第7-10章阶段练习卷(含解析)-2024-2025学年数学七年级下册苏科版(2024)
文档属性
| 名称 | 第7-10章阶段练习卷(含解析)-2024-2025学年数学七年级下册苏科版(2024) | 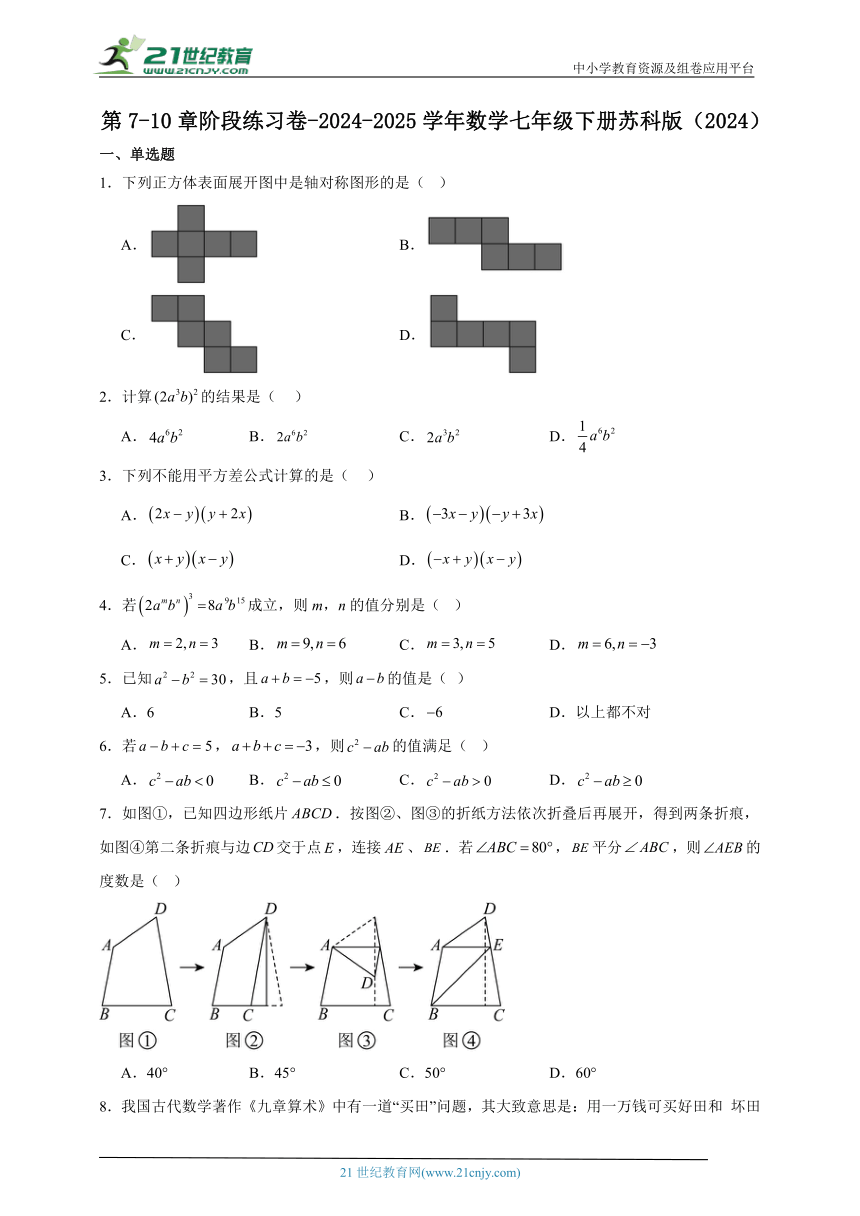 | |
| 格式 | docx | ||
| 文件大小 | 1.1MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 苏科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-05-07 21:40:06 | ||
图片预览




文档简介
中小学教育资源及组卷应用平台
第7-10章阶段练习卷-2024-2025学年数学七年级下册苏科版(2024)
一、单选题
1.下列正方体表面展开图中是轴对称图形的是( )
A. B.
C. D.
2.计算的结果是( )
A. B. C. D.
3.下列不能用平方差公式计算的是( )
A. B.
C. D.
4.若成立,则m,n的值分别是( )
A. B. C. D.
5.已知,且,则的值是( )
A.6 B.5 C. D.以上都不对
6.若,,则的值满足( )
A. B. C. D.
7.如图①,已知四边形纸片.按图②、图③的折纸方法依次折叠后再展开,得到两条折痕,如图④第二条折痕与边交于点,连接、.若,平分,则的度数是( )
A.40° B.45° C.50° D.60°
8.我国古代数学著作《九章算术》中有一道“买田”问题,其大致意思是:用一万钱可买好田和 坏田共一百亩,若……问好田和坏田分别买了多少亩?设买好田x 亩,坏田y 亩,可列出符合题意的方程组 根据已有信息,则题中用“……”表示的缺失条件应为 ( )
A.好田三百亩用一钱,坏田五百亩用七钱
B.好田七百亩用五百钱,坏田一亩用三百钱
C.好田五百亩用七钱,坏田三百亩用一钱
D.好田一亩用三百钱,坏田七亩用五百钱
二、填空题
9.,则 .
10.若,则 .
11.已知,若将的指数变为是11的两个数,则.则 (填“”“”或“”),若,比较的大小,用“”连接: .
12.如图,点是线段上一点,以,为边向两边作正方形,面积分别是和,设,两个正方形的面积之和,则的面积为 .
13.如图,已知直角三角形的周长为3.14.将的斜边放在直线上,然后将顺时针在直线上转动两次到的位置,则的长度为 .
14.已知关于,的二元一次方程组的解满足,则常数的值是 .
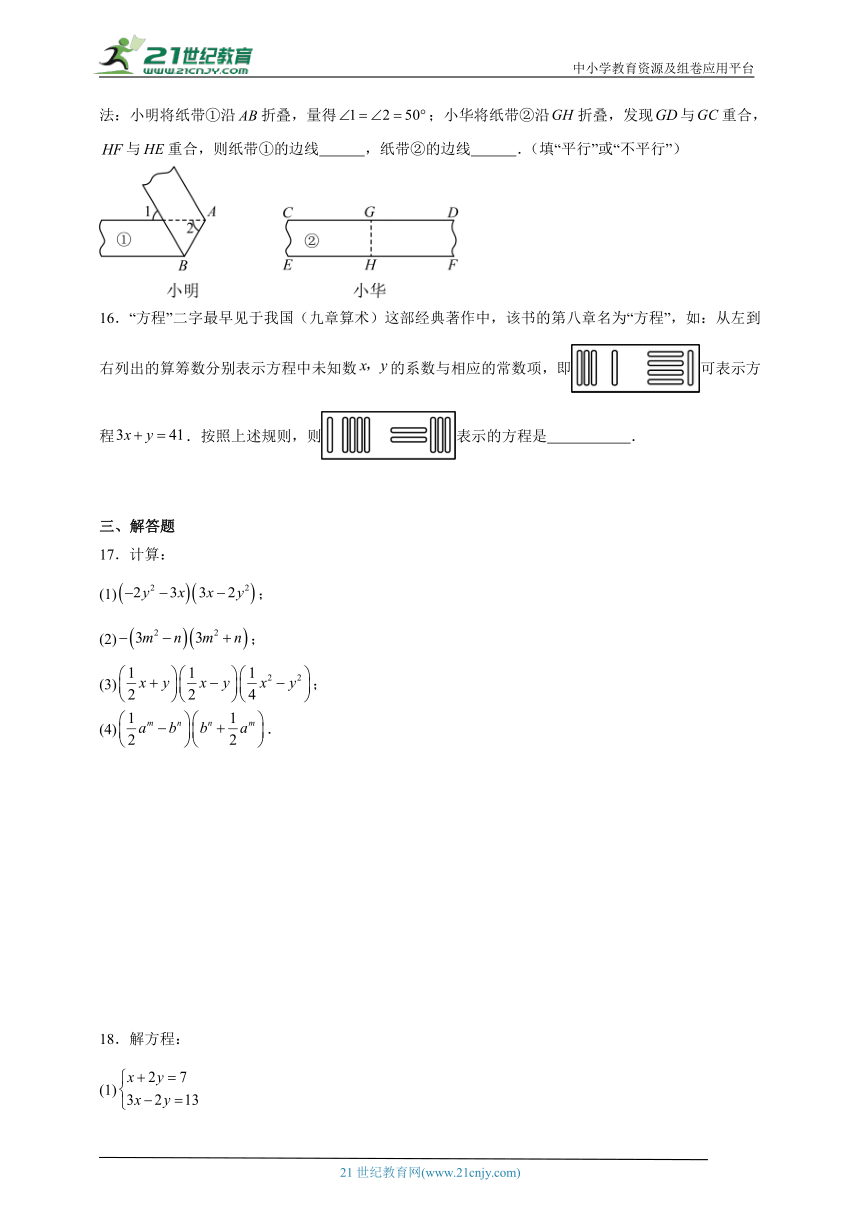
15.一次教学活动中,为检验两条纸带①②的边线是否平行(如图),小明和小华采用两种不同的方法:小明将纸带①沿折叠,量得;小华将纸带②沿折叠,发现与重合,与重合,则纸带①的边线 ,纸带②的边线 .(填“平行”或“不平行”)
16.“方程”二字最早见于我国(九章算术)这部经典著作中,该书的第八章名为“方程”,如:从左到右列出的算筹数分别表示方程中未知数的系数与相应的常数项,即可表示方程.按照上述规则,则表示的方程是 .
三、解答题
17.计算:
(1);
(2);
(3);
(4).
18.解方程:
(1)
(2)
19.若(且,m、n是正整数),则.利用上面结论解决下面的问题:
(1)如果,求x的值;
(2)如果,求x的值;
(3)若,,用含x的代数式表示y.
20.如图,在中,,点、分别在边、上,且,连接,将绕点按顺时针方向旋转一个角度得到,若,求证:.
21.在数学的奇妙世界里,我们常常会遇到一些独特的运算规则.现在定义一种新的运算“”,对于任意的有理数a和b,有,其中 m,n是正整数.同时,我们还知道整式乘法和幂运算的相关知识,比如同底数幂相乘,底数不变,指数相加,即 ;幂的乘方,底数不变,指数相乘,即.并且我们会利用二元一次方程组来解决一些未知量的问题.
(1)已知,
①求 m, n 的值;
②若,,求的值.
(2)对于任意非零实数α,b,c,若新运算“”满足,且存在某个常数k,使得,求 m,n的值和常数k.
22.已知两个正方形A,B,边长分别为.现将B放在A的内部得图甲,将A,B并列放置后构造新的正方形得图乙.
(1)用 a,b表示图甲阴影部分面积为________;图乙阴影部分面积为:_______(需化简)
(2)若图甲和图乙中阴影部分的面积分别为4和16,求正方形A,B的面积之和(请写出解题过程);
(3)在(2)的条件下,三个正方形A和两个正方形B如图丙摆放,求阴影部分的面积.
23.先阅读材料,然后解方程组.
材料:解方程组,在本题中,先将看作一个整体,将①整体代入②,得,解得.把代入①得,所以,这种解法称为“整体代入法”,请用这种方法解方程组.
24.如图,在边长均为个单位长度的小正方形组成的网格中,,,,均为格点(即每个小正方形的顶点),线段关于直线对称的线段为,
(1)线段绕点顺时针旋转得到线段,在图中画出线段、;
(2)线段绕点顺时针旋转得到线段,若,,三点共线,则与的关系为(用等式表示).
25.“脐橙结硕果,香飘引客来”,赣南脐橙以其“外表光洁美观,肉质脆嫩,风味浓甜芳香”的特点饮誉中外.现欲将一批脐橙运往外地销售,若用2辆A型车和1辆B型车载满脐橙一次可运走;用1辆A型车和2辆B型车载满脐橙一次可运走,现有脐橙,计划同时租用A型车a辆,B型车b辆,一次运完,且恰好每辆车都载满脐橙.
根据以上信息,解答下列问题:
(1)1辆A型车和1辆B型车都载满脐橙一次可分别运送多少吨?
(2)请你帮该物流公司设计租车方案,并写出所有方案;
(3)若1辆A型车需租金90元/次,1辆B型车需租金100元/次.请选出费用最少的租车方案,并求出最少租车费.
《第7-10章阶段练习卷-2024-2025学年数学七年级下册苏科版(2024)》参考答案
题号 1 2 3 4 5 6 7 8
答案 A A D C C D A D
1.A
【分析】本题考查的是轴对称图形的概念.轴对称图形的关键是寻找对称轴,图形两部分折叠后可重合.根据轴对称图形的概念逐项进行判断即可.
【详解】解:A、图形是轴对称图形,符合题意;
B、图形不是轴对称图形,不符合题意;
C、图形不是轴对称图形,不符合题意;
D、图形不是轴对称图形,不符合题意;
故选:A.
2.A
【分析】本题考查了幂的乘方及积的乘方运算,熟练掌握幂的乘方及积的乘方法则是解题的关键.根据幂的乘方及积的乘方法则计算即可.
【详解】解:.
故选:A.
3.D
【分析】本题考查平方差公式,平方差公式的式子的特点:两个二项式相乘,并且这两个二项式中有一项完全相同,另一项互为相反数.据此分析即可.
【详解】解∶ A.,故不符合题意;
B. ,故不符合题意;
C. ,故不符合题意;
D.无相同的项,故不能用平方差公式计算,符合题意.
故选D.
4.C
【分析】此题主要考查了积的乘方和幂的乘方运算,
先根据积的乘方和幂的乘方运算计算出等式左边的数,再与右边的数相比较,进而得出关于m,n的方程即可求解.
【详解】解:∵
∴,,
解得,.
故选:C.
5.C
【分析】本题考查了利用平方差公式,熟练掌握平方差公式是解题关键.利用平方差公式可得,由此即可得.
【详解】解:∵,且,
∴,即,
∴,
故选:C.
6.D
【分析】本题考查了代数式求值,完全平方公式等,根据题意,将,联立,解得与的关系,然后代入,即可求解,掌握相关知识是解题的关键.
【详解】解:∵,,
∴,,
∴,
∴
,
∵,
∴,
故选:D.
7.A
【分析】本题主要考查了轴对称的性质和图形折叠的性质,关键是熟练掌握轴对称的性质和图形折叠的性质.
根据折叠的性质可得,,可得,得到,根据角平分线的定义即可求出答案.
【详解】解:如图,
根据折叠的性质可得,,
,
,
,平分,
,
,
故选:A.
8.D
【分析】本题主要考查了二元一次方程组的应用,根据选项一一列式判断即可.
【详解】解:.好田三百亩用一钱,坏田五百亩用七钱,可列出方程,故该选项不符合题意;
.好田七百亩用五百钱,坏田一亩用三百钱,可列出方程,故该选项不符合题意;
.好田五百亩用七钱,坏田三百亩用一钱,可列出方程,故该选项不符合题意;
.好田一亩用三百钱,坏田七亩用五百钱,可列出方程,故该选项符合题意;
故选:D.
9.
【分析】本题主要考查了同底数幂的乘除法,幂的乘方等知识点,灵活运用同底数幂的乘除法,幂的乘方的运算法则是解决此题的关键.先将变形成,然后得到,解方程即可得解.
【详解】解:,
,
,
,
,
,
故答案为:.
10.3
【分析】本题主要考查多项式乘多项式,利用多项式乘多项式的法则对等式左边进行运算,再根据等式的定义进行求解即可.
【详解】解:∵,
∴,
∴,
解得:,
故答案为:3.
11.
【分析】本题主要考查幂的乘方的逆运算法则,解答的关键是利用幂的乘方的逆运算法则把各数的指数转为相等.把,,,各数的指数转为相等,再比较底数即可.
【详解】解:,
,
∴,
∵,,
,
即.
故答案为:;.
12.10
【分析】本题考查完全平方公式的几何应用.设,,根据题意得到,,利用完全平方公式求得,进而利用三角形的面积公式可求解.
【详解】解:设,,
∵,两个正方形的面积之和,
∴,,
∵,
∴,解得,
∴,
故答案为:10.
13.
【分析】本题考查了旋转,根据旋转的性质可得出,,然后根据线段的和差求解即可.
【详解】解∶由旋转可知,
∴,,
∴,
故答案为:3.14.
14.
【分析】本题考查了解二元一次方程组.用表示出方程组的解是解题的关键.先求方程组的解,用表示出,的值,再根据可得到关于的等式,从而求得的值.
【详解】解:解方程组,可得,
,
,
解得.
故答案为:.
15. 不平行 平行
【分析】本题考查平行线的判断,根据平行线的判定方法进行判断即可.
【详解】解:如图:
在图①中,,
∴,
由折叠的性质可得,
∴,
∴纸带①的边线不平行;
在图②中,
∵将纸带②沿折叠,发现与重合,与重合,
∴,
∴,
∴纸带②的边线平行;
故答案为:不平行;平行
16.
【分析】本题考查根据图意列二元一次方程,认真审题,读懂图中的意思,仿照图写出答案.解题的关键是读懂图的意思.
【详解】
解:由题意得,则表示的方程是,
故答案为:.
17.(1)
(2)
(3)
(4)
【分析】此题考查了乘法公式.
(1)利用平方差公式计算即可;
(2)利用平方差公式计算即可;
(3)利用平方差公式计算,再利用完全平方公式展开即可;
(4)利用平方差公式计算即可.
【详解】(1)解:
;
(2)解:
;
(3)解:
;
(4)解:
.
18.(1)
(2)
【分析】本题考查了解二元一次方程组的知识,解答本题的关键是熟练掌握“消元法”的应用.
(1)利用加减消元法即可解答;
(2)利用代入消元法即可解答.
【详解】(1)解:,
得,
解得,
把代入①,可得,
是原方程组的解;
(2)解:,
把①代入②可,
解得,
把代入①可得,
是原方程组的解.
19.(1)
(2)
(3)
【分析】本题考查幂的乘方,解一元一次方程,用含x的代数式表示y等.
(1)将式子变形得,再对应相等即可得到本题答案;
(2)将变形为,继而得到,后移项计算即可;
(3)根据题干可得,再代入可得,再展开整理即可.
【详解】(1)解:∵,即:,
∴,即:;
(2)解:变形为:,即:,
∴,即:,,解得:;
(3)解:∵,即:,
∵,即:,
∴.
20.见解析
【分析】本题考查了旋转的性质,平行线的性质,由旋转的性质得:, 根据,,得出,即可得出结论.
【详解】解:由旋转的性质得:, ,
∵,
∴,
∴,
∴
∴.
21.(1)①;②
(2)
【分析】本题考查定义新运算,幂的运算,熟练掌握新定义,是解题的关键:
(1)①根据新定义,得到,即可得出结果;②根据新定义,列出方程组进行求解即可;
(2)根据,推出,进而得到,根据,得到,进行求解即可.
【详解】(1)解:①∵,
∴,
∴;
②∵,,
∴,
两式相乘可得:,
∴;
(2)∵,
∴,
∴,
∵,
∴,
∴,
∵,
∴,
∵,,
∴,
∵为正整数,为常数,为任意非零有理数,
∴;
综上:.
22.(1),
(2)20
(3)44
【分析】本题考查完全平方公式与几何图形的面积,熟练掌握完全平方公式,是解题的关键:
(1)易得图甲中阴影部分的边长为,利用面积公式计算即可,分割法求出图乙的面积即可;
(2)利用完全平方公式变形计算即可;
(3)分割法表示出阴影部分的面积,利用完全平方公式变形计算求值即可.
【详解】(1)解:图甲阴影部分面积:,
图乙阴影部分面积:,
(2)设正方形A,B的边长分别为,
由图甲得,由图乙得,
∴;
答:正方形A,B的面积之和为20;
(3)∵,,
∴,
∵,
∴,
∵,且,
∴,
∴图丙的阴影部分面积
.
23.
【分析】本题考查解二元一次方程组.理解并掌握整体代入法解方程组,是解题的关键.模仿题干,利用整体代入法解方程组,即可作答.
【详解】解:
先将看作一个整体,
则整理①得,
将整体代入,得,
解得.
把代入得,
解得,
∴
24.(1)画图见解析
(2)
【分析】()根据轴对称图形和旋转的性质作图即可;
()根据题意画出图形,进而根据图形解答即可求解;
本题考查了作轴对称图形,旋转作图,掌握轴对称图形和旋转的性质是解题的关键.
【详解】(1)解:如图所示,、即为所求;
(2)解:如图,
∵,,
∴,
∴与的关系为.
25.(1)1辆A型车和1辆B型车都载满脐橙一次可分别运送、;
(2)共有三种方案:方案一:租A型车1辆,B型车8辆;方案二:租A型车5辆,B型车5辆;方案三:租A型车9辆,B型车2辆;
(3)租A型车1辆,B型车8辆费用最少,最少费用为890元.
【分析】本题主要考查了二元一次方程组和二元一次方程的应用,解题的关键是根据等量关系,列出方程.
(1)设1辆A型车载满脐橙一次可运送,1辆B 型车载满脐橙一次可运送,根据2辆A型车和1辆B型车载满脐橙一次可运走,用1辆A型车和2辆B型车载满脐橙一次可运走,列出方程组,解方程组即可;
(2)根据1辆A 型车载满脐橙一次可运送,1辆B 型车载满脐橙一次可运送,现有脐橙,列出二元一次方程,再求出二元一次方程的正整数解即可;
(3)分别求出三种方案的租车费用,然后进行比较,即可得出答案.
【详解】(1)解:设1辆 A 型车载满脐橙一次可运送,1辆B 型车载满脐橙一次可运送,依题意得:
解得:,
答:1辆A 型车载满脐橙一次可运送,1 辆B 型车载满脐橙一次可运送;
(2)解:依题意得:,
∵a,b均为正整数,
∴或或,
∴一共有3种租车方案:
方案一:租A型车1辆,B型车8辆;
方案二:租A型车5辆,B 型车5辆;
方案三:租A 型车 9辆,B 型车2辆.
(3)解:方案一所需租金为:(元);
方案二所需租金为:(元);
方案三所需租金为: (元);
∵,
∴最省钱的租车方案是方案一,即租A型车1辆,B型车8辆,最少租车费为890元.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
第7-10章阶段练习卷-2024-2025学年数学七年级下册苏科版(2024)
一、单选题
1.下列正方体表面展开图中是轴对称图形的是( )
A. B.
C. D.
2.计算的结果是( )
A. B. C. D.
3.下列不能用平方差公式计算的是( )
A. B.
C. D.
4.若成立,则m,n的值分别是( )
A. B. C. D.
5.已知,且,则的值是( )
A.6 B.5 C. D.以上都不对
6.若,,则的值满足( )
A. B. C. D.
7.如图①,已知四边形纸片.按图②、图③的折纸方法依次折叠后再展开,得到两条折痕,如图④第二条折痕与边交于点,连接、.若,平分,则的度数是( )
A.40° B.45° C.50° D.60°
8.我国古代数学著作《九章算术》中有一道“买田”问题,其大致意思是:用一万钱可买好田和 坏田共一百亩,若……问好田和坏田分别买了多少亩?设买好田x 亩,坏田y 亩,可列出符合题意的方程组 根据已有信息,则题中用“……”表示的缺失条件应为 ( )
A.好田三百亩用一钱,坏田五百亩用七钱
B.好田七百亩用五百钱,坏田一亩用三百钱
C.好田五百亩用七钱,坏田三百亩用一钱
D.好田一亩用三百钱,坏田七亩用五百钱
二、填空题
9.,则 .
10.若,则 .
11.已知,若将的指数变为是11的两个数,则.则 (填“”“”或“”),若,比较的大小,用“”连接: .
12.如图,点是线段上一点,以,为边向两边作正方形,面积分别是和,设,两个正方形的面积之和,则的面积为 .
13.如图,已知直角三角形的周长为3.14.将的斜边放在直线上,然后将顺时针在直线上转动两次到的位置,则的长度为 .
14.已知关于,的二元一次方程组的解满足,则常数的值是 .
15.一次教学活动中,为检验两条纸带①②的边线是否平行(如图),小明和小华采用两种不同的方法:小明将纸带①沿折叠,量得;小华将纸带②沿折叠,发现与重合,与重合,则纸带①的边线 ,纸带②的边线 .(填“平行”或“不平行”)
16.“方程”二字最早见于我国(九章算术)这部经典著作中,该书的第八章名为“方程”,如:从左到右列出的算筹数分别表示方程中未知数的系数与相应的常数项,即可表示方程.按照上述规则,则表示的方程是 .
三、解答题
17.计算:
(1);
(2);
(3);
(4).
18.解方程:
(1)
(2)
19.若(且,m、n是正整数),则.利用上面结论解决下面的问题:
(1)如果,求x的值;
(2)如果,求x的值;
(3)若,,用含x的代数式表示y.
20.如图,在中,,点、分别在边、上,且,连接,将绕点按顺时针方向旋转一个角度得到,若,求证:.
21.在数学的奇妙世界里,我们常常会遇到一些独特的运算规则.现在定义一种新的运算“”,对于任意的有理数a和b,有,其中 m,n是正整数.同时,我们还知道整式乘法和幂运算的相关知识,比如同底数幂相乘,底数不变,指数相加,即 ;幂的乘方,底数不变,指数相乘,即.并且我们会利用二元一次方程组来解决一些未知量的问题.
(1)已知,
①求 m, n 的值;
②若,,求的值.
(2)对于任意非零实数α,b,c,若新运算“”满足,且存在某个常数k,使得,求 m,n的值和常数k.
22.已知两个正方形A,B,边长分别为.现将B放在A的内部得图甲,将A,B并列放置后构造新的正方形得图乙.
(1)用 a,b表示图甲阴影部分面积为________;图乙阴影部分面积为:_______(需化简)
(2)若图甲和图乙中阴影部分的面积分别为4和16,求正方形A,B的面积之和(请写出解题过程);
(3)在(2)的条件下,三个正方形A和两个正方形B如图丙摆放,求阴影部分的面积.
23.先阅读材料,然后解方程组.
材料:解方程组,在本题中,先将看作一个整体,将①整体代入②,得,解得.把代入①得,所以,这种解法称为“整体代入法”,请用这种方法解方程组.
24.如图,在边长均为个单位长度的小正方形组成的网格中,,,,均为格点(即每个小正方形的顶点),线段关于直线对称的线段为,
(1)线段绕点顺时针旋转得到线段,在图中画出线段、;
(2)线段绕点顺时针旋转得到线段,若,,三点共线,则与的关系为(用等式表示).
25.“脐橙结硕果,香飘引客来”,赣南脐橙以其“外表光洁美观,肉质脆嫩,风味浓甜芳香”的特点饮誉中外.现欲将一批脐橙运往外地销售,若用2辆A型车和1辆B型车载满脐橙一次可运走;用1辆A型车和2辆B型车载满脐橙一次可运走,现有脐橙,计划同时租用A型车a辆,B型车b辆,一次运完,且恰好每辆车都载满脐橙.
根据以上信息,解答下列问题:
(1)1辆A型车和1辆B型车都载满脐橙一次可分别运送多少吨?
(2)请你帮该物流公司设计租车方案,并写出所有方案;
(3)若1辆A型车需租金90元/次,1辆B型车需租金100元/次.请选出费用最少的租车方案,并求出最少租车费.
《第7-10章阶段练习卷-2024-2025学年数学七年级下册苏科版(2024)》参考答案
题号 1 2 3 4 5 6 7 8
答案 A A D C C D A D
1.A
【分析】本题考查的是轴对称图形的概念.轴对称图形的关键是寻找对称轴,图形两部分折叠后可重合.根据轴对称图形的概念逐项进行判断即可.
【详解】解:A、图形是轴对称图形,符合题意;
B、图形不是轴对称图形,不符合题意;
C、图形不是轴对称图形,不符合题意;
D、图形不是轴对称图形,不符合题意;
故选:A.
2.A
【分析】本题考查了幂的乘方及积的乘方运算,熟练掌握幂的乘方及积的乘方法则是解题的关键.根据幂的乘方及积的乘方法则计算即可.
【详解】解:.
故选:A.
3.D
【分析】本题考查平方差公式,平方差公式的式子的特点:两个二项式相乘,并且这两个二项式中有一项完全相同,另一项互为相反数.据此分析即可.
【详解】解∶ A.,故不符合题意;
B. ,故不符合题意;
C. ,故不符合题意;
D.无相同的项,故不能用平方差公式计算,符合题意.
故选D.
4.C
【分析】此题主要考查了积的乘方和幂的乘方运算,
先根据积的乘方和幂的乘方运算计算出等式左边的数,再与右边的数相比较,进而得出关于m,n的方程即可求解.
【详解】解:∵
∴,,
解得,.
故选:C.
5.C
【分析】本题考查了利用平方差公式,熟练掌握平方差公式是解题关键.利用平方差公式可得,由此即可得.
【详解】解:∵,且,
∴,即,
∴,
故选:C.
6.D
【分析】本题考查了代数式求值,完全平方公式等,根据题意,将,联立,解得与的关系,然后代入,即可求解,掌握相关知识是解题的关键.
【详解】解:∵,,
∴,,
∴,
∴
,
∵,
∴,
故选:D.
7.A
【分析】本题主要考查了轴对称的性质和图形折叠的性质,关键是熟练掌握轴对称的性质和图形折叠的性质.
根据折叠的性质可得,,可得,得到,根据角平分线的定义即可求出答案.
【详解】解:如图,
根据折叠的性质可得,,
,
,
,平分,
,
,
故选:A.
8.D
【分析】本题主要考查了二元一次方程组的应用,根据选项一一列式判断即可.
【详解】解:.好田三百亩用一钱,坏田五百亩用七钱,可列出方程,故该选项不符合题意;
.好田七百亩用五百钱,坏田一亩用三百钱,可列出方程,故该选项不符合题意;
.好田五百亩用七钱,坏田三百亩用一钱,可列出方程,故该选项不符合题意;
.好田一亩用三百钱,坏田七亩用五百钱,可列出方程,故该选项符合题意;
故选:D.
9.
【分析】本题主要考查了同底数幂的乘除法,幂的乘方等知识点,灵活运用同底数幂的乘除法,幂的乘方的运算法则是解决此题的关键.先将变形成,然后得到,解方程即可得解.
【详解】解:,
,
,
,
,
,
故答案为:.
10.3
【分析】本题主要考查多项式乘多项式,利用多项式乘多项式的法则对等式左边进行运算,再根据等式的定义进行求解即可.
【详解】解:∵,
∴,
∴,
解得:,
故答案为:3.
11.
【分析】本题主要考查幂的乘方的逆运算法则,解答的关键是利用幂的乘方的逆运算法则把各数的指数转为相等.把,,,各数的指数转为相等,再比较底数即可.
【详解】解:,
,
∴,
∵,,
,
即.
故答案为:;.
12.10
【分析】本题考查完全平方公式的几何应用.设,,根据题意得到,,利用完全平方公式求得,进而利用三角形的面积公式可求解.
【详解】解:设,,
∵,两个正方形的面积之和,
∴,,
∵,
∴,解得,
∴,
故答案为:10.
13.
【分析】本题考查了旋转,根据旋转的性质可得出,,然后根据线段的和差求解即可.
【详解】解∶由旋转可知,
∴,,
∴,
故答案为:3.14.
14.
【分析】本题考查了解二元一次方程组.用表示出方程组的解是解题的关键.先求方程组的解,用表示出,的值,再根据可得到关于的等式,从而求得的值.
【详解】解:解方程组,可得,
,
,
解得.
故答案为:.
15. 不平行 平行
【分析】本题考查平行线的判断,根据平行线的判定方法进行判断即可.
【详解】解:如图:
在图①中,,
∴,
由折叠的性质可得,
∴,
∴纸带①的边线不平行;
在图②中,
∵将纸带②沿折叠,发现与重合,与重合,
∴,
∴,
∴纸带②的边线平行;
故答案为:不平行;平行
16.
【分析】本题考查根据图意列二元一次方程,认真审题,读懂图中的意思,仿照图写出答案.解题的关键是读懂图的意思.
【详解】
解:由题意得,则表示的方程是,
故答案为:.
17.(1)
(2)
(3)
(4)
【分析】此题考查了乘法公式.
(1)利用平方差公式计算即可;
(2)利用平方差公式计算即可;
(3)利用平方差公式计算,再利用完全平方公式展开即可;
(4)利用平方差公式计算即可.
【详解】(1)解:
;
(2)解:
;
(3)解:
;
(4)解:
.
18.(1)
(2)
【分析】本题考查了解二元一次方程组的知识,解答本题的关键是熟练掌握“消元法”的应用.
(1)利用加减消元法即可解答;
(2)利用代入消元法即可解答.
【详解】(1)解:,
得,
解得,
把代入①,可得,
是原方程组的解;
(2)解:,
把①代入②可,
解得,
把代入①可得,
是原方程组的解.
19.(1)
(2)
(3)
【分析】本题考查幂的乘方,解一元一次方程,用含x的代数式表示y等.
(1)将式子变形得,再对应相等即可得到本题答案;
(2)将变形为,继而得到,后移项计算即可;
(3)根据题干可得,再代入可得,再展开整理即可.
【详解】(1)解:∵,即:,
∴,即:;
(2)解:变形为:,即:,
∴,即:,,解得:;
(3)解:∵,即:,
∵,即:,
∴.
20.见解析
【分析】本题考查了旋转的性质,平行线的性质,由旋转的性质得:, 根据,,得出,即可得出结论.
【详解】解:由旋转的性质得:, ,
∵,
∴,
∴,
∴
∴.
21.(1)①;②
(2)
【分析】本题考查定义新运算,幂的运算,熟练掌握新定义,是解题的关键:
(1)①根据新定义,得到,即可得出结果;②根据新定义,列出方程组进行求解即可;
(2)根据,推出,进而得到,根据,得到,进行求解即可.
【详解】(1)解:①∵,
∴,
∴;
②∵,,
∴,
两式相乘可得:,
∴;
(2)∵,
∴,
∴,
∵,
∴,
∴,
∵,
∴,
∵,,
∴,
∵为正整数,为常数,为任意非零有理数,
∴;
综上:.
22.(1),
(2)20
(3)44
【分析】本题考查完全平方公式与几何图形的面积,熟练掌握完全平方公式,是解题的关键:
(1)易得图甲中阴影部分的边长为,利用面积公式计算即可,分割法求出图乙的面积即可;
(2)利用完全平方公式变形计算即可;
(3)分割法表示出阴影部分的面积,利用完全平方公式变形计算求值即可.
【详解】(1)解:图甲阴影部分面积:,
图乙阴影部分面积:,
(2)设正方形A,B的边长分别为,
由图甲得,由图乙得,
∴;
答:正方形A,B的面积之和为20;
(3)∵,,
∴,
∵,
∴,
∵,且,
∴,
∴图丙的阴影部分面积
.
23.
【分析】本题考查解二元一次方程组.理解并掌握整体代入法解方程组,是解题的关键.模仿题干,利用整体代入法解方程组,即可作答.
【详解】解:
先将看作一个整体,
则整理①得,
将整体代入,得,
解得.
把代入得,
解得,
∴
24.(1)画图见解析
(2)
【分析】()根据轴对称图形和旋转的性质作图即可;
()根据题意画出图形,进而根据图形解答即可求解;
本题考查了作轴对称图形,旋转作图,掌握轴对称图形和旋转的性质是解题的关键.
【详解】(1)解:如图所示,、即为所求;
(2)解:如图,
∵,,
∴,
∴与的关系为.
25.(1)1辆A型车和1辆B型车都载满脐橙一次可分别运送、;
(2)共有三种方案:方案一:租A型车1辆,B型车8辆;方案二:租A型车5辆,B型车5辆;方案三:租A型车9辆,B型车2辆;
(3)租A型车1辆,B型车8辆费用最少,最少费用为890元.
【分析】本题主要考查了二元一次方程组和二元一次方程的应用,解题的关键是根据等量关系,列出方程.
(1)设1辆A型车载满脐橙一次可运送,1辆B 型车载满脐橙一次可运送,根据2辆A型车和1辆B型车载满脐橙一次可运走,用1辆A型车和2辆B型车载满脐橙一次可运走,列出方程组,解方程组即可;
(2)根据1辆A 型车载满脐橙一次可运送,1辆B 型车载满脐橙一次可运送,现有脐橙,列出二元一次方程,再求出二元一次方程的正整数解即可;
(3)分别求出三种方案的租车费用,然后进行比较,即可得出答案.
【详解】(1)解:设1辆 A 型车载满脐橙一次可运送,1辆B 型车载满脐橙一次可运送,依题意得:
解得:,
答:1辆A 型车载满脐橙一次可运送,1 辆B 型车载满脐橙一次可运送;
(2)解:依题意得:,
∵a,b均为正整数,
∴或或,
∴一共有3种租车方案:
方案一:租A型车1辆,B型车8辆;
方案二:租A型车5辆,B 型车5辆;
方案三:租A 型车 9辆,B 型车2辆.
(3)解:方案一所需租金为:(元);
方案二所需租金为:(元);
方案三所需租金为: (元);
∵,
∴最省钱的租车方案是方案一,即租A型车1辆,B型车8辆,最少租车费为890元.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
同课章节目录
