第1单元简易方程应用题专项训练-2024-2025学年数学五年级下册苏教版(含解析)
文档属性
| 名称 | 第1单元简易方程应用题专项训练-2024-2025学年数学五年级下册苏教版(含解析) |

|
|
| 格式 | docx | ||
| 文件大小 | 531.4KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 苏教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-05-07 00:00:00 | ||
图片预览




文档简介
中小学教育资源及组卷应用平台
第1单元简易方程应用题专项训练-2024-2025学年数学五年级下册苏教版
1.我们穿的鞋子有新码与旧码这两种不同的鞋码。新码1码就是1厘米。它与旧码之间可以这样换算:新码(旧码+10)÷2。爸爸穿的鞋子用新码表示是26厘米。用旧码表示是多少码?(列方程解答)
2.小明和小华共有100张邮票, ,小明有多少张邮票?
(1)根据条件和问题,请补充一个信息在下面,使得问题需要两步或两步以上。
(2)先将如图补充完整,再解答。
3.一列特快列车和一列动车同时从甲城开往乙城,特快列车的速度是138千米时。经过3小时,动车比特快列车多行了201千米。动车的速度是多少千米时?(列方程解答)
4.桐桐去文具店买了6盒同样的彩笔,付了100元,找回17.2元。每盒彩笔多少元?(用方程解)
5.甲、乙两艘轮船从同一地点反向而行,0.8小时后两船相距68.8千米。已知乙船的速度是45千米时,则甲船的速度是多少千米时?(列方程解答)
6.如图,每个大球比每个小球重2千克。一个大球和一个小球各重多少千克?
7.据了解2023年第一季度,我国5G平均用户下载速率为348.31Mbps,比4G平均用户下载速率的7倍还要多8.32Mbps,4G平均用户下载速率是多少Mbps?(Mbps是一种传输速率单位)(列方程解题)
8.为绿化城市,市政公司四月份投放花草3800盆,比三月份的4倍还多200盆,三月份投放花草多少盆?
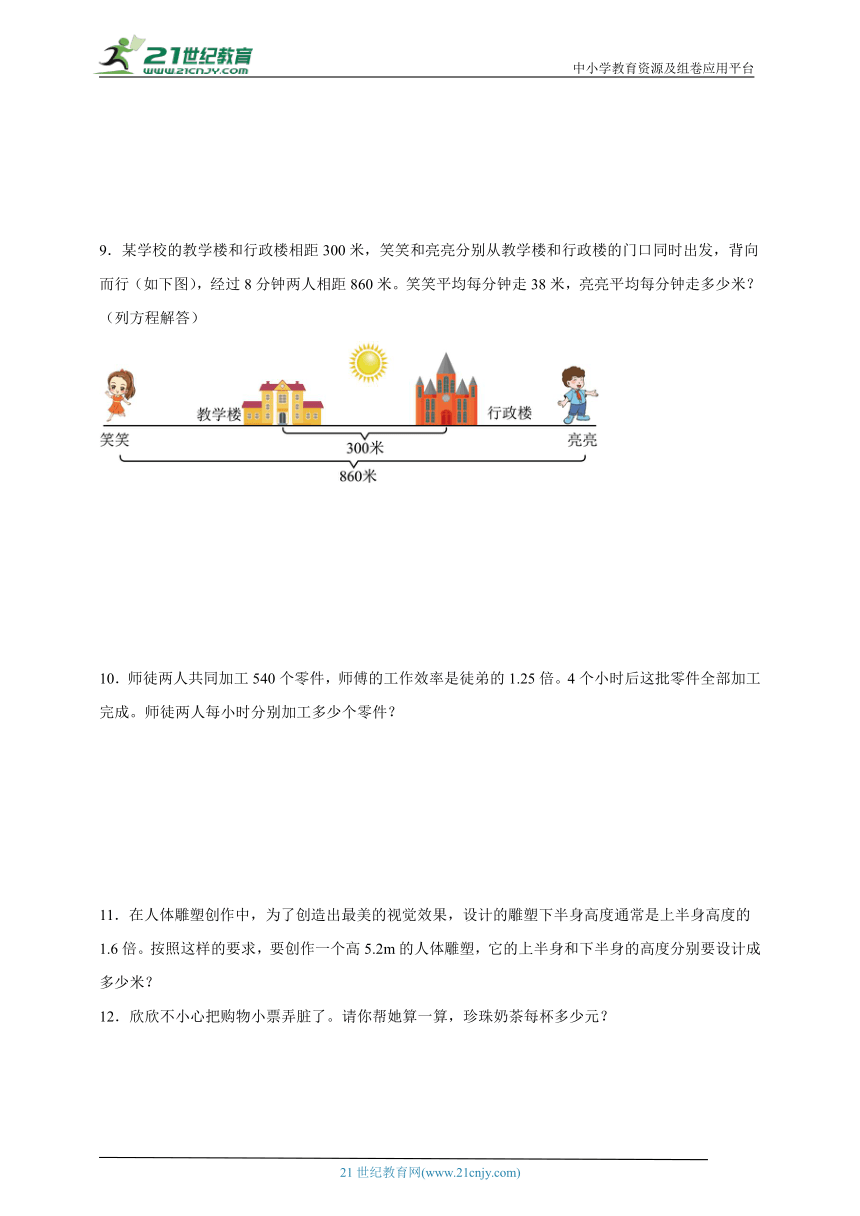
9.某学校的教学楼和行政楼相距300米,笑笑和亮亮分别从教学楼和行政楼的门口同时出发,背向而行(如下图),经过8分钟两人相距860米。笑笑平均每分钟走38米,亮亮平均每分钟走多少米?(列方程解答)
10.师徒两人共同加工540个零件,师傅的工作效率是徒弟的1.25倍。4个小时后这批零件全部加工完成。师徒两人每小时分别加工多少个零件?
11.在人体雕塑创作中,为了创造出最美的视觉效果,设计的雕塑下半身高度通常是上半身高度的1.6倍。按照这样的要求,要创作一个高5.2m的人体雕塑,它的上半身和下半身的高度分别要设计成多少米?
12.欣欣不小心把购物小票弄脏了。请你帮她算一算,珍珠奶茶每杯多少元?
13.第七届世界军人运动会吉祥物名为“兵兵”,它的设计灵感来源于中国一级重点保护野生动物中华鲟。雌性中华鲟体长2.3米,比雄性中华鲟体长的2倍少1.1米。雄性中华鲟的体长是多少米?(用方程解)
14.有“徐州之巅”之称的徐州苏宁广场主塔楼高266米,比徐州电视塔高度的2倍少133.2米,徐州电视塔高多少米?(用方程解答)
15.在4个同样的大盒和6个同样的小盒里装满球,正好是200个。每个大盒比每个小盒多装5个,每个大盒和小盒各装多少个?
16.某农场有三块菜地,总面积是500公顷,已知第一块菜地的面积比第二块少40公顷,第二块菜地的面积比第三块多60公顷。这三块菜地的面积各是多少平方米?(先画线段图表示题中的数量关系,再解答)
17.在“学习强国”活动中,王亮的爸爸昨天获得积分44分,比前天的1.5倍多5分。王亮的爸爸前天获得多少分?
18.某通信公司推出两种话费套餐:
(1)张叔叔每月通话150分钟,选哪种套餐比较合算?(计算说明理由)
(2)当通话多少分钟时,两种计费方式话费相同?
19.中国南极科考站总共有5个,分别是长城站、中山站、昆仑站、泰山站以及在建的罗斯海新站。中山站的建筑面积是泰山站的2.7倍,中山站的建筑面积比泰山站多1700平方米。中山站和泰山站的建筑面积各是多少平方米?
20.我们的地球是一个美丽的蓝色星球。朵朵同学借助网络查阅了相关资料,了解到地球的表面积一共约5.1亿平方千米。其中海洋面积大约是陆地面积的2.4倍。请你算一算地球上的海洋面积是多少亿平方千米?
21.港珠澳大桥是一座连接香港、珠海和澳门的桥隧工程,全长55千米;苏通大桥位于江苏省,是沈阳——海口高速公路跨越长江的重要枢纽。港珠澳大桥的长度比苏通大桥全长的2倍少9.8千米,苏通大桥全长多少千米?
《第1单元简易方程应用题专项训练-2024-2025学年数学五年级下册苏教版》参考答案
1.42码
【分析】设用旧码表示是码,根据等量关系:新码(旧码),代入数据列方程解答即可。
【详解】解:设用旧码表示是码。
答:用旧码表示是42码。
2.(1)小华比小明少10张
(2)图见详解,55张
【分析】(1)知道二人共有100张邮票,再补充二人邮票相差几张,形成和差问题解答即可。
(2)根据添加的信息,将线段图补充完整,再解答。
【详解】(1)小明和小华共有100张邮票,小华比小明少10张,小明有多少张邮粟?
(2)
解:设小明有x张邮票,则小华有邮票张,则可列出方程:
答:小明有55张邮票。
3.205千米时
【分析】设动车的速度是x千米/时,根据等量关系:(动车的速度-特快列车的速度)×行驶的时间 =动车比特快列车多行的路程,列方程解答即可。
【详解】解:设动车的速度是千米时。
答:动车的速度是205千米时。
【点睛】本题考查列方程解决问题,关键是根据题意找出基本数量关系,设未知数为,由此列方程解决问题。
4.13.8元
【分析】本题中的等量关系为:彩笔的总钱数+找回钱数=付了的钱数;设每盒彩笔x元,根据等量关系列出方程,解方程即可解决问题。
【详解】解:设每盒彩笔x元,根据题意列方程可得:
6x+17.2=100
6x=82.8
6x÷6=82.8÷6
x=13.8
答:每盒彩笔13.8元。
【点睛】本题考查用方程解决实际问题,关键是找出题中的等量关系。
5.41千米时
【分析】从“同一地点反向而行”可知,68.8千米是甲乙路程之和。根据路程=速度×时间,设甲船的速度是千米时,根据等量关系:甲船的速度行驶的时间乙船的速度行驶的时间千米,列方程,再根据等式性质解方程即可。
【详解】解:设甲船的速度是千米时。
答:甲船的速度是41千米时。
6.4.6千克;2.6千克
【分析】设每个小球重x千克,则每个大球重(x+2)千克,根据大球重量×个数+小球重量×个数=总重量,列出方程求出x的值是小球重量,小球重量+2千克=大球重量。
【详解】解:设每个小球重x千克。
(x+2)×3+2x=19
3x+6+2x=19
5x+6=19
5x+6-6=19-6
5x=13
5x÷5=13÷5
x=2.6
2.6+2=4.6(千克)
答:一个大球和一个小球各重4.6千克、2.6千克。
7.48.57Mbps
【分析】将4G的下载速度设为xMbps,那么它的7倍是(7x)Mbps。根据“4G速度的7倍+8.32Mbps=5G下载速度”列方程解方程即可。
【详解】解:设4G平均用户下载速率是xMbps。
7x+8.32=348.31
7x+8.32-8.32=348.31-8.32
7x=339.99
7x÷7=339.99÷7
x=48.57
答:4G平均用户下载速率是48.57Mbps。
8.900盆
【分析】设三月份投放花草x盆,四月份比三月份的4倍还是多200盆,即三月份投放花盆的盆数×4+200=四月份投放花盆的盆数,列方程:4x+200=3800,解方程,即可解答。
【详解】解:设三月份投放花草x盆。
4x+200=3800
4x+200-200=3800-200
4x=3600
4x÷4=3600÷4
x=900
答:三月份投放花草900盆。
9.32米
【分析】设亮亮平均每分钟走x米,则亮亮8分钟走了8x米;笑笑8分钟走了38×8=304(米)。根据题意可得:亮亮8分钟走的路程+笑笑8分钟走的路程+300米=860米,据此列方程解答。
【详解】解:亮亮平均每分钟走x米。
8x+38×8+300=860
8x+304+300=860
8x+604=860
8x+604-604=860-604
8x=256
8x÷8=256÷8
x=32
答:亮亮平均每分钟走32米。
10.60个;75个
【分析】可设徒弟每小时加工x个零件,则师傅每小时加工1.25x个零件。根据题意,有等式:4x+4×1.25x=540成立,解此方程即求得师徒两人每小时分别加工多少个零件。
【详解】解:设徒弟每小时加工x个零件,则师傅每小时加工1.25x个零件。
4x+4×1.25x=540
4x+5x=540
9x=540
9x÷9=540÷9
x=60
1.25×60 =75
答:徒弟每小时加工60个零件,师傅每小时加工75个零件。
11.2米;3.2米
【分析】可设上半身的高度要设计成x米,则下半身的高度要设计成1.6x米。根据题意有等式:x+1.6x=5.2 成立,解此等式即可知它的上半身和下半身的高度。
【详解】解:设它的上半身的高度要设计成x米,则下半身的高度要设计成1.6x米。
x+1.6x=5.2
2.6x=5.2
2.6x÷2.6=5.2÷2.6
x=2
1.6x=1.6×2=3.2
答:它的上半身的高度要设计成2米,下半身的高度要设计成3.2米。
12.5.5元
【分析】根据“单价×数量=总价”可得出等量关系:每杯珍珠奶茶的价钱×珍珠奶茶的杯数+5杯绿茶的价钱=珍珠奶茶和绿茶的总价,据此列出方程,并求解。
【详解】解:设珍珠奶茶每杯元。
3+30=46.5
3+30-30=46.5-30
3=16.5
3÷3=16.5÷3
=5.5
答:珍珠奶茶每杯5.5元。
13.1.7米
【分析】可设雄性中华鲟的体长为x米,根据数量关系:雌性中华鲟体长=雄性中华鲟体长×2-1.1,据此列出方程,解答方程即可。
【详解】解:设雄性中华鲟的体长是x米。
答:雄性中华鲟的体长是1.7米。
14.199.6米
【点睛】根据比徐州电视塔高度的2倍少133.2米,所以写出数量关系式是:电视塔的高度×2-133.2=塔楼的高度,根据数量关系式列方程即可。
【分析】解:设徐州电视塔高x米
答:徐州电视塔高199.6米。
【详解】重点是能够根据题目中的关键信息写出数量关系式,根据数量关系式列出方程。
15.每个大盒可以装23个,每个小盒可以装18个
【分析】由题意可知,设每个小盒可以装x个,则每个大盒可以装(x+5)个,再根据等量关系:4个大盒装的个数+6个小盒装的个数=200,据此列方程解答即可。
【详解】解:设每个小盒可以装x个,则每个大盒可以装(x+5)个。
6x+4×(x+5)=200
6x+4x+20=200
10x+20=200
10x+20-20=200-20
10x=180
10x÷10=180÷10
x=18
18+5=23(个)
答:每个大盒可以装23个,每个小盒可以装18个。
【点睛】本题考查用方程解决实际问题,明确等量关系是解题的关键。
16.第一、二、三块地分别是160公顷、200公顷、140公顷
图见详解
【分析】三块地都与第二块地进行比较,假设第二块地是x公顷,则第一块地是(x-40)公顷,第三块地是(x-60)公顷,根据总面积是500公顷,列方程解答。
【详解】线段图如下:
解:设第二块地是x公顷,则第一块地是(x-40)公顷,第三块地是(x-60)公顷。
(x-40)+x+(x-60)=500
x-40+x+x-60=500
3x-100=500
3x-100+100=500+100
3x=600
3x÷3=600÷3
x=200
x-40=200-40=160(公顷)
x-60=200-60=140(公顷)
答:第一、二、三块地分别是160公顷、200公顷、140公顷。
【点睛】已知几个数量间的和差关系及这几个数量的和,求这几个数量是多少,设其中一个数量是x,用含x的式子表示另几个量,再根据这几个数量的和列方程解答。
17.26分
【分析】已知王亮的爸爸昨天获得积分44分,而昨天的积分又比前天的1.5倍多5分,如果假设前天的积分是x分,则昨天的积分可表示为1.5x+5,故以昨天的积分为等量关系列方程为:1.5x+5=51。
【详解】解:设前天的积分是x分,可得:
1.5x+5=44
1.5x+5-5=44-5
1.5x=39
1.5x÷1.5=39÷1.5
x=26
答:王亮的爸爸前天获得26分。
【点睛】首先明确题目里昨天获得积分与前天获得积分之间的数量关系,同时结合问题设出合理的未知数,最后找出等量,列出合理的方程。
18.(1)B套餐;
(2)200分钟
【分析】(1)A套餐:月租费20元,0.15元/分钟;用0.15×150,求出150分钟通话的费用,再加上月租费20元,求出张叔叔通话费用;
B套餐:无月租,0.25元/分钟;用0.25×150,求出150分钟通话的费用,即求出张叔叔通话费用,再进行比较,即可解答。
(2)设当通话x分钟时,两种计费方式化肥相同,A套餐:20+0.15x元;B套餐:0.25x元,A套餐=B套餐,列方程:0.15x+20=0.25x,解方程,即可解答。
【详解】(1)0.15×150+20
=22.5+20
=42.5(元)
0.25×150=37.5(元)
42.5>37.5,B套餐比较合适。
答:B 套餐比较合适。
(2)设当通话x分钟时,两种计费方式话费相同。
20+0.15x=0.25x
0.25x-0.15=20
0.1x=20
x=20÷0.1
x=200
答:当通话200分钟时,两种计费方式话费相同.
【点睛】本题属于优化问题,关键是计算出两种套餐所需的费用。
19.中山站:2700平方米;泰山站:1000平方米
【分析】根据题意,设泰山站的建筑面积是x平方米,中山站的建筑面积是泰山站的2.7倍,中山站的建筑面积比泰山站多1700平方米,即中山站的建筑面积-泰山站的建筑面积=1700平方米,列方程:2.7x-x=1700,解方程,即可解答。
【详解】解:设泰山站的建筑面积是x平方米,则中山站的建筑面积是2.7x平方米。
2.7x-x=1700
1.7x=1700
1.7x÷1.7=1700÷1.7
x=1000
1000×2.7=2700(平方米)
答:中山站的建筑面积是2700平方米,泰山站的建筑面积是1000平方米。
【点睛】本题考查方程的实际应用,利用中山站的建筑面积与泰山站的建筑面积之间的关系,设出未知数,找出相关的量,列方程,解方程。
20.3.6亿平方千米
【分析】根据题意,这道题的等量关系是:海洋面积+陆地面积=5.1亿平方千米,根据这个等量关系,列方程解答。
【详解】解:设陆地面积为x亿平方千米,则海洋面积为2.4x亿平方千米。
x+2.4x=5.1
3.4x=5.1
3.4x÷3.4=5.1÷3.4
x=5.1÷3.4
x=1.5
海洋面积:1.5×2.4=3.6(亿平方千米)
答:地球上的海洋面积是3.6亿平方千米。
【点睛】本题考查列方程解应用题,解题关键是找出题目中的等量关系:海洋面积+陆地面积=5.1亿平方千米,列方程解答。
21.32.4千米
【分析】设苏通大桥全长x千米,根据题意,苏通大桥的长度×2-9.8=港珠澳大桥的长度,据此列方程解答。
【详解】解:设苏通大桥全长x千米。
2x-9.8=55
2x=55+9.8
2x=64.8
x=64.8÷2
x=32.4
答:苏通大桥全长32.4千米。
【点睛】本题用方程解答比较简便。找出题中的等量关系式是列出方程的关键。
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
第1单元简易方程应用题专项训练-2024-2025学年数学五年级下册苏教版
1.我们穿的鞋子有新码与旧码这两种不同的鞋码。新码1码就是1厘米。它与旧码之间可以这样换算:新码(旧码+10)÷2。爸爸穿的鞋子用新码表示是26厘米。用旧码表示是多少码?(列方程解答)
2.小明和小华共有100张邮票, ,小明有多少张邮票?
(1)根据条件和问题,请补充一个信息在下面,使得问题需要两步或两步以上。
(2)先将如图补充完整,再解答。
3.一列特快列车和一列动车同时从甲城开往乙城,特快列车的速度是138千米时。经过3小时,动车比特快列车多行了201千米。动车的速度是多少千米时?(列方程解答)
4.桐桐去文具店买了6盒同样的彩笔,付了100元,找回17.2元。每盒彩笔多少元?(用方程解)
5.甲、乙两艘轮船从同一地点反向而行,0.8小时后两船相距68.8千米。已知乙船的速度是45千米时,则甲船的速度是多少千米时?(列方程解答)
6.如图,每个大球比每个小球重2千克。一个大球和一个小球各重多少千克?
7.据了解2023年第一季度,我国5G平均用户下载速率为348.31Mbps,比4G平均用户下载速率的7倍还要多8.32Mbps,4G平均用户下载速率是多少Mbps?(Mbps是一种传输速率单位)(列方程解题)
8.为绿化城市,市政公司四月份投放花草3800盆,比三月份的4倍还多200盆,三月份投放花草多少盆?
9.某学校的教学楼和行政楼相距300米,笑笑和亮亮分别从教学楼和行政楼的门口同时出发,背向而行(如下图),经过8分钟两人相距860米。笑笑平均每分钟走38米,亮亮平均每分钟走多少米?(列方程解答)
10.师徒两人共同加工540个零件,师傅的工作效率是徒弟的1.25倍。4个小时后这批零件全部加工完成。师徒两人每小时分别加工多少个零件?
11.在人体雕塑创作中,为了创造出最美的视觉效果,设计的雕塑下半身高度通常是上半身高度的1.6倍。按照这样的要求,要创作一个高5.2m的人体雕塑,它的上半身和下半身的高度分别要设计成多少米?
12.欣欣不小心把购物小票弄脏了。请你帮她算一算,珍珠奶茶每杯多少元?
13.第七届世界军人运动会吉祥物名为“兵兵”,它的设计灵感来源于中国一级重点保护野生动物中华鲟。雌性中华鲟体长2.3米,比雄性中华鲟体长的2倍少1.1米。雄性中华鲟的体长是多少米?(用方程解)
14.有“徐州之巅”之称的徐州苏宁广场主塔楼高266米,比徐州电视塔高度的2倍少133.2米,徐州电视塔高多少米?(用方程解答)
15.在4个同样的大盒和6个同样的小盒里装满球,正好是200个。每个大盒比每个小盒多装5个,每个大盒和小盒各装多少个?
16.某农场有三块菜地,总面积是500公顷,已知第一块菜地的面积比第二块少40公顷,第二块菜地的面积比第三块多60公顷。这三块菜地的面积各是多少平方米?(先画线段图表示题中的数量关系,再解答)
17.在“学习强国”活动中,王亮的爸爸昨天获得积分44分,比前天的1.5倍多5分。王亮的爸爸前天获得多少分?
18.某通信公司推出两种话费套餐:
(1)张叔叔每月通话150分钟,选哪种套餐比较合算?(计算说明理由)
(2)当通话多少分钟时,两种计费方式话费相同?
19.中国南极科考站总共有5个,分别是长城站、中山站、昆仑站、泰山站以及在建的罗斯海新站。中山站的建筑面积是泰山站的2.7倍,中山站的建筑面积比泰山站多1700平方米。中山站和泰山站的建筑面积各是多少平方米?
20.我们的地球是一个美丽的蓝色星球。朵朵同学借助网络查阅了相关资料,了解到地球的表面积一共约5.1亿平方千米。其中海洋面积大约是陆地面积的2.4倍。请你算一算地球上的海洋面积是多少亿平方千米?
21.港珠澳大桥是一座连接香港、珠海和澳门的桥隧工程,全长55千米;苏通大桥位于江苏省,是沈阳——海口高速公路跨越长江的重要枢纽。港珠澳大桥的长度比苏通大桥全长的2倍少9.8千米,苏通大桥全长多少千米?
《第1单元简易方程应用题专项训练-2024-2025学年数学五年级下册苏教版》参考答案
1.42码
【分析】设用旧码表示是码,根据等量关系:新码(旧码),代入数据列方程解答即可。
【详解】解:设用旧码表示是码。
答:用旧码表示是42码。
2.(1)小华比小明少10张
(2)图见详解,55张
【分析】(1)知道二人共有100张邮票,再补充二人邮票相差几张,形成和差问题解答即可。
(2)根据添加的信息,将线段图补充完整,再解答。
【详解】(1)小明和小华共有100张邮票,小华比小明少10张,小明有多少张邮粟?
(2)
解:设小明有x张邮票,则小华有邮票张,则可列出方程:
答:小明有55张邮票。
3.205千米时
【分析】设动车的速度是x千米/时,根据等量关系:(动车的速度-特快列车的速度)×行驶的时间 =动车比特快列车多行的路程,列方程解答即可。
【详解】解:设动车的速度是千米时。
答:动车的速度是205千米时。
【点睛】本题考查列方程解决问题,关键是根据题意找出基本数量关系,设未知数为,由此列方程解决问题。
4.13.8元
【分析】本题中的等量关系为:彩笔的总钱数+找回钱数=付了的钱数;设每盒彩笔x元,根据等量关系列出方程,解方程即可解决问题。
【详解】解:设每盒彩笔x元,根据题意列方程可得:
6x+17.2=100
6x=82.8
6x÷6=82.8÷6
x=13.8
答:每盒彩笔13.8元。
【点睛】本题考查用方程解决实际问题,关键是找出题中的等量关系。
5.41千米时
【分析】从“同一地点反向而行”可知,68.8千米是甲乙路程之和。根据路程=速度×时间,设甲船的速度是千米时,根据等量关系:甲船的速度行驶的时间乙船的速度行驶的时间千米,列方程,再根据等式性质解方程即可。
【详解】解:设甲船的速度是千米时。
答:甲船的速度是41千米时。
6.4.6千克;2.6千克
【分析】设每个小球重x千克,则每个大球重(x+2)千克,根据大球重量×个数+小球重量×个数=总重量,列出方程求出x的值是小球重量,小球重量+2千克=大球重量。
【详解】解:设每个小球重x千克。
(x+2)×3+2x=19
3x+6+2x=19
5x+6=19
5x+6-6=19-6
5x=13
5x÷5=13÷5
x=2.6
2.6+2=4.6(千克)
答:一个大球和一个小球各重4.6千克、2.6千克。
7.48.57Mbps
【分析】将4G的下载速度设为xMbps,那么它的7倍是(7x)Mbps。根据“4G速度的7倍+8.32Mbps=5G下载速度”列方程解方程即可。
【详解】解:设4G平均用户下载速率是xMbps。
7x+8.32=348.31
7x+8.32-8.32=348.31-8.32
7x=339.99
7x÷7=339.99÷7
x=48.57
答:4G平均用户下载速率是48.57Mbps。
8.900盆
【分析】设三月份投放花草x盆,四月份比三月份的4倍还是多200盆,即三月份投放花盆的盆数×4+200=四月份投放花盆的盆数,列方程:4x+200=3800,解方程,即可解答。
【详解】解:设三月份投放花草x盆。
4x+200=3800
4x+200-200=3800-200
4x=3600
4x÷4=3600÷4
x=900
答:三月份投放花草900盆。
9.32米
【分析】设亮亮平均每分钟走x米,则亮亮8分钟走了8x米;笑笑8分钟走了38×8=304(米)。根据题意可得:亮亮8分钟走的路程+笑笑8分钟走的路程+300米=860米,据此列方程解答。
【详解】解:亮亮平均每分钟走x米。
8x+38×8+300=860
8x+304+300=860
8x+604=860
8x+604-604=860-604
8x=256
8x÷8=256÷8
x=32
答:亮亮平均每分钟走32米。
10.60个;75个
【分析】可设徒弟每小时加工x个零件,则师傅每小时加工1.25x个零件。根据题意,有等式:4x+4×1.25x=540成立,解此方程即求得师徒两人每小时分别加工多少个零件。
【详解】解:设徒弟每小时加工x个零件,则师傅每小时加工1.25x个零件。
4x+4×1.25x=540
4x+5x=540
9x=540
9x÷9=540÷9
x=60
1.25×60 =75
答:徒弟每小时加工60个零件,师傅每小时加工75个零件。
11.2米;3.2米
【分析】可设上半身的高度要设计成x米,则下半身的高度要设计成1.6x米。根据题意有等式:x+1.6x=5.2 成立,解此等式即可知它的上半身和下半身的高度。
【详解】解:设它的上半身的高度要设计成x米,则下半身的高度要设计成1.6x米。
x+1.6x=5.2
2.6x=5.2
2.6x÷2.6=5.2÷2.6
x=2
1.6x=1.6×2=3.2
答:它的上半身的高度要设计成2米,下半身的高度要设计成3.2米。
12.5.5元
【分析】根据“单价×数量=总价”可得出等量关系:每杯珍珠奶茶的价钱×珍珠奶茶的杯数+5杯绿茶的价钱=珍珠奶茶和绿茶的总价,据此列出方程,并求解。
【详解】解:设珍珠奶茶每杯元。
3+30=46.5
3+30-30=46.5-30
3=16.5
3÷3=16.5÷3
=5.5
答:珍珠奶茶每杯5.5元。
13.1.7米
【分析】可设雄性中华鲟的体长为x米,根据数量关系:雌性中华鲟体长=雄性中华鲟体长×2-1.1,据此列出方程,解答方程即可。
【详解】解:设雄性中华鲟的体长是x米。
答:雄性中华鲟的体长是1.7米。
14.199.6米
【点睛】根据比徐州电视塔高度的2倍少133.2米,所以写出数量关系式是:电视塔的高度×2-133.2=塔楼的高度,根据数量关系式列方程即可。
【分析】解:设徐州电视塔高x米
答:徐州电视塔高199.6米。
【详解】重点是能够根据题目中的关键信息写出数量关系式,根据数量关系式列出方程。
15.每个大盒可以装23个,每个小盒可以装18个
【分析】由题意可知,设每个小盒可以装x个,则每个大盒可以装(x+5)个,再根据等量关系:4个大盒装的个数+6个小盒装的个数=200,据此列方程解答即可。
【详解】解:设每个小盒可以装x个,则每个大盒可以装(x+5)个。
6x+4×(x+5)=200
6x+4x+20=200
10x+20=200
10x+20-20=200-20
10x=180
10x÷10=180÷10
x=18
18+5=23(个)
答:每个大盒可以装23个,每个小盒可以装18个。
【点睛】本题考查用方程解决实际问题,明确等量关系是解题的关键。
16.第一、二、三块地分别是160公顷、200公顷、140公顷
图见详解
【分析】三块地都与第二块地进行比较,假设第二块地是x公顷,则第一块地是(x-40)公顷,第三块地是(x-60)公顷,根据总面积是500公顷,列方程解答。
【详解】线段图如下:
解:设第二块地是x公顷,则第一块地是(x-40)公顷,第三块地是(x-60)公顷。
(x-40)+x+(x-60)=500
x-40+x+x-60=500
3x-100=500
3x-100+100=500+100
3x=600
3x÷3=600÷3
x=200
x-40=200-40=160(公顷)
x-60=200-60=140(公顷)
答:第一、二、三块地分别是160公顷、200公顷、140公顷。
【点睛】已知几个数量间的和差关系及这几个数量的和,求这几个数量是多少,设其中一个数量是x,用含x的式子表示另几个量,再根据这几个数量的和列方程解答。
17.26分
【分析】已知王亮的爸爸昨天获得积分44分,而昨天的积分又比前天的1.5倍多5分,如果假设前天的积分是x分,则昨天的积分可表示为1.5x+5,故以昨天的积分为等量关系列方程为:1.5x+5=51。
【详解】解:设前天的积分是x分,可得:
1.5x+5=44
1.5x+5-5=44-5
1.5x=39
1.5x÷1.5=39÷1.5
x=26
答:王亮的爸爸前天获得26分。
【点睛】首先明确题目里昨天获得积分与前天获得积分之间的数量关系,同时结合问题设出合理的未知数,最后找出等量,列出合理的方程。
18.(1)B套餐;
(2)200分钟
【分析】(1)A套餐:月租费20元,0.15元/分钟;用0.15×150,求出150分钟通话的费用,再加上月租费20元,求出张叔叔通话费用;
B套餐:无月租,0.25元/分钟;用0.25×150,求出150分钟通话的费用,即求出张叔叔通话费用,再进行比较,即可解答。
(2)设当通话x分钟时,两种计费方式化肥相同,A套餐:20+0.15x元;B套餐:0.25x元,A套餐=B套餐,列方程:0.15x+20=0.25x,解方程,即可解答。
【详解】(1)0.15×150+20
=22.5+20
=42.5(元)
0.25×150=37.5(元)
42.5>37.5,B套餐比较合适。
答:B 套餐比较合适。
(2)设当通话x分钟时,两种计费方式话费相同。
20+0.15x=0.25x
0.25x-0.15=20
0.1x=20
x=20÷0.1
x=200
答:当通话200分钟时,两种计费方式话费相同.
【点睛】本题属于优化问题,关键是计算出两种套餐所需的费用。
19.中山站:2700平方米;泰山站:1000平方米
【分析】根据题意,设泰山站的建筑面积是x平方米,中山站的建筑面积是泰山站的2.7倍,中山站的建筑面积比泰山站多1700平方米,即中山站的建筑面积-泰山站的建筑面积=1700平方米,列方程:2.7x-x=1700,解方程,即可解答。
【详解】解:设泰山站的建筑面积是x平方米,则中山站的建筑面积是2.7x平方米。
2.7x-x=1700
1.7x=1700
1.7x÷1.7=1700÷1.7
x=1000
1000×2.7=2700(平方米)
答:中山站的建筑面积是2700平方米,泰山站的建筑面积是1000平方米。
【点睛】本题考查方程的实际应用,利用中山站的建筑面积与泰山站的建筑面积之间的关系,设出未知数,找出相关的量,列方程,解方程。
20.3.6亿平方千米
【分析】根据题意,这道题的等量关系是:海洋面积+陆地面积=5.1亿平方千米,根据这个等量关系,列方程解答。
【详解】解:设陆地面积为x亿平方千米,则海洋面积为2.4x亿平方千米。
x+2.4x=5.1
3.4x=5.1
3.4x÷3.4=5.1÷3.4
x=5.1÷3.4
x=1.5
海洋面积:1.5×2.4=3.6(亿平方千米)
答:地球上的海洋面积是3.6亿平方千米。
【点睛】本题考查列方程解应用题,解题关键是找出题目中的等量关系:海洋面积+陆地面积=5.1亿平方千米,列方程解答。
21.32.4千米
【分析】设苏通大桥全长x千米,根据题意,苏通大桥的长度×2-9.8=港珠澳大桥的长度,据此列方程解答。
【详解】解:设苏通大桥全长x千米。
2x-9.8=55
2x=55+9.8
2x=64.8
x=64.8÷2
x=32.4
答:苏通大桥全长32.4千米。
【点睛】本题用方程解答比较简便。找出题中的等量关系式是列出方程的关键。
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
