【同步分层培优】4.5有趣的测量拓展卷(含解析)-2024-2025学年五年级下册数学北师大版
文档属性
| 名称 | 【同步分层培优】4.5有趣的测量拓展卷(含解析)-2024-2025学年五年级下册数学北师大版 |
|
|
| 格式 | docx | ||
| 文件大小 | 679.0KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-05-07 00:00:00 | ||
图片预览



文档简介
4.5有趣的测量
一.选择题(共3小题)
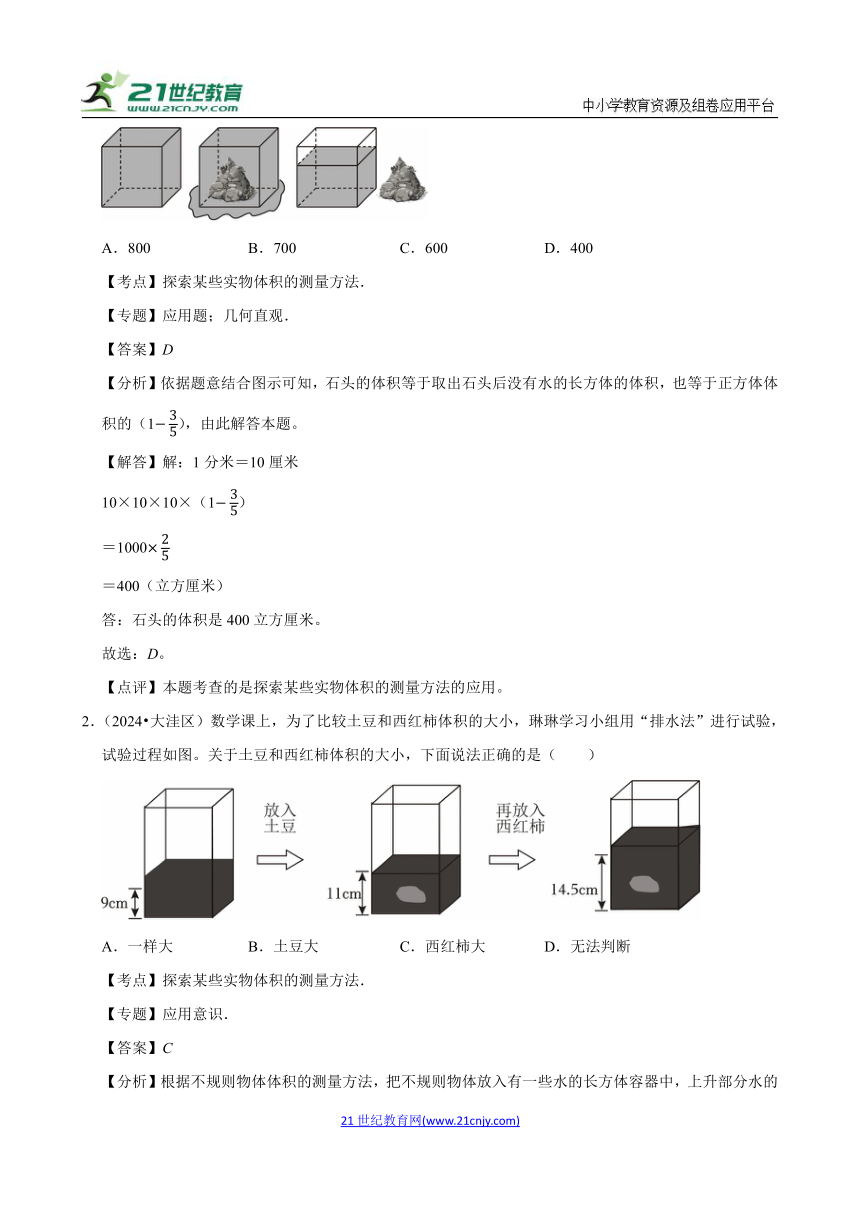
1.(2024秋 江宁区期中)如图,棱长1分米的正方体玻璃缸里装满了水,往缸里放一块石头,取出石头后,缸里的水还剩,石头的体积是( )立方厘米。
A.800 B.700 C.600 D.400
2.(2024 大洼区)数学课上,为了比较土豆和西红柿体积的大小,琳琳学习小组用“排水法”进行试验,试验过程如图。关于土豆和西红柿体积的大小,下面说法正确的是( )
A.一样大 B.土豆大 C.西红柿大 D.无法判断
3.(2024 西安)如图是测量一颗玻璃球体积的过程:(1)将300mL水倒进一个容量为500mL的杯子中;(2)将四颗相同的玻璃球放入水中,结果杯子没有满;(3)再将一颗同样的玻璃球放入水中,结果水满溢出。根据以上过程,推测这样一颗玻璃球的体积范围是( )
A.50cm3以上,60cm3以下
B.30cm3以上,40cm3以下
C.40cm3以上,50cm3以下
D.无法确定
二.填空题(共3小题)
4.(2024 昌黎县)两个大小相同的量杯中,原来都盛有450mL水。将等底等高的圆柱与圆锥零件分别放入两个量杯中,甲量杯中水面刻度如图所示,则圆柱的体积是 cm3,乙量杯中水面刻度应是 mL。
5.(2024春 长兴县期末)如图,在这个长方体的容器中装满了水,放入了一块鹅卵石后再取出发现水面下降了2cm,可知鹅卵石的体积是 cm3。
6.(2024 东莞市)如图(单位:cm),图中一个小球的体积是 cm3,一个大球的体积是 cm3。
三.判断题(共3小题)
7.(2024 盐山县)用一个盛有半杯水的水杯和一把尺子,能测量出一颗小石头的体积。
8.(2023春 南郑区期末)把一块石头投入盛了55mL水的量杯后,水位上升至78mL,这块石头的体积是78cm3。
9.(2024春 灵宝市期中)我们在求不规则物体的体积时,运用了转化的数学思想方法。
4.5有趣的测量
参考答案与试题解析
一.选择题(共3小题)
1.(2024秋 江宁区期中)如图,棱长1分米的正方体玻璃缸里装满了水,往缸里放一块石头,取出石头后,缸里的水还剩,石头的体积是( )立方厘米。
A.800 B.700 C.600 D.400
【考点】探索某些实物体积的测量方法.
【专题】应用题;几何直观.
【答案】D
【分析】依据题意结合图示可知,石头的体积等于取出石头后没有水的长方体的体积,也等于正方体体积的(1),由此解答本题。
【解答】解:1分米=10厘米
10×10×10×(1)
=1000
=400(立方厘米)
答:石头的体积是400立方厘米。
故选:D。
【点评】本题考查的是探索某些实物体积的测量方法的应用。
2.(2024 大洼区)数学课上,为了比较土豆和西红柿体积的大小,琳琳学习小组用“排水法”进行试验,试验过程如图。关于土豆和西红柿体积的大小,下面说法正确的是( )
A.一样大 B.土豆大 C.西红柿大 D.无法判断
【考点】探索某些实物体积的测量方法.
【专题】应用意识.
【答案】C
【分析】根据不规则物体体积的测量方法,把不规则物体放入有一些水的长方体容器中,上升部分水的体积就等于这个不规则体积的体积。
【解答】解:长方体容器内水的高度是9厘米,把一个土豆放入后水面高是11厘米,水面上升了11﹣9=2(厘米);再放入一个西红柿后水面高是14.5厘米,此时水面上升了14.5=11=3.5(厘米),
3.5>2
所以西红柿的如同就比土豆的体积大。
故选:C。
【点评】此题考查的目的是理解掌握不规则物体体积的测量方法及应用。
3.(2024 西安)如图是测量一颗玻璃球体积的过程:(1)将300mL水倒进一个容量为500mL的杯子中;(2)将四颗相同的玻璃球放入水中,结果杯子没有满;(3)再将一颗同样的玻璃球放入水中,结果水满溢出。根据以上过程,推测这样一颗玻璃球的体积范围是( )
A.50cm3以上,60cm3以下
B.30cm3以上,40cm3以下
C.40cm3以上,50cm3以下
D.无法确定
【考点】探索某些实物体积的测量方法.
【专题】几何直观.
【答案】C
【分析】要求每颗玻璃球的体积在哪一个范围内,根据题意,先求出5颗玻璃球的体积最少是多少,5颗玻璃球的体积最少是(500﹣300)立方厘米,进而推测这样一颗玻璃球的体积的范围即可。
【解答】解:因为把5颗玻璃球放入水中,结果水满溢出,所以5颗玻璃球的体积最少是:500﹣300=200(立方厘米)
一颗玻璃球的体积最少是:200÷5=40(立方厘米)
一颗玻璃球的体积最多是:200÷4=50(立方厘米)
答:这样一颗玻璃球的体积在40立方厘米以上,50立方厘米以下。
故选:C。
【点评】此题考查了探索某些实物体积的测量方法,结合题意分析解答即可。
二.填空题(共3小题)
4.(2024 昌黎县)两个大小相同的量杯中,原来都盛有450mL水。将等底等高的圆柱与圆锥零件分别放入两个量杯中,甲量杯中水面刻度如图所示,则圆柱的体积是 150 cm3,乙量杯中水面刻度应是 500 mL。
【考点】探索某些实物体积的测量方法.
【专题】空间观念.
【答案】150;500。
【分析】因为等底等高的圆柱的体积是圆锥体积的3倍,甲量杯中水和放入的圆柱形零件的体积和是600毫升,根据减法的意义,用减法求出圆柱形零件的体积是:600﹣450=150(立方厘米),则圆锥形零件的体积是150÷3=50(立方厘米),因为乙量杯中原来有水450毫升,现在放入体积为50立方厘米的圆锥,则圆锥和水的体积是:450+50=500ml,即可求得量杯中水面刻度。
【解答】解:600﹣450=150(立方厘米)
150÷3=50(立方厘米)
450+50=500(mL)
答:圆柱的体积是150cm3,乙量杯中水面刻度应是500mL。
故答案为:150,500。
【点评】此题考查的目的是理解掌握等底等高的圆柱与圆锥体积之间的关系及应用,注意:体积单位与容积之间的换算。
5.(2024春 长兴县期末)如图,在这个长方体的容器中装满了水,放入了一块鹅卵石后再取出发现水面下降了2cm,可知鹅卵石的体积是 30 cm3。
【考点】探索某些实物体积的测量方法.
【专题】应用意识.
【答案】30。
【分析】根据题意可知,把这块鹅卵石取出后下降部分水的体积就等于这块鹅卵石的体积,根据长方体的体积公式:V=abh,把数据代入公式解答。
【解答】解:5×3×2
=15×2
=30(立方厘米)
答:鹅卵石的体积是30立方厘米。
故答案为:30。
【点评】此题考查的目的是理解掌握不规则物体体积的测量方法及应用,长方体的体积公式及应用。
6.(2024 东莞市)如图(单位:cm),图中一个小球的体积是 15 cm3,一个大球的体积是 45 cm3。
【考点】探索某些实物体积的测量方法.
【专题】综合填空题;几何直观.
【答案】15;45。
【分析】从左往右,图一的长方体容器中没有水;图二,往装有水的圆柱体容器中放入4个小球,此时长方体容器中水深为4cm;则长方体容器中4cm高的水的体积就是4个小球的体积;根据长方体的体积=长×宽×高,求出4个小球的体积,再除以4,即是一个小球的体积;
图三,继续往圆柱体容器中放入2个大球,此时长方体容器中水深为10cm;则长方体容器中(10﹣4)cm高的水的体积就是2个大球的体积;根据长方体的体积=长×宽×高,求出2个大球的体积,再除以2,即是一个大球的体积。
【解答】解:4个小球的体积:
5×3×4=60(cm3)
一个小球的体积:
60÷4=15(cm3)
2个大球的体积:
5×3×10﹣60
=150﹣60
=90(cm3)
一个大球的体积:
90÷2=45(cm3)
答:图中一个小球的体积是15cm3,一个大球的体积是45cm3。
故答案为:15;45。
【点评】本题考查的是探索某些实物体积的测量方法的应用。
三.判断题(共3小题)
7.(2024 盐山县)用一个盛有半杯水的水杯和一把尺子,能测量出一颗小石头的体积。 √
【考点】探索某些实物体积的测量方法.
【专题】几何直观.
【答案】√
【分析】根据用排水法测量实物体积的方法,用一个盛有半杯水的水杯和一把尺子,能测量出一颗小石头的体积。操作步骤如下:
测量出杯子的底面直径和杯子水的高,然后放入小石头,再测量出水的高度,水上升的体积就是石头的体积,结合圆柱的体积公式V=πr2h,即可求出小石头的体积,据此解答即可。
【解答】解:分析可知,用一个盛有半杯水的水杯和一把尺子,能测量出一颗小石头的体积。所以原题说法正确。
故答案为:√。
【点评】本题考查了用排水法测量实物体积的方法,结合题意分析解答即可。
8.(2023春 南郑区期末)把一块石头投入盛了55mL水的量杯后,水位上升至78mL,这块石头的体积是78cm3。 ×
【考点】探索某些实物体积的测量方法.
【专题】几何直观.
【答案】×
【分析】根据这块石头的体积等于水上升的体积,结合题意分析解答即可。
【解答】解:78﹣55=23(毫升)
答:把一块石头投入盛了55mL水的量杯后,水位上升至78mL,这块石头的体积是23毫升。所以原题说法错误。
故答案为:×。
【点评】本题考查了排水法测量体积的方法,结合题意分析解答即可。
9.(2024春 灵宝市期中)我们在求不规则物体的体积时,运用了转化的数学思想方法。 √
【考点】探索某些实物体积的测量方法.
【专题】综合判断题;应用意识.
【答案】√
【分析】根据题意可知,在求不规则物体的体积时,主要是利用排水法,把不规则物体的体积转化求上升部分水的体积。据此解答。
【解答】解:我们在求不规则物体的体积时,运用了转化的数学思想方法。所以原题说法正确。
故答案为:√。
【点评】本题考查的是探索某些实物体积的测量方法的应用。
21世纪教育网(www.21cnjy.com)
一.选择题(共3小题)
1.(2024秋 江宁区期中)如图,棱长1分米的正方体玻璃缸里装满了水,往缸里放一块石头,取出石头后,缸里的水还剩,石头的体积是( )立方厘米。
A.800 B.700 C.600 D.400
2.(2024 大洼区)数学课上,为了比较土豆和西红柿体积的大小,琳琳学习小组用“排水法”进行试验,试验过程如图。关于土豆和西红柿体积的大小,下面说法正确的是( )
A.一样大 B.土豆大 C.西红柿大 D.无法判断
3.(2024 西安)如图是测量一颗玻璃球体积的过程:(1)将300mL水倒进一个容量为500mL的杯子中;(2)将四颗相同的玻璃球放入水中,结果杯子没有满;(3)再将一颗同样的玻璃球放入水中,结果水满溢出。根据以上过程,推测这样一颗玻璃球的体积范围是( )
A.50cm3以上,60cm3以下
B.30cm3以上,40cm3以下
C.40cm3以上,50cm3以下
D.无法确定
二.填空题(共3小题)
4.(2024 昌黎县)两个大小相同的量杯中,原来都盛有450mL水。将等底等高的圆柱与圆锥零件分别放入两个量杯中,甲量杯中水面刻度如图所示,则圆柱的体积是 cm3,乙量杯中水面刻度应是 mL。
5.(2024春 长兴县期末)如图,在这个长方体的容器中装满了水,放入了一块鹅卵石后再取出发现水面下降了2cm,可知鹅卵石的体积是 cm3。
6.(2024 东莞市)如图(单位:cm),图中一个小球的体积是 cm3,一个大球的体积是 cm3。
三.判断题(共3小题)
7.(2024 盐山县)用一个盛有半杯水的水杯和一把尺子,能测量出一颗小石头的体积。
8.(2023春 南郑区期末)把一块石头投入盛了55mL水的量杯后,水位上升至78mL,这块石头的体积是78cm3。
9.(2024春 灵宝市期中)我们在求不规则物体的体积时,运用了转化的数学思想方法。
4.5有趣的测量
参考答案与试题解析
一.选择题(共3小题)
1.(2024秋 江宁区期中)如图,棱长1分米的正方体玻璃缸里装满了水,往缸里放一块石头,取出石头后,缸里的水还剩,石头的体积是( )立方厘米。
A.800 B.700 C.600 D.400
【考点】探索某些实物体积的测量方法.
【专题】应用题;几何直观.
【答案】D
【分析】依据题意结合图示可知,石头的体积等于取出石头后没有水的长方体的体积,也等于正方体体积的(1),由此解答本题。
【解答】解:1分米=10厘米
10×10×10×(1)
=1000
=400(立方厘米)
答:石头的体积是400立方厘米。
故选:D。
【点评】本题考查的是探索某些实物体积的测量方法的应用。
2.(2024 大洼区)数学课上,为了比较土豆和西红柿体积的大小,琳琳学习小组用“排水法”进行试验,试验过程如图。关于土豆和西红柿体积的大小,下面说法正确的是( )
A.一样大 B.土豆大 C.西红柿大 D.无法判断
【考点】探索某些实物体积的测量方法.
【专题】应用意识.
【答案】C
【分析】根据不规则物体体积的测量方法,把不规则物体放入有一些水的长方体容器中,上升部分水的体积就等于这个不规则体积的体积。
【解答】解:长方体容器内水的高度是9厘米,把一个土豆放入后水面高是11厘米,水面上升了11﹣9=2(厘米);再放入一个西红柿后水面高是14.5厘米,此时水面上升了14.5=11=3.5(厘米),
3.5>2
所以西红柿的如同就比土豆的体积大。
故选:C。
【点评】此题考查的目的是理解掌握不规则物体体积的测量方法及应用。
3.(2024 西安)如图是测量一颗玻璃球体积的过程:(1)将300mL水倒进一个容量为500mL的杯子中;(2)将四颗相同的玻璃球放入水中,结果杯子没有满;(3)再将一颗同样的玻璃球放入水中,结果水满溢出。根据以上过程,推测这样一颗玻璃球的体积范围是( )
A.50cm3以上,60cm3以下
B.30cm3以上,40cm3以下
C.40cm3以上,50cm3以下
D.无法确定
【考点】探索某些实物体积的测量方法.
【专题】几何直观.
【答案】C
【分析】要求每颗玻璃球的体积在哪一个范围内,根据题意,先求出5颗玻璃球的体积最少是多少,5颗玻璃球的体积最少是(500﹣300)立方厘米,进而推测这样一颗玻璃球的体积的范围即可。
【解答】解:因为把5颗玻璃球放入水中,结果水满溢出,所以5颗玻璃球的体积最少是:500﹣300=200(立方厘米)
一颗玻璃球的体积最少是:200÷5=40(立方厘米)
一颗玻璃球的体积最多是:200÷4=50(立方厘米)
答:这样一颗玻璃球的体积在40立方厘米以上,50立方厘米以下。
故选:C。
【点评】此题考查了探索某些实物体积的测量方法,结合题意分析解答即可。
二.填空题(共3小题)
4.(2024 昌黎县)两个大小相同的量杯中,原来都盛有450mL水。将等底等高的圆柱与圆锥零件分别放入两个量杯中,甲量杯中水面刻度如图所示,则圆柱的体积是 150 cm3,乙量杯中水面刻度应是 500 mL。
【考点】探索某些实物体积的测量方法.
【专题】空间观念.
【答案】150;500。
【分析】因为等底等高的圆柱的体积是圆锥体积的3倍,甲量杯中水和放入的圆柱形零件的体积和是600毫升,根据减法的意义,用减法求出圆柱形零件的体积是:600﹣450=150(立方厘米),则圆锥形零件的体积是150÷3=50(立方厘米),因为乙量杯中原来有水450毫升,现在放入体积为50立方厘米的圆锥,则圆锥和水的体积是:450+50=500ml,即可求得量杯中水面刻度。
【解答】解:600﹣450=150(立方厘米)
150÷3=50(立方厘米)
450+50=500(mL)
答:圆柱的体积是150cm3,乙量杯中水面刻度应是500mL。
故答案为:150,500。
【点评】此题考查的目的是理解掌握等底等高的圆柱与圆锥体积之间的关系及应用,注意:体积单位与容积之间的换算。
5.(2024春 长兴县期末)如图,在这个长方体的容器中装满了水,放入了一块鹅卵石后再取出发现水面下降了2cm,可知鹅卵石的体积是 30 cm3。
【考点】探索某些实物体积的测量方法.
【专题】应用意识.
【答案】30。
【分析】根据题意可知,把这块鹅卵石取出后下降部分水的体积就等于这块鹅卵石的体积,根据长方体的体积公式:V=abh,把数据代入公式解答。
【解答】解:5×3×2
=15×2
=30(立方厘米)
答:鹅卵石的体积是30立方厘米。
故答案为:30。
【点评】此题考查的目的是理解掌握不规则物体体积的测量方法及应用,长方体的体积公式及应用。
6.(2024 东莞市)如图(单位:cm),图中一个小球的体积是 15 cm3,一个大球的体积是 45 cm3。
【考点】探索某些实物体积的测量方法.
【专题】综合填空题;几何直观.
【答案】15;45。
【分析】从左往右,图一的长方体容器中没有水;图二,往装有水的圆柱体容器中放入4个小球,此时长方体容器中水深为4cm;则长方体容器中4cm高的水的体积就是4个小球的体积;根据长方体的体积=长×宽×高,求出4个小球的体积,再除以4,即是一个小球的体积;
图三,继续往圆柱体容器中放入2个大球,此时长方体容器中水深为10cm;则长方体容器中(10﹣4)cm高的水的体积就是2个大球的体积;根据长方体的体积=长×宽×高,求出2个大球的体积,再除以2,即是一个大球的体积。
【解答】解:4个小球的体积:
5×3×4=60(cm3)
一个小球的体积:
60÷4=15(cm3)
2个大球的体积:
5×3×10﹣60
=150﹣60
=90(cm3)
一个大球的体积:
90÷2=45(cm3)
答:图中一个小球的体积是15cm3,一个大球的体积是45cm3。
故答案为:15;45。
【点评】本题考查的是探索某些实物体积的测量方法的应用。
三.判断题(共3小题)
7.(2024 盐山县)用一个盛有半杯水的水杯和一把尺子,能测量出一颗小石头的体积。 √
【考点】探索某些实物体积的测量方法.
【专题】几何直观.
【答案】√
【分析】根据用排水法测量实物体积的方法,用一个盛有半杯水的水杯和一把尺子,能测量出一颗小石头的体积。操作步骤如下:
测量出杯子的底面直径和杯子水的高,然后放入小石头,再测量出水的高度,水上升的体积就是石头的体积,结合圆柱的体积公式V=πr2h,即可求出小石头的体积,据此解答即可。
【解答】解:分析可知,用一个盛有半杯水的水杯和一把尺子,能测量出一颗小石头的体积。所以原题说法正确。
故答案为:√。
【点评】本题考查了用排水法测量实物体积的方法,结合题意分析解答即可。
8.(2023春 南郑区期末)把一块石头投入盛了55mL水的量杯后,水位上升至78mL,这块石头的体积是78cm3。 ×
【考点】探索某些实物体积的测量方法.
【专题】几何直观.
【答案】×
【分析】根据这块石头的体积等于水上升的体积,结合题意分析解答即可。
【解答】解:78﹣55=23(毫升)
答:把一块石头投入盛了55mL水的量杯后,水位上升至78mL,这块石头的体积是23毫升。所以原题说法错误。
故答案为:×。
【点评】本题考查了排水法测量体积的方法,结合题意分析解答即可。
9.(2024春 灵宝市期中)我们在求不规则物体的体积时,运用了转化的数学思想方法。 √
【考点】探索某些实物体积的测量方法.
【专题】综合判断题;应用意识.
【答案】√
【分析】根据题意可知,在求不规则物体的体积时,主要是利用排水法,把不规则物体的体积转化求上升部分水的体积。据此解答。
【解答】解:我们在求不规则物体的体积时,运用了转化的数学思想方法。所以原题说法正确。
故答案为:√。
【点评】本题考查的是探索某些实物体积的测量方法的应用。
21世纪教育网(www.21cnjy.com)
