沪科版七下(2024版)9.3.1 分式方程的定义及解法 课件
文档属性
| 名称 | 沪科版七下(2024版)9.3.1 分式方程的定义及解法 课件 |

|
|
| 格式 | pptx | ||
| 文件大小 | 1.4MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 沪科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-05-07 00:00:00 | ||
图片预览







文档简介
(共26张PPT)
第9章 分式
9.3.1 分式方程的定义及解法
01
教学目标
02
新知导入
03
新知讲解
04
课堂练习
05
课堂小结
06
作业布置
01
教学目标
理解分式方程的定义,能识别分母含未知数的方程。
01
掌握去分母法解分式方程的步骤,包括找最简公分母、去分母化整式方程、求解并检验根的合理性。
02
通过对比整式方程,体会分式方程的特殊性与转化思想。
03
02
新知导入
为了满足经济高速发展的需要,我国铁路部门不断进行技术革新,提高列车运行速度.兰(甘肃兰州)新(新疆乌鲁木齐)高铁里程全长约1776 km.若某直快列车改为高铁列车后,速度提高 48%运行时间缩短约6 h求直快列车的速度.
思考:题目中的等量关系是什么?你会设什么为未知数?你能列出方程吗?
02
新知导入
等量关系:提速前的运行时间=提速后的运行时间+6 h
时间=
设直快列车的速度为v km/h,
可以得到方程6.
即+6.
02
新知导入
等量关系:(1+48%)直快列车的速度=高铁列车的速度
求直快列车的速度即求.
=
设直快列车的运行时间为t h,
可以得到方程(1+48%)×.
即1.48×.
03
新知探究
+6和1.48×是整式方程吗?
结合它们的特征,想一想,它们是什么方程
分式方程的定义:
像这样,分母中含有未知数的方程叫作分式方程。
1.只含分式,或分式和整式
2.分母中含有未知数
03
新知探究
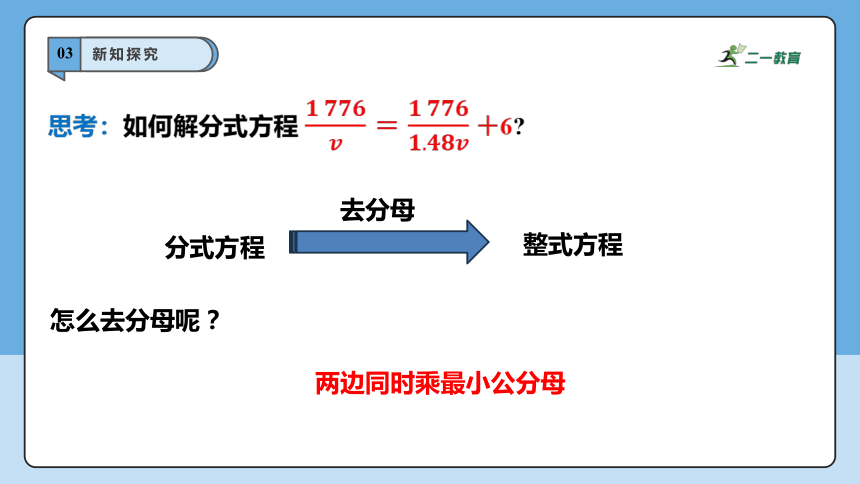
思考:如何解分式方程 6
分式方程
整式方程
去分母
怎么去分母呢?
两边同时乘最小公分母
解分式方程 6
03
新知探究
解:方程两边同乘以1.48v,得1.48×1 776=1 776+8.88x,
解这个整式方程,得x=96.
把x=96代入上述分式方程检验:
左边== +6=右边.
所以x=96是该分式方程的解.
因而,直快列车的速度为96 km/h.
探究
解方程2
解:去分母,得=.
去括号、移项,得.
解得
把解得的根代入原方程中检验,你发现了什么?
把代入原方程检验时,原方程中分式的分母为零,分式没有意义,所以不是原方程的根,原方程无解.
03
新知探究
增根:
是原方程两边同乘以最简公分母变形后,得到的整式方程的根,但不是原方程的根.像这样的根,称为增根.解分式方程时可能会产生增根,所以解分式方程必须验根.
03
新知探究
合作交流:由以上解方程的过程,你能总结出解分式方程的步骤吗?把你的结论与同学交流。
一般步骤
1.确定最简公分母
2.去分母:方程两边同时乘最简公分母,将分式方程化为整式方程
3.解整式方程:去括号、移项、合并同类项、化系数为1
4.检验:将求出的x值代入最简公分母
03
新知探究
例1
解方程:
解:方程两边同乘以最简公分母,得
展开,得.
解方程,得.
检验:当x=21时,
所以,原方程的根是x=21.
03
新知探究
分式方程根的检验方法:
解分式方程时,通常在方程两边同乘以最简公分母,验根时,只要把求得的根代入最简公分母,看它的值是否为零,使它不为零的根才是原方程的根,使它为零的根即为增根,应舍去.
04
课堂练习
【知识技能类作业】必做题:
1.下列关于的方程中,是分式方程的是( )
A. B. C. D.
2.分式方程的解是( )
A. B. C. D.
3.若关于的分式方程有增根,则的值是( )
A. B. C. D.
D
B
A
04
课堂练习
【知识技能类作业】选做题:
4.若关于的分式方程无解,则 .
5.关于的分式方程有非负数解,则的取值范围为 .
1
且
04
课堂练习
6.下列有四个结论:
①把分式中的,都扩大倍,分式的值不变;
②在实数范围内,不存在,,的值,使式子的值为;
③若,则;
④若关于的方程无解,则的值为或
其中正确的结论是 (填写序号)
①②③
04
课堂练习
【综合拓展类作业】
7.已知关于的分式方程.
(1)当时,求方程的解.
(2)若该分式方程无解,求的值.
(1)解:当时,分式方程为,
去分母,得,
解得,
经检验,是原分式方程的解;
04
课堂练习
(2)解:,
去分母,得,
整理,得,
∵原分式方程无解,
∴分式方程产生增根,增根为,
∴,
∴.
05
课堂小结
解分式方程的一般步骤
1.确定最简公分母
2.去分母:方程两边同时乘最简公分母,将分式方程化为整式方程
3.解整式方程:去括号、移项、合并同类项、化系数为1
4.检验:将求出的x值代入最简公分母
06
作业布置
【知识技能类作业】
1.已知关于的分式方程的解为正数,则非负整数的所有个数为( )
A.3 B.4 C.5 D.6
2.若分式方程无解,则的值为( )
A.2 B. C.1 D.
A
B
x的取值 4 6
分式的值 无意义 0 b
06
作业布置
【知识技能类作业】
3.已知分式(为常数)满足表格中的信息,则的积是( )
A. B.6 C.4 D.2
D
06
作业布置
【综合拓展类作业】
4.若关于x的方程恒成立,若x的值非负,则m的取值范围是?
解:
去分母得:,
解得:,
∵x的值非负,
∴
∴且.
07
板书设计
分式方程:
增根:
解分式方程的一般步骤:
9.3.1 分式方程的定义及解法
习题讲解书写部分
Thanks!
https://www.21cnjy.com/recruitment/home/fine
第9章 分式
9.3.1 分式方程的定义及解法
01
教学目标
02
新知导入
03
新知讲解
04
课堂练习
05
课堂小结
06
作业布置
01
教学目标
理解分式方程的定义,能识别分母含未知数的方程。
01
掌握去分母法解分式方程的步骤,包括找最简公分母、去分母化整式方程、求解并检验根的合理性。
02
通过对比整式方程,体会分式方程的特殊性与转化思想。
03
02
新知导入
为了满足经济高速发展的需要,我国铁路部门不断进行技术革新,提高列车运行速度.兰(甘肃兰州)新(新疆乌鲁木齐)高铁里程全长约1776 km.若某直快列车改为高铁列车后,速度提高 48%运行时间缩短约6 h求直快列车的速度.
思考:题目中的等量关系是什么?你会设什么为未知数?你能列出方程吗?
02
新知导入
等量关系:提速前的运行时间=提速后的运行时间+6 h
时间=
设直快列车的速度为v km/h,
可以得到方程6.
即+6.
02
新知导入
等量关系:(1+48%)直快列车的速度=高铁列车的速度
求直快列车的速度即求.
=
设直快列车的运行时间为t h,
可以得到方程(1+48%)×.
即1.48×.
03
新知探究
+6和1.48×是整式方程吗?
结合它们的特征,想一想,它们是什么方程
分式方程的定义:
像这样,分母中含有未知数的方程叫作分式方程。
1.只含分式,或分式和整式
2.分母中含有未知数
03
新知探究
思考:如何解分式方程 6
分式方程
整式方程
去分母
怎么去分母呢?
两边同时乘最小公分母
解分式方程 6
03
新知探究
解:方程两边同乘以1.48v,得1.48×1 776=1 776+8.88x,
解这个整式方程,得x=96.
把x=96代入上述分式方程检验:
左边== +6=右边.
所以x=96是该分式方程的解.
因而,直快列车的速度为96 km/h.
探究
解方程2
解:去分母,得=.
去括号、移项,得.
解得
把解得的根代入原方程中检验,你发现了什么?
把代入原方程检验时,原方程中分式的分母为零,分式没有意义,所以不是原方程的根,原方程无解.
03
新知探究
增根:
是原方程两边同乘以最简公分母变形后,得到的整式方程的根,但不是原方程的根.像这样的根,称为增根.解分式方程时可能会产生增根,所以解分式方程必须验根.
03
新知探究
合作交流:由以上解方程的过程,你能总结出解分式方程的步骤吗?把你的结论与同学交流。
一般步骤
1.确定最简公分母
2.去分母:方程两边同时乘最简公分母,将分式方程化为整式方程
3.解整式方程:去括号、移项、合并同类项、化系数为1
4.检验:将求出的x值代入最简公分母
03
新知探究
例1
解方程:
解:方程两边同乘以最简公分母,得
展开,得.
解方程,得.
检验:当x=21时,
所以,原方程的根是x=21.
03
新知探究
分式方程根的检验方法:
解分式方程时,通常在方程两边同乘以最简公分母,验根时,只要把求得的根代入最简公分母,看它的值是否为零,使它不为零的根才是原方程的根,使它为零的根即为增根,应舍去.
04
课堂练习
【知识技能类作业】必做题:
1.下列关于的方程中,是分式方程的是( )
A. B. C. D.
2.分式方程的解是( )
A. B. C. D.
3.若关于的分式方程有增根,则的值是( )
A. B. C. D.
D
B
A
04
课堂练习
【知识技能类作业】选做题:
4.若关于的分式方程无解,则 .
5.关于的分式方程有非负数解,则的取值范围为 .
1
且
04
课堂练习
6.下列有四个结论:
①把分式中的,都扩大倍,分式的值不变;
②在实数范围内,不存在,,的值,使式子的值为;
③若,则;
④若关于的方程无解,则的值为或
其中正确的结论是 (填写序号)
①②③
04
课堂练习
【综合拓展类作业】
7.已知关于的分式方程.
(1)当时,求方程的解.
(2)若该分式方程无解,求的值.
(1)解:当时,分式方程为,
去分母,得,
解得,
经检验,是原分式方程的解;
04
课堂练习
(2)解:,
去分母,得,
整理,得,
∵原分式方程无解,
∴分式方程产生增根,增根为,
∴,
∴.
05
课堂小结
解分式方程的一般步骤
1.确定最简公分母
2.去分母:方程两边同时乘最简公分母,将分式方程化为整式方程
3.解整式方程:去括号、移项、合并同类项、化系数为1
4.检验:将求出的x值代入最简公分母
06
作业布置
【知识技能类作业】
1.已知关于的分式方程的解为正数,则非负整数的所有个数为( )
A.3 B.4 C.5 D.6
2.若分式方程无解,则的值为( )
A.2 B. C.1 D.
A
B
x的取值 4 6
分式的值 无意义 0 b
06
作业布置
【知识技能类作业】
3.已知分式(为常数)满足表格中的信息,则的积是( )
A. B.6 C.4 D.2
D
06
作业布置
【综合拓展类作业】
4.若关于x的方程恒成立,若x的值非负,则m的取值范围是?
解:
去分母得:,
解得:,
∵x的值非负,
∴
∴且.
07
板书设计
分式方程:
增根:
解分式方程的一般步骤:
9.3.1 分式方程的定义及解法
习题讲解书写部分
Thanks!
https://www.21cnjy.com/recruitment/home/fine
