沪科版七下(2024版)9.3.2 分式方程的应用 课件
文档属性
| 名称 | 沪科版七下(2024版)9.3.2 分式方程的应用 课件 |

|
|
| 格式 | pptx | ||
| 文件大小 | 1.4MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 沪科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-05-07 16:09:37 | ||
图片预览







文档简介
(共28张PPT)
第9章 分式
9.3.2 分式方程的应用
01
教学目标
02
新知导入
03
新知讲解
04
课堂练习
05
课堂小结
06
作业布置
01
教学目标
能从实际问题中抽象数量关系,列出分式方程并求解。
01
熟练运用分式方程解决工程、行程、销售等实际问题。
02
通过“审题—设元—列式—求解—检验”的完整建模过程,发展数学建模能力。
03
02
新知导入
1.审:审清题意,找出已知量和未知量,找等量关系;
2.设:设未知数;
3.列:根据等量关系列一元一次方程;
4.解:解这个方程;
5.验:看是否是方程的解和是否符合题意;
6.答:作答,注意单位和答案完整.
列一元一次方程解应用题的一般步骤是什么?
列分式方程解应用题的一般步骤呢?
03
新知探究
列分式方程解应用题的一般步骤
1.审:审清题意,找出已知量和未知量,找等量关系;
2.设:设未知数;
3.列:根据等量关系列分式方程;
4.解:解这个分式方程;
5.验:验根(①是否是分式方程的根;②是否符合题意);
6.答:作答,注意单位和答案完整.
03
新知探究
某文教店老板到批发市场选购A、B两种品牌的绘图工具套装,每套A品牌套装进价比B品牌每套套装进价多2.5元,已知用200元购进A种套装的数量和用150元购进B种套装的数量相同.求A、B两种品牌套装每套进价分别为多少元?
等量关系:=
1
审
设A的进价为x元,B的进价为(x2.5)元
2
设
03
新知探究
=
3
列
去分母得200(x2.5)=150x
去括号得200x500=150x
移项合并同类项得50x=500
两边都除以50得x=10
4
解
左边= =20==右边
5
验
A品牌套装每套进价为10元,则 品牌套装进价为7.5元
5
答
03
新知探究
解:设品牌套装每套进价为元,则B品牌套装进价为元
由题意得
解得
经检验,是分式方程的解
答:品牌套装每套进价为元,则品牌套装进价为元
规范书写
03
新知探究
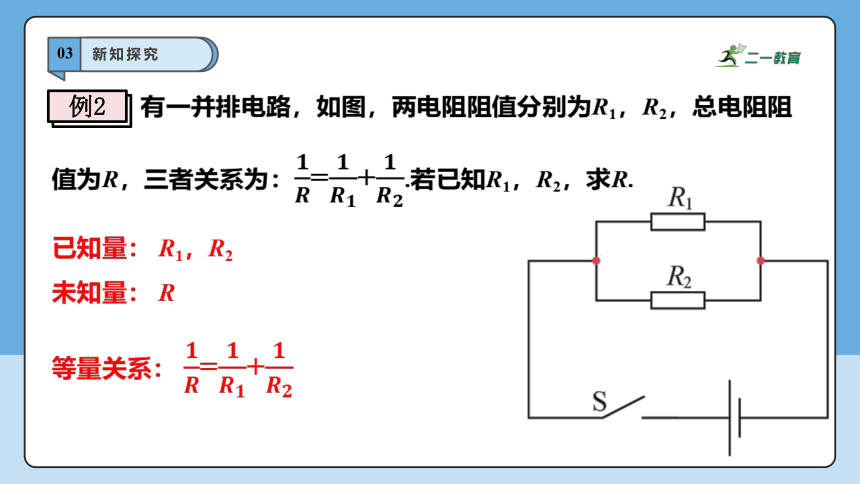
有一并排电路,如图,两电阻阻值分别为R1,R2,总电阻阻值为R,三者关系为:=+.若已知R1,R2,求R.
例2
已知量: R1,R2
未知量: R
等量关系: =+
03
新知探究
有一并排电路,如图,两电阻阻值分别为R1,R2,总电阻阻值为R,三者关系为:=+.若已知R1,R2,求R.
例2
解:方程两边同乘以R1R2R,得
R1R2=RR2+RR1,即R1R2=R(R1+R2).
因为R,R2都是正数,所以R1+R2≠0.
所以两边同除以(R1+R2),得R=.
03
新知探究
例3
七(1)、(2)两班师生前往郊区参加义务植树活动,已知七(1)班每天比七(2)班多种10棵树.如果分配给七(1)、(2)两班的植树任务分别是150棵和120棵,问两个班每天各植树多少棵,才能同时完成任务?
解:设七(2)班每天植树x棵,那么七(1)班每天植树(x+10)棵,七(1)班完成任务需天,七(2)班完成任务需天.
要求同时完成任务,即x应满足下列等式:=.
03
新知探究
例3
七(1)、(2)两班师生前往郊区参加义务植树活动,已知七(1)班每天比七(2)班多种10棵树.如果分配给七(1)、(2)两班的植树任务分别是150棵和120棵,问两个班每天各植树多少棵,才能同时完成任务?
解方程,得x=40.
经检验,x=40是原方程的根.此时x+10=50.
答:当七(2)班每天植树40棵,七(1)班每天植树50棵时,两个班能同时完成任务.
04
课堂练习
【知识技能类作业】必做题:
1. 《步辇图》是唐朝画家阎立本的作品,如图是它的局部画面,装裱前是一个长为,宽为的长方形,装裱后,整幅图画宽与长的比是,且四周边框的宽度相等,则边框的宽度应是多少?设边框的宽度为,根据题意,可列方程为( )
A.
B.
C.
D.
C
04
课堂练习
2.某学校改造过程中整修门口的道路,但是在实际施工时,,求实际每天整修道路多少米?”在这个题目中,若设实际每天整修道路 ,可得方程15,则题目中用“”表示的条件应是( )
A.每天比原计划多修,结果延期15天完成
B.每天比原计划多修,结果提前15天完成
C.每天比原计划少修,结果延期15天完成
D.每天比原计划少修,结果提前15天完成
B
04
课堂练习
3.某商场用3000元购进某种商品,售完后,第二次购进时,每件商品进价提高了20%,同样用3000元购进商品的数量比第一次少了10件,则第一次购进每件商品的进价为( )
A.50元
B.60元
C.70元
D.80元
A
04
课堂练习
【知识技能类作业】选做题:
4.一艘轮船在静水中的最大航速为30km/h,它以最大航速沿江顺流航行90km所用时间与最大航速逆流航行60km所用时间相等,则江水的流速为__________km/h.
5.在学校组织的一次汉字打字比赛中,“阳光”中队的小聪输入1000个字的时间比小明输入1200字的时间少2分钟,小聪与小明平均每分钟打字个数之比是5:4,设小聪平均每分钟打字为5x个,根据题意可列方程是________________________.
6
04
课堂练习
6.某网店用5000元购进一批新品种草莓进行试销,由于销售状况良好,网店又用11000元第二次购进的该品种草莓,但第二次的进货价比试销时每千克多了0.5元,第二次购进的草莓数量是试销时的2倍.试销时该品种草莓的进货价是每千克_________元,两次共购进草莓_______千克.
5
3000
04
课堂练习
【综合拓展类作业】
7.某网店销售甲、乙两种茶具套装,甲种茶具套装的单价比乙种茶具套装的单价少30元,花1500元购进甲种茶具套装的数量是花900元购进乙种茶具套装数量的2倍,求甲、乙两种茶具套装的单价.
解:设甲种茶具套装的单价是x元,
根据题意,得,
解得.
经检验,是所列方程的解,且符合题意,
∴.
答:甲种茶具套装的单价是150元,乙种茶具套装的单价是180元.
05
课堂小结
列分式方程解应用题的一般步骤
1.审:审清题意,找出已知量和未知量,找等量关系;
2.设:设未知数;
3.列:根据等量关系列分式方程;
4.解:解这个分式方程;
5.验:验根(①是否是分式方程的根;②是否符合题意);
6.答:作答,注意单位和答案完整.
06
作业布置
【知识技能类作业】
1.八年级学生去距学校10千米的博物馆参观,一部分同学骑自行车先走,过了20分后,其余同学乘汽车出发,结果他们同时到达.已知汽车的速度是骑车同学速度的2倍,则骑车同学的速度为( )
A.10千米/时
B.15千米/时
C.20千米/时
D.30千米/时
B
06
作业布置
【知识技能类作业】
2.数学家斐波那契编写的《算经》中有如下分钱问题:第一次由一组人平分10元钱,每人分得若干,第二次比第一次增加6人,平分40元钱,则第二次每人分得的钱与第一次相同,设第二次分钱的人数为x人,则可列方程为( )
A. B.
C. D.
D
06
作业布置
【知识技能类作业】
3.承包池塘的农民伯伯想知道自家池塘里有多少条鱼,决定通过捕鱼和标记来估计.第一次捕获了100条鱼,并对它们进行标记,然后,将这100条鱼放回了池塘.过了几天,等这些标记的鱼在池塘中均匀分布后,又捕获了200条鱼,发现其中有10条鱼是之前标记过的.请估计池塘里大概有( )条鱼.
A.500 B.1000 C.2000 D.3000
C
06
作业布置
【综合拓展类作业】
4.为了创建全国卫生城市,某社区要清理一个卫生死角内的垃圾,租用甲、乙两车运送,两车各运6趟可完成,需支付运费2400元.已知甲、乙两车单独运完此堆垃圾,乙车所运趟数是甲车的2倍,且乙车每趟运费比甲车少100元.
(1)求甲、乙两车单独运完此堆垃圾各需运多少趟?
(2)若单独租用一台车,租用哪台车合算?
06
作业布置
(1)解:设甲车单独运完此堆垃圾需运趟,则乙车单独运完此堆垃圾需运趟,根据题意得出:
解得:,
经检验得出:是原方程的解,
∴,
答:甲车单独运完需9趟,乙车单独运完需18趟;
06
作业布置
(2)解:设甲车每一趟的运费是元,由题意得:
,
解得:,
则乙车每一趟的费用是:(元),
单独租用甲车总费用是:(元),
单独租用乙车总费用是:(元),
,
∴单独租用一台车,租用甲车合算.
07
板书设计
一般步骤:
1.审:
2.设:
3.列:
4.解:
5.验:
6.答:
9.3.2 分式方程的应用
习题讲解书写部分
Thanks!
https://www.21cnjy.com/recruitment/home/fine
第9章 分式
9.3.2 分式方程的应用
01
教学目标
02
新知导入
03
新知讲解
04
课堂练习
05
课堂小结
06
作业布置
01
教学目标
能从实际问题中抽象数量关系,列出分式方程并求解。
01
熟练运用分式方程解决工程、行程、销售等实际问题。
02
通过“审题—设元—列式—求解—检验”的完整建模过程,发展数学建模能力。
03
02
新知导入
1.审:审清题意,找出已知量和未知量,找等量关系;
2.设:设未知数;
3.列:根据等量关系列一元一次方程;
4.解:解这个方程;
5.验:看是否是方程的解和是否符合题意;
6.答:作答,注意单位和答案完整.
列一元一次方程解应用题的一般步骤是什么?
列分式方程解应用题的一般步骤呢?
03
新知探究
列分式方程解应用题的一般步骤
1.审:审清题意,找出已知量和未知量,找等量关系;
2.设:设未知数;
3.列:根据等量关系列分式方程;
4.解:解这个分式方程;
5.验:验根(①是否是分式方程的根;②是否符合题意);
6.答:作答,注意单位和答案完整.
03
新知探究
某文教店老板到批发市场选购A、B两种品牌的绘图工具套装,每套A品牌套装进价比B品牌每套套装进价多2.5元,已知用200元购进A种套装的数量和用150元购进B种套装的数量相同.求A、B两种品牌套装每套进价分别为多少元?
等量关系:=
1
审
设A的进价为x元,B的进价为(x2.5)元
2
设
03
新知探究
=
3
列
去分母得200(x2.5)=150x
去括号得200x500=150x
移项合并同类项得50x=500
两边都除以50得x=10
4
解
左边= =20==右边
5
验
A品牌套装每套进价为10元,则 品牌套装进价为7.5元
5
答
03
新知探究
解:设品牌套装每套进价为元,则B品牌套装进价为元
由题意得
解得
经检验,是分式方程的解
答:品牌套装每套进价为元,则品牌套装进价为元
规范书写
03
新知探究
有一并排电路,如图,两电阻阻值分别为R1,R2,总电阻阻值为R,三者关系为:=+.若已知R1,R2,求R.
例2
已知量: R1,R2
未知量: R
等量关系: =+
03
新知探究
有一并排电路,如图,两电阻阻值分别为R1,R2,总电阻阻值为R,三者关系为:=+.若已知R1,R2,求R.
例2
解:方程两边同乘以R1R2R,得
R1R2=RR2+RR1,即R1R2=R(R1+R2).
因为R,R2都是正数,所以R1+R2≠0.
所以两边同除以(R1+R2),得R=.
03
新知探究
例3
七(1)、(2)两班师生前往郊区参加义务植树活动,已知七(1)班每天比七(2)班多种10棵树.如果分配给七(1)、(2)两班的植树任务分别是150棵和120棵,问两个班每天各植树多少棵,才能同时完成任务?
解:设七(2)班每天植树x棵,那么七(1)班每天植树(x+10)棵,七(1)班完成任务需天,七(2)班完成任务需天.
要求同时完成任务,即x应满足下列等式:=.
03
新知探究
例3
七(1)、(2)两班师生前往郊区参加义务植树活动,已知七(1)班每天比七(2)班多种10棵树.如果分配给七(1)、(2)两班的植树任务分别是150棵和120棵,问两个班每天各植树多少棵,才能同时完成任务?
解方程,得x=40.
经检验,x=40是原方程的根.此时x+10=50.
答:当七(2)班每天植树40棵,七(1)班每天植树50棵时,两个班能同时完成任务.
04
课堂练习
【知识技能类作业】必做题:
1. 《步辇图》是唐朝画家阎立本的作品,如图是它的局部画面,装裱前是一个长为,宽为的长方形,装裱后,整幅图画宽与长的比是,且四周边框的宽度相等,则边框的宽度应是多少?设边框的宽度为,根据题意,可列方程为( )
A.
B.
C.
D.
C
04
课堂练习
2.某学校改造过程中整修门口的道路,但是在实际施工时,,求实际每天整修道路多少米?”在这个题目中,若设实际每天整修道路 ,可得方程15,则题目中用“”表示的条件应是( )
A.每天比原计划多修,结果延期15天完成
B.每天比原计划多修,结果提前15天完成
C.每天比原计划少修,结果延期15天完成
D.每天比原计划少修,结果提前15天完成
B
04
课堂练习
3.某商场用3000元购进某种商品,售完后,第二次购进时,每件商品进价提高了20%,同样用3000元购进商品的数量比第一次少了10件,则第一次购进每件商品的进价为( )
A.50元
B.60元
C.70元
D.80元
A
04
课堂练习
【知识技能类作业】选做题:
4.一艘轮船在静水中的最大航速为30km/h,它以最大航速沿江顺流航行90km所用时间与最大航速逆流航行60km所用时间相等,则江水的流速为__________km/h.
5.在学校组织的一次汉字打字比赛中,“阳光”中队的小聪输入1000个字的时间比小明输入1200字的时间少2分钟,小聪与小明平均每分钟打字个数之比是5:4,设小聪平均每分钟打字为5x个,根据题意可列方程是________________________.
6
04
课堂练习
6.某网店用5000元购进一批新品种草莓进行试销,由于销售状况良好,网店又用11000元第二次购进的该品种草莓,但第二次的进货价比试销时每千克多了0.5元,第二次购进的草莓数量是试销时的2倍.试销时该品种草莓的进货价是每千克_________元,两次共购进草莓_______千克.
5
3000
04
课堂练习
【综合拓展类作业】
7.某网店销售甲、乙两种茶具套装,甲种茶具套装的单价比乙种茶具套装的单价少30元,花1500元购进甲种茶具套装的数量是花900元购进乙种茶具套装数量的2倍,求甲、乙两种茶具套装的单价.
解:设甲种茶具套装的单价是x元,
根据题意,得,
解得.
经检验,是所列方程的解,且符合题意,
∴.
答:甲种茶具套装的单价是150元,乙种茶具套装的单价是180元.
05
课堂小结
列分式方程解应用题的一般步骤
1.审:审清题意,找出已知量和未知量,找等量关系;
2.设:设未知数;
3.列:根据等量关系列分式方程;
4.解:解这个分式方程;
5.验:验根(①是否是分式方程的根;②是否符合题意);
6.答:作答,注意单位和答案完整.
06
作业布置
【知识技能类作业】
1.八年级学生去距学校10千米的博物馆参观,一部分同学骑自行车先走,过了20分后,其余同学乘汽车出发,结果他们同时到达.已知汽车的速度是骑车同学速度的2倍,则骑车同学的速度为( )
A.10千米/时
B.15千米/时
C.20千米/时
D.30千米/时
B
06
作业布置
【知识技能类作业】
2.数学家斐波那契编写的《算经》中有如下分钱问题:第一次由一组人平分10元钱,每人分得若干,第二次比第一次增加6人,平分40元钱,则第二次每人分得的钱与第一次相同,设第二次分钱的人数为x人,则可列方程为( )
A. B.
C. D.
D
06
作业布置
【知识技能类作业】
3.承包池塘的农民伯伯想知道自家池塘里有多少条鱼,决定通过捕鱼和标记来估计.第一次捕获了100条鱼,并对它们进行标记,然后,将这100条鱼放回了池塘.过了几天,等这些标记的鱼在池塘中均匀分布后,又捕获了200条鱼,发现其中有10条鱼是之前标记过的.请估计池塘里大概有( )条鱼.
A.500 B.1000 C.2000 D.3000
C
06
作业布置
【综合拓展类作业】
4.为了创建全国卫生城市,某社区要清理一个卫生死角内的垃圾,租用甲、乙两车运送,两车各运6趟可完成,需支付运费2400元.已知甲、乙两车单独运完此堆垃圾,乙车所运趟数是甲车的2倍,且乙车每趟运费比甲车少100元.
(1)求甲、乙两车单独运完此堆垃圾各需运多少趟?
(2)若单独租用一台车,租用哪台车合算?
06
作业布置
(1)解:设甲车单独运完此堆垃圾需运趟,则乙车单独运完此堆垃圾需运趟,根据题意得出:
解得:,
经检验得出:是原方程的解,
∴,
答:甲车单独运完需9趟,乙车单独运完需18趟;
06
作业布置
(2)解:设甲车每一趟的运费是元,由题意得:
,
解得:,
则乙车每一趟的费用是:(元),
单独租用甲车总费用是:(元),
单独租用乙车总费用是:(元),
,
∴单独租用一台车,租用甲车合算.
07
板书设计
一般步骤:
1.审:
2.设:
3.列:
4.解:
5.验:
6.答:
9.3.2 分式方程的应用
习题讲解书写部分
Thanks!
https://www.21cnjy.com/recruitment/home/fine
