沪科版七下(2024版)第9章 小结与复习 教案
文档属性
| 名称 | 沪科版七下(2024版)第9章 小结与复习 教案 |

|
|
| 格式 | docx | ||
| 文件大小 | 506.4KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 沪科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-05-07 00:00:00 | ||
图片预览


文档简介
中小学教育资源及组卷应用平台
分课时教学设计
《小结与复习》教学设计
课型 新授课 复习课 试卷讲评课 其他课
教学内容分析 《分式》小结与复习主要对分式的概念及基本性质、分式的加减乘除运算、分式方程的解法、分式方程的应用等进行了全面的梳理和评价。该章节旨在通过系统的复习与总结,加深学生对分式及分式方程的理解,掌握其计算方法,并能灵活应用于解决实际问题中。
学习者分析 学生已掌握分式的基本概念和简单运算,但在以下方面存在不足: 概念混淆:易忽略分母不为零的条件(如分式值为零时需同时满足分子为零、分母非零); 运算规范性差:约分时漏项、通分时未找最简公分母,或符号处理错误(如负号遗漏); 应用能力弱:难以从实际问题中提取等量关系列分式方程(如“至少”“不超过”的数学转化); 检验意识不足:解分式方程后未验证增根,导致解集错误。
教学目标 1.复习巩固分式和最简分式的概念。 2.能利用分式的基本性质进行约分和通分。 3.复习巩固分式的四则运算。 4.能根据实际问题列分式方程,并能解可化为一元一次方程的分式方程。
教学重点 1.分式的四则运算。 2.分式方程的解法与应用。
教学难点 1.分式方程的实际应用(如隐含条件挖掘)。 2.复杂分式化简(如含多项式因式分解)。 3.解集的检验与实际问题匹配性判断。
学习活动设计
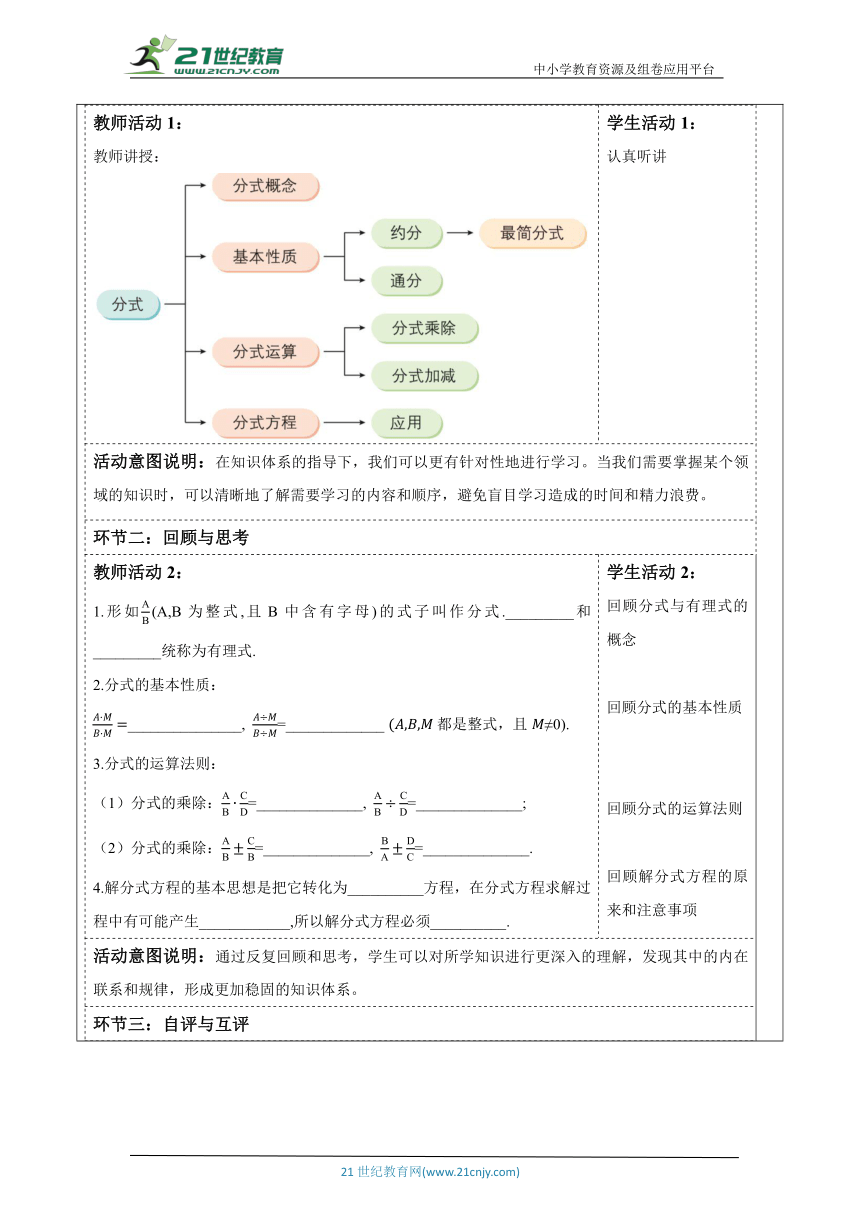
教师活动学生活动环节一:构建知识体系教师活动1: 教师讲授: 学生活动1: 认真听讲活动意图说明:在知识体系的指导下,我们可以更有针对性地进行学习。当我们需要掌握某个领域的知识时,可以清晰地了解需要学习的内容和顺序,避免盲目学习造成的时间和精力浪费。环节二:回顾与思考教师活动2: 1.形如(A,B为整式,且B中含有字母)的式子叫作分式._________和_________统称为有理式. 2.分式的基本性质: _______________, =_____________ 都是整式,且≠0). 3.分式的运算法则: (1)分式的乘除:=______________, =______________; (2)分式的乘除:=______________, =______________. 4.解分式方程的基本思想是把它转化为__________方程,在分式方程求解过程中有可能产生____________,所以解分式方程必须__________.学生活动2: 回顾分式与有理式的概念 回顾分式的基本性质 回顾分式的运算法则 回顾解分式方程的原来和注意事项活动意图说明:通过反复回顾和思考,学生可以对所学知识进行更深入的理解,发现其中的内在联系和规律,形成更加稳固的知识体系。环节三:自评与互评教师活动3: 教师讲授: 1.本章从分式的概念、性质到运算法则、都是通过和分数的有关知识 类比得到的.类比是一种重要的数学思想方法,请你举例说明前面哪些知识的学习运用了这种思想方法.与同学进行交流. 2.解分式方程是通过去分母,化归为整式方程求解.化归同样是一种重要的数学思想方法,在前面知识的学习中,哪些应用了这种思想方法 试举例说明,与同学进行交流. 3.解分式方程与解一元一次方程有什么联系和区别 4.联系实际生活,提出一个可以通过列分式方程解决的问题,与你的同学共同解决,并对解答给出评价.学生活动4: 认真思考,合作交流活动意图说明:通过自评,学生可以认识到自己的学习成果与目标的差距,从而激发内在的学习动力。同时互评过程中,学生可以分享自己的学习方法和经验,促进知识的共享和互补。
板书设计
课堂练习 【知识技能类作业】 必做题: 1.下列各式中,无论取何值,分式都有意义的是( ) A. B. C. D. 2.已知,其中,则与的关系是( ) A. B. C. D. 3.下列方程中,不是分式方程的是( ) A. B. C. D. 选做题: 4.在分式,,,中,最简分式有 个. 5.若关于的分式方程的解是负数,则的取值范围是__________. 6.化简:. 【综合拓展类作业】 7.某中学为落实《教育部办公厅关于进一步加强中小学生体质健康管理工作的通知》文件要求,决定增设篮球,足球两门选修课程,需要购进一批篮球和足球.若购买篮球的数量是足球的2倍,购买篮球用了6000元,购买足球用了2000元,篮球单价比足球单价贵30元. (1)求篮球和足球的单价分别是多少元: (2)学校计划采购篮球、足球共60个,并要求篮球多于40个,且总费用低于4900元.那么有哪几种购买方案?
作业设计 【知识技能类作业】 必做题: 1.下列等式成立的是( ) A. B. C. D. 2.两地相距1600千米,技术突破后,列车运行时速提升了50千米,而从A地运行至地的时长缩短了1小时,若设提速前的车速为千米/小时,则可列方程为( ) A. B. C. D. 3.对于代数式m,n,定义运算“”:,例如:,若,则 . 【综合拓展类作业】 4.先化简:,然后在,,,四个数中选一个你认为合适的数代入求值.
教学反思 改进方向 抽象概念具象化:部分学生对分式方程的“增根”理解模糊,需借助数轴动态演示解的变化过程; 强化逆向思维:增加“已知解集反推参数”类问题(如分式方程有增根时求字母取值); 技术辅助:引入计算器处理复杂运算,但需规范使用步骤,避免依赖。
21世纪教育网(www.21cnjy.com)
分课时教学设计
《小结与复习》教学设计
课型 新授课 复习课 试卷讲评课 其他课
教学内容分析 《分式》小结与复习主要对分式的概念及基本性质、分式的加减乘除运算、分式方程的解法、分式方程的应用等进行了全面的梳理和评价。该章节旨在通过系统的复习与总结,加深学生对分式及分式方程的理解,掌握其计算方法,并能灵活应用于解决实际问题中。
学习者分析 学生已掌握分式的基本概念和简单运算,但在以下方面存在不足: 概念混淆:易忽略分母不为零的条件(如分式值为零时需同时满足分子为零、分母非零); 运算规范性差:约分时漏项、通分时未找最简公分母,或符号处理错误(如负号遗漏); 应用能力弱:难以从实际问题中提取等量关系列分式方程(如“至少”“不超过”的数学转化); 检验意识不足:解分式方程后未验证增根,导致解集错误。
教学目标 1.复习巩固分式和最简分式的概念。 2.能利用分式的基本性质进行约分和通分。 3.复习巩固分式的四则运算。 4.能根据实际问题列分式方程,并能解可化为一元一次方程的分式方程。
教学重点 1.分式的四则运算。 2.分式方程的解法与应用。
教学难点 1.分式方程的实际应用(如隐含条件挖掘)。 2.复杂分式化简(如含多项式因式分解)。 3.解集的检验与实际问题匹配性判断。
学习活动设计
教师活动学生活动环节一:构建知识体系教师活动1: 教师讲授: 学生活动1: 认真听讲活动意图说明:在知识体系的指导下,我们可以更有针对性地进行学习。当我们需要掌握某个领域的知识时,可以清晰地了解需要学习的内容和顺序,避免盲目学习造成的时间和精力浪费。环节二:回顾与思考教师活动2: 1.形如(A,B为整式,且B中含有字母)的式子叫作分式._________和_________统称为有理式. 2.分式的基本性质: _______________, =_____________ 都是整式,且≠0). 3.分式的运算法则: (1)分式的乘除:=______________, =______________; (2)分式的乘除:=______________, =______________. 4.解分式方程的基本思想是把它转化为__________方程,在分式方程求解过程中有可能产生____________,所以解分式方程必须__________.学生活动2: 回顾分式与有理式的概念 回顾分式的基本性质 回顾分式的运算法则 回顾解分式方程的原来和注意事项活动意图说明:通过反复回顾和思考,学生可以对所学知识进行更深入的理解,发现其中的内在联系和规律,形成更加稳固的知识体系。环节三:自评与互评教师活动3: 教师讲授: 1.本章从分式的概念、性质到运算法则、都是通过和分数的有关知识 类比得到的.类比是一种重要的数学思想方法,请你举例说明前面哪些知识的学习运用了这种思想方法.与同学进行交流. 2.解分式方程是通过去分母,化归为整式方程求解.化归同样是一种重要的数学思想方法,在前面知识的学习中,哪些应用了这种思想方法 试举例说明,与同学进行交流. 3.解分式方程与解一元一次方程有什么联系和区别 4.联系实际生活,提出一个可以通过列分式方程解决的问题,与你的同学共同解决,并对解答给出评价.学生活动4: 认真思考,合作交流活动意图说明:通过自评,学生可以认识到自己的学习成果与目标的差距,从而激发内在的学习动力。同时互评过程中,学生可以分享自己的学习方法和经验,促进知识的共享和互补。
板书设计
课堂练习 【知识技能类作业】 必做题: 1.下列各式中,无论取何值,分式都有意义的是( ) A. B. C. D. 2.已知,其中,则与的关系是( ) A. B. C. D. 3.下列方程中,不是分式方程的是( ) A. B. C. D. 选做题: 4.在分式,,,中,最简分式有 个. 5.若关于的分式方程的解是负数,则的取值范围是__________. 6.化简:. 【综合拓展类作业】 7.某中学为落实《教育部办公厅关于进一步加强中小学生体质健康管理工作的通知》文件要求,决定增设篮球,足球两门选修课程,需要购进一批篮球和足球.若购买篮球的数量是足球的2倍,购买篮球用了6000元,购买足球用了2000元,篮球单价比足球单价贵30元. (1)求篮球和足球的单价分别是多少元: (2)学校计划采购篮球、足球共60个,并要求篮球多于40个,且总费用低于4900元.那么有哪几种购买方案?
作业设计 【知识技能类作业】 必做题: 1.下列等式成立的是( ) A. B. C. D. 2.两地相距1600千米,技术突破后,列车运行时速提升了50千米,而从A地运行至地的时长缩短了1小时,若设提速前的车速为千米/小时,则可列方程为( ) A. B. C. D. 3.对于代数式m,n,定义运算“”:,例如:,若,则 . 【综合拓展类作业】 4.先化简:,然后在,,,四个数中选一个你认为合适的数代入求值.
教学反思 改进方向 抽象概念具象化:部分学生对分式方程的“增根”理解模糊,需借助数轴动态演示解的变化过程; 强化逆向思维:增加“已知解集反推参数”类问题(如分式方程有增根时求字母取值); 技术辅助:引入计算器处理复杂运算,但需规范使用步骤,避免依赖。
21世纪教育网(www.21cnjy.com)
