北京市西城区第一六一中学2024-2025学年七年级下册数学期中试卷(pdf版,含答案)
文档属性
| 名称 | 北京市西城区第一六一中学2024-2025学年七年级下册数学期中试卷(pdf版,含答案) | 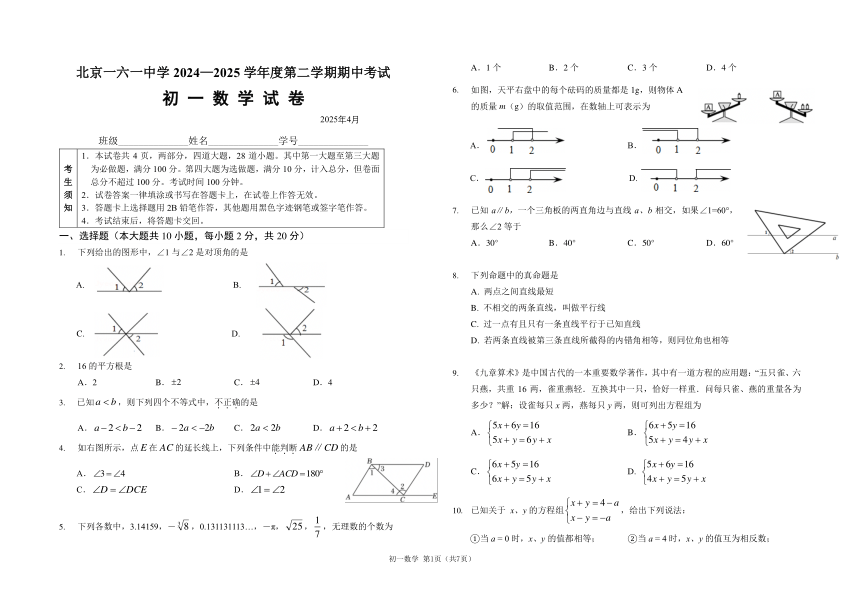 | |
| 格式 | |||
| 文件大小 | 849.9KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-05-07 16:24:08 | ||
图片预览



文档简介
北京一六一中学 2024—2025 学年度第二学期期中考试 A.1 个 B.2 个 C.3 个 D.4 个
6. 如图,天平右盘中的每个砝码的质量都是 1g,则物体 A
初 一 数 学 试 卷
的质量 m(g)的取值范围,在数轴上可表示为
2025年4月
班级______________姓名______________学号______________
A. B.
1.本试卷共 4 页,两部分,四道大题,28 道小题。其中第一大题至第三大题
考 为必做题,满分 100 分。第四大题为选做题,满分 10 分,计入总分,但卷面
生 总分不超过 100 分。考试时间 分钟。 C. D. 100
须 2.试卷答案一律填涂或书写在答题卡上,在试卷上作答无效。
知 3.答题卡上选择题用 2B 铅笔作答,其他题用黑色字迹钢笔或签字笔作答。 7. 已知 a∥b,一个三角板的两直角边与直线 a、b 相交,如果∠1=60°,
4.考试结束后,将答题卡交回。
那么∠2 等于
一、选择题(本大题共 10 小题,每小题 2 分,共 20 分)
A.30° B.40° C.50° D.60°
1. 下列给出的图形中,∠1 与∠2 是对顶角的是
8. 下列命题中的真命题是
A. B.
A. 两点之间直线最短
B. 不相交的两条直线,叫做平行线
C. 过一点有且只有一条直线平行于已知直线
C. D.
D. 若两条直线被第三条直线所截得的内错角相等,则同位角也相等
2. 16 的平方根是
9. 《九章算术》是中国古代的一本重要数学著作,其中有一道方程的应用题:“五只雀、六
A.2 B. 2 C. 4 D.4
只燕,共重 16 两,雀重燕轻.互换其中一只,恰好一样重.问每只雀、燕的重量各为
3. 已知a b,则下列四个不等式中,不.正.确.的是 多少?”解:设雀每只 x 两,燕每只 y 两,则可列出方程组为
A.a 2 b 2 B. 2a 2b C.2a 2b D.a+ 2 b+ 2 5x + 6y =16 6x + 5y =16
A. B.
5x + y = 6y + x 5x + y = 4y + x
4. 如右图所示,点 E 在 AC 的延长线上,下列条件中能.判.断.AB∥CD的是
6x + 5y =16 5x + 6y =16
A. 3= 4 B. D+ ACD =180 C. D.
6x + y = 5y + x 4x + y = 5y + x
C. D = DCE D. 1= 2
x + y = 4 a
10. 已知关于 x、y 的方程组 ,给出下列说法:
1 x y = a
5. 下列各数中,3.14159,- 3 8 ,0.131131113…,-π, 25, ,无理数的个数为
7
①当 a = 0 时,x、y 的值都相等; ②当 a = 4 时,x、y 的值互为相反数;
初一数学 第1页(共7页)
③无论 a 为何值,y 的值都不变; ④若 a 3,则 x 5 .
其中说法正确的有( )个 搭配方式 西瓜 哈密瓜 火龙果 总质量
A.1 B.2 C.3 D.4 搭配一 300g 200g 0g 500g
二、填空题:(本大题共 8 小题,每小题 2 分,共 16 分) 搭配二 200g 0g 250g 450g
11. -27 的立方根是______.
搭配三 0g 230g 200g 430g
12. 将命题“对顶角相等”用“如果……那么……”的形式可以改写为______.
13. 人教版七年级下册数学课本共有如下 6 章内容:《相交线与平行线》、《实数》、《平面直 (1)若三种水果共用了 2260g,则搭配三的数量为______;
角坐标系》、《二元一次方程组》、《不等式与不等式组》、《数据的收集、整理与描述》.若 (2)若使用的西瓜不超过 1000g,使用的火龙果不超过 800g,则搭配二的数量最多是
某期末试卷要求,每章至少有 4 个题,全卷总题数不超过 26 个题,设本期末试卷的全 ______.
卷总题数为 x 个题,则 x 的取值范围是______.
a
14. 已知 (a 3)2 + b 4 = 0,则 的值是______. 三、解答题:(19 题 20 分;20 题 5 分;21 题 7 分;22 题 5 分;23 题 7 分;
b
24 题 6 分;25 题 6 分;26 题 8 分;共 64 分)
15. 如图,AB∥CD,CE 交 AB 于 F,∠C=55°,∠AEC=15°,则∠A=______°.
1 x 2 x + y = 1,
16. 若不等式组 有解,则 k 的取值范围是______. 19. (1)解方程 组:
x k 2x 3y = 8.
计算:
17. 如图,面积为 a(a>1)的正方形 ABCD 的边 AB 在数轴上,点 B 表示的数为 1.将正
方形 ABCD 沿着数轴水平移动,移动后的正方形记为 A'B'C 'D',点 A、B、C、D 的对 (2) 2 3( 2 ) + ( 3 2 ) + 1
应点分别为 A'、B'、C '、D',移动后的正方形 A'B'C 'D'与原正方形 ABCD 重叠部分
图形的面积记为 S.当 S= √ 时,数轴上点 B’表示的数是______(用含 a 的代数式表 2
(3)求下列式子中 x 的值: (x 1) = 9
示).
2x + 6 7x 4,
(4)解不等式组 4x + 2 x 1 并写出它的所有整数解.
.
5 2
20. 如图,CD,AE 相交于点 O,∠1=∠2,∠3=∠D. E
(1)求证:BE∥AD;
C 1 2 D
(2)若 AB∥CD,∠4=65°,求∠D 的度数. O 3
18. 餐厅用西瓜、哈密瓜、火龙果三种水果两两搭配做成水果拼盘,有以下三种搭配方式:
4
B A
初一数学 第2页(共7页)
21. 如图,△ABC 的三个顶点 A、B、C 均在正方形网格的格点上,每个小正 解:过点 M 作 MN∥EF,交 AB 于 N.
方形的边长都为 1.请在网格中画图并回答下列问题: ∵MN∥EF,
(1)过 C 点画直线 AB 的垂线,垂足为点 E; ∴∠EON=∠ONM(______),
(2)过 A 点画射线 AF∥BC,交直线 CE 于点 F; ∴∠EFM=∠NMG(______),
(3)点 C 到直线 AB 的距离为线段______的长度; 又∵AB∥CD,
(4)比较线段 CE 和线段 BC 长度的大小______,并说明理由______; ∴______(两直线平行,内错角相等),
(5)将三角形 ABC 沿着直线 CE 方向向上平移 2 个单位,再向右平移 1 ∴______=∠EON(等量代换),
个单位,请画出平移后的三角形 A B C ,并计算其面积______. 又∵EF⊥AB,
2 ∴∠EON=90°.
22. 已知 (a 1) + 2a b = 0,c 是 -8 的立方根.
∴∠DMG=______.(直接填度数).
(1)求 a,b,c 的值;
(2)请你根据爱民同学在乙图添加的辅助线写出求解过程.
(2) 理解无理数的表示方法:因为 7 是无理数,而无理数是无限不循环小数,所以
24. 对于实数a ,我们规定:用符号[ a]表示不大于 a 的最大整数,称[ a]为 a 的根整
7 的小数部分我们不可能全部写出来,而2 7 3,于是可用 7 2来表示
数,例如:[ 9] = 3,[ 10] = 3;还可以对a 连续求根整数,直到结果为 1 为止,例
7 的小数部分.在(1)的条件下请解答下列问题: 2a+3b c 的整数部分是
如:对 10 连续求根整数 2 次:[ 10] = 3,[ 3] =1,得到结果为 1.
______,小数部分是______.
23. 在学完了《相交线与平行线》后,课堂上李老师呈现了这样一个问题: (1)仿照以上方法计算:[ 26] = ______;
已知,如图,AB∥CD,AB⊥ (2)对 123 连续求根整数,______次之后结果为 1;
EF,垂足为点 O,FG 交 CD 于点 (3)只需进行 3 次连续求根整数运算后结果为 1 的所有正整数中,最大的正整数是多
M,若∠EFM=126°, 少?请通过计算说明.
试求:∠DMG 的度数.
25. 学校计划为“数学文化活动”购买奖品.已知购买 3 个 A 奖品和 2 个 B 奖品共需 130 元;
购买 5 个 A 奖品和 4 个 B 奖品共需 230 元.
(1)求 A、B 两种奖品的单价;
1
(2)学校准备购买 A、B 两种奖品共 40 个,且 A 奖品的数量不少于 B 奖品数量的 .购
3
买预算金不超过 920 元,请通过计算说明,学校有几种不同的购买方案.
爱华、爱民两位同学用不同的方法添加辅助线解决问题,如上图甲 、图乙所示:
(1)爱华同学利用图甲给出了不完整的解题过程,请你帮他将过程补充完整; 26. 综合与实践
初一数学 第3页(共7页)
【问题情境】 四、选做题:(本大题共 2 个小题,共 10 分)
在数学综合与实践课上,老师让同学们以“三角板与平行线”为主题开展数学活动.已知 27. 如果一元一次方程的解是一元一次不等式组的解,则称该一元一次方程为该不等式组的
直线 l1∥l2,在直角三角板 ABC 中,∠ABC=90°. 关联方程.
【操作发现】
1
x 1
(1) 如图 1 所示,将直角三角板 ABC 顶点 A 放在直线 l2上,设边 AC 与 l1 相交于点 (1)若不等式组 2 的一个关联方程的解是整数,则这个关联方程可以是
H,边 AB 与 l1相交于点 D.当∠ADH=90°时,发现 BC∥l .请说明理由.
1+ x 3x + 22
【深入探究】 ______;(写出一个即可)
(2) 如图 2 所示,将图 1 中三角板 ABC 的直角顶点 B 放在平行线 l1和 l2 之间,两直
1 x 2x m
角边 AB,CB 分别与 l ,l 相交于点 P 和 Q,得到∠1 和∠2,试探究∠1 和∠2 (2)若方程3 x = 2x,3+ x = 2 x + 都是关于 x 的不等式组 的关联1 2
2 x 2 m
的数量关系并说明理由.
方程,直接写出m 的取值范围.
【拓展运用】
28. 学行线的性质与判定之后,我们继续探究折纸中的平行线.
(3) 同学们继续探究以下问题,在(2)的情况下,分别作∠1 和∠2 对顶角的角平
分线,它们相交于点 O,如图 3 所示,请直接写出∠POQ 的度数. (1) 如图 1,长方形纸条 ABCD 中,AB∥CD,AD∥BC,∠A=∠B=∠C=∠D=90°,
(4) 若在∠ABC 内部作射线 BE,过点 B 作射线 BF⊥BE 交直线 l2 于点 M,得到 将纸条沿直线 EF 折叠,点 A 落在 A′处,点 D 落在 D′处,A′E 交 CD 于点
∠FMQ,请在图 4 中补充完整相应图形,并直接写出∠1,∠FMQ 与∠EBC 的数
G.
量关系.
①若∠AEF=40°,求∠A′GC 的度数.
②若∠AEF=α,则∠A′GC= (用含 α 的式子表示).
(2) 如图 2,在图 1 的基础上将∠CGE 对折,点 C 落在直线 GE 上的 C’处.点 B 落在
B’处,得到折痕 GH,则折痕 EF 与 GH 有怎样的位置关系?说明理由.
(3) 如图 3,在图 2 的基础上,过点 C’ 作 AB 的平行线 MN,直接写出∠A’GC 和
∠B’C’N 的数量关系.
图 4
初一数学 第4页(共7页)
(3)解: ( 2x 1) = 9
北京一六一中学2024—2025学年度第二学期期中考试
x 1= 3..........................2分
初一数学参考答案及评分标准 x 1= 3时,x = 4.............3分
x 1= 3时,x = 2.........4分
2025年 4月 (4)解:解不等式 2x+6>7x﹣4,得:x<2. .............................................1 分
一、选择题(本大题共 10 小题,每小题 2 分,共 20 分) 4x + 2 x 1解不等式 ,得:x ≥﹣3 ...........................................3 分
1 2 3 4 5 6 7 8 9 10 5 2
C C B D B A A D D D 则不等式组的解集为﹣3 ≤ x<2 .............................................4 分
所以不等式组的整数解为-3、-2、-1、0、1 ...............................................6 分
二、填空题:(本大题共 8 小题,每小题 2 分,共 16 分)
11 12 13 14 15 16 17 18
20.(1)证明:∵∠1=∠2,∠3=∠D,∠2=∠3,
-3 如果两个角 24 x 26 3 40° k 2 2;3
a 或
是对顶角, 2 ∴∠1=∠D, .............................................1 分
那么这两个
2 a ∴BE∥AD; .............................................2 分
角相等.
(2)解:∵AB∥CD,∠4=65°,
E
∴∠3=∠4=65°, .............................................3 分
三、解答题:(19 题 20 分;20 题 5 分;21 题 7 分;22 题 5 分;23 题 7 分;
∵∠3=∠D, C 1 2 D
O 3
24 题 6 分;25 题 6 分;26 题 8 分;共 64 分) ∴∠D=65°..............................................5 分
4
19. (1)解: 2 x + 2 y = 2 .. .. .. .. ① B A
2x 3y = 8...........②
① ② : 5y = 10
图 3 分
y = -2...................................3分
代入x + y = -1 中得: 21. (3)点 C 到直线 AB 的距离为线段 CE 的长度........4 分
x =1.....................................4分
x =1 (4)CB > CE,垂线段最短......................................6 分
原方程组的解是:
y = 2..............5分
(5)三角形面积是 3............................................... ..7 分.
2 3
(2)解: (- 2 ) + (- 3 2 ) + 1 22.(1)a=1,b=2,c=﹣2;...................................................................................3 分
= 2 2 + 1..................3分
初一数学 第5页(共7页)
= 1............................5分
(2)3,√10 3.......................................................................................................5 分
(3)255 .................................................................6 分
23 . (1) 解:过点 M 作 MN∥EF,交 AB 于 N.
∵MN∥EF,
25. 解:(1)设 A 种奖品的单价为 x 元,B 种奖品的单价为 y 元,
∴∠EON=∠ONM( 两直线平行,内错角相等 ),...................1 分
3x + 2 y = 130
∴∠EFM=∠NMG( 两直线平行,同位角相等 ),...................2 分 依题意,得: ,
5x + 4 y = 230
又∵AB∥CD,
x = 30
∴ ∠ONM=∠DMN (两直线平行,内错角相等),...................3 分 解得: .
y = 20
∴ ∠DMN =∠EON(等量代换),................................................4 分
答:A 种奖品的单价为 30 元,B 种奖品的单价为 20 元.....................3 分
又∵EF⊥AB,
(2)设购买 A 种奖品 m 个,则购买 B 种奖品(40﹣m)个,
∴∠EON=90°.
1
m (40 m)
∴∠DMG= 36° (直接填度数)................................................5 分 依题意,得: 3 ,
(2)证明:过点 F 作 HN∥AB, 30m + 20(40 m) 920
∵AB⊥EF, 解得:10 m 12∵m 为整数,
∴∠1=90°, ∴m=10,11,12,
∵AB∥HN, ∴40﹣m=30,29,28.
∴∠1=∠EFN=90°, ∴学校有三种购买方案,方案一:购买 A 种奖品 10 个,B 种奖品 30 个;方案二:
∵∠EFM=126°, 购买 A 种奖品 11 个,B 种奖品 29 个;方案三:购买 A 种奖品 12 个,B 种奖品
∴∠2=∠EFM﹣∠EFN=36°, 28 个.............................................................................................................6 分
∵AB∥CD,
∴HN∥CD,
∴∠2=∠3=36°, 26. (1)证明:∵∠ADH=90°,∠B=90°,
∴∠DMG 的度数为 36°. .............................................................7 分 ∴∠B=∠ADH,
∴BC∥l1
24. (1)5 .............................................................1 分
∵l1∥l2,
(2)3 ...............................................................3 分
∴BC∥l2.。。。。。。。。。。。。。。。。。。。。。。。。。。。。。。。。。。。。。。。。。。。。。。。。。。。。。。。。。。。。。。。。。。。。。。。。。。。。。。。。。。。。。。。。。。。。2 分
初一数学 第6页(共7页)
(2)∠1+∠2=90°(证明略 4 分)
(3)∠POQ=45°.............................................................................................................6 分
(4) 1 + F M Q + E B C = 1 8 0
FMQ = 1+ EBC
............................................................................8 分
四、选做题:(共 10 分)
27. (1)整数解是 1,所以可以设方程为:2x - 2 = 0.......................................................1 分
(2)0 m 1 ..............................................................................................................3 分
28. 解:(1)①由题意得:∠A′EF=∠AEF=40°,
∴∠AEG=∠A′EF+∠AEF=40°+40°=80°,
∵AB∥CD,
∴∠CGE=∠AEG=80°,
∴∠A′GC=180°﹣∠CGE=180°﹣80°=100°;........2 分
②∠A′GC=180°﹣2α...................................................................................................3 分
(2)EF∥GH,理由如下:
1 1
由题意得:∠ = ∠ ′ = ∠ ,∠ = ∠ ′ = ∠ ,
2 2
∵AB∥CD,
∴∠CGE=∠AEG,
∴∠C′GH=∠A′EF,
∴EF∥GH...................................................................................5 分
(3)∠A′GC﹣∠B′C′N=90°.............................................7 分
初一数学 第7页(共7页)
6. 如图,天平右盘中的每个砝码的质量都是 1g,则物体 A
初 一 数 学 试 卷
的质量 m(g)的取值范围,在数轴上可表示为
2025年4月
班级______________姓名______________学号______________
A. B.
1.本试卷共 4 页,两部分,四道大题,28 道小题。其中第一大题至第三大题
考 为必做题,满分 100 分。第四大题为选做题,满分 10 分,计入总分,但卷面
生 总分不超过 100 分。考试时间 分钟。 C. D. 100
须 2.试卷答案一律填涂或书写在答题卡上,在试卷上作答无效。
知 3.答题卡上选择题用 2B 铅笔作答,其他题用黑色字迹钢笔或签字笔作答。 7. 已知 a∥b,一个三角板的两直角边与直线 a、b 相交,如果∠1=60°,
4.考试结束后,将答题卡交回。
那么∠2 等于
一、选择题(本大题共 10 小题,每小题 2 分,共 20 分)
A.30° B.40° C.50° D.60°
1. 下列给出的图形中,∠1 与∠2 是对顶角的是
8. 下列命题中的真命题是
A. B.
A. 两点之间直线最短
B. 不相交的两条直线,叫做平行线
C. 过一点有且只有一条直线平行于已知直线
C. D.
D. 若两条直线被第三条直线所截得的内错角相等,则同位角也相等
2. 16 的平方根是
9. 《九章算术》是中国古代的一本重要数学著作,其中有一道方程的应用题:“五只雀、六
A.2 B. 2 C. 4 D.4
只燕,共重 16 两,雀重燕轻.互换其中一只,恰好一样重.问每只雀、燕的重量各为
3. 已知a b,则下列四个不等式中,不.正.确.的是 多少?”解:设雀每只 x 两,燕每只 y 两,则可列出方程组为
A.a 2 b 2 B. 2a 2b C.2a 2b D.a+ 2 b+ 2 5x + 6y =16 6x + 5y =16
A. B.
5x + y = 6y + x 5x + y = 4y + x
4. 如右图所示,点 E 在 AC 的延长线上,下列条件中能.判.断.AB∥CD的是
6x + 5y =16 5x + 6y =16
A. 3= 4 B. D+ ACD =180 C. D.
6x + y = 5y + x 4x + y = 5y + x
C. D = DCE D. 1= 2
x + y = 4 a
10. 已知关于 x、y 的方程组 ,给出下列说法:
1 x y = a
5. 下列各数中,3.14159,- 3 8 ,0.131131113…,-π, 25, ,无理数的个数为
7
①当 a = 0 时,x、y 的值都相等; ②当 a = 4 时,x、y 的值互为相反数;
初一数学 第1页(共7页)
③无论 a 为何值,y 的值都不变; ④若 a 3,则 x 5 .
其中说法正确的有( )个 搭配方式 西瓜 哈密瓜 火龙果 总质量
A.1 B.2 C.3 D.4 搭配一 300g 200g 0g 500g
二、填空题:(本大题共 8 小题,每小题 2 分,共 16 分) 搭配二 200g 0g 250g 450g
11. -27 的立方根是______.
搭配三 0g 230g 200g 430g
12. 将命题“对顶角相等”用“如果……那么……”的形式可以改写为______.
13. 人教版七年级下册数学课本共有如下 6 章内容:《相交线与平行线》、《实数》、《平面直 (1)若三种水果共用了 2260g,则搭配三的数量为______;
角坐标系》、《二元一次方程组》、《不等式与不等式组》、《数据的收集、整理与描述》.若 (2)若使用的西瓜不超过 1000g,使用的火龙果不超过 800g,则搭配二的数量最多是
某期末试卷要求,每章至少有 4 个题,全卷总题数不超过 26 个题,设本期末试卷的全 ______.
卷总题数为 x 个题,则 x 的取值范围是______.
a
14. 已知 (a 3)2 + b 4 = 0,则 的值是______. 三、解答题:(19 题 20 分;20 题 5 分;21 题 7 分;22 题 5 分;23 题 7 分;
b
24 题 6 分;25 题 6 分;26 题 8 分;共 64 分)
15. 如图,AB∥CD,CE 交 AB 于 F,∠C=55°,∠AEC=15°,则∠A=______°.
1 x 2 x + y = 1,
16. 若不等式组 有解,则 k 的取值范围是______. 19. (1)解方程 组:
x k 2x 3y = 8.
计算:
17. 如图,面积为 a(a>1)的正方形 ABCD 的边 AB 在数轴上,点 B 表示的数为 1.将正
方形 ABCD 沿着数轴水平移动,移动后的正方形记为 A'B'C 'D',点 A、B、C、D 的对 (2) 2 3( 2 ) + ( 3 2 ) + 1
应点分别为 A'、B'、C '、D',移动后的正方形 A'B'C 'D'与原正方形 ABCD 重叠部分
图形的面积记为 S.当 S= √ 时,数轴上点 B’表示的数是______(用含 a 的代数式表 2
(3)求下列式子中 x 的值: (x 1) = 9
示).
2x + 6 7x 4,
(4)解不等式组 4x + 2 x 1 并写出它的所有整数解.
.
5 2
20. 如图,CD,AE 相交于点 O,∠1=∠2,∠3=∠D. E
(1)求证:BE∥AD;
C 1 2 D
(2)若 AB∥CD,∠4=65°,求∠D 的度数. O 3
18. 餐厅用西瓜、哈密瓜、火龙果三种水果两两搭配做成水果拼盘,有以下三种搭配方式:
4
B A
初一数学 第2页(共7页)
21. 如图,△ABC 的三个顶点 A、B、C 均在正方形网格的格点上,每个小正 解:过点 M 作 MN∥EF,交 AB 于 N.
方形的边长都为 1.请在网格中画图并回答下列问题: ∵MN∥EF,
(1)过 C 点画直线 AB 的垂线,垂足为点 E; ∴∠EON=∠ONM(______),
(2)过 A 点画射线 AF∥BC,交直线 CE 于点 F; ∴∠EFM=∠NMG(______),
(3)点 C 到直线 AB 的距离为线段______的长度; 又∵AB∥CD,
(4)比较线段 CE 和线段 BC 长度的大小______,并说明理由______; ∴______(两直线平行,内错角相等),
(5)将三角形 ABC 沿着直线 CE 方向向上平移 2 个单位,再向右平移 1 ∴______=∠EON(等量代换),
个单位,请画出平移后的三角形 A B C ,并计算其面积______. 又∵EF⊥AB,
2 ∴∠EON=90°.
22. 已知 (a 1) + 2a b = 0,c 是 -8 的立方根.
∴∠DMG=______.(直接填度数).
(1)求 a,b,c 的值;
(2)请你根据爱民同学在乙图添加的辅助线写出求解过程.
(2) 理解无理数的表示方法:因为 7 是无理数,而无理数是无限不循环小数,所以
24. 对于实数a ,我们规定:用符号[ a]表示不大于 a 的最大整数,称[ a]为 a 的根整
7 的小数部分我们不可能全部写出来,而2 7 3,于是可用 7 2来表示
数,例如:[ 9] = 3,[ 10] = 3;还可以对a 连续求根整数,直到结果为 1 为止,例
7 的小数部分.在(1)的条件下请解答下列问题: 2a+3b c 的整数部分是
如:对 10 连续求根整数 2 次:[ 10] = 3,[ 3] =1,得到结果为 1.
______,小数部分是______.
23. 在学完了《相交线与平行线》后,课堂上李老师呈现了这样一个问题: (1)仿照以上方法计算:[ 26] = ______;
已知,如图,AB∥CD,AB⊥ (2)对 123 连续求根整数,______次之后结果为 1;
EF,垂足为点 O,FG 交 CD 于点 (3)只需进行 3 次连续求根整数运算后结果为 1 的所有正整数中,最大的正整数是多
M,若∠EFM=126°, 少?请通过计算说明.
试求:∠DMG 的度数.
25. 学校计划为“数学文化活动”购买奖品.已知购买 3 个 A 奖品和 2 个 B 奖品共需 130 元;
购买 5 个 A 奖品和 4 个 B 奖品共需 230 元.
(1)求 A、B 两种奖品的单价;
1
(2)学校准备购买 A、B 两种奖品共 40 个,且 A 奖品的数量不少于 B 奖品数量的 .购
3
买预算金不超过 920 元,请通过计算说明,学校有几种不同的购买方案.
爱华、爱民两位同学用不同的方法添加辅助线解决问题,如上图甲 、图乙所示:
(1)爱华同学利用图甲给出了不完整的解题过程,请你帮他将过程补充完整; 26. 综合与实践
初一数学 第3页(共7页)
【问题情境】 四、选做题:(本大题共 2 个小题,共 10 分)
在数学综合与实践课上,老师让同学们以“三角板与平行线”为主题开展数学活动.已知 27. 如果一元一次方程的解是一元一次不等式组的解,则称该一元一次方程为该不等式组的
直线 l1∥l2,在直角三角板 ABC 中,∠ABC=90°. 关联方程.
【操作发现】
1
x 1
(1) 如图 1 所示,将直角三角板 ABC 顶点 A 放在直线 l2上,设边 AC 与 l1 相交于点 (1)若不等式组 2 的一个关联方程的解是整数,则这个关联方程可以是
H,边 AB 与 l1相交于点 D.当∠ADH=90°时,发现 BC∥l .请说明理由.
1+ x 3x + 22
【深入探究】 ______;(写出一个即可)
(2) 如图 2 所示,将图 1 中三角板 ABC 的直角顶点 B 放在平行线 l1和 l2 之间,两直
1 x 2x m
角边 AB,CB 分别与 l ,l 相交于点 P 和 Q,得到∠1 和∠2,试探究∠1 和∠2 (2)若方程3 x = 2x,3+ x = 2 x + 都是关于 x 的不等式组 的关联1 2
2 x 2 m
的数量关系并说明理由.
方程,直接写出m 的取值范围.
【拓展运用】
28. 学行线的性质与判定之后,我们继续探究折纸中的平行线.
(3) 同学们继续探究以下问题,在(2)的情况下,分别作∠1 和∠2 对顶角的角平
分线,它们相交于点 O,如图 3 所示,请直接写出∠POQ 的度数. (1) 如图 1,长方形纸条 ABCD 中,AB∥CD,AD∥BC,∠A=∠B=∠C=∠D=90°,
(4) 若在∠ABC 内部作射线 BE,过点 B 作射线 BF⊥BE 交直线 l2 于点 M,得到 将纸条沿直线 EF 折叠,点 A 落在 A′处,点 D 落在 D′处,A′E 交 CD 于点
∠FMQ,请在图 4 中补充完整相应图形,并直接写出∠1,∠FMQ 与∠EBC 的数
G.
量关系.
①若∠AEF=40°,求∠A′GC 的度数.
②若∠AEF=α,则∠A′GC= (用含 α 的式子表示).
(2) 如图 2,在图 1 的基础上将∠CGE 对折,点 C 落在直线 GE 上的 C’处.点 B 落在
B’处,得到折痕 GH,则折痕 EF 与 GH 有怎样的位置关系?说明理由.
(3) 如图 3,在图 2 的基础上,过点 C’ 作 AB 的平行线 MN,直接写出∠A’GC 和
∠B’C’N 的数量关系.
图 4
初一数学 第4页(共7页)
(3)解: ( 2x 1) = 9
北京一六一中学2024—2025学年度第二学期期中考试
x 1= 3..........................2分
初一数学参考答案及评分标准 x 1= 3时,x = 4.............3分
x 1= 3时,x = 2.........4分
2025年 4月 (4)解:解不等式 2x+6>7x﹣4,得:x<2. .............................................1 分
一、选择题(本大题共 10 小题,每小题 2 分,共 20 分) 4x + 2 x 1解不等式 ,得:x ≥﹣3 ...........................................3 分
1 2 3 4 5 6 7 8 9 10 5 2
C C B D B A A D D D 则不等式组的解集为﹣3 ≤ x<2 .............................................4 分
所以不等式组的整数解为-3、-2、-1、0、1 ...............................................6 分
二、填空题:(本大题共 8 小题,每小题 2 分,共 16 分)
11 12 13 14 15 16 17 18
20.(1)证明:∵∠1=∠2,∠3=∠D,∠2=∠3,
-3 如果两个角 24 x 26 3 40° k 2 2;3
a 或
是对顶角, 2 ∴∠1=∠D, .............................................1 分
那么这两个
2 a ∴BE∥AD; .............................................2 分
角相等.
(2)解:∵AB∥CD,∠4=65°,
E
∴∠3=∠4=65°, .............................................3 分
三、解答题:(19 题 20 分;20 题 5 分;21 题 7 分;22 题 5 分;23 题 7 分;
∵∠3=∠D, C 1 2 D
O 3
24 题 6 分;25 题 6 分;26 题 8 分;共 64 分) ∴∠D=65°..............................................5 分
4
19. (1)解: 2 x + 2 y = 2 .. .. .. .. ① B A
2x 3y = 8...........②
① ② : 5y = 10
图 3 分
y = -2...................................3分
代入x + y = -1 中得: 21. (3)点 C 到直线 AB 的距离为线段 CE 的长度........4 分
x =1.....................................4分
x =1 (4)CB > CE,垂线段最短......................................6 分
原方程组的解是:
y = 2..............5分
(5)三角形面积是 3............................................... ..7 分.
2 3
(2)解: (- 2 ) + (- 3 2 ) + 1 22.(1)a=1,b=2,c=﹣2;...................................................................................3 分
= 2 2 + 1..................3分
初一数学 第5页(共7页)
= 1............................5分
(2)3,√10 3.......................................................................................................5 分
(3)255 .................................................................6 分
23 . (1) 解:过点 M 作 MN∥EF,交 AB 于 N.
∵MN∥EF,
25. 解:(1)设 A 种奖品的单价为 x 元,B 种奖品的单价为 y 元,
∴∠EON=∠ONM( 两直线平行,内错角相等 ),...................1 分
3x + 2 y = 130
∴∠EFM=∠NMG( 两直线平行,同位角相等 ),...................2 分 依题意,得: ,
5x + 4 y = 230
又∵AB∥CD,
x = 30
∴ ∠ONM=∠DMN (两直线平行,内错角相等),...................3 分 解得: .
y = 20
∴ ∠DMN =∠EON(等量代换),................................................4 分
答:A 种奖品的单价为 30 元,B 种奖品的单价为 20 元.....................3 分
又∵EF⊥AB,
(2)设购买 A 种奖品 m 个,则购买 B 种奖品(40﹣m)个,
∴∠EON=90°.
1
m (40 m)
∴∠DMG= 36° (直接填度数)................................................5 分 依题意,得: 3 ,
(2)证明:过点 F 作 HN∥AB, 30m + 20(40 m) 920
∵AB⊥EF, 解得:10 m 12∵m 为整数,
∴∠1=90°, ∴m=10,11,12,
∵AB∥HN, ∴40﹣m=30,29,28.
∴∠1=∠EFN=90°, ∴学校有三种购买方案,方案一:购买 A 种奖品 10 个,B 种奖品 30 个;方案二:
∵∠EFM=126°, 购买 A 种奖品 11 个,B 种奖品 29 个;方案三:购买 A 种奖品 12 个,B 种奖品
∴∠2=∠EFM﹣∠EFN=36°, 28 个.............................................................................................................6 分
∵AB∥CD,
∴HN∥CD,
∴∠2=∠3=36°, 26. (1)证明:∵∠ADH=90°,∠B=90°,
∴∠DMG 的度数为 36°. .............................................................7 分 ∴∠B=∠ADH,
∴BC∥l1
24. (1)5 .............................................................1 分
∵l1∥l2,
(2)3 ...............................................................3 分
∴BC∥l2.。。。。。。。。。。。。。。。。。。。。。。。。。。。。。。。。。。。。。。。。。。。。。。。。。。。。。。。。。。。。。。。。。。。。。。。。。。。。。。。。。。。。。。。。。。。。2 分
初一数学 第6页(共7页)
(2)∠1+∠2=90°(证明略 4 分)
(3)∠POQ=45°.............................................................................................................6 分
(4) 1 + F M Q + E B C = 1 8 0
FMQ = 1+ EBC
............................................................................8 分
四、选做题:(共 10 分)
27. (1)整数解是 1,所以可以设方程为:2x - 2 = 0.......................................................1 分
(2)0 m 1 ..............................................................................................................3 分
28. 解:(1)①由题意得:∠A′EF=∠AEF=40°,
∴∠AEG=∠A′EF+∠AEF=40°+40°=80°,
∵AB∥CD,
∴∠CGE=∠AEG=80°,
∴∠A′GC=180°﹣∠CGE=180°﹣80°=100°;........2 分
②∠A′GC=180°﹣2α...................................................................................................3 分
(2)EF∥GH,理由如下:
1 1
由题意得:∠ = ∠ ′ = ∠ ,∠ = ∠ ′ = ∠ ,
2 2
∵AB∥CD,
∴∠CGE=∠AEG,
∴∠C′GH=∠A′EF,
∴EF∥GH...................................................................................5 分
(3)∠A′GC﹣∠B′C′N=90°.............................................7 分
初一数学 第7页(共7页)
同课章节目录
