苏科版(2024)七年级下册11.2 一元一次不等式的概念 课件 (共21张PPT)
文档属性
| 名称 | 苏科版(2024)七年级下册11.2 一元一次不等式的概念 课件 (共21张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 813.3KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-05-07 17:24:10 | ||
图片预览








文档简介
(共21张PPT)
11.2 一元一次不等式的概念
讲课人:
第十一章 一元一次不等式
教学目标
1、感受一元一次不等式概念的行程过程
2、知道不等式的解、解集的意义,会在数轴上表示不等式的解集
3、会判断一个数是不是不等式的解
4、初步感受数形结合思想
重点
了解不等式的解和解集的意义,会在数轴上表示不等式的解集
难点
不等式的解和解集的关系
一、下列各式哪些是不等式:
① x+y;② 3x>7;③ 2x+3=5;
1-y ≤ 0;⑤ 2x-3y ≠1;⑥ -2<0;
⑦ 2a - 1>5;⑧ m≤n
用不等号表示不等关系的式子叫做不等式。
不等式中常见符号:> 、≥ 、<、 ≤、 ≠
一、下列各式哪些是不等式:
① x+y;② 3x>7;③ 2x+3=5;
1-y ≤ 0;⑤ 2x-3y ≠1;⑥ -2<0;
⑦ 2a - 1>5;⑧ m≤n
一、下列各式哪些是不等式:
① x+y;② 3x>7;③ 2x+3=5;
1-y ≤ 0;⑤ 2x-3y ≠1;⑥ -2<0;
⑦ 2a - 1>5;⑧ m≤n
温故知新
3x > 7
1-y ≤ 0;
2a - 1 > 5
观察这些不等式有哪些共同特点?
(1)只含有一个未知数;
(2)未知数的次数是1,系数不等于0;
像这样的方程,叫做一元一次方程
=
=
=
像这样的不等式,叫做一元一次不等式
探究新知
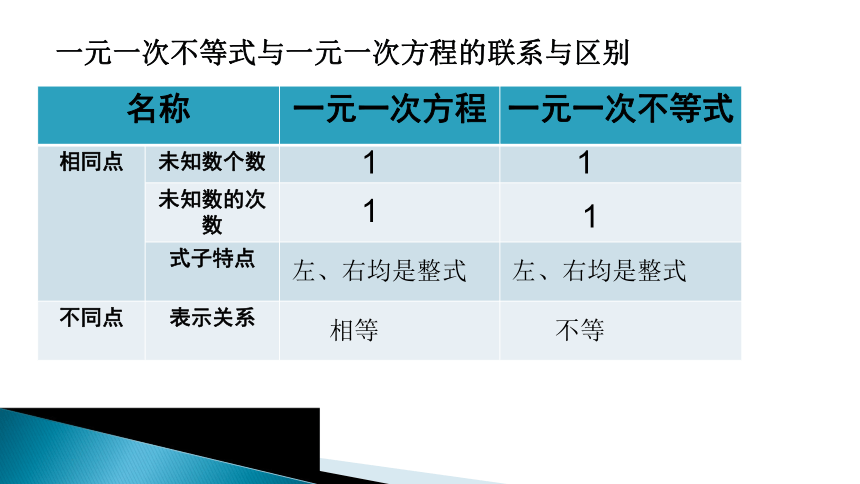
一元一次不等式与一元一次方程的联系与区别
名称 一元一次方程 一元一次不等式
相同点 未知数个数
未知数的次数
式子特点
不同点 表示关系
1
1
1
1
左、右均是整式
左、右均是整式
不等
相等
例1、下列不等式,哪些是一元一次不等式
(1) 2x-3>1
(2) 5x+2>6x-3
(3) x2+1(4) y≥0
(5) x+y<1
(7) 5+3x=240
一元一次不等式:
①是不等式;②含有一个未知数;
③未知数的的次数为1;④分母中不能含有字母;
若3x2m-1-2>1是关于x的一元一次不等式,则m=_____.
试一试
1
情境引入
我们把满足不等式的未知数的某个值称为不等式的一个解,所有的解组成的全体叫作这个不等式的解集。求不等式解集的过程叫作解不等式。
一般地,不等式的解集是某个范围,这个范围(即解集)可用一个简单的不等式 x > c 或 x < c (c为常数)的形式.
例2、判断下列说法是否正确。
(1)x=5是不等式 x+2>6的解;
解:把x=5代入不等式的左边,这时x+2=7,而7>6,即x+2>6成立,所以x=5是不等式x+2>6的解,故(1)正确。
(2)y=3不是不等式y-1>2的解;
(3)所有小于1的整数都是不等式x+1<2的解。
例3、下面五种说法:
(1)x=5是不等式x+1<2的解;
(2)不等式x+1<2的解有无数个;
(3)不等式x+1<2的解是x=1;
(4)不等式x+1<2的解集是x<1;
(5)x<0中的任何一个数都能使不等式x+1<2成立,所以x<0也是它的解集。
其中正确的有_________(填序号)。
(1)不等式的解是指在某一范围内的数,用它代替不等式中的未知数,不等式成立。
(2)不等式的解集是一个范围,在这个范围内的每一个值都是不等式的一个解。
(3)不等式的解和不等式的解集是两个不同的概念:不等式的解是能使不等式成立的未知数的值,而不等式的解集是指满足这个不等式的所有未知数的值,不等式的每一个解都是该不等式的解集中的一个元素。
不等式的解与不等式的解集的区别与联系
能使不等式成立的未知数的值都是不等式的解,一个含有未知数的不等式的解一般有无数个;
一个含有未知数的不等式的所有的解组成的全体才是这个不等式的解集,一个含有未知数的不等式的一个解或部分解不是这个不等式的解集。
方法归纳:
例4、在数轴上表示下列不等式的解集:
(1) x < -2; (2) x ≤ -2; (3) x > -2; (4) x ≥ -2.
解:(1) x < -2可以表示为:
(2) x ≤ -2可以表示为:
(3) x > -2可以表示为:
(4) x ≥ -2可以表示为:
0
-2
0
0
0
-2
-2
-2
例5、写出下列数轴上所表示的关于x的不等式的解集:
1.已知 是关于 的一元一次不等式,则 的值为 .
2.写出不等式3x+2>8的3个解,并比较它们与方程3x+2=8的解的大小,并比较它们与方程
-2x+1=5的解的大小。
拓展训练
3、填空:
(1)写出不等式x<3的所有正整数解:____________.
(2)写出不等式x ≤ 2的所有非负整数解: ____________.
(3)写出不等式 x ≥ -4所有负整数解:____________.
(4)写出不等式 x>-3的最小整数解:____________.
本节课你的收获是什么?
小结
本节课你学到了什么
一元一次不等式的定义
一元一次不等式的解和解集
在数轴上表示一元一次不等式的解集
只含有一个未知数,并且未知数的次数是 1 的不等式叫作一元一次不等式.
把满足不等式的未知数的 某个值 称为不等式的一个解,所有的解组成的 全体 叫作这个不等式的解集.求不等式 解集 的过程叫作解不等式.
不等式的解集常常可以借助数轴直观地表示出来.可以概括如下:小于向 左 画,大于向 右 画;无等号画 空心 圆圈,有等号画 实心 圆圈.
本节课你的收获是什么?
THANK YOU
11.2 一元一次不等式的概念
讲课人:
第十一章 一元一次不等式
教学目标
1、感受一元一次不等式概念的行程过程
2、知道不等式的解、解集的意义,会在数轴上表示不等式的解集
3、会判断一个数是不是不等式的解
4、初步感受数形结合思想
重点
了解不等式的解和解集的意义,会在数轴上表示不等式的解集
难点
不等式的解和解集的关系
一、下列各式哪些是不等式:
① x+y;② 3x>7;③ 2x+3=5;
1-y ≤ 0;⑤ 2x-3y ≠1;⑥ -2<0;
⑦ 2a - 1>5;⑧ m≤n
用不等号表示不等关系的式子叫做不等式。
不等式中常见符号:> 、≥ 、<、 ≤、 ≠
一、下列各式哪些是不等式:
① x+y;② 3x>7;③ 2x+3=5;
1-y ≤ 0;⑤ 2x-3y ≠1;⑥ -2<0;
⑦ 2a - 1>5;⑧ m≤n
一、下列各式哪些是不等式:
① x+y;② 3x>7;③ 2x+3=5;
1-y ≤ 0;⑤ 2x-3y ≠1;⑥ -2<0;
⑦ 2a - 1>5;⑧ m≤n
温故知新
3x > 7
1-y ≤ 0;
2a - 1 > 5
观察这些不等式有哪些共同特点?
(1)只含有一个未知数;
(2)未知数的次数是1,系数不等于0;
像这样的方程,叫做一元一次方程
=
=
=
像这样的不等式,叫做一元一次不等式
探究新知
一元一次不等式与一元一次方程的联系与区别
名称 一元一次方程 一元一次不等式
相同点 未知数个数
未知数的次数
式子特点
不同点 表示关系
1
1
1
1
左、右均是整式
左、右均是整式
不等
相等
例1、下列不等式,哪些是一元一次不等式
(1) 2x-3>1
(2) 5x+2>6x-3
(3) x2+1
(5) x+y<1
(7) 5+3x=240
一元一次不等式:
①是不等式;②含有一个未知数;
③未知数的的次数为1;④分母中不能含有字母;
若3x2m-1-2>1是关于x的一元一次不等式,则m=_____.
试一试
1
情境引入
我们把满足不等式的未知数的某个值称为不等式的一个解,所有的解组成的全体叫作这个不等式的解集。求不等式解集的过程叫作解不等式。
一般地,不等式的解集是某个范围,这个范围(即解集)可用一个简单的不等式 x > c 或 x < c (c为常数)的形式.
例2、判断下列说法是否正确。
(1)x=5是不等式 x+2>6的解;
解:把x=5代入不等式的左边,这时x+2=7,而7>6,即x+2>6成立,所以x=5是不等式x+2>6的解,故(1)正确。
(2)y=3不是不等式y-1>2的解;
(3)所有小于1的整数都是不等式x+1<2的解。
例3、下面五种说法:
(1)x=5是不等式x+1<2的解;
(2)不等式x+1<2的解有无数个;
(3)不等式x+1<2的解是x=1;
(4)不等式x+1<2的解集是x<1;
(5)x<0中的任何一个数都能使不等式x+1<2成立,所以x<0也是它的解集。
其中正确的有_________(填序号)。
(1)不等式的解是指在某一范围内的数,用它代替不等式中的未知数,不等式成立。
(2)不等式的解集是一个范围,在这个范围内的每一个值都是不等式的一个解。
(3)不等式的解和不等式的解集是两个不同的概念:不等式的解是能使不等式成立的未知数的值,而不等式的解集是指满足这个不等式的所有未知数的值,不等式的每一个解都是该不等式的解集中的一个元素。
不等式的解与不等式的解集的区别与联系
能使不等式成立的未知数的值都是不等式的解,一个含有未知数的不等式的解一般有无数个;
一个含有未知数的不等式的所有的解组成的全体才是这个不等式的解集,一个含有未知数的不等式的一个解或部分解不是这个不等式的解集。
方法归纳:
例4、在数轴上表示下列不等式的解集:
(1) x < -2; (2) x ≤ -2; (3) x > -2; (4) x ≥ -2.
解:(1) x < -2可以表示为:
(2) x ≤ -2可以表示为:
(3) x > -2可以表示为:
(4) x ≥ -2可以表示为:
0
-2
0
0
0
-2
-2
-2
例5、写出下列数轴上所表示的关于x的不等式的解集:
1.已知 是关于 的一元一次不等式,则 的值为 .
2.写出不等式3x+2>8的3个解,并比较它们与方程3x+2=8的解的大小,并比较它们与方程
-2x+1=5的解的大小。
拓展训练
3、填空:
(1)写出不等式x<3的所有正整数解:____________.
(2)写出不等式x ≤ 2的所有非负整数解: ____________.
(3)写出不等式 x ≥ -4所有负整数解:____________.
(4)写出不等式 x>-3的最小整数解:____________.
本节课你的收获是什么?
小结
本节课你学到了什么
一元一次不等式的定义
一元一次不等式的解和解集
在数轴上表示一元一次不等式的解集
只含有一个未知数,并且未知数的次数是 1 的不等式叫作一元一次不等式.
把满足不等式的未知数的 某个值 称为不等式的一个解,所有的解组成的 全体 叫作这个不等式的解集.求不等式 解集 的过程叫作解不等式.
不等式的解集常常可以借助数轴直观地表示出来.可以概括如下:小于向 左 画,大于向 右 画;无等号画 空心 圆圈,有等号画 实心 圆圈.
本节课你的收获是什么?
THANK YOU
同课章节目录
- 第7章 平面图形的认识(二)
- 7.1 探索直线平行的条件
- 7.2 探索平行线的性质
- 7.3 图形的平移
- 7.4 认识三角形
- 7.5 多边形的内角和与外角和
- 第8章 幂的运算
- 8.1 同底数幂的乘法
- 8.2 幂的乘方与积的乘方
- 8.3 同底数幂的除法
- 第9章 整式乘法与因式分解
- 9.1 单项式乘单项式
- 9.2 单项式乘多项式
- 9.3 多项式乘多项式
- 9.4 乘法公式
- 9.5 多项式的因式分解
- 第10章 二元一次方程组
- 10.1 二元一次方程
- 10.2 二元一次方程组
- 10.3 解二元一次方程组
- 10.4 三元一次方程组
- 10.5 用二元一次方程解决问题
- 第11章 一元一次不等式
- 11.1 生活中的不等式
- 11.2 不等式的解集
- 11.3 不等式的性质
- 11.4 解一元一次不等式
- 11.5 用一元一次不等式解决问题
- 11.6 一元一次不等式组
- 第12章 证明
- 12.1 定义与命题
- 12.2 证明
- 12.3 互逆命题
