第 8 章 整式乘法单元知识整合练习(含答案)
文档属性
| 名称 | 第 8 章 整式乘法单元知识整合练习(含答案) |
|
|
| 格式 | docx | ||
| 文件大小 | 114.1KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 苏科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-05-08 05:39:02 | ||
图片预览


文档简介
第 8 章 整式乘法单元知识整合练习
一、选择题
1. (2024·苏州市相城区期末)已知(x-2)· 则m+n的值是( )
A. 5 B. - 5 C. - 3 D. 7
2.若n 是整数,则 的计算结果 ( )
A. 是0 B.总是奇数
C.总是偶数 D.可能是奇数也可能是偶数
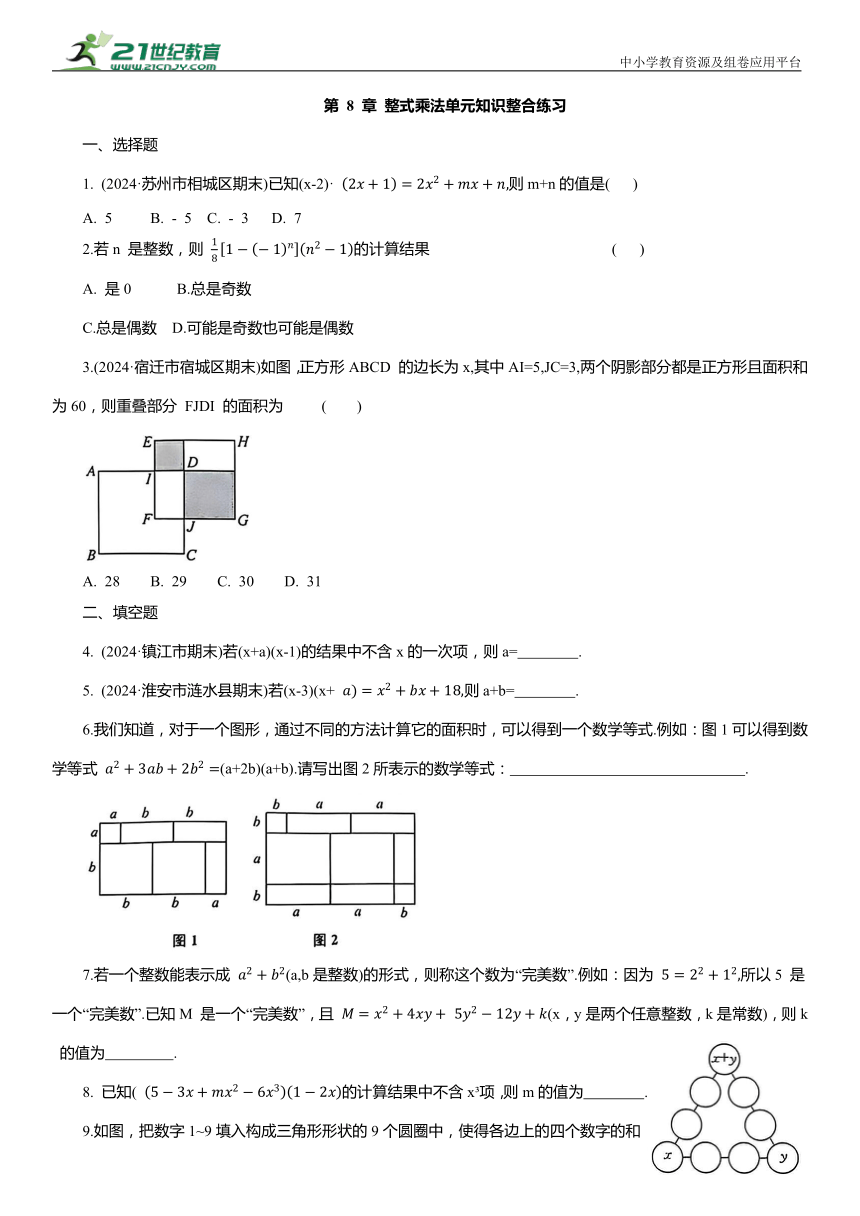
3.(2024·宿迁市宿城区期末)如图,正方形ABCD 的边长为x,其中AI=5,JC=3,两个阴影部分都是正方形且面积和为60,则重叠部分 FJDI 的面积为 ( )
A. 28 B. 29 C. 30 D. 31
二、填空题
4. (2024·镇江市期末)若(x+a)(x-1)的结果中不含x的一次项,则a= .
5. (2024·淮安市涟水县期末)若(x-3)(x+ 则a+b= .
6.我们知道,对于一个图形,通过不同的方法计算它的面积时,可以得到一个数学等式.例如:图1可以得到数学等式 (a+2b)(a+b).请写出图2所表示的数学等式: .
7.若一个整数能表示成 (a,b是整数)的形式,则称这个数为“完美数”.例如:因为 所以5 是一个“完美数”.已知M 是一个“完美数”,且 (x,y是两个任意整数,k是常数),则k 的值为 .
8. 已知( 的计算结果中不含x 项,则m的值为 .
9.如图,把数字1~9填入构成三角形形状的9个圆圈中,使得各边上的四个数字的和都等于 21,将每边四个数字的平方和分别记作 A,B,C,已知A+B+C=411.如果将位于这个三角形顶点处的三个圆圈填入的数字分别表示为x,y,x+y,那么 xy 的值为
三、解答题
10. 化简:
(2)x(3x-y)-(3x-2y) ;
(a+2b+3c)(a+2b-3c).
11.(2024·镇江市期末)“数缺形时少直观,形少数时难入微.”我们通过拼图观察、感受整式乘法,体现了“数形结合”的数学思想.下面,我们一起来探索其中的规律.
如图1,有若干张 A,B,C三种不同型号的纸片,其中 A 型纸片是边长为a 的正方形,B型纸片是长为a、宽为b(b图2
(1)用上述三种纸片拼出图2,通过两种方法计算图2的面积,可以得到一个等式: .
(2)现有 A,B,C三种型号的纸片共6张,用这6张纸片拼成一边长为a+b的长方形,每种纸片至少选一张,请画出两种符合条件的示意图.
(3)现有 A,B,C三种型号的纸片若干张,用这些纸片拼成一边长为a+b的长方形,每种纸片至少选一张.设需要 A 型纸片x张,B型纸片y张,C型纸片z张(x,y,z是正整数),写出x,y,z之间满足的等量关系,并请说明理由.
12.【阅读理解】若x 满足(30-x)(x---10)=100,求( 的值.
解:设30-x=a,x-10=b,则(30-x) ·(x--10)= ab=100,a+b=(30--x)+
【解决问题】
(1) 若x满足(2025-x)(x-2 020)=4,求 的值.
(2) 如图,在长方形ABCD 中,AB=20,BC=12,E,F 分别是BC,CD 上的点,且BE=DF=x.分别以 FC,CE为边在长方形ABCD 的外侧作正方形CFGH 和正方形CEMN.若长方形CEPF 的面积为128,求图中阴影部分的面积.
中小学教育资源及组卷应用平台
1. B 提示:( 所以m=-3,n=-2,所以m+n=-5.
2. C 提示:当n是奇数时 设 n = 2k - 1(k 为 整 数), 则 当 n 是偶数时, 因为0和k(k-1)(k为整数)都是偶数,所以选项C正确.
3. A 提示:由题意,得DI=x-5,DJ=x-3.因为 (x - 5) - (x - 3) = - 2, 所 以 即 又因为 所以60-2(x-5)(x-3)=4,所以(x-5)(x-3)=28,即重叠部分 FJDI的面积为28.
4. 1 提示:因为 1)x-a,所以a-1=0,解得a=1.
5. 一15 提示:由题意,得 所以a-3=b,-3a=18,解得a=-6,b=-9.所以a+b=-15.
7. 36 提示:因为 所以当k=36时,M 是“完美数”.
8. - 3 提示: 因为结果中不含x 项,所以-6-2m=0,解得m=-3.
9. 18 提示:数字1~9的和为1+2+3+4+5+6+7+8+9=45.因为各边上的四个数字的和都等于21,所以x+y+(x+y)=21×3-45=18,即x+y=9.又因为每边四个数字的平方和A,B,C满足A+B+C=411,且 所以. 所以. 即 所以( 所以 xy=18.
10. 解:(1) 原式
(2) 原式:
(3) 原式=[(2a---3b)(2a+3b)] =
(4) 原式=
11. 解:(1) (3a+b)(a+b)=3a +
(2)如图所示.
(3)x,y,z之间满足的等量关系是x+z=y.理由如下:
由(2)中图形,可得每1张 A 型或C型纸片,一定需要配合1张B型纸片,才能拼出满足条件的图形,因此x+z=y.
12. 解:(1)设2025--x=a,x--2020=b,则(2025--x)(x--2020)= ab=4,a+b=(2025-x)+(x--2020)=5,所以(2 025-
(2)根据题意,得1FC=20-x,EC=12-x.因为长方形 CEPF 的面积为128,所以(20--x)(12--x)=128,所以(20--x)(x-12)=--128.根据题意,可知阴影部分的面积为 设20--x=a,x-12=b,则(20-x)(x--12)= ab=--128,a+b=(20--x)+(x--12)=8,所以( (一128)=320.所以阴影部分的面积为320.
一、选择题
1. (2024·苏州市相城区期末)已知(x-2)· 则m+n的值是( )
A. 5 B. - 5 C. - 3 D. 7
2.若n 是整数,则 的计算结果 ( )
A. 是0 B.总是奇数
C.总是偶数 D.可能是奇数也可能是偶数
3.(2024·宿迁市宿城区期末)如图,正方形ABCD 的边长为x,其中AI=5,JC=3,两个阴影部分都是正方形且面积和为60,则重叠部分 FJDI 的面积为 ( )
A. 28 B. 29 C. 30 D. 31
二、填空题
4. (2024·镇江市期末)若(x+a)(x-1)的结果中不含x的一次项,则a= .
5. (2024·淮安市涟水县期末)若(x-3)(x+ 则a+b= .
6.我们知道,对于一个图形,通过不同的方法计算它的面积时,可以得到一个数学等式.例如:图1可以得到数学等式 (a+2b)(a+b).请写出图2所表示的数学等式: .
7.若一个整数能表示成 (a,b是整数)的形式,则称这个数为“完美数”.例如:因为 所以5 是一个“完美数”.已知M 是一个“完美数”,且 (x,y是两个任意整数,k是常数),则k 的值为 .
8. 已知( 的计算结果中不含x 项,则m的值为 .
9.如图,把数字1~9填入构成三角形形状的9个圆圈中,使得各边上的四个数字的和都等于 21,将每边四个数字的平方和分别记作 A,B,C,已知A+B+C=411.如果将位于这个三角形顶点处的三个圆圈填入的数字分别表示为x,y,x+y,那么 xy 的值为
三、解答题
10. 化简:
(2)x(3x-y)-(3x-2y) ;
(a+2b+3c)(a+2b-3c).
11.(2024·镇江市期末)“数缺形时少直观,形少数时难入微.”我们通过拼图观察、感受整式乘法,体现了“数形结合”的数学思想.下面,我们一起来探索其中的规律.
如图1,有若干张 A,B,C三种不同型号的纸片,其中 A 型纸片是边长为a 的正方形,B型纸片是长为a、宽为b(b
(1)用上述三种纸片拼出图2,通过两种方法计算图2的面积,可以得到一个等式: .
(2)现有 A,B,C三种型号的纸片共6张,用这6张纸片拼成一边长为a+b的长方形,每种纸片至少选一张,请画出两种符合条件的示意图.
(3)现有 A,B,C三种型号的纸片若干张,用这些纸片拼成一边长为a+b的长方形,每种纸片至少选一张.设需要 A 型纸片x张,B型纸片y张,C型纸片z张(x,y,z是正整数),写出x,y,z之间满足的等量关系,并请说明理由.
12.【阅读理解】若x 满足(30-x)(x---10)=100,求( 的值.
解:设30-x=a,x-10=b,则(30-x) ·(x--10)= ab=100,a+b=(30--x)+
【解决问题】
(1) 若x满足(2025-x)(x-2 020)=4,求 的值.
(2) 如图,在长方形ABCD 中,AB=20,BC=12,E,F 分别是BC,CD 上的点,且BE=DF=x.分别以 FC,CE为边在长方形ABCD 的外侧作正方形CFGH 和正方形CEMN.若长方形CEPF 的面积为128,求图中阴影部分的面积.
中小学教育资源及组卷应用平台
1. B 提示:( 所以m=-3,n=-2,所以m+n=-5.
2. C 提示:当n是奇数时 设 n = 2k - 1(k 为 整 数), 则 当 n 是偶数时, 因为0和k(k-1)(k为整数)都是偶数,所以选项C正确.
3. A 提示:由题意,得DI=x-5,DJ=x-3.因为 (x - 5) - (x - 3) = - 2, 所 以 即 又因为 所以60-2(x-5)(x-3)=4,所以(x-5)(x-3)=28,即重叠部分 FJDI的面积为28.
4. 1 提示:因为 1)x-a,所以a-1=0,解得a=1.
5. 一15 提示:由题意,得 所以a-3=b,-3a=18,解得a=-6,b=-9.所以a+b=-15.
7. 36 提示:因为 所以当k=36时,M 是“完美数”.
8. - 3 提示: 因为结果中不含x 项,所以-6-2m=0,解得m=-3.
9. 18 提示:数字1~9的和为1+2+3+4+5+6+7+8+9=45.因为各边上的四个数字的和都等于21,所以x+y+(x+y)=21×3-45=18,即x+y=9.又因为每边四个数字的平方和A,B,C满足A+B+C=411,且 所以. 所以. 即 所以( 所以 xy=18.
10. 解:(1) 原式
(2) 原式:
(3) 原式=[(2a---3b)(2a+3b)] =
(4) 原式=
11. 解:(1) (3a+b)(a+b)=3a +
(2)如图所示.
(3)x,y,z之间满足的等量关系是x+z=y.理由如下:
由(2)中图形,可得每1张 A 型或C型纸片,一定需要配合1张B型纸片,才能拼出满足条件的图形,因此x+z=y.
12. 解:(1)设2025--x=a,x--2020=b,则(2025--x)(x--2020)= ab=4,a+b=(2025-x)+(x--2020)=5,所以(2 025-
(2)根据题意,得1FC=20-x,EC=12-x.因为长方形 CEPF 的面积为128,所以(20--x)(12--x)=128,所以(20--x)(x-12)=--128.根据题意,可知阴影部分的面积为 设20--x=a,x-12=b,则(20-x)(x--12)= ab=--128,a+b=(20--x)+(x--12)=8,所以( (一128)=320.所以阴影部分的面积为320.
同课章节目录
- 第7章 平面图形的认识(二)
- 7.1 探索直线平行的条件
- 7.2 探索平行线的性质
- 7.3 图形的平移
- 7.4 认识三角形
- 7.5 多边形的内角和与外角和
- 第8章 幂的运算
- 8.1 同底数幂的乘法
- 8.2 幂的乘方与积的乘方
- 8.3 同底数幂的除法
- 第9章 整式乘法与因式分解
- 9.1 单项式乘单项式
- 9.2 单项式乘多项式
- 9.3 多项式乘多项式
- 9.4 乘法公式
- 9.5 多项式的因式分解
- 第10章 二元一次方程组
- 10.1 二元一次方程
- 10.2 二元一次方程组
- 10.3 解二元一次方程组
- 10.4 三元一次方程组
- 10.5 用二元一次方程解决问题
- 第11章 一元一次不等式
- 11.1 生活中的不等式
- 11.2 不等式的解集
- 11.3 不等式的性质
- 11.4 解一元一次不等式
- 11.5 用一元一次不等式解决问题
- 11.6 一元一次不等式组
- 第12章 证明
- 12.1 定义与命题
- 12.2 证明
- 12.3 互逆命题
