第 9 章 图形的变换巅峰训练7(含答案)
文档属性
| 名称 | 第 9 章 图形的变换巅峰训练7(含答案) |  | |
| 格式 | docx | ||
| 文件大小 | 246.0KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 苏科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-05-08 05:37:14 | ||
图片预览


文档简介
中小学教育资源及组卷应用平台
巅峰训练7 旋转
1.下列现象中:①地下水位逐年下降;②传送带的移动;③方向盘的转动;④钟摆的运动;⑤荡秋千运动.属于旋转的有 ( )
A. 2个 B. 3个 C. 4个 D. 5个
2.将一副三角板按如图1的位置摆放,其中含30°角的直角三角板的直角边与含45°角的直角三角板的斜边重合,含30°角的直角三角板直角顶点与含 45°角的直角三角板的锐角顶点O 重合.现将含 30°角的直角三角板绕点O 顺时针旋转至如图2 的位置,此时∠1=20°,则∠2的大小为 ( )
A. 30° B. 25° C. 20° D. 15°
3. 如图,△ABC 与△DEF 关于某点成中心对称,则其对称中心是 ( )
A. 点 P B. 点Q C. 点M D. 点 N
4.如图,如果正方形CDEF 旋转后能与正方形ABCD 重合,那么此图所在的平面上可以作为旋转中心的点共有 ( )
A. 1个 B. 2个 C. 3个 D. 4个
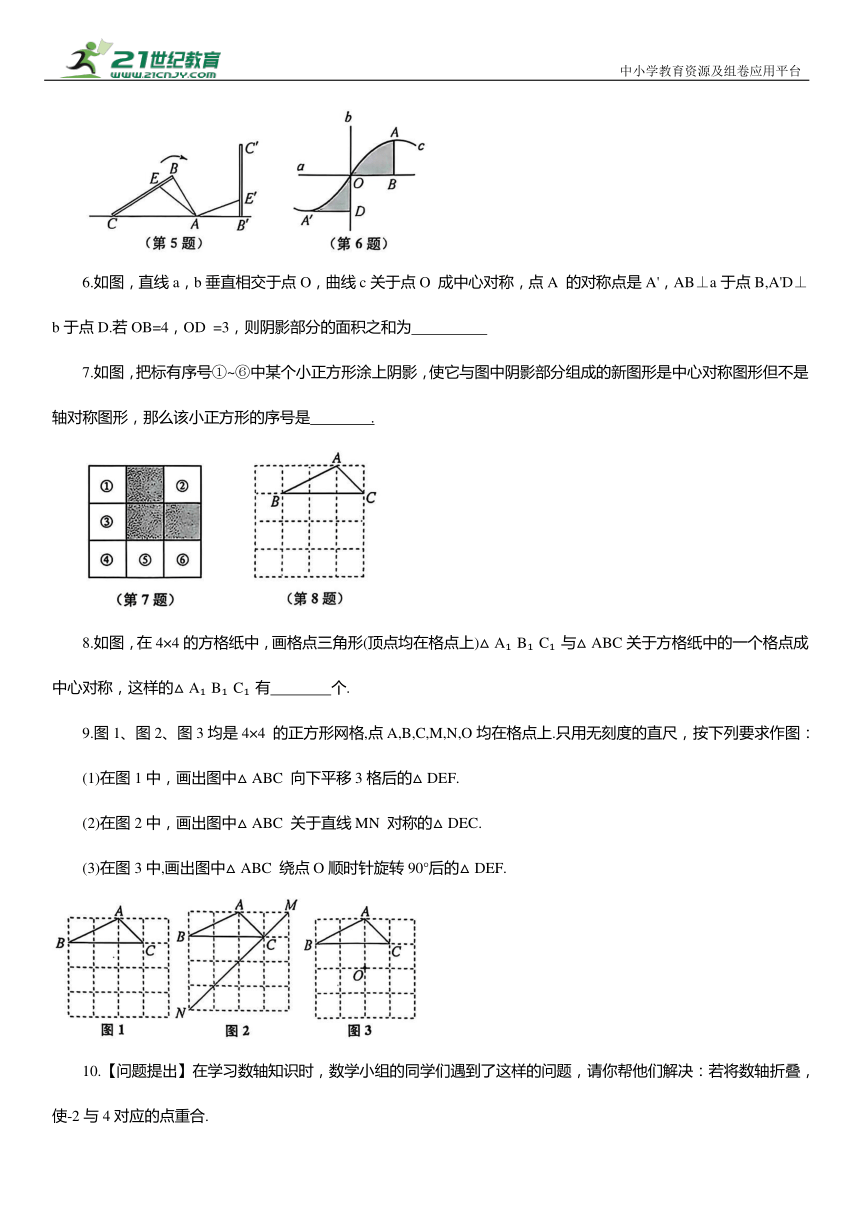
5.如图,教室内地面有个倾斜的畚箕,箕面AB 与水平地面的夹角∠CAB 为 62°,小明将它扶起(将畚箕绕点 A 顺时针旋转)后平放在地面,箕面AB 绕点A 旋转的度数为 .
6.如图,直线a,b垂直相交于点O,曲线c关于点O 成中心对称,点A 的对称点是A',AB⊥a于点B,A'D⊥b于点D.若OB=4,OD =3,则阴影部分的面积之和为
7.如图,把标有序号①~⑥中某个小正方形涂上阴影,使它与图中阴影部分组成的新图形是中心对称图形但不是轴对称图形,那么该小正方形的序号是 .
8.如图,在4×4的方格纸中,画格点三角形(顶点均在格点上)△A B C 与△ABC关于方格纸中的一个格点成中心对称,这样的△A B C 有 个.
9.图1、图2、图3均是4×4 的正方形网格,点A,B,C,M,N,O均在格点上.只用无刻度的直尺,按下列要求作图:
(1)在图1中,画出图中△ABC 向下平移3格后的△DEF.
(2)在图2中,画出图中△ABC 关于直线MN 对称的△DEC.
(3)在图3中,画出图中△ABC 绕点O顺时针旋转90°后的△DEF.
10.【问题提出】在学习数轴知识时,数学小组的同学们遇到了这样的问题,请你帮他们解决:若将数轴折叠,使-2与4对应的点重合.
(1)此时,-3对应的点与 对应的点重合.
(2)若数轴上 M,N两点之间的距离为2024,且M,N两点经过上述方法折叠后互相重合,求M,N两点表示的数.
【反思生疑】解决这个问题后,小寻同学提出了这样的问题:既然数轴可以折叠,那可不可以把数轴旋转一下呢 于是,同学们将数轴绕原点旋转180°,得到了如图所示的“新数轴”.
晓晓同学说:一般规定水平向右为数轴的正方向,但是如果规定水平向左为正方向,也可以帮助我们解决问题.我们就叫这个数轴为“新数轴”吧!我来考考大家:
(3) 在这个“新数轴”上,a= ,b= ,点A 与点 B 之间的距离为
(4)在这个“新数轴”上,若点 P 从点 A 出发,以每秒2个单位长度的速度向左移动,经过多少秒,点P 与点 A 的距离是点 P 与点 B 的距离的2 倍 此时,点P在“新数轴”上表示的数是多少
11.如图,有一副直角三角板如图1所示放置,其中∠D=45°,∠DPB=45°,∠C=30°,∠CPA=60°,PA,PB 与直线MN 重合,且三角板 PAC,三角板 PBD 均可以绕点P 逆时针旋转.
(1) 在图1中,∠DPC= .
(2)①如图2,若三角板 PBD 保持不动,三角板 PAC 绕点 P 逆时针旋转,转速为10(°)/s,转动一周三角板 PAC 就停止转动,在旋转的过程中,当旋转时间为多少时,PC∥DB
②如图3,在图1基础上,若三角板PAC 的边 PA 从 PN 处开始绕点P 逆时针旋转,转速为3(°)/s,同时三角板 PBD 的边 PB 从 PM 处开始绕点 P 逆时针旋转,转速为2(°)/s,当 PC 转到与原 PA 位置重合时,两三角板都停止转动,在旋转过程中,当∠CPD=∠BPM 时,旋转的时间是多少 1. B 提示:①②是平移现象,③④⑤是旋转现象.
2. B 提示:如图,易知 45°.因为∠2+∠1+∠3=90°,即 所以∠2=25°.
3. C 提示:如图,连接BE,CF,发现其交于点M,根据中心对称的性质,可知点 M 即为其对称中心.
4. C 提示:以点C 为旋转中心,把正方形CDEF 逆时针旋转90°,可得到正方形 BCDA;以点 D为旋转中心,把正方形 CDEF 顺时针旋转90°,可得到正方形 ADCB;以CD 的中点为旋转中心,把正方形CDEF 旋转180°,可得到正方形 DCBA.故此图所在的平面上可以作为旋转中心的点共有3个.
5. 118° 提示:因为 AB 与地面的夹角∠CAB为62°,所以, 118°,即旋转角为118°.
6. 12 提示:如图,过点A作AE⊥b于点E.因为直线a,b垂直相交于点O,曲线c关于点O成中心对称,点A 的对称点是A',AB⊥a于点B,A'D⊥b 于点D,OB=4,OD=3,所以AB=3,图形①与图形②面积相等,所以阴影部分的面积之和=长方形 ABOE 的面积=3×4=12.
7.①或⑥ 提示:把标有序号①或⑥的小正方形涂上阴影,可以与图中阴影部分组成的新图形是中心对称图形但不是轴对称图形;把标有序号②的小正方形涂上阴影,是中心对称图形也是轴对称图形;把标有序号③或④或⑤的小正方形涂上阴影,是轴对称图形.
8.2 提示:如图所示.
9. 解:(1)如图1,△DEF 即为所求.
如图2,△DEC 即为所求.
(3) 如图3,△DEF 即为所求.
10. 解:(1)5
(2)将数轴折叠,使-2与4对应的点重合,所以对折点表示的数为1.又因为数轴上M,N 两点之间的距离为2 024,且上述方法折叠后互相重合,所以点M,N到1对应的点的距离都为 1 012.若点 M 在点 N 的左侧,则点 M 为 1—1 012=—1 011,点 N 为 1+1012=1 013;若点 M 在点 N 的右侧,则点 M为1+1012=1 013,点 N 为1-1012=-1011.所以M,N 两点表示的数分别为--1 011,1 013 或1 013,-1011.
(3)-2 4 6
(4)①当点 P 在点A,B 之间时,因为点A,B之间的距离为6,点P 与点A 的距离是点P 与点 B 的距离的2倍,所以2t=2(6-2t),解得 t=2,此时点 P 表示的数为--2+2t=-2+4=2.
②当点 P 在点B 的左侧时,因为点 A,B之间的距离为6,点P 与点A 的距离是点P 与点B 的距离的2倍,所以PA=2PB=2AB=2×6=12,所以t=12÷2=6,此时点 P 表示的数为-2+2t=10.
综上所述,经过2 s或6s,点 P 与点A 的距离是点 P 与点 B 的距离的2倍,此时,点P在“新数轴”上表示的数是2 或10.
11. 解:(1)75°
(2) ①如图1,BD∥PC,所以∠CPN=∠DBP=90°,所以∠APN=30°,因为转速为10(°)/s,所以旋转时间为3 s;如图2,PC∥BD,所 以 ∠CPB = ∠DBP = 90°, 所以∠APM=30°,所以三角板 PAC 绕点 P 逆时针旋转的角度为 ,因为转速为10(°)/s,所以旋转时间为21 s.综上所述,当旋转时间为3s或21s时,PC∥DB.
②设旋转的时间为t s,由题可知0
巅峰训练7 旋转
1.下列现象中:①地下水位逐年下降;②传送带的移动;③方向盘的转动;④钟摆的运动;⑤荡秋千运动.属于旋转的有 ( )
A. 2个 B. 3个 C. 4个 D. 5个
2.将一副三角板按如图1的位置摆放,其中含30°角的直角三角板的直角边与含45°角的直角三角板的斜边重合,含30°角的直角三角板直角顶点与含 45°角的直角三角板的锐角顶点O 重合.现将含 30°角的直角三角板绕点O 顺时针旋转至如图2 的位置,此时∠1=20°,则∠2的大小为 ( )
A. 30° B. 25° C. 20° D. 15°
3. 如图,△ABC 与△DEF 关于某点成中心对称,则其对称中心是 ( )
A. 点 P B. 点Q C. 点M D. 点 N
4.如图,如果正方形CDEF 旋转后能与正方形ABCD 重合,那么此图所在的平面上可以作为旋转中心的点共有 ( )
A. 1个 B. 2个 C. 3个 D. 4个
5.如图,教室内地面有个倾斜的畚箕,箕面AB 与水平地面的夹角∠CAB 为 62°,小明将它扶起(将畚箕绕点 A 顺时针旋转)后平放在地面,箕面AB 绕点A 旋转的度数为 .
6.如图,直线a,b垂直相交于点O,曲线c关于点O 成中心对称,点A 的对称点是A',AB⊥a于点B,A'D⊥b于点D.若OB=4,OD =3,则阴影部分的面积之和为
7.如图,把标有序号①~⑥中某个小正方形涂上阴影,使它与图中阴影部分组成的新图形是中心对称图形但不是轴对称图形,那么该小正方形的序号是 .
8.如图,在4×4的方格纸中,画格点三角形(顶点均在格点上)△A B C 与△ABC关于方格纸中的一个格点成中心对称,这样的△A B C 有 个.
9.图1、图2、图3均是4×4 的正方形网格,点A,B,C,M,N,O均在格点上.只用无刻度的直尺,按下列要求作图:
(1)在图1中,画出图中△ABC 向下平移3格后的△DEF.
(2)在图2中,画出图中△ABC 关于直线MN 对称的△DEC.
(3)在图3中,画出图中△ABC 绕点O顺时针旋转90°后的△DEF.
10.【问题提出】在学习数轴知识时,数学小组的同学们遇到了这样的问题,请你帮他们解决:若将数轴折叠,使-2与4对应的点重合.
(1)此时,-3对应的点与 对应的点重合.
(2)若数轴上 M,N两点之间的距离为2024,且M,N两点经过上述方法折叠后互相重合,求M,N两点表示的数.
【反思生疑】解决这个问题后,小寻同学提出了这样的问题:既然数轴可以折叠,那可不可以把数轴旋转一下呢 于是,同学们将数轴绕原点旋转180°,得到了如图所示的“新数轴”.
晓晓同学说:一般规定水平向右为数轴的正方向,但是如果规定水平向左为正方向,也可以帮助我们解决问题.我们就叫这个数轴为“新数轴”吧!我来考考大家:
(3) 在这个“新数轴”上,a= ,b= ,点A 与点 B 之间的距离为
(4)在这个“新数轴”上,若点 P 从点 A 出发,以每秒2个单位长度的速度向左移动,经过多少秒,点P 与点 A 的距离是点 P 与点 B 的距离的2 倍 此时,点P在“新数轴”上表示的数是多少
11.如图,有一副直角三角板如图1所示放置,其中∠D=45°,∠DPB=45°,∠C=30°,∠CPA=60°,PA,PB 与直线MN 重合,且三角板 PAC,三角板 PBD 均可以绕点P 逆时针旋转.
(1) 在图1中,∠DPC= .
(2)①如图2,若三角板 PBD 保持不动,三角板 PAC 绕点 P 逆时针旋转,转速为10(°)/s,转动一周三角板 PAC 就停止转动,在旋转的过程中,当旋转时间为多少时,PC∥DB
②如图3,在图1基础上,若三角板PAC 的边 PA 从 PN 处开始绕点P 逆时针旋转,转速为3(°)/s,同时三角板 PBD 的边 PB 从 PM 处开始绕点 P 逆时针旋转,转速为2(°)/s,当 PC 转到与原 PA 位置重合时,两三角板都停止转动,在旋转过程中,当∠CPD=∠BPM 时,旋转的时间是多少 1. B 提示:①②是平移现象,③④⑤是旋转现象.
2. B 提示:如图,易知 45°.因为∠2+∠1+∠3=90°,即 所以∠2=25°.
3. C 提示:如图,连接BE,CF,发现其交于点M,根据中心对称的性质,可知点 M 即为其对称中心.
4. C 提示:以点C 为旋转中心,把正方形CDEF 逆时针旋转90°,可得到正方形 BCDA;以点 D为旋转中心,把正方形 CDEF 顺时针旋转90°,可得到正方形 ADCB;以CD 的中点为旋转中心,把正方形CDEF 旋转180°,可得到正方形 DCBA.故此图所在的平面上可以作为旋转中心的点共有3个.
5. 118° 提示:因为 AB 与地面的夹角∠CAB为62°,所以, 118°,即旋转角为118°.
6. 12 提示:如图,过点A作AE⊥b于点E.因为直线a,b垂直相交于点O,曲线c关于点O成中心对称,点A 的对称点是A',AB⊥a于点B,A'D⊥b 于点D,OB=4,OD=3,所以AB=3,图形①与图形②面积相等,所以阴影部分的面积之和=长方形 ABOE 的面积=3×4=12.
7.①或⑥ 提示:把标有序号①或⑥的小正方形涂上阴影,可以与图中阴影部分组成的新图形是中心对称图形但不是轴对称图形;把标有序号②的小正方形涂上阴影,是中心对称图形也是轴对称图形;把标有序号③或④或⑤的小正方形涂上阴影,是轴对称图形.
8.2 提示:如图所示.
9. 解:(1)如图1,△DEF 即为所求.
如图2,△DEC 即为所求.
(3) 如图3,△DEF 即为所求.
10. 解:(1)5
(2)将数轴折叠,使-2与4对应的点重合,所以对折点表示的数为1.又因为数轴上M,N 两点之间的距离为2 024,且上述方法折叠后互相重合,所以点M,N到1对应的点的距离都为 1 012.若点 M 在点 N 的左侧,则点 M 为 1—1 012=—1 011,点 N 为 1+1012=1 013;若点 M 在点 N 的右侧,则点 M为1+1012=1 013,点 N 为1-1012=-1011.所以M,N 两点表示的数分别为--1 011,1 013 或1 013,-1011.
(3)-2 4 6
(4)①当点 P 在点A,B 之间时,因为点A,B之间的距离为6,点P 与点A 的距离是点P 与点 B 的距离的2倍,所以2t=2(6-2t),解得 t=2,此时点 P 表示的数为--2+2t=-2+4=2.
②当点 P 在点B 的左侧时,因为点 A,B之间的距离为6,点P 与点A 的距离是点P 与点B 的距离的2倍,所以PA=2PB=2AB=2×6=12,所以t=12÷2=6,此时点 P 表示的数为-2+2t=10.
综上所述,经过2 s或6s,点 P 与点A 的距离是点 P 与点 B 的距离的2倍,此时,点P在“新数轴”上表示的数是2 或10.
11. 解:(1)75°
(2) ①如图1,BD∥PC,所以∠CPN=∠DBP=90°,所以∠APN=30°,因为转速为10(°)/s,所以旋转时间为3 s;如图2,PC∥BD,所 以 ∠CPB = ∠DBP = 90°, 所以∠APM=30°,所以三角板 PAC 绕点 P 逆时针旋转的角度为 ,因为转速为10(°)/s,所以旋转时间为21 s.综上所述,当旋转时间为3s或21s时,PC∥DB.
②设旋转的时间为t s,由题可知0
同课章节目录
- 第7章 平面图形的认识(二)
- 7.1 探索直线平行的条件
- 7.2 探索平行线的性质
- 7.3 图形的平移
- 7.4 认识三角形
- 7.5 多边形的内角和与外角和
- 第8章 幂的运算
- 8.1 同底数幂的乘法
- 8.2 幂的乘方与积的乘方
- 8.3 同底数幂的除法
- 第9章 整式乘法与因式分解
- 9.1 单项式乘单项式
- 9.2 单项式乘多项式
- 9.3 多项式乘多项式
- 9.4 乘法公式
- 9.5 多项式的因式分解
- 第10章 二元一次方程组
- 10.1 二元一次方程
- 10.2 二元一次方程组
- 10.3 解二元一次方程组
- 10.4 三元一次方程组
- 10.5 用二元一次方程解决问题
- 第11章 一元一次不等式
- 11.1 生活中的不等式
- 11.2 不等式的解集
- 11.3 不等式的性质
- 11.4 解一元一次不等式
- 11.5 用一元一次不等式解决问题
- 11.6 一元一次不等式组
- 第12章 证明
- 12.1 定义与命题
- 12.2 证明
- 12.3 互逆命题
