核心素养综合练(2) (含答案)2024-2025学年苏科版七年级数学下册
文档属性
| 名称 | 核心素养综合练(2) (含答案)2024-2025学年苏科版七年级数学下册 |

|
|
| 格式 | docx | ||
| 文件大小 | 238.8KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 苏科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-05-08 00:00:00 | ||
图片预览

文档简介
核心素养综合练(2)
1、 观察; x -1,….据此规律,当( 时,代数式. 的值为 ( )
A. 1 B. 0
C. 1 或 1 D. 0或-2
2. 若关于x 的方程5ax+3bx---9x-3a+16+17-0有无穷多个解,则a+b的值为( )
A. - 1 B. 0 C. 1 D. 5
3. 若43'-2021,47'=2021,则[(x-1)·(1-y)] 的值为 ( )
A. 1 B. 2021
C. -1 D. 2°021
4. 如果|x|+x+y=10,|y|+x-y=12,那么x+y的值是 ( )
A. - 2 B. 2 C. D.
5.定义:有两个相邻内角互余的四边形称为一邻余四边形”,这两个角的夹边称为“邻余线”.如图,在4×2的方格纸中,点A,B在格点上,如果点C,D在格点上,且AB是“邻余线”,那么该方格纸中符合条件的一邻余四边形”ABCD 的个数是 .
6.如图,按下面的程序进行运算.规定:程序运行到“判断结果是否大于28”为一轮循环.若运算进行了3轮才停止,则x 的取值范围是 .
7. 已知a,b 满足 7)<10,则a+2b·· .
8.利用两块相同的长方体木块测量一张桌子的高度.首先按图]方式放置,再交换两木块的位置,按图2方式放置,测量的数据如图,则桌子的高度是 cm.
已知:x ,x ,x ,…,x 006是整数,且满足下列条件: 求 的最小值和最大值.
10.学校捐资购买了一批物资 120 t打算支援山区,现有甲、乙、丙三种车型供选择,每辆车的运载能力和运费如下表(假设每辆车均满载)所示:
车型 甲 乙 丙
汽车运载量(t/辆) 5 8 10
汽车运费(元/辆) 400 500 600
(1)若全部物资都用甲、乙两种车型来运送,需运费 8 200 元,则分别需甲、乙两种车型各几辆
(2)为了节省运费,该学校打算用甲、乙、丙三种车型同时参与运送,已知它们的总辆数为14辆,请分别求出三种车型的辆数及所需的运费.
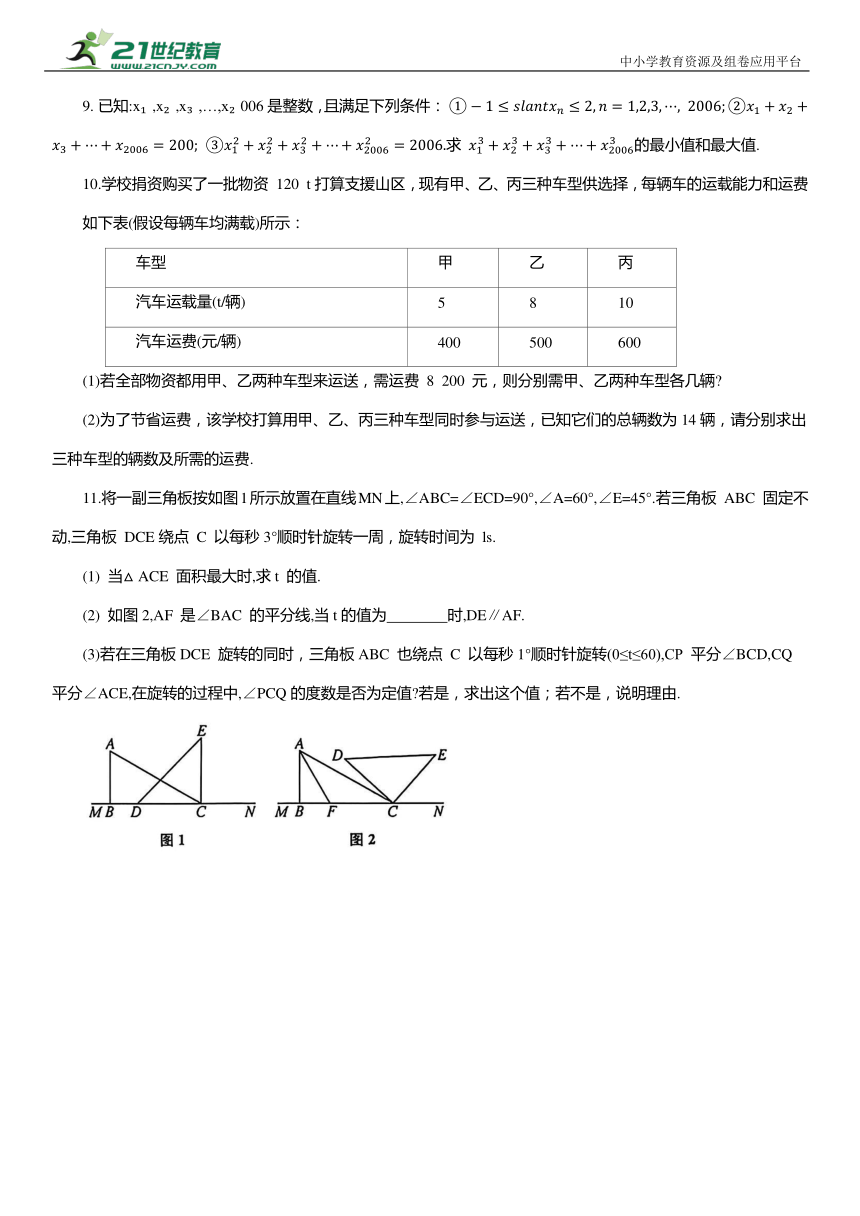
11.将一副三角板按如图1所示放置在直线MN上,∠ABC=∠ECD=90°,∠A=60°,∠E=45°.若三角板 ABC 固定不动,三角板 DCE绕点 C 以每秒3°顺时针旋转一周,旋转时间为 ls.
(1) 当△ACE 面积最大时,求t 的值.
(2) 如图2,AF 是∠BAC 的平分线,当t的值为 时,DE∥AF.
(3)若在三角板DCE 旋转的同时,三角板ABC 也绕点 C 以每秒1°顺时针旋转(0≤t≤60),CP 平分∠BCD,CQ 平分∠ACE,在旋转的过程中,∠PCQ的度数是否为定值 若是,求出这个值;若不是,说明理由.
中小学教育资源及组卷应用平台
核心素养综合练(2)
1. D 提示:因为( x+1)=0,所以. 所以 所以 所以 所以x=±1.当x=1时,原式: 1=0.当x=-1时,原式=
2. C 提示:该方程整理,得((5a+3b-9)x+(-3a+4b+17)=0.根据题意,得 解得 所以a+b=1.
3. C 提示:因为43°=2021°,47°=2021°,所 因为43×47=2021,所以xy=x+y,所以(x-1)(1-y)=x-xy-1+y=-1,所以
4. C 提示:①当x≥0,y≥0时, 解得 (舍去);②当.x≥0,y<0时, 解得 比时 ③:当x<0,y≥0时, 解得 (舍去);④当x<0,y<0时 解得 (舍去).
5.6 提示:如图,该方格纸中符合条件的“邻余四边形”ABCD的个数是6.
6. 27.0 提示:因为( 10,所以 所以 易知( 所以( 所以 所以a+2=0,b-1=0,所以a=-2,b=1,所以a+2b=0.
8.75 提示:设长方体木块的长和宽分别为a cm,b cm,桌子高为 h cm.根据题意,得 解得h=75.
9. 解:由①,知x ,x ,……,x 006的取值范围为-1,0,1,2四个.设值为--1有a个,0有b个,1有c个,2有d个.
根据题意,得 对
比①③,可知 b =3d,进一步可解得
根据题意,得
该式只比②的左侧大6d,所以-a+c+8d=6d+200.因为
所以 因为d 为整数,所以200≤6d+200≤2 402,即 的最小值为200,最大值为2 402.
10.解:(1)设需甲种车型x辆,乙种车型y辆,根据题意,得 解得
答:需甲种车型8辆,乙种车型10辆.
(2)设甲种车型有a辆,乙种车型有b辆,则丙种车型有(14-a-b)辆.根据题意,得5a+8b+10(14-a-b)=120.化简,得5a+2b=20,即 因为a,b,14-a--b均为正整数,所以b只能等于5,从而a=2,14-a--b=7,所以需运费为400×2+500×5+600×7=7500(元).
答:甲种车型2辆、乙种车型5辆、丙种车型7辆,需运费7500元.
解:(1)如图1,当△DCE 绕点C 顺时针旋转30°时,CE⊥AC,此时△ACE 的边AC上的高最大,最大值为 CE 的长,所以此时△ACE 面积最大.因为30÷3=10(s),所以当△ACE 面积最大时,t=10.
(2)35 或95 提示:如图2,因为在 Rt△ABC中,∠BAC=60°,∠ABC=90°,AF 平分∠BAC,所以∠BAF=30°,所以∠AFB=60°.当 DE∥AF 时,设 DE交直线MN 于点G,可知∠DGC=∠AFB=60°.又易得∠D=45°,所以∠DCG=180°-∠DGC-∠D=75°,所以∠DCM=180°-∠DCG=105°.所以3t=105,解得t=35.根据中心对称的性质,可知三角板 DCE 绕点C再旋转180°,此时DE 也平行于.AF, 综上所述,当t的值为35或95时,DE∥AF.
(3)∠PCQ 的度数为定值,∠PCQ=60°.理由如下:
如图3,由题意,可知旋转后∠BCM=t°, 因为CP 平分∠BCD,CQ 平分∠ACE,所以∠BCP=∠DCP=t°,∠ECQ= 所以∠PCM=∠BCM+∠BCP=2t°.因为 所以∠PCQ=∠MCE-∠PCM-∠ECQ=90°+
1、 观察; x -1,….据此规律,当( 时,代数式. 的值为 ( )
A. 1 B. 0
C. 1 或 1 D. 0或-2
2. 若关于x 的方程5ax+3bx---9x-3a+16+17-0有无穷多个解,则a+b的值为( )
A. - 1 B. 0 C. 1 D. 5
3. 若43'-2021,47'=2021,则[(x-1)·(1-y)] 的值为 ( )
A. 1 B. 2021
C. -1 D. 2°021
4. 如果|x|+x+y=10,|y|+x-y=12,那么x+y的值是 ( )
A. - 2 B. 2 C. D.
5.定义:有两个相邻内角互余的四边形称为一邻余四边形”,这两个角的夹边称为“邻余线”.如图,在4×2的方格纸中,点A,B在格点上,如果点C,D在格点上,且AB是“邻余线”,那么该方格纸中符合条件的一邻余四边形”ABCD 的个数是 .
6.如图,按下面的程序进行运算.规定:程序运行到“判断结果是否大于28”为一轮循环.若运算进行了3轮才停止,则x 的取值范围是 .
7. 已知a,b 满足 7)<10,则a+2b·· .
8.利用两块相同的长方体木块测量一张桌子的高度.首先按图]方式放置,再交换两木块的位置,按图2方式放置,测量的数据如图,则桌子的高度是 cm.
已知:x ,x ,x ,…,x 006是整数,且满足下列条件: 求 的最小值和最大值.
10.学校捐资购买了一批物资 120 t打算支援山区,现有甲、乙、丙三种车型供选择,每辆车的运载能力和运费如下表(假设每辆车均满载)所示:
车型 甲 乙 丙
汽车运载量(t/辆) 5 8 10
汽车运费(元/辆) 400 500 600
(1)若全部物资都用甲、乙两种车型来运送,需运费 8 200 元,则分别需甲、乙两种车型各几辆
(2)为了节省运费,该学校打算用甲、乙、丙三种车型同时参与运送,已知它们的总辆数为14辆,请分别求出三种车型的辆数及所需的运费.
11.将一副三角板按如图1所示放置在直线MN上,∠ABC=∠ECD=90°,∠A=60°,∠E=45°.若三角板 ABC 固定不动,三角板 DCE绕点 C 以每秒3°顺时针旋转一周,旋转时间为 ls.
(1) 当△ACE 面积最大时,求t 的值.
(2) 如图2,AF 是∠BAC 的平分线,当t的值为 时,DE∥AF.
(3)若在三角板DCE 旋转的同时,三角板ABC 也绕点 C 以每秒1°顺时针旋转(0≤t≤60),CP 平分∠BCD,CQ 平分∠ACE,在旋转的过程中,∠PCQ的度数是否为定值 若是,求出这个值;若不是,说明理由.
中小学教育资源及组卷应用平台
核心素养综合练(2)
1. D 提示:因为( x+1)=0,所以. 所以 所以 所以 所以x=±1.当x=1时,原式: 1=0.当x=-1时,原式=
2. C 提示:该方程整理,得((5a+3b-9)x+(-3a+4b+17)=0.根据题意,得 解得 所以a+b=1.
3. C 提示:因为43°=2021°,47°=2021°,所 因为43×47=2021,所以xy=x+y,所以(x-1)(1-y)=x-xy-1+y=-1,所以
4. C 提示:①当x≥0,y≥0时, 解得 (舍去);②当.x≥0,y<0时, 解得 比时 ③:当x<0,y≥0时, 解得 (舍去);④当x<0,y<0时 解得 (舍去).
5.6 提示:如图,该方格纸中符合条件的“邻余四边形”ABCD的个数是6.
6. 2
8.75 提示:设长方体木块的长和宽分别为a cm,b cm,桌子高为 h cm.根据题意,得 解得h=75.
9. 解:由①,知x ,x ,……,x 006的取值范围为-1,0,1,2四个.设值为--1有a个,0有b个,1有c个,2有d个.
根据题意,得 对
比①③,可知 b =3d,进一步可解得
根据题意,得
该式只比②的左侧大6d,所以-a+c+8d=6d+200.因为
所以 因为d 为整数,所以200≤6d+200≤2 402,即 的最小值为200,最大值为2 402.
10.解:(1)设需甲种车型x辆,乙种车型y辆,根据题意,得 解得
答:需甲种车型8辆,乙种车型10辆.
(2)设甲种车型有a辆,乙种车型有b辆,则丙种车型有(14-a-b)辆.根据题意,得5a+8b+10(14-a-b)=120.化简,得5a+2b=20,即 因为a,b,14-a--b均为正整数,所以b只能等于5,从而a=2,14-a--b=7,所以需运费为400×2+500×5+600×7=7500(元).
答:甲种车型2辆、乙种车型5辆、丙种车型7辆,需运费7500元.
解:(1)如图1,当△DCE 绕点C 顺时针旋转30°时,CE⊥AC,此时△ACE 的边AC上的高最大,最大值为 CE 的长,所以此时△ACE 面积最大.因为30÷3=10(s),所以当△ACE 面积最大时,t=10.
(2)35 或95 提示:如图2,因为在 Rt△ABC中,∠BAC=60°,∠ABC=90°,AF 平分∠BAC,所以∠BAF=30°,所以∠AFB=60°.当 DE∥AF 时,设 DE交直线MN 于点G,可知∠DGC=∠AFB=60°.又易得∠D=45°,所以∠DCG=180°-∠DGC-∠D=75°,所以∠DCM=180°-∠DCG=105°.所以3t=105,解得t=35.根据中心对称的性质,可知三角板 DCE 绕点C再旋转180°,此时DE 也平行于.AF, 综上所述,当t的值为35或95时,DE∥AF.
(3)∠PCQ 的度数为定值,∠PCQ=60°.理由如下:
如图3,由题意,可知旋转后∠BCM=t°, 因为CP 平分∠BCD,CQ 平分∠ACE,所以∠BCP=∠DCP=t°,∠ECQ= 所以∠PCM=∠BCM+∠BCP=2t°.因为 所以∠PCQ=∠MCE-∠PCM-∠ECQ=90°+
同课章节目录
