核心素养综合练(3) (含答案)2024-2025学年苏科版七年级数学下册
文档属性
| 名称 | 核心素养综合练(3) (含答案)2024-2025学年苏科版七年级数学下册 |  | |
| 格式 | docx | ||
| 文件大小 | 232.4KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 苏科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-05-08 05:44:13 | ||
图片预览

文档简介
中小学教育资源及组卷应用平台
核心素养综合练(3)
1. 用 min(a,b)表示a,b 两数中的较小者,用max(a,b)表示a,b两数中的较大者,例如min(3,5)=3, max(3,5)=5, min(3,3)=3, max(5,5)=5.若a,b,c,d 是互不相等的自然数, min(a,b)=p, min(c,d)=q,max(p,q)=x, max(a,b)=m, max(c,d)=n, min(m,n)=y,则 ( )
A. x>y
B. xC. x=y
D. x>y和x2.一停车场上有24 辆车,其中一辆汽车有4个轮子,一辆摩托车有3个轮子,且停车场只有汽车和摩托车,这些车共有86个轮子,那么摩托车应为 ( )
A. 14辆 B. 12辆
C. 16辆 D. 10辆
3. 如图,AD∥BC,∠D=∠ABC,E 是边DC上一点,连接AE,交BC 的延长线于点H,F 是边 AB 上一点,使得∠FBE =∠FEB,作∠FEH 的平分线EG,交 BH于点G.若∠DEH=100°,则∠BEG 的度数为 ( )
A. 30° B. 40°
C. 50° D. 60°
4.甲、乙、丙三人进行智力抢答比赛,规定:第一个问题由乙提出,由甲、丙抢答.以后在抢答过程中若甲答对1题,就可提6个问题,乙答对1题就可提5个问题,丙答对1题就可提4个问题,供另两人抢答.抢答结束后,总共有16个问题没有任何人答对,则丙答对的题数是 ( )
A. 1 或2 B. 0或1
C. 1 或5 D. 1或3
5.我们知道下面的结论:若 且a≠1),则m=n.利用这个结论解决下列问题.已知 现给出m,n,p三者之间的三个关系式:①m+p=2n;②m+n=2p-3;③n -mp=2.其中正确的是 (填序号).
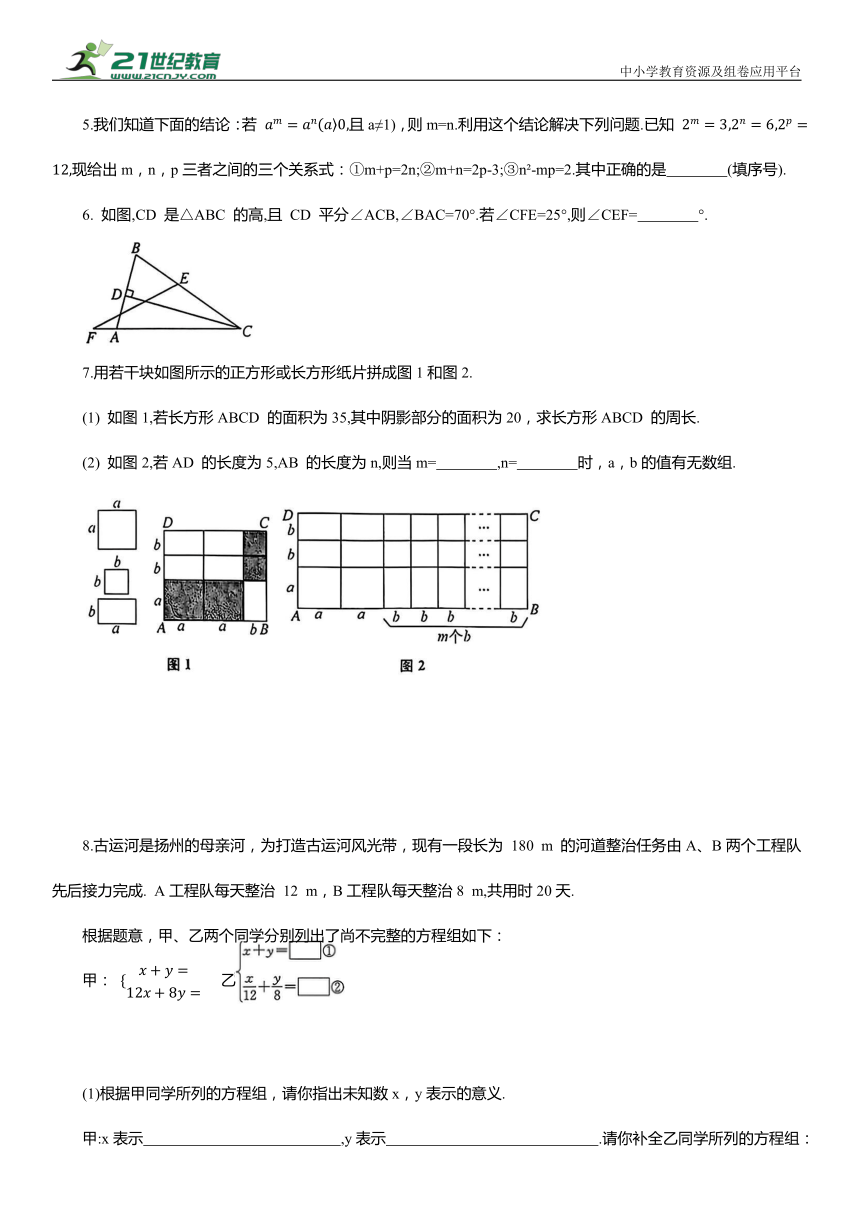
6. 如图,CD 是△ABC 的高,且 CD 平分∠ACB,∠BAC=70°.若∠CFE=25°,则∠CEF= °.
7.用若干块如图所示的正方形或长方形纸片拼成图1和图2.
(1) 如图1,若长方形ABCD 的面积为35,其中阴影部分的面积为20,求长方形ABCD 的周长.
(2) 如图2,若AD 的长度为5,AB 的长度为n,则当m= ,n= 时,a,b的值有无数组.
8.古运河是扬州的母亲河,为打造古运河风光带,现有一段长为 180 m 的河道整治任务由A、B两个工程队先后接力完成. A工程队每天整治 12 m,B工程队每天整治8 m,共用时20天.
根据题意,甲、乙两个同学分别列出了尚不完整的方程组如下:
甲: 乙
(1)根据甲同学所列的方程组,请你指出未知数x,y表示的意义.
甲:x表示 ,y表示 .请你补全乙同学所列的方程组:乙:① ,② .
(2)求A,B两工程队分别整治河道多少米 (写出完整的解答过程)
9. 如图,直线l ∥l ,线段AB 的端点A 在l 上,端点 B 在l 上.
(1)如图1,平行移动线段AB 到 CD,点M在线段CD 上,连接AM,BM.如果△AMC 的面积为S ,△BMD 的面积为S ,△AMB 的面积为S ,写出S ,S ,S 的数量关系式,并给出推理过程.
(2)如图2,平行移动线段AB 到 CD,直线CE 交线段BD 于点E,点 N 在直线l 上点 D 的右侧;连接 AE;把△CDE 沿着直线CE 翻折,点 D 的对应点 F 恰好落在线段AE 上;线段AB 与直线l 的夹角为α.
①若α=60°,∠ACF=10°,求∠DCE的度数.
②探究:如果∠CAE=∠CED,那么是否存在α,使得直线CF⊥AE,同时CE,CF 把∠ACD 三等分 如果存在,请求出α的值;如果不存在,请说明理由.
核心素养综合练(3)
1. D 提示:取a,b,c,d依次为4,3,2,1,则x=3,y=2,x>y;取a,b,c,d依次为4,2,3,1,则x=2,y=3,xy和y>x都有可能.
2. D 提示:设摩托车应为x辆,汽车应为y辆.根据题意,得 解得 所以摩托车应为10辆.
3. B 提示:设∠FBE=∠FEB=α,∠GEH=∠GEF-β,则∠AFE=2a.因为AD∥BC,所以∠ABC+∠BAD=180°,而∠D=∠ABC,所以∠D+∠BAD=180°,所以AB∥CD.因为∠DEH=100°,所以∠FAE=∠CEH=80°.因为. 180°-2β,∠AEF=180°-∠AFE-∠FAE=100°-2α,所以β-α=40°,所以∠BEG=∠GEF-∠FEB=β-α=40°.
4. A 提示:设甲、乙、丙答对的题数分别是x,y,z.根据题意,得6x+5y+4z+1=x+y+z+16.整理,得5x+4y+3z=15.因为 且x,y,z为整数,所以x=3,y=0,z=0(不合题意,舍去)或x=1,y=1,z=2或x=0,y=3,z=1或x=0,y=0,z=5(不合题意,舍去),所以丙答对的题数是2或1.
5. ①② 提示:因为2"=6=2×3=2×2"= 所以n=1+m.因为2 所以p=2+m.所以p=n+1.所以m+p=n-1+n+1=2n,所以①正确;因为m+n=p-2+p-1=2p-3,所以②正确;因为 所以③错误.
6. 115 提示:因为 CD 是△ABC 的高,所以∠ADC=∠BDC=90°,所以. 20°.因为 CD 平分∠ACB,所以∠ACB=2∠ACD=40°.因为∠CFE=25°,所以, ∠ACB=115°.
7. (1) 解:根据题意,得 整理,得 ②---①×2,得5ab=15,即 ab=3.所以 b +2ab=16,a+b=4,所以C长方形ABCD =2(2b+a+2a+b)=6(a+b)=24.
(2)4 10 提示:根据题意,得 因为a,b的值有无数组,所以 所以m=4,n=10.
8.解:(1)A工程队工作的时间 B工程队工作的时间 ①180 ②20
(2)解法1 选择甲同学的思路,根据题意,得 解得 所 以12x=60,8y=120.
答:A工程队整治河道60m,B工程队整治河道120 m.
解法2 选择乙同学的思路,根据题意,得 解得
答:A工程队整治河道60m,B工程队整治河道120 m.
9. 解: 理由如下:
根据题意,得AB∥CD,AB=CD.如图,过点 A,B 分别作AE⊥CD,BH⊥CD,垂足分别为E 和H,过点 M 作MN⊥AB,垂足为N.易知AE∥MN∥BH,AE=MN=BH.因为△AMC 的面积为S ,△BMD 的面积为S ,△AMB 的面积为S ,所以 所以 所以 S +
(2) ①根据题意,得 AB∥CD,所以∠ABD=∠CDN=α=60°.因为直线l ∥l ,所以∠CDN=∠ACD=60°.因为△CDE 沿着直线 CE 翻折,所以∠DCE = ∠ECF. 因为∠DCE + ∠ECF + ∠ACF = ∠ACD, 即 所以∠DCE=25°.
②存在.当α=90°时,直线CF⊥AE,同时CE,CF 把∠ACD 三等分.理由如下:
根据题意,得AB∥CD,∠CFE=∠CDE,∠ECF = ∠ECD,∠FEC = ∠CED. 要使CF⊥AE,则有∠CDE=∠CFE=90°,所以∠CDN=90°,所以∠ABD=∠CDN=α=90°.因为直线l ∥l ,所以∠ACD=∠CDN=90°,∠CED =∠ACE,∠CAE +∠AED =180°,即∠CAE+∠FEC+∠CED=180°.因为∠CAE=∠CED,所以∠CED=∠FEC=∠CAE=60°,所以∠CED=∠ACE=60°.因为∠ACD = 90°,所以∠ECD =∠ACD -∠ACE=30°.又因为∠ECD=∠ECF,所以∠ECD=∠ECF=30°,所以∠ACF=30°,所以 即CE,CF 把∠ACD 三等分.所以当α=90°时,直线 CF⊥AE,同时 CE,CF 把∠ACD 三等分.
核心素养综合练(3)
1. 用 min(a,b)表示a,b 两数中的较小者,用max(a,b)表示a,b两数中的较大者,例如min(3,5)=3, max(3,5)=5, min(3,3)=3, max(5,5)=5.若a,b,c,d 是互不相等的自然数, min(a,b)=p, min(c,d)=q,max(p,q)=x, max(a,b)=m, max(c,d)=n, min(m,n)=y,则 ( )
A. x>y
B. x
D. x>y和x
A. 14辆 B. 12辆
C. 16辆 D. 10辆
3. 如图,AD∥BC,∠D=∠ABC,E 是边DC上一点,连接AE,交BC 的延长线于点H,F 是边 AB 上一点,使得∠FBE =∠FEB,作∠FEH 的平分线EG,交 BH于点G.若∠DEH=100°,则∠BEG 的度数为 ( )
A. 30° B. 40°
C. 50° D. 60°
4.甲、乙、丙三人进行智力抢答比赛,规定:第一个问题由乙提出,由甲、丙抢答.以后在抢答过程中若甲答对1题,就可提6个问题,乙答对1题就可提5个问题,丙答对1题就可提4个问题,供另两人抢答.抢答结束后,总共有16个问题没有任何人答对,则丙答对的题数是 ( )
A. 1 或2 B. 0或1
C. 1 或5 D. 1或3
5.我们知道下面的结论:若 且a≠1),则m=n.利用这个结论解决下列问题.已知 现给出m,n,p三者之间的三个关系式:①m+p=2n;②m+n=2p-3;③n -mp=2.其中正确的是 (填序号).
6. 如图,CD 是△ABC 的高,且 CD 平分∠ACB,∠BAC=70°.若∠CFE=25°,则∠CEF= °.
7.用若干块如图所示的正方形或长方形纸片拼成图1和图2.
(1) 如图1,若长方形ABCD 的面积为35,其中阴影部分的面积为20,求长方形ABCD 的周长.
(2) 如图2,若AD 的长度为5,AB 的长度为n,则当m= ,n= 时,a,b的值有无数组.
8.古运河是扬州的母亲河,为打造古运河风光带,现有一段长为 180 m 的河道整治任务由A、B两个工程队先后接力完成. A工程队每天整治 12 m,B工程队每天整治8 m,共用时20天.
根据题意,甲、乙两个同学分别列出了尚不完整的方程组如下:
甲: 乙
(1)根据甲同学所列的方程组,请你指出未知数x,y表示的意义.
甲:x表示 ,y表示 .请你补全乙同学所列的方程组:乙:① ,② .
(2)求A,B两工程队分别整治河道多少米 (写出完整的解答过程)
9. 如图,直线l ∥l ,线段AB 的端点A 在l 上,端点 B 在l 上.
(1)如图1,平行移动线段AB 到 CD,点M在线段CD 上,连接AM,BM.如果△AMC 的面积为S ,△BMD 的面积为S ,△AMB 的面积为S ,写出S ,S ,S 的数量关系式,并给出推理过程.
(2)如图2,平行移动线段AB 到 CD,直线CE 交线段BD 于点E,点 N 在直线l 上点 D 的右侧;连接 AE;把△CDE 沿着直线CE 翻折,点 D 的对应点 F 恰好落在线段AE 上;线段AB 与直线l 的夹角为α.
①若α=60°,∠ACF=10°,求∠DCE的度数.
②探究:如果∠CAE=∠CED,那么是否存在α,使得直线CF⊥AE,同时CE,CF 把∠ACD 三等分 如果存在,请求出α的值;如果不存在,请说明理由.
核心素养综合练(3)
1. D 提示:取a,b,c,d依次为4,3,2,1,则x=3,y=2,x>y;取a,b,c,d依次为4,2,3,1,则x=2,y=3,x
2. D 提示:设摩托车应为x辆,汽车应为y辆.根据题意,得 解得 所以摩托车应为10辆.
3. B 提示:设∠FBE=∠FEB=α,∠GEH=∠GEF-β,则∠AFE=2a.因为AD∥BC,所以∠ABC+∠BAD=180°,而∠D=∠ABC,所以∠D+∠BAD=180°,所以AB∥CD.因为∠DEH=100°,所以∠FAE=∠CEH=80°.因为. 180°-2β,∠AEF=180°-∠AFE-∠FAE=100°-2α,所以β-α=40°,所以∠BEG=∠GEF-∠FEB=β-α=40°.
4. A 提示:设甲、乙、丙答对的题数分别是x,y,z.根据题意,得6x+5y+4z+1=x+y+z+16.整理,得5x+4y+3z=15.因为 且x,y,z为整数,所以x=3,y=0,z=0(不合题意,舍去)或x=1,y=1,z=2或x=0,y=3,z=1或x=0,y=0,z=5(不合题意,舍去),所以丙答对的题数是2或1.
5. ①② 提示:因为2"=6=2×3=2×2"= 所以n=1+m.因为2 所以p=2+m.所以p=n+1.所以m+p=n-1+n+1=2n,所以①正确;因为m+n=p-2+p-1=2p-3,所以②正确;因为 所以③错误.
6. 115 提示:因为 CD 是△ABC 的高,所以∠ADC=∠BDC=90°,所以. 20°.因为 CD 平分∠ACB,所以∠ACB=2∠ACD=40°.因为∠CFE=25°,所以, ∠ACB=115°.
7. (1) 解:根据题意,得 整理,得 ②---①×2,得5ab=15,即 ab=3.所以 b +2ab=16,a+b=4,所以C长方形ABCD =2(2b+a+2a+b)=6(a+b)=24.
(2)4 10 提示:根据题意,得 因为a,b的值有无数组,所以 所以m=4,n=10.
8.解:(1)A工程队工作的时间 B工程队工作的时间 ①180 ②20
(2)解法1 选择甲同学的思路,根据题意,得 解得 所 以12x=60,8y=120.
答:A工程队整治河道60m,B工程队整治河道120 m.
解法2 选择乙同学的思路,根据题意,得 解得
答:A工程队整治河道60m,B工程队整治河道120 m.
9. 解: 理由如下:
根据题意,得AB∥CD,AB=CD.如图,过点 A,B 分别作AE⊥CD,BH⊥CD,垂足分别为E 和H,过点 M 作MN⊥AB,垂足为N.易知AE∥MN∥BH,AE=MN=BH.因为△AMC 的面积为S ,△BMD 的面积为S ,△AMB 的面积为S ,所以 所以 所以 S +
(2) ①根据题意,得 AB∥CD,所以∠ABD=∠CDN=α=60°.因为直线l ∥l ,所以∠CDN=∠ACD=60°.因为△CDE 沿着直线 CE 翻折,所以∠DCE = ∠ECF. 因为∠DCE + ∠ECF + ∠ACF = ∠ACD, 即 所以∠DCE=25°.
②存在.当α=90°时,直线CF⊥AE,同时CE,CF 把∠ACD 三等分.理由如下:
根据题意,得AB∥CD,∠CFE=∠CDE,∠ECF = ∠ECD,∠FEC = ∠CED. 要使CF⊥AE,则有∠CDE=∠CFE=90°,所以∠CDN=90°,所以∠ABD=∠CDN=α=90°.因为直线l ∥l ,所以∠ACD=∠CDN=90°,∠CED =∠ACE,∠CAE +∠AED =180°,即∠CAE+∠FEC+∠CED=180°.因为∠CAE=∠CED,所以∠CED=∠FEC=∠CAE=60°,所以∠CED=∠ACE=60°.因为∠ACD = 90°,所以∠ECD =∠ACD -∠ACE=30°.又因为∠ECD=∠ECF,所以∠ECD=∠ECF=30°,所以∠ACF=30°,所以 即CE,CF 把∠ACD 三等分.所以当α=90°时,直线 CF⊥AE,同时 CE,CF 把∠ACD 三等分.
同课章节目录
