期末压轴题汇总(含答案) 2024-2025学年苏科版七年级数学下册
文档属性
| 名称 | 期末压轴题汇总(含答案) 2024-2025学年苏科版七年级数学下册 |  | |
| 格式 | docx | ||
| 文件大小 | 1.0MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 苏科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-05-08 05:43:47 | ||
图片预览



文档简介
期末压轴题1
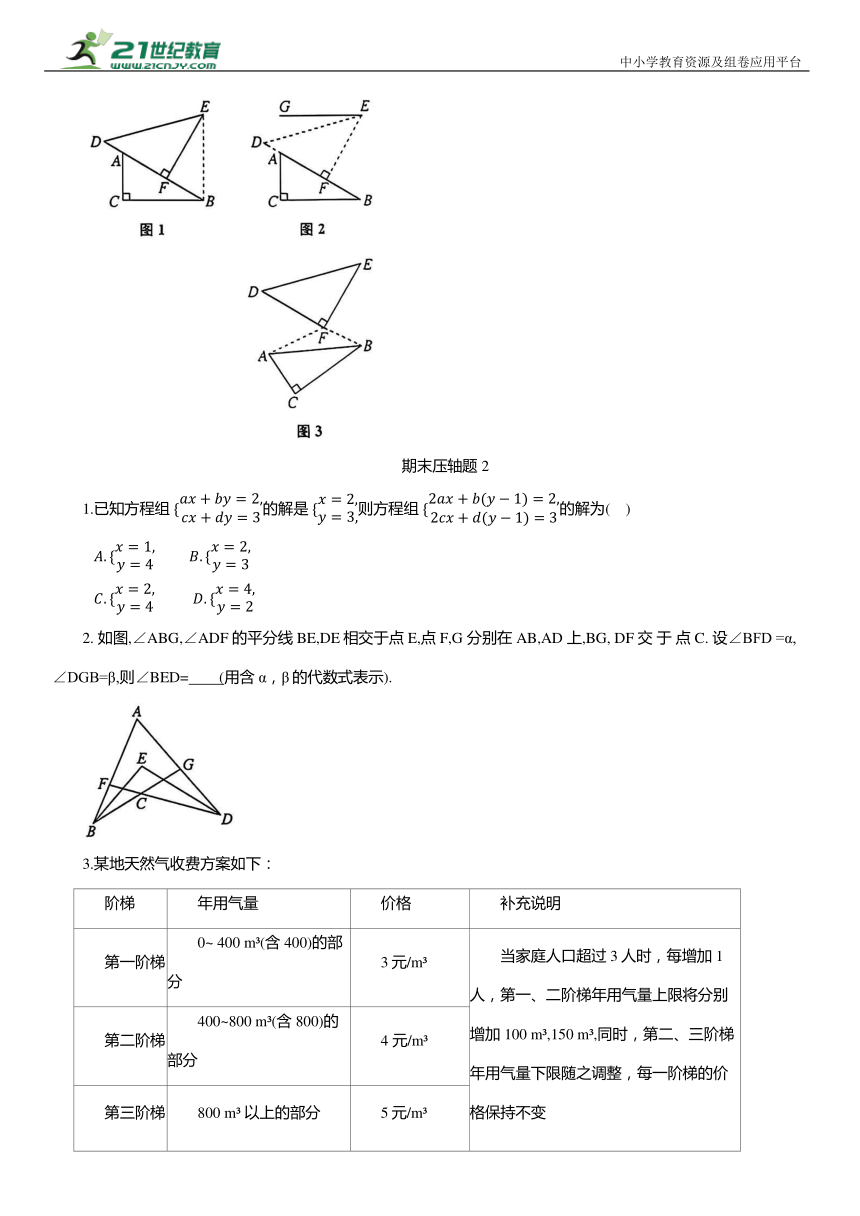
1.在矩形 ABCD 中,将边长分别为a 和b的两张正方形纸片(a>b)按图1 和图2两种方式放置(两张正方形纸片均有部分重叠),矩形中未被这两张正方形纸片覆盖的部分用阴影表示,设图1、图2中阴影部分的面积分别为 S 、S .当 时, 的值为 ( )
A. a/2 B. b
2. 如图,点 D,E,F 分别在△ABC 的各边上,DE∥AC,DF∥AB.将△ABC 沿DE翻折,使得点 B 落在点 B'处,沿DF 翻折,使得点C 落在点C'处.若. 40°,则∠A= .
3. 在几何软件中,将△ABC 和△DEF 按图1所示的方式摆放,其中∠ACB=∠DFE=90°,∠D=45°,∠ABC=30°,点 D,A,F,B在同一条直线上,点E 在点 B 的正上方,且EB(1) 如图1,将△DEF 绕点 F 顺时针旋转,当BC第一次与DE 平行时,∠DFA= °.
(2)将图1 中的△DEF 绕点 E 逆时针旋转一定角度,使点 D 落在边BC 上,过点 E 作 EG∥BC(点 G 在点 E 的左侧),直线 DM 平分∠FDB,直线 EN平分∠GED,交直线 DM 于点 N.在图2中按以上叙述补全图形(无需尺规作图),并直接写出∠END 的度数.
(3) 如图3,将图 1中的△ABC 绕点 B 逆时针旋转.
①当 BC∥DE 时,连接 AF,BF,则∠DFA-∠FAB= ;
②若∠E 与∠ABC 的平分线所在直线相交于点Q,∠EQB=27°,直接写出∠DBA 的度数.
期末压轴题2
1.已知方程组 的解是 则方程组 的解为( )
2. 如图,∠ABG,∠ADF 的平分线 BE,DE相交于点E,点 F,G 分别在AB,AD 上,BG, DF 交 于 点 C. 设∠BFD =α,∠DGB=β,则∠BED= (用含α,β的代数式表示).
3.某地天然气收费方案如下:
阶梯 年用气量 价格 补充说明
第一阶梯 0~ 400 m (含 400)的部分 3元/m 当家庭人口超过3人时,每增加1人,第一、二阶梯年用气量上限将分别增加 100 m ,150 m ,同时,第二、三阶梯年用气量下限随之调整,每一阶梯的价格保持不变
第二阶梯 400~800 m (含 800)的部分 4 元/m
第三阶梯 800 m 以上的部分 5元/m
(1)某家庭当年用气量为500 m .若该家庭人口为3人,则需缴纳燃气费用 元;若该家庭人口为4人,则需缴纳燃气费用 元.
(2)甲户家庭人口为3人,乙户家庭人口为4人.某年甲、乙两户年用气量之和为1 000 m ,甲户年用气量大于乙户年用气量.已知甲、乙两户一共缴纳燃气费用3 200元,求甲、乙两户年用气量分别是多少.
(3)某公司共有 22名员工,员工宿舍有3人间和4人间两种类型的房间可供选择,且员工所选择的房间必须住满.结算天然气费用时,将每间宿舍视作一户家庭,收费标准按上表进行收费.假定每位员工的年用气量为 250 m ,要使该公司员工宿舍当年总天然气费最低,则3人间的房间数为 .
期末压轴题3
1.从前,一位庄园主把一块长为a m、宽为b m(a>b>100)的长方形土地租给租户张老汉,第二年,他对张老汉说:“我把这块地的长增加10m、宽减少10m,继续租给你,租金不变,你也没有吃亏,你看如何 ”如果这样,你觉得张老汉的租地面积会 ( )
A.变小了 B.变大了
C.没有变化 D.无法确定
2. 如图,AB∥CD,∠AEF 的平分线与∠EFC 的平分线交于点O.若∠A=20°,则∠O= °.
3.定义:只有一组对角相等的四边形叫作等角四边形.如:在四边形 ABCD 中,若∠A=∠C,且∠B≠∠D,则称四边形ABCD 为等角四边形,记作(A,C)等角四边形.
【初步认识】
(1) 如图1,四边形ABCD 是(A,C)等角四边形,∠A=80°,∠B=65°,则∠D= °.
【继续探索】
(2) 如图2,四边形 ABCD 是(B,D)等角四边形,AE 平分∠DAB 交CD 于点E,CF 平分∠DCB 交AB 于点 F,求证:AE∥CF.
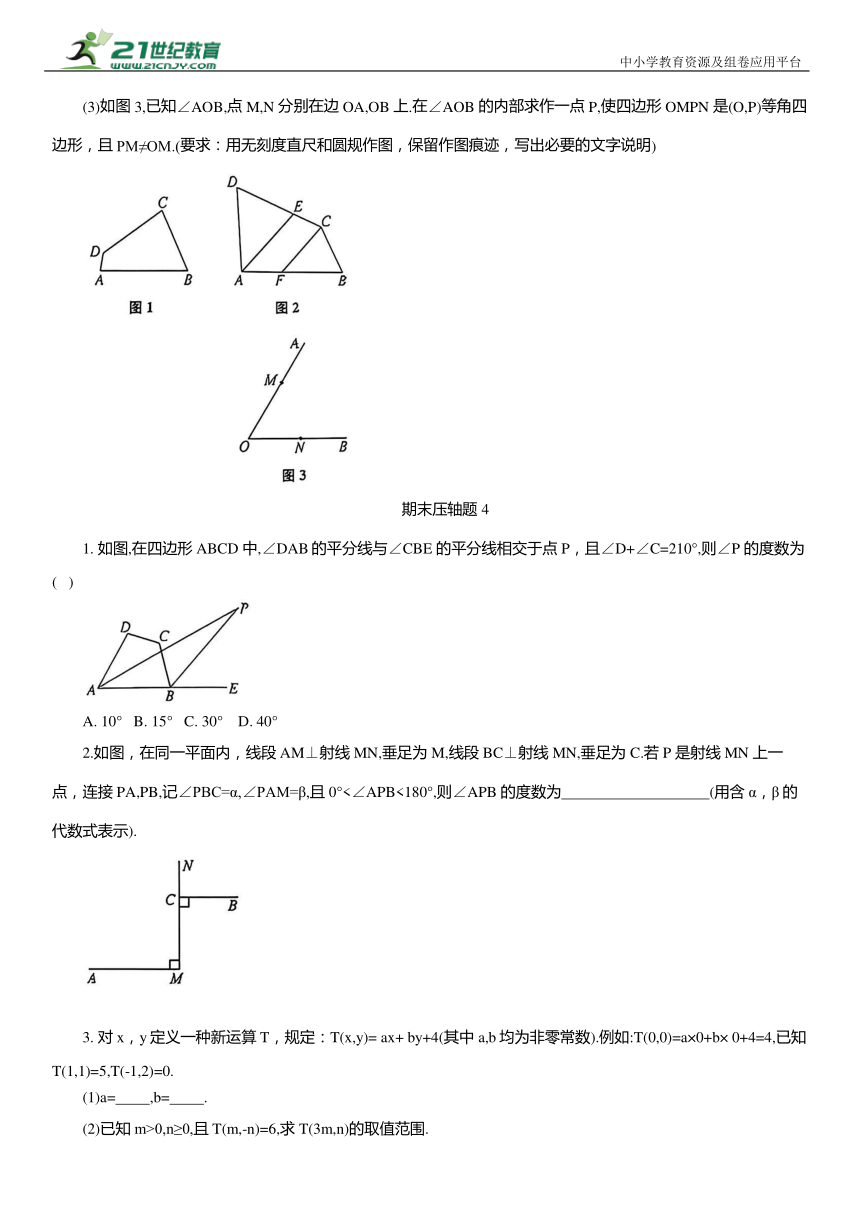
(3)如图3,已知∠AOB,点 M,N 分别在边OA,OB 上.在∠AOB 的内部求作一点 P,使四边形 OMPN 是(O,P)等角四边形,且PM≠OM.(要求:用无刻度直尺和圆规作图,保留作图痕迹,写出必要的文字说明)
期末压轴题4
1. 如图,在四边形ABCD 中,∠DAB的平分线与∠CBE 的平分线相交于点 P,且∠D+∠C=210°,则∠P 的度数为( )
A. 10° B. 15° C. 30° D. 40°
2.如图,在同一平面内,线段 AM⊥射线MN,垂足为 M,线段 BC⊥射线 MN,垂足为C.若P 是射线 MN 上一点,连接PA,PB,记∠PBC=α,∠PAM=β,且0°<∠APB<180°,则∠APB 的度数为 (用含α,β的代数式表示).
3. 对x,y定义一种新运算 T,规定:T(x,y)= ax+ by+4(其中a,b均为非零常数).例如:T(0,0)=a×0+b× 0+4=4,已知T(1,1)=5,T(-1,2)=0.
(1)a= ,b= .
(2)已知m>0,n≥0,且T(m,-n)=6,求T(3m,n)的取值范围.
(3)求 的最小值.
期末压轴题5
1. 如图, ,点 B,C分别在 AM,AN 上运动(不与点 A 重合),连接BC,将△ABC 沿BC 折叠,点A落在点A'的位置.现有下列结论:①当点A′落在∠MAN 的一边上时,△ABC 为直角三角形;②当点 A'落在边 AN 上时,∠NA'B=2∠A;③当点 A'落在∠MAN内部时、 ④当点A'落在∠MAN 外部时,|∠MBA'一 .其中正确的是 ( )
A. ①② B. ①③
C. ②④ D. ①③④
2. 如图,AD,CE 是△ABC 的两条高,它们相交于点 P,已知∠BAC 的度数为α,∠BCA 的度数为β,则∠APC 的度数是 (用含α,β的代数式表示).
3.我们把关于x,y的二元一次方程 ax+by+c=0的系数a,b,c称为该方程的伴随数,记作(a,b,c).例如:二元一次方程5x-y+3=0的伴随数是(5,-1,3).
(1)二元一次方程3x+2y=1的伴随数是 .
(2)已知关于x,y的二元一次方程的伴随数是(3,m,n).
①若是该方程的两组解,求m,n的值;
②若 是该方程的一组解,且满足m+n>7,求代数式3m+4π的值的范围.
期末压轴题6
1. 如图,在长方形ABCD 中,AB=6,第1次平移将长方形 ABCD 沿AB 的方向向右平移5个单位长度,得到长方形. 第2次平移将长方形A B C D 沿. 的方向向右平移5个单位长度,得到长方形A B C D ……以此类推,第n次平移将长方形 沿 的方向向右平移5个单位长度,得到长方形AnBnCnDn(n>2),,则ABn的长为 ( )
A. 5n+6 B. 5n+1
C. 5n+4 D. 5n+3
2.我们知道:三角形的外角等于与它不相邻的两个内角的和.如图,若n边形的一个外角是x°,与它不相邻的所有内角之和是y°,则x,y与n之间的数量关系是 .
3. 画. ,在∠A 的两边上分别取点B,C,P 是平面内一点(点 P 不在直线AB,AC,BC 上),连接 PB,PC.分别记. 为α,β,γ.(本题中涉及的所有角均不超过
(1) 若点 P 在图1所示位置,则∠BPC= (用含α,β,γ的代数式表示).
(2)若点 P 在图2所示位置,则 与α,β,γ之间有怎样的数量关系 请证明你的结论.
(3)当点 P 的位置发生变化时,探索 与α,β,γ之间的数量关系(不同于第(1)(2)问),画出图形并直接写出结论.
期末压轴题8
1. 如图,在△ABC中,AD 是边 BC 上的高,且∠ACB=∠BAD,AE 平分∠CAD,交 BC于点 E,过点 E 作 EF∥AC,分别交 AB,AD 于点 F,G.有下列结论:①∠BAC=90°; ② ∠AEF = ∠BEF; ③ ∠BAE =∠BEA;④∠B=2∠AEF.其中正确的有 (填序号).
2.正方形 ABCD 和正方形 EFCG 如图放置,点F,G 分别在边 BC,CD 上,已知两个正方形的边长 BC 与 FC 的和为8,且 BC 与FC 的积为6,则阴影部分的面积为 ( )
A. 23 B. 24 C. 26 D. 29
3.【阅读】《九章算术》记载,淳风等按:平分知,诸分参差,欲令齐等,减彼之多,增此之少,故曰平分也.在我们的数学中也经常体现平分思想.
例如:如图 1,C是线段AB 的中点,则
【尝试】已知三角形纸片ABC 的面积为6.
(1)如图2,若 D 是线段BC 的中点,则△ABD 的面积等于 .
(2)如图3,将三角形纸片ABC 的∠A 折叠,使得点A 落在边 BC 上的点A'的位置,折痕与AB,AC 分别交于点E,F.若△A'EF 的面积等于四边形BEFC 面积的一半,则△AEF 的面积等于 .
【探究】在△ABC 中,∠A=70°.
(3) 如图4,△ABC 的内角∠ABC 的平分线与△ABC 的外角∠ACD 的平分线交于点 P,求∠P 的度数.
(4) 如图 5,△ABC 的外角∠CBE 和∠BCF 的平分线交于点Q,求∠Q 的度数.
【应用】如图6,两条平行公路l ,l 上分别有点A,D 与点B,C,连接AB,CD,测量得到∠ABC=100°,∠ADC=60°,计划在点 P 处建一个加油站,满足直线 AP 与CP 所形成的锐角为 20°.请利用量角器和直尺画出一个符合题意的加油站(用点 P表示)的位置,并说明理由.
期末压轴题9
中小学教育资源及组卷应用平台
1. 如图,∠ABD 和∠ACE 是△ABC 的外角,BF 和 CG 分别是∠ABD 和∠ACE的平分线,延长 FB 和GC 交于点 H.设∠A=α,∠H=β,则α与β之间的数量关系为 .
2.已知关于x,y的方程组 其中-3≤a≤1,给出下列说法:①当a=1时,方程组的解也是方程x+y=2-a的一个解;②当a=-2时,x,y 的值互为相反数;③若x≤1,则1≤y≤4; 是方程组的解.其中说法错误的是 ( )
A. ①②③④ B. ①②③
C. ②④ D. ②③
3.【教材回顾】苏科版七年级下册数学教材的部分内容:
活动:
如图1,在边长为a 的正方形纸片上剪去一个边长为b的(b思路1:直接用大正方形面积减去小正方形面积,那么它的面积为 .
思路2:将剩余部分剪开拼成图2所示的长方形,那么它的面积为 ;由此得到等式 .
【知识应用】如图3,一“L”形纸片,其面积为27,各边长度如图所示,则m= ,n= .
【知识迁移】上面是通过不同的方法表示同一图形的面积,从而得出相应的等式.其实,通过不同的方法表示同一几何体的体积,也可以探求相应的等式.如图4是棱长为(a+b)的正方体,被如图所示的分割线分成8块.
(1)用不同方法计算这个正方体体积,就可以得到一个等式,这个等式可以为
(2)已知3m--n=4, mn=2,利用上面的知识求 的值.
期末压轴题10
1. 已知a、b、c 是 三个非负数、且满足a+b=2,3a+b-2c -4,则式子2a - b+3c的最大值为 ( )
A. 1 B. 5 (`. 7 D. 9
2.如图,6个形状、大小完全相同的小长方形放在一个大长方形中,已知大长方形的周长为28,小长方形的周长为12,则 AB 与CD 的差为 .
3.【问题探究】如何证明三角形内角和定理
(1) 方法1:过△ABC 的顶点A 作DE∥BC,就能证明“三角形内角和定理”,请你完成这个证明.
如图1,在△ABC中,过顶点A 作DE∥BC,求证:∠BAC+∠B+∠C=180°.
(2)方法2:如果将顶点 A 这个特殊的位置换成△ABC 边AB 上的任意一点P,过点 P 分别作出另外两边的平行线,也能证明“三角形内角和定理”,请你先画出辅助线,再完成这个证明.
如图2,在△ABC中,P 是边 AB 上的任意一点,求证:∠A+∠B+∠C=180°.
【定理应用】
(3) 如图3,P 是△ABC 边AB 上的任意一点,射线 PE∥BC,BD 平分∠PBE交PE 于点D,N 为线段PE 上一点(点 N 不与点 P,D,E 重合),且∠PNB=2∠PEB.若∠ABC=60°,∠DBE =α,试用含 α 的式子表示∠DBN.
期末压轴题11
1. 如图,在△ABC 中,∠A =48°,∠ABC 与∠ACD 的平分线交于点 A ,得∠A ;∠A BC与∠A CD的平分线交于点A ,得 与∠A . CD的平分线交于点 A,,要使∠A,,的度数为整数,则n的最大值为 ( )
A. 2 B. 3 C. 4 D. 5
2. 如图,已知∠F=16°,在△ABC中,BD,CD分别平分∠ABC,∠ACB,点 M,N,Q 分别在DB,DC,BC的延长线上,BE,CE 分别平分∠MBC,∠BCN,BF,CF 分别平分∠EBC,∠ECQ,则∠A= .
3.如图1,大到市民广场,小到家居装修,常常用形状各异的瓷砖来铺设.
探究:正多边形的平面图形密铺
正多边形是指各边相等、各角相等的多边形.用一种或几种正多边形在公共顶点处进行拼接,彼此之间既无空隙又不重叠,这就是正多边形的共顶点密铺.共顶点密铺其实就是围绕一点的几个正多边形的内角的和为360°.
共顶点单一密铺:仅用同一种正多边形密铺.
如图2,可知,正五边形不能共顶点单一密铺,可用下面的方法说明.
解:设有x个正五边形.
因为正五边形的每一个内角为108°,若想用x个108°围成360°,则108x=360°,解得 (不合题意).
所以正五边形不可以共顶点单一密铺.
(1)探索正三角形能不能共顶点单一密铺 请用上述方法说明.
(2)符合共顶点单一密铺的正多边形不止一种,请尝试再找出一种,并说明理由.共顶点组合密铺:用两种或两种以上正多边形密铺.
(3)某中学图书馆拟用正多边形地砖铺设地面.已有正三角形形状的地砖,现打算购买另外一种形状不同,但边长相等的正多边形地砖,与已有正三角形地砖进行共顶点组合密铺.请设计两种不同的共顶点组合密铺方案,并说明理由.
(4)创意设计:选取三种形状不同,但边长相等的正多边形进行共顶点组合密铺,请写出设计方案.
期末压轴题12
1.有下列命题:①同位角相等,两直线平行;②如果两个角是直角,那么它们相等;③如果 ab>0,那么a<0,b<0;④如果两个有理数相等,那么它们的平方相等.它们的逆命题成立的个数有 ( )
A. 1 B. 2 C. 3 D. 4
2.下列表格是某超市对 A,B,C三种品牌商品连续五天的销售记录,第三天的总收入登记时不慎被油墨污染.已知 A,B,C三种品牌商品这五天的销售单价保持不变,请根据表中数据,补全第三天的总收入为 元.
时间 销量/个 总收入/元
A B C
第一天 1 5 3 1 000
第二天 7 3 0 880
第三天 4 4 2
第四天 3 6 0 660
第五天 4 5 1 900
3.一副直角三角板如图1所示放置,∠A=∠E=90°,∠F=60°,∠C=45°,它们的斜边在同一直线上,D为边BC 上一点,三角板DEF 绕点D 按顺时针方向旋转α(0°<α≤60°).
(1)当α= 时,DF∥AC;当α= 时,DE⊥AB.
(2) 设 DE 交边AB 于点 N,直线 DF 交直线 AC 于点 M,记∠CMD 为∠1,∠BND 为∠2.
①如图 2,当α=30°,求∠2-∠1的值;
②当3∠1+∠2<160°时,求α的取值范围.
期末压轴题13
1.如图,长为4、宽为3的长方形ABCD 内有一正方形 BEFG.若直线 AF 将长方形的面积分为1 :3的两部分,则正方形的边长为 ( )
A. 1 B. 1.2 C. 1.4 D. 1.6
2.如图,已知线段 AB 与直线 BC 的夹角∠ABC=75°,D 是直线 BC 上的一个动点,平移线段 AB,使点 B 移到点 D 的位置,得到线段 DE,连接BE,再将△BDE沿BE 折叠,点 D 落在点 F 处.若 BF 平分∠ABE,则∠BED 的度数为 .
3.我们规定,若一元一次方程的解在一元一次不等式组解集范围内,则称该一元一次方程为该不等式组的“关联方程”,例如:x--1=2的解为 的解集为--3≤x<4,不难发现x=3在-3≤x<4的范围内,所以x-1=2是 的“关联方程”.
问题解决:
(1) 方程 3x + 3 = 6 是 不 等式组 的“关联方程”吗 请说明理由.
(2)若关于x的方程2x+k=2是不等式组 的“关联方程”,求k的取值范围.
(3)若关于x的不等式组 的所有“关联方程”只有 3 个不同整数解,试求m的取值范围.
期末压轴题14
1. 如图,点 B,C分别在AM,AN 上运动(不与点 A 重合),CD 是∠BCN 的平分线,CD 的反向延长线交∠ABC 的平分线于点 P. 现给出下列条件:①∠ABC +∠ACB 的值;②∠A 的值;③∠NCD一∠ABP 的值;④∠ABC 的值.其中不能求出∠P 大小的是 ( )
A. ① B. ② C. ③ D. ④
2.小聪在学习完乘法公式后,发现完全平方公式经过适当的变形或数形结合,可以解决很多数学问题.如图摆放两个正方形卡片,点A,M,B在同一直线上.若AB=5,且两个正方形面积之和为13,则阴影部分的面积为 .
3.定义:在一个三角形中,如果一个内角α的度数比另一个内角度数大36°,那么这样的三角形我们称为“似黄金三角形”,其中α称为“黄金角”.例如:一个三角形三个内角的度数分别是 30°,84°,66°,这个三角形就是“似黄金三角形”,其中 66°为“黄金角”.
(1)一个“似黄金三角形”的一个内角为92°,若“黄金角”为锐角,则这个“黄金角”的度数为 .
(2) 如图1,在△ABC中,∠A=70°,∠B=60°,D 为线段 AB 上一点(点 D 不与点A,B 重合).若△BCD 是“似黄金三角形”,求∠BDC 的度数.
(3)如图 2,在△ABC 中,点 D 在边 AB上,DE 平分∠ADC 交AC 于点E,过点 E 作 EF∥AB 交CD 于点 F,且∠DEF=∠B.若△BCD 和△ACD都是“似黄金三角形”,直接写出∠A的度数.
期末压轴题15
1.如图是可调躺椅示意图(数据如图),AE与 BD 的交点为 C,且∠CAB,∠CBA,∠D 的大小保持不变.为了舒适,需调整∠E 的大小,使∠EFD = 110°,则图中∠E 应 ( )
A. 增加10° B. 减少10°
C. 增加20° D. 减少20°
2.定义一种新的取整符号[],即[x]表示不超过 x 的最大整数.例如:[2.3]=2,[--1.7]=-2.有下列结论:①[-2.1]+[0.99]=--3;②[x]+[-x]=0;③若[x+1]=3,则x的取值范围是2≤x<3;④方程 的解有无数多个.其中正确的是 (填序号).
3.如图1,直角三角板 DEF 与直角三角板ABC 的斜边在同一直线上,∠EDF=30°,∠ABC=45°,∠ACB=∠E=90°,CD 平分∠ACB,△ABC 不动,将△DEF 绕点D 按逆时针方向旋转,记∠ADF 为α ,在旋转过程中:
(1) 如图2,当α= 时,DE∥BC;当α= 时,EF∥AB.
(2)将△DEF 绕点 D 按逆时针方向旋转到如图3的位置,边 DE 与BC 延长线交于点 P,边 DF 与AC 交于点Q,求∠BPD+∠AQD 的值.
(3)当顶点C 不在△DEF 内部时,α的取值范围是 (三角形的内部不包含三角形的边).
(4)在旋转过程中,当α的度数为 时,△DEF 的一边与AC平行.
期末压轴题16
1.为了传承中华民族传统文化,邗江区某学校组织“端午”知识微竞赛.竞赛的试题由6道判断题组成,参赛人员只要画“ ”或画“×”表示出对各题的正误判断即可,每小题判断正确得1分,判断错误得0分.竞赛 A小组共有甲、乙、丙、丁四位同学,他们对6道试题的判断与得分的结果如下图所示,由此可以推断丁同学的得分为 ( )
项目 第 1题 第2题 第3 题 第 4 题 第 5题 第 6题 得分
甲 ∨ 4 分
乙 4 分
丙 ∨ 4 分
丁
A. 6分 B. 5分
C. 4分 D. 3分
2.若关于x的不等式组 至少有 4个整数解,且关于 y 的方程2+my=10-y的解为整数,则所有满足条件的整数m 的值之和为 .
3.在七年级的“平行线的性质与判定”的学习中,我们常借助于三角板来研究其相关知识,现有一副三角板如图 1 所示,其中∠ACB=∠EDF=90°,∠A=30°,∠E=45°.请同学们结合已有的知识及活动经验,解决下列问题:
【初步感知】
(1)如图2,将上述三角板的直角顶点重合在一起.当CE∥AB时,∠BCF= .
(2) 如图3,当CA 平分∠ECF 时,请写出图中两条平行的直线,并说明理由.
【深度探究】
(3)将上述三角板按图4 所示的方式摆放,点A,B 在直线GH 上,点D,F 在直线 MN 上,直线GH∥MN,保持三角板ABC 不动,现将三角板 DEF 绕点D 以每秒3°的速度顺时针旋转,设旋转时间为 t s,且0≤t≤60,则是否存在 t 的值,使边 BC 与另一块三角板DEF 的一条边平行 若存在,请求出 t 的值;若不存在,请说明理由.
(4)将上述三角板按图5 所示的方式摆放,点C 与点 D 重合,保持三角板ABC 不动,将三角板 DEF 绕点 C 旋转,使点 F 在直线BC 上方,当两块三角板的两条边互相平行时,若∠BCF度数的最大值为m,最小值为 n,则m-n= .
期末压轴题17
1.如图,在2×2的方格纸中有一个以格点为顶点的△ABC,则与△ABC 成轴对称且以格点为顶点的三角形共有 ( )
A. 3个 B. 4个 C. 5个 D. 6个
2. 已 知6 = 192, 32” = 192, 则
3. 已知△ABC,点 D 在直线 AB 上,连接CD.
(1) 如图1,若∠ACB=90°,CD⊥AB.求证:∠ACD=∠ABC.
(2) 若∠ACD=∠ABC,∠BAC 的平分线与CB,CD分别交于点E,F.
①如图2,当点 D 在边AB 上(不与点A,B 重合)时,求证:∠CFE =∠CEF.
②当点 D 在 AB 的延长线上时,“∠CFE=∠CEF”是否依然成立 画出图形,并说明理由.
期末压轴题18
1.如图,边长相等的正五边形和正n边形(n>5)拼接在一起,则∠ACB 的度数可能是 ( )
A. 54° B. 30° C. 24° D. 18°
2.有两个数值转换机 A、B、将数字x输入数值转换机 A,则可得 如:输入数字3、则输出数字为1;输入数字-11,则输出数字为-3.将数字y输入数值转换机 B,则可得不大于 y 的最大整数,如:输入3.14,则输出数字为3;输入一1.414,则输出数字为-2.现将某整数 m 先输入数值转换机A,再将输出的数字输入数值转换机 B,发现从数值转换机 B输出的数字为5,则符合条件的整数m有 个.
3.【项目式学习】
项目主题:数学智慧拼图
项目背景:为了缓解同学们的学习压力,提高思维能力,增强学习兴趣,并促进同学们的全面发展,王老师将数学学习小组分成三组,每组领取一些矩形卡片,开展以“数学智慧拼图”为主题的项目式学习.
任务一:观察建模
(1)如图1,第一小组领了8个大小、形状完全相同的小矩形,拼成一个大矩形,每个小矩形的长和宽分别为y,x(x任务二:推理分析
(2)第二小组也领了8个大小、形状完全相同的小矩形,把它们按图2方式放置在一个大矩形中,求图2中阴影部分的面积.
任务三:设计方案
(3)第三小组领了A,B,C三种类型的矩形卡片,它们的长都为 18.宽分别为a,b,c,其中a期末压轴题19
1.如图,甲、乙两名同学玩抢硬币游戏,将7枚硬币排成一行,两人轮流从中取一枚或相邻的两枚硬币,如果两枚硬币中间有空位,那么不能将这两枚硬币同时拿走,谁取走最后一枚硬币谁就获胜.如果甲同学先取,并确保获胜,那么甲会先取 ( )
A. 2号 B. 3号
C. 4号 D. 5号或6号
2.如果一个三角形的一个内角等于另一个内角的2倍,我们称这样的三角形为“倍角三角形”.若△ABC 为“倍角三角形”,∠A=100°,则∠B 的度数为 .
3.【观察计算】用等号或不等号填空:
……
【猜想说明】
(2)仿照上面,再任意取几组数值,进行计算比较,你能发现什么大小关系,请用不等式进行表达,并说明理由.
【思考应用】
(用等号或不等号填空).
(4)如图,已知一个长方形的面积为16,分别以它的宽和长(宽和长不相等)为边向外画正方形,记这两个正方形的面积分别为S ,S ,则 的取值范 围是 .
S
S 16
期末压轴题20
1. 如图,在四边形ABCD 中,AB=AD,点B关于AC 的对称点B'恰好落在CD 上.若∠BAD=α,则∠ACB 的度数为 ( )
A. 45°
·2.某校奖励学生:七年级获奖学生中,有一人获奖品3件,其余每人获奖品7件;八年级获奖学生中,有一人获奖品4件,其余每人获奖品9件.如果两个年级获奖人数不等,但奖品数目相等,且每个年级奖品数大于50而不超过 100,那么两个年级获奖学生共有 人.
3. 如图1,由线段AB,AM,CM,CD 组成的图形像∑,称为“∑形 BAMCD”.
(1) 如图2,在“∑形 BAMCD”中,若AB∥CD,∠AMC=70°,则∠A +∠C= °.
(2) 如图3,在“∑形BAMCD”中,若AB∥CD,∠AMC =70°,则∠C--∠A = °.
(3) 如图4,连接“∑形BAMCD”中的 B,D 两点,若∠ABD+∠BDC=160°,∠AMC=α,试猜想∠BAM 与∠MCD的数量关系,并说明理由.
(4)在(3)的条件下,当点 M 在射线 BD上从上向下移动的过程中,请直接写出∠BAM 与∠MCD 所有可能的数
量关系.
期末压轴题21
1. 设a,b为有理数,多项式(x+a)(2x+b)展开后x 的一次项系数为p,多项式(2x+a)(x+b)展开后x 的一次项系数为q.若p+q=6,且p,q均为正整数,则( )
A. ab 与 的最大值相等,ab 与a/b的最小值也相等
B. ab 与a/b的最大值相等, ab 与a/b的最小值不相等
C. ab 与a/b的最大值不相等, ab 与a/b的最小值相等
D. ab与a/b的最大值不相等, ab 与a/b的最小值也不相等
2.如图,在△ABC 中有两个内角相等,且BD 是△ABC 的角平分线,点 E 在 BD上,DF∥BC,交AE于点F.若∠DAE=3∠BAE,∠ADF=3∠EDF,则∠BAE 的度数为 .
3.【新知情境】如图 1,在△ABC 中,∠B=∠C,点 P,Q 分别在AB,AC上.若边 BC上存在一点O,满足∠POQ=∠B,则称O是△ABC 的“一线三等角点”.
【理解新知】
(1) 如图2,在△ABC中,∠B=∠C,AD是边 BC 上的高,DE 是△ABD 中边AB 上的高.求证:D 是△ABC 的“一线三等角点”.
(2)如图1,在【新知情境】的条件和结论下,求证:∠BPO=∠COQ.
【操作探究】
(3) 如图3,在△ABC 中,∠B=∠C,点P,Q 分别在 AB,AC 上. 点 D 在△ABC 内,且∠PDQ=∠B.
①由于点 D 不在边BC 上,所以点 D不是△ABC 的一个“一线三等角点”.小明想沿着 QD 方向,将∠PDQ 平移到 BC 上,使得点 D的对应点为 D ,平移后的∠PDQ的边DP 与AB 的交点为点 P .请用无刻度的直尺和圆规作出∠P D Q.(不写作法,保留清晰的作图痕迹,标明字母)
②如图4,若∠B=∠C=∠PDQ=α(0°<α<60°),∠BPD 与∠CQD的平分线所在直线交于点 E,直接写出∠PEQ与α之间的数量关系.
期末压轴题1
1. B 提示:由题图,得 所以S 一S =[-b(AB-a)]-[-b(AD-a)]=b(AD-AB).因为 所.以 所以
2. 70°提示:设 由翻折的性质,得 因为 所以∠C'DE= 所以. .由翻折的性质,得 因为 DE∥AC,DF∥AB,所以∠C=∠BDE=x°,∠B=∠CDF= 由三角形的内角和定理,得∠A=180°一∠C-∠B=70°.
3. 解:(1)15 提示:如图1,延长DF 交BC 于点 M.因为 BC∥DE,∠D=45°,所以∠CMD=∠D=45°.由三角形外角的性质,得∠BFM=∠CMD -∠B=15°,所以∠DFA=∠BFM=15°.
(2) 补全图形如图2所示,∠END= 22.5°.提示:过点 N 作 NQ∥BC.设∠END=α,∠DNQ=β,则∠ENQ=α+β.因为EG∥BC,所以 EG∥BC∥NQ,所以∠GEN=∠ENQ=α+β,∠MDB=∠DNQ=β.因为 EN 为∠GED 的平分线,DM 为∠FDB 的平分线,所以∠GED=2∠GEN=2(α+β),∠FDB=2∠MDB=2β.又因为∠EDF=45°,所以∠EDB= . 因为 EG∥BC,所以∠GED=∠EDB,即2(α+β)=45°+2β,解得α=22.5°.所以∠END=α=22.5°.
(3) ①15°或165° 提示:分情况讨论:如图3,当△ABC 绕点B 逆时针旋转,第一次满足BC∥DE 时,由题意可知.点D,F,B在同一条直线上.因为 BC∥DE.所以∠CBD=∠D=45°,又因为∠ABC=30°,所以∠ABF=∠CBD-∠ABC=15°.由三角形外角的性质.得∠DFA-∠FAB=∠ABF =15°.如图 4,当△ABC 绕点B 逆时针旋转,第二次满足 BC∥DE时,同理由题意可知,点D,F,B在同一条直线上.因为BC∥DE,∠D=45°,所以. 所以∠ABF=∠CBD+∠ABC=165°,由三角形外角的性质,得∠DFA-∠FAB=∠ABF=165°.
②25.5°或 154.5°或 100.5°或 79.5°.提示:分情况讨论:如图5,当点Q 在直线BD 左下方时,△ABC 绕点B 逆时针旋转会由现两种情形.设射线EQ交DF 于点 P.因为∠DFE=90°,∠D=45°,所以∠DEF=45°.因为 BQ 是∠ABC 的平分线,EQ 是∠DEF 的平分线,所以 由三角形外角的性质,得∠DPQ=∠EQB+∠PBQ=∠D+∠DEQ=67.5°.又因为∠EQB=27°,所以∠PBQ=∠DPQ-∠EQB=40.5°.所以∠DBA=∠PBQ-∠ABQ=25.5°.易知A,B,A'三点共线,所以. 154.5°.如图6,当点Q 在直线BD 右上方时,△ABC 绕点B 逆时针旋转同样会出现两种情形.设直线 EQ 交DF 于点 P.同理可得, 由三角形的内角和定理,得∠DPQ=180°-∠DEP-∠D=112.5°.由三角形外角的性质,得∠DPQ=∠Q+∠PBQ.又因为∠Q=27°,所以∠PBQ =∠DPQ--∠Q =·85.5°. 所以∠DBA=∠PBQ+∠ABQ=100.5°.易知A,B,A'三点共线,所以∠DBA'=180°-∠DBA=79.5°.综上所述,∠DBA 的度数为25.5°或154.5°或 100.5°或79.5°.
期末压轴2
1. A 提 示:将题 中 方 程 组 整 理,得 运用整体换元的思想,得 解得
提示:如图,连接AE 并延长至点H.因为∠ABG,∠ADF 的平分线BE,DE 相交于点E,所以∠ABG=2∠ABE,∠ADF=2∠ADE.由三角形外角的性质,得∠BEH=∠BAE+∠ABE,∠DEH=∠DAE+∠ADE,α=∠BFD=∠BAD+∠ADF,β=∠DGB=∠BAD+∠ABG,所以α+β=∠BAD+∠ADF+∠BAD+∠ABG=2(∠BAD+∠ADE+∠ABE),所以∠BED=∠BEH+∠DEH=∠BAE+∠ABE+∠DAE +∠ADE =∠BAD +∠ABE +
3. 解:(1) 1 600 1 500
(2)设甲户年用气量为xm ,则乙户年用气量为 由题意,得x>1000-x.解得x>500.所以1 000-x<500.所以 3×400+4(x--400)+3(1000--x)=3200,解得x=600.所以1000-x=400.
答:甲、乙两户年用气量分别是600 m ,400 m .
(3)6 提示:设3人间有a间,4人间有b间,则3a+4b=22.因为a,b均为自然数,所以a=2,b=4或a=6,b=1.由题意可知,3人间年用气量为3×250=750(m ),4人间年用气量为
①当a=2,b=4时,公司需缴纳总天然气费用为2×[3×400+4×(750-400)]+4×[3×500+4×(950-500)+5×(1000-950)]=19 400(元).
②当a=6,b=1时.公司需缴纳总天然气费用为6×[3×400+4×(750-400)]+[3×500+4×(950-500)+5×(1000-950)]=19 150(元).
因为19400>19150,所以要使该公司员工宿舍当年总天然气费最低,则3人间的房间数为6.
期末压轴3
2024年南京市联合体期末压轴题
1. A 提示:由题意可知,原租地面积为 ab m .第二年按照庄园主的想法,则租地面积变为(a+10)·(b-10)= ab-10a+10b-100=[ab-10(a-b)-100]m .因为a>b,所以 ab-10(a-b)-100< ab,所以租地面积会变小.
2. 100 提示:如图,作∠AME 的平分线MK 交OE 于点 K,则 因为 OE 平分∠AEM,所以 所以∠EMK+ 80°,所以 因为 AB∥CD,所以∠AME=∠CFM.因为 OF 平分∠CFM,所以 又因为∠EMK= 所以∠EMK=∠OFM,所以MK∥OF,所以∠O=∠MKE=100°.
— 50 —
3. (1) 135
(2) 证明:因为四边形ABCD 是(B,D)等角四边形,所以∠B=∠D.设∠B=∠D=α.由四边形的内角和为360°,得∠DAB+∠B+∠DCB+∠D=360°,所以∠DAB+∠DCB=360°---2α. 因为 AE 平分∠DAB,CF 平分∠DCB,所以 所以 ∠DCB)=180°-α.由三角形的内角和定理,得∠BCF+∠CFB+∠B=180°,所以∠BCF+∠CFB=180°---α=∠EAB +∠BCF,所以∠EAB=∠CFB,所以AE∥CF.
(3)解:如图,由题意可知,四边形OMPN是(O,P)等角四边形,即∠O=∠MPN,∠OMP≠∠ONP.连接MN,由三角形的内角和定理,得∠O+∠OMN+∠ONM=180°,∠P+∠PMN+∠PNM=180°,所以∠OMN +∠ONM =∠PMN+∠PNM.作法:先构造∠CMN =∠OMN+∠ONM=∠PMN+∠PNM,即作∠OMC=∠ONM;再在∠CMN 内部任作不与射线 MO 重合且∠NMD≠∠ONM 的射线 MD,作∠NME = ∠NMD,∠MNF =∠CMD,射线 ME,NF 交于点 P,则点 P 即为所求.
期末压轴4
2024年苏州市期末压轴题
1. B 提示:因为∠D+∠C=210°,∠DAB+∠ABC+∠C+∠D=360°,所以∠DAB+∠ABC=150°.又因为∠DAB 的平分线与∠CBE 的平分线相交于点 P,所以 165°,所以∠P=180°-(∠PAB+∠ABP)=15°.
2. 180°-α+β或180°+α-β或 180°-α—β 提示:连接AB 交MC 于点D,分三种情况讨论:①如图 1,当点 P 在线段 MD 上时,∠APB =∠APD+∠BPD,因为∠APD=∠M+∠PAM=90°+β,∠BPD=90°-∠PBC=90°-α,所以∠APB=∠APD+∠BPD=90°+β+90°-α=180°-α+β;②如图2,当点P 在线段 CD 上时,同理可得∠APB=∠APM+∠BPM=90°-β+90°+α=180°+α-β;③如图3,当点P 在射线 CN 上时,∠APB=∠APM+∠BPM=90°-β+90°-α=180°-α-β.综上所述,∠APB 的度数为180°-α+β或 180°+α-β或 180°-α-β.
3. 解:(1)2 — 1 提示:因为 T(1,1)=5,T(-1,2)=0,所以 解得
(2)由(1)可知,T(x,y)=2x--y+4.因为T(m,--n)=6,所以2m+n+4=6,所以n=-2m+2,所以T(3m,n)=6m--n+4=6m+2m--2+4=8m+2.因为m>0,n≥0,所以--2m+2≥0,所以0(3) 因为 所以T(2x , 所以 的最小值为6.
期末压轴5
2024年无锡市期末压轴题
1. D 提示:如图1,当点A'落在∠MAN 的边AN 上时,由折叠的性质可知,BC 垂直平分AA',所以 .同理,当点 A'落在∠MAN 的边AM上时,. 即△ABC是直角三角形,故①正确.由图 1 可知,∠NA'B+∠A = 但 不一定成立,故②错误.如图2,当点A′落在∠MAN 内部时,连接 AA'. 因为∠MBA',∠NCA'分别是△ABA'和△ACA'的外角,所以. 又因为∠MAN=∠BA'C,所以, 故③正确.如图3,当点A′落在∠MAN的边AN 下方时,分别过点B,A'可作BF∥AN∥A'E,所以∠MBF=∠A, 所以. (设A'B 交边AN于点 P. 因为∠MBA',∠APB 分别是△ABP 和△CPA'的外角,故也可根据三角形外角的性质解之);如图4,当点A'落在∠MAN 的边 AM 上方时,同理可作BF∥AN∥A'E,所以∠MBF=∠A,∠EA'B=∠FBA'= 所以 (设A'C交边AM 于点Q.因为∠NCA',∠AQC 分别是△ACQ 和△BQA'的外角,故也可根据三角形外角的性质解之).所以
故④正确.
2.α+β 提示:由三角形的内角和定理,得∠B=180°-∠BAC-∠BCA=180°-(α+β).因为AD⊥BC,CE⊥AB,所以∠AEC=∠ADB=90°,所以 由三角形外角的性质,得∠APC=∠AEC+∠BAD=α+β.
3. 解:(1)(3,2,-1)
(2)①由题可知,该二元一次方程为3x+ my+n=0.将分别代入3x+ my+n=0,得 解得
②将 代入3x+ my+n=0,得-9+2m+n=0,所以n=9-2m,所以3m+4n=3m+4(9-2m)=36-5m.因为m+n>7,所以m+(9--2m)>7,解得 m<2.所以m<2且m≠0,所以-5m>--10且m≠0,所以36-5m>26且36--5m≠36,即 3m+4n>26且3m+4n≠36.
期末压轴6
2024年常州市期末压轴题
1. A 提示:由题可知,每次平移5个单位长度,n次平移5n个单位长度,即AAn=BBn=5n,所以ABn=AB+BBn=5n+6.
2. y--x=180(n--3)提示:易知n边形的内角和为(n-2)·180°.由题意,得(n-2)×180=y+(180-x),所以y-x=180(n-3).
3. 解:(
(2)∠BPC=α-β-γ.
证法1 如图1,连接 BC.在△ABC中,∠BAC+∠ABC+∠ACB=180°,所以∠ABC+ 在△PBC 中,∠BPC+∠PBC +∠PCB = 180°, 即∠BPC +β+∠ABC+γ+∠ACB =180°,所以∠BPC=180°-(∠ABC+∠ACB)-β-γ=α-β-γ.
证法2 如图2,连接PA 并延长至点D.由三角形外角的性质,得∠BAD=∠BPA+∠PBA =∠BPA +β,∠CAD =∠CPA +∠PCA = ∠CPA + γ. 所 以 ∠BAC =∠BAD+∠CAD=∠BPA+β+∠CPA+γ=∠BPC+β+γ=α,所以∠BPC=α-β-γ.
(3)如图3,∠BPC=α+β+γ;如图4,∠BPC=α+γ-β;如图5,∠BPC=β--α-γ;如图 6,∠BPC =α+β---γ;如图 7,∠BPC=γ-α-β. 提示:连接BC.由题可知,点P 不在直线AB,AC,BC上.易知直线 AB,AC,BC将平面划分为7个区域,除第(1)(2)问两种情况外,还有以下5种情况:
①如图3,由(2)中证法2,得∠BPC=∠BAC+∠PBA+∠PCA=α+β+γ;②如图4,设 PC 交AB 于点O,由三角形外角的性质,得∠BOC=∠BPC+∠PBA=∠BAC+∠PCA,所以∠BPC=∠BAC+∠PCA-∠PBA=α+γ-β;③如图5,设 PC 交直线AB 于点 O,由三角形外角的性质,得∠POB =∠BAC + ∠PCA,∠PBA = ∠BPC + ∠POB =∠BPC+∠BAC+∠PCA,所以∠BPC=∠PBA-∠BAC-∠PCA=β-α-γ;④如图6,同②可得,∠BPC+∠PCA=∠BAC+∠PBA,所以∠BPC=α+β-γ;⑤如图7,同③可得,∠PCA =∠BPC+∠BAC+∠PBA,所以∠BPC=∠PCA-∠BAC-∠PBA=γ-α-β.
期末压轴7
2024年镇江市期末压轴题
1. ①③④ 提示:因为 AD⊥BC,所以∠ADC=90°,所以∠C+∠CAD=90°.因为∠BAD=∠C,所以∠BAD+∠CAD=90°,即∠BAC=90°,故①正确.无法判定∠AEF =∠BEF(仅当 E 为 BC 的中点时,∠AEF=∠BEF),故②错误.因为 AE 平分∠CAD,所以∠DAE =∠CAE. 又因为∠BAD =∠C,所以∠BAD+∠DAE=∠C+∠CAE,即∠BAE=∠BEA,故③正确.因为 EF∥AC,所以∠AEF=∠CAE,所以∠CAD=2∠CAE=2∠AEF.因为∠CAD+∠BAD=90°,∠BAD+∠B=90°,所以∠B=∠CAD=2∠AEF,故④正确.
2. A 提示:设 BC=a,FC=b,则a+b=8,ab=6.由正方形的性质,得CD=BC=a,CG=EG=FC=b,所以 DG=CD-CG=a-b.所以 因为 所以 所以
3. 解:(1) 3 提示:△ABD 和△ACD 为等底等高的三角形,面积均为△ABC 面积的一半.
(2)2 提示:由折叠的性质,得 所以
(3) 因为 BP 平分∠ABC,CP 平分∠ACD,所以 由三角形外角的性质,得∠DCP=∠P+∠CBP,∠ACD=∠ABC+∠A,所以 又因为 所以
(4)由三角形的内角和定理,得∠ABC+∠ACB=180°--∠A =110°,所以∠CBE + 360°--(∠ABC+∠ACB)=250°.因为 BQ平分∠CBE,CQ 平分∠BCF,所以∠CBQ = 所以∠CBQ+ 所以
【应用】如图,延长 DC 至点E,作∠BCE和∠BAF 的平分线交于点 P,则点 P 即为所求.理由如下:
因为l ∥l ,所以∠BAF=∠ABC=100°,∠BCE=∠ADC=60°.因为AP 平分∠BAF,CP平分∠BCE,所以 因为l ∥l ,]所以∠AGB=∠FAP=50°.由三角形外角的性质,得∠P=∠AGB-∠BCP=20°.
2024年镇江市丹徒区期末压轴题
1.α+2β=180° 提示:因为 BF和CG分别是∠ABD 和∠ACE 的平分线,所以∠CBH=∠DBF= 所 以 ∠CBH + 由三角形的内角和定理,得∠H+∠CBH+∠BCH=180°,即 整理,得α+2β=180°.
2. A 提示:当 a=1 时, 解得 斤以x+y=0≠2-1,故①错误.当a=-2时 解得 此时x与y不互为相反数,故②错误.由 解得 若x≤1.即 解得a≥0,所以 0≤a≤1,则 1≤ 即 故③错误.当 时、解得 此时 故④错误.
3.解:【教材回顾】
【知识应用】6 3 提示:由题意,得 27. m-n=3,所以m+n=9,联立方程组,解得m=6,n=3.
【知识迁移】 提示:由题图可知,该正方体被分成的8块分别为:1个棱长为a的小正方体;1个棱长为b的小正方体,3个底面积为a ,高为b的长方体;3个底面积为b ,高为a的长方体.利用大正方体体积的两种算法可得等式.
(2) 对于 令a=3m,b=-n,则( 9mn·(3m-n).将3m-n=4, mn=2代入,得 所以
期末压轴9
2024年南通市期末压轴题
1. C
2.2 提示:设小长方形的长为a、宽为 b.由题意,得 解得 设点 A 到大长方形左边的距离为x,则AB=a-x=5-x,CD=a+3b-u-x=3-x.所以AB-CD=5-x--(3-x)=2.
3. (1) 证明:因为 DE∥BC,所以∠1=∠B,∠2=∠C.因为∠BAC+∠1+∠2=180°,所以∠BAC+∠B+∠C=180°.
(2)证明:如图1,过点 P 分别作PM∥BC交AC于点M,PN∥AC 交BC 于点N,所以∠1=∠B,∠2=∠A,∠3=∠4=∠C.因为∠1+∠2+∠3=180°,所以∠A +∠B+∠C=180°.
解:分情况讨论:①如图2,当点 N 在线段 PD 上时,因为 BD 平分∠PBE,所以∠PBD=∠DBE=α.因为∠ABC=60°,所以∠CBE = ∠ABC - ∠PBE = 60° - 2α,∠CBD=∠ABC-∠PBD=60°--α.因为PE∥BC,所以∠PEB=∠CBE=60°--2α,∠PDB=∠CBD=60°-α.所以∠PNB= .由三角形外角的性质,得∠DBN =∠PNB - ∠PDB =120°--4α-
②如图3,当点 N 在线段DE 上时,同理可得,∠DBN=∠PDB--∠PNB=(60°- .综上所述,∠DBN=60°-3α或∠DBN=3α-60°.
期末压轴10
2024年盐城市期末压轴题
1. C 提示:因为 BA 和CA 分别是∠ABC和∠ACD 的平分线,所以∠ABC=2∠A BC,∠ACD=2∠A CD.由三角形外角的性质,得∠ACD=∠A+∠ABC=∠A+2∠A BC,∠A CD=∠A BC+∠A .所以 ,所以 同理, 所以要使∠A 的度数为整数,则n的最大值为4.
2.52° 提示:由三角形外角的性质,得∠ECQ=∠E+∠EBC,∠FCQ=∠FBC+∠F.因为 BF,CF 分别平分∠EBC,∠ECQ,所以∠EBC=2∠FBC,∠ECQ=2∠FCQ. 所以∠E+∠EBC=2(∠FBC+∠F),即∠E+2∠FBC=2∠FBC+2∠F,所以∠E=2∠F=32°.因为 BE,CE 分别平分∠MBC,∠BCN,所以∠MBC=2∠EBC,∠BCN=2∠BCE,所以∠MBC+∠BCN=2(∠EBC+∠BCE)=2(180°-∠E)=296°,所以 ∠BCN=360°-(∠MBC+∠BCN)=64°.因为 BD,
CD分别平分∠ABC,∠ACB,所以∠ABC=2∠DBC,∠ACB=2∠DCB,所以∠A = 180°--(∠ABC +∠ACB)=180°-2(∠DBC+∠DCB)=52°.
3.解:(1)能,6个正三角形可以共顶点单一密铺.理由如下:
设有x 个正三角形.因为正三角形的每一个内角为 60°,若想用x 个 60°围成 360°,则60x=360,解得x=6.所以6个正三角形可以共顶点单一密铺.
(2)4个正方形可以共顶点单一密铺.理由如下:
设有x个正方形.因为正方形的每一个内角为90°,若想用x个90°围成360°,则 90x=360,解得x=4.所以4个正方形可以共顶点单一密铺.
(3)方案:2个正三角形、2个正六边形或4个正三角形、1个正六边形.理由如下:
设有x 个正三角形、y个正六边形.因为正三角形的每一个内角为60°,正六边形的每一个内角为 若想用x个60°与 y 个 120°围成 360°,则 60x+120y=360.因为x,y均为正整数,所以x=2,y=2或x=4,y=1.
(4)方案:1个正三角形、2个正方形、1个正六边形.理由如下:
设有x个正三角形、y个正方形、z个正六边形.因为正三角形的每一个内角为60°,正方形的每一个内角为90°,正六边形的每一个内角为120°,若想用x个60°、y 个90°与z 个120°围成360°,则60x+90y+120z=360°.因为x,y,z均为正整数,所以x=1,y=2,z=1.
期末压轴11
2024年泰州市靖江市期末压轴题
1. B 提示:①原命题的逆命题为“两直线平行,同位角相等”,是真命题;②原命题的逆命题为“如果两个角相等,那么它们都是直角”,是假命题;③原命题的逆命题为“如果a<0,b<0,那么 ab>0”,是真命题;④原命题的逆命题为“如果两个有理数的平方相等,那么这两个有理数相等”,是假命题.
2. 1 040 提示:设A,B,C三种品牌商品的销售单价分别为x元、y元、z元.由题意,得 解得 所以4x+4y+2z=1040,所以第三天的
总收入为 1 040元.
3. 解:(1) 45°15°提示:如图1,当DF∥AC时,α=∠BDF=∠C=45°;如图2,当 DE⊥AB 时,则 DE∥AC,所以∠BDE=∠C=45°,所以α=∠BDF=∠BDE-∠FDE=15°.
(2) ①因为 α = 30°, 即∠BDF = 30°,∠EDF = 90°--∠F = 30°, 所 以∠CDM =∠BDF=30°,∠BDN=∠BDF+∠EDF=60°,所以∠2=∠BND=180°-∠B-∠BDN=75°.由三角形外角的性质,得∠1=∠CMD =∠ACB-∠CDM=15°.所以∠2-∠1=60°.
②因为当α=45°时, DF∥AC 不合题意,所以分情况讨论:当0°20°,所以20°<α<45°.当45°<α≤60°时,如图3,射线 DF 与射线CA 交于点M,则∠CDM=180°-∠BDF=180°-α,∠BDN=∠BDF +∠EDF =α+ 30°, 所 以∠2 =∠BND=180°-∠B-∠BDN =105°-α,∠1=∠CMD=180°-∠C-∠CDM=α-45°.所以3∠1+∠2=3(α--45°)+(105°-α)=2α--30°<160°,解得α<95°,所以45°<α≤60°.综上所述,α的取值范围是20°<α≤60°且α≠45°.
期末压轴12
2024年泰州市兴化市期末压轴题
1. B 提示:设直线AF 交 BC 于点 H.由题意,得 即 所以 BH=2.设正方形 BEFG 的边长为x,则AG=3-x,EH=2-x.所以 整理,得 解得x=1.2,即正方形的边长为1.2.
2. 50°或70° 提示:分情况讨论:①如图1,当点D 在点 B 的右侧时,因为 BF 平分∠ABE,所以∠ABF=∠EBF.由折叠的性质,得∠EBF=∠EBD.所以 75°=25°.由题可知,DE∥AB.所以∠BED=∠ABE=2∠ABF=2×25°=50°.②如图2,当点 D 在点 B 的左侧时,同理可得 15°或 105°或 135°.
期末压轴15
2024年扬州市邗江区期末压轴题
1. D 提示:由题可知,该测试共有6道题目,每题判断正确得1分,判断错误得0分,甲、乙的得分都是4分,则甲、乙至少有2道题目的结果相同且为正确答案.由题表可知,甲、乙的第3道题和第6道题判断相同,所以第3道题和第6道题的正确答案均为“×”,所以丙的第3道题和第6道题判断错误,而丙也得了4分,说明丙其余题目全部判断正确,所以这6道题目的正确答案是:1×,2 ,3×,4 ,5×,6×.所以丁做对了3道,得了3分.
2. 一14 提示:解关 于 x 的不等式组得 因为该不等式组至少有4个整数解,所以 解得m<-3.解关于y的方程2+ my=10-y,得 因为y为整数,所以m+1的值为±1或±2或±4或±8,即m 的值为0或-2或1或-3或3或-5或7或-9.因为m<-3,所以所有满足条件的整数m的值为-5,-9,其和为--5-9=-14.
3. 解:(1) 30°
(2) BC∥EF.理由如下:
因为 CA 平分∠ECF,∠ECF =90°,所以 因为∠ACB=∠EDF = 90°, 即 ∠ACF + ∠BCF = 90°,∠ACF+∠ACE=90°,所以∠BCF=∠ACE=45°.因为∠F=∠E=45°,所以∠F=∠BCF,所以BC∥EF.
分情况讨论:①如图1,当 DE∥BC时,延长AC 交MN 于点 P,延长 BC 交MN于点Q,则∠PDE=∠PQB.因为MN∥GH,所以∠PQB=∠ABC=90°-∠BAC=60°,所以∠PDE = 60°, 所 以 ∠FDM = 180°-∠EDF--∠PDE = 30°.由题可知,旋转角∠FDM=3t°,所以: 解得t=10.②如图2,当BC∥DF时,延长BC 交MN 于点T.同理可得,∠FDN=∠BTN=∠ABC=60°.所以 解得 t =40.③如图 3,当 EF∥BC 时,设 EF交MN 于点K,延长EF 交GH 于点O.同理可得,∠FKN=∠AOF=∠ABC=60°.由三角形外角的性质,得∠FDN=∠FKN-∠DFE=15°,所以∠FDM=180°-∠FDN= 解得t=55.综上所述,t 的值为10或40或55.
135° 提示:当三角板DEF 绕点C旋转时,因为点 F 在直线BC 上方,所以0°<∠BCF<180°.分情况讨论:①如图4,当AB∥DE 时,∠ACE=∠A=30°.因为∠ACB-∠ACF=∠EDF-∠ACF,所以∠BCF=∠ACE =30°;②如图 5,当 BC∥EF 时,∠BCF=∠F=45°;③如图6,当AB∥DF 时,∠BCF=180°-∠B=120°;④如图 7,当 AC∥EF 时,∠ACF=∠F=45°,所以∠BCF=∠ACF+∠ACB=135°;⑤如图8,当 AB∥EF 时,延长 BC 交 EF 于点 G,则∠CGE=∠B=60°,由三角形外角的性质,得∠GCF=∠CGE-∠F=15°,所以, 165°.综上所述,∠BCF 度数的最大值; 最小值n=30°,所以m-n=135°.
期末压轴16
2024年徐州市期末压轴题
1. C 提示:如图,与△ABC 成轴对称且以格点为顶点的三角形有△ABG,△CDF,△AEF,△DBH,
提示:因为6'=192,32'=192,所以 所以 所以( 即 所以(x-1)(y-1)=1,所以(
3. (1) 证明: 因为 CD⊥AB,所以∠CDB=90°.所以∠ABC+∠BCD=90°.因为∠ACB=90°,所以∠ACD+∠BCD=90°.所以∠ACD=∠ABC.
(2)①证明:由三角形外角的性质,得∠CFE=∠CAE+∠ACD,∠CEF=∠BAE+∠ABC.因为AE 平分∠BAC,所以∠CAE=∠BAE.又因为∠ACD=∠ABC,所以∠CFE=∠CEF.
②解:画出图形,如图所示.∠CFE =∠CEF 依然成立.理由如下:因为 AE 平分∠BAC,所以∠CAE=∠BAE.由三角形的内角和定理,得∠CFE = 180°--∠CAE -∠ACD,∠AEB=180°-∠BAE-∠ABC.又因为∠ACD=∠ABC,所以∠CFE=∠AEB.因为∠CEF=∠AEB,所以∠CFE=∠CEF.
期末压轴17
2024年宿迁市泗阳县期末压轴题
1. C 提示:因为 所以∠BAC=360°- 因为 AB=AC,所以△ABC 为等腰三角形,两底角相等,即∠ABC=∠ACB,所以 因为n>5且为整数,所以若n=6,则∠ACB=24°.验证可知选项A,B,D均不符合题意.
2.4 提示:由题意可知,将整数m输入数值转换机 A,输出的数为 再将 输入数值转换机B,由于从数值转换机 B输出的数字为5,所以5≤ 解得17≤m<20.5,所以整数m 的值为17,18,19,20,共4个.
3. 解:(1) 6 10
(2)设小矩形的长为m、宽为 n.由题意,得 解得 则 13×(5+3n)-8mn=31.
(3)由题意,得
解得 因为a36 ,故此时不能放置;当a=1时,b=8-2a=6,c=a+10=11,分别取A,B,C卡片3,2,5张,拼成的不重叠的图形面积为3×18×1+2×18×6+5×18×11= 此时能放置,放置方式如下图:
期末压轴18
2024年宿迁市宿豫区期末压轴题
1. C 提示:甲先取走正中间的1枚(即4号硬币),这样使左右两边硬币形成对称,乙取多少数量的硬币,甲在另一边对称的位置就取相同数量的硬币,乙每取完一次,甲都会再取一次,这样甲会最终取走最后一枚硬币,从而确保获胜.
2. 50°或30°或 或 提示:分情况讨论:当∠A=2∠B 时, 当∠A=2∠C时, 所以. 当∠B=2∠C 时, 解得 当∠C=2∠B 时, ,解得 综上所述,∠B 的度数为 50°或 30°或 或
3. 解:【观察计算】(1) ①= ②> ③>
(2)举例如下:
;用不等式表示为 理由如下:
因为 所以
(3)>
提示:设长方形的长为a、宽为b,则 所以 b .因为a≠b,所以. 即
期末压轴19
2024年淮安市期末压轴题
1. D 提示:如图,连接AB'.设∠ACB=x,∠BAC=y.由轴对称的性质,得 ∠B'AC=∠BAC=y,AB'=AB.因为AB=AD,所以 ,所以△ADB'为等腰三角形,两底角相等,即 因为∠BAD=α,所以∠B'AD=∠BAD-∠B'AB=α-2y.由三角形外角的性质,得 .由三角形的内角和定理,得. 即α--2y+x+y+x+y=180°,解得 即
2.25 提示:设七年级获奖人数为(n+1),八年级获奖人数为(m+1)(n≠m,且n,m均为正整数).由题意,得3+7n=4+9m,即7n=9m+1①.解50<3+7n≤100,50<4+9m≤100,得 所以n的值为7,8,9,10,11,12,13,m的值为6,7,8,9,10.因为满足3+7n=4+9m的解只有n=13,m=10,所以n+1=14,m+1=11.所以两个年级获奖学生共有14+11=25(人).
3. 解:(1) 70 提示:过点 M向左侧作 MN∥AB.因为AB∥CD,所以AB∥MN∥CD,所以∠AMN=∠A,∠CMN=∠C,所以∠A+∠C=∠AMN+∠CMN=∠AMC=70°.
(2) 70 提示:设 AB 与 MC 交于点E.因为AB∥CD,所以∠C=∠MEB.由三角形外角的性质,得∠MEB=∠AMC+∠A.所以∠C=∠AMC+∠A,所以∠C-∠A=∠AMC=70°.
(3) ∠BAM+∠MCD=α+20°.理由如下:
如图1,过点 A 作AP∥CD 交BD 于点P,则∠APB=∠BDC.由三角形的内角和定理,得∠BAP+∠APB+∠ABD =180°,即∠BAP + ∠BDC + ∠ABD = 180°. 因 为∠ABD+∠BDC=160°,所以∠BAP=20°.由(1)可知,∠AMC=∠PAM+∠MCD=α.所以∠BAM + ∠MCD = ∠BAP + ∠PAM +∠MCD=α+20°.
(4) 当点 M 在线段BD 上时,∠BAM+∠MCD=α+20°;当点 C,D 位于AM 两侧时,∠BAM--∠MCD=α+20°;当A,C,M三点共线时,∠BAM--∠MCD=20°;当点 C,D位于AM 同侧时,∠MCD-∠BAM=α-20°.提示:分情况讨论:①当点M 在线段BD上时,由(3)可知,∠BAM+∠MCD=α+20°.②如图2,当点C,D 位于 AM 两侧时,延长 BM 至点 O. 因为∠ABD +∠BDC=160°,∠CDM+∠BDC=180°,所以∠CDM-∠ABD=20°. 由三角形外角的性质,得∠AMO=∠ABD+∠BAM,∠CMO=∠MCD+∠CDM.所以α=∠AMC =∠AMO - ∠CMO = ∠ABD +∠BAM -(∠MCD+∠CDM)=∠BAM-∠MCD - 20°,即∠BAM-∠MCD=α+20°.③当A,C,M三点共线时,∠AMC=α=0°.由四边形内角和为 360°,得∠ABD+∠BDC+∠BAM+∠ACD=360°. 因为∠ABD +∠BDC=160°,所以∠BAM+∠ACD=200°. 因为∠ACD+∠MCD=180°,所以∠BAM-∠MCD=20°.④如图3,当点C,D位于AM 同侧时,延长BM 至点O.同理可得,∠CDM--∠ABD =20°,α=∠AMC =∠CMO-∠AMO=∠MCD+∠CDM-(∠ABD+∠BAM) =∠MCD-∠BAM +20°, 即∠MCD -∠BAM=α-20°.
期末压轴20
2024年连云港市期末压轴题
1. A 提示:因为( ,所以p=b+2a,q=2b+a.因为p+q=6,即b+2a+2b+a=6,整理,得a+b=2.所以p=b+2a=a+2,q=2b+a=b+2.因为p+q=6,p与q均为正整数,所以 即 所 以 或 或 或 或 可得 ab=a(2- ,易知当a=1时,ab取得最大值,为l;当a=-1或a=3时, ab取得最小值,为—3.由题意知,当a/b有意义时,b≠0,所以a≠2.因为 所以当b=1时,a/b取得最大值,为1;当b=-1时, ab取得最小值,为-3.
或 提示:设∠BAE=α,∠EDF =β,则∠DAE =3∠BAE =3α,∠ADF =3∠EDF=3β,所以∠BAC=∠DAE+∠BAE=4α.因为DF∥BC,所以∠CBD=∠EDF=β,∠C=∠ADF=3β.因为 BD 是△ABC 的角平分线,所以∠ABC=2∠CBD=2β.分情况讨论:①若∠BAC=∠C,即4α=3β,则 由三角形的内角和定理,得∠BAC+∠ABC+∠C=180°,即4α+2β+3β=180°.将 代入,得 解得 ②若∠ABC=∠BAC,即2β=4α,则β=2α.同理可得,4α+2β+3β=180°,即14α=180°,解得 ③若∠ABC=∠C,即2β=3β,则β=0,易知这种情况不存在,综上所述,∠BAE 的度数为 或
3. (1) 证明:因为 AD 是边 BC 上的高,DE 是 △ABD 中 边 AB 上的高, 所 以∠ADB=∠AED=90°,所以∠B+∠BAD=90°,∠ADE +∠BAD = 90°, 所以∠B =∠ADE.因为∠B=∠C,所以D 是△ABC 的“一线三等角点”.
(2) 证明:因为在△BOP 中,∠B +∠BOP +∠BPO=180°,又因为∠BOP +∠POQ+∠COQ=180°,∠POQ=∠B,所以∠BPO=∠COQ.
(3)解:①如图1,∠P D Q 即为所求.
②2∠PEQ+3α=180°. 提示:如图2,连接EA 并延长至点F.因为∠B=∠C=∠PDQ=α(0°<α<60°),由三角形的内角和定理,得. ∠B--∠C= 180°--2α. 由三角形外角的性质,得∠APE=∠PAF--∠AEP,∠AQE=∠QAF--∠AEQ,所以∠APE+∠AQE=∠PAF--∠AEP+∠QAF-∠AEQ=∠BAC--∠PEQ.因为∠APE=∠BPM,∠AQE=∠CQN,所以∠BPM+∠CQN=∠BAC-∠PEQ.因为∠BPD 与∠CQD 的平分线分别是 PM,QN,所以∠DPM=∠BPM,∠DQN=∠CQN.所以∠DPM+∠DQN=∠BAC-∠PEQ.所以∠APD+∠AQD= 180° - (∠APE +∠DPM) + 180°- 因为∠BAC +∠APD +∠AQD +∠D = 360°,即∠BAC+360°-2(∠BAC-∠PEQ)+α=360°,所以∠BAC=2∠PEQ+α.所以: 即2∠PEQ +3α= 180°.(此题也可连接 AD,通过∠BPD+∠CQD=∠BAC+∠PDQ 解之)
1.在矩形 ABCD 中,将边长分别为a 和b的两张正方形纸片(a>b)按图1 和图2两种方式放置(两张正方形纸片均有部分重叠),矩形中未被这两张正方形纸片覆盖的部分用阴影表示,设图1、图2中阴影部分的面积分别为 S 、S .当 时, 的值为 ( )
A. a/2 B. b
2. 如图,点 D,E,F 分别在△ABC 的各边上,DE∥AC,DF∥AB.将△ABC 沿DE翻折,使得点 B 落在点 B'处,沿DF 翻折,使得点C 落在点C'处.若. 40°,则∠A= .
3. 在几何软件中,将△ABC 和△DEF 按图1所示的方式摆放,其中∠ACB=∠DFE=90°,∠D=45°,∠ABC=30°,点 D,A,F,B在同一条直线上,点E 在点 B 的正上方,且EB
(2)将图1 中的△DEF 绕点 E 逆时针旋转一定角度,使点 D 落在边BC 上,过点 E 作 EG∥BC(点 G 在点 E 的左侧),直线 DM 平分∠FDB,直线 EN平分∠GED,交直线 DM 于点 N.在图2中按以上叙述补全图形(无需尺规作图),并直接写出∠END 的度数.
(3) 如图3,将图 1中的△ABC 绕点 B 逆时针旋转.
①当 BC∥DE 时,连接 AF,BF,则∠DFA-∠FAB= ;
②若∠E 与∠ABC 的平分线所在直线相交于点Q,∠EQB=27°,直接写出∠DBA 的度数.
期末压轴题2
1.已知方程组 的解是 则方程组 的解为( )
2. 如图,∠ABG,∠ADF 的平分线 BE,DE相交于点E,点 F,G 分别在AB,AD 上,BG, DF 交 于 点 C. 设∠BFD =α,∠DGB=β,则∠BED= (用含α,β的代数式表示).
3.某地天然气收费方案如下:
阶梯 年用气量 价格 补充说明
第一阶梯 0~ 400 m (含 400)的部分 3元/m 当家庭人口超过3人时,每增加1人,第一、二阶梯年用气量上限将分别增加 100 m ,150 m ,同时,第二、三阶梯年用气量下限随之调整,每一阶梯的价格保持不变
第二阶梯 400~800 m (含 800)的部分 4 元/m
第三阶梯 800 m 以上的部分 5元/m
(1)某家庭当年用气量为500 m .若该家庭人口为3人,则需缴纳燃气费用 元;若该家庭人口为4人,则需缴纳燃气费用 元.
(2)甲户家庭人口为3人,乙户家庭人口为4人.某年甲、乙两户年用气量之和为1 000 m ,甲户年用气量大于乙户年用气量.已知甲、乙两户一共缴纳燃气费用3 200元,求甲、乙两户年用气量分别是多少.
(3)某公司共有 22名员工,员工宿舍有3人间和4人间两种类型的房间可供选择,且员工所选择的房间必须住满.结算天然气费用时,将每间宿舍视作一户家庭,收费标准按上表进行收费.假定每位员工的年用气量为 250 m ,要使该公司员工宿舍当年总天然气费最低,则3人间的房间数为 .
期末压轴题3
1.从前,一位庄园主把一块长为a m、宽为b m(a>b>100)的长方形土地租给租户张老汉,第二年,他对张老汉说:“我把这块地的长增加10m、宽减少10m,继续租给你,租金不变,你也没有吃亏,你看如何 ”如果这样,你觉得张老汉的租地面积会 ( )
A.变小了 B.变大了
C.没有变化 D.无法确定
2. 如图,AB∥CD,∠AEF 的平分线与∠EFC 的平分线交于点O.若∠A=20°,则∠O= °.
3.定义:只有一组对角相等的四边形叫作等角四边形.如:在四边形 ABCD 中,若∠A=∠C,且∠B≠∠D,则称四边形ABCD 为等角四边形,记作(A,C)等角四边形.
【初步认识】
(1) 如图1,四边形ABCD 是(A,C)等角四边形,∠A=80°,∠B=65°,则∠D= °.
【继续探索】
(2) 如图2,四边形 ABCD 是(B,D)等角四边形,AE 平分∠DAB 交CD 于点E,CF 平分∠DCB 交AB 于点 F,求证:AE∥CF.
(3)如图3,已知∠AOB,点 M,N 分别在边OA,OB 上.在∠AOB 的内部求作一点 P,使四边形 OMPN 是(O,P)等角四边形,且PM≠OM.(要求:用无刻度直尺和圆规作图,保留作图痕迹,写出必要的文字说明)
期末压轴题4
1. 如图,在四边形ABCD 中,∠DAB的平分线与∠CBE 的平分线相交于点 P,且∠D+∠C=210°,则∠P 的度数为( )
A. 10° B. 15° C. 30° D. 40°
2.如图,在同一平面内,线段 AM⊥射线MN,垂足为 M,线段 BC⊥射线 MN,垂足为C.若P 是射线 MN 上一点,连接PA,PB,记∠PBC=α,∠PAM=β,且0°<∠APB<180°,则∠APB 的度数为 (用含α,β的代数式表示).
3. 对x,y定义一种新运算 T,规定:T(x,y)= ax+ by+4(其中a,b均为非零常数).例如:T(0,0)=a×0+b× 0+4=4,已知T(1,1)=5,T(-1,2)=0.
(1)a= ,b= .
(2)已知m>0,n≥0,且T(m,-n)=6,求T(3m,n)的取值范围.
(3)求 的最小值.
期末压轴题5
1. 如图, ,点 B,C分别在 AM,AN 上运动(不与点 A 重合),连接BC,将△ABC 沿BC 折叠,点A落在点A'的位置.现有下列结论:①当点A′落在∠MAN 的一边上时,△ABC 为直角三角形;②当点 A'落在边 AN 上时,∠NA'B=2∠A;③当点 A'落在∠MAN内部时、 ④当点A'落在∠MAN 外部时,|∠MBA'一 .其中正确的是 ( )
A. ①② B. ①③
C. ②④ D. ①③④
2. 如图,AD,CE 是△ABC 的两条高,它们相交于点 P,已知∠BAC 的度数为α,∠BCA 的度数为β,则∠APC 的度数是 (用含α,β的代数式表示).
3.我们把关于x,y的二元一次方程 ax+by+c=0的系数a,b,c称为该方程的伴随数,记作(a,b,c).例如:二元一次方程5x-y+3=0的伴随数是(5,-1,3).
(1)二元一次方程3x+2y=1的伴随数是 .
(2)已知关于x,y的二元一次方程的伴随数是(3,m,n).
①若是该方程的两组解,求m,n的值;
②若 是该方程的一组解,且满足m+n>7,求代数式3m+4π的值的范围.
期末压轴题6
1. 如图,在长方形ABCD 中,AB=6,第1次平移将长方形 ABCD 沿AB 的方向向右平移5个单位长度,得到长方形. 第2次平移将长方形A B C D 沿. 的方向向右平移5个单位长度,得到长方形A B C D ……以此类推,第n次平移将长方形 沿 的方向向右平移5个单位长度,得到长方形AnBnCnDn(n>2),,则ABn的长为 ( )
A. 5n+6 B. 5n+1
C. 5n+4 D. 5n+3
2.我们知道:三角形的外角等于与它不相邻的两个内角的和.如图,若n边形的一个外角是x°,与它不相邻的所有内角之和是y°,则x,y与n之间的数量关系是 .
3. 画. ,在∠A 的两边上分别取点B,C,P 是平面内一点(点 P 不在直线AB,AC,BC 上),连接 PB,PC.分别记. 为α,β,γ.(本题中涉及的所有角均不超过
(1) 若点 P 在图1所示位置,则∠BPC= (用含α,β,γ的代数式表示).
(2)若点 P 在图2所示位置,则 与α,β,γ之间有怎样的数量关系 请证明你的结论.
(3)当点 P 的位置发生变化时,探索 与α,β,γ之间的数量关系(不同于第(1)(2)问),画出图形并直接写出结论.
期末压轴题8
1. 如图,在△ABC中,AD 是边 BC 上的高,且∠ACB=∠BAD,AE 平分∠CAD,交 BC于点 E,过点 E 作 EF∥AC,分别交 AB,AD 于点 F,G.有下列结论:①∠BAC=90°; ② ∠AEF = ∠BEF; ③ ∠BAE =∠BEA;④∠B=2∠AEF.其中正确的有 (填序号).
2.正方形 ABCD 和正方形 EFCG 如图放置,点F,G 分别在边 BC,CD 上,已知两个正方形的边长 BC 与 FC 的和为8,且 BC 与FC 的积为6,则阴影部分的面积为 ( )
A. 23 B. 24 C. 26 D. 29
3.【阅读】《九章算术》记载,淳风等按:平分知,诸分参差,欲令齐等,减彼之多,增此之少,故曰平分也.在我们的数学中也经常体现平分思想.
例如:如图 1,C是线段AB 的中点,则
【尝试】已知三角形纸片ABC 的面积为6.
(1)如图2,若 D 是线段BC 的中点,则△ABD 的面积等于 .
(2)如图3,将三角形纸片ABC 的∠A 折叠,使得点A 落在边 BC 上的点A'的位置,折痕与AB,AC 分别交于点E,F.若△A'EF 的面积等于四边形BEFC 面积的一半,则△AEF 的面积等于 .
【探究】在△ABC 中,∠A=70°.
(3) 如图4,△ABC 的内角∠ABC 的平分线与△ABC 的外角∠ACD 的平分线交于点 P,求∠P 的度数.
(4) 如图 5,△ABC 的外角∠CBE 和∠BCF 的平分线交于点Q,求∠Q 的度数.
【应用】如图6,两条平行公路l ,l 上分别有点A,D 与点B,C,连接AB,CD,测量得到∠ABC=100°,∠ADC=60°,计划在点 P 处建一个加油站,满足直线 AP 与CP 所形成的锐角为 20°.请利用量角器和直尺画出一个符合题意的加油站(用点 P表示)的位置,并说明理由.
期末压轴题9
中小学教育资源及组卷应用平台
1. 如图,∠ABD 和∠ACE 是△ABC 的外角,BF 和 CG 分别是∠ABD 和∠ACE的平分线,延长 FB 和GC 交于点 H.设∠A=α,∠H=β,则α与β之间的数量关系为 .
2.已知关于x,y的方程组 其中-3≤a≤1,给出下列说法:①当a=1时,方程组的解也是方程x+y=2-a的一个解;②当a=-2时,x,y 的值互为相反数;③若x≤1,则1≤y≤4; 是方程组的解.其中说法错误的是 ( )
A. ①②③④ B. ①②③
C. ②④ D. ②③
3.【教材回顾】苏科版七年级下册数学教材的部分内容:
活动:
如图1,在边长为a 的正方形纸片上剪去一个边长为b的(b
思路2:将剩余部分剪开拼成图2所示的长方形,那么它的面积为 ;由此得到等式 .
【知识应用】如图3,一“L”形纸片,其面积为27,各边长度如图所示,则m= ,n= .
【知识迁移】上面是通过不同的方法表示同一图形的面积,从而得出相应的等式.其实,通过不同的方法表示同一几何体的体积,也可以探求相应的等式.如图4是棱长为(a+b)的正方体,被如图所示的分割线分成8块.
(1)用不同方法计算这个正方体体积,就可以得到一个等式,这个等式可以为
(2)已知3m--n=4, mn=2,利用上面的知识求 的值.
期末压轴题10
1. 已知a、b、c 是 三个非负数、且满足a+b=2,3a+b-2c -4,则式子2a - b+3c的最大值为 ( )
A. 1 B. 5 (`. 7 D. 9
2.如图,6个形状、大小完全相同的小长方形放在一个大长方形中,已知大长方形的周长为28,小长方形的周长为12,则 AB 与CD 的差为 .
3.【问题探究】如何证明三角形内角和定理
(1) 方法1:过△ABC 的顶点A 作DE∥BC,就能证明“三角形内角和定理”,请你完成这个证明.
如图1,在△ABC中,过顶点A 作DE∥BC,求证:∠BAC+∠B+∠C=180°.
(2)方法2:如果将顶点 A 这个特殊的位置换成△ABC 边AB 上的任意一点P,过点 P 分别作出另外两边的平行线,也能证明“三角形内角和定理”,请你先画出辅助线,再完成这个证明.
如图2,在△ABC中,P 是边 AB 上的任意一点,求证:∠A+∠B+∠C=180°.
【定理应用】
(3) 如图3,P 是△ABC 边AB 上的任意一点,射线 PE∥BC,BD 平分∠PBE交PE 于点D,N 为线段PE 上一点(点 N 不与点 P,D,E 重合),且∠PNB=2∠PEB.若∠ABC=60°,∠DBE =α,试用含 α 的式子表示∠DBN.
期末压轴题11
1. 如图,在△ABC 中,∠A =48°,∠ABC 与∠ACD 的平分线交于点 A ,得∠A ;∠A BC与∠A CD的平分线交于点A ,得 与∠A . CD的平分线交于点 A,,要使∠A,,的度数为整数,则n的最大值为 ( )
A. 2 B. 3 C. 4 D. 5
2. 如图,已知∠F=16°,在△ABC中,BD,CD分别平分∠ABC,∠ACB,点 M,N,Q 分别在DB,DC,BC的延长线上,BE,CE 分别平分∠MBC,∠BCN,BF,CF 分别平分∠EBC,∠ECQ,则∠A= .
3.如图1,大到市民广场,小到家居装修,常常用形状各异的瓷砖来铺设.
探究:正多边形的平面图形密铺
正多边形是指各边相等、各角相等的多边形.用一种或几种正多边形在公共顶点处进行拼接,彼此之间既无空隙又不重叠,这就是正多边形的共顶点密铺.共顶点密铺其实就是围绕一点的几个正多边形的内角的和为360°.
共顶点单一密铺:仅用同一种正多边形密铺.
如图2,可知,正五边形不能共顶点单一密铺,可用下面的方法说明.
解:设有x个正五边形.
因为正五边形的每一个内角为108°,若想用x个108°围成360°,则108x=360°,解得 (不合题意).
所以正五边形不可以共顶点单一密铺.
(1)探索正三角形能不能共顶点单一密铺 请用上述方法说明.
(2)符合共顶点单一密铺的正多边形不止一种,请尝试再找出一种,并说明理由.共顶点组合密铺:用两种或两种以上正多边形密铺.
(3)某中学图书馆拟用正多边形地砖铺设地面.已有正三角形形状的地砖,现打算购买另外一种形状不同,但边长相等的正多边形地砖,与已有正三角形地砖进行共顶点组合密铺.请设计两种不同的共顶点组合密铺方案,并说明理由.
(4)创意设计:选取三种形状不同,但边长相等的正多边形进行共顶点组合密铺,请写出设计方案.
期末压轴题12
1.有下列命题:①同位角相等,两直线平行;②如果两个角是直角,那么它们相等;③如果 ab>0,那么a<0,b<0;④如果两个有理数相等,那么它们的平方相等.它们的逆命题成立的个数有 ( )
A. 1 B. 2 C. 3 D. 4
2.下列表格是某超市对 A,B,C三种品牌商品连续五天的销售记录,第三天的总收入登记时不慎被油墨污染.已知 A,B,C三种品牌商品这五天的销售单价保持不变,请根据表中数据,补全第三天的总收入为 元.
时间 销量/个 总收入/元
A B C
第一天 1 5 3 1 000
第二天 7 3 0 880
第三天 4 4 2
第四天 3 6 0 660
第五天 4 5 1 900
3.一副直角三角板如图1所示放置,∠A=∠E=90°,∠F=60°,∠C=45°,它们的斜边在同一直线上,D为边BC 上一点,三角板DEF 绕点D 按顺时针方向旋转α(0°<α≤60°).
(1)当α= 时,DF∥AC;当α= 时,DE⊥AB.
(2) 设 DE 交边AB 于点 N,直线 DF 交直线 AC 于点 M,记∠CMD 为∠1,∠BND 为∠2.
①如图 2,当α=30°,求∠2-∠1的值;
②当3∠1+∠2<160°时,求α的取值范围.
期末压轴题13
1.如图,长为4、宽为3的长方形ABCD 内有一正方形 BEFG.若直线 AF 将长方形的面积分为1 :3的两部分,则正方形的边长为 ( )
A. 1 B. 1.2 C. 1.4 D. 1.6
2.如图,已知线段 AB 与直线 BC 的夹角∠ABC=75°,D 是直线 BC 上的一个动点,平移线段 AB,使点 B 移到点 D 的位置,得到线段 DE,连接BE,再将△BDE沿BE 折叠,点 D 落在点 F 处.若 BF 平分∠ABE,则∠BED 的度数为 .
3.我们规定,若一元一次方程的解在一元一次不等式组解集范围内,则称该一元一次方程为该不等式组的“关联方程”,例如:x--1=2的解为 的解集为--3≤x<4,不难发现x=3在-3≤x<4的范围内,所以x-1=2是 的“关联方程”.
问题解决:
(1) 方程 3x + 3 = 6 是 不 等式组 的“关联方程”吗 请说明理由.
(2)若关于x的方程2x+k=2是不等式组 的“关联方程”,求k的取值范围.
(3)若关于x的不等式组 的所有“关联方程”只有 3 个不同整数解,试求m的取值范围.
期末压轴题14
1. 如图,点 B,C分别在AM,AN 上运动(不与点 A 重合),CD 是∠BCN 的平分线,CD 的反向延长线交∠ABC 的平分线于点 P. 现给出下列条件:①∠ABC +∠ACB 的值;②∠A 的值;③∠NCD一∠ABP 的值;④∠ABC 的值.其中不能求出∠P 大小的是 ( )
A. ① B. ② C. ③ D. ④
2.小聪在学习完乘法公式后,发现完全平方公式经过适当的变形或数形结合,可以解决很多数学问题.如图摆放两个正方形卡片,点A,M,B在同一直线上.若AB=5,且两个正方形面积之和为13,则阴影部分的面积为 .
3.定义:在一个三角形中,如果一个内角α的度数比另一个内角度数大36°,那么这样的三角形我们称为“似黄金三角形”,其中α称为“黄金角”.例如:一个三角形三个内角的度数分别是 30°,84°,66°,这个三角形就是“似黄金三角形”,其中 66°为“黄金角”.
(1)一个“似黄金三角形”的一个内角为92°,若“黄金角”为锐角,则这个“黄金角”的度数为 .
(2) 如图1,在△ABC中,∠A=70°,∠B=60°,D 为线段 AB 上一点(点 D 不与点A,B 重合).若△BCD 是“似黄金三角形”,求∠BDC 的度数.
(3)如图 2,在△ABC 中,点 D 在边 AB上,DE 平分∠ADC 交AC 于点E,过点 E 作 EF∥AB 交CD 于点 F,且∠DEF=∠B.若△BCD 和△ACD都是“似黄金三角形”,直接写出∠A的度数.
期末压轴题15
1.如图是可调躺椅示意图(数据如图),AE与 BD 的交点为 C,且∠CAB,∠CBA,∠D 的大小保持不变.为了舒适,需调整∠E 的大小,使∠EFD = 110°,则图中∠E 应 ( )
A. 增加10° B. 减少10°
C. 增加20° D. 减少20°
2.定义一种新的取整符号[],即[x]表示不超过 x 的最大整数.例如:[2.3]=2,[--1.7]=-2.有下列结论:①[-2.1]+[0.99]=--3;②[x]+[-x]=0;③若[x+1]=3,则x的取值范围是2≤x<3;④方程 的解有无数多个.其中正确的是 (填序号).
3.如图1,直角三角板 DEF 与直角三角板ABC 的斜边在同一直线上,∠EDF=30°,∠ABC=45°,∠ACB=∠E=90°,CD 平分∠ACB,△ABC 不动,将△DEF 绕点D 按逆时针方向旋转,记∠ADF 为α ,在旋转过程中:
(1) 如图2,当α= 时,DE∥BC;当α= 时,EF∥AB.
(2)将△DEF 绕点 D 按逆时针方向旋转到如图3的位置,边 DE 与BC 延长线交于点 P,边 DF 与AC 交于点Q,求∠BPD+∠AQD 的值.
(3)当顶点C 不在△DEF 内部时,α的取值范围是 (三角形的内部不包含三角形的边).
(4)在旋转过程中,当α的度数为 时,△DEF 的一边与AC平行.
期末压轴题16
1.为了传承中华民族传统文化,邗江区某学校组织“端午”知识微竞赛.竞赛的试题由6道判断题组成,参赛人员只要画“ ”或画“×”表示出对各题的正误判断即可,每小题判断正确得1分,判断错误得0分.竞赛 A小组共有甲、乙、丙、丁四位同学,他们对6道试题的判断与得分的结果如下图所示,由此可以推断丁同学的得分为 ( )
项目 第 1题 第2题 第3 题 第 4 题 第 5题 第 6题 得分
甲 ∨ 4 分
乙 4 分
丙 ∨ 4 分
丁
A. 6分 B. 5分
C. 4分 D. 3分
2.若关于x的不等式组 至少有 4个整数解,且关于 y 的方程2+my=10-y的解为整数,则所有满足条件的整数m 的值之和为 .
3.在七年级的“平行线的性质与判定”的学习中,我们常借助于三角板来研究其相关知识,现有一副三角板如图 1 所示,其中∠ACB=∠EDF=90°,∠A=30°,∠E=45°.请同学们结合已有的知识及活动经验,解决下列问题:
【初步感知】
(1)如图2,将上述三角板的直角顶点重合在一起.当CE∥AB时,∠BCF= .
(2) 如图3,当CA 平分∠ECF 时,请写出图中两条平行的直线,并说明理由.
【深度探究】
(3)将上述三角板按图4 所示的方式摆放,点A,B 在直线GH 上,点D,F 在直线 MN 上,直线GH∥MN,保持三角板ABC 不动,现将三角板 DEF 绕点D 以每秒3°的速度顺时针旋转,设旋转时间为 t s,且0≤t≤60,则是否存在 t 的值,使边 BC 与另一块三角板DEF 的一条边平行 若存在,请求出 t 的值;若不存在,请说明理由.
(4)将上述三角板按图5 所示的方式摆放,点C 与点 D 重合,保持三角板ABC 不动,将三角板 DEF 绕点 C 旋转,使点 F 在直线BC 上方,当两块三角板的两条边互相平行时,若∠BCF度数的最大值为m,最小值为 n,则m-n= .
期末压轴题17
1.如图,在2×2的方格纸中有一个以格点为顶点的△ABC,则与△ABC 成轴对称且以格点为顶点的三角形共有 ( )
A. 3个 B. 4个 C. 5个 D. 6个
2. 已 知6 = 192, 32” = 192, 则
3. 已知△ABC,点 D 在直线 AB 上,连接CD.
(1) 如图1,若∠ACB=90°,CD⊥AB.求证:∠ACD=∠ABC.
(2) 若∠ACD=∠ABC,∠BAC 的平分线与CB,CD分别交于点E,F.
①如图2,当点 D 在边AB 上(不与点A,B 重合)时,求证:∠CFE =∠CEF.
②当点 D 在 AB 的延长线上时,“∠CFE=∠CEF”是否依然成立 画出图形,并说明理由.
期末压轴题18
1.如图,边长相等的正五边形和正n边形(n>5)拼接在一起,则∠ACB 的度数可能是 ( )
A. 54° B. 30° C. 24° D. 18°
2.有两个数值转换机 A、B、将数字x输入数值转换机 A,则可得 如:输入数字3、则输出数字为1;输入数字-11,则输出数字为-3.将数字y输入数值转换机 B,则可得不大于 y 的最大整数,如:输入3.14,则输出数字为3;输入一1.414,则输出数字为-2.现将某整数 m 先输入数值转换机A,再将输出的数字输入数值转换机 B,发现从数值转换机 B输出的数字为5,则符合条件的整数m有 个.
3.【项目式学习】
项目主题:数学智慧拼图
项目背景:为了缓解同学们的学习压力,提高思维能力,增强学习兴趣,并促进同学们的全面发展,王老师将数学学习小组分成三组,每组领取一些矩形卡片,开展以“数学智慧拼图”为主题的项目式学习.
任务一:观察建模
(1)如图1,第一小组领了8个大小、形状完全相同的小矩形,拼成一个大矩形,每个小矩形的长和宽分别为y,x(x
(2)第二小组也领了8个大小、形状完全相同的小矩形,把它们按图2方式放置在一个大矩形中,求图2中阴影部分的面积.
任务三:设计方案
(3)第三小组领了A,B,C三种类型的矩形卡片,它们的长都为 18.宽分别为a,b,c,其中a
1.如图,甲、乙两名同学玩抢硬币游戏,将7枚硬币排成一行,两人轮流从中取一枚或相邻的两枚硬币,如果两枚硬币中间有空位,那么不能将这两枚硬币同时拿走,谁取走最后一枚硬币谁就获胜.如果甲同学先取,并确保获胜,那么甲会先取 ( )
A. 2号 B. 3号
C. 4号 D. 5号或6号
2.如果一个三角形的一个内角等于另一个内角的2倍,我们称这样的三角形为“倍角三角形”.若△ABC 为“倍角三角形”,∠A=100°,则∠B 的度数为 .
3.【观察计算】用等号或不等号填空:
……
【猜想说明】
(2)仿照上面,再任意取几组数值,进行计算比较,你能发现什么大小关系,请用不等式进行表达,并说明理由.
【思考应用】
(用等号或不等号填空).
(4)如图,已知一个长方形的面积为16,分别以它的宽和长(宽和长不相等)为边向外画正方形,记这两个正方形的面积分别为S ,S ,则 的取值范 围是 .
S
S 16
期末压轴题20
1. 如图,在四边形ABCD 中,AB=AD,点B关于AC 的对称点B'恰好落在CD 上.若∠BAD=α,则∠ACB 的度数为 ( )
A. 45°
·2.某校奖励学生:七年级获奖学生中,有一人获奖品3件,其余每人获奖品7件;八年级获奖学生中,有一人获奖品4件,其余每人获奖品9件.如果两个年级获奖人数不等,但奖品数目相等,且每个年级奖品数大于50而不超过 100,那么两个年级获奖学生共有 人.
3. 如图1,由线段AB,AM,CM,CD 组成的图形像∑,称为“∑形 BAMCD”.
(1) 如图2,在“∑形 BAMCD”中,若AB∥CD,∠AMC=70°,则∠A +∠C= °.
(2) 如图3,在“∑形BAMCD”中,若AB∥CD,∠AMC =70°,则∠C--∠A = °.
(3) 如图4,连接“∑形BAMCD”中的 B,D 两点,若∠ABD+∠BDC=160°,∠AMC=α,试猜想∠BAM 与∠MCD的数量关系,并说明理由.
(4)在(3)的条件下,当点 M 在射线 BD上从上向下移动的过程中,请直接写出∠BAM 与∠MCD 所有可能的数
量关系.
期末压轴题21
1. 设a,b为有理数,多项式(x+a)(2x+b)展开后x 的一次项系数为p,多项式(2x+a)(x+b)展开后x 的一次项系数为q.若p+q=6,且p,q均为正整数,则( )
A. ab 与 的最大值相等,ab 与a/b的最小值也相等
B. ab 与a/b的最大值相等, ab 与a/b的最小值不相等
C. ab 与a/b的最大值不相等, ab 与a/b的最小值相等
D. ab与a/b的最大值不相等, ab 与a/b的最小值也不相等
2.如图,在△ABC 中有两个内角相等,且BD 是△ABC 的角平分线,点 E 在 BD上,DF∥BC,交AE于点F.若∠DAE=3∠BAE,∠ADF=3∠EDF,则∠BAE 的度数为 .
3.【新知情境】如图 1,在△ABC 中,∠B=∠C,点 P,Q 分别在AB,AC上.若边 BC上存在一点O,满足∠POQ=∠B,则称O是△ABC 的“一线三等角点”.
【理解新知】
(1) 如图2,在△ABC中,∠B=∠C,AD是边 BC 上的高,DE 是△ABD 中边AB 上的高.求证:D 是△ABC 的“一线三等角点”.
(2)如图1,在【新知情境】的条件和结论下,求证:∠BPO=∠COQ.
【操作探究】
(3) 如图3,在△ABC 中,∠B=∠C,点P,Q 分别在 AB,AC 上. 点 D 在△ABC 内,且∠PDQ=∠B.
①由于点 D 不在边BC 上,所以点 D不是△ABC 的一个“一线三等角点”.小明想沿着 QD 方向,将∠PDQ 平移到 BC 上,使得点 D的对应点为 D ,平移后的∠PDQ的边DP 与AB 的交点为点 P .请用无刻度的直尺和圆规作出∠P D Q.(不写作法,保留清晰的作图痕迹,标明字母)
②如图4,若∠B=∠C=∠PDQ=α(0°<α<60°),∠BPD 与∠CQD的平分线所在直线交于点 E,直接写出∠PEQ与α之间的数量关系.
期末压轴题1
1. B 提示:由题图,得 所以S 一S =[-b(AB-a)]-[-b(AD-a)]=b(AD-AB).因为 所.以 所以
2. 70°提示:设 由翻折的性质,得 因为 所以∠C'DE= 所以. .由翻折的性质,得 因为 DE∥AC,DF∥AB,所以∠C=∠BDE=x°,∠B=∠CDF= 由三角形的内角和定理,得∠A=180°一∠C-∠B=70°.
3. 解:(1)15 提示:如图1,延长DF 交BC 于点 M.因为 BC∥DE,∠D=45°,所以∠CMD=∠D=45°.由三角形外角的性质,得∠BFM=∠CMD -∠B=15°,所以∠DFA=∠BFM=15°.
(2) 补全图形如图2所示,∠END= 22.5°.提示:过点 N 作 NQ∥BC.设∠END=α,∠DNQ=β,则∠ENQ=α+β.因为EG∥BC,所以 EG∥BC∥NQ,所以∠GEN=∠ENQ=α+β,∠MDB=∠DNQ=β.因为 EN 为∠GED 的平分线,DM 为∠FDB 的平分线,所以∠GED=2∠GEN=2(α+β),∠FDB=2∠MDB=2β.又因为∠EDF=45°,所以∠EDB= . 因为 EG∥BC,所以∠GED=∠EDB,即2(α+β)=45°+2β,解得α=22.5°.所以∠END=α=22.5°.
(3) ①15°或165° 提示:分情况讨论:如图3,当△ABC 绕点B 逆时针旋转,第一次满足BC∥DE 时,由题意可知.点D,F,B在同一条直线上.因为 BC∥DE.所以∠CBD=∠D=45°,又因为∠ABC=30°,所以∠ABF=∠CBD-∠ABC=15°.由三角形外角的性质.得∠DFA-∠FAB=∠ABF =15°.如图 4,当△ABC 绕点B 逆时针旋转,第二次满足 BC∥DE时,同理由题意可知,点D,F,B在同一条直线上.因为BC∥DE,∠D=45°,所以. 所以∠ABF=∠CBD+∠ABC=165°,由三角形外角的性质,得∠DFA-∠FAB=∠ABF=165°.
②25.5°或 154.5°或 100.5°或 79.5°.提示:分情况讨论:如图5,当点Q 在直线BD 左下方时,△ABC 绕点B 逆时针旋转会由现两种情形.设射线EQ交DF 于点 P.因为∠DFE=90°,∠D=45°,所以∠DEF=45°.因为 BQ 是∠ABC 的平分线,EQ 是∠DEF 的平分线,所以 由三角形外角的性质,得∠DPQ=∠EQB+∠PBQ=∠D+∠DEQ=67.5°.又因为∠EQB=27°,所以∠PBQ=∠DPQ-∠EQB=40.5°.所以∠DBA=∠PBQ-∠ABQ=25.5°.易知A,B,A'三点共线,所以. 154.5°.如图6,当点Q 在直线BD 右上方时,△ABC 绕点B 逆时针旋转同样会出现两种情形.设直线 EQ 交DF 于点 P.同理可得, 由三角形的内角和定理,得∠DPQ=180°-∠DEP-∠D=112.5°.由三角形外角的性质,得∠DPQ=∠Q+∠PBQ.又因为∠Q=27°,所以∠PBQ =∠DPQ--∠Q =·85.5°. 所以∠DBA=∠PBQ+∠ABQ=100.5°.易知A,B,A'三点共线,所以∠DBA'=180°-∠DBA=79.5°.综上所述,∠DBA 的度数为25.5°或154.5°或 100.5°或79.5°.
期末压轴2
1. A 提 示:将题 中 方 程 组 整 理,得 运用整体换元的思想,得 解得
提示:如图,连接AE 并延长至点H.因为∠ABG,∠ADF 的平分线BE,DE 相交于点E,所以∠ABG=2∠ABE,∠ADF=2∠ADE.由三角形外角的性质,得∠BEH=∠BAE+∠ABE,∠DEH=∠DAE+∠ADE,α=∠BFD=∠BAD+∠ADF,β=∠DGB=∠BAD+∠ABG,所以α+β=∠BAD+∠ADF+∠BAD+∠ABG=2(∠BAD+∠ADE+∠ABE),所以∠BED=∠BEH+∠DEH=∠BAE+∠ABE+∠DAE +∠ADE =∠BAD +∠ABE +
3. 解:(1) 1 600 1 500
(2)设甲户年用气量为xm ,则乙户年用气量为 由题意,得x>1000-x.解得x>500.所以1 000-x<500.所以 3×400+4(x--400)+3(1000--x)=3200,解得x=600.所以1000-x=400.
答:甲、乙两户年用气量分别是600 m ,400 m .
(3)6 提示:设3人间有a间,4人间有b间,则3a+4b=22.因为a,b均为自然数,所以a=2,b=4或a=6,b=1.由题意可知,3人间年用气量为3×250=750(m ),4人间年用气量为
①当a=2,b=4时,公司需缴纳总天然气费用为2×[3×400+4×(750-400)]+4×[3×500+4×(950-500)+5×(1000-950)]=19 400(元).
②当a=6,b=1时.公司需缴纳总天然气费用为6×[3×400+4×(750-400)]+[3×500+4×(950-500)+5×(1000-950)]=19 150(元).
因为19400>19150,所以要使该公司员工宿舍当年总天然气费最低,则3人间的房间数为6.
期末压轴3
2024年南京市联合体期末压轴题
1. A 提示:由题意可知,原租地面积为 ab m .第二年按照庄园主的想法,则租地面积变为(a+10)·(b-10)= ab-10a+10b-100=[ab-10(a-b)-100]m .因为a>b,所以 ab-10(a-b)-100< ab,所以租地面积会变小.
2. 100 提示:如图,作∠AME 的平分线MK 交OE 于点 K,则 因为 OE 平分∠AEM,所以 所以∠EMK+ 80°,所以 因为 AB∥CD,所以∠AME=∠CFM.因为 OF 平分∠CFM,所以 又因为∠EMK= 所以∠EMK=∠OFM,所以MK∥OF,所以∠O=∠MKE=100°.
— 50 —
3. (1) 135
(2) 证明:因为四边形ABCD 是(B,D)等角四边形,所以∠B=∠D.设∠B=∠D=α.由四边形的内角和为360°,得∠DAB+∠B+∠DCB+∠D=360°,所以∠DAB+∠DCB=360°---2α. 因为 AE 平分∠DAB,CF 平分∠DCB,所以 所以 ∠DCB)=180°-α.由三角形的内角和定理,得∠BCF+∠CFB+∠B=180°,所以∠BCF+∠CFB=180°---α=∠EAB +∠BCF,所以∠EAB=∠CFB,所以AE∥CF.
(3)解:如图,由题意可知,四边形OMPN是(O,P)等角四边形,即∠O=∠MPN,∠OMP≠∠ONP.连接MN,由三角形的内角和定理,得∠O+∠OMN+∠ONM=180°,∠P+∠PMN+∠PNM=180°,所以∠OMN +∠ONM =∠PMN+∠PNM.作法:先构造∠CMN =∠OMN+∠ONM=∠PMN+∠PNM,即作∠OMC=∠ONM;再在∠CMN 内部任作不与射线 MO 重合且∠NMD≠∠ONM 的射线 MD,作∠NME = ∠NMD,∠MNF =∠CMD,射线 ME,NF 交于点 P,则点 P 即为所求.
期末压轴4
2024年苏州市期末压轴题
1. B 提示:因为∠D+∠C=210°,∠DAB+∠ABC+∠C+∠D=360°,所以∠DAB+∠ABC=150°.又因为∠DAB 的平分线与∠CBE 的平分线相交于点 P,所以 165°,所以∠P=180°-(∠PAB+∠ABP)=15°.
2. 180°-α+β或180°+α-β或 180°-α—β 提示:连接AB 交MC 于点D,分三种情况讨论:①如图 1,当点 P 在线段 MD 上时,∠APB =∠APD+∠BPD,因为∠APD=∠M+∠PAM=90°+β,∠BPD=90°-∠PBC=90°-α,所以∠APB=∠APD+∠BPD=90°+β+90°-α=180°-α+β;②如图2,当点P 在线段 CD 上时,同理可得∠APB=∠APM+∠BPM=90°-β+90°+α=180°+α-β;③如图3,当点P 在射线 CN 上时,∠APB=∠APM+∠BPM=90°-β+90°-α=180°-α-β.综上所述,∠APB 的度数为180°-α+β或 180°+α-β或 180°-α-β.
3. 解:(1)2 — 1 提示:因为 T(1,1)=5,T(-1,2)=0,所以 解得
(2)由(1)可知,T(x,y)=2x--y+4.因为T(m,--n)=6,所以2m+n+4=6,所以n=-2m+2,所以T(3m,n)=6m--n+4=6m+2m--2+4=8m+2.因为m>0,n≥0,所以--2m+2≥0,所以0
期末压轴5
2024年无锡市期末压轴题
1. D 提示:如图1,当点A'落在∠MAN 的边AN 上时,由折叠的性质可知,BC 垂直平分AA',所以 .同理,当点 A'落在∠MAN 的边AM上时,. 即△ABC是直角三角形,故①正确.由图 1 可知,∠NA'B+∠A = 但 不一定成立,故②错误.如图2,当点A′落在∠MAN 内部时,连接 AA'. 因为∠MBA',∠NCA'分别是△ABA'和△ACA'的外角,所以. 又因为∠MAN=∠BA'C,所以, 故③正确.如图3,当点A′落在∠MAN的边AN 下方时,分别过点B,A'可作BF∥AN∥A'E,所以∠MBF=∠A, 所以. (设A'B 交边AN于点 P. 因为∠MBA',∠APB 分别是△ABP 和△CPA'的外角,故也可根据三角形外角的性质解之);如图4,当点A'落在∠MAN 的边 AM 上方时,同理可作BF∥AN∥A'E,所以∠MBF=∠A,∠EA'B=∠FBA'= 所以 (设A'C交边AM 于点Q.因为∠NCA',∠AQC 分别是△ACQ 和△BQA'的外角,故也可根据三角形外角的性质解之).所以
故④正确.
2.α+β 提示:由三角形的内角和定理,得∠B=180°-∠BAC-∠BCA=180°-(α+β).因为AD⊥BC,CE⊥AB,所以∠AEC=∠ADB=90°,所以 由三角形外角的性质,得∠APC=∠AEC+∠BAD=α+β.
3. 解:(1)(3,2,-1)
(2)①由题可知,该二元一次方程为3x+ my+n=0.将分别代入3x+ my+n=0,得 解得
②将 代入3x+ my+n=0,得-9+2m+n=0,所以n=9-2m,所以3m+4n=3m+4(9-2m)=36-5m.因为m+n>7,所以m+(9--2m)>7,解得 m<2.所以m<2且m≠0,所以-5m>--10且m≠0,所以36-5m>26且36--5m≠36,即 3m+4n>26且3m+4n≠36.
期末压轴6
2024年常州市期末压轴题
1. A 提示:由题可知,每次平移5个单位长度,n次平移5n个单位长度,即AAn=BBn=5n,所以ABn=AB+BBn=5n+6.
2. y--x=180(n--3)提示:易知n边形的内角和为(n-2)·180°.由题意,得(n-2)×180=y+(180-x),所以y-x=180(n-3).
3. 解:(
(2)∠BPC=α-β-γ.
证法1 如图1,连接 BC.在△ABC中,∠BAC+∠ABC+∠ACB=180°,所以∠ABC+ 在△PBC 中,∠BPC+∠PBC +∠PCB = 180°, 即∠BPC +β+∠ABC+γ+∠ACB =180°,所以∠BPC=180°-(∠ABC+∠ACB)-β-γ=α-β-γ.
证法2 如图2,连接PA 并延长至点D.由三角形外角的性质,得∠BAD=∠BPA+∠PBA =∠BPA +β,∠CAD =∠CPA +∠PCA = ∠CPA + γ. 所 以 ∠BAC =∠BAD+∠CAD=∠BPA+β+∠CPA+γ=∠BPC+β+γ=α,所以∠BPC=α-β-γ.
(3)如图3,∠BPC=α+β+γ;如图4,∠BPC=α+γ-β;如图5,∠BPC=β--α-γ;如图 6,∠BPC =α+β---γ;如图 7,∠BPC=γ-α-β. 提示:连接BC.由题可知,点P 不在直线AB,AC,BC上.易知直线 AB,AC,BC将平面划分为7个区域,除第(1)(2)问两种情况外,还有以下5种情况:
①如图3,由(2)中证法2,得∠BPC=∠BAC+∠PBA+∠PCA=α+β+γ;②如图4,设 PC 交AB 于点O,由三角形外角的性质,得∠BOC=∠BPC+∠PBA=∠BAC+∠PCA,所以∠BPC=∠BAC+∠PCA-∠PBA=α+γ-β;③如图5,设 PC 交直线AB 于点 O,由三角形外角的性质,得∠POB =∠BAC + ∠PCA,∠PBA = ∠BPC + ∠POB =∠BPC+∠BAC+∠PCA,所以∠BPC=∠PBA-∠BAC-∠PCA=β-α-γ;④如图6,同②可得,∠BPC+∠PCA=∠BAC+∠PBA,所以∠BPC=α+β-γ;⑤如图7,同③可得,∠PCA =∠BPC+∠BAC+∠PBA,所以∠BPC=∠PCA-∠BAC-∠PBA=γ-α-β.
期末压轴7
2024年镇江市期末压轴题
1. ①③④ 提示:因为 AD⊥BC,所以∠ADC=90°,所以∠C+∠CAD=90°.因为∠BAD=∠C,所以∠BAD+∠CAD=90°,即∠BAC=90°,故①正确.无法判定∠AEF =∠BEF(仅当 E 为 BC 的中点时,∠AEF=∠BEF),故②错误.因为 AE 平分∠CAD,所以∠DAE =∠CAE. 又因为∠BAD =∠C,所以∠BAD+∠DAE=∠C+∠CAE,即∠BAE=∠BEA,故③正确.因为 EF∥AC,所以∠AEF=∠CAE,所以∠CAD=2∠CAE=2∠AEF.因为∠CAD+∠BAD=90°,∠BAD+∠B=90°,所以∠B=∠CAD=2∠AEF,故④正确.
2. A 提示:设 BC=a,FC=b,则a+b=8,ab=6.由正方形的性质,得CD=BC=a,CG=EG=FC=b,所以 DG=CD-CG=a-b.所以 因为 所以 所以
3. 解:(1) 3 提示:△ABD 和△ACD 为等底等高的三角形,面积均为△ABC 面积的一半.
(2)2 提示:由折叠的性质,得 所以
(3) 因为 BP 平分∠ABC,CP 平分∠ACD,所以 由三角形外角的性质,得∠DCP=∠P+∠CBP,∠ACD=∠ABC+∠A,所以 又因为 所以
(4)由三角形的内角和定理,得∠ABC+∠ACB=180°--∠A =110°,所以∠CBE + 360°--(∠ABC+∠ACB)=250°.因为 BQ平分∠CBE,CQ 平分∠BCF,所以∠CBQ = 所以∠CBQ+ 所以
【应用】如图,延长 DC 至点E,作∠BCE和∠BAF 的平分线交于点 P,则点 P 即为所求.理由如下:
因为l ∥l ,所以∠BAF=∠ABC=100°,∠BCE=∠ADC=60°.因为AP 平分∠BAF,CP平分∠BCE,所以 因为l ∥l ,]所以∠AGB=∠FAP=50°.由三角形外角的性质,得∠P=∠AGB-∠BCP=20°.
2024年镇江市丹徒区期末压轴题
1.α+2β=180° 提示:因为 BF和CG分别是∠ABD 和∠ACE 的平分线,所以∠CBH=∠DBF= 所 以 ∠CBH + 由三角形的内角和定理,得∠H+∠CBH+∠BCH=180°,即 整理,得α+2β=180°.
2. A 提示:当 a=1 时, 解得 斤以x+y=0≠2-1,故①错误.当a=-2时 解得 此时x与y不互为相反数,故②错误.由 解得 若x≤1.即 解得a≥0,所以 0≤a≤1,则 1≤ 即 故③错误.当 时、解得 此时 故④错误.
3.解:【教材回顾】
【知识应用】6 3 提示:由题意,得 27. m-n=3,所以m+n=9,联立方程组,解得m=6,n=3.
【知识迁移】 提示:由题图可知,该正方体被分成的8块分别为:1个棱长为a的小正方体;1个棱长为b的小正方体,3个底面积为a ,高为b的长方体;3个底面积为b ,高为a的长方体.利用大正方体体积的两种算法可得等式.
(2) 对于 令a=3m,b=-n,则( 9mn·(3m-n).将3m-n=4, mn=2代入,得 所以
期末压轴9
2024年南通市期末压轴题
1. C
2.2 提示:设小长方形的长为a、宽为 b.由题意,得 解得 设点 A 到大长方形左边的距离为x,则AB=a-x=5-x,CD=a+3b-u-x=3-x.所以AB-CD=5-x--(3-x)=2.
3. (1) 证明:因为 DE∥BC,所以∠1=∠B,∠2=∠C.因为∠BAC+∠1+∠2=180°,所以∠BAC+∠B+∠C=180°.
(2)证明:如图1,过点 P 分别作PM∥BC交AC于点M,PN∥AC 交BC 于点N,所以∠1=∠B,∠2=∠A,∠3=∠4=∠C.因为∠1+∠2+∠3=180°,所以∠A +∠B+∠C=180°.
解:分情况讨论:①如图2,当点 N 在线段 PD 上时,因为 BD 平分∠PBE,所以∠PBD=∠DBE=α.因为∠ABC=60°,所以∠CBE = ∠ABC - ∠PBE = 60° - 2α,∠CBD=∠ABC-∠PBD=60°--α.因为PE∥BC,所以∠PEB=∠CBE=60°--2α,∠PDB=∠CBD=60°-α.所以∠PNB= .由三角形外角的性质,得∠DBN =∠PNB - ∠PDB =120°--4α-
②如图3,当点 N 在线段DE 上时,同理可得,∠DBN=∠PDB--∠PNB=(60°- .综上所述,∠DBN=60°-3α或∠DBN=3α-60°.
期末压轴10
2024年盐城市期末压轴题
1. C 提示:因为 BA 和CA 分别是∠ABC和∠ACD 的平分线,所以∠ABC=2∠A BC,∠ACD=2∠A CD.由三角形外角的性质,得∠ACD=∠A+∠ABC=∠A+2∠A BC,∠A CD=∠A BC+∠A .所以 ,所以 同理, 所以要使∠A 的度数为整数,则n的最大值为4.
2.52° 提示:由三角形外角的性质,得∠ECQ=∠E+∠EBC,∠FCQ=∠FBC+∠F.因为 BF,CF 分别平分∠EBC,∠ECQ,所以∠EBC=2∠FBC,∠ECQ=2∠FCQ. 所以∠E+∠EBC=2(∠FBC+∠F),即∠E+2∠FBC=2∠FBC+2∠F,所以∠E=2∠F=32°.因为 BE,CE 分别平分∠MBC,∠BCN,所以∠MBC=2∠EBC,∠BCN=2∠BCE,所以∠MBC+∠BCN=2(∠EBC+∠BCE)=2(180°-∠E)=296°,所以 ∠BCN=360°-(∠MBC+∠BCN)=64°.因为 BD,
CD分别平分∠ABC,∠ACB,所以∠ABC=2∠DBC,∠ACB=2∠DCB,所以∠A = 180°--(∠ABC +∠ACB)=180°-2(∠DBC+∠DCB)=52°.
3.解:(1)能,6个正三角形可以共顶点单一密铺.理由如下:
设有x 个正三角形.因为正三角形的每一个内角为 60°,若想用x 个 60°围成 360°,则60x=360,解得x=6.所以6个正三角形可以共顶点单一密铺.
(2)4个正方形可以共顶点单一密铺.理由如下:
设有x个正方形.因为正方形的每一个内角为90°,若想用x个90°围成360°,则 90x=360,解得x=4.所以4个正方形可以共顶点单一密铺.
(3)方案:2个正三角形、2个正六边形或4个正三角形、1个正六边形.理由如下:
设有x 个正三角形、y个正六边形.因为正三角形的每一个内角为60°,正六边形的每一个内角为 若想用x个60°与 y 个 120°围成 360°,则 60x+120y=360.因为x,y均为正整数,所以x=2,y=2或x=4,y=1.
(4)方案:1个正三角形、2个正方形、1个正六边形.理由如下:
设有x个正三角形、y个正方形、z个正六边形.因为正三角形的每一个内角为60°,正方形的每一个内角为90°,正六边形的每一个内角为120°,若想用x个60°、y 个90°与z 个120°围成360°,则60x+90y+120z=360°.因为x,y,z均为正整数,所以x=1,y=2,z=1.
期末压轴11
2024年泰州市靖江市期末压轴题
1. B 提示:①原命题的逆命题为“两直线平行,同位角相等”,是真命题;②原命题的逆命题为“如果两个角相等,那么它们都是直角”,是假命题;③原命题的逆命题为“如果a<0,b<0,那么 ab>0”,是真命题;④原命题的逆命题为“如果两个有理数的平方相等,那么这两个有理数相等”,是假命题.
2. 1 040 提示:设A,B,C三种品牌商品的销售单价分别为x元、y元、z元.由题意,得 解得 所以4x+4y+2z=1040,所以第三天的
总收入为 1 040元.
3. 解:(1) 45°15°提示:如图1,当DF∥AC时,α=∠BDF=∠C=45°;如图2,当 DE⊥AB 时,则 DE∥AC,所以∠BDE=∠C=45°,所以α=∠BDF=∠BDE-∠FDE=15°.
(2) ①因为 α = 30°, 即∠BDF = 30°,∠EDF = 90°--∠F = 30°, 所 以∠CDM =∠BDF=30°,∠BDN=∠BDF+∠EDF=60°,所以∠2=∠BND=180°-∠B-∠BDN=75°.由三角形外角的性质,得∠1=∠CMD =∠ACB-∠CDM=15°.所以∠2-∠1=60°.
②因为当α=45°时, DF∥AC 不合题意,所以分情况讨论:当0°
期末压轴12
2024年泰州市兴化市期末压轴题
1. B 提示:设直线AF 交 BC 于点 H.由题意,得 即 所以 BH=2.设正方形 BEFG 的边长为x,则AG=3-x,EH=2-x.所以 整理,得 解得x=1.2,即正方形的边长为1.2.
2. 50°或70° 提示:分情况讨论:①如图1,当点D 在点 B 的右侧时,因为 BF 平分∠ABE,所以∠ABF=∠EBF.由折叠的性质,得∠EBF=∠EBD.所以 75°=25°.由题可知,DE∥AB.所以∠BED=∠ABE=2∠ABF=2×25°=50°.②如图2,当点 D 在点 B 的左侧时,同理可得 15°或 105°或 135°.
期末压轴15
2024年扬州市邗江区期末压轴题
1. D 提示:由题可知,该测试共有6道题目,每题判断正确得1分,判断错误得0分,甲、乙的得分都是4分,则甲、乙至少有2道题目的结果相同且为正确答案.由题表可知,甲、乙的第3道题和第6道题判断相同,所以第3道题和第6道题的正确答案均为“×”,所以丙的第3道题和第6道题判断错误,而丙也得了4分,说明丙其余题目全部判断正确,所以这6道题目的正确答案是:1×,2 ,3×,4 ,5×,6×.所以丁做对了3道,得了3分.
2. 一14 提示:解关 于 x 的不等式组得 因为该不等式组至少有4个整数解,所以 解得m<-3.解关于y的方程2+ my=10-y,得 因为y为整数,所以m+1的值为±1或±2或±4或±8,即m 的值为0或-2或1或-3或3或-5或7或-9.因为m<-3,所以所有满足条件的整数m的值为-5,-9,其和为--5-9=-14.
3. 解:(1) 30°
(2) BC∥EF.理由如下:
因为 CA 平分∠ECF,∠ECF =90°,所以 因为∠ACB=∠EDF = 90°, 即 ∠ACF + ∠BCF = 90°,∠ACF+∠ACE=90°,所以∠BCF=∠ACE=45°.因为∠F=∠E=45°,所以∠F=∠BCF,所以BC∥EF.
分情况讨论:①如图1,当 DE∥BC时,延长AC 交MN 于点 P,延长 BC 交MN于点Q,则∠PDE=∠PQB.因为MN∥GH,所以∠PQB=∠ABC=90°-∠BAC=60°,所以∠PDE = 60°, 所 以 ∠FDM = 180°-∠EDF--∠PDE = 30°.由题可知,旋转角∠FDM=3t°,所以: 解得t=10.②如图2,当BC∥DF时,延长BC 交MN 于点T.同理可得,∠FDN=∠BTN=∠ABC=60°.所以 解得 t =40.③如图 3,当 EF∥BC 时,设 EF交MN 于点K,延长EF 交GH 于点O.同理可得,∠FKN=∠AOF=∠ABC=60°.由三角形外角的性质,得∠FDN=∠FKN-∠DFE=15°,所以∠FDM=180°-∠FDN= 解得t=55.综上所述,t 的值为10或40或55.
135° 提示:当三角板DEF 绕点C旋转时,因为点 F 在直线BC 上方,所以0°<∠BCF<180°.分情况讨论:①如图4,当AB∥DE 时,∠ACE=∠A=30°.因为∠ACB-∠ACF=∠EDF-∠ACF,所以∠BCF=∠ACE =30°;②如图 5,当 BC∥EF 时,∠BCF=∠F=45°;③如图6,当AB∥DF 时,∠BCF=180°-∠B=120°;④如图 7,当 AC∥EF 时,∠ACF=∠F=45°,所以∠BCF=∠ACF+∠ACB=135°;⑤如图8,当 AB∥EF 时,延长 BC 交 EF 于点 G,则∠CGE=∠B=60°,由三角形外角的性质,得∠GCF=∠CGE-∠F=15°,所以, 165°.综上所述,∠BCF 度数的最大值; 最小值n=30°,所以m-n=135°.
期末压轴16
2024年徐州市期末压轴题
1. C 提示:如图,与△ABC 成轴对称且以格点为顶点的三角形有△ABG,△CDF,△AEF,△DBH,
提示:因为6'=192,32'=192,所以 所以 所以( 即 所以(x-1)(y-1)=1,所以(
3. (1) 证明: 因为 CD⊥AB,所以∠CDB=90°.所以∠ABC+∠BCD=90°.因为∠ACB=90°,所以∠ACD+∠BCD=90°.所以∠ACD=∠ABC.
(2)①证明:由三角形外角的性质,得∠CFE=∠CAE+∠ACD,∠CEF=∠BAE+∠ABC.因为AE 平分∠BAC,所以∠CAE=∠BAE.又因为∠ACD=∠ABC,所以∠CFE=∠CEF.
②解:画出图形,如图所示.∠CFE =∠CEF 依然成立.理由如下:因为 AE 平分∠BAC,所以∠CAE=∠BAE.由三角形的内角和定理,得∠CFE = 180°--∠CAE -∠ACD,∠AEB=180°-∠BAE-∠ABC.又因为∠ACD=∠ABC,所以∠CFE=∠AEB.因为∠CEF=∠AEB,所以∠CFE=∠CEF.
期末压轴17
2024年宿迁市泗阳县期末压轴题
1. C 提示:因为 所以∠BAC=360°- 因为 AB=AC,所以△ABC 为等腰三角形,两底角相等,即∠ABC=∠ACB,所以 因为n>5且为整数,所以若n=6,则∠ACB=24°.验证可知选项A,B,D均不符合题意.
2.4 提示:由题意可知,将整数m输入数值转换机 A,输出的数为 再将 输入数值转换机B,由于从数值转换机 B输出的数字为5,所以5≤ 解得17≤m<20.5,所以整数m 的值为17,18,19,20,共4个.
3. 解:(1) 6 10
(2)设小矩形的长为m、宽为 n.由题意,得 解得 则 13×(5+3n)-8mn=31.
(3)由题意,得
解得 因为a
期末压轴18
2024年宿迁市宿豫区期末压轴题
1. C 提示:甲先取走正中间的1枚(即4号硬币),这样使左右两边硬币形成对称,乙取多少数量的硬币,甲在另一边对称的位置就取相同数量的硬币,乙每取完一次,甲都会再取一次,这样甲会最终取走最后一枚硬币,从而确保获胜.
2. 50°或30°或 或 提示:分情况讨论:当∠A=2∠B 时, 当∠A=2∠C时, 所以. 当∠B=2∠C 时, 解得 当∠C=2∠B 时, ,解得 综上所述,∠B 的度数为 50°或 30°或 或
3. 解:【观察计算】(1) ①= ②> ③>
(2)举例如下:
;用不等式表示为 理由如下:
因为 所以
(3)>
提示:设长方形的长为a、宽为b,则 所以 b .因为a≠b,所以. 即
期末压轴19
2024年淮安市期末压轴题
1. D 提示:如图,连接AB'.设∠ACB=x,∠BAC=y.由轴对称的性质,得 ∠B'AC=∠BAC=y,AB'=AB.因为AB=AD,所以 ,所以△ADB'为等腰三角形,两底角相等,即 因为∠BAD=α,所以∠B'AD=∠BAD-∠B'AB=α-2y.由三角形外角的性质,得 .由三角形的内角和定理,得. 即α--2y+x+y+x+y=180°,解得 即
2.25 提示:设七年级获奖人数为(n+1),八年级获奖人数为(m+1)(n≠m,且n,m均为正整数).由题意,得3+7n=4+9m,即7n=9m+1①.解50<3+7n≤100,50<4+9m≤100,得 所以n的值为7,8,9,10,11,12,13,m的值为6,7,8,9,10.因为满足3+7n=4+9m的解只有n=13,m=10,所以n+1=14,m+1=11.所以两个年级获奖学生共有14+11=25(人).
3. 解:(1) 70 提示:过点 M向左侧作 MN∥AB.因为AB∥CD,所以AB∥MN∥CD,所以∠AMN=∠A,∠CMN=∠C,所以∠A+∠C=∠AMN+∠CMN=∠AMC=70°.
(2) 70 提示:设 AB 与 MC 交于点E.因为AB∥CD,所以∠C=∠MEB.由三角形外角的性质,得∠MEB=∠AMC+∠A.所以∠C=∠AMC+∠A,所以∠C-∠A=∠AMC=70°.
(3) ∠BAM+∠MCD=α+20°.理由如下:
如图1,过点 A 作AP∥CD 交BD 于点P,则∠APB=∠BDC.由三角形的内角和定理,得∠BAP+∠APB+∠ABD =180°,即∠BAP + ∠BDC + ∠ABD = 180°. 因 为∠ABD+∠BDC=160°,所以∠BAP=20°.由(1)可知,∠AMC=∠PAM+∠MCD=α.所以∠BAM + ∠MCD = ∠BAP + ∠PAM +∠MCD=α+20°.
(4) 当点 M 在线段BD 上时,∠BAM+∠MCD=α+20°;当点 C,D 位于AM 两侧时,∠BAM--∠MCD=α+20°;当A,C,M三点共线时,∠BAM--∠MCD=20°;当点 C,D位于AM 同侧时,∠MCD-∠BAM=α-20°.提示:分情况讨论:①当点M 在线段BD上时,由(3)可知,∠BAM+∠MCD=α+20°.②如图2,当点C,D 位于 AM 两侧时,延长 BM 至点 O. 因为∠ABD +∠BDC=160°,∠CDM+∠BDC=180°,所以∠CDM-∠ABD=20°. 由三角形外角的性质,得∠AMO=∠ABD+∠BAM,∠CMO=∠MCD+∠CDM.所以α=∠AMC =∠AMO - ∠CMO = ∠ABD +∠BAM -(∠MCD+∠CDM)=∠BAM-∠MCD - 20°,即∠BAM-∠MCD=α+20°.③当A,C,M三点共线时,∠AMC=α=0°.由四边形内角和为 360°,得∠ABD+∠BDC+∠BAM+∠ACD=360°. 因为∠ABD +∠BDC=160°,所以∠BAM+∠ACD=200°. 因为∠ACD+∠MCD=180°,所以∠BAM-∠MCD=20°.④如图3,当点C,D位于AM 同侧时,延长BM 至点O.同理可得,∠CDM--∠ABD =20°,α=∠AMC =∠CMO-∠AMO=∠MCD+∠CDM-(∠ABD+∠BAM) =∠MCD-∠BAM +20°, 即∠MCD -∠BAM=α-20°.
期末压轴20
2024年连云港市期末压轴题
1. A 提示:因为( ,所以p=b+2a,q=2b+a.因为p+q=6,即b+2a+2b+a=6,整理,得a+b=2.所以p=b+2a=a+2,q=2b+a=b+2.因为p+q=6,p与q均为正整数,所以 即 所 以 或 或 或 或 可得 ab=a(2- ,易知当a=1时,ab取得最大值,为l;当a=-1或a=3时, ab取得最小值,为—3.由题意知,当a/b有意义时,b≠0,所以a≠2.因为 所以当b=1时,a/b取得最大值,为1;当b=-1时, ab取得最小值,为-3.
或 提示:设∠BAE=α,∠EDF =β,则∠DAE =3∠BAE =3α,∠ADF =3∠EDF=3β,所以∠BAC=∠DAE+∠BAE=4α.因为DF∥BC,所以∠CBD=∠EDF=β,∠C=∠ADF=3β.因为 BD 是△ABC 的角平分线,所以∠ABC=2∠CBD=2β.分情况讨论:①若∠BAC=∠C,即4α=3β,则 由三角形的内角和定理,得∠BAC+∠ABC+∠C=180°,即4α+2β+3β=180°.将 代入,得 解得 ②若∠ABC=∠BAC,即2β=4α,则β=2α.同理可得,4α+2β+3β=180°,即14α=180°,解得 ③若∠ABC=∠C,即2β=3β,则β=0,易知这种情况不存在,综上所述,∠BAE 的度数为 或
3. (1) 证明:因为 AD 是边 BC 上的高,DE 是 △ABD 中 边 AB 上的高, 所 以∠ADB=∠AED=90°,所以∠B+∠BAD=90°,∠ADE +∠BAD = 90°, 所以∠B =∠ADE.因为∠B=∠C,所以D 是△ABC 的“一线三等角点”.
(2) 证明:因为在△BOP 中,∠B +∠BOP +∠BPO=180°,又因为∠BOP +∠POQ+∠COQ=180°,∠POQ=∠B,所以∠BPO=∠COQ.
(3)解:①如图1,∠P D Q 即为所求.
②2∠PEQ+3α=180°. 提示:如图2,连接EA 并延长至点F.因为∠B=∠C=∠PDQ=α(0°<α<60°),由三角形的内角和定理,得. ∠B--∠C= 180°--2α. 由三角形外角的性质,得∠APE=∠PAF--∠AEP,∠AQE=∠QAF--∠AEQ,所以∠APE+∠AQE=∠PAF--∠AEP+∠QAF-∠AEQ=∠BAC--∠PEQ.因为∠APE=∠BPM,∠AQE=∠CQN,所以∠BPM+∠CQN=∠BAC-∠PEQ.因为∠BPD 与∠CQD 的平分线分别是 PM,QN,所以∠DPM=∠BPM,∠DQN=∠CQN.所以∠DPM+∠DQN=∠BAC-∠PEQ.所以∠APD+∠AQD= 180° - (∠APE +∠DPM) + 180°- 因为∠BAC +∠APD +∠AQD +∠D = 360°,即∠BAC+360°-2(∠BAC-∠PEQ)+α=360°,所以∠BAC=2∠PEQ+α.所以: 即2∠PEQ +3α= 180°.(此题也可连接 AD,通过∠BPD+∠CQD=∠BAC+∠PDQ 解之)
同课章节目录
