2025年成都市中考数学模拟试卷(一)(含解析)
文档属性
| 名称 | 2025年成都市中考数学模拟试卷(一)(含解析) |  | |
| 格式 | docx | ||
| 文件大小 | 259.2KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 通用版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-05-08 05:46:49 | ||
图片预览




文档简介
中小学教育资源及组卷应用平台
2025年成都市中考数学模拟试卷(一)
注意事项:
1.全卷分A卷和B卷,A卷满分100分,B卷满分50分;考试时间120分钟。
2.在作答前,考生务必将自己的姓名、准考证号涂写在试卷和答题卡规定的地方。考试结束,监考人员将试卷和答题卡一并收回。
3.选择题部分必须使用2B铅笔填涂;非选择题部分必须使用0.5毫米黑色签字笔书写,字体工整,笔迹清楚。
4.请按照题号在答题卡上各题目对应的答题区域内作答,超出答题区域书写的答案无效;在草稿纸、试卷上答题均无效。
5.保持答题卡清洁,不得折叠、污染、破损等。
A卷(共100分)
第Ⅰ卷(选择题,共32分)
一、选择题(本大题共8个小题,每小题4分,共32分,每小题均有四个选项,其中只有一项符合题目要求)
1. 实数0,- ,1,- 中,最小的数是
(A)0 (C) 1
2.作为新兴力量,DeepSeek承载着打破国外技术垄断、为中国AI开拓新局的使命,在全球AI竞技场上崭露头角,助力中国迈向AI强国之列.数据显示,随着访问使用量急速上升,在2月1日 Deep-Seek已经成为目前最快突破3000万日活跃用户量的应用程序.则将数据3000万用科学记数法可以表示为
3.下列计算结果为4x 的是
4. 如图,在△CBE和△EAD中,点B,E,A在同一条直线上,∠C=∠AED,CE=ED,只添加一个条件,能判定△CBE≌△EAD的是
(A) ∠B=∠CED
(B) ∠A=∠C
(C) BE=AD
(D) BC=AE
5.中共中央、国务院印发了《教育强国建设规划纲要(2024—2035年)》,其中明确提出了中小学生每天综合体育活动时间不低于2小时的要求.某校为了解学生的综合体育活动情况,对部分学生在一周内的综合体育活动时间统计如下表:
时间/h 12 13 14 15 16
人数 12 20 10 5 3
则这些学生综合体育活动时间的众数和中位数分别是
(A) 13,13 (B) 12,14 (C) 13,15 (D) 13,14
6.如图是小明用两个含45°的全等直角三角形拼成的平行四边形,若BC=10,则BD的长为
7.中国古代数学著作《增删算法统宗》记载:现在有绫3尺,绢4尺,共值4钱8分;又有绫7尺,绢2尺,共值6钱8分,则每尺绫、每尺绢各值多少分 已知1钱等于10分,设1尺绫值x分,1尺绢值y分,则可列方程组为
8. 如图,在Rt△ABC中,∠BAC=90°,按以下步骤作图:①以点A为圆心,AB长为半径作弧,交BC于点D;②分别以点B,D为圆心,大于 BD长为半径作弧,两弧在BC下方交于点E;③连接AE交BC于点F.若BF=2,CF=6,则下列结论错误的是
(A)AF⊥BC
(B)AB=3
(C) ∠B=∠CAF
第Ⅱ卷(非选择题,共68分)
二、填空题(本大题共5个小题,每小题4分,共20分)
9. 若 则x+y= .
10.一个不透明的布袋内有x个白色乒乓球和2个黄色乒乓球,这些球除颜色外无其他差别,若随机摸出一个球是黄色乒乓球的概率为 ,则x的值为 .
11. 如下图,正六边形内接于⊙O,OC⊥AB,OC=3,则⊙O的面积为 .
12.黄金分割是汉字结构最基本的规律,借助如图的正方形田字格书写的汉字“蓉”端庄稳重、舒展美观.已知一条分割线的端点A,B分别在田字格的边MN,PQ上,且AB∥NQ,“蓉”字笔画的第八笔“丶”经过AB的黄金分割点C,即 若 则AC的长为 cm.
13.已知二次函数 的图象经过点 若 ,则b的取值范围是 .
三、解答题(本大题共5个小题,共48分)
14.(本小题满分12分,每题6分)
(1)计算: (2)解不等式组
15.(本小题满分8分)
2025年世界运动会将于2025年8月7日至8月17日在中国四川成都举行,是中国大陆第一次举办世界运动会,项目设置获得批准通过35个正式比赛项目,其中航空运动、体育舞蹈、拔河、轮滑这四个项目最受年轻人喜爱,某校随机抽取部分学生进行“心中最期待的一个项目”调查,并根据选择结果绘制成如下统计图表.
项目 人数
航空运动 120
体育舞蹈 a
拔河 75
轮滑 60
根据图表信息,解答下列问题:
(1)本次参与调查的学生共有 人,表中a的值为 ;
(2)在扇形统计图中,求“轮滑”所占百分比;
(3)若该校共有2500人,请你根据调查结果,估计该校最期待拔河项目的学生人数.
16.(本小题满分8分)
随着音频技术的不断发展,新的麦克风技术和产品不断涌现,用户可以根据自身需求和预算选择合适的品牌和型号.图1是某款桌面麦克风,图2为其侧面示意图,其中话筒AB长为14.5cm,支架OC长为11cm,使用时,用户可以绕点O旋转话筒AB 调节高度.当话筒AB与水平线的夹角为 时,测得点A,C所在直线与桌面DE的夹角为 ,求此时点 B到桌面的距离.(结果精确到0.1cm.参考数据: sin ≈0.47,tan62°≈1.88)
17. (本小题满分10分)
如图,在⊙O中,C是直径AB延长线上一点,D为⊙O上一点,连接CD并延长交⊙O于点E,连接AE,AD,BD,BE.
(1)求证:AC·DB=DC·AE;
(2)若 求tan∠ADE的值.
18. (本小题满分10分)
如图,在平面直角坐标系中,直线y=-x-2与y轴交于点A,与反比例函数 的图象交于点B(b,1),点C在线段AB上(不与点A,B重合),过点C作y轴的平行线交反比例函数的图象于点 D.
(1)求反比例函数的表达式;
(2)将点D沿直线AB 翻折后的对应点为 当点D'落在x轴上时,求点 D 的坐标;
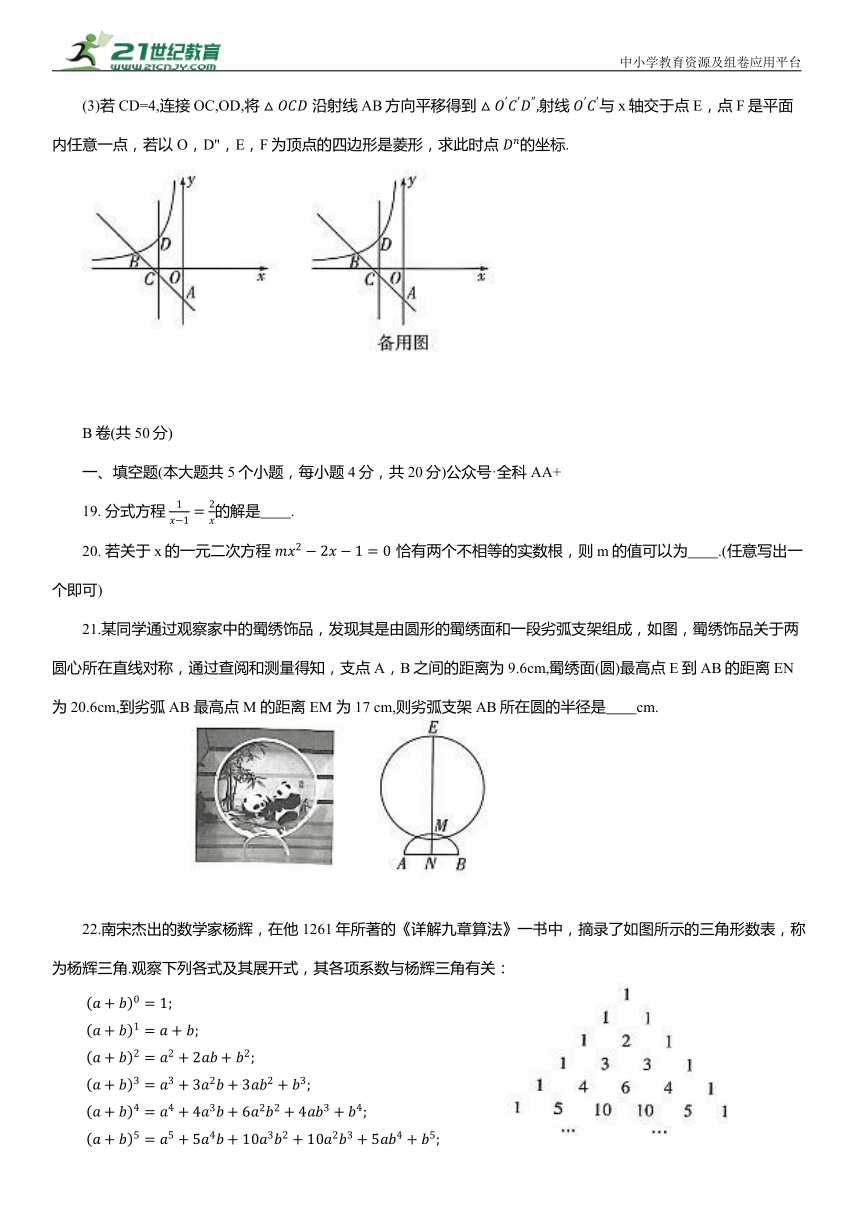
(3)若CD=4,连接OC,OD,将 沿射线AB方向平移得到 射线 与x轴交于点E,点F是平面内任意一点,若以O,D",E,F为顶点的四边形是菱形,求此时点 的坐标.
B卷(共50分)
一、填空题(本大题共5个小题,每小题4分,共20分)公众号·全科AA+
19. 分式方程 的解是 .
20. 若关于x的一元二次方程 恰有两个不相等的实数根,则m的值可以为 .(任意写出一个即可)
21.某同学通过观察家中的蜀绣饰品,发现其是由圆形的蜀绣面和一段劣弧支架组成,如图,蜀绣饰品关于两圆心所在直线对称,通过查阅和测量得知,支点A,B之间的距离为9.6cm,蜀绣面(圆)最高点E到AB的距离EN为20.6cm,到劣弧AB 最高点 M 的距离EM 为17 cm,则劣弧支架 AB所在圆的半径是 cm.
22.南宋杰出的数学家杨辉,在他1261年所著的《详解九章算法》一书中,摘录了如图所示的三角形数表,称为杨辉三角.观察下列各式及其展开式,其各项系数与杨辉三角有关:
…
根据前面各式的规律,则( 的展开式中 的系数是 .
23. 如图,在菱形ABCD中,AB=6,∠ABC=60°,点E在边AB上,且BE=2,点F为边BC上的动点,连接EF,AC.将△BEF 沿 EF 所在直线翻折得到△B'EF,点B'到直线AC的最小距离是 ;连接B'D,则B'D的最小值是 .
二、解答题(本大题共3个小题,共30分)
24.(本小题满分8分)
2024年,我国快递业务量首次突破1700亿件,提高分拣效率、降低分拣成本、提高分拣准确性对于物流公司越发迫切.某快递公司引进了具有分拣功能的智能机器人,发现每台机器人和每个人1小时分拣快递量如下表:
每台机器人 每人 合计(件)
1 小时分拣快递量/件 5x+10 x 730
(1)分别求每个人和每台机器人1小时分拣快递的数量;
(2)若该快递公司每天需要使用机器人分拣10万件快递,一台机器人每天的工作时间为15小时,则至少需要购买多少台机器人才能满足快递公司的需求
25. (本小题满分10分)
如图,在平面直角坐标系xOy中,抛物线 与x轴交于O,A两点,与直线 交于B,C(3,m)两点,对称轴为直线
(1)求抛物线的函数表达式;
(2)P为抛物线上一动点,连接OB,OC,PB,PC,若 求点P的横坐标;
(3)E,F为射线CB上两个动点,作直线OE,OF分别交抛物线于M,N两点(不同于点O),若E,F两点的横坐标之积为3,试探究:直线MN是否经过定点 若经过,请求出该定点的坐标;若不经过,请说明理由.
26. (本小题满分12分)
如图,四边形ABCD是正方形,等腰直角三角形AEF绕着A点旋转,其中 5,连接EB,FC,AC. H为线段EB的中点,连接HF.
(1)证明:
(2)当k=5,E,F,C在一条直线上时,求HF的长;
(3)当点E旋转至线段AB上,要使HF最小,求此时k的值和HF 的长.
1. B 【解析
2. C
3. C
4. D
5. A 【解析】由表格可知,这些学生在一周内的综合体育活动时间为13 h的有20人,人数最多,∴这些学生在一周内的综合体育活动时间的众数是13;∵共有12+20+10+5+3=50(人),∴中位数是将数据按从小到大(或从大到小)的顺序排列后第25,26个数据的平均数,即
6. B 【解析】∵ 四边形ABCD 是平行四边形,∴AO=CO,BO=DO,∵△ABC是等腰直角三角形,∴AC= 在 Rt△BOC 中,BO=
7. D 【解析】由题意可知,绫3尺+绢4尺=48分,可建立方程3x+4y=48;绫7尺+绢2尺=68分,可建立方程7x+2y=68,联立可得方程组为 新考法解读 试题情境取材于《增删算法统宗》,《增删算法统宗》是中国古代重要的数学著作之一.本题将“方程组的实际应用”与“数学文化”相结合,展现了中国古代数学的优秀成果,弘扬传统文化的同时,增强学生对中国古代数学成就的了解,并且为便于学生理解,题干将原题的文言文翻译成现代文,保障了考查的公平性.
8. B 【解析】由尺规作图可知,AF是△ABC 底边 BC上的高线,∴ AF⊥BC,∴ ∠B+∠BAF=90°.∵∠CAF+∠BAF=90°,∴ ∠B =∠CAF.∵ ∠AFB =∠CFA=90°,∴ Rt△ABF∽Rt△CAF,∴AFCF=FAF,∴AF =BF·CF.∵ BF=2,CF=6,∴AF=2 在Rt△ABF中,由勾股定理得,
9. 3 【解析】∵| 解得.x=1,y=2,∴x+y=1+2=3.
10.3 【解析】由题意可知, 解得x=3,经检验x=3是原方程的解,且符合题意,∴x的值为3.
11. 12π 【解析】∵正六边形内接于⊙O,∴ ∠AOB= ×360°=60°,∵OA=OB,OC⊥AB,∴△AOB是等边三角形,∠AOC=30°,在Rt△AOC中,OC=3,∴ ∴⊙O 的面积 =12π.
知识精准回顾
正n边形的内角和为(n-2)×180°,
每个内角均为
【解析】∵四边形 MNQP 是正方形,AB∥NQ,∴四边形 ANQB 是矩形,∴AB=NQ=4 cm.又∵
13. - 2y ,∴b的取值范围为-214. 解:(1)原式 … 4分
=2; ……………………………… 6分
(2)解不等式①,得x>-2, 2分
解不等式②,得x≥1, 4分
故不等式组的解集是x≥1. 6分
15. 解:(1)300,45; 4分
【解法提示】本次调查的学生共有120÷40%=300(人),表中a的值为300-120-75-60=45.
答:在扇形统计图中,“轮滑”所占百分比为20%; 6分
(人),
答:估计该校最期待拔河项目的学生人数为625人. 8分
16. 解:如解图,过点 B 作 BF⊥DE 于点 F,过点 O 作OG⊥BF于点G,过点A作AN⊥BF 于点 N,交OC于点 M,则四边形OMNG 和四边形OCFG均为矩形,
∴OM=GN,OC=GF. 2分
在Rt△ABN中,BN=AB·sin∠BAN=14.5×sin55°≈11.89,
在Rt△AMO中,OM=AM·tan∠OAM,
在Rt△AMC中,CM=AM·tan∠MAC,
则AM·tan∠OAM+AM·tan∠MAC=OM+CM=OC,即 解得,AM≈3.32, 6分
∴OM=AM·tan∠OAM≈4.75,
∴BF=BN-GN+GF=11.89-4.75+11≈18.1,
∴ 点 B 到桌面的距离约为 18.1 cm. ……… 8分
新考法解读 本题以麦克风为背景,让学生通过提取、理解和分析情境中的相关信息,抽离几何图形,设问具有实际意义,体现了数学的应用价值,使考试内容与生活情境相结合,真正考查学生理解和运用所学知识解决问题的能力.教育部《关于加强初中学业水平考试命题工作的意见》和《义务教育数学课程标准(2022 年版)》中均指出:情境创设的真实性.
17. (1)证明:∵四边形AEDB是⊙O 的内接四边形,
∴∠AED+∠ABD=180°,
∵∠ABD+∠DBC=180°,
∴∠DBC=∠AEC,………………………………… 3分
∵∠ACE=∠DCB,
∴△AEC∽△DBC,
∴AC·DB=DC·AE; 4分
(2)解:如解图,连接OE,过点 E作AC 的垂线,垂足为F,
∵∠BEC=∠DAC,∠ECB=∠ACD,
∴△BEC∽△DAC,
. .…… 5分
∵∠C=2∠EAC,∠EOC=2∠EAC,
∴∠C=∠EOC,
∴OE=CE,
∴OF=CF,
设BF=m,BC=n,则OF=CF=m+n,OE=OB=2m+n.
∵在 Rt△BFE中,
在 Rt△OFE中,
即 方程两边同时除以n ,
得
解得 (舍去)或
… 8分
在Rt△BEF中,
∴tan∠ADE=tan∠EBF=EFF=2m=2. 10分
18. 解:(1)将B(b,1)代入y=-x-2中,
解得b=-3,则B(-3,1),
将B(-3,1)代入 中,
解得k=-3,
∴反比例函数的表达式为 …3分
(2)如解图①,连接DD',设.D'(d,0),D(t,- ),
∴ DD'的中点坐标为
解得
由翻折的性质可知,DD'⊥BC,CD=CD',
∴易得∠D'DC=45°,
∴tan∠D'DC=1,
解得t=-2或t=0(舍去), …………………………………………………5分当t=-2时,
∴ 当点 D'落在x轴上时,点D 的坐标是 6分
(3)如解图②,连接OO',设点 C 的坐标是(c,-c-2),则点 D 的坐标是
∵CD=4,
解得c=3(舍去)或c=-1.
∴点C 的坐标是(-1,-1),点 D 的坐标是(-1,3).
设直线 OC 的表达式为y= mx,将点 C(-1,-1)代入,得-1=-m,解得m=1,
∴ 直线OC 的表达式为y=x,根据平移的性质可得O'C'∥OC,
∴设直线 O'C'的表达式为y=x+n.
∵直线AC的表达式是y=-x-2,OO'∥AC,
∴直线OO'的表达式为y=-x.
设平移后点 O'的坐标为(a,-a),其中a<0,则点D"(a-1,-a+3),
将点O'的坐标代入y=x+n,得-a=a+n,解得n=-2a,
∴直线O'C'的表达式为y=x-2a,当y=0时,x=2a,
∴E(2a,0),
4a+10,
以O,D",E,F为顶点的四边形是菱形时,分三种情况讨论:
①当D"E 为菱形的对角线时,OE=OD",
,解得a=-5或a=1(舍去),则点 D"(-6,8); 7分
②当OD"为菱形的对角线时,OE=D"E,
解得 或 (舍去),则点 ……………………… 8分
③当OE 为菱形的对角线时,OD"=D"E,
解得a=0(舍去), 9分
∴此种情况不存在.
综上所述,点D"的坐标为(-6,8)或( ). 10分
19. x=2 【解析】解 去分母,得x=2(x-1),去括号,得x=2x-2,解得x=2,检验:把x=2代入得,x(x-1)≠0,∴x=2是原分式方程的解.
20. 1(答案不唯一,m>-1,且m≠0即可) 【解析】由题可得 且m≠0,∴m>-1,且m≠0.
21. 5 【解析】设 P,Q分别为两圆心,连接NQ,AQ.由题意可知点E,P,M,N,Q在同一直线上,MN=EN 在Rt△ANQ中,设AQ=r cm,则.NQ=(r-3.6) cm,由勾股定理得, 解得r=5,∴劣弧支架AB所在圆的半径是5cm .
22.81 【解析】依据规律可得到 的展开式的系数是杨辉三角第7行的数,第7行的数分别为1,6,15,20,15,6,1.
解题思路引导
观察所给展开式的系数和杨辉三角中各数的关系,先写出所求展开式中的系数
展开式中x 的系数为 135,同理( 展开式中x 的系数为10×9× 展开式中x 的系数为6×9 展开式中x 的系数为3×9 展开式中x 的系数为1×9=9,∴ 原式展开式中x 的系数为135-90+54-27+9=81.
解题思路引导
根据发现的规律得出每个展开式中x 的系数,进行相加
【解析】如解图①,∵ EB'=EB=2,∴点 B'在以点 E 为圆心,半径为2 的圆弧上运动.
解题思路引导
根据点 B'的运动轨迹,再结合直线外一点与直线上各点连接的所有线段中,垂线段最短求解.
过点 E作 EI⊥AC 于点I,当点 B'位于线段 EI 与圆弧的交点处时,点B'到AC的距离最小,为B'I的长,∵四边形 ABCD 是菱形,∠ABC =60°,∴△ABC为等边三角形,∠BAC=60°.∵AE=AB-BE 即点 B'到直线AC 的最小距离是 如解图②,同理,点B'在以点 E 为圆心,半径为2的圆弧上运动.连接ED,当点 B'位于 ED 与圆弧的交点处时,B'D的值最小.
解题思路引导
根据圆外一点到圆上的最短距离为点与圆心形成的线段减去半径的长即可求解.
过点 E 作 EK⊥DA 交 DA 的延长线于点 K.∵ 四边形ABCD 是菱形,∴AD∥BC,∴∠KAE=∠ABC= 2 ,∴ DK=AD+AK=8,∴ DE = √DK +EK = ,即B'D 的最小值是
【解题妙招】
已知:如图,点E 为⊙O 上一动点,D为平面内不在⊙O上的一点.
计算:DE 的最大、最小值.
作辅助线:如图,作直线OD 交⊙O 于两点 E',E".
结论:DE'即为 DE 的最小值,DE"即为 DE 的最大值.
24. 解:(1)由题意,可列方程:5x+10+x=730,解得x=120, …………………………………… 3分
∴5x+10=5×120+10=610(件),
答:每个人1小时分拣快递的数量为120件,每台机器人1小时分拣快递的数量为610件;…4分(2)设需要购买y台机器人,
则15×610y≥100 000,
9 150y≥100 000,
…………………… …6分
∵y为正整数,
∴y的最小值为11,
答:至少需要购买11台机器人才能满足快递公司的需求.……………………………………………8分
25. 解:(1)由题知 则C(3,-3),… ………………… 1分根据题意,得 解得
∴ 抛物线的函数表达式为 …… 3分
(2)如解图①,过点 P 作 PQ⊥x轴交 BC 于点 Q,记BC与y轴交于点 T.
将x=0代入直线
得 则
设 则
∴PQ=2OT=3,………………………………… 4分
5分
解得
故点P的横坐标为1或 3
……………………………………………… 6分
(3)直线MN经过定点.如解图②,设 直线MN的表达式为y= kx+n(k≠0),
直线OE 的表达式为y=k x,直线OF的表达式为
解得
∴直线OE 的表达式为
联立直线 OE与 BC 的表达式,得 解得 ……………………… 7分
同理得
即
联立直线MN与抛物线的函数表达式,整理得 (k-2)x+n=0,
, 8分
∴4n-10(2-k)+25=3,∴n=- k-
∴直线 MN的表达式为
∴直线MN经过定点 … 10分
26. (1)证明:∵△AEF与△ABC为等腰直角三角形, 且∠EAF=∠BAC=45°,
∴ ∠EAF-∠BAF = ∠BAC - ∠BAF, 即 ∠EAB=∠FAC,
∴△AEB∽△AFC; 3分
(2)解:当点 E 在点 F 上方时,如解图①,过点 H作HM⊥EC,垂足为M.
∵AB=kAE=5,k=5,
在Rt△AEC中,由勾股定理得,
∵EF=AE=1,
∴FC=EC-EF=7-1=6.
由(1)可知,△AEB∽△AFC,
∴EB=3 ,∠BEF=∠AEB-∠AEF=45°,
∵H为线段EB的中点,
由HM⊥EC,∠BEF=45°,可知△EHM 为等腰直角三角形,
在Rt△HMF中, ……………………………… 5分
当点 F 在点 E 的上方时,如解图②,过点 H 作 HN垂直EC于点N,
同理易得 E
由(1)可知,△AEB∽△AFC,
∴∠ABE=∠ACF,
∵∠ABC+∠BCA=135°,
∴∠EBC+∠BCE=135°,
∴∠BEC=45°,
则HN=EN=2,FN=3,
综上所述,HF 的长为 或 … 7分
(3)解:如解图③,延长EF至点M,使得FM=EF,连接AM,BM.
∵H为EB的中点,FM=EF,
∴HF为△EBM的中位线,
∵AE=EF=FM,∠AEM=90°,
∵AD∥EM,
∴ ∠MAD 为定角. 9分
如解图④,因此点 M 的轨迹在射线AM 上,故当BM⊥AM时,MB最小,
此时 最小.
则∠BAM+∠DAM=90°,∠ABM+∠BAM=90°,∴ ∠MAD=∠ABM.
在Rt△ABM中,设AM=x,则BM=2x,
得
10分
在 Rt△AEM中, ,设AE=EF=FM=a,则
解得a=1(负值已舍去),
∴AE=EF=1,
∵AB=kAE=5,
∴k=5.
综上所述,当HF 最小时,此时k的值为5,HF 的长为 . 12分
2025年成都市中考数学模拟试卷(一)
注意事项:
1.全卷分A卷和B卷,A卷满分100分,B卷满分50分;考试时间120分钟。
2.在作答前,考生务必将自己的姓名、准考证号涂写在试卷和答题卡规定的地方。考试结束,监考人员将试卷和答题卡一并收回。
3.选择题部分必须使用2B铅笔填涂;非选择题部分必须使用0.5毫米黑色签字笔书写,字体工整,笔迹清楚。
4.请按照题号在答题卡上各题目对应的答题区域内作答,超出答题区域书写的答案无效;在草稿纸、试卷上答题均无效。
5.保持答题卡清洁,不得折叠、污染、破损等。
A卷(共100分)
第Ⅰ卷(选择题,共32分)
一、选择题(本大题共8个小题,每小题4分,共32分,每小题均有四个选项,其中只有一项符合题目要求)
1. 实数0,- ,1,- 中,最小的数是
(A)0 (C) 1
2.作为新兴力量,DeepSeek承载着打破国外技术垄断、为中国AI开拓新局的使命,在全球AI竞技场上崭露头角,助力中国迈向AI强国之列.数据显示,随着访问使用量急速上升,在2月1日 Deep-Seek已经成为目前最快突破3000万日活跃用户量的应用程序.则将数据3000万用科学记数法可以表示为
3.下列计算结果为4x 的是
4. 如图,在△CBE和△EAD中,点B,E,A在同一条直线上,∠C=∠AED,CE=ED,只添加一个条件,能判定△CBE≌△EAD的是
(A) ∠B=∠CED
(B) ∠A=∠C
(C) BE=AD
(D) BC=AE
5.中共中央、国务院印发了《教育强国建设规划纲要(2024—2035年)》,其中明确提出了中小学生每天综合体育活动时间不低于2小时的要求.某校为了解学生的综合体育活动情况,对部分学生在一周内的综合体育活动时间统计如下表:
时间/h 12 13 14 15 16
人数 12 20 10 5 3
则这些学生综合体育活动时间的众数和中位数分别是
(A) 13,13 (B) 12,14 (C) 13,15 (D) 13,14
6.如图是小明用两个含45°的全等直角三角形拼成的平行四边形,若BC=10,则BD的长为
7.中国古代数学著作《增删算法统宗》记载:现在有绫3尺,绢4尺,共值4钱8分;又有绫7尺,绢2尺,共值6钱8分,则每尺绫、每尺绢各值多少分 已知1钱等于10分,设1尺绫值x分,1尺绢值y分,则可列方程组为
8. 如图,在Rt△ABC中,∠BAC=90°,按以下步骤作图:①以点A为圆心,AB长为半径作弧,交BC于点D;②分别以点B,D为圆心,大于 BD长为半径作弧,两弧在BC下方交于点E;③连接AE交BC于点F.若BF=2,CF=6,则下列结论错误的是
(A)AF⊥BC
(B)AB=3
(C) ∠B=∠CAF
第Ⅱ卷(非选择题,共68分)
二、填空题(本大题共5个小题,每小题4分,共20分)
9. 若 则x+y= .
10.一个不透明的布袋内有x个白色乒乓球和2个黄色乒乓球,这些球除颜色外无其他差别,若随机摸出一个球是黄色乒乓球的概率为 ,则x的值为 .
11. 如下图,正六边形内接于⊙O,OC⊥AB,OC=3,则⊙O的面积为 .
12.黄金分割是汉字结构最基本的规律,借助如图的正方形田字格书写的汉字“蓉”端庄稳重、舒展美观.已知一条分割线的端点A,B分别在田字格的边MN,PQ上,且AB∥NQ,“蓉”字笔画的第八笔“丶”经过AB的黄金分割点C,即 若 则AC的长为 cm.
13.已知二次函数 的图象经过点 若 ,则b的取值范围是 .
三、解答题(本大题共5个小题,共48分)
14.(本小题满分12分,每题6分)
(1)计算: (2)解不等式组
15.(本小题满分8分)
2025年世界运动会将于2025年8月7日至8月17日在中国四川成都举行,是中国大陆第一次举办世界运动会,项目设置获得批准通过35个正式比赛项目,其中航空运动、体育舞蹈、拔河、轮滑这四个项目最受年轻人喜爱,某校随机抽取部分学生进行“心中最期待的一个项目”调查,并根据选择结果绘制成如下统计图表.
项目 人数
航空运动 120
体育舞蹈 a
拔河 75
轮滑 60
根据图表信息,解答下列问题:
(1)本次参与调查的学生共有 人,表中a的值为 ;
(2)在扇形统计图中,求“轮滑”所占百分比;
(3)若该校共有2500人,请你根据调查结果,估计该校最期待拔河项目的学生人数.
16.(本小题满分8分)
随着音频技术的不断发展,新的麦克风技术和产品不断涌现,用户可以根据自身需求和预算选择合适的品牌和型号.图1是某款桌面麦克风,图2为其侧面示意图,其中话筒AB长为14.5cm,支架OC长为11cm,使用时,用户可以绕点O旋转话筒AB 调节高度.当话筒AB与水平线的夹角为 时,测得点A,C所在直线与桌面DE的夹角为 ,求此时点 B到桌面的距离.(结果精确到0.1cm.参考数据: sin ≈0.47,tan62°≈1.88)
17. (本小题满分10分)
如图,在⊙O中,C是直径AB延长线上一点,D为⊙O上一点,连接CD并延长交⊙O于点E,连接AE,AD,BD,BE.
(1)求证:AC·DB=DC·AE;
(2)若 求tan∠ADE的值.
18. (本小题满分10分)
如图,在平面直角坐标系中,直线y=-x-2与y轴交于点A,与反比例函数 的图象交于点B(b,1),点C在线段AB上(不与点A,B重合),过点C作y轴的平行线交反比例函数的图象于点 D.
(1)求反比例函数的表达式;
(2)将点D沿直线AB 翻折后的对应点为 当点D'落在x轴上时,求点 D 的坐标;
(3)若CD=4,连接OC,OD,将 沿射线AB方向平移得到 射线 与x轴交于点E,点F是平面内任意一点,若以O,D",E,F为顶点的四边形是菱形,求此时点 的坐标.
B卷(共50分)
一、填空题(本大题共5个小题,每小题4分,共20分)公众号·全科AA+
19. 分式方程 的解是 .
20. 若关于x的一元二次方程 恰有两个不相等的实数根,则m的值可以为 .(任意写出一个即可)
21.某同学通过观察家中的蜀绣饰品,发现其是由圆形的蜀绣面和一段劣弧支架组成,如图,蜀绣饰品关于两圆心所在直线对称,通过查阅和测量得知,支点A,B之间的距离为9.6cm,蜀绣面(圆)最高点E到AB的距离EN为20.6cm,到劣弧AB 最高点 M 的距离EM 为17 cm,则劣弧支架 AB所在圆的半径是 cm.
22.南宋杰出的数学家杨辉,在他1261年所著的《详解九章算法》一书中,摘录了如图所示的三角形数表,称为杨辉三角.观察下列各式及其展开式,其各项系数与杨辉三角有关:
…
根据前面各式的规律,则( 的展开式中 的系数是 .
23. 如图,在菱形ABCD中,AB=6,∠ABC=60°,点E在边AB上,且BE=2,点F为边BC上的动点,连接EF,AC.将△BEF 沿 EF 所在直线翻折得到△B'EF,点B'到直线AC的最小距离是 ;连接B'D,则B'D的最小值是 .
二、解答题(本大题共3个小题,共30分)
24.(本小题满分8分)
2024年,我国快递业务量首次突破1700亿件,提高分拣效率、降低分拣成本、提高分拣准确性对于物流公司越发迫切.某快递公司引进了具有分拣功能的智能机器人,发现每台机器人和每个人1小时分拣快递量如下表:
每台机器人 每人 合计(件)
1 小时分拣快递量/件 5x+10 x 730
(1)分别求每个人和每台机器人1小时分拣快递的数量;
(2)若该快递公司每天需要使用机器人分拣10万件快递,一台机器人每天的工作时间为15小时,则至少需要购买多少台机器人才能满足快递公司的需求
25. (本小题满分10分)
如图,在平面直角坐标系xOy中,抛物线 与x轴交于O,A两点,与直线 交于B,C(3,m)两点,对称轴为直线
(1)求抛物线的函数表达式;
(2)P为抛物线上一动点,连接OB,OC,PB,PC,若 求点P的横坐标;
(3)E,F为射线CB上两个动点,作直线OE,OF分别交抛物线于M,N两点(不同于点O),若E,F两点的横坐标之积为3,试探究:直线MN是否经过定点 若经过,请求出该定点的坐标;若不经过,请说明理由.
26. (本小题满分12分)
如图,四边形ABCD是正方形,等腰直角三角形AEF绕着A点旋转,其中 5,连接EB,FC,AC. H为线段EB的中点,连接HF.
(1)证明:
(2)当k=5,E,F,C在一条直线上时,求HF的长;
(3)当点E旋转至线段AB上,要使HF最小,求此时k的值和HF 的长.
1. B 【解析
2. C
3. C
4. D
5. A 【解析】由表格可知,这些学生在一周内的综合体育活动时间为13 h的有20人,人数最多,∴这些学生在一周内的综合体育活动时间的众数是13;∵共有12+20+10+5+3=50(人),∴中位数是将数据按从小到大(或从大到小)的顺序排列后第25,26个数据的平均数,即
6. B 【解析】∵ 四边形ABCD 是平行四边形,∴AO=CO,BO=DO,∵△ABC是等腰直角三角形,∴AC= 在 Rt△BOC 中,BO=
7. D 【解析】由题意可知,绫3尺+绢4尺=48分,可建立方程3x+4y=48;绫7尺+绢2尺=68分,可建立方程7x+2y=68,联立可得方程组为 新考法解读 试题情境取材于《增删算法统宗》,《增删算法统宗》是中国古代重要的数学著作之一.本题将“方程组的实际应用”与“数学文化”相结合,展现了中国古代数学的优秀成果,弘扬传统文化的同时,增强学生对中国古代数学成就的了解,并且为便于学生理解,题干将原题的文言文翻译成现代文,保障了考查的公平性.
8. B 【解析】由尺规作图可知,AF是△ABC 底边 BC上的高线,∴ AF⊥BC,∴ ∠B+∠BAF=90°.∵∠CAF+∠BAF=90°,∴ ∠B =∠CAF.∵ ∠AFB =∠CFA=90°,∴ Rt△ABF∽Rt△CAF,∴AFCF=FAF,∴AF =BF·CF.∵ BF=2,CF=6,∴AF=2 在Rt△ABF中,由勾股定理得,
9. 3 【解析】∵| 解得.x=1,y=2,∴x+y=1+2=3.
10.3 【解析】由题意可知, 解得x=3,经检验x=3是原方程的解,且符合题意,∴x的值为3.
11. 12π 【解析】∵正六边形内接于⊙O,∴ ∠AOB= ×360°=60°,∵OA=OB,OC⊥AB,∴△AOB是等边三角形,∠AOC=30°,在Rt△AOC中,OC=3,∴ ∴⊙O 的面积 =12π.
知识精准回顾
正n边形的内角和为(n-2)×180°,
每个内角均为
【解析】∵四边形 MNQP 是正方形,AB∥NQ,∴四边形 ANQB 是矩形,∴AB=NQ=4 cm.又∵
13. - 2
=2; ……………………………… 6分
(2)解不等式①,得x>-2, 2分
解不等式②,得x≥1, 4分
故不等式组的解集是x≥1. 6分
15. 解:(1)300,45; 4分
【解法提示】本次调查的学生共有120÷40%=300(人),表中a的值为300-120-75-60=45.
答:在扇形统计图中,“轮滑”所占百分比为20%; 6分
(人),
答:估计该校最期待拔河项目的学生人数为625人. 8分
16. 解:如解图,过点 B 作 BF⊥DE 于点 F,过点 O 作OG⊥BF于点G,过点A作AN⊥BF 于点 N,交OC于点 M,则四边形OMNG 和四边形OCFG均为矩形,
∴OM=GN,OC=GF. 2分
在Rt△ABN中,BN=AB·sin∠BAN=14.5×sin55°≈11.89,
在Rt△AMO中,OM=AM·tan∠OAM,
在Rt△AMC中,CM=AM·tan∠MAC,
则AM·tan∠OAM+AM·tan∠MAC=OM+CM=OC,即 解得,AM≈3.32, 6分
∴OM=AM·tan∠OAM≈4.75,
∴BF=BN-GN+GF=11.89-4.75+11≈18.1,
∴ 点 B 到桌面的距离约为 18.1 cm. ……… 8分
新考法解读 本题以麦克风为背景,让学生通过提取、理解和分析情境中的相关信息,抽离几何图形,设问具有实际意义,体现了数学的应用价值,使考试内容与生活情境相结合,真正考查学生理解和运用所学知识解决问题的能力.教育部《关于加强初中学业水平考试命题工作的意见》和《义务教育数学课程标准(2022 年版)》中均指出:情境创设的真实性.
17. (1)证明:∵四边形AEDB是⊙O 的内接四边形,
∴∠AED+∠ABD=180°,
∵∠ABD+∠DBC=180°,
∴∠DBC=∠AEC,………………………………… 3分
∵∠ACE=∠DCB,
∴△AEC∽△DBC,
∴AC·DB=DC·AE; 4分
(2)解:如解图,连接OE,过点 E作AC 的垂线,垂足为F,
∵∠BEC=∠DAC,∠ECB=∠ACD,
∴△BEC∽△DAC,
. .…… 5分
∵∠C=2∠EAC,∠EOC=2∠EAC,
∴∠C=∠EOC,
∴OE=CE,
∴OF=CF,
设BF=m,BC=n,则OF=CF=m+n,OE=OB=2m+n.
∵在 Rt△BFE中,
在 Rt△OFE中,
即 方程两边同时除以n ,
得
解得 (舍去)或
… 8分
在Rt△BEF中,
∴tan∠ADE=tan∠EBF=EFF=2m=2. 10分
18. 解:(1)将B(b,1)代入y=-x-2中,
解得b=-3,则B(-3,1),
将B(-3,1)代入 中,
解得k=-3,
∴反比例函数的表达式为 …3分
(2)如解图①,连接DD',设.D'(d,0),D(t,- ),
∴ DD'的中点坐标为
解得
由翻折的性质可知,DD'⊥BC,CD=CD',
∴易得∠D'DC=45°,
∴tan∠D'DC=1,
解得t=-2或t=0(舍去), …………………………………………………5分当t=-2时,
∴ 当点 D'落在x轴上时,点D 的坐标是 6分
(3)如解图②,连接OO',设点 C 的坐标是(c,-c-2),则点 D 的坐标是
∵CD=4,
解得c=3(舍去)或c=-1.
∴点C 的坐标是(-1,-1),点 D 的坐标是(-1,3).
设直线 OC 的表达式为y= mx,将点 C(-1,-1)代入,得-1=-m,解得m=1,
∴ 直线OC 的表达式为y=x,根据平移的性质可得O'C'∥OC,
∴设直线 O'C'的表达式为y=x+n.
∵直线AC的表达式是y=-x-2,OO'∥AC,
∴直线OO'的表达式为y=-x.
设平移后点 O'的坐标为(a,-a),其中a<0,则点D"(a-1,-a+3),
将点O'的坐标代入y=x+n,得-a=a+n,解得n=-2a,
∴直线O'C'的表达式为y=x-2a,当y=0时,x=2a,
∴E(2a,0),
4a+10,
以O,D",E,F为顶点的四边形是菱形时,分三种情况讨论:
①当D"E 为菱形的对角线时,OE=OD",
,解得a=-5或a=1(舍去),则点 D"(-6,8); 7分
②当OD"为菱形的对角线时,OE=D"E,
解得 或 (舍去),则点 ……………………… 8分
③当OE 为菱形的对角线时,OD"=D"E,
解得a=0(舍去), 9分
∴此种情况不存在.
综上所述,点D"的坐标为(-6,8)或( ). 10分
19. x=2 【解析】解 去分母,得x=2(x-1),去括号,得x=2x-2,解得x=2,检验:把x=2代入得,x(x-1)≠0,∴x=2是原分式方程的解.
20. 1(答案不唯一,m>-1,且m≠0即可) 【解析】由题可得 且m≠0,∴m>-1,且m≠0.
21. 5 【解析】设 P,Q分别为两圆心,连接NQ,AQ.由题意可知点E,P,M,N,Q在同一直线上,MN=EN 在Rt△ANQ中,设AQ=r cm,则.NQ=(r-3.6) cm,由勾股定理得, 解得r=5,∴劣弧支架AB所在圆的半径是5cm .
22.81 【解析】依据规律可得到 的展开式的系数是杨辉三角第7行的数,第7行的数分别为1,6,15,20,15,6,1.
解题思路引导
观察所给展开式的系数和杨辉三角中各数的关系,先写出所求展开式中的系数
展开式中x 的系数为 135,同理( 展开式中x 的系数为10×9× 展开式中x 的系数为6×9 展开式中x 的系数为3×9 展开式中x 的系数为1×9=9,∴ 原式展开式中x 的系数为135-90+54-27+9=81.
解题思路引导
根据发现的规律得出每个展开式中x 的系数,进行相加
【解析】如解图①,∵ EB'=EB=2,∴点 B'在以点 E 为圆心,半径为2 的圆弧上运动.
解题思路引导
根据点 B'的运动轨迹,再结合直线外一点与直线上各点连接的所有线段中,垂线段最短求解.
过点 E作 EI⊥AC 于点I,当点 B'位于线段 EI 与圆弧的交点处时,点B'到AC的距离最小,为B'I的长,∵四边形 ABCD 是菱形,∠ABC =60°,∴△ABC为等边三角形,∠BAC=60°.∵AE=AB-BE 即点 B'到直线AC 的最小距离是 如解图②,同理,点B'在以点 E 为圆心,半径为2的圆弧上运动.连接ED,当点 B'位于 ED 与圆弧的交点处时,B'D的值最小.
解题思路引导
根据圆外一点到圆上的最短距离为点与圆心形成的线段减去半径的长即可求解.
过点 E 作 EK⊥DA 交 DA 的延长线于点 K.∵ 四边形ABCD 是菱形,∴AD∥BC,∴∠KAE=∠ABC= 2 ,∴ DK=AD+AK=8,∴ DE = √DK +EK = ,即B'D 的最小值是
【解题妙招】
已知:如图,点E 为⊙O 上一动点,D为平面内不在⊙O上的一点.
计算:DE 的最大、最小值.
作辅助线:如图,作直线OD 交⊙O 于两点 E',E".
结论:DE'即为 DE 的最小值,DE"即为 DE 的最大值.
24. 解:(1)由题意,可列方程:5x+10+x=730,解得x=120, …………………………………… 3分
∴5x+10=5×120+10=610(件),
答:每个人1小时分拣快递的数量为120件,每台机器人1小时分拣快递的数量为610件;…4分(2)设需要购买y台机器人,
则15×610y≥100 000,
9 150y≥100 000,
…………………… …6分
∵y为正整数,
∴y的最小值为11,
答:至少需要购买11台机器人才能满足快递公司的需求.……………………………………………8分
25. 解:(1)由题知 则C(3,-3),… ………………… 1分根据题意,得 解得
∴ 抛物线的函数表达式为 …… 3分
(2)如解图①,过点 P 作 PQ⊥x轴交 BC 于点 Q,记BC与y轴交于点 T.
将x=0代入直线
得 则
设 则
∴PQ=2OT=3,………………………………… 4分
5分
解得
故点P的横坐标为1或 3
……………………………………………… 6分
(3)直线MN经过定点.如解图②,设 直线MN的表达式为y= kx+n(k≠0),
直线OE 的表达式为y=k x,直线OF的表达式为
解得
∴直线OE 的表达式为
联立直线 OE与 BC 的表达式,得 解得 ……………………… 7分
同理得
即
联立直线MN与抛物线的函数表达式,整理得 (k-2)x+n=0,
, 8分
∴4n-10(2-k)+25=3,∴n=- k-
∴直线 MN的表达式为
∴直线MN经过定点 … 10分
26. (1)证明:∵△AEF与△ABC为等腰直角三角形, 且∠EAF=∠BAC=45°,
∴ ∠EAF-∠BAF = ∠BAC - ∠BAF, 即 ∠EAB=∠FAC,
∴△AEB∽△AFC; 3分
(2)解:当点 E 在点 F 上方时,如解图①,过点 H作HM⊥EC,垂足为M.
∵AB=kAE=5,k=5,
在Rt△AEC中,由勾股定理得,
∵EF=AE=1,
∴FC=EC-EF=7-1=6.
由(1)可知,△AEB∽△AFC,
∴EB=3 ,∠BEF=∠AEB-∠AEF=45°,
∵H为线段EB的中点,
由HM⊥EC,∠BEF=45°,可知△EHM 为等腰直角三角形,
在Rt△HMF中, ……………………………… 5分
当点 F 在点 E 的上方时,如解图②,过点 H 作 HN垂直EC于点N,
同理易得 E
由(1)可知,△AEB∽△AFC,
∴∠ABE=∠ACF,
∵∠ABC+∠BCA=135°,
∴∠EBC+∠BCE=135°,
∴∠BEC=45°,
则HN=EN=2,FN=3,
综上所述,HF 的长为 或 … 7分
(3)解:如解图③,延长EF至点M,使得FM=EF,连接AM,BM.
∵H为EB的中点,FM=EF,
∴HF为△EBM的中位线,
∵AE=EF=FM,∠AEM=90°,
∵AD∥EM,
∴ ∠MAD 为定角. 9分
如解图④,因此点 M 的轨迹在射线AM 上,故当BM⊥AM时,MB最小,
此时 最小.
则∠BAM+∠DAM=90°,∠ABM+∠BAM=90°,∴ ∠MAD=∠ABM.
在Rt△ABM中,设AM=x,则BM=2x,
得
10分
在 Rt△AEM中, ,设AE=EF=FM=a,则
解得a=1(负值已舍去),
∴AE=EF=1,
∵AB=kAE=5,
∴k=5.
综上所述,当HF 最小时,此时k的值为5,HF 的长为 . 12分
同课章节目录
