期末综合练(4) (含答案) 2024-2025学年苏科版七年级数学下册
文档属性
| 名称 | 期末综合练(4) (含答案) 2024-2025学年苏科版七年级数学下册 | 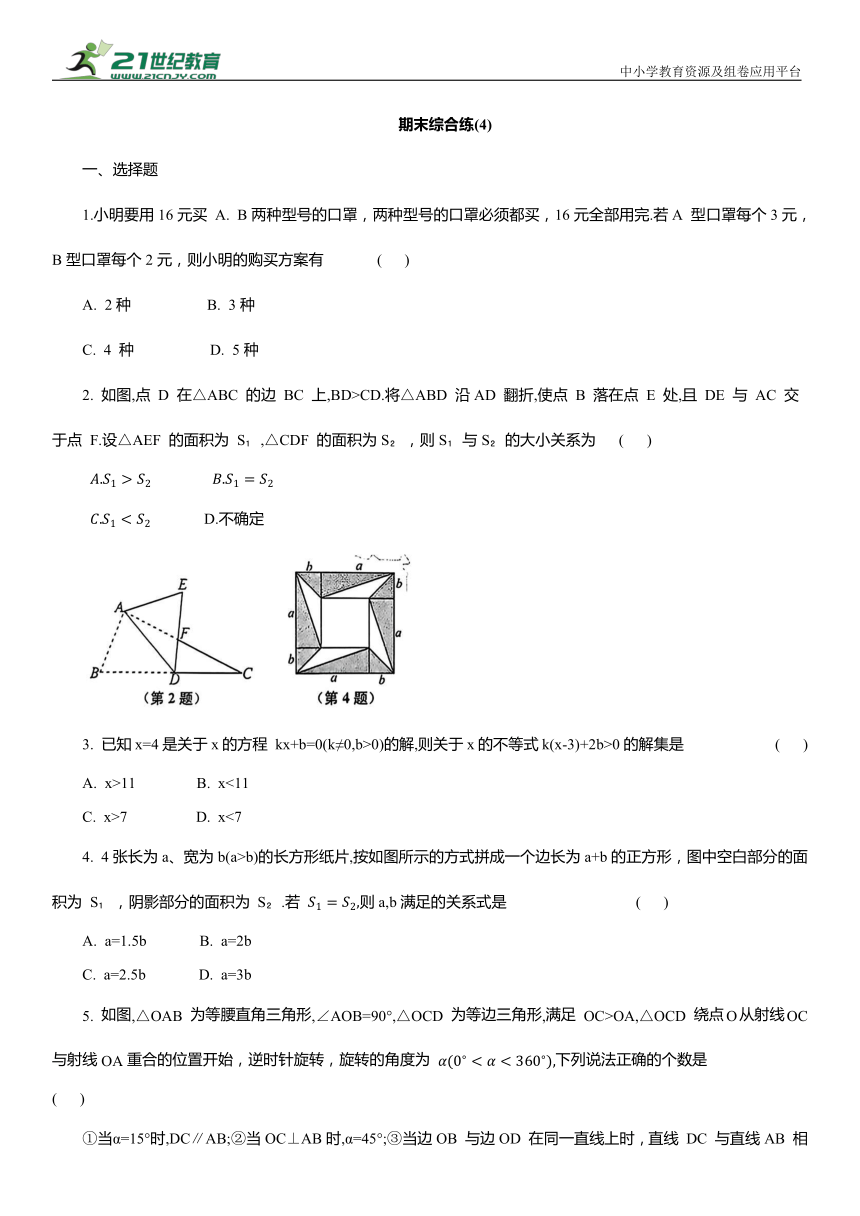 | |
| 格式 | docx | ||
| 文件大小 | 234.9KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 苏科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-05-08 05:42:57 | ||
图片预览



文档简介
中小学教育资源及组卷应用平台
期末综合练(4)
一、选择题
1.小明要用16元买 A. B两种型号的口罩,两种型号的口罩必须都买,16元全部用完.若A 型口罩每个3元,B型口罩每个2元,则小明的购买方案有 ( )
A. 2种 B. 3种
C. 4 种 D. 5种
2. 如图,点 D 在△ABC 的边 BC 上,BD>CD.将△ABD 沿AD 翻折,使点 B 落在点 E 处,且 DE 与 AC 交于点 F.设△AEF 的面积为 S ,△CDF 的面积为S ,则S 与S 的大小关系为 ( )
D.不确定
3. 已知x=4是关于x的方程 kx+b=0(k≠0,b>0)的解,则关于x的不等式k(x-3)+2b>0的解集是 ( )
A. x>11 B. x<11
C. x>7 D. x<7
4. 4张长为a、宽为b(a>b)的长方形纸片,按如图所示的方式拼成一个边长为a+b的正方形,图中空白部分的面积为 S ,阴影部分的面积为 S .若 则a,b满足的关系式是 ( )
A. a=1.5b B. a=2b
C. a=2.5b D. a=3b
5. 如图,△OAB 为等腰直角三角形,∠AOB=90°,△OCD 为等边三角形,满足 OC>OA,△OCD 绕点O从射线OC 与射线OA重合的位置开始,逆时针旋转,旋转的角度为 下列说法正确的个数是 ( )
①当α=15°时,DC∥AB;②当OC⊥AB时,α=45°;③当边OB 与边OD 在同一直线上时,直线 DC 与直线AB 相交形成的锐角为15°;④整个旋转过程,共有10个位置使得△OAB 与△OCD 有一条边平行.
A. 1 111 B. 2 C. 3 D. 4
二、填空题
6.一次数学测试,满分为100分.测试分数出来后,同桌的李华和吴珊同学把他俩的分数进行计算,李华说:“我俩分数的和是160分.”吴珊说:“我俩分数的差是60分.”给出下列关于两人说法的判断:①俩人的说法都是正确的;②至少有一人说错了;③俩人的说法都是错的.其中判断正确的是 (填序号).
7.观察等式: 已知按一定规律排列的一组数:2 ,2 ,2 ,……,2 ,2 .若 则用含a 的代数式表示这组数的和是 .
8.某风景区有4个相同的出口、4个相同的入口,假设在任何情况下每个入口的人均是匀速进入,每个出口的人均是匀速出去.当风景区人数达到可容纳人数的20%时:若同时开放4个入口和2个出口,则经过1.6h刚好达到可容纳人数;若同时开放2个入口和2个出口,则经过8h刚好达到可容纳人数.当风景区人数达到可容纳人数的10%时,若同时开放3个入口和2个出口,则经过 h刚好达到可容纳人数的60%.
9. 如图,在△ABC中,∠ABC=50°,∠ACB=100°,M 是射线AB 上的一个动点,过点 M作MN∥BC 交射线AC 于点 N,连接BN.若△BMN 中有两个角相等,则∠MNB 的度数可能是 .
三、解答题
10.用方程组和不等式解决问题.
本地某快递公司规定:寄件不超过1 kg的部分为首重,按起步价计费;寄件超过1 kg的部分(以1kg为计重单位,四舍五入取整数)为续重,按千克计费.受江浙沪经济圈的影响,本地发往上海的快件,首重起步价比发往北京要便宜3元,续重计费比发往北京每千克要便宜4元.已知小丽从本地寄3kg的快件到上海需付费11元,寄4kg的快件到北京需付费28元.问:用不超过28元的费用通过该快递公司从本地寄件到上海,最多可寄多重的快件 (以1kg为计重单位)
11.【探究结论】
(1) 如图1,AB∥CD,E 为平行线内一点,连接AE,CE,则∠AEC,∠A,∠C 的关系是 .
【探究应用】利用(1)中结论解决下面问题:
(2) 如图2,AB∥CD,直线 MN 分别交AB,CD 于点 E,F,EG 和 EG 为∠BEF 内满足∠1=∠2 的两条射线,分别与∠EFD 的平分线交于点G ,G ,求证:
(3)如图3,已知AB∥CD,F 为CD 上一点,∠EFD=60°,∠AEC=3∠CEF.若8°<∠BAE<20°,∠C 的度数为整数,则∠C 的度数为 .
期末综合练(4)
1. A 提示:设购买A型口罩x个,购买B型口罩y个.根据题意,得3x+2y=16.化简,得 y=8一 x.因为x,y都是正整数,所以x=2,y=5或x=4,y-2.所以小明的购买方案有2种.
2. A 提示:因为点 D 在△ABC 的边 BC 上,BD>CD,所以, 由折叠的性质,可得 所以 所以 S△AFD一 即
3. B 提示:将x - 4代入 kx+b=0,得4k+b=0,即b ·-4k.因为b>0,所以k<0.将b- -4k代入k(x-3)+2b>0,得k(x-3)-8k>0,即k(x-11)>0.所以x-11<0,解得x<11.
4. D 提示:根据题意,得 因为 所以 所以2b(a+b)=(a-b)(a+b).因为a+b>0、所以2b: a-b,所以a=3b.
5. C 提示:设OC与AB 交点为M,OD 与AB交点为 N.当α=15°时,∠OMN=α+∠A=60°,所以∠OMN=∠C,所以 DC∥AB,故①正确.当OC⊥AB时,a+∠A=90°或( ,所以α=45°或α=225°,故②错误.当边OB 与边OD 在同一直线上时,设直线 DC与直线AB 的交点为E,分以下两种情况:()如图1,当射线OB 与射线OD 重合时,∠EBD=∠ABO=45°,∠EDB =180°--∠ODC=120°,所以 ;( )如图2,当射线 OB 与射线 OD 在同一条直线上且不重合时,∠EBD=45°,∠EDB =180°--∠ODC=120°,所以∠E=180°-∠EBD--∠EDB=15°,故③正确.整个旋转过程,因为OC,OB,OD,OA 都有公共交点O,所以有CD分别与AB,OA,OB 存在平行,AB 分别与OC,OD存在平行,根据图形的对称性可判断共有10个位置使得△OAB 与△OCD 有一条边平行,故④正确.
6. ②
提示:
8. 提示:设1个入口每小时进a人,1个出口每小时出b人,景区可容纳的总人数是c.根据题意,得1.6(4a-2b)=(1-20%)c,8(2a-2b)=(1-20%)c,所以 经过 (h)刚好达到可容纳人数的60%.
9. 25°或50°或80°或65° 提示:①如图1,当点M在线段AB 上时,因为MN∥BC,所以∠AMN=∠ABC=50°,所以∠BMN=130°.因为△BMN 中有两个角相等,所以只有∠MNB=∠MBN=25°.②如图2,当点M 在AB 的延长线上时:(|)当∠BMN=∠MNB 时,∠MNB=50°;(Ⅱ) 当∠BMN=∠MBN=50°时,∠MNB=180°--∠BMN--∠MBN=80°;③当∠MBN=∠MNB 时, 综上所述,∠MNB 的度数可能为 25°或 50°或 80°或65°.
解:设本地发往北京的快件起步价为x元,续重计费为 y 元/kg.根据题意,得
解得 设通过该快递公司从本地寄m kg重的快件到上海.根据题意,得(10--3)+(m--1)(6--4)≤28,解得 因为以1 kg为计重单位,所以m的最大值为11.
答:用不超过28元的费用通过该快递公司从本地寄件到上海,最多可寄11kg的快件.
11. (1)∠AEC=∠A+∠C
(2)证明:由(1)知 因为 FG 平分∠EFD, 所以. ∠DFG .又因为∠1=∠2,所以. ∠EFG .因为∠FG E+∠2+∠EFG =180°,所以.
(3) 42°或 41° 提示:由(1)知∠AEF =∠BAE+∠EFD.设∠CEF=x,则∠AEC=3x.因为∠EFD= 60°,所以 x+3x=∠BAE+60°,所以∠BAE=4x-60°.因为8°<∠BAE<20°,即8°<4x- 解得 .因为∠EFD 是△CEF 的外角,所以∠C=∠EFD-∠CEF=60°-x.因为∠C的度数为整数,所以x=18°或 19°,所以∠C=60°- 或
期末综合练(4)
一、选择题
1.小明要用16元买 A. B两种型号的口罩,两种型号的口罩必须都买,16元全部用完.若A 型口罩每个3元,B型口罩每个2元,则小明的购买方案有 ( )
A. 2种 B. 3种
C. 4 种 D. 5种
2. 如图,点 D 在△ABC 的边 BC 上,BD>CD.将△ABD 沿AD 翻折,使点 B 落在点 E 处,且 DE 与 AC 交于点 F.设△AEF 的面积为 S ,△CDF 的面积为S ,则S 与S 的大小关系为 ( )
D.不确定
3. 已知x=4是关于x的方程 kx+b=0(k≠0,b>0)的解,则关于x的不等式k(x-3)+2b>0的解集是 ( )
A. x>11 B. x<11
C. x>7 D. x<7
4. 4张长为a、宽为b(a>b)的长方形纸片,按如图所示的方式拼成一个边长为a+b的正方形,图中空白部分的面积为 S ,阴影部分的面积为 S .若 则a,b满足的关系式是 ( )
A. a=1.5b B. a=2b
C. a=2.5b D. a=3b
5. 如图,△OAB 为等腰直角三角形,∠AOB=90°,△OCD 为等边三角形,满足 OC>OA,△OCD 绕点O从射线OC 与射线OA重合的位置开始,逆时针旋转,旋转的角度为 下列说法正确的个数是 ( )
①当α=15°时,DC∥AB;②当OC⊥AB时,α=45°;③当边OB 与边OD 在同一直线上时,直线 DC 与直线AB 相交形成的锐角为15°;④整个旋转过程,共有10个位置使得△OAB 与△OCD 有一条边平行.
A. 1 111 B. 2 C. 3 D. 4
二、填空题
6.一次数学测试,满分为100分.测试分数出来后,同桌的李华和吴珊同学把他俩的分数进行计算,李华说:“我俩分数的和是160分.”吴珊说:“我俩分数的差是60分.”给出下列关于两人说法的判断:①俩人的说法都是正确的;②至少有一人说错了;③俩人的说法都是错的.其中判断正确的是 (填序号).
7.观察等式: 已知按一定规律排列的一组数:2 ,2 ,2 ,……,2 ,2 .若 则用含a 的代数式表示这组数的和是 .
8.某风景区有4个相同的出口、4个相同的入口,假设在任何情况下每个入口的人均是匀速进入,每个出口的人均是匀速出去.当风景区人数达到可容纳人数的20%时:若同时开放4个入口和2个出口,则经过1.6h刚好达到可容纳人数;若同时开放2个入口和2个出口,则经过8h刚好达到可容纳人数.当风景区人数达到可容纳人数的10%时,若同时开放3个入口和2个出口,则经过 h刚好达到可容纳人数的60%.
9. 如图,在△ABC中,∠ABC=50°,∠ACB=100°,M 是射线AB 上的一个动点,过点 M作MN∥BC 交射线AC 于点 N,连接BN.若△BMN 中有两个角相等,则∠MNB 的度数可能是 .
三、解答题
10.用方程组和不等式解决问题.
本地某快递公司规定:寄件不超过1 kg的部分为首重,按起步价计费;寄件超过1 kg的部分(以1kg为计重单位,四舍五入取整数)为续重,按千克计费.受江浙沪经济圈的影响,本地发往上海的快件,首重起步价比发往北京要便宜3元,续重计费比发往北京每千克要便宜4元.已知小丽从本地寄3kg的快件到上海需付费11元,寄4kg的快件到北京需付费28元.问:用不超过28元的费用通过该快递公司从本地寄件到上海,最多可寄多重的快件 (以1kg为计重单位)
11.【探究结论】
(1) 如图1,AB∥CD,E 为平行线内一点,连接AE,CE,则∠AEC,∠A,∠C 的关系是 .
【探究应用】利用(1)中结论解决下面问题:
(2) 如图2,AB∥CD,直线 MN 分别交AB,CD 于点 E,F,EG 和 EG 为∠BEF 内满足∠1=∠2 的两条射线,分别与∠EFD 的平分线交于点G ,G ,求证:
(3)如图3,已知AB∥CD,F 为CD 上一点,∠EFD=60°,∠AEC=3∠CEF.若8°<∠BAE<20°,∠C 的度数为整数,则∠C 的度数为 .
期末综合练(4)
1. A 提示:设购买A型口罩x个,购买B型口罩y个.根据题意,得3x+2y=16.化简,得 y=8一 x.因为x,y都是正整数,所以x=2,y=5或x=4,y-2.所以小明的购买方案有2种.
2. A 提示:因为点 D 在△ABC 的边 BC 上,BD>CD,所以, 由折叠的性质,可得 所以 所以 S△AFD一 即
3. B 提示:将x - 4代入 kx+b=0,得4k+b=0,即b ·-4k.因为b>0,所以k<0.将b- -4k代入k(x-3)+2b>0,得k(x-3)-8k>0,即k(x-11)>0.所以x-11<0,解得x<11.
4. D 提示:根据题意,得 因为 所以 所以2b(a+b)=(a-b)(a+b).因为a+b>0、所以2b: a-b,所以a=3b.
5. C 提示:设OC与AB 交点为M,OD 与AB交点为 N.当α=15°时,∠OMN=α+∠A=60°,所以∠OMN=∠C,所以 DC∥AB,故①正确.当OC⊥AB时,a+∠A=90°或( ,所以α=45°或α=225°,故②错误.当边OB 与边OD 在同一直线上时,设直线 DC与直线AB 的交点为E,分以下两种情况:()如图1,当射线OB 与射线OD 重合时,∠EBD=∠ABO=45°,∠EDB =180°--∠ODC=120°,所以 ;( )如图2,当射线 OB 与射线 OD 在同一条直线上且不重合时,∠EBD=45°,∠EDB =180°--∠ODC=120°,所以∠E=180°-∠EBD--∠EDB=15°,故③正确.整个旋转过程,因为OC,OB,OD,OA 都有公共交点O,所以有CD分别与AB,OA,OB 存在平行,AB 分别与OC,OD存在平行,根据图形的对称性可判断共有10个位置使得△OAB 与△OCD 有一条边平行,故④正确.
6. ②
提示:
8. 提示:设1个入口每小时进a人,1个出口每小时出b人,景区可容纳的总人数是c.根据题意,得1.6(4a-2b)=(1-20%)c,8(2a-2b)=(1-20%)c,所以 经过 (h)刚好达到可容纳人数的60%.
9. 25°或50°或80°或65° 提示:①如图1,当点M在线段AB 上时,因为MN∥BC,所以∠AMN=∠ABC=50°,所以∠BMN=130°.因为△BMN 中有两个角相等,所以只有∠MNB=∠MBN=25°.②如图2,当点M 在AB 的延长线上时:(|)当∠BMN=∠MNB 时,∠MNB=50°;(Ⅱ) 当∠BMN=∠MBN=50°时,∠MNB=180°--∠BMN--∠MBN=80°;③当∠MBN=∠MNB 时, 综上所述,∠MNB 的度数可能为 25°或 50°或 80°或65°.
解:设本地发往北京的快件起步价为x元,续重计费为 y 元/kg.根据题意,得
解得 设通过该快递公司从本地寄m kg重的快件到上海.根据题意,得(10--3)+(m--1)(6--4)≤28,解得 因为以1 kg为计重单位,所以m的最大值为11.
答:用不超过28元的费用通过该快递公司从本地寄件到上海,最多可寄11kg的快件.
11. (1)∠AEC=∠A+∠C
(2)证明:由(1)知 因为 FG 平分∠EFD, 所以. ∠DFG .又因为∠1=∠2,所以. ∠EFG .因为∠FG E+∠2+∠EFG =180°,所以.
(3) 42°或 41° 提示:由(1)知∠AEF =∠BAE+∠EFD.设∠CEF=x,则∠AEC=3x.因为∠EFD= 60°,所以 x+3x=∠BAE+60°,所以∠BAE=4x-60°.因为8°<∠BAE<20°,即8°<4x- 解得 .因为∠EFD 是△CEF 的外角,所以∠C=∠EFD-∠CEF=60°-x.因为∠C的度数为整数,所以x=18°或 19°,所以∠C=60°- 或
同课章节目录
