第12 章巅峰训练19 定理(2) (含答案)
文档属性
| 名称 | 第12 章巅峰训练19 定理(2) (含答案) |

|
|
| 格式 | docx | ||
| 文件大小 | 297.3KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 苏科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-05-08 00:00:00 | ||
图片预览


文档简介
中小学教育资源及组卷应用平台
巅峰训练19 定理(2)
热食单糖等
1.下列命题中,逆命题是真命题的个数是( )
①若 则 ②若-1≤x≤2,则1≤|x|≤2;③四边形的外角和为 360°;④在△ABC 中,若∠A+∠B=90°,则∠C=90°.
A. 4 B. 3 C. 2 D. 1
2.用反证法证明命题“在四边形中,至少有一个角是钝角或直角”时,首先应该假设这个四边形中 ( )
A.有一个角是钝角或直角
B.每一个角都是钝角
C.每一个角都是直角
D.每一个角都是锐角
3.如图,由6个各边相等、各内角也相等的九边形拼接成一个美丽的图案,则图中∠α的度数为 ( )
A. 80° B. 60° C. 50° D. 100°
4. (2024·盐城市东台市期末)如图,点 D 在BC 的延长线上,DE⊥AB 于点 E,交 AC于点F.若∠A=35°,∠D=15°,则∠ACB的度数为 .
5.用反证法证明命题“同位角不相等时,两直线不平行”,应假设: .
6.(2024·镇江市期末)足球的表面是由12个正五边形和20个正六边形组成的.如图,将足球上的一个正六边形和它相邻的一个正五边形展开放平,则图中的∠ABC= .
7.(2024·宿迁市沭阳县期末)已知:如图1,三条线段 B C ,B C ,B C 两两相交于点A ,A ,A .
(1) 求∠B ,∠C ,∠B ,∠C ,∠B ,∠C 的度数之和.
(2)如图2,四条线段两两相交于点 A ,A ,A ,A ,求∠B ,∠C ,∠B ,∠C ,∠B ,∠C ,∠B ,∠C 的度数之和.
(3)猜想:类比图1、图2的画法,n条线段两两相交于点 A ,A ,A ,A ,…,A ,那么
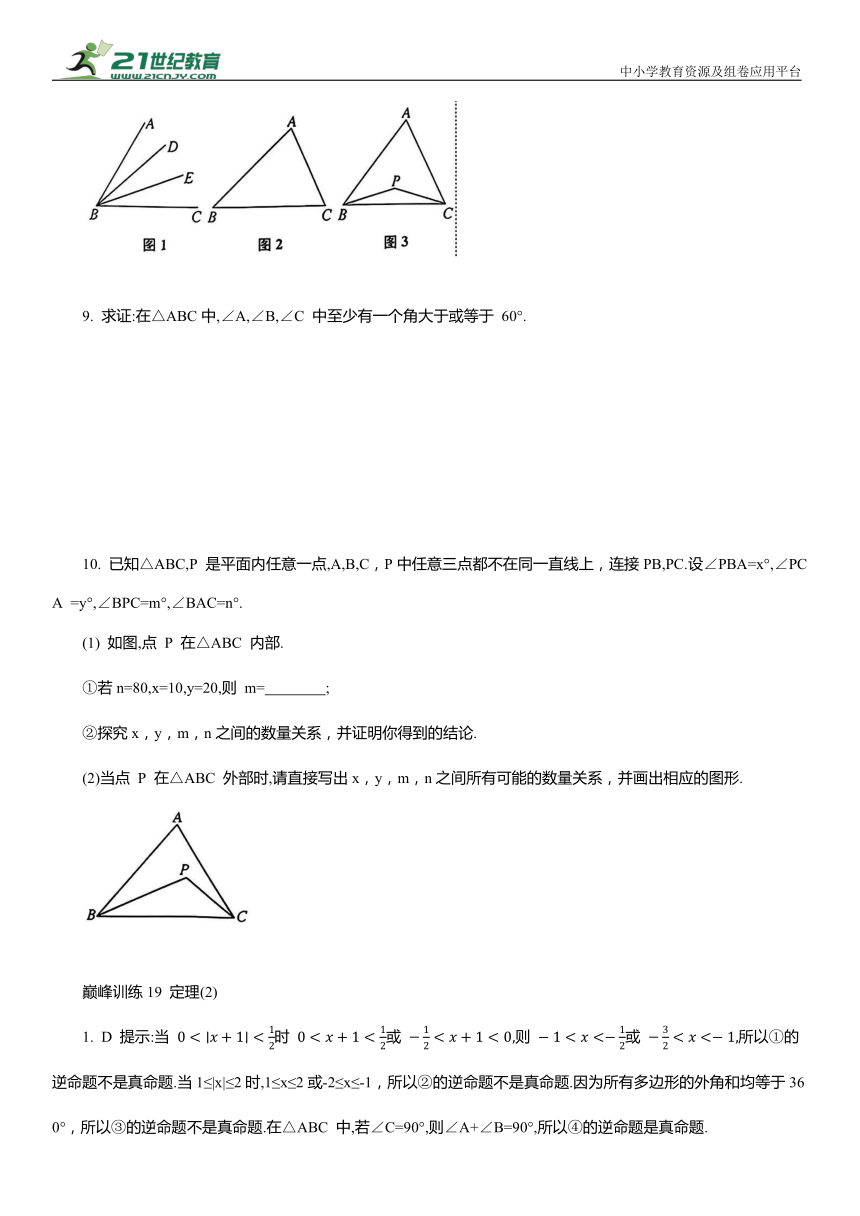
8.(2024·常州市武进区校级月考)【概念认识】如图1,在∠ABC中,若∠ABD=∠DBE=∠EBC,则 BD,BE 叫作∠ABC 的“三分线”.其中,BD 是“邻AB 三分线”,BE 是“邻 BC 三分线”.
【问题解决】
(1) 如图2,在△ABC中,∠A=80°,∠B=45°.若∠B 的“三分线” BD 交AC 于点D,求∠BDC的度数.
(2) 如图3,在△ABC 中,BP,CP 分别是∠ABC 的“邻 BC 三分线”和∠ACB的“邻 BC 三分线”,且∠BPC=140°,求∠A 的度数.
【延伸推广】
(3) 在△ABC 中,∠ACD 是△ABC 的外角,∠B 的“三分线”所在的直线与∠ACD 的“三分线”所在的直线交于点 P.若 54°,请直接写出∠BPC 的度数(用含m 的代数式表示).
9. 求证:在△ABC中,∠A,∠B,∠C 中至少有一个角大于或等于 60°.
10. 已知△ABC,P 是平面内任意一点,A,B,C,P中任意三点都不在同一直线上,连接PB,PC.设∠PBA=x°,∠PCA =y°,∠BPC=m°,∠BAC=n°.
(1) 如图,点 P 在△ABC 内部.
①若n=80,x=10,y=20,则 m= ;
②探究x,y,m,n之间的数量关系,并证明你得到的结论.
(2)当点 P 在△ABC 外部时,请直接写出x,y,m,n之间所有可能的数量关系,并画出相应的图形.
巅峰训练19 定理(2)
1. D 提示:当 时 或 则 或 所以①的逆命题不是真命题.当1≤|x|≤2时,1≤x≤2或-2≤x≤-1,所以②的逆命题不是真命题.因为所有多边形的外角和均等于360°,所以③的逆命题不是真命题.在△ABC 中,若∠C=90°,则∠A+∠B=90°,所以④的逆命题是真命题.
2. D
3. A 提示:根据题意,得题图中九边形的每个内角都等于 所以
4.70° 5.同位角不相等时,两直线平行
6. 132°
7. 解:(1) 因为. ,所以∠B + 因为 ,所以∠B +
(2) 同(1)可得, ∠B A C ).因为. 所以∠B +
(3) 360° 提示:由(1)可知, 由(2)可知, 以此类推.
8. 解:(1)如图1,当 BD 是∠ABC的“邻AB 三分线”时, 95°;当 BD 是∠ABC 的“邻 BC 三分线”时, 综上所述,∠BDC 的度数为95°或110°.
(2) 在△BPC 中,因为∠BPC=140°,所以∠PBC+∠PCB=40°.又因为 BP,CP 分别是∠ABC 的“邻 BC 三分线”和∠ACB 的“邻BC 三分线”,所以 所以 40°,所以∠ABC+∠ACB=120°.在△ABC中,∠A +∠ABC +∠ACB = 180°, 所以∠A=180°-(∠ABC+∠ACB)=60°.
或 或 或 18°. 提示:分4种情况进行画图计算:
如图2,当 BP 和CP 分别是∠ABC 的“邻AB 三分线”和∠ACD 的“邻 AC 三分线”时,∠A+∠ABP=∠BPC+∠ACP,即 因为∠ACD=∠A+∠ABC,所以
如图3,当 BP 和CP 分别是∠ABC 的“邻BC 三分线”和∠ACD 的“邻CD 三分线”时,∠A+∠ABP =∠BPC+∠ACP,即 因为∠ACD=∠A+∠ABC,所以
如图4,当 BP 和CP 分别是∠ABC 的“邻BC 三分线”和∠ACD 的“邻AC 三分线”时,∠A+∠ABP=∠BPC+∠ACP,即 因为∠ACD=∠A+∠ABC,所以∠BPC=
如图5,当BP 和CP 分别是∠ABC 的“邻AB 三分线”和∠ACD 的“邻CD 三分线”时,∠A+∠ABP=∠BPC+∠ACP,即 因为∠ACD=∠A+∠ABC,所以∠BPC=
综上所述,∠BPC 的度数为 或 或 18°或
9.证明:假设△ABC 中每个内角都小于60°,则∠A+∠B+∠C<180°,这与三角形内角和定理矛盾,故假设错误,所以在△ABC中,∠A,∠B,∠C 中至少有一个角大于或等于60°.
10. 解:(1) ①110
②x,y,m,n 之间的数量关系为m=n+x+y.证明如下:
因为在△ABC 中,∠BAC+∠ABC+∠ACB = 180°, 所 以 ∠BAC +∠PBA + 因为在△PBC 中,∠BPC+∠PCB+∠PBC=180°,所以 所以∠BPC=∠BAC+∠PBA+∠PCA,即m=n+x+y.
(2)x,y,m,n之间所有可能的数量关系:①m+x=n+y,如图1所示;②n=m+x+y,如图2所示;③n+x=m+y,如图3所示;④x=m+n+y,如图4所示;⑤y=m+n+x,如图5所示;⑥m+n+x+y=360,如图6所示.
巅峰训练19 定理(2)
热食单糖等
1.下列命题中,逆命题是真命题的个数是( )
①若 则 ②若-1≤x≤2,则1≤|x|≤2;③四边形的外角和为 360°;④在△ABC 中,若∠A+∠B=90°,则∠C=90°.
A. 4 B. 3 C. 2 D. 1
2.用反证法证明命题“在四边形中,至少有一个角是钝角或直角”时,首先应该假设这个四边形中 ( )
A.有一个角是钝角或直角
B.每一个角都是钝角
C.每一个角都是直角
D.每一个角都是锐角
3.如图,由6个各边相等、各内角也相等的九边形拼接成一个美丽的图案,则图中∠α的度数为 ( )
A. 80° B. 60° C. 50° D. 100°
4. (2024·盐城市东台市期末)如图,点 D 在BC 的延长线上,DE⊥AB 于点 E,交 AC于点F.若∠A=35°,∠D=15°,则∠ACB的度数为 .
5.用反证法证明命题“同位角不相等时,两直线不平行”,应假设: .
6.(2024·镇江市期末)足球的表面是由12个正五边形和20个正六边形组成的.如图,将足球上的一个正六边形和它相邻的一个正五边形展开放平,则图中的∠ABC= .
7.(2024·宿迁市沭阳县期末)已知:如图1,三条线段 B C ,B C ,B C 两两相交于点A ,A ,A .
(1) 求∠B ,∠C ,∠B ,∠C ,∠B ,∠C 的度数之和.
(2)如图2,四条线段两两相交于点 A ,A ,A ,A ,求∠B ,∠C ,∠B ,∠C ,∠B ,∠C ,∠B ,∠C 的度数之和.
(3)猜想:类比图1、图2的画法,n条线段两两相交于点 A ,A ,A ,A ,…,A ,那么
8.(2024·常州市武进区校级月考)【概念认识】如图1,在∠ABC中,若∠ABD=∠DBE=∠EBC,则 BD,BE 叫作∠ABC 的“三分线”.其中,BD 是“邻AB 三分线”,BE 是“邻 BC 三分线”.
【问题解决】
(1) 如图2,在△ABC中,∠A=80°,∠B=45°.若∠B 的“三分线” BD 交AC 于点D,求∠BDC的度数.
(2) 如图3,在△ABC 中,BP,CP 分别是∠ABC 的“邻 BC 三分线”和∠ACB的“邻 BC 三分线”,且∠BPC=140°,求∠A 的度数.
【延伸推广】
(3) 在△ABC 中,∠ACD 是△ABC 的外角,∠B 的“三分线”所在的直线与∠ACD 的“三分线”所在的直线交于点 P.若 54°,请直接写出∠BPC 的度数(用含m 的代数式表示).
9. 求证:在△ABC中,∠A,∠B,∠C 中至少有一个角大于或等于 60°.
10. 已知△ABC,P 是平面内任意一点,A,B,C,P中任意三点都不在同一直线上,连接PB,PC.设∠PBA=x°,∠PCA =y°,∠BPC=m°,∠BAC=n°.
(1) 如图,点 P 在△ABC 内部.
①若n=80,x=10,y=20,则 m= ;
②探究x,y,m,n之间的数量关系,并证明你得到的结论.
(2)当点 P 在△ABC 外部时,请直接写出x,y,m,n之间所有可能的数量关系,并画出相应的图形.
巅峰训练19 定理(2)
1. D 提示:当 时 或 则 或 所以①的逆命题不是真命题.当1≤|x|≤2时,1≤x≤2或-2≤x≤-1,所以②的逆命题不是真命题.因为所有多边形的外角和均等于360°,所以③的逆命题不是真命题.在△ABC 中,若∠C=90°,则∠A+∠B=90°,所以④的逆命题是真命题.
2. D
3. A 提示:根据题意,得题图中九边形的每个内角都等于 所以
4.70° 5.同位角不相等时,两直线平行
6. 132°
7. 解:(1) 因为. ,所以∠B + 因为 ,所以∠B +
(2) 同(1)可得, ∠B A C ).因为. 所以∠B +
(3) 360° 提示:由(1)可知, 由(2)可知, 以此类推.
8. 解:(1)如图1,当 BD 是∠ABC的“邻AB 三分线”时, 95°;当 BD 是∠ABC 的“邻 BC 三分线”时, 综上所述,∠BDC 的度数为95°或110°.
(2) 在△BPC 中,因为∠BPC=140°,所以∠PBC+∠PCB=40°.又因为 BP,CP 分别是∠ABC 的“邻 BC 三分线”和∠ACB 的“邻BC 三分线”,所以 所以 40°,所以∠ABC+∠ACB=120°.在△ABC中,∠A +∠ABC +∠ACB = 180°, 所以∠A=180°-(∠ABC+∠ACB)=60°.
或 或 或 18°. 提示:分4种情况进行画图计算:
如图2,当 BP 和CP 分别是∠ABC 的“邻AB 三分线”和∠ACD 的“邻 AC 三分线”时,∠A+∠ABP=∠BPC+∠ACP,即 因为∠ACD=∠A+∠ABC,所以
如图3,当 BP 和CP 分别是∠ABC 的“邻BC 三分线”和∠ACD 的“邻CD 三分线”时,∠A+∠ABP =∠BPC+∠ACP,即 因为∠ACD=∠A+∠ABC,所以
如图4,当 BP 和CP 分别是∠ABC 的“邻BC 三分线”和∠ACD 的“邻AC 三分线”时,∠A+∠ABP=∠BPC+∠ACP,即 因为∠ACD=∠A+∠ABC,所以∠BPC=
如图5,当BP 和CP 分别是∠ABC 的“邻AB 三分线”和∠ACD 的“邻CD 三分线”时,∠A+∠ABP=∠BPC+∠ACP,即 因为∠ACD=∠A+∠ABC,所以∠BPC=
综上所述,∠BPC 的度数为 或 或 18°或
9.证明:假设△ABC 中每个内角都小于60°,则∠A+∠B+∠C<180°,这与三角形内角和定理矛盾,故假设错误,所以在△ABC中,∠A,∠B,∠C 中至少有一个角大于或等于60°.
10. 解:(1) ①110
②x,y,m,n 之间的数量关系为m=n+x+y.证明如下:
因为在△ABC 中,∠BAC+∠ABC+∠ACB = 180°, 所 以 ∠BAC +∠PBA + 因为在△PBC 中,∠BPC+∠PCB+∠PBC=180°,所以 所以∠BPC=∠BAC+∠PBA+∠PCA,即m=n+x+y.
(2)x,y,m,n之间所有可能的数量关系:①m+x=n+y,如图1所示;②n=m+x+y,如图2所示;③n+x=m+y,如图3所示;④x=m+n+y,如图4所示;⑤y=m+n+x,如图5所示;⑥m+n+x+y=360,如图6所示.
同课章节目录
- 第7章 平面图形的认识(二)
- 7.1 探索直线平行的条件
- 7.2 探索平行线的性质
- 7.3 图形的平移
- 7.4 认识三角形
- 7.5 多边形的内角和与外角和
- 第8章 幂的运算
- 8.1 同底数幂的乘法
- 8.2 幂的乘方与积的乘方
- 8.3 同底数幂的除法
- 第9章 整式乘法与因式分解
- 9.1 单项式乘单项式
- 9.2 单项式乘多项式
- 9.3 多项式乘多项式
- 9.4 乘法公式
- 9.5 多项式的因式分解
- 第10章 二元一次方程组
- 10.1 二元一次方程
- 10.2 二元一次方程组
- 10.3 解二元一次方程组
- 10.4 三元一次方程组
- 10.5 用二元一次方程解决问题
- 第11章 一元一次不等式
- 11.1 生活中的不等式
- 11.2 不等式的解集
- 11.3 不等式的性质
- 11.4 解一元一次不等式
- 11.5 用一元一次不等式解决问题
- 11.6 一元一次不等式组
- 第12章 证明
- 12.1 定义与命题
- 12.2 证明
- 12.3 互逆命题
