第12 章 定义 命题 证明单元知识整合练习2(含答案)
文档属性
| 名称 | 第12 章 定义 命题 证明单元知识整合练习2(含答案) |

|
|
| 格式 | docx | ||
| 文件大小 | 241.4KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 苏科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-05-08 00:00:00 | ||
图片预览

文档简介
中小学教育资源及组卷应用平台
第12 章 定义 命题 证明单元知识整合练习2
一、选择题
1.给出下列命题:①数轴上的点与有理数一一对应;②同一平面内垂直于同一条直线的两条直线平行;③两点之间,线段最短.其中是假命题的个数是 ( )
A. 0 B. 1 C. 2 D. 3
2. (2024·无锡市梁溪区校级月考)如图,在△ABC 中, ∠A = 84°, O 是 ∠ABC,∠ACB 的平分线的交点,P 是∠BOC,∠OCB 的平分线的交点.若∠P=100°,则∠ACB 的度数是 ( )
A. 42° B. 60° C. 56° D. 65°
3. A,B,C,D四个队赛球,比赛之前,甲和乙两人猜测比赛的名次顺序.甲:从第一名开始,名次顺序是 A,D,C,B;乙:从第一名开始,名次顺序是A,C,B,D.比赛之后,两人都只猜对了一个队的名次,已知第一名是B队,则这四个队的名次顺序是( )
A. B,A,C,D B. B,C,A,D
C. D,B,A,C D. B,A,D,C
二、填空题
4. 命题“两直线平行,同旁内角相等”是 (填“真”或“假”)命题.
5. 用反证法证明“如果|a|>a,那么a<0”是真命题时,第一步应先假设 .
6. (2024·苏州市期末) 如图,在△ABC 中,∠A=70°,∠C=44°,BD 平分∠ABC,交AC 于点 D,DE⊥AC,交 BC 于点 E,则∠BDE= °.
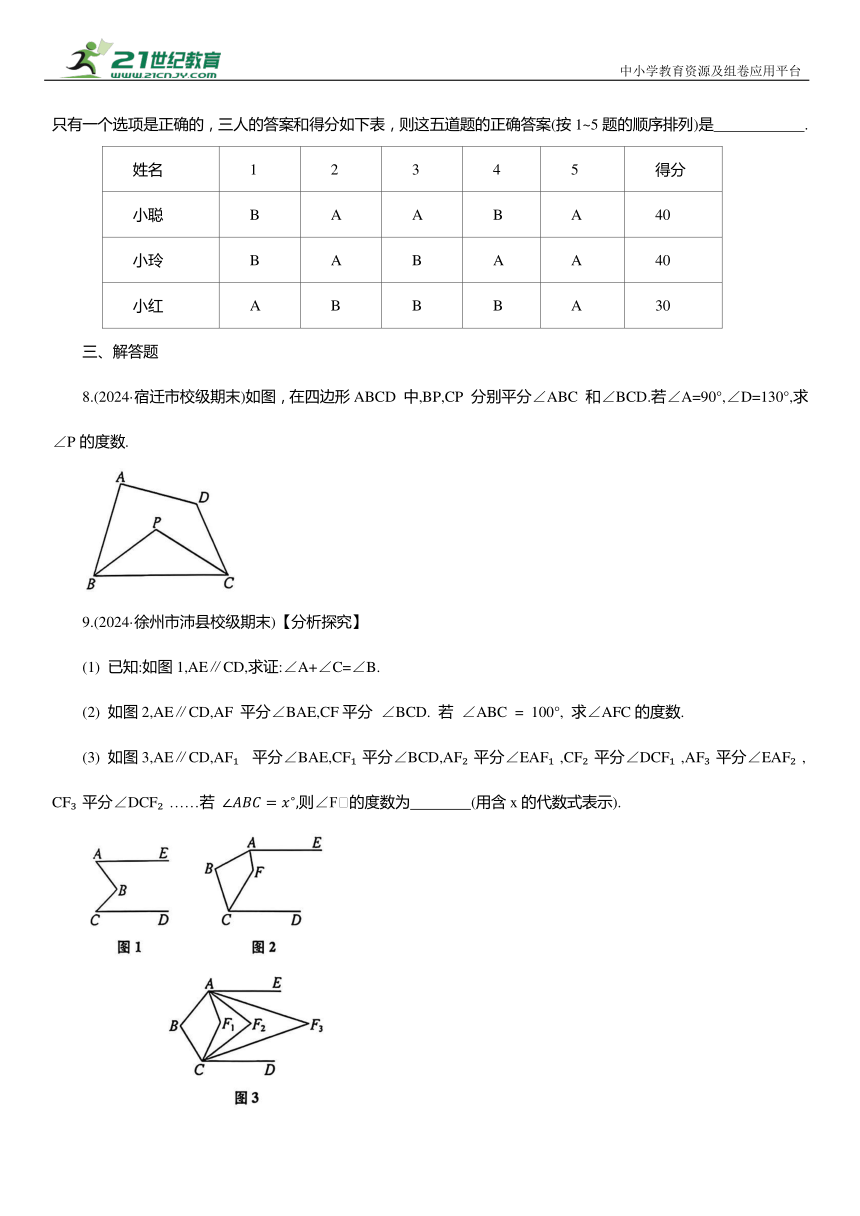
7.小聪、小玲、小红三人参加“普法知识竞赛”,其中前5题是选择题,每题10分,每题有 A,B两个选项,且只有一个选项是正确的,三人的答案和得分如下表,则这五道题的正确答案(按1~5题的顺序排列)是 .
姓名 1 2 3 4 5 得分
小聪 B A A B A 40
小玲 B A B A A 40
小红 A B B B A 30
三、解答题
8.(2024·宿迁市校级期末)如图,在四边形ABCD 中,BP,CP 分别平分∠ABC 和∠BCD.若∠A=90°,∠D=130°,求∠P的度数.
9.(2024·徐州市沛县校级期末)【分析探究】
(1) 已知:如图1,AE∥CD,求证:∠A+∠C=∠B.
(2) 如图2,AE∥CD,AF 平分∠BAE,CF平分 ∠BCD. 若 ∠ABC = 100°, 求∠AFC的度数.
(3) 如图3,AE∥CD,AF 平分∠BAE,CF 平分∠BCD,AF 平分∠EAF ,CF 平分∠DCF ,AF 平分∠EAF ,CF 平分∠DCF ……若 则∠F 的度数为 (用含x的代数式表示).
10.【阅读材料】
运用基本事实“同位角相等,两直线平行”证明“两直线平行,同位角相等”.
已知:如图1,直线AB,CD 被直线EF 所截,AB∥CD.求证:∠1=∠2.
证明:首先,假设∠1≠∠2,那么可以过点O作直线GH,使得∠EOH=∠2.根据“同位角相等,两直线平行”可以得到 GH∥CD,这样,过点 O 就有两条直线AB,GH 都与CD 平行,这与基本事实“过直线外一点有且只有一条直线与已知直线平行”矛盾.所以假设不正确,于是∠1=∠2.
【解决问题】
(1)仿照上面的证明方法,补全下面证明“两条平行线之间的距离处处相等”的过程.已知:如图 2,AB∥CD,EF⊥AB,GH⊥AB.求证:EF=GH.
首先,假设 ,将GH 沿着直线 BA 的方向平移,使点 G 与点 E 重合,点H 的对应点Q 在直线AB 上.因为EF≠GH,所以点 Q 与点 F 不重合.由EQ∥GH,GH⊥AB,易得 EQ⊥AB,而EF⊥AB,同时EQ⊥AB,这与基本事实 矛盾.所以假设不正确,于是EF=GH.
(2) 如图3,AB∥CD,S 表示△EFO的面积,S 表示△GHO 的面积.求证:
(3)按照要求,画出图形,并简要说明画法.
①如图4,过点 A 画一条直线,将△ABC 分割成面积相等的两部分;
②如图5,在△ABC 中,N 是 AB 上的一点(不是中点),过点 N 画一条直线将△ABC 分割成面积相等的两部分.
1. B
2. C 提示:设∠BCP=∠PCO=α,∠BOP=∠COP=β,因为∠P=100°,所以∠PCO+∠COP=α+β=80°.所以2α+2β=160°,所以. .因为 BO平分∠ABC,所以∠ABC=40°.因为∠A=84°,所以
3. A 提示:由第一名是B队,可知甲猜错了第一名和第四名,乙猜错了第一名和第三名.又因为甲、乙两人都只猜对了一个队的名次,所以可推知甲猜对了第三名,乙猜对了第四名.结合两人的猜测结果,可得正确的名次顺序是 B,A,C,D.
4. 假 5. a≥0
6. 13 提示:因为∠A=70°,∠C=44°,)所以 因为 BD平分∠ABC,所以 所以∠BDC=∠A+∠ABD=103°.因为 DE⊥AC,所以∠EDC=90°.所以∠BDE=∠BDC-∠EDC=13°.
7. BABBA 提示:根据得分,可知小聪和小玲都只有1题错误,小红有2题错误.第5题,三人选项相同,若不是选 A,则小聪和小玲的其他题目的答案一定相同,这与已知矛盾,故第5题的答案是 A;小聪和小玲第3题和第4题的答案不同,则一定在这两题上其中一人有错误,所以第1,2题两人答案正确,故第1题的答案是B,第2题的答案是 A;可知小红的错题是第1题和第2题,所以第3题和第4题正确,故第3题的答案是B,第4题的答案是 B.所以正确答案(按1~5题的顺序排列)是 BABBA.
8. 解:因为∠A=90°,∠D=130°,所以 因为 BP,CP 分别平分∠ABC 和∠BCD,所以 所以 所以∠P=180°-
9. (1) 证明:如图,过点 B 作 BM∥AE.因为AE∥CD,所以AE∥BM∥CD,所以∠ABM=∠A,∠CBM=∠C,所以∠A+∠C=∠ABM+∠CBM,即∠A+∠C=∠ABC.
(2) 解:因为 AF 平分∠BAE,CF 平分∠BCD,所以∠EAF =∠BAF,∠DCF =∠BCF. 由(1)可知,∠AFC = ∠EAF +∠DCF,所以∠BAF+∠BCF =∠EAF +∠DCF=∠AFC.由四边形的内角和等于360°, 得 ∠ABC + ∠BAF + ∠BCF +∠AFC=360°,即∠ABC+2∠AFC=360°,所以 因为∠ABC=100°,所以∠AFC=130°.
提示:因为 AF 平分∠EAF ,CF 平分∠DCF ,所以 所以 由(1)可知,. 所以. 由(2)可知, 又因为∠ABC=x°,所以 所以 同理 以此类推,
10. (1) 解:EF≠GH “在同一平面内,过一点有且仅有一条直线与已知直线垂直”
(2)证明:过点 E 作EP⊥AB 于点 P,过点G 作GQ⊥AB 于点Q.由(1)可知,EP=GQ. 因为 所以S△EFH=S△GFH.因为 所以
(3) 解:①如图1,取 BC 的中点 D,连接AD,则直线AD 即为所求.
②如图2,取 BC 的中点D,连接 ND,过点A 作AM∥ND,交BC 于点M,连接MN,则直线MN 即为所求.
第12 章 定义 命题 证明单元知识整合练习2
一、选择题
1.给出下列命题:①数轴上的点与有理数一一对应;②同一平面内垂直于同一条直线的两条直线平行;③两点之间,线段最短.其中是假命题的个数是 ( )
A. 0 B. 1 C. 2 D. 3
2. (2024·无锡市梁溪区校级月考)如图,在△ABC 中, ∠A = 84°, O 是 ∠ABC,∠ACB 的平分线的交点,P 是∠BOC,∠OCB 的平分线的交点.若∠P=100°,则∠ACB 的度数是 ( )
A. 42° B. 60° C. 56° D. 65°
3. A,B,C,D四个队赛球,比赛之前,甲和乙两人猜测比赛的名次顺序.甲:从第一名开始,名次顺序是 A,D,C,B;乙:从第一名开始,名次顺序是A,C,B,D.比赛之后,两人都只猜对了一个队的名次,已知第一名是B队,则这四个队的名次顺序是( )
A. B,A,C,D B. B,C,A,D
C. D,B,A,C D. B,A,D,C
二、填空题
4. 命题“两直线平行,同旁内角相等”是 (填“真”或“假”)命题.
5. 用反证法证明“如果|a|>a,那么a<0”是真命题时,第一步应先假设 .
6. (2024·苏州市期末) 如图,在△ABC 中,∠A=70°,∠C=44°,BD 平分∠ABC,交AC 于点 D,DE⊥AC,交 BC 于点 E,则∠BDE= °.
7.小聪、小玲、小红三人参加“普法知识竞赛”,其中前5题是选择题,每题10分,每题有 A,B两个选项,且只有一个选项是正确的,三人的答案和得分如下表,则这五道题的正确答案(按1~5题的顺序排列)是 .
姓名 1 2 3 4 5 得分
小聪 B A A B A 40
小玲 B A B A A 40
小红 A B B B A 30
三、解答题
8.(2024·宿迁市校级期末)如图,在四边形ABCD 中,BP,CP 分别平分∠ABC 和∠BCD.若∠A=90°,∠D=130°,求∠P的度数.
9.(2024·徐州市沛县校级期末)【分析探究】
(1) 已知:如图1,AE∥CD,求证:∠A+∠C=∠B.
(2) 如图2,AE∥CD,AF 平分∠BAE,CF平分 ∠BCD. 若 ∠ABC = 100°, 求∠AFC的度数.
(3) 如图3,AE∥CD,AF 平分∠BAE,CF 平分∠BCD,AF 平分∠EAF ,CF 平分∠DCF ,AF 平分∠EAF ,CF 平分∠DCF ……若 则∠F 的度数为 (用含x的代数式表示).
10.【阅读材料】
运用基本事实“同位角相等,两直线平行”证明“两直线平行,同位角相等”.
已知:如图1,直线AB,CD 被直线EF 所截,AB∥CD.求证:∠1=∠2.
证明:首先,假设∠1≠∠2,那么可以过点O作直线GH,使得∠EOH=∠2.根据“同位角相等,两直线平行”可以得到 GH∥CD,这样,过点 O 就有两条直线AB,GH 都与CD 平行,这与基本事实“过直线外一点有且只有一条直线与已知直线平行”矛盾.所以假设不正确,于是∠1=∠2.
【解决问题】
(1)仿照上面的证明方法,补全下面证明“两条平行线之间的距离处处相等”的过程.已知:如图 2,AB∥CD,EF⊥AB,GH⊥AB.求证:EF=GH.
首先,假设 ,将GH 沿着直线 BA 的方向平移,使点 G 与点 E 重合,点H 的对应点Q 在直线AB 上.因为EF≠GH,所以点 Q 与点 F 不重合.由EQ∥GH,GH⊥AB,易得 EQ⊥AB,而EF⊥AB,同时EQ⊥AB,这与基本事实 矛盾.所以假设不正确,于是EF=GH.
(2) 如图3,AB∥CD,S 表示△EFO的面积,S 表示△GHO 的面积.求证:
(3)按照要求,画出图形,并简要说明画法.
①如图4,过点 A 画一条直线,将△ABC 分割成面积相等的两部分;
②如图5,在△ABC 中,N 是 AB 上的一点(不是中点),过点 N 画一条直线将△ABC 分割成面积相等的两部分.
1. B
2. C 提示:设∠BCP=∠PCO=α,∠BOP=∠COP=β,因为∠P=100°,所以∠PCO+∠COP=α+β=80°.所以2α+2β=160°,所以. .因为 BO平分∠ABC,所以∠ABC=40°.因为∠A=84°,所以
3. A 提示:由第一名是B队,可知甲猜错了第一名和第四名,乙猜错了第一名和第三名.又因为甲、乙两人都只猜对了一个队的名次,所以可推知甲猜对了第三名,乙猜对了第四名.结合两人的猜测结果,可得正确的名次顺序是 B,A,C,D.
4. 假 5. a≥0
6. 13 提示:因为∠A=70°,∠C=44°,)所以 因为 BD平分∠ABC,所以 所以∠BDC=∠A+∠ABD=103°.因为 DE⊥AC,所以∠EDC=90°.所以∠BDE=∠BDC-∠EDC=13°.
7. BABBA 提示:根据得分,可知小聪和小玲都只有1题错误,小红有2题错误.第5题,三人选项相同,若不是选 A,则小聪和小玲的其他题目的答案一定相同,这与已知矛盾,故第5题的答案是 A;小聪和小玲第3题和第4题的答案不同,则一定在这两题上其中一人有错误,所以第1,2题两人答案正确,故第1题的答案是B,第2题的答案是 A;可知小红的错题是第1题和第2题,所以第3题和第4题正确,故第3题的答案是B,第4题的答案是 B.所以正确答案(按1~5题的顺序排列)是 BABBA.
8. 解:因为∠A=90°,∠D=130°,所以 因为 BP,CP 分别平分∠ABC 和∠BCD,所以 所以 所以∠P=180°-
9. (1) 证明:如图,过点 B 作 BM∥AE.因为AE∥CD,所以AE∥BM∥CD,所以∠ABM=∠A,∠CBM=∠C,所以∠A+∠C=∠ABM+∠CBM,即∠A+∠C=∠ABC.
(2) 解:因为 AF 平分∠BAE,CF 平分∠BCD,所以∠EAF =∠BAF,∠DCF =∠BCF. 由(1)可知,∠AFC = ∠EAF +∠DCF,所以∠BAF+∠BCF =∠EAF +∠DCF=∠AFC.由四边形的内角和等于360°, 得 ∠ABC + ∠BAF + ∠BCF +∠AFC=360°,即∠ABC+2∠AFC=360°,所以 因为∠ABC=100°,所以∠AFC=130°.
提示:因为 AF 平分∠EAF ,CF 平分∠DCF ,所以 所以 由(1)可知,. 所以. 由(2)可知, 又因为∠ABC=x°,所以 所以 同理 以此类推,
10. (1) 解:EF≠GH “在同一平面内,过一点有且仅有一条直线与已知直线垂直”
(2)证明:过点 E 作EP⊥AB 于点 P,过点G 作GQ⊥AB 于点Q.由(1)可知,EP=GQ. 因为 所以S△EFH=S△GFH.因为 所以
(3) 解:①如图1,取 BC 的中点 D,连接AD,则直线AD 即为所求.
②如图2,取 BC 的中点D,连接 ND,过点A 作AM∥ND,交BC 于点M,连接MN,则直线MN 即为所求.
同课章节目录
- 第7章 平面图形的认识(二)
- 7.1 探索直线平行的条件
- 7.2 探索平行线的性质
- 7.3 图形的平移
- 7.4 认识三角形
- 7.5 多边形的内角和与外角和
- 第8章 幂的运算
- 8.1 同底数幂的乘法
- 8.2 幂的乘方与积的乘方
- 8.3 同底数幂的除法
- 第9章 整式乘法与因式分解
- 9.1 单项式乘单项式
- 9.2 单项式乘多项式
- 9.3 多项式乘多项式
- 9.4 乘法公式
- 9.5 多项式的因式分解
- 第10章 二元一次方程组
- 10.1 二元一次方程
- 10.2 二元一次方程组
- 10.3 解二元一次方程组
- 10.4 三元一次方程组
- 10.5 用二元一次方程解决问题
- 第11章 一元一次不等式
- 11.1 生活中的不等式
- 11.2 不等式的解集
- 11.3 不等式的性质
- 11.4 解一元一次不等式
- 11.5 用一元一次不等式解决问题
- 11.6 一元一次不等式组
- 第12章 证明
- 12.1 定义与命题
- 12.2 证明
- 12.3 互逆命题
