期末综合练(2) (含答案)2024-2025学年苏科版七年级数学下册
文档属性
| 名称 | 期末综合练(2) (含答案)2024-2025学年苏科版七年级数学下册 |  | |
| 格式 | docx | ||
| 文件大小 | 229.3KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 苏科版 | ||
| 科目 | 数学 | ||
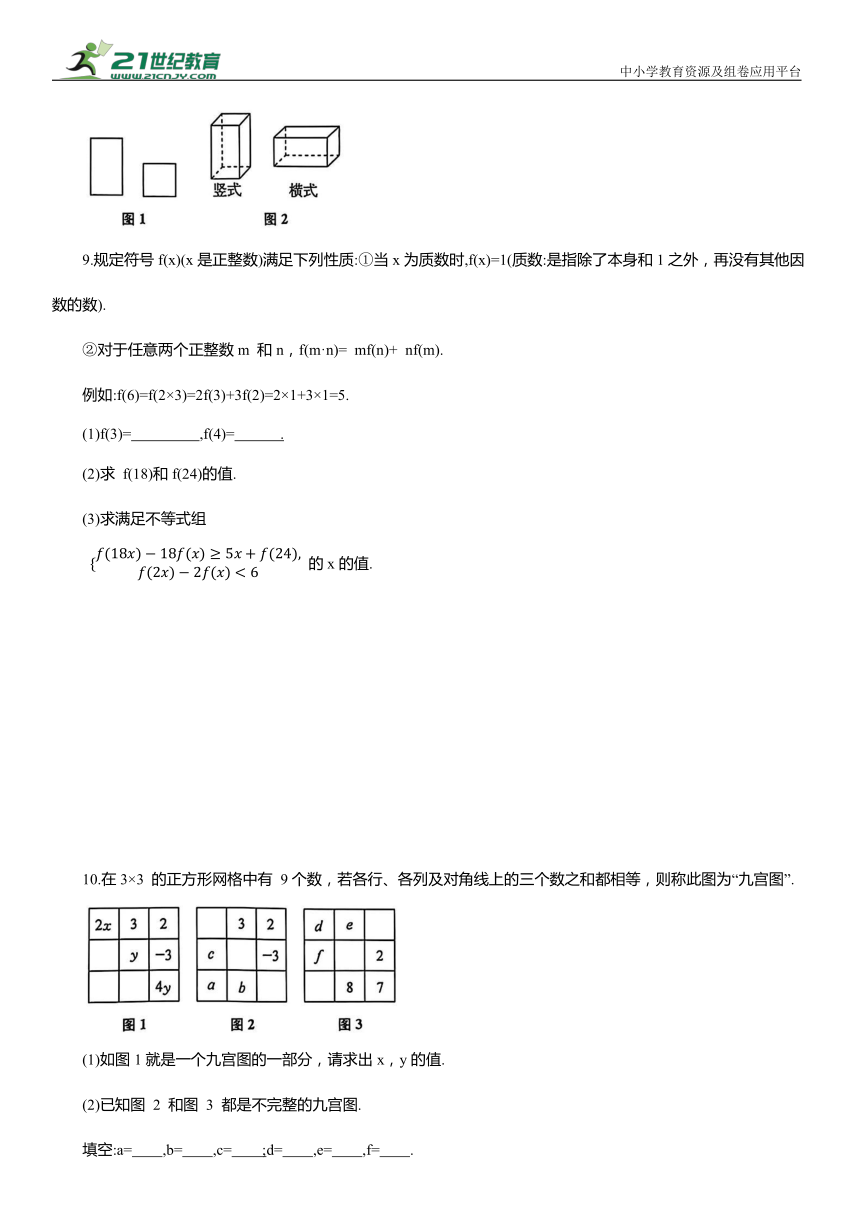
| 更新时间 | 2025-05-08 05:49:35 | ||
图片预览

文档简介
中小学教育资源及组卷应用平台
期末综合练(2)
一、选择题
1.下列命题中,属于真命题的是 ( )
A.同旁内角互补
B. 若a<1,则(
C.直角都相等
D.相等的角是对顶角
2. 古希腊数学家把数1,3,6,10,15,21,…叫作三角数,它们有一定的规律性.若把第1个三角数记为a ,第2个三角数记为a ……第 n个三角数记为 an,计算( 由此推算a +a 的值为 ( )
A. 20 000 B. 40 000
C. 39 701 D. 19 701
3.甲、乙、丙3人从图书馆各借了一本书(如下表所示),他们相约在每个星期天相互交换读完的书,经过数次交换后,他们都读完了这3本书.已知甲读的第三本书是乙读的第二本书,则丙读的第二本书是( )
甲 乙 丙
书 A 书 B 书C
A. 书A B. 书B
C. 书C D.无法确定
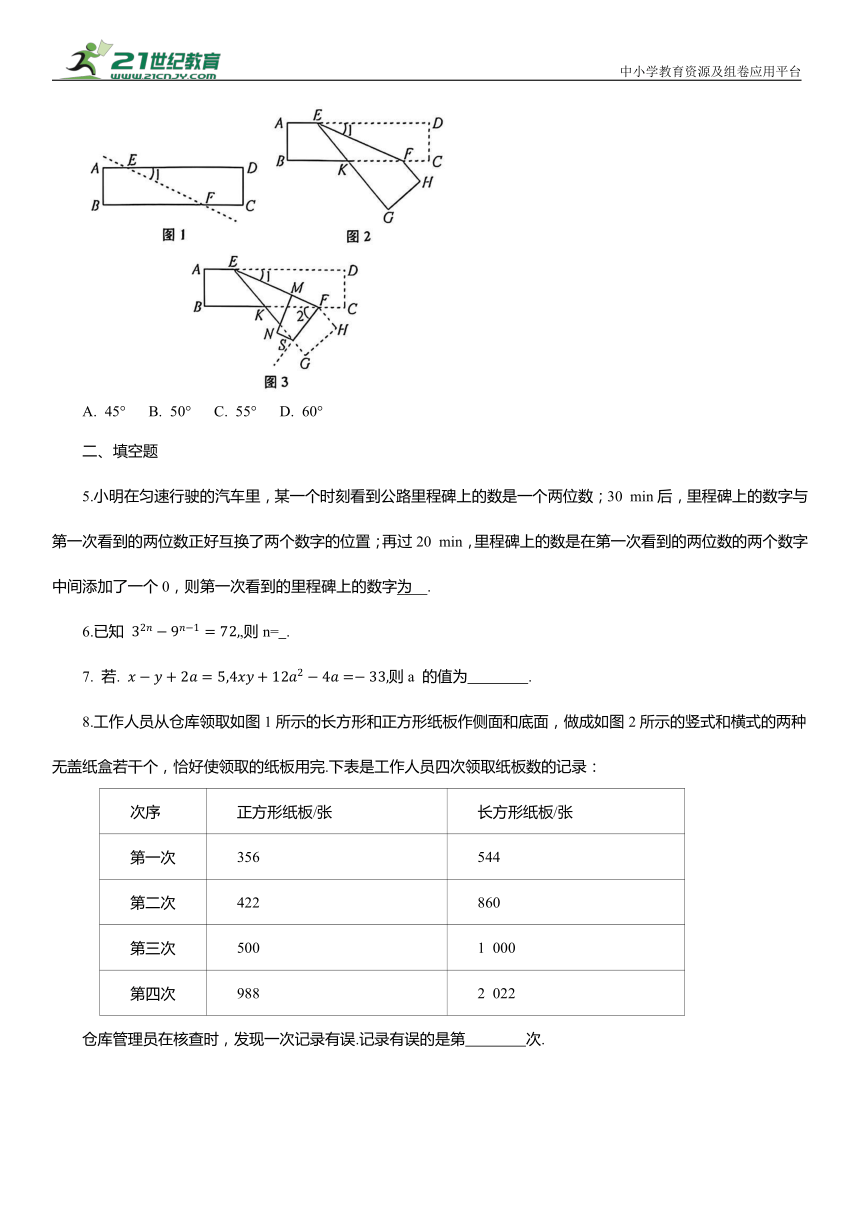
4. 如图 1,已知长方形纸带 ABCD,AB∥CD,AD∥BC,∠C=90°,点 E,F 分别在边AD,BC上,∠1=20°.如图2,将纸带先沿直线 EF 折叠后,点C,D分别落在点H,G的位置.如图3,将纸带再沿 FS 折叠一次,使点 H 落在线段EF 上点 M 的位置,则∠2的度数为 ( )
A. 45° B. 50° C. 55° D. 60°
二、填空题
5.小明在匀速行驶的汽车里,某一个时刻看到公路里程碑上的数是一个两位数;30 min后,里程碑上的数字与第一次看到的两位数正好互换了两个数字的位置;再过20 min,里程碑上的数是在第一次看到的两位数的两个数字中间添加了一个0,则第一次看到的里程碑上的数字为 .
6.已知 ,则n= .
7. 若. 则a 的值为 .
8.工作人员从仓库领取如图1所示的长方形和正方形纸板作侧面和底面,做成如图2所示的竖式和横式的两种无盖纸盒若干个,恰好使领取的纸板用完.下表是工作人员四次领取纸板数的记录:
次序 正方形纸板/张 长方形纸板/张
第一次 356 544
第二次 422 860
第三次 500 1 000
第四次 988 2 022
仓库管理员在核查时,发现一次记录有误.记录有误的是第 次.
9.规定符号f(x)(x是正整数)满足下列性质:①当x为质数时,f(x)=1(质数:是指除了本身和1之外,再没有其他因数的数).
②对于任意两个正整数m 和n,f(m·n)= mf(n)+ nf(m).
例如:f(6)=f(2×3)=2f(3)+3f(2)=2×1+3×1=5.
(1)f(3)= ,f(4)= .
(2)求 f(18)和f(24)的值.
(3)求满足不等式组
的x的值.
10.在3×3 的正方形网格中有 9个数,若各行、各列及对角线上的三个数之和都相等,则称此图为“九宫图”.
(1)如图1就是一个九宫图的一部分,请求出x,y的值.
(2)已知图 2 和图 3 都是不完整的九宫图.
填空:a= ,b= ,c= ;d= ,e= ,f= .
11. 在△ABC中,∠BAC=90°,D 是BC 上一点,将△ABD 沿AD 翻折后得到△AED,边AE 交射线BC 于点F.
(1) 如图1,当AE⊥BC时,求证:DE∥AC.
(2)若
①如图2,当DE⊥BC时,求x的值.
②是否存在这样的x的值,使得△DEF中有两个角相等 若存在,求出x的值;若不存在,请说明理由.
期末综合练(2)
1. C
2. B 提示:因为 所以, 所以
3. A 提示:因为甲读的第三本书是乙读的第二本书,且必然不是各自所读的第一本书,即不是书A,书B,所以乙读的第二本书为书C.所以乙读书的先后顺序为书B,书C,书A;甲读书的先后顺序为书 A,书B,书C;丙读书的先后顺序为书C,书A,书B.
4. D 提示:由折叠的性质,可得∠GEF=∠1=20°.因为 AD∥BC,所以 FH∥EG.所以∠GEF+∠EFH= 180°,所以∠EFH =160°,所以∠EFS = 因为 AD∥BC,所以∠EFB=∠1=20°,所以∠2=∠EFS-∠EFB=60°.
5.17 提示:设第一次看到的两位数十位上的数字为x,个位上的数字为 y,则第一个里程碑上的数为(10x+y),第二个里程碑上的数为(10y+x),第三个里程碑上的数为(100x+y).因为小亮是匀速行驶,所以 解得y=7x.因为x,y都为整数,且1≤x≤9,1≤y≤9,所以x=1,y=7.所以第一次看到的里程碑上的数字为17.
6.2 提示:因为 ,所以 3 ,即2n-2=2,解得n=2.
7. - 1 提示:因为x-y+2a=5,所以x--y=5-2a,所以( 即 因为 所以①+②,得 即 所以 因为 1) ≥0,所以a+1=0,所以a=-1.
8.二 提示:设可以做成x个竖式无盖纸盒,y个横式无盖纸盒.解法1 第一次: 解得 数据无误;第二次: 解得 因为x,y应当为正整数,所以不符合题意,即数据错误;第三次; 解得 数据无误;第四次: 解得 数据无误.
解法2 易知需要正方形纸板(x+2y)张,需要长方形纸板(4x+3y)张.因为((x+2y)+(4x+3y)=5(x+y),所以二者之和应该是5的倍数.第二次领取记录显然不符合题意.
9. 解:(1)1 4
(2) f(18)=f(3×6)=3f(6)+6f(3)=3×5+6×1=21,f(24)=f(4×6)=4f(6)+6f(4)=4×5+6×4=44.
(3) 因为 f(18x)=18f(x)+ xf(18)=18f(x)+21x,f(2x)=2f(x)+ xf(2)=2f(x)+x,所以代入原不等式组,整理可得 解得 又因为x为正整数,所以x的值为3或4或5.
10. 解: (1) 根 据 题 意, 得 解得
(2) 0 — 1 5 5 4 10 提示:根据题意,得 解得
11. (1) 证明:因为∠BAC=90°,AE⊥BC,所以∠CAF +∠BAF = 90°,∠B +∠BAF=90°,所以∠CAF=∠B.由翻折的性质,可知∠E=∠B,所以∠CAF=∠E,所以DE∥AC.
(2) 解:①因为∠C=2∠B,易知∠C+∠B=90°,所以∠C=60°,∠B=30°.因为DE⊥BC,∠E=∠B=30°,所以∠BFE=60°. 因为 ∠BFE = ∠B +∠BAF,所以∠BAF=30°.由翻折的性质,可知∠BAD= 即x=15.
②存在.因为∠FDA=∠B+∠BAD=(30+x)°,∠ADE=∠ADB=180°-∠B-∠BAD=(150-x)°,所以∠FDE=∠ADE--∠FDA=(120-2x)°,所以. ∠E--∠FDE =(2x+30)°. 当∠FDE =∠DFE时,120-2x=2x+30,解得x=22.5;当∠DFE=∠E=30°时,2x+30=30,解得x=0,因为0
期末综合练(2)
一、选择题
1.下列命题中,属于真命题的是 ( )
A.同旁内角互补
B. 若a<1,则(
C.直角都相等
D.相等的角是对顶角
2. 古希腊数学家把数1,3,6,10,15,21,…叫作三角数,它们有一定的规律性.若把第1个三角数记为a ,第2个三角数记为a ……第 n个三角数记为 an,计算( 由此推算a +a 的值为 ( )
A. 20 000 B. 40 000
C. 39 701 D. 19 701
3.甲、乙、丙3人从图书馆各借了一本书(如下表所示),他们相约在每个星期天相互交换读完的书,经过数次交换后,他们都读完了这3本书.已知甲读的第三本书是乙读的第二本书,则丙读的第二本书是( )
甲 乙 丙
书 A 书 B 书C
A. 书A B. 书B
C. 书C D.无法确定
4. 如图 1,已知长方形纸带 ABCD,AB∥CD,AD∥BC,∠C=90°,点 E,F 分别在边AD,BC上,∠1=20°.如图2,将纸带先沿直线 EF 折叠后,点C,D分别落在点H,G的位置.如图3,将纸带再沿 FS 折叠一次,使点 H 落在线段EF 上点 M 的位置,则∠2的度数为 ( )
A. 45° B. 50° C. 55° D. 60°
二、填空题
5.小明在匀速行驶的汽车里,某一个时刻看到公路里程碑上的数是一个两位数;30 min后,里程碑上的数字与第一次看到的两位数正好互换了两个数字的位置;再过20 min,里程碑上的数是在第一次看到的两位数的两个数字中间添加了一个0,则第一次看到的里程碑上的数字为 .
6.已知 ,则n= .
7. 若. 则a 的值为 .
8.工作人员从仓库领取如图1所示的长方形和正方形纸板作侧面和底面,做成如图2所示的竖式和横式的两种无盖纸盒若干个,恰好使领取的纸板用完.下表是工作人员四次领取纸板数的记录:
次序 正方形纸板/张 长方形纸板/张
第一次 356 544
第二次 422 860
第三次 500 1 000
第四次 988 2 022
仓库管理员在核查时,发现一次记录有误.记录有误的是第 次.
9.规定符号f(x)(x是正整数)满足下列性质:①当x为质数时,f(x)=1(质数:是指除了本身和1之外,再没有其他因数的数).
②对于任意两个正整数m 和n,f(m·n)= mf(n)+ nf(m).
例如:f(6)=f(2×3)=2f(3)+3f(2)=2×1+3×1=5.
(1)f(3)= ,f(4)= .
(2)求 f(18)和f(24)的值.
(3)求满足不等式组
的x的值.
10.在3×3 的正方形网格中有 9个数,若各行、各列及对角线上的三个数之和都相等,则称此图为“九宫图”.
(1)如图1就是一个九宫图的一部分,请求出x,y的值.
(2)已知图 2 和图 3 都是不完整的九宫图.
填空:a= ,b= ,c= ;d= ,e= ,f= .
11. 在△ABC中,∠BAC=90°,D 是BC 上一点,将△ABD 沿AD 翻折后得到△AED,边AE 交射线BC 于点F.
(1) 如图1,当AE⊥BC时,求证:DE∥AC.
(2)若
①如图2,当DE⊥BC时,求x的值.
②是否存在这样的x的值,使得△DEF中有两个角相等 若存在,求出x的值;若不存在,请说明理由.
期末综合练(2)
1. C
2. B 提示:因为 所以, 所以
3. A 提示:因为甲读的第三本书是乙读的第二本书,且必然不是各自所读的第一本书,即不是书A,书B,所以乙读的第二本书为书C.所以乙读书的先后顺序为书B,书C,书A;甲读书的先后顺序为书 A,书B,书C;丙读书的先后顺序为书C,书A,书B.
4. D 提示:由折叠的性质,可得∠GEF=∠1=20°.因为 AD∥BC,所以 FH∥EG.所以∠GEF+∠EFH= 180°,所以∠EFH =160°,所以∠EFS = 因为 AD∥BC,所以∠EFB=∠1=20°,所以∠2=∠EFS-∠EFB=60°.
5.17 提示:设第一次看到的两位数十位上的数字为x,个位上的数字为 y,则第一个里程碑上的数为(10x+y),第二个里程碑上的数为(10y+x),第三个里程碑上的数为(100x+y).因为小亮是匀速行驶,所以 解得y=7x.因为x,y都为整数,且1≤x≤9,1≤y≤9,所以x=1,y=7.所以第一次看到的里程碑上的数字为17.
6.2 提示:因为 ,所以 3 ,即2n-2=2,解得n=2.
7. - 1 提示:因为x-y+2a=5,所以x--y=5-2a,所以( 即 因为 所以①+②,得 即 所以 因为 1) ≥0,所以a+1=0,所以a=-1.
8.二 提示:设可以做成x个竖式无盖纸盒,y个横式无盖纸盒.解法1 第一次: 解得 数据无误;第二次: 解得 因为x,y应当为正整数,所以不符合题意,即数据错误;第三次; 解得 数据无误;第四次: 解得 数据无误.
解法2 易知需要正方形纸板(x+2y)张,需要长方形纸板(4x+3y)张.因为((x+2y)+(4x+3y)=5(x+y),所以二者之和应该是5的倍数.第二次领取记录显然不符合题意.
9. 解:(1)1 4
(2) f(18)=f(3×6)=3f(6)+6f(3)=3×5+6×1=21,f(24)=f(4×6)=4f(6)+6f(4)=4×5+6×4=44.
(3) 因为 f(18x)=18f(x)+ xf(18)=18f(x)+21x,f(2x)=2f(x)+ xf(2)=2f(x)+x,所以代入原不等式组,整理可得 解得 又因为x为正整数,所以x的值为3或4或5.
10. 解: (1) 根 据 题 意, 得 解得
(2) 0 — 1 5 5 4 10 提示:根据题意,得 解得
11. (1) 证明:因为∠BAC=90°,AE⊥BC,所以∠CAF +∠BAF = 90°,∠B +∠BAF=90°,所以∠CAF=∠B.由翻折的性质,可知∠E=∠B,所以∠CAF=∠E,所以DE∥AC.
(2) 解:①因为∠C=2∠B,易知∠C+∠B=90°,所以∠C=60°,∠B=30°.因为DE⊥BC,∠E=∠B=30°,所以∠BFE=60°. 因为 ∠BFE = ∠B +∠BAF,所以∠BAF=30°.由翻折的性质,可知∠BAD= 即x=15.
②存在.因为∠FDA=∠B+∠BAD=(30+x)°,∠ADE=∠ADB=180°-∠B-∠BAD=(150-x)°,所以∠FDE=∠ADE--∠FDA=(120-2x)°,所以. ∠E--∠FDE =(2x+30)°. 当∠FDE =∠DFE时,120-2x=2x+30,解得x=22.5;当∠DFE=∠E=30°时,2x+30=30,解得x=0,因为0
同课章节目录
