29.1 投影(课时1)同步练习 (含答案)人教版数学九年级下册
文档属性
| 名称 | 29.1 投影(课时1)同步练习 (含答案)人教版数学九年级下册 |

|
|
| 格式 | docx | ||
| 文件大小 | 201.2KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-05-08 07:57:52 | ||
图片预览


文档简介
《29.1 投影》同步练习
(课时1 平行投影与中心投影)
一、基础巩固
知识点1 投影的概念
1. 下列现象是物体的投影的是( )
A.小明看到镜子里的自己
B.灯光下猫咪映在墙上的影子
C.自行车行驶过后车轮留下的痕迹
D.掉在地上的树叶
知识点2 平行投影
2. [2022河北唐山路北区期末]下列投影是平行投影的是( )
A.太阳光下窗户的影子
B.台灯下书本的影子
C.在手电筒照射下纸片的影子
D.路灯下行人的影子
3. [2022河南濮阳三模]下列四幅图中,能表示两棵树在同一时刻太阳光下的影子的图是( )
4. 矩形窗框在太阳光下的影子不可能是( )
A.平行四边形 B.矩形 C.梯形 D.线段
5. [2020山东济南长清区期末]如图,已知AB和DE是直立在地面上的两根立柱.AB=5 m,某一时刻AB在阳光下的投影BC=3 m.
(1)请你在图中画出此时DE在阳光下的投影;
(2)在测量AB的投影时,同时测量出DE在阳光下的投影长为6 m,请你计算DE的长.
知识点3 中心投影
6. 下列影子不是中心投影的是( )
A.皮影戏中的影子
B.晚上在房间内墙上的手影
C.舞厅中霓虹灯形成的影子
D.太阳光下林荫道上的树影
7. 一幢4层楼房只有一个窗户亮着一盏灯,一棵小树和一根电线杆在窗口灯光下的影子如图所示,则亮着灯的窗口是( )
A.1号窗口 B.2号窗口
C.3号窗口 D.4号窗口
8. [2021江西景德镇期末]如图,某小区内有一条笔直的小路,路的旁边有一盏路灯,晚上小红由A处走到B处,则表示她在该路灯照射下的影长l与行走的路程s之间关系的大致图象是( )
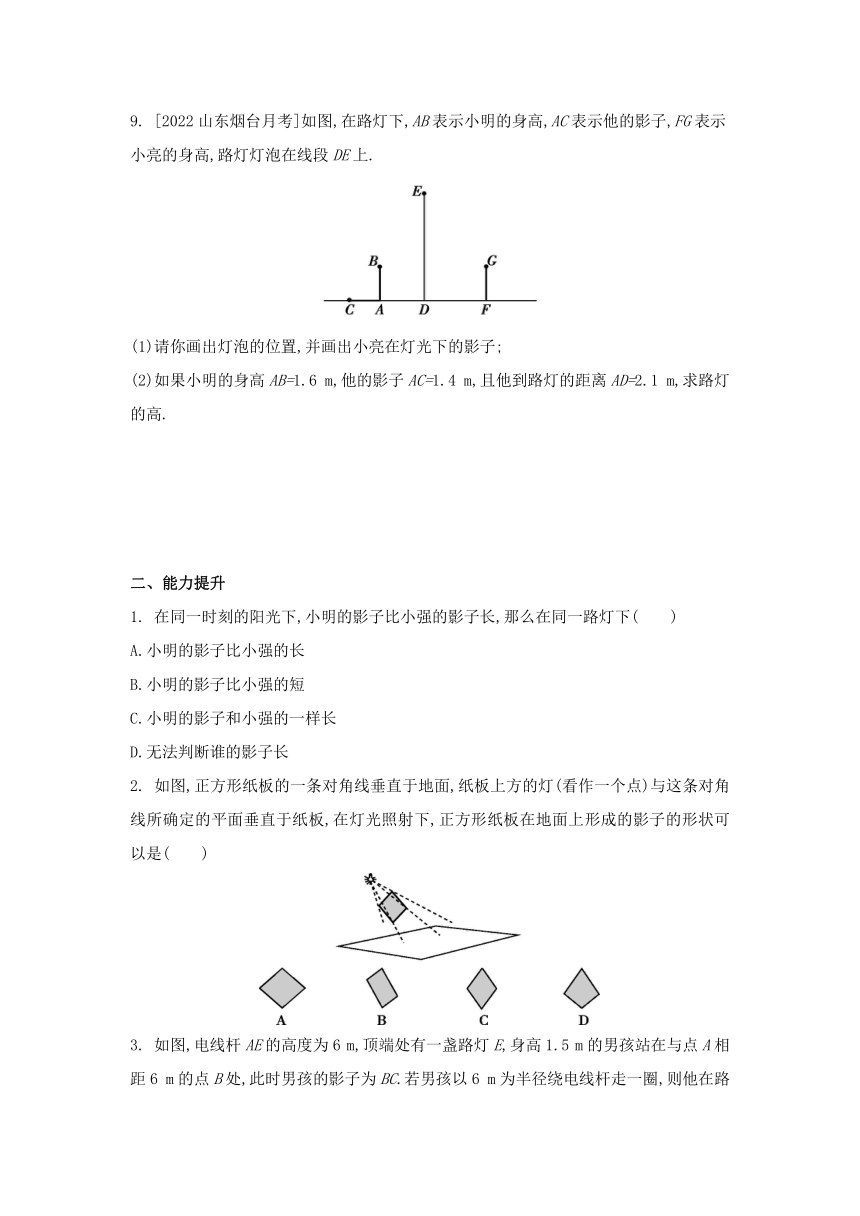
9. [2022山东烟台月考]如图,在路灯下,AB表示小明的身高,AC表示他的影子,FG表示小亮的身高,路灯灯泡在线段DE上.
(1)请你画出灯泡的位置,并画出小亮在灯光下的影子;
(2)如果小明的身高AB=1.6 m,他的影子AC=1.4 m,且他到路灯的距离AD=2.1 m,求路灯的高.
二、能力提升
1. 在同一时刻的阳光下,小明的影子比小强的影子长,那么在同一路灯下( )
A.小明的影子比小强的长
B.小明的影子比小强的短
C.小明的影子和小强的一样长
D.无法判断谁的影子长
2. 如图,正方形纸板的一条对角线垂直于地面,纸板上方的灯(看作一个点)与这条对角线所确定的平面垂直于纸板,在灯光照射下,正方形纸板在地面上形成的影子的形状可以是( )
3. 如图,电线杆AE的高度为6 m,顶端处有一盏路灯E,身高1.5 m的男孩站在与点A相距6 m的点B处,此时男孩的影子为BC.若男孩以6 m为半径绕电线杆走一圈,则他在路灯下的影子扫过的面积为 m2.
4. 在长、宽都为4 m,高为3 m的房间的正中央的天花板上悬挂一个灯泡,为了集中光线,加上了灯罩,如图所示.已知灯罩深8 cm,灯泡A离地面2 m,为了使光线恰好照到墙角,问灯罩的直径BC应为多少.(结果精确到0.01 m,≈1.414)
参考答案
一、基础巩固
1.B 【解析】 一般地,用光线照射物体,在某个平面(地面、墙壁等)上得到的影子叫做物体的投影.A项、C项、D项都和影子无关.
2.A
3.C 【解析】 同一时刻太阳光下树的影子是平行的,影子方向相同,且影长与树高成正比.选项A,B中的两棵树的影子方向都相反,故可排除;选项D中影长和树高不成正比,故可排除.
4.C
5.【解析】 (1)如图,连接AC,过点D作DF∥AC,交地面于点F,线段EF即DE在阳光下的投影.
(2)∵AC∥DF,∴∠ACB=∠DFE,
又∠ABC=∠DEF=90°,∴△ABC∽△DEF.
∴=, 即=,∴DE=10 m.
∴DE的长为10 m.
6.D
7.B 【解析】 如图所示,亮着灯的窗口是2号窗口.
8.C 【解析】 小红由A处走到路灯正下方这一过程中,l随s的增加而减小;当小红走到路灯正下方时,l等于0;小红由路灯正下方走到B处这一过程中,l随s的增大而增大.结合选项,知选C.
9.【解析】 (1)如图,点O为灯泡的位置,FH为小亮在灯光下的影子.
(2)∵AB∥OD,∴△ABC∽△DOC,
∴=,即=,∴DO=4 m.
∴路灯的高为4 m.
二、能力提升
1.D 【解析】 路灯下的投影为中心投影,由于不知道他们距离光源的远近,所以无法判断谁的影子长.
2.D 【解析】 由题意知,正方形纸板越靠近光源的边,影子越长.如图,由于正方形纸板有一条对角线与地面垂直,且该对角线与灯所确定的平面垂直于纸板,故AB,AD的影子相等,CB,CD的影子相等,且AB,AD的影子长.
3.28π 【解析】 ∵AE∥BD,∴△CBD∽△CAE,∴=,即=,∴CB=2 m,∴AC=8 m,∴男孩以6 m为半径绕电线杆走一圈,他在路灯下的影子扫过的面积为π×82-π×62=28π(m2).
4.【解析】 如图,由于光线要照到墙角,因此点A,B,D和点A,C,E分别在同一条直线上,
∵房间的长、宽都为4 m,∴DE=4 m.
过点A作AM⊥DE于点M,AM交BC于点N.
由DE∥BC,易得△ABC∽△ADE,∴= .
∵AN=0.08 m,AM=2 m,DE=4 m,
∴BC=≈0.23(m).
答:灯罩的直径BC应约为0.23 m.
(课时1 平行投影与中心投影)
一、基础巩固
知识点1 投影的概念
1. 下列现象是物体的投影的是( )
A.小明看到镜子里的自己
B.灯光下猫咪映在墙上的影子
C.自行车行驶过后车轮留下的痕迹
D.掉在地上的树叶
知识点2 平行投影
2. [2022河北唐山路北区期末]下列投影是平行投影的是( )
A.太阳光下窗户的影子
B.台灯下书本的影子
C.在手电筒照射下纸片的影子
D.路灯下行人的影子
3. [2022河南濮阳三模]下列四幅图中,能表示两棵树在同一时刻太阳光下的影子的图是( )
4. 矩形窗框在太阳光下的影子不可能是( )
A.平行四边形 B.矩形 C.梯形 D.线段
5. [2020山东济南长清区期末]如图,已知AB和DE是直立在地面上的两根立柱.AB=5 m,某一时刻AB在阳光下的投影BC=3 m.
(1)请你在图中画出此时DE在阳光下的投影;
(2)在测量AB的投影时,同时测量出DE在阳光下的投影长为6 m,请你计算DE的长.
知识点3 中心投影
6. 下列影子不是中心投影的是( )
A.皮影戏中的影子
B.晚上在房间内墙上的手影
C.舞厅中霓虹灯形成的影子
D.太阳光下林荫道上的树影
7. 一幢4层楼房只有一个窗户亮着一盏灯,一棵小树和一根电线杆在窗口灯光下的影子如图所示,则亮着灯的窗口是( )
A.1号窗口 B.2号窗口
C.3号窗口 D.4号窗口
8. [2021江西景德镇期末]如图,某小区内有一条笔直的小路,路的旁边有一盏路灯,晚上小红由A处走到B处,则表示她在该路灯照射下的影长l与行走的路程s之间关系的大致图象是( )
9. [2022山东烟台月考]如图,在路灯下,AB表示小明的身高,AC表示他的影子,FG表示小亮的身高,路灯灯泡在线段DE上.
(1)请你画出灯泡的位置,并画出小亮在灯光下的影子;
(2)如果小明的身高AB=1.6 m,他的影子AC=1.4 m,且他到路灯的距离AD=2.1 m,求路灯的高.
二、能力提升
1. 在同一时刻的阳光下,小明的影子比小强的影子长,那么在同一路灯下( )
A.小明的影子比小强的长
B.小明的影子比小强的短
C.小明的影子和小强的一样长
D.无法判断谁的影子长
2. 如图,正方形纸板的一条对角线垂直于地面,纸板上方的灯(看作一个点)与这条对角线所确定的平面垂直于纸板,在灯光照射下,正方形纸板在地面上形成的影子的形状可以是( )
3. 如图,电线杆AE的高度为6 m,顶端处有一盏路灯E,身高1.5 m的男孩站在与点A相距6 m的点B处,此时男孩的影子为BC.若男孩以6 m为半径绕电线杆走一圈,则他在路灯下的影子扫过的面积为 m2.
4. 在长、宽都为4 m,高为3 m的房间的正中央的天花板上悬挂一个灯泡,为了集中光线,加上了灯罩,如图所示.已知灯罩深8 cm,灯泡A离地面2 m,为了使光线恰好照到墙角,问灯罩的直径BC应为多少.(结果精确到0.01 m,≈1.414)
参考答案
一、基础巩固
1.B 【解析】 一般地,用光线照射物体,在某个平面(地面、墙壁等)上得到的影子叫做物体的投影.A项、C项、D项都和影子无关.
2.A
3.C 【解析】 同一时刻太阳光下树的影子是平行的,影子方向相同,且影长与树高成正比.选项A,B中的两棵树的影子方向都相反,故可排除;选项D中影长和树高不成正比,故可排除.
4.C
5.【解析】 (1)如图,连接AC,过点D作DF∥AC,交地面于点F,线段EF即DE在阳光下的投影.
(2)∵AC∥DF,∴∠ACB=∠DFE,
又∠ABC=∠DEF=90°,∴△ABC∽△DEF.
∴=, 即=,∴DE=10 m.
∴DE的长为10 m.
6.D
7.B 【解析】 如图所示,亮着灯的窗口是2号窗口.
8.C 【解析】 小红由A处走到路灯正下方这一过程中,l随s的增加而减小;当小红走到路灯正下方时,l等于0;小红由路灯正下方走到B处这一过程中,l随s的增大而增大.结合选项,知选C.
9.【解析】 (1)如图,点O为灯泡的位置,FH为小亮在灯光下的影子.
(2)∵AB∥OD,∴△ABC∽△DOC,
∴=,即=,∴DO=4 m.
∴路灯的高为4 m.
二、能力提升
1.D 【解析】 路灯下的投影为中心投影,由于不知道他们距离光源的远近,所以无法判断谁的影子长.
2.D 【解析】 由题意知,正方形纸板越靠近光源的边,影子越长.如图,由于正方形纸板有一条对角线与地面垂直,且该对角线与灯所确定的平面垂直于纸板,故AB,AD的影子相等,CB,CD的影子相等,且AB,AD的影子长.
3.28π 【解析】 ∵AE∥BD,∴△CBD∽△CAE,∴=,即=,∴CB=2 m,∴AC=8 m,∴男孩以6 m为半径绕电线杆走一圈,他在路灯下的影子扫过的面积为π×82-π×62=28π(m2).
4.【解析】 如图,由于光线要照到墙角,因此点A,B,D和点A,C,E分别在同一条直线上,
∵房间的长、宽都为4 m,∴DE=4 m.
过点A作AM⊥DE于点M,AM交BC于点N.
由DE∥BC,易得△ABC∽△ADE,∴= .
∵AN=0.08 m,AM=2 m,DE=4 m,
∴BC=≈0.23(m).
答:灯罩的直径BC应约为0.23 m.
