【同步分层】3.2图形的旋转(二)拓展卷(含解析)-2024-2025学年六年级下册数学北师大版
文档属性
| 名称 | 【同步分层】3.2图形的旋转(二)拓展卷(含解析)-2024-2025学年六年级下册数学北师大版 |

|
|
| 格式 | docx | ||
| 文件大小 | 1.8MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-05-07 19:52:25 | ||
图片预览



文档简介
3.2图形的旋转(二)
一.选择题(共3小题)
1.(2024 于洪区)如图,图形A( )可以得到图形B。
A.绕点Q逆时针旋转90°,再向下平移2格。
B.绕点Q顺时针旋转90°,再向下平移2格。
C.绕点P顺时针旋转90°,再向左平移2格。
2.(2024春 顺义区期末)观察并思考图1到图2的运动过程,下面说法正确的是( )
A.图1先绕E点顺时针旋转90°,再向右平移7格
B.图1先绕E点逆时针旋转90°,再向右平移7格
C.图1先绕F点顺时针旋转90°,再向右平移4格
D.图1先绕F点逆时针旋转90°,再向右平移4格
3.(2023秋 青岛期末)如图是( )后得到的图形。
A.平移 B.逆时针旋转90°
C.顺时针旋转90° D.逆时针旋转270°
二.填空题(共3小题)
4.如图,线段AB绕点A旋转到AB1、的位置,是按 时针方向旋转 度;线段AB绕A点旋转到AB2的位置,是按 时针方向旋转 度.
5.找规律。
一个等边三角形绕它的3条对称轴的交点旋转120°,得到的图形与原图形重合;
一个正方形绕它的4条对称轴的交点旋转90°,得到的图形与原图形重合;
一个正五边形绕它的5条对称轴的交点旋转72°,得到的图形与原图形重合;
……
(1)一个正n边形绕它的n条对称轴的交点旋转,得到的图形与原图形重合。
(2)根据以上的规律,下列图形中,旋转120°后能与原图形重合的是 。
A.正方形B.正五边形C.正六边形D.正八边形
6.(2022春 临川区期末)图形A绕O点顺时针旋转了 。图形B绕O点 旋转了90°。
三.应用题(共1小题)
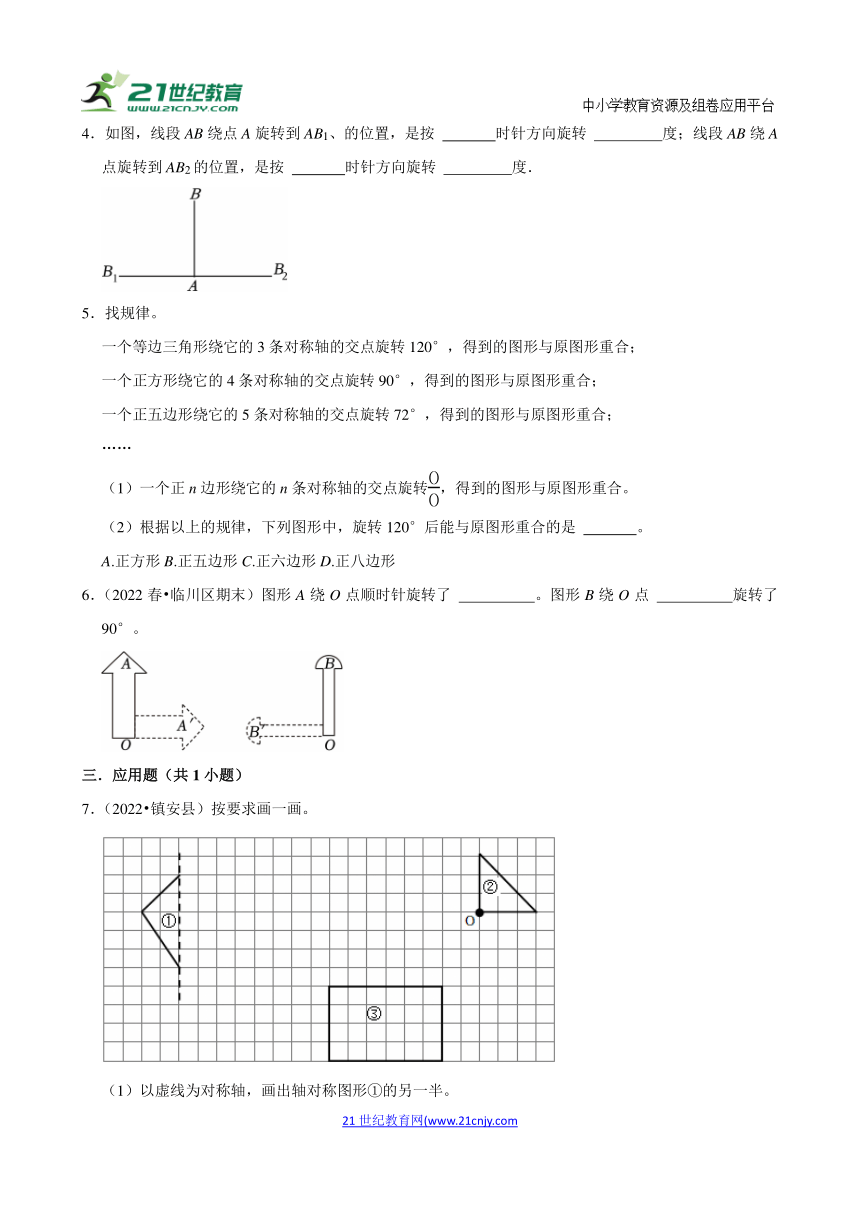
7.(2022 镇安县)按要求画一画。
(1)以虚线为对称轴,画出轴对称图形①的另一半。
(2)画出图形②绕点O顺时针旋转90°后的图形。
(3)将图形③缩小,使缩小后的图形与原图形对应线段长的比为1:2。
四.操作题(共3小题)
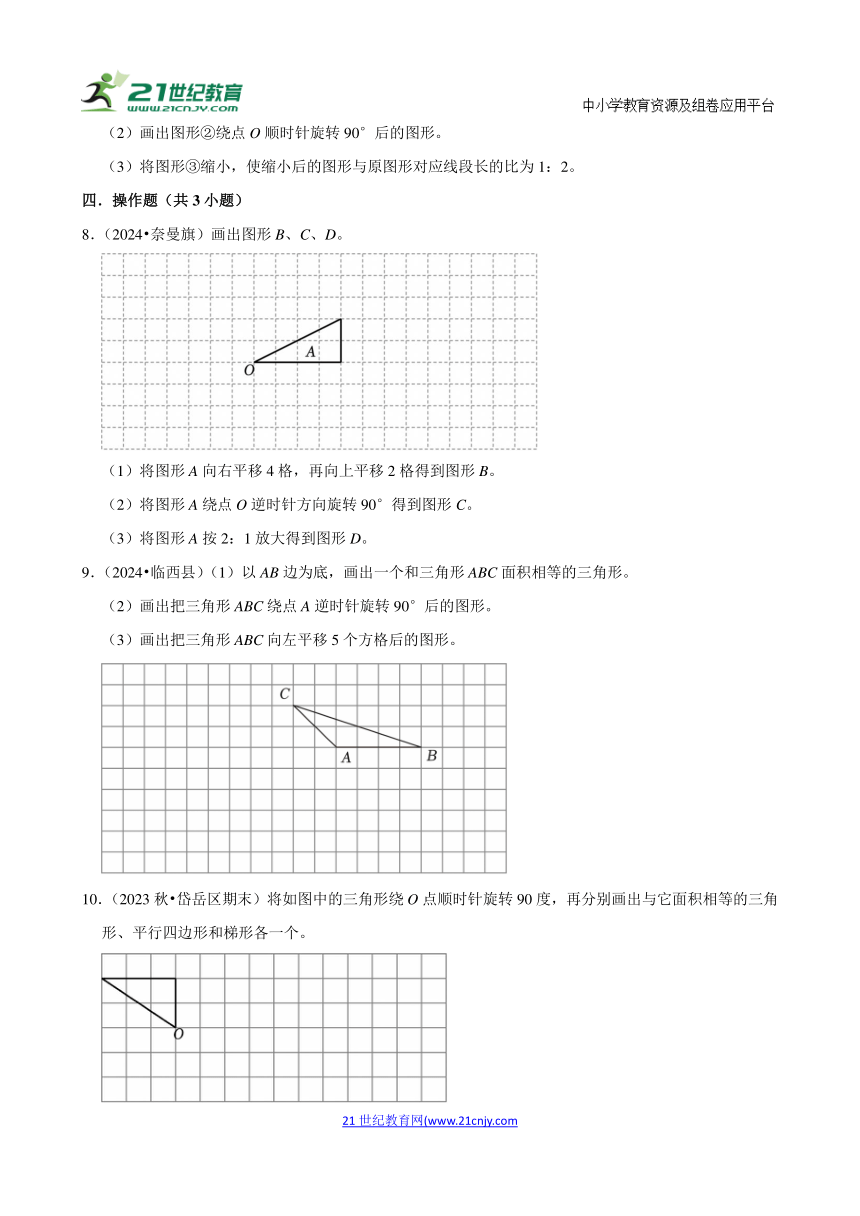
8.(2024 奈曼旗)画出图形B、C、D。
(1)将图形A向右平移4格,再向上平移2格得到图形B。
(2)将图形A绕点O逆时针方向旋转90°得到图形C。
(3)将图形A按2:1放大得到图形D。
9.(2024 临西县)(1)以AB边为底,画出一个和三角形ABC面积相等的三角形。
(2)画出把三角形ABC绕点A逆时针旋转90°后的图形。
(3)画出把三角形ABC向左平移5个方格后的图形。
10.(2023秋 岱岳区期末)将如图中的三角形绕O点顺时针旋转90度,再分别画出与它面积相等的三角形、平行四边形和梯形各一个。
3.2图形的旋转(二)
参考答案与试题解析
一.选择题(共3小题)
1.(2024 于洪区)如图,图形A( )可以得到图形B。
A.绕点Q逆时针旋转90°,再向下平移2格。
B.绕点Q顺时针旋转90°,再向下平移2格。
C.绕点P顺时针旋转90°,再向左平移2格。
【考点】作旋转一定角度后的图形;作平移后的图形.
【专题】几何直观.
【答案】B
【分析】根据图形的旋转和平移知识,图形A经过绕Q点顺时针旋转90°,再向下平移2格运动后可变成图形B,据此解答即可。
【解答】解:分析可知,图形A经过绕Q点顺时针旋转90°,再向下平移2格运动后可变成图形B。
故选:B。
【点评】本题考查了图形的旋转和平移知识,解答的关键是看清是顺时针还是逆时针旋转,旋转多少度,结合题意分析解答即可。
2.(2024春 顺义区期末)观察并思考图1到图2的运动过程,下面说法正确的是( )
A.图1先绕E点顺时针旋转90°,再向右平移7格
B.图1先绕E点逆时针旋转90°,再向右平移7格
C.图1先绕F点顺时针旋转90°,再向右平移4格
D.图1先绕F点逆时针旋转90°,再向右平移4格
【考点】作旋转一定角度后的图形;作平移后的图形.
【专题】空间与图形;几何直观.
【答案】D
【分析】根据旋转的特征,点F的位置不动,其余各部分均绕此点按相同方向旋转相同的度数,得到旋转后的图形;再根据平移的方向和距离解答。
【解答】解:图1先绕F点逆时针旋转90°,再向右平移4格。
故选:D。
【点评】本题考查了图形的平移、旋转方法。
3.(2023秋 青岛期末)如图是( )后得到的图形。
A.平移 B.逆时针旋转90°
C.顺时针旋转90° D.逆时针旋转270°
【考点】作旋转一定角度后的图形.
【专题】几何直观.
【答案】C
【分析】根据旋转的特征及箭头指向,左边的三角形绕点O顺时针方程旋转90°即可得到右边的三角形。
【解答】解:如图:
左边的三角形绕点O顺时针旋转90°即可得到右边的三角形。
故选:C。
【点评】旋转作图要注意:①旋转方向;②旋转角度。整个旋转作图,就是把整个图案的每一个特征点绕旋转中心按一定的旋转方向和一定的旋转角度旋转移动。
二.填空题(共3小题)
4.如图,线段AB绕点A旋转到AB1、的位置,是按 逆 时针方向旋转 90 度;线段AB绕A点旋转到AB2的位置,是按 顺 时针方向旋转 90 度.
【考点】作旋转一定角度后的图形.
【专题】图形与位置.
【答案】见试题解答内容
【分析】根据图示可知,线段AB垂直与线段B1B2,点A是垂直,所以线段AB绕点A旋转到AB1或绕点A旋转到AB2的角度都是90°,线段AB绕点A旋转到AB1是作逆时针旋转,绕点A旋转到AB2时是作顺时针旋转,据此解答即可.
【解答】解:线段AB绕点A旋转到AB1、的位置,是按逆时针方向旋转90度;线段AB绕A点旋转到AB2的位置,是按顺时针方向旋转90度.
故答案为:逆、90、顺、90.
【点评】本题考查了图形的旋转变化,要看清是顺时针还是逆时针旋转,旋转多少度,难度不大,但易错.
5.找规律。
一个等边三角形绕它的3条对称轴的交点旋转120°,得到的图形与原图形重合;
一个正方形绕它的4条对称轴的交点旋转90°,得到的图形与原图形重合;
一个正五边形绕它的5条对称轴的交点旋转72°,得到的图形与原图形重合;
……
(1)一个正n边形绕它的n条对称轴的交点旋转,得到的图形与原图形重合。
(2)根据以上的规律,下列图形中,旋转120°后能与原图形重合的是 C 。
A.正方形
B.正五边形
C.正六边形
D.正八边形
【考点】作旋转一定角度后的图形;轴对称图形的辨识.
【专题】压轴题;应用意识.
【答案】(1);(2)C。
【分析】(1)结合已知,120×3=360,90×4=360,72×5=360,据此解答;
(2)由正多边形旋转一定的角度后与原图形重合,结合题中旋转120°,不难解答本题。
【解答】解:(1)一个正n边形绕它的n条对称轴的交点旋转,得到的图形与原图形重合。
(2)因为120°=60°×2,360°÷60°=6
所以正六边形沿同一方向绕中心旋转两次,每次旋转60°,即可与原图形重合,即C正六边形正确。
故答案为:(1);(2)C。
【点评】本题考查了轴对称图形认识的题目,熟练掌握正多边形的特征是解题的关键。
6.(2022春 临川区期末)图形A绕O点顺时针旋转了 90° 。图形B绕O点 逆时针 旋转了90°。
【考点】作旋转一定角度后的图形.
【专题】空间与图形;几何直观.
【答案】90°,逆时针。
【分析】图形A连接O点的两条边绕O点顺时针旋转了90°,整个图形绕O点旋转了90°。图形B连接O点的两条绕O点 逆时针旋转了90°,图形B绕O点逆时针旋转了90°。
【解答】解:图形A绕O点顺时针旋转了90°。图形B绕O点逆时针旋转了90°。
故答案为:90°,逆时针。
【点评】熟悉图形旋转的方法是解决本题的关键。
三.应用题(共1小题)
7.(2022 镇安县)按要求画一画。
(1)以虚线为对称轴,画出轴对称图形①的另一半。
(2)画出图形②绕点O顺时针旋转90°后的图形。
(3)将图形③缩小,使缩小后的图形与原图形对应线段长的比为1:2。
【考点】作旋转一定角度后的图形;图形的放大与缩小.
【专题】作图题;空间观念;几何直观.
【答案】(1)图中红色部分。
(2)图中绿色部分。
(3)图中蓝色部分。
【分析】(1)根据轴对称图形的特征,对称点到对称轴的距离相等,对称点的连线垂直于对称轴,在对称轴的右边画出图形①的关键对称点,依次连接即可以画出图形①的另一半。
(2)根据旋转的特征,图形②绕点O顺时针旋转90°,点O的位置不动,其余各部分均绕此点按相同方向旋转相同的度数即可画出旋转后的图形。
(3)根据图形的放大和缩小的意义,图形③的长和宽都缩小2倍,变为长和宽分别是3格和2格的长方形,据此画图即可。
【解答】解:(1)以虚线为对称轴,画出轴对称图形①的另一半(图中红色部分)。
(2)画出图形②绕点O顺时针旋转90°后的图形(图中绿色部分)。
(3)将图形③缩小,使缩小后的图形与原图形对应线段长的比为1:2(图中蓝色部分)。
【点评】此题考查了作轴对称图形和作旋转一定角度后的图形的方法,还考查了对图形的放大和缩小的意义的灵活运用。
四.操作题(共3小题)
8.(2024 奈曼旗)画出图形B、C、D。
(1)将图形A向右平移4格,再向上平移2格得到图形B。
(2)将图形A绕点O逆时针方向旋转90°得到图形C。
(3)将图形A按2:1放大得到图形D。
【考点】作旋转一定角度后的图形;图形的放大与缩小;作平移后的图形.
【专题】作图题;几何直观.
【答案】
【分析】(1)根据平移图形的特征,把三角形A的3个顶点分别向右平移4格,再向上平移2格后首尾连接各点,即可得到三角形A向右平移4格,再向上平移2格得到图形B;
(2)根据旋转的意义,找出图中三角形A3个关键点,再画出按逆时针方向绕点O旋转90度后的三角形C即可;
(3)按2:1的比例画出三角形A放大后的图形,就是把三角形A的三条边分别扩大到原来的2倍,据此画出放大后的三角形D。
【解答】解:(1)、(2)、(3)如下图所示:
【点评】本题考查了图形的平移、旋转和放大。
9.(2024 临西县)(1)以AB边为底,画出一个和三角形ABC面积相等的三角形。
(2)画出把三角形ABC绕点A逆时针旋转90°后的图形。
(3)画出把三角形ABC向左平移5个方格后的图形。
【考点】作旋转一定角度后的图形;作平移后的图形.
【专题】几何直观.
【答案】(画出一个和三角形ABC面积相等的三角形,画法不唯一)。
【分析】(1)画法不唯一。等底、等高的三角形面积相等,以AB边为底,画一个与三角形ABC等高的三角形,其面积就与三角形ABC的面积相等。
(2)根据旋转的特征,三角形ABC绕点A逆时针旋转90°,点A的位置不动,这个图形的各部分均绕此点按相同方向旋转相同的度数即可画出旋转后的图形。
(3)根据平移的特征,把三角形ABC的各顶点分别向左平移5格,依次连接即可得到平移后的图形。
【解答】解:(1)、(2)、(3)画图如下(画出一个和三角形ABC面积相等的三角形,画法不唯一):
【点评】图形平移注意三要素:即原位置、平移方向、平移距离。图形旋转注意四要素:即原位置、旋转中心、旋转方向、旋转角。等底、等高的三角形面积相等。
10.(2023秋 岱岳区期末)将如图中的三角形绕O点顺时针旋转90度,再分别画出与它面积相等的三角形、平行四边形和梯形各一个。
【考点】作旋转一定角度后的图形.
【专题】几何直观;应用意识.
【答案】(除旋转后的三角形外,其余图形画法均不唯一)。
【分析】根据旋转的特征,三角形绕点O顺时针旋转90°,点O的位置不动,这个图形的各部分均绕此点按相同方向旋转相同的度数即可画出旋转后的图形。画一个底、高分别为这个三角形两条边的三角形,其面积与这个三角形的面积相等;根据平行四边形面积计算公式“S=ah”、三角形面积计算公式“S=ah÷2”、梯形面积计算公式“S=(a+b)h÷2”与平行四边形底(或高)相等,高(或底)为平行四边形高(或底)2倍的三角形面积与平行四边形面积相等;上、下底之和等于三角形底,与三角形等高的梯形面积与三角形面积相等。
【解答】解:根据题意画图如下(除旋转后的三角形外,其余图形画法均不唯一):
【点评】此题考查的知识点:作旋转一定度数后的图形、三角形面积的计算、平行四边形面积的计算、梯形面积的计算。
21世纪教育网(www.21cnjy.com
一.选择题(共3小题)
1.(2024 于洪区)如图,图形A( )可以得到图形B。
A.绕点Q逆时针旋转90°,再向下平移2格。
B.绕点Q顺时针旋转90°,再向下平移2格。
C.绕点P顺时针旋转90°,再向左平移2格。
2.(2024春 顺义区期末)观察并思考图1到图2的运动过程,下面说法正确的是( )
A.图1先绕E点顺时针旋转90°,再向右平移7格
B.图1先绕E点逆时针旋转90°,再向右平移7格
C.图1先绕F点顺时针旋转90°,再向右平移4格
D.图1先绕F点逆时针旋转90°,再向右平移4格
3.(2023秋 青岛期末)如图是( )后得到的图形。
A.平移 B.逆时针旋转90°
C.顺时针旋转90° D.逆时针旋转270°
二.填空题(共3小题)
4.如图,线段AB绕点A旋转到AB1、的位置,是按 时针方向旋转 度;线段AB绕A点旋转到AB2的位置,是按 时针方向旋转 度.
5.找规律。
一个等边三角形绕它的3条对称轴的交点旋转120°,得到的图形与原图形重合;
一个正方形绕它的4条对称轴的交点旋转90°,得到的图形与原图形重合;
一个正五边形绕它的5条对称轴的交点旋转72°,得到的图形与原图形重合;
……
(1)一个正n边形绕它的n条对称轴的交点旋转,得到的图形与原图形重合。
(2)根据以上的规律,下列图形中,旋转120°后能与原图形重合的是 。
A.正方形B.正五边形C.正六边形D.正八边形
6.(2022春 临川区期末)图形A绕O点顺时针旋转了 。图形B绕O点 旋转了90°。
三.应用题(共1小题)
7.(2022 镇安县)按要求画一画。
(1)以虚线为对称轴,画出轴对称图形①的另一半。
(2)画出图形②绕点O顺时针旋转90°后的图形。
(3)将图形③缩小,使缩小后的图形与原图形对应线段长的比为1:2。
四.操作题(共3小题)
8.(2024 奈曼旗)画出图形B、C、D。
(1)将图形A向右平移4格,再向上平移2格得到图形B。
(2)将图形A绕点O逆时针方向旋转90°得到图形C。
(3)将图形A按2:1放大得到图形D。
9.(2024 临西县)(1)以AB边为底,画出一个和三角形ABC面积相等的三角形。
(2)画出把三角形ABC绕点A逆时针旋转90°后的图形。
(3)画出把三角形ABC向左平移5个方格后的图形。
10.(2023秋 岱岳区期末)将如图中的三角形绕O点顺时针旋转90度,再分别画出与它面积相等的三角形、平行四边形和梯形各一个。
3.2图形的旋转(二)
参考答案与试题解析
一.选择题(共3小题)
1.(2024 于洪区)如图,图形A( )可以得到图形B。
A.绕点Q逆时针旋转90°,再向下平移2格。
B.绕点Q顺时针旋转90°,再向下平移2格。
C.绕点P顺时针旋转90°,再向左平移2格。
【考点】作旋转一定角度后的图形;作平移后的图形.
【专题】几何直观.
【答案】B
【分析】根据图形的旋转和平移知识,图形A经过绕Q点顺时针旋转90°,再向下平移2格运动后可变成图形B,据此解答即可。
【解答】解:分析可知,图形A经过绕Q点顺时针旋转90°,再向下平移2格运动后可变成图形B。
故选:B。
【点评】本题考查了图形的旋转和平移知识,解答的关键是看清是顺时针还是逆时针旋转,旋转多少度,结合题意分析解答即可。
2.(2024春 顺义区期末)观察并思考图1到图2的运动过程,下面说法正确的是( )
A.图1先绕E点顺时针旋转90°,再向右平移7格
B.图1先绕E点逆时针旋转90°,再向右平移7格
C.图1先绕F点顺时针旋转90°,再向右平移4格
D.图1先绕F点逆时针旋转90°,再向右平移4格
【考点】作旋转一定角度后的图形;作平移后的图形.
【专题】空间与图形;几何直观.
【答案】D
【分析】根据旋转的特征,点F的位置不动,其余各部分均绕此点按相同方向旋转相同的度数,得到旋转后的图形;再根据平移的方向和距离解答。
【解答】解:图1先绕F点逆时针旋转90°,再向右平移4格。
故选:D。
【点评】本题考查了图形的平移、旋转方法。
3.(2023秋 青岛期末)如图是( )后得到的图形。
A.平移 B.逆时针旋转90°
C.顺时针旋转90° D.逆时针旋转270°
【考点】作旋转一定角度后的图形.
【专题】几何直观.
【答案】C
【分析】根据旋转的特征及箭头指向,左边的三角形绕点O顺时针方程旋转90°即可得到右边的三角形。
【解答】解:如图:
左边的三角形绕点O顺时针旋转90°即可得到右边的三角形。
故选:C。
【点评】旋转作图要注意:①旋转方向;②旋转角度。整个旋转作图,就是把整个图案的每一个特征点绕旋转中心按一定的旋转方向和一定的旋转角度旋转移动。
二.填空题(共3小题)
4.如图,线段AB绕点A旋转到AB1、的位置,是按 逆 时针方向旋转 90 度;线段AB绕A点旋转到AB2的位置,是按 顺 时针方向旋转 90 度.
【考点】作旋转一定角度后的图形.
【专题】图形与位置.
【答案】见试题解答内容
【分析】根据图示可知,线段AB垂直与线段B1B2,点A是垂直,所以线段AB绕点A旋转到AB1或绕点A旋转到AB2的角度都是90°,线段AB绕点A旋转到AB1是作逆时针旋转,绕点A旋转到AB2时是作顺时针旋转,据此解答即可.
【解答】解:线段AB绕点A旋转到AB1、的位置,是按逆时针方向旋转90度;线段AB绕A点旋转到AB2的位置,是按顺时针方向旋转90度.
故答案为:逆、90、顺、90.
【点评】本题考查了图形的旋转变化,要看清是顺时针还是逆时针旋转,旋转多少度,难度不大,但易错.
5.找规律。
一个等边三角形绕它的3条对称轴的交点旋转120°,得到的图形与原图形重合;
一个正方形绕它的4条对称轴的交点旋转90°,得到的图形与原图形重合;
一个正五边形绕它的5条对称轴的交点旋转72°,得到的图形与原图形重合;
……
(1)一个正n边形绕它的n条对称轴的交点旋转,得到的图形与原图形重合。
(2)根据以上的规律,下列图形中,旋转120°后能与原图形重合的是 C 。
A.正方形
B.正五边形
C.正六边形
D.正八边形
【考点】作旋转一定角度后的图形;轴对称图形的辨识.
【专题】压轴题;应用意识.
【答案】(1);(2)C。
【分析】(1)结合已知,120×3=360,90×4=360,72×5=360,据此解答;
(2)由正多边形旋转一定的角度后与原图形重合,结合题中旋转120°,不难解答本题。
【解答】解:(1)一个正n边形绕它的n条对称轴的交点旋转,得到的图形与原图形重合。
(2)因为120°=60°×2,360°÷60°=6
所以正六边形沿同一方向绕中心旋转两次,每次旋转60°,即可与原图形重合,即C正六边形正确。
故答案为:(1);(2)C。
【点评】本题考查了轴对称图形认识的题目,熟练掌握正多边形的特征是解题的关键。
6.(2022春 临川区期末)图形A绕O点顺时针旋转了 90° 。图形B绕O点 逆时针 旋转了90°。
【考点】作旋转一定角度后的图形.
【专题】空间与图形;几何直观.
【答案】90°,逆时针。
【分析】图形A连接O点的两条边绕O点顺时针旋转了90°,整个图形绕O点旋转了90°。图形B连接O点的两条绕O点 逆时针旋转了90°,图形B绕O点逆时针旋转了90°。
【解答】解:图形A绕O点顺时针旋转了90°。图形B绕O点逆时针旋转了90°。
故答案为:90°,逆时针。
【点评】熟悉图形旋转的方法是解决本题的关键。
三.应用题(共1小题)
7.(2022 镇安县)按要求画一画。
(1)以虚线为对称轴,画出轴对称图形①的另一半。
(2)画出图形②绕点O顺时针旋转90°后的图形。
(3)将图形③缩小,使缩小后的图形与原图形对应线段长的比为1:2。
【考点】作旋转一定角度后的图形;图形的放大与缩小.
【专题】作图题;空间观念;几何直观.
【答案】(1)图中红色部分。
(2)图中绿色部分。
(3)图中蓝色部分。
【分析】(1)根据轴对称图形的特征,对称点到对称轴的距离相等,对称点的连线垂直于对称轴,在对称轴的右边画出图形①的关键对称点,依次连接即可以画出图形①的另一半。
(2)根据旋转的特征,图形②绕点O顺时针旋转90°,点O的位置不动,其余各部分均绕此点按相同方向旋转相同的度数即可画出旋转后的图形。
(3)根据图形的放大和缩小的意义,图形③的长和宽都缩小2倍,变为长和宽分别是3格和2格的长方形,据此画图即可。
【解答】解:(1)以虚线为对称轴,画出轴对称图形①的另一半(图中红色部分)。
(2)画出图形②绕点O顺时针旋转90°后的图形(图中绿色部分)。
(3)将图形③缩小,使缩小后的图形与原图形对应线段长的比为1:2(图中蓝色部分)。
【点评】此题考查了作轴对称图形和作旋转一定角度后的图形的方法,还考查了对图形的放大和缩小的意义的灵活运用。
四.操作题(共3小题)
8.(2024 奈曼旗)画出图形B、C、D。
(1)将图形A向右平移4格,再向上平移2格得到图形B。
(2)将图形A绕点O逆时针方向旋转90°得到图形C。
(3)将图形A按2:1放大得到图形D。
【考点】作旋转一定角度后的图形;图形的放大与缩小;作平移后的图形.
【专题】作图题;几何直观.
【答案】
【分析】(1)根据平移图形的特征,把三角形A的3个顶点分别向右平移4格,再向上平移2格后首尾连接各点,即可得到三角形A向右平移4格,再向上平移2格得到图形B;
(2)根据旋转的意义,找出图中三角形A3个关键点,再画出按逆时针方向绕点O旋转90度后的三角形C即可;
(3)按2:1的比例画出三角形A放大后的图形,就是把三角形A的三条边分别扩大到原来的2倍,据此画出放大后的三角形D。
【解答】解:(1)、(2)、(3)如下图所示:
【点评】本题考查了图形的平移、旋转和放大。
9.(2024 临西县)(1)以AB边为底,画出一个和三角形ABC面积相等的三角形。
(2)画出把三角形ABC绕点A逆时针旋转90°后的图形。
(3)画出把三角形ABC向左平移5个方格后的图形。
【考点】作旋转一定角度后的图形;作平移后的图形.
【专题】几何直观.
【答案】(画出一个和三角形ABC面积相等的三角形,画法不唯一)。
【分析】(1)画法不唯一。等底、等高的三角形面积相等,以AB边为底,画一个与三角形ABC等高的三角形,其面积就与三角形ABC的面积相等。
(2)根据旋转的特征,三角形ABC绕点A逆时针旋转90°,点A的位置不动,这个图形的各部分均绕此点按相同方向旋转相同的度数即可画出旋转后的图形。
(3)根据平移的特征,把三角形ABC的各顶点分别向左平移5格,依次连接即可得到平移后的图形。
【解答】解:(1)、(2)、(3)画图如下(画出一个和三角形ABC面积相等的三角形,画法不唯一):
【点评】图形平移注意三要素:即原位置、平移方向、平移距离。图形旋转注意四要素:即原位置、旋转中心、旋转方向、旋转角。等底、等高的三角形面积相等。
10.(2023秋 岱岳区期末)将如图中的三角形绕O点顺时针旋转90度,再分别画出与它面积相等的三角形、平行四边形和梯形各一个。
【考点】作旋转一定角度后的图形.
【专题】几何直观;应用意识.
【答案】(除旋转后的三角形外,其余图形画法均不唯一)。
【分析】根据旋转的特征,三角形绕点O顺时针旋转90°,点O的位置不动,这个图形的各部分均绕此点按相同方向旋转相同的度数即可画出旋转后的图形。画一个底、高分别为这个三角形两条边的三角形,其面积与这个三角形的面积相等;根据平行四边形面积计算公式“S=ah”、三角形面积计算公式“S=ah÷2”、梯形面积计算公式“S=(a+b)h÷2”与平行四边形底(或高)相等,高(或底)为平行四边形高(或底)2倍的三角形面积与平行四边形面积相等;上、下底之和等于三角形底,与三角形等高的梯形面积与三角形面积相等。
【解答】解:根据题意画图如下(除旋转后的三角形外,其余图形画法均不唯一):
【点评】此题考查的知识点:作旋转一定度数后的图形、三角形面积的计算、平行四边形面积的计算、梯形面积的计算。
21世纪教育网(www.21cnjy.com
