第22章 二次函数的最值 练习(含答案) 人教版数学九年级上册
文档属性
| 名称 | 第22章 二次函数的最值 练习(含答案) 人教版数学九年级上册 |

|
|
| 格式 | docx | ||
| 文件大小 | 76.4KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-05-08 00:00:00 | ||
图片预览



文档简介
二次函数的最值
一、单选题
1.已知关于x的二次函数y=x2+(1﹣a)x+1,当x的取值范围是1≤x≤3时,y在x=1时取得最大值,则实数a的取值范围是( )
A.a=5 B.a≥5 C.a=3 D.a≥3
2.关于二次函数y=-x2+2x的最值,下列叙述正确的是( )
A.当x=2时,y有最小值0 B.当x=2时,y有最大值0
C.当x=1时,y有最小值1 D.当x=1时,y有最大值1
3.如图1,在矩形 中,动点 从点 出发,沿 的路线运动,当点 到达点 时停止运动.若 ,交 于点 设点 运动的路程为 , ,已知 关于 的图象如图2所示,则 的值为( )
A. B.2 C.1 D.
4.点P(a,b)在以y轴为对称轴的二次函数y= +mx+5的图象上,则2a-b的最大值等于( )
A.4 B.-4 C.-4.5 D.4.5
5.二次函数y=﹣x2+2x+4的最大值为( )
A.3 B.4 C.5 D.6
6.已知抛物线,当时,y的最小值为,则当时,y的最大值为( )
A.2 B.1 C.0 D.
7.下列函数中函数值有最大值的是( )
A. B. C. D.
8.某公园草坪的防护栏由100段形状相同的抛物线形构件组成,为了牢固起见,每段护栏需要间距0.4m加设一根不锈钢的支柱,防护栏的最高点距底部0.5m(如图),则这防护栏需要不锈钢支柱的总长度至少为( )
A.50m B.100m C.160m D.200m
9.关于二次函数y=﹣2x2+1,下列说法错误的是( )
A.图象开口向下 B.图象的对称轴为x=
C.函数最大值为1 D.当x>1时,y随x的增大而减小
10.二次函教y=x2+2x-5有( )
A.最大值-5 B.最小值-5 C.最大值-6 D.最小值-6
11.已知抛物线 .当 时,y随x的增大而增大;当 时,y的最大值为10.那么与抛物线 关于y轴对称的抛物线在 内的函数最大值为( )
A.10 B.17 C.5 D.2
12.已知二次函数的解析式为:y=-3(x+5)2﹣7,那么下列说法正确的是( )
A.顶点的坐标是(5,-7) B.顶点的坐标是(-7,-5)
C.当x=-5时,函数有最大值y=-7 D.当x=-5时,函数有最小值y=-7
二、填空题
13.二次函数y=2x2﹣2x+6的最小值是 .
14.如图,P是抛物线y=﹣x2+x+2在第一象限上的点,过点P分别向x轴和y轴引垂线,垂足分别为A,B,则四边形OAPB周长的最大值为 .
15.如图所示,二次函数 ( , , , 为实数)的图象过点 ,对称轴为直线 ,给出以下结论:① ;② ;③ ;④若 、 为函数图象上的两点,则 .其中正确的有 .(填写序号即可)
16.已知实数x,y满足x2-3x+4y=7,则3x+4y的最大值为 。
17.二次函数y=x2+4x+5(﹣3≤x≤0)的最大值和最小值分别是 .
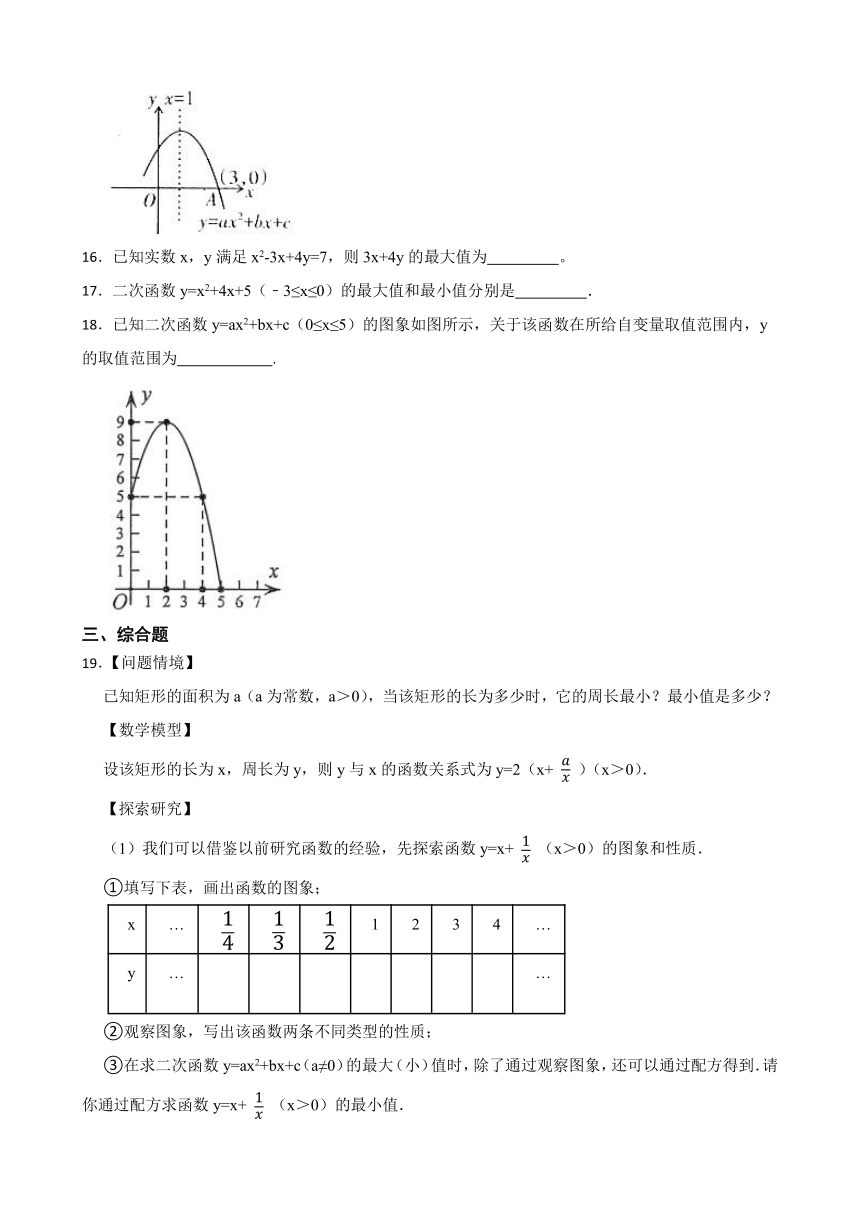
18.已知二次函数y=ax2+bx+c(0≤x≤5)的图象如图所示,关于该函数在所给自变量取值范围内,y的取值范围为 .
三、综合题
19.【问题情境】
已知矩形的面积为a(a为常数,a>0),当该矩形的长为多少时,它的周长最小?最小值是多少?
【数学模型】
设该矩形的长为x,周长为y,则y与x的函数关系式为y=2(x+ )(x>0).
【探索研究】
(1)我们可以借鉴以前研究函数的经验,先探索函数y=x+ (x>0)的图象和性质.
①填写下表,画出函数的图象;
x … 1 2 3 4 …
y … …
②观察图象,写出该函数两条不同类型的性质;
③在求二次函数y=ax2+bx+c(a≠0)的最大(小)值时,除了通过观察图象,还可以通过配方得到.请你通过配方求函数y=x+ (x>0)的最小值.
(2)用上述方法解决“问题情境”中的问题,直接写出答案.
20.某商店将成本为30元的文化衫标价50元出售.
(1)为了搞促销活动经过两次降价调至每件40.5元,若两次降价的百分率相同,求每次降价的百分率
(2)经调查,该文化衫每降5元,每月可多售出100件,若该品牌文化衫按原标价出售,每月可销售200件,那么销售价定为多少元,可以使该商品获得最大的利润?最大的利润是多少?
21.已知 是关于x的二次函数.
(1)满足条件的m的值;
(2)m为何值时,抛物线有最低点?求出这个最低点,这时当x为何值时,y随x的增大而增大?
(3)m为何值时,函数有最大值?最大值是多少?这时当x为何值时,y随x的增大而减小?
22.已知函数 (b为常数).
(1)若图象经过点 ,判断图象经过点 吗?请说明理由;
(2)设该函数图象的顶点坐标为 ,当b的值变化时,求m与n的关系式;
(3)若该函数图象不经过第三象限,当 时,函数的最大值与最小值之差为16,求b的值.
23.某商品的进价为每件40元,在销售过程中发现,每周的销售量y(件)与销售单价x(元)之间的关系可以近似看作一次函数 ,且当售价定为50元/件时,每周销售30件,当售价定为70元/件时,每周销售10件.
(1)求k,b的值;
(2)求销售该商品每周的利润w(元)与销售单价x(元)之间的函数解析式,并求出销售该商品每周可获得的最大利润.
24.甲、乙两公司同时销售一款进价为40元/千克的产品.图①中折线ABC表示甲公司销售价y1(元/千克)与销售量x(千克)之间的函数关系,图②中抛物线表示乙公司销售这款产品获得的利润y2(元)与销售量x(千克)之间的函数关系.
(1)分别求出图①中线段AB、图②中抛物线所表示的函数表达式;
(2)当该产品销售量为多少千克时,甲、乙两公司获得的利润的差最大?最大值为多少?
答案解析部分
1.【答案】B
2.【答案】D
3.【答案】D
4.【答案】B
5.【答案】C
6.【答案】A
7.【答案】C
8.【答案】C
9.【答案】B
10.【答案】D
11.【答案】B
12.【答案】C
13.【答案】
14.【答案】6
15.【答案】①②③
16.【答案】16
17.【答案】5,1
18.【答案】0≤y≤9
19.【答案】(1)解:①故答案为: , , ,2, , , .
函数y=x+ 的图象如图:
②答:函数两条不同类型的性质是:当0<x<1时,y 随x的增大而减小,当x>1时,y 随x的增大而增大;当x=1时,函数y=x+ (x>0)的最小值是2.
③y=x+ = = +2= +2,
∵x>0,所以 ≥0,
所以当x=1时, 的最小值为0,
∴函数y=x+ (x>0)的最小值是2
(2)解:答:矩形的面积为a(a为常数,a>0),当该矩形的长为 时,它的周长最小,最小值是4 .
20.【答案】(1)解:设每次降价率为n,则
50(1﹣n)2=40.5,
解得:n1=0.1=10%,n2=1.9(不合,舍去).
故每次降价的百分率为10%;
(2)设销售定价为每件x元,每月利润为y元,则
y=(x﹣30)(200+×100)=﹣20(x﹣45)2+4450
∵a=﹣20<0,
∴当x=45时,y取最大值为4450元.
21.【答案】(1)因为函数为二次函数
∴m+2≠0,m2+m-4=2
∴m≠-2,m2+m-6=0
∴m≠-2,(m+3)(m-2)=0
∴m=-3,m=2
(2)当m=2时,函数为y=4x2+1,有最低点,最低点为(0,1),且x≥0时,y随x的增大而增大
(3)m=-3时,函数为-x2+1,有最大值,最大值为1,x≥0时,y随x的增大而减小
22.【答案】(1)解:经过,
把点(﹣2,4)代入y=x2+bx+3b中得:
4﹣2b+3b=4,
解得b=0,
∴此函数表达式为:y=x2,
当x=2时,y=4,
∴图象经过点(2,4);
(2)解:∵抛物线函数y=x2+bx+3b(b为常数)的顶点坐标是 (m,n),
∴﹣ =m, =n,
∴b=﹣2m,
把b=﹣2m代入 =n得n= =﹣m2﹣6m.
即n关于m的函数解析式为n=﹣m2﹣6m.
(3)解:把x=0代入y=x2+bx+3b得y=3b,
∵抛物线不经过第三象限,
∴3b≥0,即b≥0,
∵y=x2+bx+3b=(x+ )2﹣ +3b,
∴抛物线顶点(﹣ ,﹣ +3b),
∵﹣ ≤0,
∴当﹣ +3b≥0时,抛物线不经过第三象限,
解得b≤12,
∴0≤b≤12,﹣6≤﹣ ≤0,
∴当﹣6≤x≤1时,函数最小值为y=﹣ +3b,
把x=﹣6代入y=x2+bx+3b得y=36﹣3b,
把x=1代入y=x2+bx+3b得y=1+4b,
当36﹣3b﹣(﹣ +3b)=16时,
解得b=20(不符合题意,舍去)或b=4.
当1+4b﹣(﹣ +3b)=16时,
解得b=6或b=﹣10(不符合题意,舍去).
综上所述,b=4或6.
23.【答案】(1)解:由题意可得,当x=50时,y=30;当x=70时,y=10,
代入 中得:
,解得: ,
∴k=-1,b=80;
(2)解:由(1)可知,y=-x+80,
∴ ,
∵y=-x+80≥0,
∴
∵-1<0,
∴当x=60时,w有最大值,此时w=400,
即最大利润为400元.
24.【答案】(1)解:设y1与x之间的函数表达式为y1=kx+b.
根据题意,当x=0时,y1=120;当x=80时,y1=72.
所以 ,解得
所以,y1与x之间的函数表达式为y1=-0.6x+120.
设y2与x之间的函数表达式为y2=a(x―75)2+2250,
当x=0时,y2=0,解得a=―0.4.
所以,y2与x之间的函数表达式为y2=―0.4(x―75)2+2250
(2)解:设甲、乙两公司的销售总利润的差为w(元).当0<x≤80时,
w=(y1-40)x―y2= (-0.6x+120―40)x-[(-0.4(x―75)2+2250]
=-0.2x2+20x=-0.2(x-50)2+500.∵-0.2<0,0<x≤80∴当x=50时, w有最大值,最大值为500.
当80<x≤84时,
w=(72―40)x―[―0.4(x―75)2+2250]=0.4x2―28x,
∵当80<x≤84时,w随x的增大而增大,∴当x=84时, 有最大值,最大值为470.4.
综上所述,当销售量为50千克时,甲乙两公司获得的利润的差最大,最大是500元
一、单选题
1.已知关于x的二次函数y=x2+(1﹣a)x+1,当x的取值范围是1≤x≤3时,y在x=1时取得最大值,则实数a的取值范围是( )
A.a=5 B.a≥5 C.a=3 D.a≥3
2.关于二次函数y=-x2+2x的最值,下列叙述正确的是( )
A.当x=2时,y有最小值0 B.当x=2时,y有最大值0
C.当x=1时,y有最小值1 D.当x=1时,y有最大值1
3.如图1,在矩形 中,动点 从点 出发,沿 的路线运动,当点 到达点 时停止运动.若 ,交 于点 设点 运动的路程为 , ,已知 关于 的图象如图2所示,则 的值为( )
A. B.2 C.1 D.
4.点P(a,b)在以y轴为对称轴的二次函数y= +mx+5的图象上,则2a-b的最大值等于( )
A.4 B.-4 C.-4.5 D.4.5
5.二次函数y=﹣x2+2x+4的最大值为( )
A.3 B.4 C.5 D.6
6.已知抛物线,当时,y的最小值为,则当时,y的最大值为( )
A.2 B.1 C.0 D.
7.下列函数中函数值有最大值的是( )
A. B. C. D.
8.某公园草坪的防护栏由100段形状相同的抛物线形构件组成,为了牢固起见,每段护栏需要间距0.4m加设一根不锈钢的支柱,防护栏的最高点距底部0.5m(如图),则这防护栏需要不锈钢支柱的总长度至少为( )
A.50m B.100m C.160m D.200m
9.关于二次函数y=﹣2x2+1,下列说法错误的是( )
A.图象开口向下 B.图象的对称轴为x=
C.函数最大值为1 D.当x>1时,y随x的增大而减小
10.二次函教y=x2+2x-5有( )
A.最大值-5 B.最小值-5 C.最大值-6 D.最小值-6
11.已知抛物线 .当 时,y随x的增大而增大;当 时,y的最大值为10.那么与抛物线 关于y轴对称的抛物线在 内的函数最大值为( )
A.10 B.17 C.5 D.2
12.已知二次函数的解析式为:y=-3(x+5)2﹣7,那么下列说法正确的是( )
A.顶点的坐标是(5,-7) B.顶点的坐标是(-7,-5)
C.当x=-5时,函数有最大值y=-7 D.当x=-5时,函数有最小值y=-7
二、填空题
13.二次函数y=2x2﹣2x+6的最小值是 .
14.如图,P是抛物线y=﹣x2+x+2在第一象限上的点,过点P分别向x轴和y轴引垂线,垂足分别为A,B,则四边形OAPB周长的最大值为 .
15.如图所示,二次函数 ( , , , 为实数)的图象过点 ,对称轴为直线 ,给出以下结论:① ;② ;③ ;④若 、 为函数图象上的两点,则 .其中正确的有 .(填写序号即可)
16.已知实数x,y满足x2-3x+4y=7,则3x+4y的最大值为 。
17.二次函数y=x2+4x+5(﹣3≤x≤0)的最大值和最小值分别是 .
18.已知二次函数y=ax2+bx+c(0≤x≤5)的图象如图所示,关于该函数在所给自变量取值范围内,y的取值范围为 .
三、综合题
19.【问题情境】
已知矩形的面积为a(a为常数,a>0),当该矩形的长为多少时,它的周长最小?最小值是多少?
【数学模型】
设该矩形的长为x,周长为y,则y与x的函数关系式为y=2(x+ )(x>0).
【探索研究】
(1)我们可以借鉴以前研究函数的经验,先探索函数y=x+ (x>0)的图象和性质.
①填写下表,画出函数的图象;
x … 1 2 3 4 …
y … …
②观察图象,写出该函数两条不同类型的性质;
③在求二次函数y=ax2+bx+c(a≠0)的最大(小)值时,除了通过观察图象,还可以通过配方得到.请你通过配方求函数y=x+ (x>0)的最小值.
(2)用上述方法解决“问题情境”中的问题,直接写出答案.
20.某商店将成本为30元的文化衫标价50元出售.
(1)为了搞促销活动经过两次降价调至每件40.5元,若两次降价的百分率相同,求每次降价的百分率
(2)经调查,该文化衫每降5元,每月可多售出100件,若该品牌文化衫按原标价出售,每月可销售200件,那么销售价定为多少元,可以使该商品获得最大的利润?最大的利润是多少?
21.已知 是关于x的二次函数.
(1)满足条件的m的值;
(2)m为何值时,抛物线有最低点?求出这个最低点,这时当x为何值时,y随x的增大而增大?
(3)m为何值时,函数有最大值?最大值是多少?这时当x为何值时,y随x的增大而减小?
22.已知函数 (b为常数).
(1)若图象经过点 ,判断图象经过点 吗?请说明理由;
(2)设该函数图象的顶点坐标为 ,当b的值变化时,求m与n的关系式;
(3)若该函数图象不经过第三象限,当 时,函数的最大值与最小值之差为16,求b的值.
23.某商品的进价为每件40元,在销售过程中发现,每周的销售量y(件)与销售单价x(元)之间的关系可以近似看作一次函数 ,且当售价定为50元/件时,每周销售30件,当售价定为70元/件时,每周销售10件.
(1)求k,b的值;
(2)求销售该商品每周的利润w(元)与销售单价x(元)之间的函数解析式,并求出销售该商品每周可获得的最大利润.
24.甲、乙两公司同时销售一款进价为40元/千克的产品.图①中折线ABC表示甲公司销售价y1(元/千克)与销售量x(千克)之间的函数关系,图②中抛物线表示乙公司销售这款产品获得的利润y2(元)与销售量x(千克)之间的函数关系.
(1)分别求出图①中线段AB、图②中抛物线所表示的函数表达式;
(2)当该产品销售量为多少千克时,甲、乙两公司获得的利润的差最大?最大值为多少?
答案解析部分
1.【答案】B
2.【答案】D
3.【答案】D
4.【答案】B
5.【答案】C
6.【答案】A
7.【答案】C
8.【答案】C
9.【答案】B
10.【答案】D
11.【答案】B
12.【答案】C
13.【答案】
14.【答案】6
15.【答案】①②③
16.【答案】16
17.【答案】5,1
18.【答案】0≤y≤9
19.【答案】(1)解:①故答案为: , , ,2, , , .
函数y=x+ 的图象如图:
②答:函数两条不同类型的性质是:当0<x<1时,y 随x的增大而减小,当x>1时,y 随x的增大而增大;当x=1时,函数y=x+ (x>0)的最小值是2.
③y=x+ = = +2= +2,
∵x>0,所以 ≥0,
所以当x=1时, 的最小值为0,
∴函数y=x+ (x>0)的最小值是2
(2)解:答:矩形的面积为a(a为常数,a>0),当该矩形的长为 时,它的周长最小,最小值是4 .
20.【答案】(1)解:设每次降价率为n,则
50(1﹣n)2=40.5,
解得:n1=0.1=10%,n2=1.9(不合,舍去).
故每次降价的百分率为10%;
(2)设销售定价为每件x元,每月利润为y元,则
y=(x﹣30)(200+×100)=﹣20(x﹣45)2+4450
∵a=﹣20<0,
∴当x=45时,y取最大值为4450元.
21.【答案】(1)因为函数为二次函数
∴m+2≠0,m2+m-4=2
∴m≠-2,m2+m-6=0
∴m≠-2,(m+3)(m-2)=0
∴m=-3,m=2
(2)当m=2时,函数为y=4x2+1,有最低点,最低点为(0,1),且x≥0时,y随x的增大而增大
(3)m=-3时,函数为-x2+1,有最大值,最大值为1,x≥0时,y随x的增大而减小
22.【答案】(1)解:经过,
把点(﹣2,4)代入y=x2+bx+3b中得:
4﹣2b+3b=4,
解得b=0,
∴此函数表达式为:y=x2,
当x=2时,y=4,
∴图象经过点(2,4);
(2)解:∵抛物线函数y=x2+bx+3b(b为常数)的顶点坐标是 (m,n),
∴﹣ =m, =n,
∴b=﹣2m,
把b=﹣2m代入 =n得n= =﹣m2﹣6m.
即n关于m的函数解析式为n=﹣m2﹣6m.
(3)解:把x=0代入y=x2+bx+3b得y=3b,
∵抛物线不经过第三象限,
∴3b≥0,即b≥0,
∵y=x2+bx+3b=(x+ )2﹣ +3b,
∴抛物线顶点(﹣ ,﹣ +3b),
∵﹣ ≤0,
∴当﹣ +3b≥0时,抛物线不经过第三象限,
解得b≤12,
∴0≤b≤12,﹣6≤﹣ ≤0,
∴当﹣6≤x≤1时,函数最小值为y=﹣ +3b,
把x=﹣6代入y=x2+bx+3b得y=36﹣3b,
把x=1代入y=x2+bx+3b得y=1+4b,
当36﹣3b﹣(﹣ +3b)=16时,
解得b=20(不符合题意,舍去)或b=4.
当1+4b﹣(﹣ +3b)=16时,
解得b=6或b=﹣10(不符合题意,舍去).
综上所述,b=4或6.
23.【答案】(1)解:由题意可得,当x=50时,y=30;当x=70时,y=10,
代入 中得:
,解得: ,
∴k=-1,b=80;
(2)解:由(1)可知,y=-x+80,
∴ ,
∵y=-x+80≥0,
∴
∵-1<0,
∴当x=60时,w有最大值,此时w=400,
即最大利润为400元.
24.【答案】(1)解:设y1与x之间的函数表达式为y1=kx+b.
根据题意,当x=0时,y1=120;当x=80时,y1=72.
所以 ,解得
所以,y1与x之间的函数表达式为y1=-0.6x+120.
设y2与x之间的函数表达式为y2=a(x―75)2+2250,
当x=0时,y2=0,解得a=―0.4.
所以,y2与x之间的函数表达式为y2=―0.4(x―75)2+2250
(2)解:设甲、乙两公司的销售总利润的差为w(元).当0<x≤80时,
w=(y1-40)x―y2= (-0.6x+120―40)x-[(-0.4(x―75)2+2250]
=-0.2x2+20x=-0.2(x-50)2+500.∵-0.2<0,0<x≤80∴当x=50时, w有最大值,最大值为500.
当80<x≤84时,
w=(72―40)x―[―0.4(x―75)2+2250]=0.4x2―28x,
∵当80<x≤84时,w随x的增大而增大,∴当x=84时, 有最大值,最大值为470.4.
综上所述,当销售量为50千克时,甲乙两公司获得的利润的差最大,最大是500元
同课章节目录
