第8章 三角形 小专题12 三角形中内、外角平分线的常见模型 2025中考数学二轮复习课件(共16张PPT)
文档属性
| 名称 | 第8章 三角形 小专题12 三角形中内、外角平分线的常见模型 2025中考数学二轮复习课件(共16张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 1.1MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 通用版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-05-08 07:19:08 | ||
图片预览


文档简介
(共16张PPT)
第8章 三角形
小专题12 三角形中内、外角平分线的常见模型
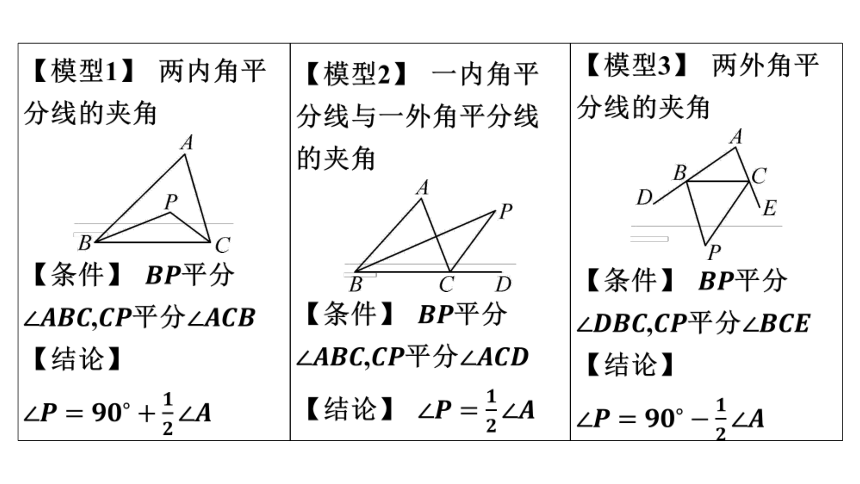
【模型1】 两内角平 分线的夹角 ________________________________________ 【条件】 平分 ,平分 【结论】 【模型2】 一内角平 分线与一外角平分线 的夹角 ___________________________________________ 【条件】 平分 ,平分 【结论】 【模型3】 两外角平
分线的夹角
______________________________________
【条件】 平分
,平分
【结论】
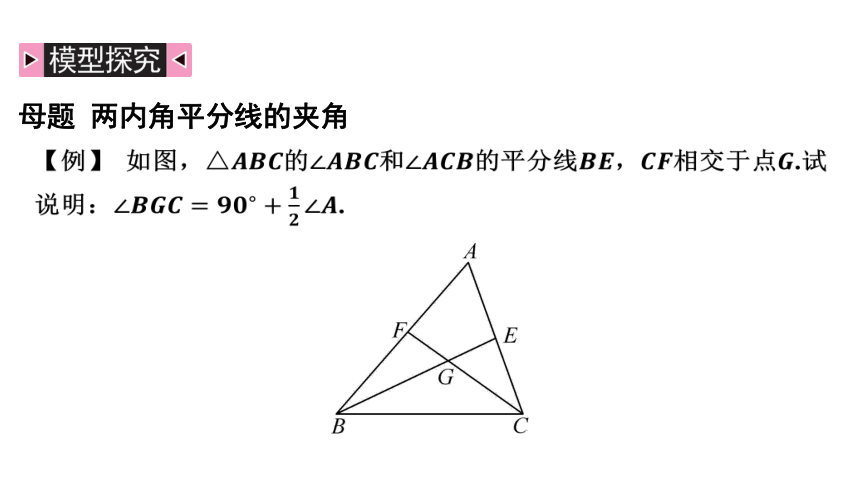
母题 两内角平分线的夹角
【例】 如图,的和的平分线,相交于点 .试
说明: .
解:,分别是, 的平分线,
.
.
又 ,
.
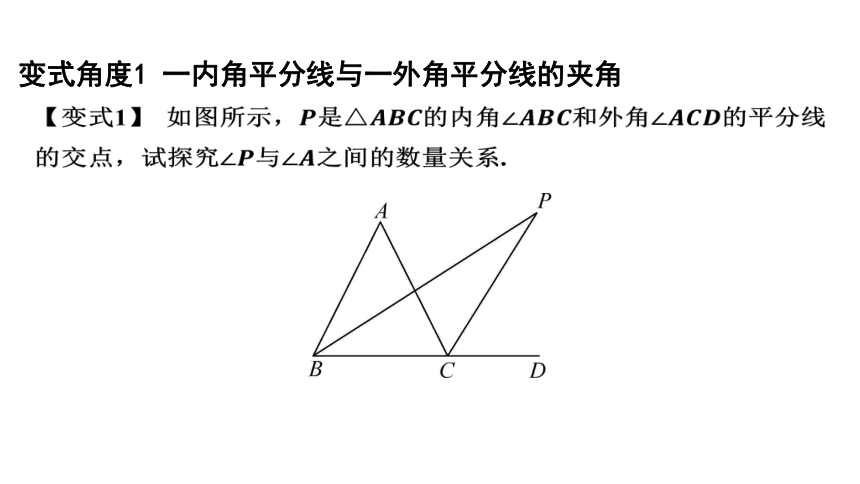
变式角度1 一内角平分线与一外角平分线的夹角
【变式1】 如图所示,是的内角和外角 的平分线
的交点,试探究与 之间的数量关系.
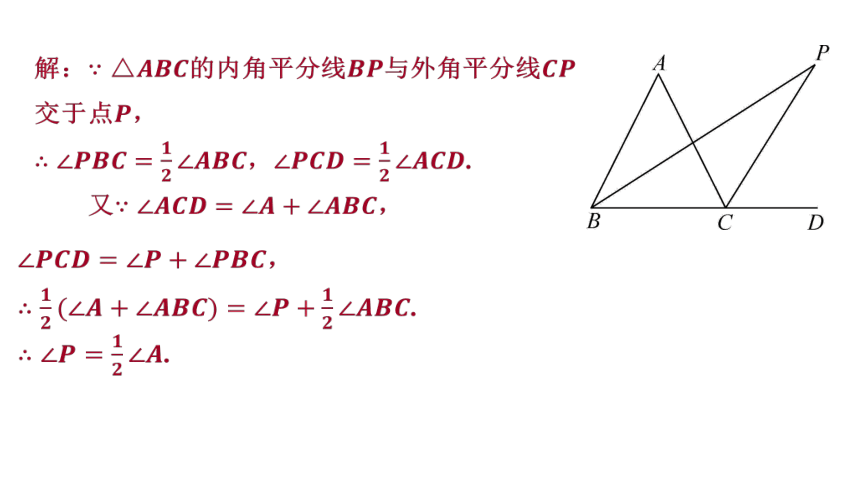
解:的内角平分线与外角平分线
交于点 ,
, .
又 ,
,
.
.
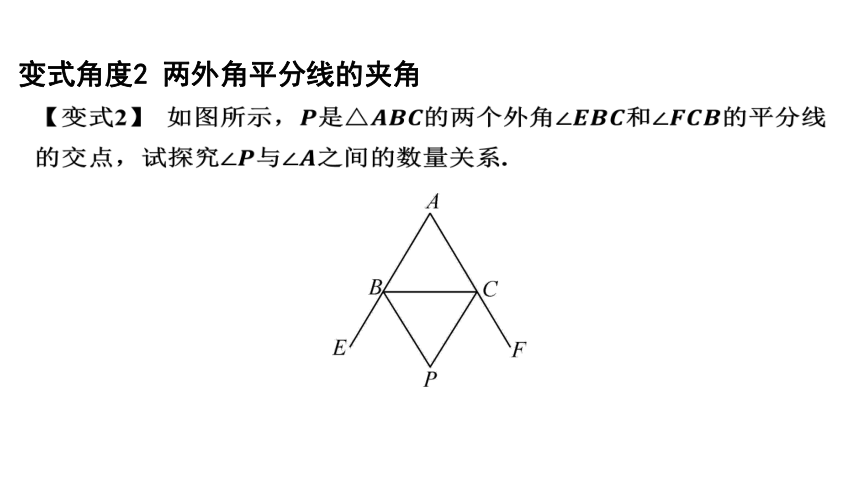
变式角度2 两外角平分线的夹角
【变式2】 如图所示,是的两个外角和 的平分线
的交点,试探究与 之间的数量关系.
解: ,
.
,分别是, 的平分线,
, .
.
.
变式角度3 三等分线
【变式3】 如图,已知,,试探究
与 之间的数量关系.
解: ,
.
, ,
.
.
1.如图, ,,分别是, 的三等分线
(即,),则 ______.
2.(2023·长葛期中)在图1、图2、图3中, , ,
,则 ______.
图1
图2
图3
3.如图,在中, ,与的平分线交于点 ,
得,与的平分线相交于点,得 与
的平分线相交于点,得,则 的度数为( )
B
A. B. C. D.
4.如图, ,点,分别在射线, 上移动
(不与点重合),平分,的反向延长线与 的平分
线相交于点 .
(1)当 时, _____;
(2)随着点,的移动,试问 的大小是否发生变化?请说出你的
理由.
解: 的大小不变.理由如下:
, 平
分 ,
.
平分 ,
.
又 ,
.
的大小不发生变化.
第8章 三角形
小专题12 三角形中内、外角平分线的常见模型
【模型1】 两内角平 分线的夹角 ________________________________________ 【条件】 平分 ,平分 【结论】 【模型2】 一内角平 分线与一外角平分线 的夹角 ___________________________________________ 【条件】 平分 ,平分 【结论】 【模型3】 两外角平
分线的夹角
______________________________________
【条件】 平分
,平分
【结论】
母题 两内角平分线的夹角
【例】 如图,的和的平分线,相交于点 .试
说明: .
解:,分别是, 的平分线,
.
.
又 ,
.
变式角度1 一内角平分线与一外角平分线的夹角
【变式1】 如图所示,是的内角和外角 的平分线
的交点,试探究与 之间的数量关系.
解:的内角平分线与外角平分线
交于点 ,
, .
又 ,
,
.
.
变式角度2 两外角平分线的夹角
【变式2】 如图所示,是的两个外角和 的平分线
的交点,试探究与 之间的数量关系.
解: ,
.
,分别是, 的平分线,
, .
.
.
变式角度3 三等分线
【变式3】 如图,已知,,试探究
与 之间的数量关系.
解: ,
.
, ,
.
.
1.如图, ,,分别是, 的三等分线
(即,),则 ______.
2.(2023·长葛期中)在图1、图2、图3中, , ,
,则 ______.
图1
图2
图3
3.如图,在中, ,与的平分线交于点 ,
得,与的平分线相交于点,得 与
的平分线相交于点,得,则 的度数为( )
B
A. B. C. D.
4.如图, ,点,分别在射线, 上移动
(不与点重合),平分,的反向延长线与 的平分
线相交于点 .
(1)当 时, _____;
(2)随着点,的移动,试问 的大小是否发生变化?请说出你的
理由.
解: 的大小不变.理由如下:
, 平
分 ,
.
平分 ,
.
又 ,
.
的大小不发生变化.
同课章节目录
