【期末高频考点】三角形的内角和高频易错提高卷(含解析)-2024-2025学年四年级下册数学人教版
文档属性
| 名称 | 【期末高频考点】三角形的内角和高频易错提高卷(含解析)-2024-2025学年四年级下册数学人教版 |

|
|
| 格式 | docx | ||
| 文件大小 | 551.7KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-05-07 00:00:00 | ||
图片预览




文档简介
三角形的内角和
一.选择题(共5小题)
1.(2024春 宣汉县期末)用100倍的放大镜看一个三角形,这个三角形的内角和是( )
A.180° B.360° C.1800°
2.(2024春 吐鲁番市期末)一个三角形中最多有( )个钝角.
A.1 B.2 C.3
3.(2023秋 黔南州期末)一个三角板上有( )个直角.
A.1 B.2 C.3
4.(2024秋 龙口市期中)在一个三角形中,有一个角是60°,另外的两个角可能是( )
A.50°和50° B.50°和60° C.50°和70° D.60°和70°
5.(2023秋 宁波期末)乐乐不小心把家里的一块玻璃摔成3块(如图),他只拿其中一块玻璃去玻璃店切割出一块与原来一样大的玻璃,你知道他拿的是哪一块玻璃吗?( )
A.3 B.2 C.1 D.都可以
二.填空题(共5小题)
6.(2024秋 定安县期末)一个直角三角形,它其中一个锐角是35°,它的另一个锐角是 。
7.(2024秋 莱芜区期末)一个等腰三角形的顶角是80°,它的底角是 °
8.(2023秋 高新区期末)将三角形的三个角撕下来拼在一起(如图),我发现: 。
9.(2024春 宣汉县期末)在35°,95°,60°和85°这四个角中,可能组成为同一个三角形的三个内角分别是 , , .
10.(2023秋 如东县期末)等腰三角形的一个顶角是70°,那它的一个底角是 °。一个三角形的两条边长分别是8厘米和12厘米,那第三条边最长是 厘米(长度均为整厘米数)。
三.判断题(共5小题)
11.(2024秋 道外区期末)一个三角形中最多有两个锐角。
12.(2024秋 桓台县期末)两把相同的三角尺拼成大三角形的内角和是180°。
13.(2024秋 钢城区期中)两个三角形拼成的一个大三角形的内角和是360度。
14.(2024秋 甘州区期中)一个三角板有三个角,其中有两个直角。
15.(2024 泗水县)钝角三角形的两个锐角之和一定小于90°。
四.计算题(共1小题)
16.(2023春 兴文县期末)计算下面各未知角的度数。
(1)
(2)
五.应用题(共4小题)
17.(2024春 灵川县期末)“三月三”活动日当天,二(2)班节目可谓精彩纷呈:跳竹竿舞、抛绣球、尝美食……,最后玩起了猫抓老鼠的游戏,各个角色需要佩戴头饰。其中,老鼠头饰是一个直角三角形(如图所示),你知道另一个锐角是多少度吗?
18.(2024春 南沙区期末)2024潍坊国际风筝嘉年华开幕,本届嘉年华创新扎制了众多特色鲜明的主题风筝。例如,以庆祝新中国成立75周年为主题的“祖国万岁”风筝、港珠澳大桥风筝和“蛟龙”号风筝等。小红买了一个形状是等腰三角形的风筝,已知该风筝的一个角是50°,另外两个角可能是多少度?
19.(2024春 乐东县期末)红领巾是少先队员的标志,象征着革命的胜利和无数英雄的心血。少先队员佩戴的红领巾的一个底角是30°,它的顶角是多少度?
20.(2024春 南海区期末)明明做了一个等腰三角形的风筝,如果这个风筝的一个内角是50°,那么它的另外两个内角分别是多少度?
六.解答题(共2小题)
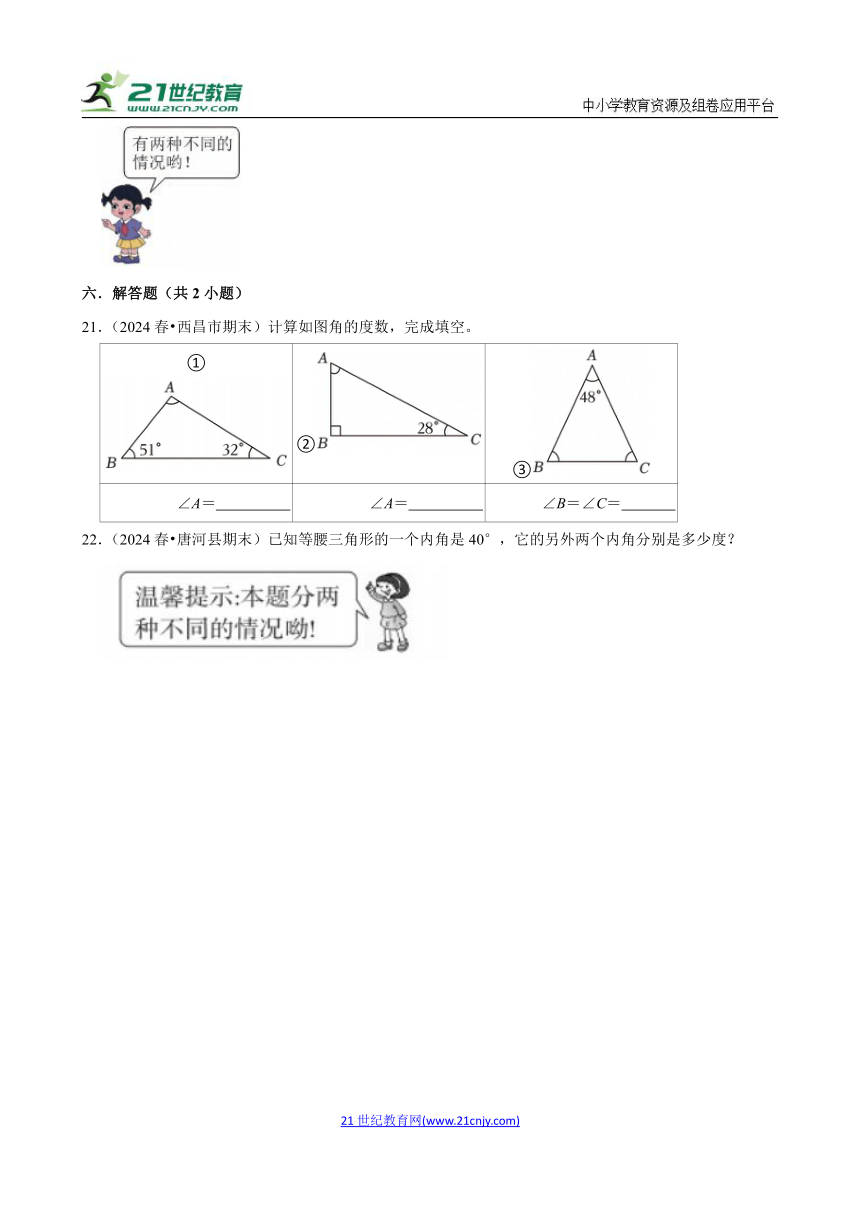
21.(2024春 西昌市期末)计算如图角的度数,完成填空。
① ② ③
∠A= ∠A= ∠B=∠C=
22.(2024春 唐河县期末)已知等腰三角形的一个内角是40°,它的另外两个内角分别是多少度?
三角形的内角和
参考答案与试题解析
题号 1 2 3 4 5
答案 A A A C A
一.选择题(共5小题)
1.(2024春 宣汉县期末)用100倍的放大镜看一个三角形,这个三角形的内角和是( )
A.180° B.360° C.1800°
【考点】三角形的内角和.
【专题】应用意识.
【答案】A
【分析】三角形的内角和是180°;用放大镜放大一个三角形,三角形的边长变长了,但是每个角度的大小都没变,内角和也不会变;据此解答。
【解答】解:用100倍的放大镜看一个三角形,这个三角形的内角和是180°。
故选:A。
【点评】本题主要考查三角形内角和定理的应用。
2.(2024春 吐鲁番市期末)一个三角形中最多有( )个钝角.
A.1 B.2 C.3
【考点】三角形的内角和.
【专题】平面图形的认识与计算.
【答案】A
【分析】依据三角形的内角和是180度,假设一个三角形中可以有多于1个的钝角,则会得出违背三角形内角和是180度的结论,假设不成立,从而可以作出正确的选择.
【解答】解:假设三角形中,出现2个或3个钝角,那么三角形的内角和就大于180°,
不符合三角形内角和是180°,因而假设不成立,
所以一个三角形中最多有一个钝角;
故选:A.
【点评】此题主要考查三角形的内角和是180度的灵活应用,利用假设法即可进行解答.
3.(2023秋 黔南州期末)一个三角板上有( )个直角.
A.1 B.2 C.3
【考点】三角形的内角和.
【答案】A
【分析】本题主要运用了三角形的内角和是180°,这道题要运用“假设法”解答,假设一副三角板上有2个直角则内角和为90°+90°+另一个角度数>180°,即可求得答案.
【解答】解:假设一副三角板上的3个角中有2个直角.
则内角和为:90°+90°+第三个角=180+(不为0的数)>180°.
因为三角形的内角和是180°.
所以在一个三角板中只有一个直角.
故选:A.
【点评】此题考查了三角形内角和是180°.
4.(2024秋 龙口市期中)在一个三角形中,有一个角是60°,另外的两个角可能是( )
A.50°和50° B.50°和60° C.50°和70° D.60°和70°
【考点】三角形的内角和.
【专题】综合判断题;应用意识.
【答案】C
【分析】根据三角形的内角和等于180度来判断即可。
【解答】解:180°﹣60°=120°
50°+50°=100°,不符合题意;
50°+60°=110°,不符合题意;
50°+70°=120°,符合题意;
60°+70°=130°,不符合题意。
即只有C选项符合题意。
故选:C。
【点评】本题考查了三角形内角和的应用。
5.(2023秋 宁波期末)乐乐不小心把家里的一块玻璃摔成3块(如图),他只拿其中一块玻璃去玻璃店切割出一块与原来一样大的玻璃,你知道他拿的是哪一块玻璃吗?( )
A.3 B.2 C.1 D.都可以
【考点】三角形的内角和.
【专题】应用意识.
【答案】A
【分析】三角形的内角和是180°,已知三角形的一条边的长度和这条边上的两个角的度数即可求出另一个角的度数与另外两条边的长度。据此解答。
【解答】解:由分析得:乐乐不小心把家里的一块玻璃摔成3块(如图),他只拿其中一块玻璃去玻璃店切割出一块与原来一样大的玻璃,我知道他拿的是第3块玻璃。
故选:A。
【点评】此题考查的目的是理解掌握三角形的特征及应用,三角形内角和及应用。
二.填空题(共5小题)
6.(2024秋 定安县期末)一个直角三角形,它其中一个锐角是35°,它的另一个锐角是 55° 。
【考点】三角形的内角和.
【专题】空间观念.
【答案】见试题解答内容
【分析】因为三角形的内角和是180度,直角是90度,所以直角三角形中的两个锐角的和是90度,所以用90度减去35度的角,就是另一个角的度数。
【解答】解:90°﹣35°=55°
答:另一个锐角是55°。
故答案为:55°。
【点评】本题主要考查学生三角形的内角和是180度和直角三角形特征的掌握情况。
7.(2024秋 莱芜区期末)一个等腰三角形的顶角是80°,它的底角是 50 °
【考点】三角形的内角和.
【专题】应用意识.
【答案】50。
【分析】三角形的内角和是180度,先用“180﹣80”求出两个底角的度数和,进而用“三角形两个底角的度数和÷2”解答求出一个底角的度数。
【解答】解:(180°﹣80°)÷2
=100°÷2
=50°
答:它的一个底角度数是50°。
故答案为:50。
【点评】解答此题用到的知识点:(1)三角形的内角和是180度;(2)等腰三角形的特征。
8.(2023秋 高新区期末)将三角形的三个角撕下来拼在一起(如图),我发现: 三角形的内角和是180° 。
【考点】三角形的内角和.
【专题】应用意识.
【答案】三角形的内角和是180°。
【分析】根据平角的意义,平角是180°,将三角形的三个角撕下来拼在一起,正好拼成一个平角,所以三角形的内角和是180°。据此解答。
【解答】解:将三角形的三个角撕下来拼在一起,正好拼成一个平角,所以三角形三个内角的和是180°。
故答案为:三角形的内角和是180°。
【点评】此题考查的目的是理解掌握三角形内角和的推算方法及应用,平角的意义及应用。
9.(2024春 宣汉县期末)在35°,95°,60°和85°这四个角中,可能组成为同一个三角形的三个内角分别是 35° , 60° , 85° .
【考点】三角形的内角和.
【答案】见试题解答内容
【分析】根据三角形的内角和是180度,将所给3个角相加,等于180度的符合要求,不符合的就不能组成一个三角形.据此解答即可.
【解答】解:35°+60°+85°=180°
故答案为:35°,60°,85°.
【点评】此题考查了三角形内角和定理的应用,根据三角形的内角和等于180°,进行解答即可.
10.(2023秋 如东县期末)等腰三角形的一个顶角是70°,那它的一个底角是 55 °。一个三角形的两条边长分别是8厘米和12厘米,那第三条边最长是 19 厘米(长度均为整厘米数)。
【考点】三角形的内角和;三角形边的关系.
【专题】平面图形的认识与计算;应用意识.
【答案】55,19。
【分析】根据三角形内角和是180°,再根据等腰三角形的两个底角相等,即可求出底角,根据三角形两边之和大于第三边,两边之差小于第三边,即可解答。
【解答】解:(180°﹣70°)÷2
=110°÷2
=55°
12+8=20(厘米)
12﹣8=4(厘米)
所以4厘米<第三边<20厘米
20﹣1=19(厘米)
答:它的一个底角是55°,第三条边最长是19厘米。
故答案为:55,19。
【点评】本题考查的是三角形内角和以及三角形三条边的关系,掌握三角形内角和是180°和三角形三条边的关系是解答关键。
三.判断题(共5小题)
11.(2024秋 道外区期末)一个三角形中最多有两个锐角。 ×
【考点】三角形的内角和.
【专题】应用意识.
【答案】×
【分析】根据三角形的内角和是180度举例即可解答。
【解答】解:等边三角形的三个角都是60度,60度是锐角,所以一个三角形中最多有三个锐角。
所以原题说法错误。
故答案为:×。
【点评】熟练掌握三角形的内角和是180度以及三角形按角的分类是解题的关键。
12.(2024秋 桓台县期末)两把相同的三角尺拼成大三角形的内角和是180°。 √
【考点】三角形的内角和.
【专题】模型思想;应用意识.
【答案】√。
【分析】利用三角形内角和定理判断即可。
【解答】解:两把相同的三角尺拼成大三角形的内角和是180°,原题说法正确。
故答案为:√。
【点评】本题主要考查三角形内角和定理的应用。
13.(2024秋 钢城区期中)两个三角形拼成的一个大三角形的内角和是360度。 ×
【考点】三角形的内角和.
【专题】应用意识.
【答案】×。
【分析】只要是三角形,它的内角和就是180度,不管三角形是大还是小,它的内角和都是180度,据此解答。
【解答】解:两个三角形拼成的一个大三角形的内角和是180°,故原题说法错误。
故答案为:×。
【点评】解答此题的主要依据是:三角形的内角和是180度。
14.(2024秋 甘州区期中)一个三角板有三个角,其中有两个直角。 ×
【考点】三角形的内角和.
【专题】常规题型;能力层次.
【答案】×
【分析】根据三角形的内角和等于180°可知,一个三角形最多有一个直角,据此解答即可。
【解答】解:一个三角板有三个角,其中有两个锐角,一个直角。
所以题干说法是错误的。
故答案为:×。
【点评】熟练掌握三角形的内角和,是解答此题的关键。
15.(2024 泗水县)钝角三角形的两个锐角之和一定小于90°。 ∨
【考点】三角形的内角和.
【专题】常规题型;能力层次.
【答案】∨
【分析】根据三角形的内角和等于180度,和钝角三角形的定义,解答此题即可。
【解答】解:因为三角形的内角和等于180度,钝角三角形有一个钝角大于90度,所以钝角三角形的两个锐角之和一定小于90°。
所以题干说法是正确的。
故答案为:∨。
【点评】熟练掌握三角形的内角和定理,是解答此题的关键。
四.计算题(共1小题)
16.(2023春 兴文县期末)计算下面各未知角的度数。
(1)
(2)
【考点】三角形的内角和.
【专题】应用意识.
【答案】(1)64°,(2)120°。
【分析】(1)根据三角形的内角和是180度,用内角和减去两个已知角的度数即可解答;
(2)由两条边相等的三角形是等腰三角形,等腰三角形的顶角等于180度减去底角度数的2倍,据此列式解答。
【解答】解:(1)180﹣86﹣30
=94﹣30
=64(度)
答:未知角64°。
(2)180﹣30×2
=180﹣60
=120(度)
答:未知角是120°。
【点评】熟练掌握三角形的内角和是180度以及等腰三角形的特征是解题的关键。
五.应用题(共4小题)
17.(2024春 灵川县期末)“三月三”活动日当天,二(2)班节目可谓精彩纷呈:跳竹竿舞、抛绣球、尝美食……,最后玩起了猫抓老鼠的游戏,各个角色需要佩戴头饰。其中,老鼠头饰是一个直角三角形(如图所示),你知道另一个锐角是多少度吗?
【考点】三角形的内角和.
【专题】应用意识.
【答案】60度。
【分析】三角形的内角和是180度,用180度减去90度,再减去30度就是另一个锐角的度数。
【解答】解:180°﹣90°﹣30°
=90°﹣30°
=60°
答:另一个锐角是60度。
【点评】熟练掌握三角形的内角和是180度是解题的关键。
18.(2024春 南沙区期末)2024潍坊国际风筝嘉年华开幕,本届嘉年华创新扎制了众多特色鲜明的主题风筝。例如,以庆祝新中国成立75周年为主题的“祖国万岁”风筝、港珠澳大桥风筝和“蛟龙”号风筝等。小红买了一个形状是等腰三角形的风筝,已知该风筝的一个角是50°,另外两个角可能是多少度?
【考点】三角形的内角和.
【专题】几何直观.
【答案】65°、65°或50°、80°。
【分析】等腰三角形的两个底角相等,所以50°的角可作底角,也可作顶角,故分两种情况进行计算即可。
【解答】解:①当50°的角是顶角,则两个底角是:
(180°﹣50°)÷2
=130°÷2
=65°
②当50°的角是底角,则顶角是:
180﹣50°×2
=180°﹣100°
=80°
答:另外两个角可能是65°、65°或50°、80°。
【点评】本题考查了等腰三角形的性质,解题的关键是注意分情况进行讨论。
19.(2024春 乐东县期末)红领巾是少先队员的标志,象征着革命的胜利和无数英雄的心血。少先队员佩戴的红领巾的一个底角是30°,它的顶角是多少度?
【考点】三角形的内角和.
【专题】平面图形的认识与计算;应用意识.
【答案】120°。
【分析】根据红领巾是等腰三角形,所以两个底角相等,再根据三角形内角和是180°,即可解答。
【解答】解:180°﹣30°﹣30°
=150°﹣30°
=120°
答:它的顶角是 120°。
【点评】本题考查的是三角形内角和的有关计算,掌握三角形内角和是180°是解答关键。
20.(2024春 南海区期末)明明做了一个等腰三角形的风筝,如果这个风筝的一个内角是50°,那么它的另外两个内角分别是多少度?
【考点】三角形的内角和.
【专题】应用题;应用意识.
【答案】50°、80°;65°、65°。
【分析】由题意可知:可以假设这个内角分别为底角和顶角,再依据三角形的内角和是180度和等腰三角形的底角相等的特点,即可分别计算出两种情况下其他内角的度数。
【解答】解:(1)假设这个内角是底角,则另一个底角也是50°。
顶角为:180°﹣50°×2
=180°﹣100°
=80°
(2)假设这个内角是顶角。
每个底角的度数为:(180°﹣50°)÷2
=130°÷2
=65°
故答案为:50°、80°;65°、65°。
【点评】解答此题的主要依据是:三角形的内角和是180度和等腰三角形的底角相等的特点,利用假设法,分两种情况求解。
六.解答题(共2小题)
21.(2024春 西昌市期末)计算如图角的度数,完成填空。
① ② ③
∠A= 97° ∠A= 62° ∠B=∠C= 66°
【考点】三角形的内角和.
【专题】综合填空题;几何直观.
【答案】①97°;②62°;③66°。
【分析】依据题意结合图示可知,利用三角形内角和是180°分别去计算即可。
【解答】解:①∠A=180°﹣51°﹣32°=97°
②∠A=180°﹣90°﹣28°=62°
③∠B=∠C=(180°﹣48°)÷2=66°
故答案为:①97°;②62°;③66°。
【点评】熟练掌握三角形的内角和知识与等腰三角形的性质是解答此题的关键。
22.(2024春 唐河县期末)已知等腰三角形的一个内角是40°,它的另外两个内角分别是多少度?
【考点】三角形的内角和.
【专题】应用意识.
【答案】两个内角分别是70°,70°或40°,100°。
【分析】根据题意,假设40°的角是顶角,根据三角形的内角和是180°计算另外两个内角分别是多少度;再假设40°的角是底角,用同样的方法计算另外两个内角分别是多少度即可。
【解答】解:如果顶角是40°,那么另外两个内角是底角,
(180°﹣40°)÷2
=140°÷2
=70°
如果底角是40°,那么顶角是:
180°﹣40°×2
=180°﹣80°
=100°
即另外两个内角分别是70°,70°或40°,100°。
答:两个内角分别是70°,70°或40°,100°。
【点评】本题考查三角形的内角和,需要掌握三角形的内角和是180°。
21世纪教育网(www.21cnjy.com)
一.选择题(共5小题)
1.(2024春 宣汉县期末)用100倍的放大镜看一个三角形,这个三角形的内角和是( )
A.180° B.360° C.1800°
2.(2024春 吐鲁番市期末)一个三角形中最多有( )个钝角.
A.1 B.2 C.3
3.(2023秋 黔南州期末)一个三角板上有( )个直角.
A.1 B.2 C.3
4.(2024秋 龙口市期中)在一个三角形中,有一个角是60°,另外的两个角可能是( )
A.50°和50° B.50°和60° C.50°和70° D.60°和70°
5.(2023秋 宁波期末)乐乐不小心把家里的一块玻璃摔成3块(如图),他只拿其中一块玻璃去玻璃店切割出一块与原来一样大的玻璃,你知道他拿的是哪一块玻璃吗?( )
A.3 B.2 C.1 D.都可以
二.填空题(共5小题)
6.(2024秋 定安县期末)一个直角三角形,它其中一个锐角是35°,它的另一个锐角是 。
7.(2024秋 莱芜区期末)一个等腰三角形的顶角是80°,它的底角是 °
8.(2023秋 高新区期末)将三角形的三个角撕下来拼在一起(如图),我发现: 。
9.(2024春 宣汉县期末)在35°,95°,60°和85°这四个角中,可能组成为同一个三角形的三个内角分别是 , , .
10.(2023秋 如东县期末)等腰三角形的一个顶角是70°,那它的一个底角是 °。一个三角形的两条边长分别是8厘米和12厘米,那第三条边最长是 厘米(长度均为整厘米数)。
三.判断题(共5小题)
11.(2024秋 道外区期末)一个三角形中最多有两个锐角。
12.(2024秋 桓台县期末)两把相同的三角尺拼成大三角形的内角和是180°。
13.(2024秋 钢城区期中)两个三角形拼成的一个大三角形的内角和是360度。
14.(2024秋 甘州区期中)一个三角板有三个角,其中有两个直角。
15.(2024 泗水县)钝角三角形的两个锐角之和一定小于90°。
四.计算题(共1小题)
16.(2023春 兴文县期末)计算下面各未知角的度数。
(1)
(2)
五.应用题(共4小题)
17.(2024春 灵川县期末)“三月三”活动日当天,二(2)班节目可谓精彩纷呈:跳竹竿舞、抛绣球、尝美食……,最后玩起了猫抓老鼠的游戏,各个角色需要佩戴头饰。其中,老鼠头饰是一个直角三角形(如图所示),你知道另一个锐角是多少度吗?
18.(2024春 南沙区期末)2024潍坊国际风筝嘉年华开幕,本届嘉年华创新扎制了众多特色鲜明的主题风筝。例如,以庆祝新中国成立75周年为主题的“祖国万岁”风筝、港珠澳大桥风筝和“蛟龙”号风筝等。小红买了一个形状是等腰三角形的风筝,已知该风筝的一个角是50°,另外两个角可能是多少度?
19.(2024春 乐东县期末)红领巾是少先队员的标志,象征着革命的胜利和无数英雄的心血。少先队员佩戴的红领巾的一个底角是30°,它的顶角是多少度?
20.(2024春 南海区期末)明明做了一个等腰三角形的风筝,如果这个风筝的一个内角是50°,那么它的另外两个内角分别是多少度?
六.解答题(共2小题)
21.(2024春 西昌市期末)计算如图角的度数,完成填空。
① ② ③
∠A= ∠A= ∠B=∠C=
22.(2024春 唐河县期末)已知等腰三角形的一个内角是40°,它的另外两个内角分别是多少度?
三角形的内角和
参考答案与试题解析
题号 1 2 3 4 5
答案 A A A C A
一.选择题(共5小题)
1.(2024春 宣汉县期末)用100倍的放大镜看一个三角形,这个三角形的内角和是( )
A.180° B.360° C.1800°
【考点】三角形的内角和.
【专题】应用意识.
【答案】A
【分析】三角形的内角和是180°;用放大镜放大一个三角形,三角形的边长变长了,但是每个角度的大小都没变,内角和也不会变;据此解答。
【解答】解:用100倍的放大镜看一个三角形,这个三角形的内角和是180°。
故选:A。
【点评】本题主要考查三角形内角和定理的应用。
2.(2024春 吐鲁番市期末)一个三角形中最多有( )个钝角.
A.1 B.2 C.3
【考点】三角形的内角和.
【专题】平面图形的认识与计算.
【答案】A
【分析】依据三角形的内角和是180度,假设一个三角形中可以有多于1个的钝角,则会得出违背三角形内角和是180度的结论,假设不成立,从而可以作出正确的选择.
【解答】解:假设三角形中,出现2个或3个钝角,那么三角形的内角和就大于180°,
不符合三角形内角和是180°,因而假设不成立,
所以一个三角形中最多有一个钝角;
故选:A.
【点评】此题主要考查三角形的内角和是180度的灵活应用,利用假设法即可进行解答.
3.(2023秋 黔南州期末)一个三角板上有( )个直角.
A.1 B.2 C.3
【考点】三角形的内角和.
【答案】A
【分析】本题主要运用了三角形的内角和是180°,这道题要运用“假设法”解答,假设一副三角板上有2个直角则内角和为90°+90°+另一个角度数>180°,即可求得答案.
【解答】解:假设一副三角板上的3个角中有2个直角.
则内角和为:90°+90°+第三个角=180+(不为0的数)>180°.
因为三角形的内角和是180°.
所以在一个三角板中只有一个直角.
故选:A.
【点评】此题考查了三角形内角和是180°.
4.(2024秋 龙口市期中)在一个三角形中,有一个角是60°,另外的两个角可能是( )
A.50°和50° B.50°和60° C.50°和70° D.60°和70°
【考点】三角形的内角和.
【专题】综合判断题;应用意识.
【答案】C
【分析】根据三角形的内角和等于180度来判断即可。
【解答】解:180°﹣60°=120°
50°+50°=100°,不符合题意;
50°+60°=110°,不符合题意;
50°+70°=120°,符合题意;
60°+70°=130°,不符合题意。
即只有C选项符合题意。
故选:C。
【点评】本题考查了三角形内角和的应用。
5.(2023秋 宁波期末)乐乐不小心把家里的一块玻璃摔成3块(如图),他只拿其中一块玻璃去玻璃店切割出一块与原来一样大的玻璃,你知道他拿的是哪一块玻璃吗?( )
A.3 B.2 C.1 D.都可以
【考点】三角形的内角和.
【专题】应用意识.
【答案】A
【分析】三角形的内角和是180°,已知三角形的一条边的长度和这条边上的两个角的度数即可求出另一个角的度数与另外两条边的长度。据此解答。
【解答】解:由分析得:乐乐不小心把家里的一块玻璃摔成3块(如图),他只拿其中一块玻璃去玻璃店切割出一块与原来一样大的玻璃,我知道他拿的是第3块玻璃。
故选:A。
【点评】此题考查的目的是理解掌握三角形的特征及应用,三角形内角和及应用。
二.填空题(共5小题)
6.(2024秋 定安县期末)一个直角三角形,它其中一个锐角是35°,它的另一个锐角是 55° 。
【考点】三角形的内角和.
【专题】空间观念.
【答案】见试题解答内容
【分析】因为三角形的内角和是180度,直角是90度,所以直角三角形中的两个锐角的和是90度,所以用90度减去35度的角,就是另一个角的度数。
【解答】解:90°﹣35°=55°
答:另一个锐角是55°。
故答案为:55°。
【点评】本题主要考查学生三角形的内角和是180度和直角三角形特征的掌握情况。
7.(2024秋 莱芜区期末)一个等腰三角形的顶角是80°,它的底角是 50 °
【考点】三角形的内角和.
【专题】应用意识.
【答案】50。
【分析】三角形的内角和是180度,先用“180﹣80”求出两个底角的度数和,进而用“三角形两个底角的度数和÷2”解答求出一个底角的度数。
【解答】解:(180°﹣80°)÷2
=100°÷2
=50°
答:它的一个底角度数是50°。
故答案为:50。
【点评】解答此题用到的知识点:(1)三角形的内角和是180度;(2)等腰三角形的特征。
8.(2023秋 高新区期末)将三角形的三个角撕下来拼在一起(如图),我发现: 三角形的内角和是180° 。
【考点】三角形的内角和.
【专题】应用意识.
【答案】三角形的内角和是180°。
【分析】根据平角的意义,平角是180°,将三角形的三个角撕下来拼在一起,正好拼成一个平角,所以三角形的内角和是180°。据此解答。
【解答】解:将三角形的三个角撕下来拼在一起,正好拼成一个平角,所以三角形三个内角的和是180°。
故答案为:三角形的内角和是180°。
【点评】此题考查的目的是理解掌握三角形内角和的推算方法及应用,平角的意义及应用。
9.(2024春 宣汉县期末)在35°,95°,60°和85°这四个角中,可能组成为同一个三角形的三个内角分别是 35° , 60° , 85° .
【考点】三角形的内角和.
【答案】见试题解答内容
【分析】根据三角形的内角和是180度,将所给3个角相加,等于180度的符合要求,不符合的就不能组成一个三角形.据此解答即可.
【解答】解:35°+60°+85°=180°
故答案为:35°,60°,85°.
【点评】此题考查了三角形内角和定理的应用,根据三角形的内角和等于180°,进行解答即可.
10.(2023秋 如东县期末)等腰三角形的一个顶角是70°,那它的一个底角是 55 °。一个三角形的两条边长分别是8厘米和12厘米,那第三条边最长是 19 厘米(长度均为整厘米数)。
【考点】三角形的内角和;三角形边的关系.
【专题】平面图形的认识与计算;应用意识.
【答案】55,19。
【分析】根据三角形内角和是180°,再根据等腰三角形的两个底角相等,即可求出底角,根据三角形两边之和大于第三边,两边之差小于第三边,即可解答。
【解答】解:(180°﹣70°)÷2
=110°÷2
=55°
12+8=20(厘米)
12﹣8=4(厘米)
所以4厘米<第三边<20厘米
20﹣1=19(厘米)
答:它的一个底角是55°,第三条边最长是19厘米。
故答案为:55,19。
【点评】本题考查的是三角形内角和以及三角形三条边的关系,掌握三角形内角和是180°和三角形三条边的关系是解答关键。
三.判断题(共5小题)
11.(2024秋 道外区期末)一个三角形中最多有两个锐角。 ×
【考点】三角形的内角和.
【专题】应用意识.
【答案】×
【分析】根据三角形的内角和是180度举例即可解答。
【解答】解:等边三角形的三个角都是60度,60度是锐角,所以一个三角形中最多有三个锐角。
所以原题说法错误。
故答案为:×。
【点评】熟练掌握三角形的内角和是180度以及三角形按角的分类是解题的关键。
12.(2024秋 桓台县期末)两把相同的三角尺拼成大三角形的内角和是180°。 √
【考点】三角形的内角和.
【专题】模型思想;应用意识.
【答案】√。
【分析】利用三角形内角和定理判断即可。
【解答】解:两把相同的三角尺拼成大三角形的内角和是180°,原题说法正确。
故答案为:√。
【点评】本题主要考查三角形内角和定理的应用。
13.(2024秋 钢城区期中)两个三角形拼成的一个大三角形的内角和是360度。 ×
【考点】三角形的内角和.
【专题】应用意识.
【答案】×。
【分析】只要是三角形,它的内角和就是180度,不管三角形是大还是小,它的内角和都是180度,据此解答。
【解答】解:两个三角形拼成的一个大三角形的内角和是180°,故原题说法错误。
故答案为:×。
【点评】解答此题的主要依据是:三角形的内角和是180度。
14.(2024秋 甘州区期中)一个三角板有三个角,其中有两个直角。 ×
【考点】三角形的内角和.
【专题】常规题型;能力层次.
【答案】×
【分析】根据三角形的内角和等于180°可知,一个三角形最多有一个直角,据此解答即可。
【解答】解:一个三角板有三个角,其中有两个锐角,一个直角。
所以题干说法是错误的。
故答案为:×。
【点评】熟练掌握三角形的内角和,是解答此题的关键。
15.(2024 泗水县)钝角三角形的两个锐角之和一定小于90°。 ∨
【考点】三角形的内角和.
【专题】常规题型;能力层次.
【答案】∨
【分析】根据三角形的内角和等于180度,和钝角三角形的定义,解答此题即可。
【解答】解:因为三角形的内角和等于180度,钝角三角形有一个钝角大于90度,所以钝角三角形的两个锐角之和一定小于90°。
所以题干说法是正确的。
故答案为:∨。
【点评】熟练掌握三角形的内角和定理,是解答此题的关键。
四.计算题(共1小题)
16.(2023春 兴文县期末)计算下面各未知角的度数。
(1)
(2)
【考点】三角形的内角和.
【专题】应用意识.
【答案】(1)64°,(2)120°。
【分析】(1)根据三角形的内角和是180度,用内角和减去两个已知角的度数即可解答;
(2)由两条边相等的三角形是等腰三角形,等腰三角形的顶角等于180度减去底角度数的2倍,据此列式解答。
【解答】解:(1)180﹣86﹣30
=94﹣30
=64(度)
答:未知角64°。
(2)180﹣30×2
=180﹣60
=120(度)
答:未知角是120°。
【点评】熟练掌握三角形的内角和是180度以及等腰三角形的特征是解题的关键。
五.应用题(共4小题)
17.(2024春 灵川县期末)“三月三”活动日当天,二(2)班节目可谓精彩纷呈:跳竹竿舞、抛绣球、尝美食……,最后玩起了猫抓老鼠的游戏,各个角色需要佩戴头饰。其中,老鼠头饰是一个直角三角形(如图所示),你知道另一个锐角是多少度吗?
【考点】三角形的内角和.
【专题】应用意识.
【答案】60度。
【分析】三角形的内角和是180度,用180度减去90度,再减去30度就是另一个锐角的度数。
【解答】解:180°﹣90°﹣30°
=90°﹣30°
=60°
答:另一个锐角是60度。
【点评】熟练掌握三角形的内角和是180度是解题的关键。
18.(2024春 南沙区期末)2024潍坊国际风筝嘉年华开幕,本届嘉年华创新扎制了众多特色鲜明的主题风筝。例如,以庆祝新中国成立75周年为主题的“祖国万岁”风筝、港珠澳大桥风筝和“蛟龙”号风筝等。小红买了一个形状是等腰三角形的风筝,已知该风筝的一个角是50°,另外两个角可能是多少度?
【考点】三角形的内角和.
【专题】几何直观.
【答案】65°、65°或50°、80°。
【分析】等腰三角形的两个底角相等,所以50°的角可作底角,也可作顶角,故分两种情况进行计算即可。
【解答】解:①当50°的角是顶角,则两个底角是:
(180°﹣50°)÷2
=130°÷2
=65°
②当50°的角是底角,则顶角是:
180﹣50°×2
=180°﹣100°
=80°
答:另外两个角可能是65°、65°或50°、80°。
【点评】本题考查了等腰三角形的性质,解题的关键是注意分情况进行讨论。
19.(2024春 乐东县期末)红领巾是少先队员的标志,象征着革命的胜利和无数英雄的心血。少先队员佩戴的红领巾的一个底角是30°,它的顶角是多少度?
【考点】三角形的内角和.
【专题】平面图形的认识与计算;应用意识.
【答案】120°。
【分析】根据红领巾是等腰三角形,所以两个底角相等,再根据三角形内角和是180°,即可解答。
【解答】解:180°﹣30°﹣30°
=150°﹣30°
=120°
答:它的顶角是 120°。
【点评】本题考查的是三角形内角和的有关计算,掌握三角形内角和是180°是解答关键。
20.(2024春 南海区期末)明明做了一个等腰三角形的风筝,如果这个风筝的一个内角是50°,那么它的另外两个内角分别是多少度?
【考点】三角形的内角和.
【专题】应用题;应用意识.
【答案】50°、80°;65°、65°。
【分析】由题意可知:可以假设这个内角分别为底角和顶角,再依据三角形的内角和是180度和等腰三角形的底角相等的特点,即可分别计算出两种情况下其他内角的度数。
【解答】解:(1)假设这个内角是底角,则另一个底角也是50°。
顶角为:180°﹣50°×2
=180°﹣100°
=80°
(2)假设这个内角是顶角。
每个底角的度数为:(180°﹣50°)÷2
=130°÷2
=65°
故答案为:50°、80°;65°、65°。
【点评】解答此题的主要依据是:三角形的内角和是180度和等腰三角形的底角相等的特点,利用假设法,分两种情况求解。
六.解答题(共2小题)
21.(2024春 西昌市期末)计算如图角的度数,完成填空。
① ② ③
∠A= 97° ∠A= 62° ∠B=∠C= 66°
【考点】三角形的内角和.
【专题】综合填空题;几何直观.
【答案】①97°;②62°;③66°。
【分析】依据题意结合图示可知,利用三角形内角和是180°分别去计算即可。
【解答】解:①∠A=180°﹣51°﹣32°=97°
②∠A=180°﹣90°﹣28°=62°
③∠B=∠C=(180°﹣48°)÷2=66°
故答案为:①97°;②62°;③66°。
【点评】熟练掌握三角形的内角和知识与等腰三角形的性质是解答此题的关键。
22.(2024春 唐河县期末)已知等腰三角形的一个内角是40°,它的另外两个内角分别是多少度?
【考点】三角形的内角和.
【专题】应用意识.
【答案】两个内角分别是70°,70°或40°,100°。
【分析】根据题意,假设40°的角是顶角,根据三角形的内角和是180°计算另外两个内角分别是多少度;再假设40°的角是底角,用同样的方法计算另外两个内角分别是多少度即可。
【解答】解:如果顶角是40°,那么另外两个内角是底角,
(180°﹣40°)÷2
=140°÷2
=70°
如果底角是40°,那么顶角是:
180°﹣40°×2
=180°﹣80°
=100°
即另外两个内角分别是70°,70°或40°,100°。
答:两个内角分别是70°,70°或40°,100°。
【点评】本题考查三角形的内角和,需要掌握三角形的内角和是180°。
21世纪教育网(www.21cnjy.com)
