6.4分数加减法的简便算法 (课件)(共22张PPT)人教版数学五年级下册
文档属性
| 名称 | 6.4分数加减法的简便算法 (课件)(共22张PPT)人教版数学五年级下册 |  | |
| 格式 | pptx | ||
| 文件大小 | 4.9MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-05-07 21:17:59 | ||
图片预览







文档简介
(共22张PPT)
6.4 分数加减法的简便算法
6 分数的加法和减法
人教版五年级数学下册
学习目标
能运用所学知识解决简单的实际问题,感受异分母分效加减计算在生活中的应用。
在具体的计算过程中,体会整数加减法的运算律对分数加减法同样适用,并会用其进行简便运算,进步提高简算意识与能力;
结合具体情境,会比较异分母分数的大小,理解整数加法运算定律的意义,能正确进行计算;
课前导入
-( + )
3
10
4
3
2
5
19
30
=
= -
7
10
4
3
= -
40
30
21
30
+ -
9
14
1
4
5
7
= + -
7
28
18
28
20
28
18
28
= -
27
28
9
28
=
【选自教材P100 练习二十五 第1题】
计算。
+( - )
1
2
5
9
3
4
29
36
=
= +
1
4
5
9
= +
20
36
9
36
【选自教材P100 练习二十五 第1题】
= -
30
24
15
24
+ -
3
4
3
6
5
8
= + -
12
24
18
24
15
24
5
8
=
-( + )
1
3
3
5
2
15
= -
7
15
3
5
2
15
=
= -
9
15
7
15
【选自教材P100 练习二十五 第1题】
+ -
1
10
3
8
2
5
3
40
=
= -
19
40
16
40
= + -
15
40
4
40
16
40
新知探究
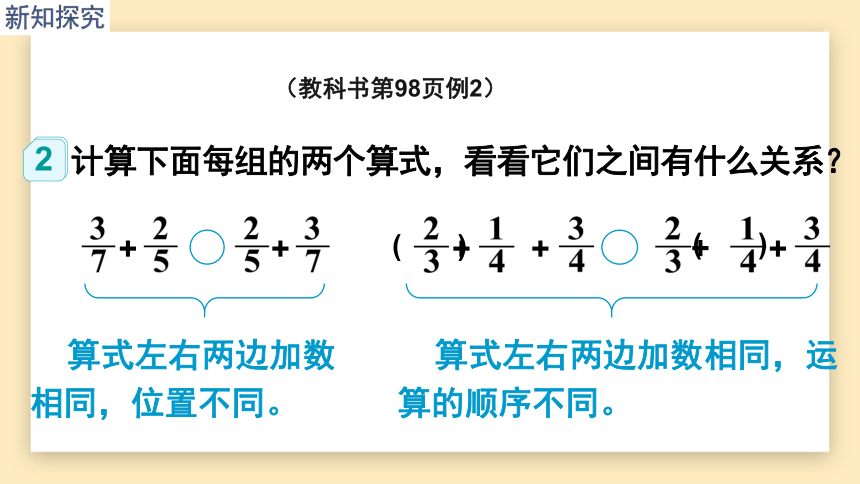
计算下面每组的两个算式,看看它们之间有什么关系?
2
(教科书第98页例2)
+
+
( )
( )
+
+
+
+
算式左右两边加数相同,位置不同。
算式左右两边加数相同,运算的顺序不同。
算一算:
+
+
+
=
+
=
+
=
+
=
它们的和相同。
=
a+b=b+a
整数加法的交换律同样适用于分数的加法混合运算。
算一算:
( )
+
+
( )
+
+
( )
+
+
=( )
+
+
=
+
=
=
( )
+
+
=
+1
=
=
=
整数加法的结合律(a+b)+c= a+(b+c)一样可以用于分数的加法混合运算。
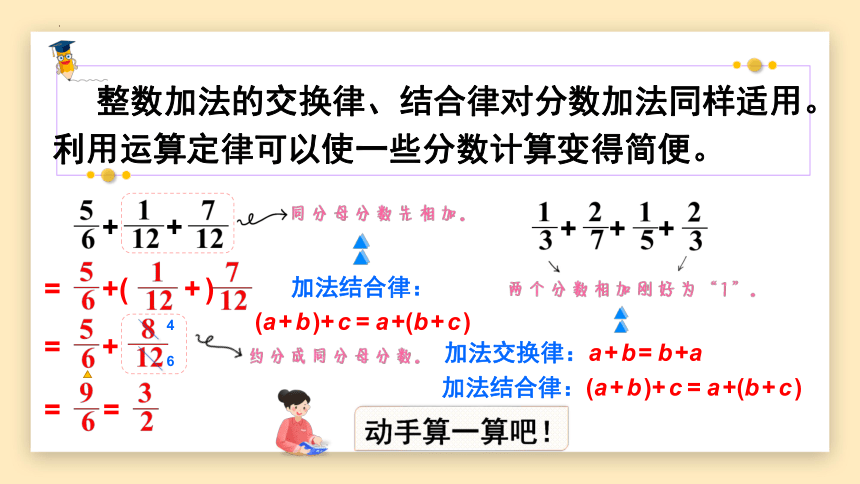
整数加法的交换律、结合律对分数加法同样适用。利用运算定律可以使一些分数计算变得简便。
+
+
+
+
+
加法结合律: (a+b)+c=a+(b+c)
( )
+
+
=
+
=
6
4
=
=
加法结合律:(a+b)+c=a+(b+c)
加法交换律:a+b=b+a
动手算一算吧!
+
+
+
+
+
( )
+
+
=
+
=
6
4
=
=
( )
( )
+
+
=
+
1
( )
+
=
+
1
=
整数加法的交换律、结合律对分数加法同样适用。利用运算定律可以使一些分数计算变得简便。
培优范例
计算:
1
+
+
+
+
异分母相加,你是选择分步通分计算,还是一次通分计算?
+
+
+
以此类推,算式可以写成:
解:
原式=
=
0
0
0
0
0
0
0
=
=
随堂练习
1. 用简便算法计算下面各题。
教材第98页“做一做”第2题
加法交换律
加法交换律和结合律
教材第98页“做一做”第2题
加法交换律和结合律
教材第98页“做一做”第2题
2. 把下面的算式填写完整。
(1)
6
1
2
1
3
6
+
=
+
(2)
7
5
2
3
( )
2
5
7
8
7
7
+
=
+
+
+
(3)
24
3
5
5
( )
5
3
5
24
12
24
24
12
-
=
-
-
○
(4)
11
3
6
7
( )
3
2
( )
11
9
11
9
+
=
+
+
+
+
+
2
3
3
8
6
11
7
9
2
9
+
加法交换律
加法结合律
加法交换律和结合律
连减的性质
3. 怎样简便怎样算。
4
1
这里可用连减的性质a–b–c=a-(b+c)进行简便。
胜利村修一条水渠,第一天修了 千米,第二天修了 千米,还剩 千米。这条水渠共长多少千米?
4.
9
2
9
7
5
2
水渠
9
2
km
5
2
km
9
7
km
?km
5
2
+
9
7
2
9
+
=
9
7
+
5
2
2
9
+
=
5
2
1
(km)
答:这条水渠共长 千米。
5
2
1
运用加法交换律
课堂小结
整数加法的交换律和结合律对分数加法同样适用。利用运算定律可以使一些分数计算变得简便。
谢谢观看
人教版五年级数学下册
6.4 分数加减法的简便算法
6 分数的加法和减法
人教版五年级数学下册
学习目标
能运用所学知识解决简单的实际问题,感受异分母分效加减计算在生活中的应用。
在具体的计算过程中,体会整数加减法的运算律对分数加减法同样适用,并会用其进行简便运算,进步提高简算意识与能力;
结合具体情境,会比较异分母分数的大小,理解整数加法运算定律的意义,能正确进行计算;
课前导入
-( + )
3
10
4
3
2
5
19
30
=
= -
7
10
4
3
= -
40
30
21
30
+ -
9
14
1
4
5
7
= + -
7
28
18
28
20
28
18
28
= -
27
28
9
28
=
【选自教材P100 练习二十五 第1题】
计算。
+( - )
1
2
5
9
3
4
29
36
=
= +
1
4
5
9
= +
20
36
9
36
【选自教材P100 练习二十五 第1题】
= -
30
24
15
24
+ -
3
4
3
6
5
8
= + -
12
24
18
24
15
24
5
8
=
-( + )
1
3
3
5
2
15
= -
7
15
3
5
2
15
=
= -
9
15
7
15
【选自教材P100 练习二十五 第1题】
+ -
1
10
3
8
2
5
3
40
=
= -
19
40
16
40
= + -
15
40
4
40
16
40
新知探究
计算下面每组的两个算式,看看它们之间有什么关系?
2
(教科书第98页例2)
+
+
( )
( )
+
+
+
+
算式左右两边加数相同,位置不同。
算式左右两边加数相同,运算的顺序不同。
算一算:
+
+
+
=
+
=
+
=
+
=
它们的和相同。
=
a+b=b+a
整数加法的交换律同样适用于分数的加法混合运算。
算一算:
( )
+
+
( )
+
+
( )
+
+
=( )
+
+
=
+
=
=
( )
+
+
=
+1
=
=
=
整数加法的结合律(a+b)+c= a+(b+c)一样可以用于分数的加法混合运算。
整数加法的交换律、结合律对分数加法同样适用。利用运算定律可以使一些分数计算变得简便。
+
+
+
+
+
加法结合律: (a+b)+c=a+(b+c)
( )
+
+
=
+
=
6
4
=
=
加法结合律:(a+b)+c=a+(b+c)
加法交换律:a+b=b+a
动手算一算吧!
+
+
+
+
+
( )
+
+
=
+
=
6
4
=
=
( )
( )
+
+
=
+
1
( )
+
=
+
1
=
整数加法的交换律、结合律对分数加法同样适用。利用运算定律可以使一些分数计算变得简便。
培优范例
计算:
1
+
+
+
+
异分母相加,你是选择分步通分计算,还是一次通分计算?
+
+
+
以此类推,算式可以写成:
解:
原式=
=
0
0
0
0
0
0
0
=
=
随堂练习
1. 用简便算法计算下面各题。
教材第98页“做一做”第2题
加法交换律
加法交换律和结合律
教材第98页“做一做”第2题
加法交换律和结合律
教材第98页“做一做”第2题
2. 把下面的算式填写完整。
(1)
6
1
2
1
3
6
+
=
+
(2)
7
5
2
3
( )
2
5
7
8
7
7
+
=
+
+
+
(3)
24
3
5
5
( )
5
3
5
24
12
24
24
12
-
=
-
-
○
(4)
11
3
6
7
( )
3
2
( )
11
9
11
9
+
=
+
+
+
+
+
2
3
3
8
6
11
7
9
2
9
+
加法交换律
加法结合律
加法交换律和结合律
连减的性质
3. 怎样简便怎样算。
4
1
这里可用连减的性质a–b–c=a-(b+c)进行简便。
胜利村修一条水渠,第一天修了 千米,第二天修了 千米,还剩 千米。这条水渠共长多少千米?
4.
9
2
9
7
5
2
水渠
9
2
km
5
2
km
9
7
km
?km
5
2
+
9
7
2
9
+
=
9
7
+
5
2
2
9
+
=
5
2
1
(km)
答:这条水渠共长 千米。
5
2
1
运用加法交换律
课堂小结
整数加法的交换律和结合律对分数加法同样适用。利用运算定律可以使一些分数计算变得简便。
谢谢观看
人教版五年级数学下册
