【小升初押题卷】计算面积高频易错冲刺卷(含解析)-2024-2025学年六年级下学期数学苏教版
文档属性
| 名称 | 【小升初押题卷】计算面积高频易错冲刺卷(含解析)-2024-2025学年六年级下学期数学苏教版 |  | |
| 格式 | docx | ||
| 文件大小 | 2.7MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 苏教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-05-07 21:31:57 | ||
图片预览



文档简介
计算面积
1.一块茄子地的形状是三角形,它的底是28米,高是30米,如果每棵茄子占地0.5平方米,那么这块地可以种多少棵茄子?
2.阳光小区有一块梯形空地,物业为增加小区的绿化带区域,决定在这块空地上铺一块平行四边形草坪和一块三角形草坪,两个草坪之间留一条平行四边形的小路(如图)。如果铺草坪每平方米要花2.5元,那么铺这两块草坪一共要花多少元?
3.滨海盐场有40块同样大的长方形盐田,每块盐田长100米,宽50米。这些盐田一共占地多少公顷?
4.在冬天,园林工人采用粗麻绳紧致地环绕树木,用“穿冬衣”的方法给树木御寒。一位工人叔叔给一棵树穿“衣服”时,用了约301.44分米长的麻绳一共捆了16周,这棵树干的横截面面积大约是多少平方分米?(麻绳的粗细忽略不计)
5.公园里有一个周长是94.2米的圆形草坪,准备在正中间安装自动旋转喷水器进行喷艇。
(1)你认为安装射程为多少米的装置最合适?
(2)在草坪周围建一条1米宽的环形石子路,这条小路的面积是多少平方米?
6.一个牡丹园的形状是三角形,它的底是160米,高是100米,种1m2的牡丹幼苗能卖20元,这个牡丹园种满牡丹幼苗可以卖多少元?
7.如图这块长方形绿地的宽增加36米,长不变,扩大后绿地的面积是多少平方米?
8.超市门口的装饰牌是等腰梯形。它的上底是16米,下底是22米,高是3米。用油漆刷这块装饰牌的一面,每平方米需用油漆2.5千克,刷这块装饰牌需要多少千克油漆?
9.如图是一个梯形花园,上底6m,下底16m,较大三角形的面积是72m2。
(1)梯形的高是多少米?
(2)每平方米花园年产值约60元,梯形花园的产值每年约为多少元?
10.有一块周长是62.8米的圆形草坪。
(1)准备在这块草坪的中心位置安装自动旋转喷灌装置,自动旋转喷灌装置的射程分别为5米、10米、20米,选择哪种比较合适?
(2)在这块圆形草坪周围铺一条宽1米的小路,这条小路的面积是多少平方米?
11.一个正方形果园的周长是1200米,这个果园的占地面积是多少平方米?合多少公顷?
12.王大爷在一块长300米、宽100米的长方形地里种棉花,种植棉花的株距是0.3米,行距是0.5米。
(1)这块地能种植多少株棉花?
(2)如果每千克籽棉能卖6.2元,这块棉花地大约能收入多少元?
13.学校有一块长方形试验田。现在将长增加5米或宽增加3米,面积都比原来增加45平方米。原来试验田的面积是多少平方米?(先在图上画一画,再解答)
14.土楼是福建、广东等地区的一种建筑形式,被列入“世界物质文化名录”,其外形有圆形、方形、椭圆形等。一座圆环形土楼外直径为26米,内直径为14米。这座土楼的占地面积是多少平方米?
15.李叔叔家有一个圆木桌。
(1)李叔叔想做一个和桌面大小形状都相同的桌垫,桌垫的面积是多少平方米?
(2)如果给这个桌垫的边缘围一圈花边,花边的长是多少米?
16.同学们,这学期我们进行了多边形面积的“探究之旅”。下面我们再来跟淘气、笑笑、奇思和妙想开启新一轮的“探究之旅”吧!
(1)如图,淘气、笑笑和奇思在研究如何解决平行四边形面积的计算问题时,想到了以下的方法。下面的推导方法中,谁的方法是合理的,请你在他的名字后面括号画“√”。
(2)从上面你认可的推导方法中任选一个,将其推导过程和结论写下来。
(3)妙想用这学期学习的知识,解决了以下的问题:
小区内有一块面积为129.6平方米的平行四边形的草坪,为了优化生态环境,在原来平行四边形草坪旁边,又扩建了一块三角形草坪。如图,平行四边形草坪的高是多少?
(4)请你算一算,扩建后草坪的面积一共有多大?
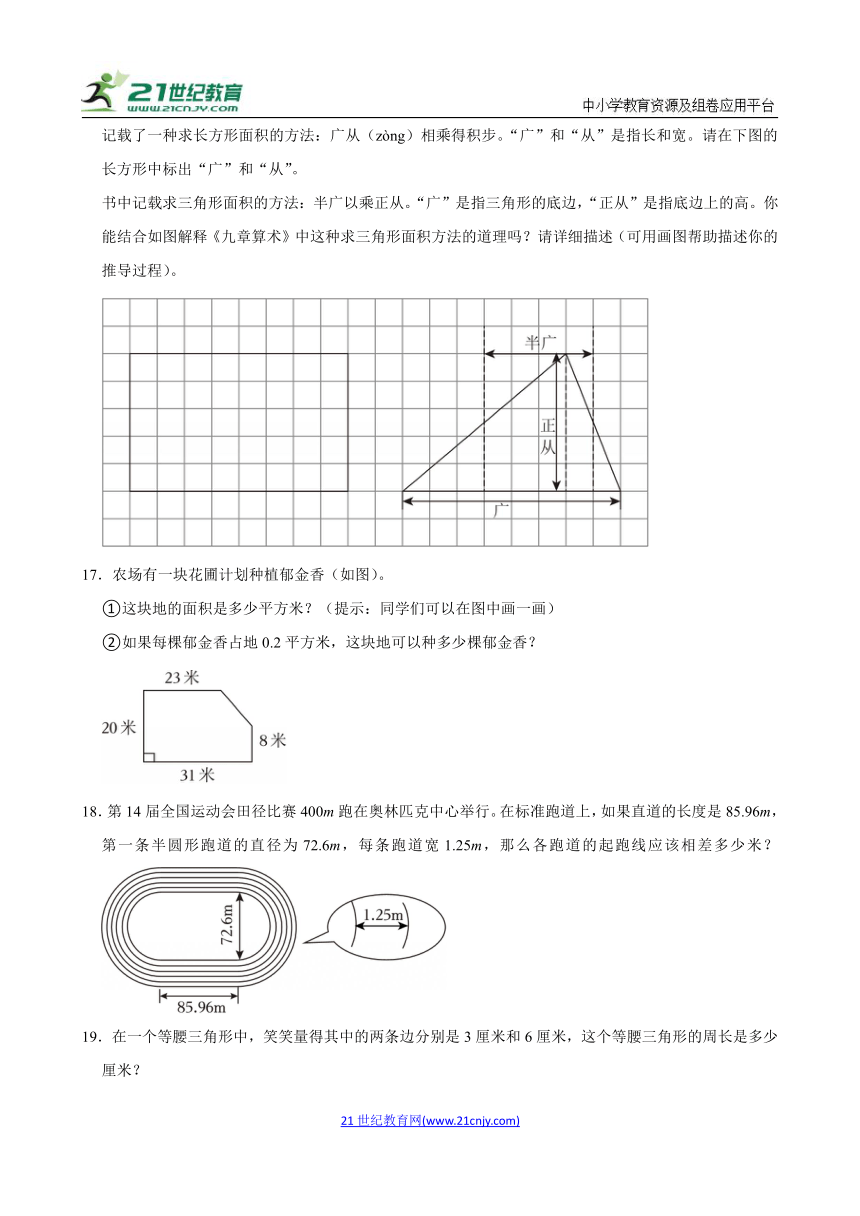
(5)在解决上面问题的过程中,妙想还用到了三角形的面积公式。你知道吗?早在2000多年前,我国数学名著《九章算术》中就记载了一种可以由长方形面积计算方法推导出三角形面积的计算方法。书中记载了一种求长方形面积的方法:广从(zòng)相乘得积步。“广”和“从”是指长和宽。请在下图的长方形中标出“广”和“从”。
书中记载求三角形面积的方法:半广以乘正从。“广”是指三角形的底边,“正从”是指底边上的高。你能结合如图解释《九章算术》中这种求三角形面积方法的道理吗?请详细描述(可用画图帮助描述你的推导过程)。
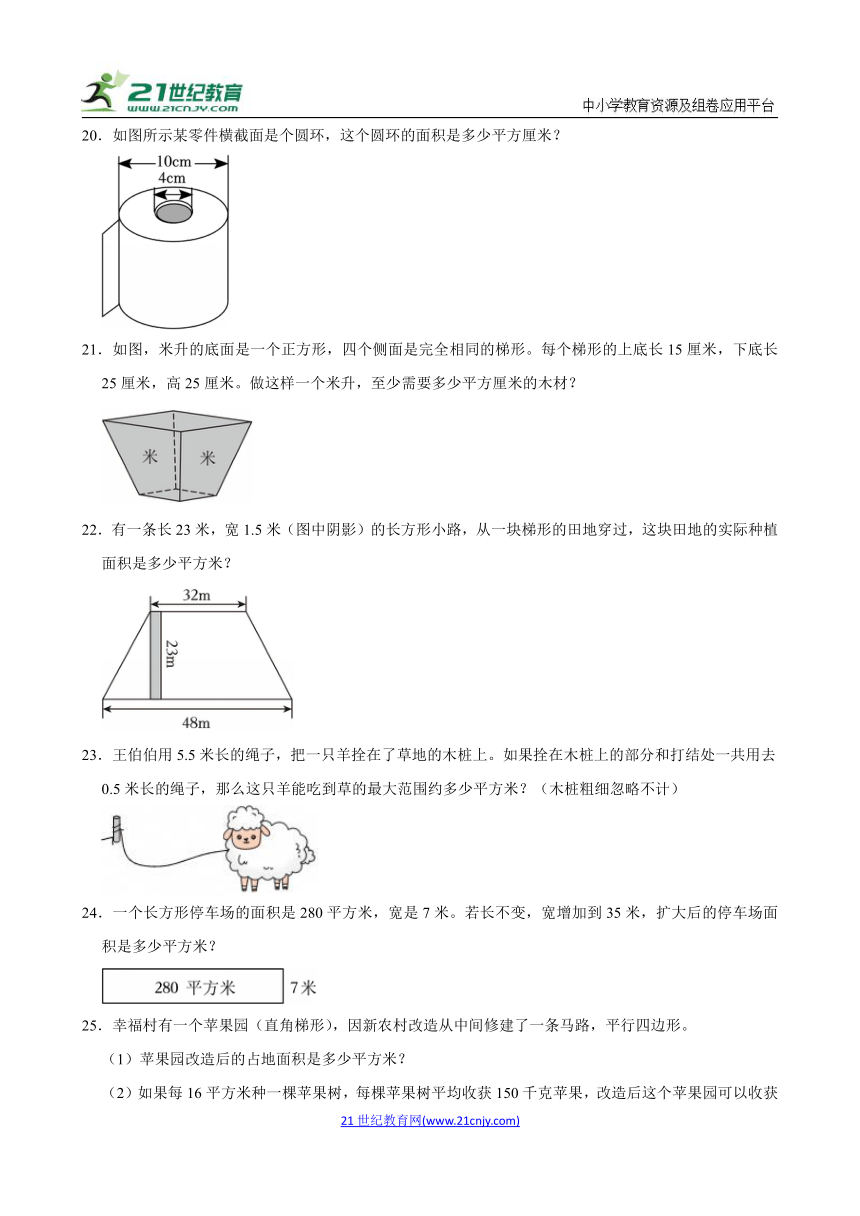
17.农场有一块花圃计划种植郁金香(如图)。
①这块地的面积是多少平方米?(提示:同学们可以在图中画一画)
②如果每棵郁金香占地0.2平方米,这块地可以种多少棵郁金香?
18.第14届全国运动会田径比赛400m跑在奥林匹克中心举行。在标准跑道上,如果直道的长度是85.96m,第一条半圆形跑道的直径为72.6m,每条跑道宽1.25m,那么各跑道的起跑线应该相差多少米?
19.在一个等腰三角形中,笑笑量得其中的两条边分别是3厘米和6厘米,这个等腰三角形的周长是多少厘米?
20.如图所示某零件横截面是个圆环,这个圆环的面积是多少平方厘米?
21.如图,米升的底面是一个正方形,四个侧面是完全相同的梯形。每个梯形的上底长15厘米,下底长25厘米,高25厘米。做这样一个米升,至少需要多少平方厘米的木材?
22.有一条长23米,宽1.5米(图中阴影)的长方形小路,从一块梯形的田地穿过,这块田地的实际种植面积是多少平方米?
23.王伯伯用5.5米长的绳子,把一只羊拴在了草地的木桩上。如果拴在木桩上的部分和打结处一共用去0.5米长的绳子,那么这只羊能吃到草的最大范围约多少平方米?(木桩粗细忽略不计)
24.一个长方形停车场的面积是280平方米,宽是7米。若长不变,宽增加到35米,扩大后的停车场面积是多少平方米?
25.幸福村有一个苹果园(直角梯形),因新农村改造从中间修建了一条马路,平行四边形。
(1)苹果园改造后的占地面积是多少平方米?
(2)如果每16平方米种一棵苹果树,每棵苹果树平均收获150千克苹果,改造后这个苹果园可以收获苹果多少吨?
26.小林周末去市杂技团看演出,最让人感到惊险刺激的节目是骑独轮车走钢丝,主持人介绍说:“独轮车的车轮半径约为15cm,体重达到80kg的表演人员要骑着独轮车经过一根离地面高3米,长度为18.84米,且绷得笔直的钢丝绳。”小林一边仰头观看一边想,怎样计算出,走完钢丝车轮要转动多少圈呢?同学们,你们能帮小林算一算吗?(π≈3.14)
27.有一条宽4米的长方形人行道,占地面积是360平方米。为了行走方便,道路的宽增加到12米,长不变,扩宽后的人行道的面积是多少平方米?
28.王爷爷有一块面积为72平方米的长方形菜园,里面种了黄瓜和番茄(如图)。其中黄瓜地的面积比番茄地多16平方米。番茄地有多少平方米?
29.如图,在房屋的一面墙上,用42.5米长的篱笆围成一块梯形麦田(靠墙这一面不用围篱笆)。
(1)这块麦田的面积是多少平方米?
(2)如果一平方米麦田能生产小麦大约0.2吨,那这块麦田的总产量约是多少吨?
30.育才小学有一个长方形草坪。如果草坪的长增加5米,面积就增加75平方米。如果草坪的宽增加5米,面积就增加125平方米。原来草坪的面积是多少平方米?(先在图中画一画,再解答)
31.学校有一个三角形的花坛,底边为12米,高为4.5米。要把这个花坛栽满鲜花,施工公司报价每平方米80元。给这个花坛栽满鲜花一共要多少元?
32.如图是张老师新房的平面图。如果客厅、厨房和卫生间铺地板的费用,按平均每平方米150元计算,共需要多少元?
33.一柄遮阳大伞完全打开后,从上往下看伞面尺寸和形状如图所示(单位:米)。这个伞面的面积是多少平方米?
34.一个平行四边形的街头广告牌,底是13.5米,高是6米,如果要油饰这块广告牌(只油饰正面),每平方米用油漆0.62千克,需要多少千克油漆?
35.如图1,ABCD、CEFG是两个正方形,边长分别为5厘米和4厘米,将GC边擦去,留下一个轮廓,然后连结AE、BF相交于点H,连结BG与AE相交于点I,则图2中阴影部分的面积是多少平方厘米?
36.如图所示,一块长方形绿地,面积为360平方米,现在要扩大,如果长不变,宽增加到32米,扩大后的绿地面积是多少平方米?
37.从一张纸上剪下8个相同大小的等腰直角三角形,组成装饰图案(如图)。这个图案的面积是多少平方厘米?
38.为了确保游客在游览时的安全,避免发生踩踏事故,室外景点每人所占用的活动面积必须大于或等于0.75平方米。在一个旅游景区依墙搭建了一个直径是20米的半圆形室外观看区。为了保证安全,这个观看区最多能同时容纳多少人?
39.位于湖南省东北部的张谷英村,因其错落相连的房屋建构,使人在村中行走能做到晴不曝日、雨不湿鞋,有“天下第一村”的美誉。无人机拍摄发现村中一户房顶因无人居住出现了大面积损坏,旅游局打算重新铺瓦。检修部分的房顶形状如图,通常一平方米需要铺设140块小青瓦片,重铺这块房顶需要准备多少块小青瓦片?
40.小明家要买一张吃饭用的圆桌,要求最多能坐8人。如果每人在圆周上大约站位60cm,小明家需要买直径多大的圆桌?(本题π取近似值3)
41.张大伯有一块3.6公顷的土地,要在这块地里栽种核桃,种植的行距为4米,株距为4.5米。这块地可栽多少棵核桃树?
42.张爷爷靠墙围了一个平行四边形的菜园(如图),围菜园的篱笆长23米。这个菜园的面积是多少平方米?
43.根据相关研究,室内景点人均活动面积低于1m2室外景点人均活动面积低于0.75m2时,就有发生踩踏事故的危险。在某古镇景点戏台前,有一个上底是32m、下底是48m、高是30m的梯形室外场地,为保证安全,这个场地最多能容纳多少人同时看戏?
44.采摘园原来有一块宽是26米的长方形菜地(如图),现在正在扩建。如果长不变,宽增加8米,扩建后面积增加680平方米。这块菜地原来的面积有多大?
(1)画一画,在右图画出扩建的区域,并标数据。
(2)算一算,这块菜地原来的面积有多大?
45.一个圆的周长是12.56米,半径增加2米后,圆的面积是多少平方米?
46.公园里的圆形花坛周长是37.68米,现在要在花坛周围铺一条宽1米的石板路,如果每平方米要投资50元,铺这条石板路要投资多少元?
47.一块三角形广告牌,底5米,高是1.8米。将这块广告牌的正反两面都刷上油漆,如果每平方米需要刷漆450克,准备4千克油漆够不够?(请用计算说明)
48.淘气爷爷一面靠墙围了一个养鸡圈(如图)。
(1)如果要给它围上一圈篱笆,篱笆至少长多少米?
(2)这养鸡圈的占地面积有多大?
49.一块铁皮的形状如图。请你算算这块铁皮的面积是多少?(单位:dm)
50.叔叔家果园的形状为梯形,它的上底22米,下底38米,高24米。叔叔计划在果园里栽果树,若每棵果树占地约6平方米,可以栽多少棵果树?
51.为保障市民安全合理观看比赛,组委会在跑道两侧设置观看区域。某一跑道旁有一块直角梯形的观看区域,面积是34.8平方米。组委会在观看区域的三面围上护栏(如图),只测得梯形的高为3.2米,请你算出护栏的总长是多少米?
52.哈尔滨亚冬会期间冰雪大世界有一块室外游乐场地(如图),相关研究表明:室外景点低于0.75平方米/人时,就有发生踩踏事故的危险。要避免踩踏事故的出现这块场地最多能容纳多少人同时活动?
53.盛安小学原有一个长方形花坛,后来因修路的需要,长减少了5米,这个花圃的面积减少了100平方米。减少后的花坛正好是一个正方形,原来长方形花圃的面积是多少平方米?(先在图中画出减少部分,再解答)
54.如图的平行四边形底是6厘米,高是4.5厘米,请你画一条线将它分成两个大小形状完全相同的梯形,并算出其中一个梯形的面积。
55.一扇老式木门,最上面有个梯形的透光窗,窗架的上底是5分米,下底9分米,高4分米。如果要为这个窗架配一块玻璃,这块玻璃的面积至少有多大?(忽略玻璃与窗架镶嵌处的面积)
56.李明经常在自家小区圆形的游泳池边散步。这天,他以每分钟62.8m的速度绕泳池走了一圈,恰好用了5分钟。这个泳池的面积是多少平方米?
57.旧城改造,准备修建一个花坛,形状如图,它的边是4个直径相等的半圆。这个花坛的面积是多少平方米?
58.大约在两千年前,我国数学名著《九章算术》中的“方田章”就论述了平面图形面积的算法。书中说:“圭田术曰,半广以乘正从。”其中“圭田”就是指三角形田地,“广”和“从”是指三角形的底和高,已知三角形的面积是35.2平方米,底是4.4米,它的高是多少米?
59.用一根长15dm的铁丝围成一个等腰梯形。已知这个梯形的两腰共长8.6dm,高是3dm,这个梯形的面积是多少dm2?
60.中国少年先锋队是中国少年儿童的群团组织,是少年儿童学习中国特色社会主义和共产主义的学校,是建设社会主义和共产主义的预备队,我们每一个班级中队就是中国少先队的一个小集体。兴华小学要做12面中队旗,共需要多少平方米布?
计算面积
参考答案与试题解析
1.一块茄子地的形状是三角形,它的底是28米,高是30米,如果每棵茄子占地0.5平方米,那么这块地可以种多少棵茄子?
【答案】840棵。
【分析】三角形的面积=底×高÷2,据此代入数据计算,求出这块地的面积,再除以每棵茄子占地面积,即可求出茄子棵数。
【解答】解:28×30÷2÷0.5
=840÷2÷0.5
=420÷0.5
=840(棵)
答:这块地可以种840棵茄子。
【点评】此题考查三角形面积的计算及应用。
2.阳光小区有一块梯形空地,物业为增加小区的绿化带区域,决定在这块空地上铺一块平行四边形草坪和一块三角形草坪,两个草坪之间留一条平行四边形的小路(如图)。如果铺草坪每平方米要花2.5元,那么铺这两块草坪一共要花多少元?
【答案】120元。
【分析】一个平行四边形的面积加上一个三角形的面积即可,单价乘面积即可总钱数。
【解答】解:4×6+8×6÷2
=24+24
=48(平方米)
48×2.5=120(元)
答:这两块草坪一共要花120元。
【点评】本题主要考查组合图形的面积,关键利用规则平面图形的面积公式计算。
3.滨海盐场有40块同样大的长方形盐田,每块盐田长100米,宽50米。这些盐田一共占地多少公顷?
【答案】20公顷。
【分析】根据长方形的面积=长×宽,把数据代入公式求出一块盐田的面积,然后再乘盐田的块数即可。
【解答】解:100×50×40
=5000×40
=200000(平方米)
200000平方米=20公顷
答:这些盐田一共占地20公顷。
【点评】此题主要考查长方形面积公式的灵活运用,关键是熟记公式。
4.在冬天,园林工人采用粗麻绳紧致地环绕树木,用“穿冬衣”的方法给树木御寒。一位工人叔叔给一棵树穿“衣服”时,用了约301.44分米长的麻绳一共捆了16周,这棵树干的横截面面积大约是多少平方分米?(麻绳的粗细忽略不计)
【答案】28.26平方分米。
【分析】先用301.44÷16计算出绕树的树干1圈的长度(即树干的周长),然后根据“圆的半径=圆的周长÷π÷2”求出圆的半径,进而利用圆的面积公式解答即可。
【解答】解:301.44÷16=18.84(分米)
18.84÷3.14÷2=3(分米)
3.14×32
=3.14×9
=28.26(平方分米)
答:这棵树干的横截面面积大约是28.26平方分米。
【点评】解答此题的关键是先计算出树的树干1圈的长度,继而根据圆的周长和面积公式进行解答。
5.公园里有一个周长是94.2米的圆形草坪,准备在正中间安装自动旋转喷水器进行喷艇。
(1)你认为安装射程为多少米的装置最合适?
(2)在草坪周围建一条1米宽的环形石子路,这条小路的面积是多少平方米?
【答案】(1)15米;(2)97.34平方米。
【分析】(1)根据“圆周长=2πr”求出圆半径,即为所求;
(2)根据圆环的面积等于大圆的面积减去小圆的面积即可求解。
【解答】解:(1)94.2÷3.14÷2=15(米)
答:安装射程为15米的装置最合适。
(2)3.14×[(15+1)2﹣152]
=3.14×31
=97.34(平方米)
答:这条小路的面积是97.34平方米。
【点评】本题考查了圆周长和圆环面积计算的应用。
6.一个牡丹园的形状是三角形,它的底是160米,高是100米,种1m2的牡丹幼苗能卖20元,这个牡丹园种满牡丹幼苗可以卖多少元?
【答案】16000元。
【分析】根据三角形面积=底×高÷2,求出三角形面积,再乘20,即可解答。
【解答】解:160×100÷2×20
=16000÷2×20
=8000×20
=16000(元)
答:这个牡丹园种满牡丹幼苗可以卖16000元。
【点评】本题考查的是三角形面积的计算,熟记公式是解答关键。
7.如图这块长方形绿地的宽增加36米,长不变,扩大后绿地的面积是多少平方米?
【答案】2880平方米。
【分析】长方形的长=长方形面积÷宽,据此用720÷12计算出长,宽增加36米,用12+36计算出扩大后长方形绿地的宽,再根据长方形面积=长×宽解题即可。
【解答】解:720÷12×(12+36)
=60×48
=2880(平方米)
答:扩大后绿地的面积是2880平方米。
【点评】此题主要考查长方形面积公式的灵活运用,关键是熟记公式。
8.超市门口的装饰牌是等腰梯形。它的上底是16米,下底是22米,高是3米。用油漆刷这块装饰牌的一面,每平方米需用油漆2.5千克,刷这块装饰牌需要多少千克油漆?
【答案】142.5千克。
【分析】梯形的面积公式:S=(a+b)h÷2,已知上底是16米,下底是22米,高是3米,据此可求出梯形的面积,再乘0.5就是需要油漆的重量,据此解答。
【解答】解:(16+22)×3÷2
=38×3÷2
=57(平方米)
57×2.5=142.5(千克)
答:一共需要142.5千克油漆。
【点评】本题主要考查了学生对梯形面积公式的实际运用。
9.如图是一个梯形花园,上底6m,下底16m,较大三角形的面积是72m2。
(1)梯形的高是多少米?
(2)每平方米花园年产值约60元,梯形花园的产值每年约为多少元?
【答案】(1)9米;(2)5940元。
【分析】(1)用72乘2除以16求出梯形的高;
(2)用梯形的面积乘60就是梯形花园的产值每年约为多少元。
【解答】解:(1)72×2÷16
=144÷16
=9(米)
答:梯形的高是90米。
(2)(16+6)×9÷2×60
=22×9÷2×60
=198÷2×60
=99×60
=5940(元)
答:梯形花园的产值每年约为5940元。
【点评】解答此题要运用三角形和梯形的面积公式。
10.有一块周长是62.8米的圆形草坪。
(1)准备在这块草坪的中心位置安装自动旋转喷灌装置,自动旋转喷灌装置的射程分别为5米、10米、20米,选择哪种比较合适?
(2)在这块圆形草坪周围铺一条宽1米的小路,这条小路的面积是多少平方米?
【答案】(1)10米;
(2)65.94平方米。
【分析】(1)根据圆的周长C=2πr,r=C÷2π,代入数据计算后,即可选择哪种射程的合适。
(2)圆环的面积等于大圆的面积减去小圆的面积即可。
【解答】解:(1)62.8÷(2×3.14)
=62.8÷6.28
=10(米)
答:自动旋转喷灌装置的射程为10米比较合适。
(2)3.14×[(10+1)2﹣102]
=3.14×[121﹣100]
=3.14×21
=65.94(平方米)
答:这条小路的面积是65.94平方米。
【点评】本题考查了圆的周长公式和圆环的面积计算。
11.一个正方形果园的周长是1200米,这个果园的占地面积是多少平方米?合多少公顷?
【答案】见试题解答内容
【分析】已知正方形的周长是800米,根据正方形的周长公式:C=4a知:a=C÷4可求正方形的边长,再根据正方形的面积公式:S=a2可求出果园的面积是多少平方米,再化成公顷即可.
【解答】解:1200÷4=300(米)
300×300=90000(平方米)=9(公顷)
答:这个果园的占地面积是90000平方米,合9公顷.
【点评】本题主要考查了学生对正方形面积和周长公式的应用.
12.王大爷在一块长300米、宽100米的长方形地里种棉花,种植棉花的株距是0.3米,行距是0.5米。
(1)这块地能种植多少株棉花?
(2)如果每千克籽棉能卖6.2元,这块棉花地大约能收入多少元?
【答案】(1)200000株;
(2)992000元。
【分析】(1)根据长方形的面积=长×宽,把数据代入公式分别求出这块地的面积、每株棉花的占地面积,然后根据“包含”除法的意义,用除法解答。
(2)根据总产量=单产量×数量,求出这块地一共收籽棉多少千克,再根据总价=单价×数量,列式解答即可。
【解答】解:(300×100)÷(0.5×0.3)
=30000÷0.15
=200000(株)
答:这块地能种植200000株棉花。
(2)0.08×200000×6.2
=16000×6.2
=99200(元)
答:这块棉花地大约能收入99200元。
【点评】此题主要考查长方形面积公式的灵活运用,以及单产量、数量、总产量三者之间的关系及应用、单价、数量、总价三者之间的关系及应用。
13.学校有一块长方形试验田。现在将长增加5米或宽增加3米,面积都比原来增加45平方米。原来试验田的面积是多少平方米?(先在图上画一画,再解答)
【答案】135平方米。
【分析】根据长方形的面积公式:S=ab,那么a=S÷b,b=S÷a,据此求出原来的长、宽,然后把数据代入公式求出原来的面积。
【解答】解:如图:
(45÷3)×(45÷5)
=15×9
=135(平方米)
答:原来试验田的面积是135平方米。
【点评】此题主要考查长方形面积公式的灵活运用关键是熟记公式。
14.土楼是福建、广东等地区的一种建筑形式,被列入“世界物质文化名录”,其外形有圆形、方形、椭圆形等。一座圆环形土楼外直径为26米,内直径为14米。这座土楼的占地面积是多少平方米?
【答案】见试题解答内容
【分析】根据环形面积公式:S=π(R2﹣r2),把数据代入公式解答。
【解答】解:3.14×[(26÷2)2﹣(14÷2)2]
=3.14×[169﹣49]
=3.14×120
=376.8(平方米)
答:这座土楼的占地面积是376.8平方米。
【点评】此题主要考查环形面积公式的灵活运用,关键是熟记公式。
15.李叔叔家有一个圆木桌。
(1)李叔叔想做一个和桌面大小形状都相同的桌垫,桌垫的面积是多少平方米?
(2)如果给这个桌垫的边缘围一圈花边,花边的长是多少米?
【答案】(1)0.785平方米;(2)3.14米。
【分析】(1)桌垫的面积就是直径是1米的圆形面积,根据圆形面积S=πr2,把数据代入公式解答即可;
(2)花边的长是直径是1米的圆形周长,根据圆形周长C=πd,把数据代入公式解答即可。
【解答】解:(1)3.14×(1÷2)2
=3.14×0.52
=3.14×0.25
=0.785(平方米)
答:桌垫的面积是0.785平方米。
(2)3.14×1=3.14(米)
答:花边的长是3.14米。
【点评】本题考查的是圆形周长和圆形面积计算公式的运用。
16.同学们,这学期我们进行了多边形面积的“探究之旅”。下面我们再来跟淘气、笑笑、奇思和妙想开启新一轮的“探究之旅”吧!
(1)如图,淘气、笑笑和奇思在研究如何解决平行四边形面积的计算问题时,想到了以下的方法。下面的推导方法中,谁的方法是合理的,请你在他的名字后面括号画“√”。
(2)从上面你认可的推导方法中任选一个,将其推导过程和结论写下来。
(3)妙想用这学期学习的知识,解决了以下的问题:
小区内有一块面积为129.6平方米的平行四边形的草坪,为了优化生态环境,在原来平行四边形草坪旁边,又扩建了一块三角形草坪。如图,平行四边形草坪的高是多少?
(4)请你算一算,扩建后草坪的面积一共有多大?
(5)在解决上面问题的过程中,妙想还用到了三角形的面积公式。你知道吗?早在2000多年前,我国数学名著《九章算术》中就记载了一种可以由长方形面积计算方法推导出三角形面积的计算方法。书中记载了一种求长方形面积的方法:广从(zòng)相乘得积步。“广”和“从”是指长和宽。请在下图的长方形中标出“广”和“从”。
书中记载求三角形面积的方法:半广以乘正从。“广”是指三角形的底边,“正从”是指底边上的高。你能结合如图解释《九章算术》中这种求三角形面积方法的道理吗?请详细描述(可用画图帮助描述你的推导过程)。
【答案】(1);
(2)选淘气的方法:把直角三角形剪下,并补到另一边,组成的图形是长方形,这个长方形的长是a,宽是h,利用长方形的面积公式可知,平行四边形的面积=ah。(答案不唯一)
(3)7.2米;
(4)151.2平方米;
(5),红色三角形向上翻折为绿色三角形,紫色三角形向上翻折为蓝色三角形,所以三角形的面积=半广×正从=广×从÷2。(答案不唯一)
【分析】(1)依据题意结合图示可知,笑笑和淘气通过图形的切割来计算平行四边形的面积,奇思的方法中长方形和平行四边形的周长相等,但是面积不同;
(2)选择淘气的方法去解答;(答案不唯一)
(3)利用平行四边形的面积=底×高,结合题中数据计算即可;
(4)利用三角形的面积公式计算三角形草坪的面积,然后计算扩建后草坪的面积;
(5)依据题意结合图示可知,把三角形进行切割,然后利用长方形的面积公式计算三角形的面积。(答案不唯一)
【解答】解:(1)如图:
(2)选淘气的方法:把直角三角形剪下,并补到另一边,组成的图形是长方形,这个长方形的长是a,宽是h,利用长方形的面积公式可知,平行四边形的面积=ah。(答案不唯一)
(3)129.6÷18=7.2(米)
答:平行四边形草坪的高是7.2米。
(4)6×7.2÷2+129.6
=21.6+129.6
=151.2(平方米)
答:扩建后草坪的面积一共151.2平方米。
(5)如图:
红色三角形向上翻折为绿色三角形,紫色三角形向上翻折为蓝色三角形,所以三角形的面积=半广×正从=广×从÷2。(答案不唯一)
【点评】本题考查的是长方形、三角形、平行四边形的面积的应用。
17.农场有一块花圃计划种植郁金香(如图)。
①这块地的面积是多少平方米?(提示:同学们可以在图中画一画)
②如果每棵郁金香占地0.2平方米,这块地可以种多少棵郁金香?
【答案】见试题解答内容
【分析】①把这块地分成左面一个长方形、右面一个梯形,利用长方形面积公式:S=ab,梯形面积公式:S=(a+b)h÷2计算即可。
②用这块地的面积除以每棵郁金香的占地面积,计算种的棵数即可。
【解答】解:①23×20+(8+20)×(31﹣23)÷2
=460+112
=572(平方米)
答:这块地的面积是572平方米。
②572÷0.2=2860(棵)
答:这块地可以种2860棵。
【点评】本题主要考查组合图形的面积的计算,关键是应用长方形和梯形面积公式。
18.第14届全国运动会田径比赛400m跑在奥林匹克中心举行。在标准跑道上,如果直道的长度是85.96m,第一条半圆形跑道的直径为72.6m,每条跑道宽1.25m,那么各跑道的起跑线应该相差多少米?
【答案】7.85米。
【分析】根据题意可知,相邻两个跑道的差也就是两端弯道的差,第一条半圆形跑道的直径为72.6米,那么第二跑道的直径是(72.6+1.25×2)米,根据圆的周长公式:C=πd,把数据代入公式求出外圆周长与内圆周长的差即可。
【解答】解:3.14×(72.6+1.25×2)﹣3.14×72.6
=3.14×(72.6+2.5)﹣227.964
=3.14×75.1﹣227.964
=235.814﹣227.964
=7.85(米)
答:各跑道的起跑线应该相差7.85米。
【点评】此题主要考查圆的周长公式的灵活运用,关键是熟记公式,重点是明确:外跑道和内跑道的差,也就是弯道的差。
19.在一个等腰三角形中,笑笑量得其中的两条边分别是3厘米和6厘米,这个等腰三角形的周长是多少厘米?
【答案】15厘米。
【分析】根据三角形的特性:两边之和大于第三边,三角形的两边的差一定小于第三边;判断出该三角形的腰为6厘米,进而根据三角形的周长计算方法解答即可。
【解答】解:6+6+3
=12+3
=15(厘米)
答:这个等腰三角形的周长是15厘米。
【点评】此题主要考查了三角形的特性和三角形周长的计算方法。
20.如图所示某零件横截面是个圆环,这个圆环的面积是多少平方厘米?
【答案】65.94平方厘米。
【分析】因为光盘是圆环,知道了内圆和外圆直径,求出半径,代入圆环面积公式S环=π(R2﹣r2)计算即可。
【解答】解:3.14×[(10÷2)2﹣(4÷2)2]
=3.14×(25﹣4)
=3.14×21
=65.94(平方厘米)
答:圆环面积是65.94平方厘米。
【点评】此题是考查圆环的面积计算,可利用其公式S环=π(R2﹣r2)计算即可。
21.如图,米升的底面是一个正方形,四个侧面是完全相同的梯形。每个梯形的上底长15厘米,下底长25厘米,高25厘米。做这样一个米升,至少需要多少平方厘米的木材?
【答案】4225平方厘米。
【分析】依据题意可知,木材的面积等于4个侧面梯形的面积加上底面正方形的面积,利用梯形的面积=(上底+下底)×高÷2,正方形的面积=边长×边长,结合题中数据计算即可。
【解答】解:(15+25)×25×4+15×15
=4000+225
=4225(平方厘米)
答:至少需要4225平方厘米的木材。
【点评】本题考查的是梯形的面积公式的应用。
22.有一条长23米,宽1.5米(图中阴影)的长方形小路,从一块梯形的田地穿过,这块田地的实际种植面积是多少平方米?
【答案】885.5平方米。
【分析】这块田地的实际种植面积等于梯形面积减去阴影小长方形面积,据此计算。
【解答】解:(32+48)×23÷2﹣23×1.5
=920﹣34.5
=885.5(m2)
答:这块田地的实际种植面积是885.5平方米。
【点评】本题考查了梯形面积和长方形面积计算的应用。
23.王伯伯用5.5米长的绳子,把一只羊拴在了草地的木桩上。如果拴在木桩上的部分和打结处一共用去0.5米长的绳子,那么这只羊能吃到草的最大范围约多少平方米?(木桩粗细忽略不计)
【答案】78.5平方米。
【分析】根据题意可知,这只羊能吃到草的最大面积为半径是(5.5﹣0.5)米的圆的面积,根据圆的面积公式:S=πr2,把数据代入公式解答。
【解答】解:5.5﹣0.5=5(米)
3.14×52
=3.14×25
=78.5(平方米)
答:这只羊能吃到草的最大范围约78.5平方米。
【点评】此题主要考查圆的面积公式的灵活运用,关键是熟记公式。
24.一个长方形停车场的面积是280平方米,宽是7米。若长不变,宽增加到35米,扩大后的停车场面积是多少平方米?
【答案】1400平方米。
【分析】根据长方形的面积=长×宽,再根据因数与积的变化规律,先求出扩大后的宽是原来宽的几倍,进而求出扩大后的面积。
【解答】解:280×(35÷7)
=280×5
=1400(平方米)
答:扩大后的停车场面积是400平方米。
【点评】此题主要考查长方形面积公式的灵活运用,因数与积的变化规律及应用。
25.幸福村有一个苹果园(直角梯形),因新农村改造从中间修建了一条马路,平行四边形。
(1)苹果园改造后的占地面积是多少平方米?
(2)如果每16平方米种一棵苹果树,每棵苹果树平均收获150千克苹果,改造后这个苹果园可以收获苹果多少吨?
【答案】(1)4800平方米;
(2)45吨。
【分析】(1)用梯形面积减去平行四边形的面积计算改造后的面积即可;
(2)用改造后的面积除以16,计算种苹果树的棵数,再乘150,再换算单位即可。
【解答】解:(1)(80+120)×60÷2﹣20×60
=6000﹣1200
=4800(平方米)
答:苹果园改造后的占地面积是4800平方米。
(2)4800÷16×150
=300×150
=45000(千克)
45000千克=45吨
答:改造后这个苹果园可以收获苹果45吨。
【点评】本题主要考查组合图形的面积的计算,关键是利用规则图形的面积公式计算。
26.小林周末去市杂技团看演出,最让人感到惊险刺激的节目是骑独轮车走钢丝,主持人介绍说:“独轮车的车轮半径约为15cm,体重达到80kg的表演人员要骑着独轮车经过一根离地面高3米,长度为18.84米,且绷得笔直的钢丝绳。”小林一边仰头观看一边想,怎样计算出,走完钢丝车轮要转动多少圈呢?同学们,你们能帮小林算一算吗?(π≈3.14)
【答案】20圈。
【分析】绳长除以车轮周长即可解答。
【解答】解:(18.84×100)÷(2×3.14×15)
=1884÷94.2
=20(圈)
答:走完钢丝车轮要转动20圈。
【点评】本题考查了圆周长计算的应用。
27.有一条宽4米的长方形人行道,占地面积是360平方米。为了行走方便,道路的宽增加到12米,长不变,扩宽后的人行道的面积是多少平方米?
【答案】1080平方米。
【分析】首先用360除以4求出长方形人行道原来的长是多少米,再用长乘扩建后的宽12米就是扩宽后的人行道的面积。
【解答】解:360÷4×12
=90×12
=1080(平方米)
答:扩宽后的人行道的面积是1080平方米。
【点评】解答此题要运用长方形的面积公式。
28.王爷爷有一块面积为72平方米的长方形菜园,里面种了黄瓜和番茄(如图)。其中黄瓜地的面积比番茄地多16平方米。番茄地有多少平方米?
【答案】28平方米。
【分析】根据题意,用72减去16求出两块番茄地的面积,再除以2即可。
【解答】解:(72﹣16)÷2
=56÷2
=28(平方米)
答:番茄地有28平方米。
【点评】此题考查的是长方形的面积公式。
29.如图,在房屋的一面墙上,用42.5米长的篱笆围成一块梯形麦田(靠墙这一面不用围篱笆)。
(1)这块麦田的面积是多少平方米?
(2)如果一平方米麦田能生产小麦大约0.2吨,那这块麦田的总产量约是多少吨?
【答案】(1)105平方米;(2)21吨。
【分析】(1)用42.5减去7.5,求出梯形上底和下底的和,再根据梯形面积=(上底+下底)×高÷2,即可解答;
(2)用梯形面积乘0.2,即可解答。
【解答】解:(1)(42.5﹣7.5)×6÷2
=210÷2
=105(平方米)
答:这块麦田的面积是105平方米。
(2)0.2×105=21(吨)
答:这块麦田的总产量约是21吨。
【点评】本题考查的是梯形面积的计算,熟记公式是解答关键。
30.育才小学有一个长方形草坪。如果草坪的长增加5米,面积就增加75平方米。如果草坪的宽增加5米,面积就增加125平方米。原来草坪的面积是多少平方米?(先在图中画一画,再解答)
【答案】;375平方米。
【分析】根据长方形的面积公式:S=ab,用增加的面积除以增加的宽,求出原来的长;用增加的面积除以增加的长,求出原来的宽,然后把数据代入公式解答。
【解答】解:
(75÷5)×(125÷5)
=15×25
=375(平方米)
答:原来草坪的面积是375平方米。
【点评】此题主要考查长方形面积公式的灵活运用,关键是熟记公式。
31.学校有一个三角形的花坛,底边为12米,高为4.5米。要把这个花坛栽满鲜花,施工公司报价每平方米80元。给这个花坛栽满鲜花一共要多少元?
【答案】2160元。
【分析】三角形面积=底×高÷2,结合题意求出花坛面积,然后乘80解答即可。
【解答】解:12×4.5÷2×80
=27×80
=2160(元)
答:给这个花坛栽满鲜花一共要2160元。
【点评】本题考查了三角形面积公式的灵活运用,结合题意分析解答即可。
32.如图是张老师新房的平面图。如果客厅、厨房和卫生间铺地板的费用,按平均每平方米150元计算,共需要多少元?
【答案】5700元。
【分析】客厅、厨房和卫生间地面是长(5.2+4.8)米、宽3.8米的长方形,利用长方形面积公式:S=ab计算客厅、厨房和卫生间地面的面积,再乘150即可计算所需钱数。
【解答】解:(5.2+4.8)×3.8×150
=38×150
=5700(元)
答:共需要5700元。
【点评】本题主要考查组合图形的面积,关键是利用规则图形的面积公式计算。
33.一柄遮阳大伞完全打开后,从上往下看伞面尺寸和形状如图所示(单位:米)。这个伞面的面积是多少平方米?
【答案】2.4平方米。
【分析】根据图示,这个伞面的面积等于8个三角形的面积之和,每个三角形的底是0.6米,高是1米,结合三角形的面积=底×高÷2,解答即可。
【解答】解:0.6×1÷2×8
=0.3×8
=2.4(平方米)
答:这个伞面的面积是2.4平方米。
【点评】本题考查了组合图形面积计算知识,结合三角形的面积公式解答即可。
34.一个平行四边形的街头广告牌,底是13.5米,高是6米,如果要油饰这块广告牌(只油饰正面),每平方米用油漆0.62千克,需要多少千克油漆?
【答案】50.22千克。
【分析】广告牌的底和高已知,利用平行四边形的面积公式即可求得其面积;每平方米的用漆量已知,乘广告牌的总面积,就能求得总的用漆量。
【解答】解:13.5×6×0.62
=81×0.62
=50.22(千克)
答:需要50.22千克油漆。
【点评】解答此题的关键是先求出广告牌的面积,进而求得总的用漆量。
35.如图1,ABCD、CEFG是两个正方形,边长分别为5厘米和4厘米,将GC边擦去,留下一个轮廓,然后连结AE、BF相交于点H,连结BG与AE相交于点I,则图2中阴影部分的面积是多少平方厘米?
【答案】cm2。
【分析】连接CH,AG,如图:,观察沙漏模型AEFB,有AH:HE=AB:EF=5:4,由于BC:CE=5:4=AH:HE,所以HC∥AB,即H在CD上,由于HC∥AB,所以HC:AB=EC:EB=4:9,计算HC,GH,梯形AGHB的面积,又GH:AB:5=16:45,由蝴蝶模型,可知S△GHI:SAGHB=162:(16+45)2=162:612,由此计算阴影部分的面积。
【解答】解:连接CH,AG,如图:观察沙漏模型AEFB,AH:HE=AB:EF=5:4,由于BC:CE=5:4=AH:HE,所以HC∥AB,即H在CD上。
由于HC∥AB,所以HC:AB=EC:EB=4:9,则HC(cm),所以GH=4(cm)。
SAGHB(5)×5(cm2),又GH:AB:5=16:45,由蝴蝶模型,可知S△GHI:SAGHB=162:(16+45)2=162:612=256:3721;
S△GHISAGHB(cm2)
答:图2中阴影部分的面积是cm2。
【点评】本题考查的是三角形的面积的应用。
36.如图所示,一块长方形绿地,面积为360平方米,现在要扩大,如果长不变,宽增加到32米,扩大后的绿地面积是多少平方米?
【答案】1440平方米。
【分析】第一种解法:用长方形的面积÷宽=长方形的长,再用长方形的长×新的宽=扩大后的面积。
第二种解法:一个因数不变,另一个因数乘几,积也乘几。这里长不变,就相当于一个因数不变。宽由8米增加到32米,相当于宽乘4,那么面积也应该乘4,据此解答。
【解答】解:解法一:360÷8=45(米)
45×32=1440(平方米)
解法二:32÷8=4
360×4=1440(平方米)
答:扩大后的绿地面积是1440平方米。
【点评】此题主要考查长方形面积公式的灵活运用,因数与积的变化规律及应用。
37.从一张纸上剪下8个相同大小的等腰直角三角形,组成装饰图案(如图)。这个图案的面积是多少平方厘米?
【答案】100平方厘米。
【分析】由图可知:三角形的直角边是20÷4=5(厘米),再运用三角形的面积公式:S=ah÷2求出一个三角形的面积,乘8即可得到图形的面积。
【解答】解:20÷4=5(厘米)
5×5÷2×8
=25×4
=100(平方厘米)
答:这个图案的面积是100平方厘米。
【点评】此题主要考查三角形的面积公式的计算应用。
38.为了确保游客在游览时的安全,避免发生踩踏事故,室外景点每人所占用的活动面积必须大于或等于0.75平方米。在一个旅游景区依墙搭建了一个直径是20米的半圆形室外观看区。为了保证安全,这个观看区最多能同时容纳多少人?
【答案】209人。
【分析】运用圆的面积公式S=πr2求出半圆的面积;然后除以每人所占用的活动面积;由此即可求得答案。
【解答】解:20÷2=10(米)
3.14×102÷2
=3.14×25
=157(平方米)
157÷0.75≈209(人)
答:这个观看区最多能同时容纳209人。
【点评】本题考查了圆的面积公式的应用。
39.位于湖南省东北部的张谷英村,因其错落相连的房屋建构,使人在村中行走能做到晴不曝日、雨不湿鞋,有“天下第一村”的美誉。无人机拍摄发现村中一户房顶因无人居住出现了大面积损坏,旅游局打算重新铺瓦。检修部分的房顶形状如图,通常一平方米需要铺设140块小青瓦片,重铺这块房顶需要准备多少块小青瓦片?
【答案】10640块。
【分析】根据图示,检修部分的房顶面积等于上底是16米,下底是7+4.5=11.5(米),高是4+2=6(米)的梯形的面积,减去上底是2米,下底是4.5米,高是2米的梯形的面积,然后用检修部分的房顶面积乘140解答即可。
【解答】解:(16+7+4.5)×(4+2)÷2﹣(2+4.5)×2÷2
=82.5﹣6.5
=76(平方米)
76×140=10640(块)
答:重铺这块房顶需要准备10640块小青瓦片。
【点评】本题考查了组合图形面积计算知识,结合题意分析解答即可。
40.小明家要买一张吃饭用的圆桌,要求最多能坐8人。如果每人在圆周上大约站位60cm,小明家需要买直径多大的圆桌?(本题π取近似值3)
【答案】160厘米。
【分析】根据题意,首先求出这个圆桌的周长,再根据圆的周长公式:C=πd,那么d=C÷π,把数据代入公式解答。
【解答】解:60×8÷3
=480÷3
=160(厘米)
答:小明家需要买直径160厘米的圆桌。
【点评】此题主要考查圆的周长公式的灵活运用,关键是熟记公式。
41.张大伯有一块3.6公顷的土地,要在这块地里栽种核桃,种植的行距为4米,株距为4.5米。这块地可栽多少棵核桃树?
【答案】2000棵。
【分析】首先把3.6公顷化成36000平方米,根据长方形的面积公式:S=ab,把数据代入公式求出每棵桃树的占地面积,然后用果园的面积除以每棵桃树的占地面积求出栽桃树的棵数。
【解答】解:3.6公顷=36000平方米
4×4.5=18(平方米)
36000÷18=2000(棵)
答:这块地可栽2000棵核桃树。
【点评】此题主要考查长方形的面积公式的灵活运用,关键是熟记公式。
42.张爷爷靠墙围了一个平行四边形的菜园(如图),围菜园的篱笆长23米。这个菜园的面积是多少平方米?
【答案】52.2平方米。
【分析】依据题意结合图示可知,平行四边形的底等于篱笆长减去2个7米,利用平行四边形的面积公式计算即可。
【解答】解:(23﹣7×2)×5.8
=9×5.8
=52.2(平方米)
答:菜园的面积是52.2平方米。
【点评】本题考查的是平行四边形的面积的应用。
43.根据相关研究,室内景点人均活动面积低于1m2室外景点人均活动面积低于0.75m2时,就有发生踩踏事故的危险。在某古镇景点戏台前,有一个上底是32m、下底是48m、高是30m的梯形室外场地,为保证安全,这个场地最多能容纳多少人同时看戏?
【答案】1600人。
【分析】根据梯形的面积=(上底+下底)×高÷2代入数据求出室外场地的面积,然后再除以0.75计算即可。
【解答】解:(32+48)×30÷2÷0.75
=80×30÷2÷0.75
=2400÷2÷0.75
=1200÷0.75
=1600(人)
答:这个场地最多能容纳1600人同时看戏。
【点评】解答此题要运用梯形的面积公式。
44.采摘园原来有一块宽是26米的长方形菜地(如图),现在正在扩建。如果长不变,宽增加8米,扩建后面积增加680平方米。这块菜地原来的面积有多大?
(1)画一画,在右图画出扩建的区域,并标数据。
(2)算一算,这块菜地原来的面积有多大?
【答案】(1);(2)2210平方米。
【分析】(1)根据题意,用扩建后的面积除以8,求出长是多少米,据此画图即可;(2)用原来的宽乘长就是原来的面积。
【解答】解:(1)680÷8=85(米)
(2)85×26=2210(平方米)
答:这块菜地原来的面积有2210平方米。
【点评】解答此题要灵活运用长方形的面积公式。
45.一个圆的周长是12.56米,半径增加2米后,圆的面积是多少平方米?
【答案】50.24平方米。
【分析】根据题意先用圆形周长除以圆周率,再除以2得出原来的半径,再加2得出变化后的半径,最后根据圆形面积S=πr2,代入数据解答即可。
【解答】解:12.56÷3.14÷2
=4÷2
=2(米)
3.14×(2+2)2
=3.14×16
=50.24(平方米)
答:圆的面积是50.24平方米。
【点评】此题主要考查圆形面积公式的灵活运用,关键是熟记公式。
46.公园里的圆形花坛周长是37.68米,现在要在花坛周围铺一条宽1米的石板路,如果每平方米要投资50元,铺这条石板路要投资多少元?
【答案】2041元。
【分析】根据“圆周长=2πr”求出圆形花坛的半径,根据“圆环面积=大圆面积﹣小圆面积”求出石板路的面积,用石板路的面积乘每平方米投掷额即可解答。
【解答】解:37.68÷2÷3.14=6(米)
(6+1)2π﹣62π
=49π﹣36π
=13π
=13×3.14
=40.82(平方米)
40.82×50=2041(元)
答:铺这条石板路要投资2041元。
【点评】本题考查了圆环面积计算的应用。
47.一块三角形广告牌,底5米,高是1.8米。将这块广告牌的正反两面都刷上油漆,如果每平方米需要刷漆450克,准备4千克油漆够不够?(请用计算说明)
【答案】不够。
【分析】根据三角形面积=底×高÷2,计算出广告牌一面的面积,乘2,是正反两面的面积和,即刷油漆的面积,刷油漆的面积×每平方米需要的油漆质量=需要的油漆总质量,与准备的油漆质量比较即可。注意统一单位。
【解答】解:根据三角形的面积公式可知:
5×1.8÷2×2=9(平方米)
450克=0.45千克
9×0.45=4.05(千克)
4.05>4
答:准备4千克油漆不够。
【点评】熟练掌握三角形的面积公式,是解答此题的关键。
48.淘气爷爷一面靠墙围了一个养鸡圈(如图)。
(1)如果要给它围上一圈篱笆,篱笆至少长多少米?
(2)这养鸡圈的占地面积有多大?
【答案】(1)9.14米;(2)7.57平方米。
【分析】(1)篱笆的长度是两个3米长度的和,加上直径是2米的圆的周长的一半,据此列式计算即可;
(2)鸡圈的占地面积是长是3米、宽是2米的长方形的面积的和,加上直径是2米的圆的面积的一半,据此列式计算即可。
【解答】解:(1)3×2+3.14×2÷2
=6+3.14
=9.14(米)
答:篱笆至少长9.14米。
(2)3×2+3.14×(2÷2)2÷2
=6+3.14×1÷2
=6+1.57
=7.57(平方米)
答:这养鸡圈的占地面积是7.57平方米。
【点评】解答此题要灵活运用长方形和圆的周长和面积公式。
49.一块铁皮的形状如图。请你算算这块铁皮的面积是多少?(单位:dm)
【答案】30dm2。
【分析】根据图示可知,铁皮的面积等于左侧三角形面积和右侧梯形面积之和,据此计算。
【解答】解:5×2÷2+(3.5+6.5)×5÷2
=5+25
=30(dm2)
答:这块铁皮的面积是30dm2。
【点评】本题考查了组合图形面积计算,牢记三角形和梯形面积公式是解题关键。
50.叔叔家果园的形状为梯形,它的上底22米,下底38米,高24米。叔叔计划在果园里栽果树,若每棵果树占地约6平方米,可以栽多少棵果树?
【答案】120棵。
【分析】根据梯形面积公式:梯形的面积=(上底+下底)×高÷2,代入数据,求出果园的面积,再用果园的面积除以每棵果树占地的面积,即可解答。
【解答】解:(22+38)×24÷2÷6
=60×24÷2÷6
=720÷6
=120(棵)
答:可以栽120棵果树。
【点评】熟练掌握梯形的面积公式是解答本题的关键。
51.为保障市民安全合理观看比赛,组委会在跑道两侧设置观看区域。某一跑道旁有一块直角梯形的观看区域,面积是34.8平方米。组委会在观看区域的三面围上护栏(如图),只测得梯形的高为3.2米,请你算出护栏的总长是多少米?
【答案】24.95米。
【分析】由题意,已知梯形的面积和高,用梯形的面积乘2除以高即得上下底之和,再加上高就是护栏总长,代入数据即可解答。
【解答】解:34.8×2÷3.2+3.2
=69.6÷3.2+3.2
=21.75+3.2
=24.95(米)
答:护栏总长有24.95米。
【点评】此题考查了梯形的面积公式的实际应用,关键是明确上下底的和。
52.哈尔滨亚冬会期间冰雪大世界有一块室外游乐场地(如图),相关研究表明:室外景点低于0.75平方米/人时,就有发生踩踏事故的危险。要避免踩踏事故的出现这块场地最多能容纳多少人同时活动?
【答案】152人。
【分析】根据图示可知,该游乐场所为一个长方形和梯形的组合图形场所,右侧为长7米,宽6米的长方形,左侧为上底6米,下底12米,高(15﹣7)米的梯形。根据“长方形面积=长×宽,梯形面积=(上底+下底)×高÷2”分别计算出长方形和梯形的面积后相加求和即为该游乐场所的面积;再根据低于0.75平方米/人时,就有发生踩踏事故的危险,用游乐场所面积除以0.75即是组多可容纳人数,据此解答。
【解答】解:6×7=42(平方米)
(6+12)×(15﹣7)÷2=72(平方米)
72+42=114(平方米)
114÷0.75=152(人)
答:要避免踩踏事故的出现这块场地最多能容纳152人同时活动。
【点评】本题考查了组合图形面积计算的应用。
53.盛安小学原有一个长方形花坛,后来因修路的需要,长减少了5米,这个花圃的面积减少了100平方米。减少后的花坛正好是一个正方形,原来长方形花圃的面积是多少平方米?(先在图中画出减少部分,再解答)
【答案】;500平方米。
【分析】根据画图策略,画出示意图,从图中分析,从长减少了5米,花圃的面积减少了100平方米,则先用减少的面积除以减少的长,求出原来长方形的宽,再根据面积减少后花圃正好是一个正方形,故原来长方形的长是(宽+5)米,最后再根据“长方形的面积=长×宽”,求出原来长方形花圃的面积即可解答。
【解答】解:如图所示:
(100÷5+5)×(100÷5)
=(20+5)×20
=25×20
=500(平方米)
答:原来长方形花圃的面积是500平方米。
【点评】解答此题要运用长方形的面积公式。
54.如图的平行四边形底是6厘米,高是4.5厘米,请你画一条线将它分成两个大小形状完全相同的梯形,并算出其中一个梯形的面积。
【答案】(画法不唯一);13.5平方厘米。
【分析】连接平行四边形的两条对角线,找出对角线的交点,即平行四边形的中心点,过平行四边形的中心点,任意画一条线段(线段的两个端点不能是梯形的顶点和梯形四条边的中点),即可分成两个大小形状完全相同的梯形;再根据一个梯形的面积等于原来平行四边的面积÷2,据此计算即可求出面积。
【解答】解:画图如下:(画法不唯一)
6×4.5÷2
=27÷2
=13.5(平方厘米)
答:其中一个梯形的面积是13.5平方厘米。
【点评】本题考查了平行四边形的性质以及梯形的面积计算。
55.一扇老式木门,最上面有个梯形的透光窗,窗架的上底是5分米,下底9分米,高4分米。如果要为这个窗架配一块玻璃,这块玻璃的面积至少有多大?(忽略玻璃与窗架镶嵌处的面积)
【答案】28平方分米。
【分析】根据梯形面积=(上底+下底)×高÷2,即可解答。
【解答】解:(5+9)×4÷2
=56÷2
=28(平方分米)
答:这块玻璃的面积至少有28平方分米。
【点评】本题考查的是梯形面积的计算,熟记公式是解答关键。
56.李明经常在自家小区圆形的游泳池边散步。这天,他以每分钟62.8m的速度绕泳池走了一圈,恰好用了5分钟。这个泳池的面积是多少平方米?
【答案】7850平方米。
【分析】首先根据路程=速度×时间,求出这个圆形游泳池的周长,再根据圆的周长公式:C=2πr,那么r=C÷2π,据此求出半径,然后根据圆的面积公式:S=πr2,把数据代入公式解答。
【解答】解:62.8×5=314(米)
314÷3.14÷2=50(米)
3.14×502
=3.14×2500
=7850(平方米)
答:这个游泳池的占地面积是7850平方米。
【点评】此题主要考查圆的周长公式、面积公式的灵活运用,关键是熟记公式。
57.旧城改造,准备修建一个花坛,形状如图,它的边是4个直径相等的半圆。这个花坛的面积是多少平方米?
【答案】164.48平方米。
【分析】花坛面积即为直径为8米的2个圆面积以及边长为8米的正方形面积,根据“圆面积=πr2以及正方形面积=边长×边长”分别求解圆面积和正方形面积,然后相加求和即可。
【解答】解:3.14×(8÷2)2×2+8×8
=100.48+64
=164.48(平方米)
答:这个花坛的面积是164.48平方米。
【点评】本题考查了组合图形面积计算的应用。
58.大约在两千年前,我国数学名著《九章算术》中的“方田章”就论述了平面图形面积的算法。书中说:“圭田术曰,半广以乘正从。”其中“圭田”就是指三角形田地,“广”和“从”是指三角形的底和高,已知三角形的面积是35.2平方米,底是4.4米,它的高是多少米?
【答案】16米。
【分析】根据三角形的面积公式:S=ah÷2,那么h=2S÷a,把数据代入公式解答。
【解答】解:35.2×2÷4.4
=70.8÷4.4
=16(米)
答:它的高是16米。
【点评】此题主要考查三角形面积公式的灵活运用,关键是熟记公式。
59.用一根长15dm的铁丝围成一个等腰梯形。已知这个梯形的两腰共长8.6dm,高是3dm,这个梯形的面积是多少dm2?
【答案】9.6平方分米。
【分析】根据梯形的周长公式,用梯形的周长减去两腰的长度即可求出梯形上、下底之和,再根据梯形的面积公式:S=(a+b)×h÷2,把数据代入公式解答。
【解答】解:(15﹣8.6)×3÷2
=6.4×3÷2
=9.6(平方分米)
答:这个等腰梯形的面积是9.6平方分米。
【点评】此题主要考查梯形的周长公式、面积公式的灵活运用。
60.中国少年先锋队是中国少年儿童的群团组织,是少年儿童学习中国特色社会主义和共产主义的学校,是建设社会主义和共产主义的预备队,我们每一个班级中队就是中国少先队的一个小集体。兴华小学要做12面中队旗,共需要多少平方米布?
【答案】5.04平方米。
【分析】先用长为80厘米、宽为60厘米的长方形面积减去底为60厘米、高为20厘米的三角形面积,求出做1面中队旗需要多少平方厘米布,再乘12,求出做12面中队旗要多少平方厘米布,然后将单位换算成平方米即可。
【解答】解:(80×60﹣60×20÷2)×12
=4200×12
=50400(平方厘米)
50400平方厘米=5.04平方米
答:共需要5.04平方米布。
【点评】解答本题需准确分析图形的组成,数据长方形和商量下面积公式。
21世纪教育网(www.21cnjy.com)
1.一块茄子地的形状是三角形,它的底是28米,高是30米,如果每棵茄子占地0.5平方米,那么这块地可以种多少棵茄子?
2.阳光小区有一块梯形空地,物业为增加小区的绿化带区域,决定在这块空地上铺一块平行四边形草坪和一块三角形草坪,两个草坪之间留一条平行四边形的小路(如图)。如果铺草坪每平方米要花2.5元,那么铺这两块草坪一共要花多少元?
3.滨海盐场有40块同样大的长方形盐田,每块盐田长100米,宽50米。这些盐田一共占地多少公顷?
4.在冬天,园林工人采用粗麻绳紧致地环绕树木,用“穿冬衣”的方法给树木御寒。一位工人叔叔给一棵树穿“衣服”时,用了约301.44分米长的麻绳一共捆了16周,这棵树干的横截面面积大约是多少平方分米?(麻绳的粗细忽略不计)
5.公园里有一个周长是94.2米的圆形草坪,准备在正中间安装自动旋转喷水器进行喷艇。
(1)你认为安装射程为多少米的装置最合适?
(2)在草坪周围建一条1米宽的环形石子路,这条小路的面积是多少平方米?
6.一个牡丹园的形状是三角形,它的底是160米,高是100米,种1m2的牡丹幼苗能卖20元,这个牡丹园种满牡丹幼苗可以卖多少元?
7.如图这块长方形绿地的宽增加36米,长不变,扩大后绿地的面积是多少平方米?
8.超市门口的装饰牌是等腰梯形。它的上底是16米,下底是22米,高是3米。用油漆刷这块装饰牌的一面,每平方米需用油漆2.5千克,刷这块装饰牌需要多少千克油漆?
9.如图是一个梯形花园,上底6m,下底16m,较大三角形的面积是72m2。
(1)梯形的高是多少米?
(2)每平方米花园年产值约60元,梯形花园的产值每年约为多少元?
10.有一块周长是62.8米的圆形草坪。
(1)准备在这块草坪的中心位置安装自动旋转喷灌装置,自动旋转喷灌装置的射程分别为5米、10米、20米,选择哪种比较合适?
(2)在这块圆形草坪周围铺一条宽1米的小路,这条小路的面积是多少平方米?
11.一个正方形果园的周长是1200米,这个果园的占地面积是多少平方米?合多少公顷?
12.王大爷在一块长300米、宽100米的长方形地里种棉花,种植棉花的株距是0.3米,行距是0.5米。
(1)这块地能种植多少株棉花?
(2)如果每千克籽棉能卖6.2元,这块棉花地大约能收入多少元?
13.学校有一块长方形试验田。现在将长增加5米或宽增加3米,面积都比原来增加45平方米。原来试验田的面积是多少平方米?(先在图上画一画,再解答)
14.土楼是福建、广东等地区的一种建筑形式,被列入“世界物质文化名录”,其外形有圆形、方形、椭圆形等。一座圆环形土楼外直径为26米,内直径为14米。这座土楼的占地面积是多少平方米?
15.李叔叔家有一个圆木桌。
(1)李叔叔想做一个和桌面大小形状都相同的桌垫,桌垫的面积是多少平方米?
(2)如果给这个桌垫的边缘围一圈花边,花边的长是多少米?
16.同学们,这学期我们进行了多边形面积的“探究之旅”。下面我们再来跟淘气、笑笑、奇思和妙想开启新一轮的“探究之旅”吧!
(1)如图,淘气、笑笑和奇思在研究如何解决平行四边形面积的计算问题时,想到了以下的方法。下面的推导方法中,谁的方法是合理的,请你在他的名字后面括号画“√”。
(2)从上面你认可的推导方法中任选一个,将其推导过程和结论写下来。
(3)妙想用这学期学习的知识,解决了以下的问题:
小区内有一块面积为129.6平方米的平行四边形的草坪,为了优化生态环境,在原来平行四边形草坪旁边,又扩建了一块三角形草坪。如图,平行四边形草坪的高是多少?
(4)请你算一算,扩建后草坪的面积一共有多大?
(5)在解决上面问题的过程中,妙想还用到了三角形的面积公式。你知道吗?早在2000多年前,我国数学名著《九章算术》中就记载了一种可以由长方形面积计算方法推导出三角形面积的计算方法。书中记载了一种求长方形面积的方法:广从(zòng)相乘得积步。“广”和“从”是指长和宽。请在下图的长方形中标出“广”和“从”。
书中记载求三角形面积的方法:半广以乘正从。“广”是指三角形的底边,“正从”是指底边上的高。你能结合如图解释《九章算术》中这种求三角形面积方法的道理吗?请详细描述(可用画图帮助描述你的推导过程)。
17.农场有一块花圃计划种植郁金香(如图)。
①这块地的面积是多少平方米?(提示:同学们可以在图中画一画)
②如果每棵郁金香占地0.2平方米,这块地可以种多少棵郁金香?
18.第14届全国运动会田径比赛400m跑在奥林匹克中心举行。在标准跑道上,如果直道的长度是85.96m,第一条半圆形跑道的直径为72.6m,每条跑道宽1.25m,那么各跑道的起跑线应该相差多少米?
19.在一个等腰三角形中,笑笑量得其中的两条边分别是3厘米和6厘米,这个等腰三角形的周长是多少厘米?
20.如图所示某零件横截面是个圆环,这个圆环的面积是多少平方厘米?
21.如图,米升的底面是一个正方形,四个侧面是完全相同的梯形。每个梯形的上底长15厘米,下底长25厘米,高25厘米。做这样一个米升,至少需要多少平方厘米的木材?
22.有一条长23米,宽1.5米(图中阴影)的长方形小路,从一块梯形的田地穿过,这块田地的实际种植面积是多少平方米?
23.王伯伯用5.5米长的绳子,把一只羊拴在了草地的木桩上。如果拴在木桩上的部分和打结处一共用去0.5米长的绳子,那么这只羊能吃到草的最大范围约多少平方米?(木桩粗细忽略不计)
24.一个长方形停车场的面积是280平方米,宽是7米。若长不变,宽增加到35米,扩大后的停车场面积是多少平方米?
25.幸福村有一个苹果园(直角梯形),因新农村改造从中间修建了一条马路,平行四边形。
(1)苹果园改造后的占地面积是多少平方米?
(2)如果每16平方米种一棵苹果树,每棵苹果树平均收获150千克苹果,改造后这个苹果园可以收获苹果多少吨?
26.小林周末去市杂技团看演出,最让人感到惊险刺激的节目是骑独轮车走钢丝,主持人介绍说:“独轮车的车轮半径约为15cm,体重达到80kg的表演人员要骑着独轮车经过一根离地面高3米,长度为18.84米,且绷得笔直的钢丝绳。”小林一边仰头观看一边想,怎样计算出,走完钢丝车轮要转动多少圈呢?同学们,你们能帮小林算一算吗?(π≈3.14)
27.有一条宽4米的长方形人行道,占地面积是360平方米。为了行走方便,道路的宽增加到12米,长不变,扩宽后的人行道的面积是多少平方米?
28.王爷爷有一块面积为72平方米的长方形菜园,里面种了黄瓜和番茄(如图)。其中黄瓜地的面积比番茄地多16平方米。番茄地有多少平方米?
29.如图,在房屋的一面墙上,用42.5米长的篱笆围成一块梯形麦田(靠墙这一面不用围篱笆)。
(1)这块麦田的面积是多少平方米?
(2)如果一平方米麦田能生产小麦大约0.2吨,那这块麦田的总产量约是多少吨?
30.育才小学有一个长方形草坪。如果草坪的长增加5米,面积就增加75平方米。如果草坪的宽增加5米,面积就增加125平方米。原来草坪的面积是多少平方米?(先在图中画一画,再解答)
31.学校有一个三角形的花坛,底边为12米,高为4.5米。要把这个花坛栽满鲜花,施工公司报价每平方米80元。给这个花坛栽满鲜花一共要多少元?
32.如图是张老师新房的平面图。如果客厅、厨房和卫生间铺地板的费用,按平均每平方米150元计算,共需要多少元?
33.一柄遮阳大伞完全打开后,从上往下看伞面尺寸和形状如图所示(单位:米)。这个伞面的面积是多少平方米?
34.一个平行四边形的街头广告牌,底是13.5米,高是6米,如果要油饰这块广告牌(只油饰正面),每平方米用油漆0.62千克,需要多少千克油漆?
35.如图1,ABCD、CEFG是两个正方形,边长分别为5厘米和4厘米,将GC边擦去,留下一个轮廓,然后连结AE、BF相交于点H,连结BG与AE相交于点I,则图2中阴影部分的面积是多少平方厘米?
36.如图所示,一块长方形绿地,面积为360平方米,现在要扩大,如果长不变,宽增加到32米,扩大后的绿地面积是多少平方米?
37.从一张纸上剪下8个相同大小的等腰直角三角形,组成装饰图案(如图)。这个图案的面积是多少平方厘米?
38.为了确保游客在游览时的安全,避免发生踩踏事故,室外景点每人所占用的活动面积必须大于或等于0.75平方米。在一个旅游景区依墙搭建了一个直径是20米的半圆形室外观看区。为了保证安全,这个观看区最多能同时容纳多少人?
39.位于湖南省东北部的张谷英村,因其错落相连的房屋建构,使人在村中行走能做到晴不曝日、雨不湿鞋,有“天下第一村”的美誉。无人机拍摄发现村中一户房顶因无人居住出现了大面积损坏,旅游局打算重新铺瓦。检修部分的房顶形状如图,通常一平方米需要铺设140块小青瓦片,重铺这块房顶需要准备多少块小青瓦片?
40.小明家要买一张吃饭用的圆桌,要求最多能坐8人。如果每人在圆周上大约站位60cm,小明家需要买直径多大的圆桌?(本题π取近似值3)
41.张大伯有一块3.6公顷的土地,要在这块地里栽种核桃,种植的行距为4米,株距为4.5米。这块地可栽多少棵核桃树?
42.张爷爷靠墙围了一个平行四边形的菜园(如图),围菜园的篱笆长23米。这个菜园的面积是多少平方米?
43.根据相关研究,室内景点人均活动面积低于1m2室外景点人均活动面积低于0.75m2时,就有发生踩踏事故的危险。在某古镇景点戏台前,有一个上底是32m、下底是48m、高是30m的梯形室外场地,为保证安全,这个场地最多能容纳多少人同时看戏?
44.采摘园原来有一块宽是26米的长方形菜地(如图),现在正在扩建。如果长不变,宽增加8米,扩建后面积增加680平方米。这块菜地原来的面积有多大?
(1)画一画,在右图画出扩建的区域,并标数据。
(2)算一算,这块菜地原来的面积有多大?
45.一个圆的周长是12.56米,半径增加2米后,圆的面积是多少平方米?
46.公园里的圆形花坛周长是37.68米,现在要在花坛周围铺一条宽1米的石板路,如果每平方米要投资50元,铺这条石板路要投资多少元?
47.一块三角形广告牌,底5米,高是1.8米。将这块广告牌的正反两面都刷上油漆,如果每平方米需要刷漆450克,准备4千克油漆够不够?(请用计算说明)
48.淘气爷爷一面靠墙围了一个养鸡圈(如图)。
(1)如果要给它围上一圈篱笆,篱笆至少长多少米?
(2)这养鸡圈的占地面积有多大?
49.一块铁皮的形状如图。请你算算这块铁皮的面积是多少?(单位:dm)
50.叔叔家果园的形状为梯形,它的上底22米,下底38米,高24米。叔叔计划在果园里栽果树,若每棵果树占地约6平方米,可以栽多少棵果树?
51.为保障市民安全合理观看比赛,组委会在跑道两侧设置观看区域。某一跑道旁有一块直角梯形的观看区域,面积是34.8平方米。组委会在观看区域的三面围上护栏(如图),只测得梯形的高为3.2米,请你算出护栏的总长是多少米?
52.哈尔滨亚冬会期间冰雪大世界有一块室外游乐场地(如图),相关研究表明:室外景点低于0.75平方米/人时,就有发生踩踏事故的危险。要避免踩踏事故的出现这块场地最多能容纳多少人同时活动?
53.盛安小学原有一个长方形花坛,后来因修路的需要,长减少了5米,这个花圃的面积减少了100平方米。减少后的花坛正好是一个正方形,原来长方形花圃的面积是多少平方米?(先在图中画出减少部分,再解答)
54.如图的平行四边形底是6厘米,高是4.5厘米,请你画一条线将它分成两个大小形状完全相同的梯形,并算出其中一个梯形的面积。
55.一扇老式木门,最上面有个梯形的透光窗,窗架的上底是5分米,下底9分米,高4分米。如果要为这个窗架配一块玻璃,这块玻璃的面积至少有多大?(忽略玻璃与窗架镶嵌处的面积)
56.李明经常在自家小区圆形的游泳池边散步。这天,他以每分钟62.8m的速度绕泳池走了一圈,恰好用了5分钟。这个泳池的面积是多少平方米?
57.旧城改造,准备修建一个花坛,形状如图,它的边是4个直径相等的半圆。这个花坛的面积是多少平方米?
58.大约在两千年前,我国数学名著《九章算术》中的“方田章”就论述了平面图形面积的算法。书中说:“圭田术曰,半广以乘正从。”其中“圭田”就是指三角形田地,“广”和“从”是指三角形的底和高,已知三角形的面积是35.2平方米,底是4.4米,它的高是多少米?
59.用一根长15dm的铁丝围成一个等腰梯形。已知这个梯形的两腰共长8.6dm,高是3dm,这个梯形的面积是多少dm2?
60.中国少年先锋队是中国少年儿童的群团组织,是少年儿童学习中国特色社会主义和共产主义的学校,是建设社会主义和共产主义的预备队,我们每一个班级中队就是中国少先队的一个小集体。兴华小学要做12面中队旗,共需要多少平方米布?
计算面积
参考答案与试题解析
1.一块茄子地的形状是三角形,它的底是28米,高是30米,如果每棵茄子占地0.5平方米,那么这块地可以种多少棵茄子?
【答案】840棵。
【分析】三角形的面积=底×高÷2,据此代入数据计算,求出这块地的面积,再除以每棵茄子占地面积,即可求出茄子棵数。
【解答】解:28×30÷2÷0.5
=840÷2÷0.5
=420÷0.5
=840(棵)
答:这块地可以种840棵茄子。
【点评】此题考查三角形面积的计算及应用。
2.阳光小区有一块梯形空地,物业为增加小区的绿化带区域,决定在这块空地上铺一块平行四边形草坪和一块三角形草坪,两个草坪之间留一条平行四边形的小路(如图)。如果铺草坪每平方米要花2.5元,那么铺这两块草坪一共要花多少元?
【答案】120元。
【分析】一个平行四边形的面积加上一个三角形的面积即可,单价乘面积即可总钱数。
【解答】解:4×6+8×6÷2
=24+24
=48(平方米)
48×2.5=120(元)
答:这两块草坪一共要花120元。
【点评】本题主要考查组合图形的面积,关键利用规则平面图形的面积公式计算。
3.滨海盐场有40块同样大的长方形盐田,每块盐田长100米,宽50米。这些盐田一共占地多少公顷?
【答案】20公顷。
【分析】根据长方形的面积=长×宽,把数据代入公式求出一块盐田的面积,然后再乘盐田的块数即可。
【解答】解:100×50×40
=5000×40
=200000(平方米)
200000平方米=20公顷
答:这些盐田一共占地20公顷。
【点评】此题主要考查长方形面积公式的灵活运用,关键是熟记公式。
4.在冬天,园林工人采用粗麻绳紧致地环绕树木,用“穿冬衣”的方法给树木御寒。一位工人叔叔给一棵树穿“衣服”时,用了约301.44分米长的麻绳一共捆了16周,这棵树干的横截面面积大约是多少平方分米?(麻绳的粗细忽略不计)
【答案】28.26平方分米。
【分析】先用301.44÷16计算出绕树的树干1圈的长度(即树干的周长),然后根据“圆的半径=圆的周长÷π÷2”求出圆的半径,进而利用圆的面积公式解答即可。
【解答】解:301.44÷16=18.84(分米)
18.84÷3.14÷2=3(分米)
3.14×32
=3.14×9
=28.26(平方分米)
答:这棵树干的横截面面积大约是28.26平方分米。
【点评】解答此题的关键是先计算出树的树干1圈的长度,继而根据圆的周长和面积公式进行解答。
5.公园里有一个周长是94.2米的圆形草坪,准备在正中间安装自动旋转喷水器进行喷艇。
(1)你认为安装射程为多少米的装置最合适?
(2)在草坪周围建一条1米宽的环形石子路,这条小路的面积是多少平方米?
【答案】(1)15米;(2)97.34平方米。
【分析】(1)根据“圆周长=2πr”求出圆半径,即为所求;
(2)根据圆环的面积等于大圆的面积减去小圆的面积即可求解。
【解答】解:(1)94.2÷3.14÷2=15(米)
答:安装射程为15米的装置最合适。
(2)3.14×[(15+1)2﹣152]
=3.14×31
=97.34(平方米)
答:这条小路的面积是97.34平方米。
【点评】本题考查了圆周长和圆环面积计算的应用。
6.一个牡丹园的形状是三角形,它的底是160米,高是100米,种1m2的牡丹幼苗能卖20元,这个牡丹园种满牡丹幼苗可以卖多少元?
【答案】16000元。
【分析】根据三角形面积=底×高÷2,求出三角形面积,再乘20,即可解答。
【解答】解:160×100÷2×20
=16000÷2×20
=8000×20
=16000(元)
答:这个牡丹园种满牡丹幼苗可以卖16000元。
【点评】本题考查的是三角形面积的计算,熟记公式是解答关键。
7.如图这块长方形绿地的宽增加36米,长不变,扩大后绿地的面积是多少平方米?
【答案】2880平方米。
【分析】长方形的长=长方形面积÷宽,据此用720÷12计算出长,宽增加36米,用12+36计算出扩大后长方形绿地的宽,再根据长方形面积=长×宽解题即可。
【解答】解:720÷12×(12+36)
=60×48
=2880(平方米)
答:扩大后绿地的面积是2880平方米。
【点评】此题主要考查长方形面积公式的灵活运用,关键是熟记公式。
8.超市门口的装饰牌是等腰梯形。它的上底是16米,下底是22米,高是3米。用油漆刷这块装饰牌的一面,每平方米需用油漆2.5千克,刷这块装饰牌需要多少千克油漆?
【答案】142.5千克。
【分析】梯形的面积公式:S=(a+b)h÷2,已知上底是16米,下底是22米,高是3米,据此可求出梯形的面积,再乘0.5就是需要油漆的重量,据此解答。
【解答】解:(16+22)×3÷2
=38×3÷2
=57(平方米)
57×2.5=142.5(千克)
答:一共需要142.5千克油漆。
【点评】本题主要考查了学生对梯形面积公式的实际运用。
9.如图是一个梯形花园,上底6m,下底16m,较大三角形的面积是72m2。
(1)梯形的高是多少米?
(2)每平方米花园年产值约60元,梯形花园的产值每年约为多少元?
【答案】(1)9米;(2)5940元。
【分析】(1)用72乘2除以16求出梯形的高;
(2)用梯形的面积乘60就是梯形花园的产值每年约为多少元。
【解答】解:(1)72×2÷16
=144÷16
=9(米)
答:梯形的高是90米。
(2)(16+6)×9÷2×60
=22×9÷2×60
=198÷2×60
=99×60
=5940(元)
答:梯形花园的产值每年约为5940元。
【点评】解答此题要运用三角形和梯形的面积公式。
10.有一块周长是62.8米的圆形草坪。
(1)准备在这块草坪的中心位置安装自动旋转喷灌装置,自动旋转喷灌装置的射程分别为5米、10米、20米,选择哪种比较合适?
(2)在这块圆形草坪周围铺一条宽1米的小路,这条小路的面积是多少平方米?
【答案】(1)10米;
(2)65.94平方米。
【分析】(1)根据圆的周长C=2πr,r=C÷2π,代入数据计算后,即可选择哪种射程的合适。
(2)圆环的面积等于大圆的面积减去小圆的面积即可。
【解答】解:(1)62.8÷(2×3.14)
=62.8÷6.28
=10(米)
答:自动旋转喷灌装置的射程为10米比较合适。
(2)3.14×[(10+1)2﹣102]
=3.14×[121﹣100]
=3.14×21
=65.94(平方米)
答:这条小路的面积是65.94平方米。
【点评】本题考查了圆的周长公式和圆环的面积计算。
11.一个正方形果园的周长是1200米,这个果园的占地面积是多少平方米?合多少公顷?
【答案】见试题解答内容
【分析】已知正方形的周长是800米,根据正方形的周长公式:C=4a知:a=C÷4可求正方形的边长,再根据正方形的面积公式:S=a2可求出果园的面积是多少平方米,再化成公顷即可.
【解答】解:1200÷4=300(米)
300×300=90000(平方米)=9(公顷)
答:这个果园的占地面积是90000平方米,合9公顷.
【点评】本题主要考查了学生对正方形面积和周长公式的应用.
12.王大爷在一块长300米、宽100米的长方形地里种棉花,种植棉花的株距是0.3米,行距是0.5米。
(1)这块地能种植多少株棉花?
(2)如果每千克籽棉能卖6.2元,这块棉花地大约能收入多少元?
【答案】(1)200000株;
(2)992000元。
【分析】(1)根据长方形的面积=长×宽,把数据代入公式分别求出这块地的面积、每株棉花的占地面积,然后根据“包含”除法的意义,用除法解答。
(2)根据总产量=单产量×数量,求出这块地一共收籽棉多少千克,再根据总价=单价×数量,列式解答即可。
【解答】解:(300×100)÷(0.5×0.3)
=30000÷0.15
=200000(株)
答:这块地能种植200000株棉花。
(2)0.08×200000×6.2
=16000×6.2
=99200(元)
答:这块棉花地大约能收入99200元。
【点评】此题主要考查长方形面积公式的灵活运用,以及单产量、数量、总产量三者之间的关系及应用、单价、数量、总价三者之间的关系及应用。
13.学校有一块长方形试验田。现在将长增加5米或宽增加3米,面积都比原来增加45平方米。原来试验田的面积是多少平方米?(先在图上画一画,再解答)
【答案】135平方米。
【分析】根据长方形的面积公式:S=ab,那么a=S÷b,b=S÷a,据此求出原来的长、宽,然后把数据代入公式求出原来的面积。
【解答】解:如图:
(45÷3)×(45÷5)
=15×9
=135(平方米)
答:原来试验田的面积是135平方米。
【点评】此题主要考查长方形面积公式的灵活运用关键是熟记公式。
14.土楼是福建、广东等地区的一种建筑形式,被列入“世界物质文化名录”,其外形有圆形、方形、椭圆形等。一座圆环形土楼外直径为26米,内直径为14米。这座土楼的占地面积是多少平方米?
【答案】见试题解答内容
【分析】根据环形面积公式:S=π(R2﹣r2),把数据代入公式解答。
【解答】解:3.14×[(26÷2)2﹣(14÷2)2]
=3.14×[169﹣49]
=3.14×120
=376.8(平方米)
答:这座土楼的占地面积是376.8平方米。
【点评】此题主要考查环形面积公式的灵活运用,关键是熟记公式。
15.李叔叔家有一个圆木桌。
(1)李叔叔想做一个和桌面大小形状都相同的桌垫,桌垫的面积是多少平方米?
(2)如果给这个桌垫的边缘围一圈花边,花边的长是多少米?
【答案】(1)0.785平方米;(2)3.14米。
【分析】(1)桌垫的面积就是直径是1米的圆形面积,根据圆形面积S=πr2,把数据代入公式解答即可;
(2)花边的长是直径是1米的圆形周长,根据圆形周长C=πd,把数据代入公式解答即可。
【解答】解:(1)3.14×(1÷2)2
=3.14×0.52
=3.14×0.25
=0.785(平方米)
答:桌垫的面积是0.785平方米。
(2)3.14×1=3.14(米)
答:花边的长是3.14米。
【点评】本题考查的是圆形周长和圆形面积计算公式的运用。
16.同学们,这学期我们进行了多边形面积的“探究之旅”。下面我们再来跟淘气、笑笑、奇思和妙想开启新一轮的“探究之旅”吧!
(1)如图,淘气、笑笑和奇思在研究如何解决平行四边形面积的计算问题时,想到了以下的方法。下面的推导方法中,谁的方法是合理的,请你在他的名字后面括号画“√”。
(2)从上面你认可的推导方法中任选一个,将其推导过程和结论写下来。
(3)妙想用这学期学习的知识,解决了以下的问题:
小区内有一块面积为129.6平方米的平行四边形的草坪,为了优化生态环境,在原来平行四边形草坪旁边,又扩建了一块三角形草坪。如图,平行四边形草坪的高是多少?
(4)请你算一算,扩建后草坪的面积一共有多大?
(5)在解决上面问题的过程中,妙想还用到了三角形的面积公式。你知道吗?早在2000多年前,我国数学名著《九章算术》中就记载了一种可以由长方形面积计算方法推导出三角形面积的计算方法。书中记载了一种求长方形面积的方法:广从(zòng)相乘得积步。“广”和“从”是指长和宽。请在下图的长方形中标出“广”和“从”。
书中记载求三角形面积的方法:半广以乘正从。“广”是指三角形的底边,“正从”是指底边上的高。你能结合如图解释《九章算术》中这种求三角形面积方法的道理吗?请详细描述(可用画图帮助描述你的推导过程)。
【答案】(1);
(2)选淘气的方法:把直角三角形剪下,并补到另一边,组成的图形是长方形,这个长方形的长是a,宽是h,利用长方形的面积公式可知,平行四边形的面积=ah。(答案不唯一)
(3)7.2米;
(4)151.2平方米;
(5),红色三角形向上翻折为绿色三角形,紫色三角形向上翻折为蓝色三角形,所以三角形的面积=半广×正从=广×从÷2。(答案不唯一)
【分析】(1)依据题意结合图示可知,笑笑和淘气通过图形的切割来计算平行四边形的面积,奇思的方法中长方形和平行四边形的周长相等,但是面积不同;
(2)选择淘气的方法去解答;(答案不唯一)
(3)利用平行四边形的面积=底×高,结合题中数据计算即可;
(4)利用三角形的面积公式计算三角形草坪的面积,然后计算扩建后草坪的面积;
(5)依据题意结合图示可知,把三角形进行切割,然后利用长方形的面积公式计算三角形的面积。(答案不唯一)
【解答】解:(1)如图:
(2)选淘气的方法:把直角三角形剪下,并补到另一边,组成的图形是长方形,这个长方形的长是a,宽是h,利用长方形的面积公式可知,平行四边形的面积=ah。(答案不唯一)
(3)129.6÷18=7.2(米)
答:平行四边形草坪的高是7.2米。
(4)6×7.2÷2+129.6
=21.6+129.6
=151.2(平方米)
答:扩建后草坪的面积一共151.2平方米。
(5)如图:
红色三角形向上翻折为绿色三角形,紫色三角形向上翻折为蓝色三角形,所以三角形的面积=半广×正从=广×从÷2。(答案不唯一)
【点评】本题考查的是长方形、三角形、平行四边形的面积的应用。
17.农场有一块花圃计划种植郁金香(如图)。
①这块地的面积是多少平方米?(提示:同学们可以在图中画一画)
②如果每棵郁金香占地0.2平方米,这块地可以种多少棵郁金香?
【答案】见试题解答内容
【分析】①把这块地分成左面一个长方形、右面一个梯形,利用长方形面积公式:S=ab,梯形面积公式:S=(a+b)h÷2计算即可。
②用这块地的面积除以每棵郁金香的占地面积,计算种的棵数即可。
【解答】解:①23×20+(8+20)×(31﹣23)÷2
=460+112
=572(平方米)
答:这块地的面积是572平方米。
②572÷0.2=2860(棵)
答:这块地可以种2860棵。
【点评】本题主要考查组合图形的面积的计算,关键是应用长方形和梯形面积公式。
18.第14届全国运动会田径比赛400m跑在奥林匹克中心举行。在标准跑道上,如果直道的长度是85.96m,第一条半圆形跑道的直径为72.6m,每条跑道宽1.25m,那么各跑道的起跑线应该相差多少米?
【答案】7.85米。
【分析】根据题意可知,相邻两个跑道的差也就是两端弯道的差,第一条半圆形跑道的直径为72.6米,那么第二跑道的直径是(72.6+1.25×2)米,根据圆的周长公式:C=πd,把数据代入公式求出外圆周长与内圆周长的差即可。
【解答】解:3.14×(72.6+1.25×2)﹣3.14×72.6
=3.14×(72.6+2.5)﹣227.964
=3.14×75.1﹣227.964
=235.814﹣227.964
=7.85(米)
答:各跑道的起跑线应该相差7.85米。
【点评】此题主要考查圆的周长公式的灵活运用,关键是熟记公式,重点是明确:外跑道和内跑道的差,也就是弯道的差。
19.在一个等腰三角形中,笑笑量得其中的两条边分别是3厘米和6厘米,这个等腰三角形的周长是多少厘米?
【答案】15厘米。
【分析】根据三角形的特性:两边之和大于第三边,三角形的两边的差一定小于第三边;判断出该三角形的腰为6厘米,进而根据三角形的周长计算方法解答即可。
【解答】解:6+6+3
=12+3
=15(厘米)
答:这个等腰三角形的周长是15厘米。
【点评】此题主要考查了三角形的特性和三角形周长的计算方法。
20.如图所示某零件横截面是个圆环,这个圆环的面积是多少平方厘米?
【答案】65.94平方厘米。
【分析】因为光盘是圆环,知道了内圆和外圆直径,求出半径,代入圆环面积公式S环=π(R2﹣r2)计算即可。
【解答】解:3.14×[(10÷2)2﹣(4÷2)2]
=3.14×(25﹣4)
=3.14×21
=65.94(平方厘米)
答:圆环面积是65.94平方厘米。
【点评】此题是考查圆环的面积计算,可利用其公式S环=π(R2﹣r2)计算即可。
21.如图,米升的底面是一个正方形,四个侧面是完全相同的梯形。每个梯形的上底长15厘米,下底长25厘米,高25厘米。做这样一个米升,至少需要多少平方厘米的木材?
【答案】4225平方厘米。
【分析】依据题意可知,木材的面积等于4个侧面梯形的面积加上底面正方形的面积,利用梯形的面积=(上底+下底)×高÷2,正方形的面积=边长×边长,结合题中数据计算即可。
【解答】解:(15+25)×25×4+15×15
=4000+225
=4225(平方厘米)
答:至少需要4225平方厘米的木材。
【点评】本题考查的是梯形的面积公式的应用。
22.有一条长23米,宽1.5米(图中阴影)的长方形小路,从一块梯形的田地穿过,这块田地的实际种植面积是多少平方米?
【答案】885.5平方米。
【分析】这块田地的实际种植面积等于梯形面积减去阴影小长方形面积,据此计算。
【解答】解:(32+48)×23÷2﹣23×1.5
=920﹣34.5
=885.5(m2)
答:这块田地的实际种植面积是885.5平方米。
【点评】本题考查了梯形面积和长方形面积计算的应用。
23.王伯伯用5.5米长的绳子,把一只羊拴在了草地的木桩上。如果拴在木桩上的部分和打结处一共用去0.5米长的绳子,那么这只羊能吃到草的最大范围约多少平方米?(木桩粗细忽略不计)
【答案】78.5平方米。
【分析】根据题意可知,这只羊能吃到草的最大面积为半径是(5.5﹣0.5)米的圆的面积,根据圆的面积公式:S=πr2,把数据代入公式解答。
【解答】解:5.5﹣0.5=5(米)
3.14×52
=3.14×25
=78.5(平方米)
答:这只羊能吃到草的最大范围约78.5平方米。
【点评】此题主要考查圆的面积公式的灵活运用,关键是熟记公式。
24.一个长方形停车场的面积是280平方米,宽是7米。若长不变,宽增加到35米,扩大后的停车场面积是多少平方米?
【答案】1400平方米。
【分析】根据长方形的面积=长×宽,再根据因数与积的变化规律,先求出扩大后的宽是原来宽的几倍,进而求出扩大后的面积。
【解答】解:280×(35÷7)
=280×5
=1400(平方米)
答:扩大后的停车场面积是400平方米。
【点评】此题主要考查长方形面积公式的灵活运用,因数与积的变化规律及应用。
25.幸福村有一个苹果园(直角梯形),因新农村改造从中间修建了一条马路,平行四边形。
(1)苹果园改造后的占地面积是多少平方米?
(2)如果每16平方米种一棵苹果树,每棵苹果树平均收获150千克苹果,改造后这个苹果园可以收获苹果多少吨?
【答案】(1)4800平方米;
(2)45吨。
【分析】(1)用梯形面积减去平行四边形的面积计算改造后的面积即可;
(2)用改造后的面积除以16,计算种苹果树的棵数,再乘150,再换算单位即可。
【解答】解:(1)(80+120)×60÷2﹣20×60
=6000﹣1200
=4800(平方米)
答:苹果园改造后的占地面积是4800平方米。
(2)4800÷16×150
=300×150
=45000(千克)
45000千克=45吨
答:改造后这个苹果园可以收获苹果45吨。
【点评】本题主要考查组合图形的面积的计算,关键是利用规则图形的面积公式计算。
26.小林周末去市杂技团看演出,最让人感到惊险刺激的节目是骑独轮车走钢丝,主持人介绍说:“独轮车的车轮半径约为15cm,体重达到80kg的表演人员要骑着独轮车经过一根离地面高3米,长度为18.84米,且绷得笔直的钢丝绳。”小林一边仰头观看一边想,怎样计算出,走完钢丝车轮要转动多少圈呢?同学们,你们能帮小林算一算吗?(π≈3.14)
【答案】20圈。
【分析】绳长除以车轮周长即可解答。
【解答】解:(18.84×100)÷(2×3.14×15)
=1884÷94.2
=20(圈)
答:走完钢丝车轮要转动20圈。
【点评】本题考查了圆周长计算的应用。
27.有一条宽4米的长方形人行道,占地面积是360平方米。为了行走方便,道路的宽增加到12米,长不变,扩宽后的人行道的面积是多少平方米?
【答案】1080平方米。
【分析】首先用360除以4求出长方形人行道原来的长是多少米,再用长乘扩建后的宽12米就是扩宽后的人行道的面积。
【解答】解:360÷4×12
=90×12
=1080(平方米)
答:扩宽后的人行道的面积是1080平方米。
【点评】解答此题要运用长方形的面积公式。
28.王爷爷有一块面积为72平方米的长方形菜园,里面种了黄瓜和番茄(如图)。其中黄瓜地的面积比番茄地多16平方米。番茄地有多少平方米?
【答案】28平方米。
【分析】根据题意,用72减去16求出两块番茄地的面积,再除以2即可。
【解答】解:(72﹣16)÷2
=56÷2
=28(平方米)
答:番茄地有28平方米。
【点评】此题考查的是长方形的面积公式。
29.如图,在房屋的一面墙上,用42.5米长的篱笆围成一块梯形麦田(靠墙这一面不用围篱笆)。
(1)这块麦田的面积是多少平方米?
(2)如果一平方米麦田能生产小麦大约0.2吨,那这块麦田的总产量约是多少吨?
【答案】(1)105平方米;(2)21吨。
【分析】(1)用42.5减去7.5,求出梯形上底和下底的和,再根据梯形面积=(上底+下底)×高÷2,即可解答;
(2)用梯形面积乘0.2,即可解答。
【解答】解:(1)(42.5﹣7.5)×6÷2
=210÷2
=105(平方米)
答:这块麦田的面积是105平方米。
(2)0.2×105=21(吨)
答:这块麦田的总产量约是21吨。
【点评】本题考查的是梯形面积的计算,熟记公式是解答关键。
30.育才小学有一个长方形草坪。如果草坪的长增加5米,面积就增加75平方米。如果草坪的宽增加5米,面积就增加125平方米。原来草坪的面积是多少平方米?(先在图中画一画,再解答)
【答案】;375平方米。
【分析】根据长方形的面积公式:S=ab,用增加的面积除以增加的宽,求出原来的长;用增加的面积除以增加的长,求出原来的宽,然后把数据代入公式解答。
【解答】解:
(75÷5)×(125÷5)
=15×25
=375(平方米)
答:原来草坪的面积是375平方米。
【点评】此题主要考查长方形面积公式的灵活运用,关键是熟记公式。
31.学校有一个三角形的花坛,底边为12米,高为4.5米。要把这个花坛栽满鲜花,施工公司报价每平方米80元。给这个花坛栽满鲜花一共要多少元?
【答案】2160元。
【分析】三角形面积=底×高÷2,结合题意求出花坛面积,然后乘80解答即可。
【解答】解:12×4.5÷2×80
=27×80
=2160(元)
答:给这个花坛栽满鲜花一共要2160元。
【点评】本题考查了三角形面积公式的灵活运用,结合题意分析解答即可。
32.如图是张老师新房的平面图。如果客厅、厨房和卫生间铺地板的费用,按平均每平方米150元计算,共需要多少元?
【答案】5700元。
【分析】客厅、厨房和卫生间地面是长(5.2+4.8)米、宽3.8米的长方形,利用长方形面积公式:S=ab计算客厅、厨房和卫生间地面的面积,再乘150即可计算所需钱数。
【解答】解:(5.2+4.8)×3.8×150
=38×150
=5700(元)
答:共需要5700元。
【点评】本题主要考查组合图形的面积,关键是利用规则图形的面积公式计算。
33.一柄遮阳大伞完全打开后,从上往下看伞面尺寸和形状如图所示(单位:米)。这个伞面的面积是多少平方米?
【答案】2.4平方米。
【分析】根据图示,这个伞面的面积等于8个三角形的面积之和,每个三角形的底是0.6米,高是1米,结合三角形的面积=底×高÷2,解答即可。
【解答】解:0.6×1÷2×8
=0.3×8
=2.4(平方米)
答:这个伞面的面积是2.4平方米。
【点评】本题考查了组合图形面积计算知识,结合三角形的面积公式解答即可。
34.一个平行四边形的街头广告牌,底是13.5米,高是6米,如果要油饰这块广告牌(只油饰正面),每平方米用油漆0.62千克,需要多少千克油漆?
【答案】50.22千克。
【分析】广告牌的底和高已知,利用平行四边形的面积公式即可求得其面积;每平方米的用漆量已知,乘广告牌的总面积,就能求得总的用漆量。
【解答】解:13.5×6×0.62
=81×0.62
=50.22(千克)
答:需要50.22千克油漆。
【点评】解答此题的关键是先求出广告牌的面积,进而求得总的用漆量。
35.如图1,ABCD、CEFG是两个正方形,边长分别为5厘米和4厘米,将GC边擦去,留下一个轮廓,然后连结AE、BF相交于点H,连结BG与AE相交于点I,则图2中阴影部分的面积是多少平方厘米?
【答案】cm2。
【分析】连接CH,AG,如图:,观察沙漏模型AEFB,有AH:HE=AB:EF=5:4,由于BC:CE=5:4=AH:HE,所以HC∥AB,即H在CD上,由于HC∥AB,所以HC:AB=EC:EB=4:9,计算HC,GH,梯形AGHB的面积,又GH:AB:5=16:45,由蝴蝶模型,可知S△GHI:SAGHB=162:(16+45)2=162:612,由此计算阴影部分的面积。
【解答】解:连接CH,AG,如图:观察沙漏模型AEFB,AH:HE=AB:EF=5:4,由于BC:CE=5:4=AH:HE,所以HC∥AB,即H在CD上。
由于HC∥AB,所以HC:AB=EC:EB=4:9,则HC(cm),所以GH=4(cm)。
SAGHB(5)×5(cm2),又GH:AB:5=16:45,由蝴蝶模型,可知S△GHI:SAGHB=162:(16+45)2=162:612=256:3721;
S△GHISAGHB(cm2)
答:图2中阴影部分的面积是cm2。
【点评】本题考查的是三角形的面积的应用。
36.如图所示,一块长方形绿地,面积为360平方米,现在要扩大,如果长不变,宽增加到32米,扩大后的绿地面积是多少平方米?
【答案】1440平方米。
【分析】第一种解法:用长方形的面积÷宽=长方形的长,再用长方形的长×新的宽=扩大后的面积。
第二种解法:一个因数不变,另一个因数乘几,积也乘几。这里长不变,就相当于一个因数不变。宽由8米增加到32米,相当于宽乘4,那么面积也应该乘4,据此解答。
【解答】解:解法一:360÷8=45(米)
45×32=1440(平方米)
解法二:32÷8=4
360×4=1440(平方米)
答:扩大后的绿地面积是1440平方米。
【点评】此题主要考查长方形面积公式的灵活运用,因数与积的变化规律及应用。
37.从一张纸上剪下8个相同大小的等腰直角三角形,组成装饰图案(如图)。这个图案的面积是多少平方厘米?
【答案】100平方厘米。
【分析】由图可知:三角形的直角边是20÷4=5(厘米),再运用三角形的面积公式:S=ah÷2求出一个三角形的面积,乘8即可得到图形的面积。
【解答】解:20÷4=5(厘米)
5×5÷2×8
=25×4
=100(平方厘米)
答:这个图案的面积是100平方厘米。
【点评】此题主要考查三角形的面积公式的计算应用。
38.为了确保游客在游览时的安全,避免发生踩踏事故,室外景点每人所占用的活动面积必须大于或等于0.75平方米。在一个旅游景区依墙搭建了一个直径是20米的半圆形室外观看区。为了保证安全,这个观看区最多能同时容纳多少人?
【答案】209人。
【分析】运用圆的面积公式S=πr2求出半圆的面积;然后除以每人所占用的活动面积;由此即可求得答案。
【解答】解:20÷2=10(米)
3.14×102÷2
=3.14×25
=157(平方米)
157÷0.75≈209(人)
答:这个观看区最多能同时容纳209人。
【点评】本题考查了圆的面积公式的应用。
39.位于湖南省东北部的张谷英村,因其错落相连的房屋建构,使人在村中行走能做到晴不曝日、雨不湿鞋,有“天下第一村”的美誉。无人机拍摄发现村中一户房顶因无人居住出现了大面积损坏,旅游局打算重新铺瓦。检修部分的房顶形状如图,通常一平方米需要铺设140块小青瓦片,重铺这块房顶需要准备多少块小青瓦片?
【答案】10640块。
【分析】根据图示,检修部分的房顶面积等于上底是16米,下底是7+4.5=11.5(米),高是4+2=6(米)的梯形的面积,减去上底是2米,下底是4.5米,高是2米的梯形的面积,然后用检修部分的房顶面积乘140解答即可。
【解答】解:(16+7+4.5)×(4+2)÷2﹣(2+4.5)×2÷2
=82.5﹣6.5
=76(平方米)
76×140=10640(块)
答:重铺这块房顶需要准备10640块小青瓦片。
【点评】本题考查了组合图形面积计算知识,结合题意分析解答即可。
40.小明家要买一张吃饭用的圆桌,要求最多能坐8人。如果每人在圆周上大约站位60cm,小明家需要买直径多大的圆桌?(本题π取近似值3)
【答案】160厘米。
【分析】根据题意,首先求出这个圆桌的周长,再根据圆的周长公式:C=πd,那么d=C÷π,把数据代入公式解答。
【解答】解:60×8÷3
=480÷3
=160(厘米)
答:小明家需要买直径160厘米的圆桌。
【点评】此题主要考查圆的周长公式的灵活运用,关键是熟记公式。
41.张大伯有一块3.6公顷的土地,要在这块地里栽种核桃,种植的行距为4米,株距为4.5米。这块地可栽多少棵核桃树?
【答案】2000棵。
【分析】首先把3.6公顷化成36000平方米,根据长方形的面积公式:S=ab,把数据代入公式求出每棵桃树的占地面积,然后用果园的面积除以每棵桃树的占地面积求出栽桃树的棵数。
【解答】解:3.6公顷=36000平方米
4×4.5=18(平方米)
36000÷18=2000(棵)
答:这块地可栽2000棵核桃树。
【点评】此题主要考查长方形的面积公式的灵活运用,关键是熟记公式。
42.张爷爷靠墙围了一个平行四边形的菜园(如图),围菜园的篱笆长23米。这个菜园的面积是多少平方米?
【答案】52.2平方米。
【分析】依据题意结合图示可知,平行四边形的底等于篱笆长减去2个7米,利用平行四边形的面积公式计算即可。
【解答】解:(23﹣7×2)×5.8
=9×5.8
=52.2(平方米)
答:菜园的面积是52.2平方米。
【点评】本题考查的是平行四边形的面积的应用。
43.根据相关研究,室内景点人均活动面积低于1m2室外景点人均活动面积低于0.75m2时,就有发生踩踏事故的危险。在某古镇景点戏台前,有一个上底是32m、下底是48m、高是30m的梯形室外场地,为保证安全,这个场地最多能容纳多少人同时看戏?
【答案】1600人。
【分析】根据梯形的面积=(上底+下底)×高÷2代入数据求出室外场地的面积,然后再除以0.75计算即可。
【解答】解:(32+48)×30÷2÷0.75
=80×30÷2÷0.75
=2400÷2÷0.75
=1200÷0.75
=1600(人)
答:这个场地最多能容纳1600人同时看戏。
【点评】解答此题要运用梯形的面积公式。
44.采摘园原来有一块宽是26米的长方形菜地(如图),现在正在扩建。如果长不变,宽增加8米,扩建后面积增加680平方米。这块菜地原来的面积有多大?
(1)画一画,在右图画出扩建的区域,并标数据。
(2)算一算,这块菜地原来的面积有多大?
【答案】(1);(2)2210平方米。
【分析】(1)根据题意,用扩建后的面积除以8,求出长是多少米,据此画图即可;(2)用原来的宽乘长就是原来的面积。
【解答】解:(1)680÷8=85(米)
(2)85×26=2210(平方米)
答:这块菜地原来的面积有2210平方米。
【点评】解答此题要灵活运用长方形的面积公式。
45.一个圆的周长是12.56米,半径增加2米后,圆的面积是多少平方米?
【答案】50.24平方米。
【分析】根据题意先用圆形周长除以圆周率,再除以2得出原来的半径,再加2得出变化后的半径,最后根据圆形面积S=πr2,代入数据解答即可。
【解答】解:12.56÷3.14÷2
=4÷2
=2(米)
3.14×(2+2)2
=3.14×16
=50.24(平方米)
答:圆的面积是50.24平方米。
【点评】此题主要考查圆形面积公式的灵活运用,关键是熟记公式。
46.公园里的圆形花坛周长是37.68米,现在要在花坛周围铺一条宽1米的石板路,如果每平方米要投资50元,铺这条石板路要投资多少元?
【答案】2041元。
【分析】根据“圆周长=2πr”求出圆形花坛的半径,根据“圆环面积=大圆面积﹣小圆面积”求出石板路的面积,用石板路的面积乘每平方米投掷额即可解答。
【解答】解:37.68÷2÷3.14=6(米)
(6+1)2π﹣62π
=49π﹣36π
=13π
=13×3.14
=40.82(平方米)
40.82×50=2041(元)
答:铺这条石板路要投资2041元。
【点评】本题考查了圆环面积计算的应用。
47.一块三角形广告牌,底5米,高是1.8米。将这块广告牌的正反两面都刷上油漆,如果每平方米需要刷漆450克,准备4千克油漆够不够?(请用计算说明)
【答案】不够。
【分析】根据三角形面积=底×高÷2,计算出广告牌一面的面积,乘2,是正反两面的面积和,即刷油漆的面积,刷油漆的面积×每平方米需要的油漆质量=需要的油漆总质量,与准备的油漆质量比较即可。注意统一单位。
【解答】解:根据三角形的面积公式可知:
5×1.8÷2×2=9(平方米)
450克=0.45千克
9×0.45=4.05(千克)
4.05>4
答:准备4千克油漆不够。
【点评】熟练掌握三角形的面积公式,是解答此题的关键。
48.淘气爷爷一面靠墙围了一个养鸡圈(如图)。
(1)如果要给它围上一圈篱笆,篱笆至少长多少米?
(2)这养鸡圈的占地面积有多大?
【答案】(1)9.14米;(2)7.57平方米。
【分析】(1)篱笆的长度是两个3米长度的和,加上直径是2米的圆的周长的一半,据此列式计算即可;
(2)鸡圈的占地面积是长是3米、宽是2米的长方形的面积的和,加上直径是2米的圆的面积的一半,据此列式计算即可。
【解答】解:(1)3×2+3.14×2÷2
=6+3.14
=9.14(米)
答:篱笆至少长9.14米。
(2)3×2+3.14×(2÷2)2÷2
=6+3.14×1÷2
=6+1.57
=7.57(平方米)
答:这养鸡圈的占地面积是7.57平方米。
【点评】解答此题要灵活运用长方形和圆的周长和面积公式。
49.一块铁皮的形状如图。请你算算这块铁皮的面积是多少?(单位:dm)
【答案】30dm2。
【分析】根据图示可知,铁皮的面积等于左侧三角形面积和右侧梯形面积之和,据此计算。
【解答】解:5×2÷2+(3.5+6.5)×5÷2
=5+25
=30(dm2)
答:这块铁皮的面积是30dm2。
【点评】本题考查了组合图形面积计算,牢记三角形和梯形面积公式是解题关键。
50.叔叔家果园的形状为梯形,它的上底22米,下底38米,高24米。叔叔计划在果园里栽果树,若每棵果树占地约6平方米,可以栽多少棵果树?
【答案】120棵。
【分析】根据梯形面积公式:梯形的面积=(上底+下底)×高÷2,代入数据,求出果园的面积,再用果园的面积除以每棵果树占地的面积,即可解答。
【解答】解:(22+38)×24÷2÷6
=60×24÷2÷6
=720÷6
=120(棵)
答:可以栽120棵果树。
【点评】熟练掌握梯形的面积公式是解答本题的关键。
51.为保障市民安全合理观看比赛,组委会在跑道两侧设置观看区域。某一跑道旁有一块直角梯形的观看区域,面积是34.8平方米。组委会在观看区域的三面围上护栏(如图),只测得梯形的高为3.2米,请你算出护栏的总长是多少米?
【答案】24.95米。
【分析】由题意,已知梯形的面积和高,用梯形的面积乘2除以高即得上下底之和,再加上高就是护栏总长,代入数据即可解答。
【解答】解:34.8×2÷3.2+3.2
=69.6÷3.2+3.2
=21.75+3.2
=24.95(米)
答:护栏总长有24.95米。
【点评】此题考查了梯形的面积公式的实际应用,关键是明确上下底的和。
52.哈尔滨亚冬会期间冰雪大世界有一块室外游乐场地(如图),相关研究表明:室外景点低于0.75平方米/人时,就有发生踩踏事故的危险。要避免踩踏事故的出现这块场地最多能容纳多少人同时活动?
【答案】152人。
【分析】根据图示可知,该游乐场所为一个长方形和梯形的组合图形场所,右侧为长7米,宽6米的长方形,左侧为上底6米,下底12米,高(15﹣7)米的梯形。根据“长方形面积=长×宽,梯形面积=(上底+下底)×高÷2”分别计算出长方形和梯形的面积后相加求和即为该游乐场所的面积;再根据低于0.75平方米/人时,就有发生踩踏事故的危险,用游乐场所面积除以0.75即是组多可容纳人数,据此解答。
【解答】解:6×7=42(平方米)
(6+12)×(15﹣7)÷2=72(平方米)
72+42=114(平方米)
114÷0.75=152(人)
答:要避免踩踏事故的出现这块场地最多能容纳152人同时活动。
【点评】本题考查了组合图形面积计算的应用。
53.盛安小学原有一个长方形花坛,后来因修路的需要,长减少了5米,这个花圃的面积减少了100平方米。减少后的花坛正好是一个正方形,原来长方形花圃的面积是多少平方米?(先在图中画出减少部分,再解答)
【答案】;500平方米。
【分析】根据画图策略,画出示意图,从图中分析,从长减少了5米,花圃的面积减少了100平方米,则先用减少的面积除以减少的长,求出原来长方形的宽,再根据面积减少后花圃正好是一个正方形,故原来长方形的长是(宽+5)米,最后再根据“长方形的面积=长×宽”,求出原来长方形花圃的面积即可解答。
【解答】解:如图所示:
(100÷5+5)×(100÷5)
=(20+5)×20
=25×20
=500(平方米)
答:原来长方形花圃的面积是500平方米。
【点评】解答此题要运用长方形的面积公式。
54.如图的平行四边形底是6厘米,高是4.5厘米,请你画一条线将它分成两个大小形状完全相同的梯形,并算出其中一个梯形的面积。
【答案】(画法不唯一);13.5平方厘米。
【分析】连接平行四边形的两条对角线,找出对角线的交点,即平行四边形的中心点,过平行四边形的中心点,任意画一条线段(线段的两个端点不能是梯形的顶点和梯形四条边的中点),即可分成两个大小形状完全相同的梯形;再根据一个梯形的面积等于原来平行四边的面积÷2,据此计算即可求出面积。
【解答】解:画图如下:(画法不唯一)
6×4.5÷2
=27÷2
=13.5(平方厘米)
答:其中一个梯形的面积是13.5平方厘米。
【点评】本题考查了平行四边形的性质以及梯形的面积计算。
55.一扇老式木门,最上面有个梯形的透光窗,窗架的上底是5分米,下底9分米,高4分米。如果要为这个窗架配一块玻璃,这块玻璃的面积至少有多大?(忽略玻璃与窗架镶嵌处的面积)
【答案】28平方分米。
【分析】根据梯形面积=(上底+下底)×高÷2,即可解答。
【解答】解:(5+9)×4÷2
=56÷2
=28(平方分米)
答:这块玻璃的面积至少有28平方分米。
【点评】本题考查的是梯形面积的计算,熟记公式是解答关键。
56.李明经常在自家小区圆形的游泳池边散步。这天,他以每分钟62.8m的速度绕泳池走了一圈,恰好用了5分钟。这个泳池的面积是多少平方米?
【答案】7850平方米。
【分析】首先根据路程=速度×时间,求出这个圆形游泳池的周长,再根据圆的周长公式:C=2πr,那么r=C÷2π,据此求出半径,然后根据圆的面积公式:S=πr2,把数据代入公式解答。
【解答】解:62.8×5=314(米)
314÷3.14÷2=50(米)
3.14×502
=3.14×2500
=7850(平方米)
答:这个游泳池的占地面积是7850平方米。
【点评】此题主要考查圆的周长公式、面积公式的灵活运用,关键是熟记公式。
57.旧城改造,准备修建一个花坛,形状如图,它的边是4个直径相等的半圆。这个花坛的面积是多少平方米?
【答案】164.48平方米。
【分析】花坛面积即为直径为8米的2个圆面积以及边长为8米的正方形面积,根据“圆面积=πr2以及正方形面积=边长×边长”分别求解圆面积和正方形面积,然后相加求和即可。
【解答】解:3.14×(8÷2)2×2+8×8
=100.48+64
=164.48(平方米)
答:这个花坛的面积是164.48平方米。
【点评】本题考查了组合图形面积计算的应用。
58.大约在两千年前,我国数学名著《九章算术》中的“方田章”就论述了平面图形面积的算法。书中说:“圭田术曰,半广以乘正从。”其中“圭田”就是指三角形田地,“广”和“从”是指三角形的底和高,已知三角形的面积是35.2平方米,底是4.4米,它的高是多少米?
【答案】16米。
【分析】根据三角形的面积公式:S=ah÷2,那么h=2S÷a,把数据代入公式解答。
【解答】解:35.2×2÷4.4
=70.8÷4.4
=16(米)
答:它的高是16米。
【点评】此题主要考查三角形面积公式的灵活运用,关键是熟记公式。
59.用一根长15dm的铁丝围成一个等腰梯形。已知这个梯形的两腰共长8.6dm,高是3dm,这个梯形的面积是多少dm2?
【答案】9.6平方分米。
【分析】根据梯形的周长公式,用梯形的周长减去两腰的长度即可求出梯形上、下底之和,再根据梯形的面积公式:S=(a+b)×h÷2,把数据代入公式解答。
【解答】解:(15﹣8.6)×3÷2
=6.4×3÷2
=9.6(平方分米)
答:这个等腰梯形的面积是9.6平方分米。
【点评】此题主要考查梯形的周长公式、面积公式的灵活运用。
60.中国少年先锋队是中国少年儿童的群团组织,是少年儿童学习中国特色社会主义和共产主义的学校,是建设社会主义和共产主义的预备队,我们每一个班级中队就是中国少先队的一个小集体。兴华小学要做12面中队旗,共需要多少平方米布?
【答案】5.04平方米。
【分析】先用长为80厘米、宽为60厘米的长方形面积减去底为60厘米、高为20厘米的三角形面积,求出做1面中队旗需要多少平方厘米布,再乘12,求出做12面中队旗要多少平方厘米布,然后将单位换算成平方米即可。
【解答】解:(80×60﹣60×20÷2)×12
=4200×12
=50400(平方厘米)
50400平方厘米=5.04平方米
答:共需要5.04平方米布。
【点评】解答本题需准确分析图形的组成,数据长方形和商量下面积公式。
21世纪教育网(www.21cnjy.com)
同课章节目录
