【小升初押题卷】圆柱与圆锥高频易错冲刺卷(含解析)-2024-2025学年六年级下学期数学苏教版
文档属性
| 名称 | 【小升初押题卷】圆柱与圆锥高频易错冲刺卷(含解析)-2024-2025学年六年级下学期数学苏教版 |  | |
| 格式 | docx | ||
| 文件大小 | 971.9KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 苏教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-05-07 22:01:03 | ||
图片预览


文档简介
圆柱与圆锥
1.一个圆柱侧面展开是一个正方形,这个正方形的周长是50.24厘米,这个圆柱的底面半径是多少厘米?
2.如图是一个生日蛋糕的包装盒。这个圆柱形包装盒的底面直径是30cm,高是20cm。像图中这样捆扎,打结处在上底面圆的圆心处,至少需要多少厘米的彩带?(打结处需要35cm的彩带)
3.奶奶过生日,爸爸买了一个大蛋糕。蛋糕盒是圆柱形的,爸爸准备用十字交叉的方法系一条丝带并打一个蝴蝶结(如图),至少需要买多长的丝带?(蝴蝶结需要3.5分米丝带)
4.将一个底面直径是26厘米、高是5厘米的圆锥形木块分成形状、大小完全相同的两个木块后,表面积比原来增加了多少平方厘米?
5.一种圆柱形饮料罐,底面直径是7cm,高是12cm。将20罐这种饮料放入一个长方体纸箱内(如图)。这个纸箱内部的长、宽、高至少是多少厘米?
6.妈妈给小军买了一个生日蛋糕,并用一个圆柱形蛋糕盒包装(如图)。用彩带捆扎这个蛋糕盒,至少需要彩带多少厘米?(打结处彩带大约长30厘米)
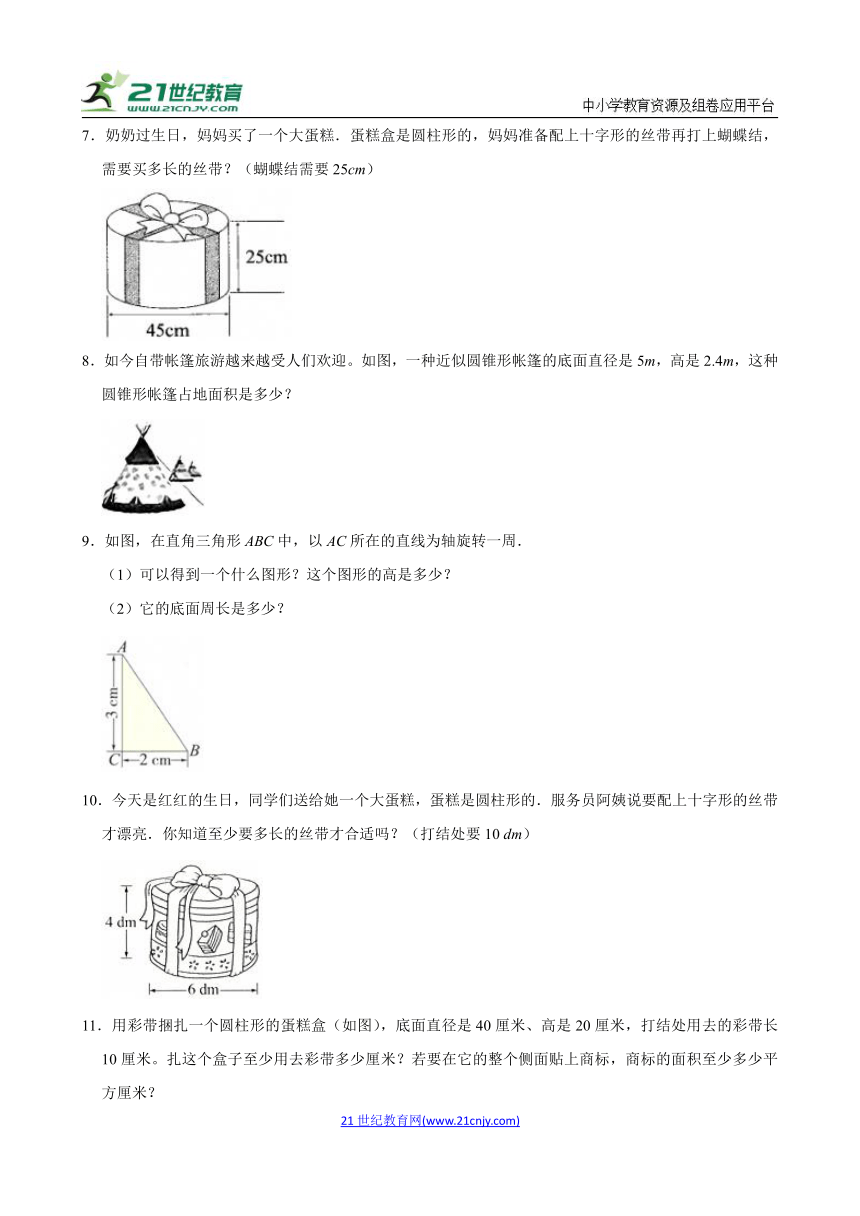
7.奶奶过生日,妈妈买了一个大蛋糕.蛋糕盒是圆柱形的,妈妈准备配上十字形的丝带再打上蝴蝶结,需要买多长的丝带?(蝴蝶结需要25cm)
8.如今自带帐篷旅游越来越受人们欢迎。如图,一种近似圆锥形帐篷的底面直径是5m,高是2.4m,这种圆锥形帐篷占地面积是多少?
9.如图,在直角三角形ABC中,以AC所在的直线为轴旋转一周.
(1)可以得到一个什么图形?这个图形的高是多少?
(2)它的底面周长是多少?
10.今天是红红的生日,同学们送给她一个大蛋糕,蛋糕是圆柱形的.服务员阿姨说要配上十字形的丝带才漂亮.你知道至少要多长的丝带才合适吗?(打结处要10 dm)
11.用彩带捆扎一个圆柱形的蛋糕盒(如图),底面直径是40厘米、高是20厘米,打结处用去的彩带长10厘米。扎这个盒子至少用去彩带多少厘米?若要在它的整个侧面贴上商标,商标的面积至少多少平方厘米?
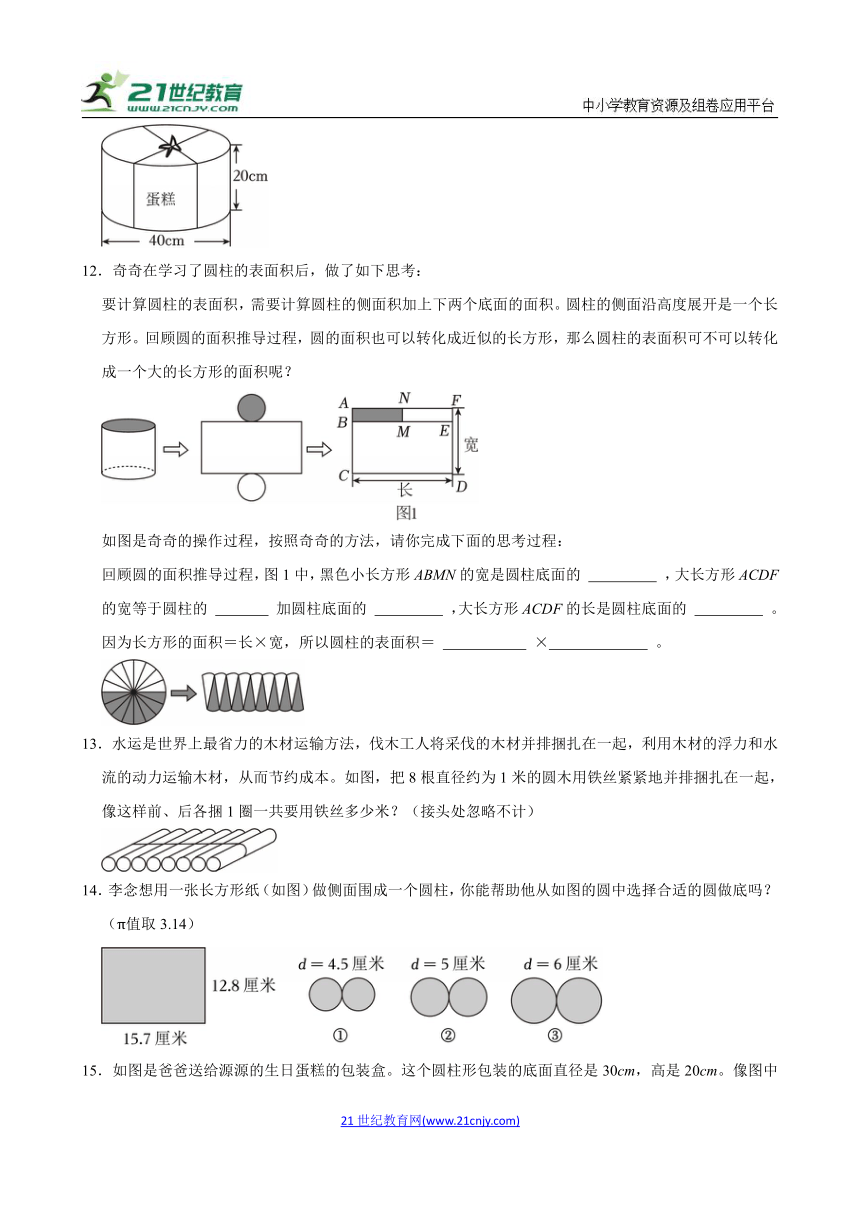
12.奇奇在学习了圆柱的表面积后,做了如下思考:
要计算圆柱的表面积,需要计算圆柱的侧面积加上下两个底面的面积。圆柱的侧面沿高度展开是一个长方形。回顾圆的面积推导过程,圆的面积也可以转化成近似的长方形,那么圆柱的表面积可不可以转化成一个大的长方形的面积呢?
如图是奇奇的操作过程,按照奇奇的方法,请你完成下面的思考过程:
回顾圆的面积推导过程,图1中,黑色小长方形ABMN的宽是圆柱底面的 ,大长方形ACDF的宽等于圆柱的 加圆柱底面的 ,大长方形ACDF的长是圆柱底面的 。
因为长方形的面积=长×宽,所以圆柱的表面积= × 。
13.水运是世界上最省力的木材运输方法,伐木工人将采伐的木材并排捆扎在一起,利用木材的浮力和水流的动力运输木材,从而节约成本。如图,把8根直径约为1米的圆木用铁丝紧紧地并排捆扎在一起,像这样前、后各捆1圈一共要用铁丝多少米?(接头处忽略不计)
14.李念想用一张长方形纸(如图)做侧面围成一个圆柱,你能帮助他从如图的圆中选择合适的圆做底吗?(π值取3.14)
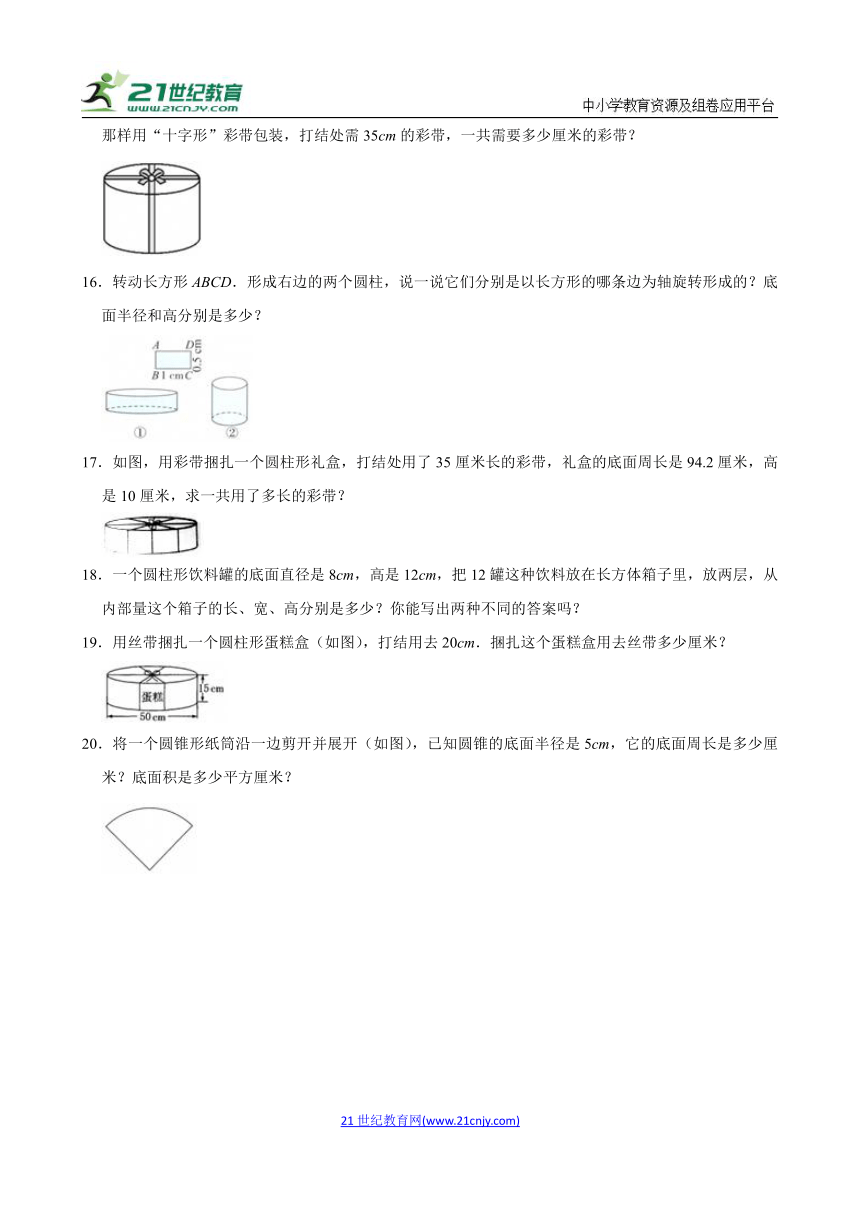
15.如图是爸爸送给源源的生日蛋糕的包装盒。这个圆柱形包装的底面直径是30cm,高是20cm。像图中那样用“十字形”彩带包装,打结处需35cm的彩带,一共需要多少厘米的彩带?
16.转动长方形ABCD.形成右边的两个圆柱,说一说它们分别是以长方形的哪条边为轴旋转形成的?底面半径和高分别是多少?
17.如图,用彩带捆扎一个圆柱形礼盒,打结处用了35厘米长的彩带,礼盒的底面周长是94.2厘米,高是10厘米,求一共用了多长的彩带?
18.一个圆柱形饮料罐的底面直径是8cm,高是12cm,把12罐这种饮料放在长方体箱子里,放两层,从内部量这个箱子的长、宽、高分别是多少?你能写出两种不同的答案吗?
19.用丝带捆扎一个圆柱形蛋糕盒(如图),打结用去20cm.捆扎这个蛋糕盒用去丝带多少厘米?
20.将一个圆锥形纸筒沿一边剪开并展开(如图),已知圆锥的底面半径是5cm,它的底面周长是多少厘米?底面积是多少平方厘米?
圆柱与圆锥
参考答案与试题解析
1.一个圆柱侧面展开是一个正方形,这个正方形的周长是50.24厘米,这个圆柱的底面半径是多少厘米?
【答案】2厘米。
【分析】根据圆柱侧面展开图的特征可知,如果圆柱的侧面沿高展开是一个正方形,那么这个圆柱的底面周长和高相等,根据正方形的周长=边长×4,那么边长=周长÷4,据此求出圆柱的底面周长,再根据圆的周长公式:C=2πr,那么r=C÷π÷2,把数据代入公式解答。
【解答】解:50.24÷4=12.56(厘米)
12.56÷3.14÷2=2(厘米)
答:这个圆柱的底面半径是2厘米。
【点评】此题考查的目的是理解掌握圆柱侧面展开图的特征及应用,正方形的周长公式、圆的周长公式及应用,关键是熟记公式。
2.如图是一个生日蛋糕的包装盒。这个圆柱形包装盒的底面直径是30cm,高是20cm。像图中这样捆扎,打结处在上底面圆的圆心处,至少需要多少厘米的彩带?(打结处需要35cm的彩带)
【答案】235厘米。
【分析】彩带的长为4条直径加上4条高和打结处用去的彩带长,据此即可求解。
【解答】解:30×4+20×4+35
=120+80+35
=235(厘米)
答:一共需要235厘米的彩带。
【点评】此题主要考查利用圆柱的特征来解决实际问题。
3.奶奶过生日,爸爸买了一个大蛋糕。蛋糕盒是圆柱形的,爸爸准备用十字交叉的方法系一条丝带并打一个蝴蝶结(如图),至少需要买多长的丝带?(蝴蝶结需要3.5分米丝带)
【答案】35.5分米。
【分析】通过观察,捆扎这个盒子至少用去丝带4个蛋糕盒底面直径和4个蛋糕盒高,再加上打结用去丝带长3.5分米,由此得解。
【解答】解:5×4+3×4+3.5
=20+12+3.5
=35.5(分米)
答:至少需要买35.5分米长的丝带。
【点评】此题要求学生要有空间想象力,能够想到底面和背面也有和我们现在看到的一样多的丝带。
4.将一个底面直径是26厘米、高是5厘米的圆锥形木块分成形状、大小完全相同的两个木块后,表面积比原来增加了多少平方厘米?
【答案】130平方厘米。
【分析】要把圆锥形木块分成形状、大小完全相同的两个木块,应沿着圆锥的高切开,得到两个切面,切面是两个相同的等腰三角形。切开后,表面积比原来增加的部分为两个等腰三角形的面积。等腰三角形的高是圆锥的高,等腰三角形的底是圆锥的底面直径。根据“三角形的面积=底×高÷2”可求出两个等腰三角形的面积,也就是表面积比原来增加的部分。
【解答】解:26×5÷2×2
=130÷2×2
=65×2
=130(平方厘米)
答:表面积比原来增加了130平方厘米。
【点评】此题考查圆锥的特征。明确切割的方式和切面的特征是解答的关键。
5.一种圆柱形饮料罐,底面直径是7cm,高是12cm。将20罐这种饮料放入一个长方体纸箱内(如图)。这个纸箱内部的长、宽、高至少是多少厘米?
【答案】35厘米,28厘米,12厘米。
【分析】由右图可看出:纸箱的长是5个圆柱形饮料罐的底面直径;纸箱的宽是4个圆柱形饮料罐的底面直径;纸箱的高等于圆柱形饮料罐的高;据此解答。
【解答】解:纸箱的长是:7×5=35(厘米)
纸箱的宽是:7×4=28(厘米)
答:这个纸箱内部的长、宽、高至少是35厘米,28厘米,12厘米。
【点评】解题关键是纸箱的长、宽、高和圆柱形饮料罐的关系。
6.妈妈给小军买了一个生日蛋糕,并用一个圆柱形蛋糕盒包装(如图)。用彩带捆扎这个蛋糕盒,至少需要彩带多少厘米?(打结处彩带大约长30厘米)
【答案】270。
【分析】通过观察图形可知,需要彩带的长度等于这个圆柱的4条直径加上4条高的长度,再加上打结用的30厘米。据此即可得出答案。
【解答】解:40×4+20×4+30
=160+80+30
=240+30
=270(厘米)
答:至少需要彩带270厘米。
【点评】本题考查学生对圆柱特征的掌握和运用。
7.奶奶过生日,妈妈买了一个大蛋糕.蛋糕盒是圆柱形的,妈妈准备配上十字形的丝带再打上蝴蝶结,需要买多长的丝带?(蝴蝶结需要25cm)
【答案】见试题解答内容
【分析】通过观察,捆扎这个盒子至少用去丝带4个蛋糕盒底面直径和4个蛋糕盒高,再加上打结用去丝带长25厘米,由此得解.
【解答】解:45×4+25×4+25
=180+100+25
=305(厘米)
答:需要买305厘米长的丝带.
【点评】此题要求学生要有空间想象力,能够想到底面和背面也有和我们现在看到的一样多的丝带.
8.如今自带帐篷旅游越来越受人们欢迎。如图,一种近似圆锥形帐篷的底面直径是5m,高是2.4m,这种圆锥形帐篷占地面积是多少?
【答案】19.625平方米。
【分析】根据题意,求的是圆锥的底面积,运用圆的面积公式S=πr2,代入数据计算即可。
【解答】解:3.14×(5÷2)2
=3.14×6.25
=19.625(平方米)
答:这种圆锥形帐篷占地面积是19.625平方米。
【点评】此题主要考查圆的面积计算公式的灵活运用,结合题意分析解答即可。
9.如图,在直角三角形ABC中,以AC所在的直线为轴旋转一周.
(1)可以得到一个什么图形?这个图形的高是多少?
(2)它的底面周长是多少?
【答案】见试题解答内容
【分析】(1)直角三角形ABC中,以AC所在的直线为轴旋转一周,可以得到一个圆锥,这个图形的高是原三角形的高,即3cm;
(2)圆锥的底面是个圆,底面半径是原三角形的底,是2cm,所以底面周长是2×2×3.14=12.56厘米.
【解答】解:(1)可以得到一个圆锥,这个图形的高是3cm.
(2)2×2×3.14
=4×3.14
=12.56(cm)
答:它的底面周长是12.56厘米.
【点评】解答此题的关键是掌握圆锥的特征和面动成体的规律.
10.今天是红红的生日,同学们送给她一个大蛋糕,蛋糕是圆柱形的.服务员阿姨说要配上十字形的丝带才漂亮.你知道至少要多长的丝带才合适吗?(打结处要10 dm)
【答案】见试题解答内容
【分析】通过观察,捆扎这个盒子至少用去4个底面直径和4个高长度的和,再加上打结用去丝带的长度10分米,由此得解.
【解答】解:6×4+4×4+10
=24+16+10
=50(分米)
答:至少要50分米的丝带才合适.
【点评】此题要求学生要有空间想象力,能够想到底面和背面也有和我们现在看到的一样多的丝带.
11.用彩带捆扎一个圆柱形的蛋糕盒(如图),底面直径是40厘米、高是20厘米,打结处用去的彩带长10厘米。扎这个盒子至少用去彩带多少厘米?若要在它的整个侧面贴上商标,商标的面积至少多少平方厘米?
【答案】250厘米,2512平方厘米。
【分析】(1)要求扎这个盒子至少用去塑料绳多少厘米,就是求4条直径、4条高和打结用去的绳长的总和。
(2)求商标的面积是多少平方厘米,就是求圆柱形蛋糕盒的侧面积,根据圆柱的侧面积=πdh,解答即可。
【解答】解:彩带的长度:20×4+40×4+10
=80+160+10
=250(厘米)
答:扎这个盒子至少用去彩带250厘米。
商标的面积:3.14×40×20
=125.6×20
=2512(平方厘米)
答:商标的面积至少2512平方厘米。
【点评】解答此题用到的知识点:①圆柱的侧面积的计算方法;②圆柱的特征。
12.奇奇在学习了圆柱的表面积后,做了如下思考:
要计算圆柱的表面积,需要计算圆柱的侧面积加上下两个底面的面积。圆柱的侧面沿高度展开是一个长方形。回顾圆的面积推导过程,圆的面积也可以转化成近似的长方形,那么圆柱的表面积可不可以转化成一个大的长方形的面积呢?
如图是奇奇的操作过程,按照奇奇的方法,请你完成下面的思考过程:
回顾圆的面积推导过程,图1中,黑色小长方形ABMN的宽是圆柱底面的 半径 ,大长方形ACDF的宽等于圆柱的 高 加圆柱底面的 半径 ,大长方形ACDF的长是圆柱底面的 周长 。
因为长方形的面积=长×宽,所以圆柱的表面积= 底面周长 × (高+半径) 。
【答案】见试题解答内容
【分析】利用转化法解答,由图可知:将圆柱的两个底面的圆切分并拼成近似的长方形,拼成的大长方形的长即为圆柱的底面圆周长,宽为圆柱的底面半径加上圆柱的高,圆柱的展开所拼成的大长方形面积即为圆柱表面积,得出圆柱表面积=底面周长×(h+r)。
【解答】解:图1中,黑色小长方形ABMN的宽是圆柱底面的 半径,大长方形ACDF的宽等于圆柱的 高加圆柱底面的 半径,大长方形ACDF的长是圆柱底面的 周长。
因为长方形的面积=长×宽,所以圆柱的表面积=底面周长×(高+半径)。
故答案为:半径,高,半径,周长,底面周长,(高+半径)。
【点评】本题考查了圆柱表面积公式推导的过程。
13.水运是世界上最省力的木材运输方法,伐木工人将采伐的木材并排捆扎在一起,利用木材的浮力和水流的动力运输木材,从而节约成本。如图,把8根直径约为1米的圆木用铁丝紧紧地并排捆扎在一起,像这样前、后各捆1圈一共要用铁丝多少米?(接头处忽略不计)
【答案】34.28米。
【分析】由图可知铁丝紧紧地捆绑一圈,最左边和最右边各一个半圆,上面的铁丝是7个直径,下面的铁丝是7个直径,所以总的长度实际上是由一个圆的周长加上14个直径的长度,前、后各捆1圈是2圈,再乘2即可得解。
【解答】解:3.14×1=3.14(米)
[3.14+1×(7+7)]×2
=(3.14+14)×2
=17.14×2
=34.28(米)
答:像这样前、后各捆1圈一共要用铁丝34.28米。
【点评】此题考查了学生的观察能力以及求圆的周长的方法。
14.李念想用一张长方形纸(如图)做侧面围成一个圆柱,你能帮助他从如图的圆中选择合适的圆做底吗?(π值取3.14)
【答案】②
【分析】根据圆的周长=πd,分别用长方形的长和宽作为圆的周长,计算出直径,在选项中找出符合题意的直径即可。
【解答】解:12.8÷3.14≈4.1(厘米)
15.7÷3.14=5(厘米)
以15.7为底面周长,5厘米为底面直径,即可围成一个圆柱。
答:选择②作为圆柱的底。
【点评】本题考查圆柱的特征以及底面直径的计算。
15.如图是爸爸送给源源的生日蛋糕的包装盒。这个圆柱形包装的底面直径是30cm,高是20cm。像图中那样用“十字形”彩带包装,打结处需35cm的彩带,一共需要多少厘米的彩带?
【答案】235厘米。
【分析】彩带的长为4条直径加上4条高和打结处用去的彩带长,据此即可求解。
【解答】解:30×4+20×4+35
=120+80+35
=235(厘米)
答:一共需要235厘米的彩带。
【点评】此题主要考查利用圆柱的特征来解决实际问题。
16.转动长方形ABCD.形成右边的两个圆柱,说一说它们分别是以长方形的哪条边为轴旋转形成的?底面半径和高分别是多少?
【答案】见试题解答内容
【分析】根据面动成体,转动长方形ABCD,以AB或CD边为轴旋转一周,得到的圆柱高为0.5厘米,底面半径为1厘米,生成圆柱①;以AD或BC为轴旋转一周得到的圆柱高为1厘米,底面半径为0.5厘米,生成圆柱②.
【解答】解:圆柱①是长方形ABCD以AB或CD边为轴旋转一周得到的,底面半径为1厘米,圆柱高为0.5厘米.
圆柱②是长方形ABCD以AD或BC边为轴旋转一周得到的,底面半径为0.5厘米,圆柱高为1厘米.
【点评】一个长方形绕长(或宽)为旋转轴转动一周,将得到一个以长(或宽)为高宽(或长)为底面半径的圆柱.
17.如图,用彩带捆扎一个圆柱形礼盒,打结处用了35厘米长的彩带,礼盒的底面周长是94.2厘米,高是10厘米,求一共用了多长的彩带?
【答案】355厘米。
【分析】根据题意和图形可知,礼盒是圆柱体,底面周长是94.2厘米,高是10厘米,彩带长是圆柱体的8条直径的长度+8条高的长度+接头处用去35厘米,由此解答即可。
【解答】解:94.2÷3.14×8+10×8+35
=240+80+35
=355(厘米)
答:一共用了355厘米的彩带。
【点评】题的解答主要根据圆柱体的特征,它的上下底面是两个完全相同的圆,两个底面之间的距离是它的高。
18.一个圆柱形饮料罐的底面直径是8cm,高是12cm,把12罐这种饮料放在长方体箱子里,放两层,从内部量这个箱子的长、宽、高分别是多少?你能写出两种不同的答案吗?
【答案】见试题解答内容
【分析】根据题意,可以把圆柱形的饮料罐横放,一排6罐,放2层,这样箱子的长等于圆柱底面直径6倍,箱子的宽等于圆柱的高,箱子的高等于圆柱底面直径的2倍;还可以竖放,一排6罐,放2层,这样箱子的长等于这个圆柱底面直径的6倍,宽等于圆柱的底面直径,高等于圆柱高的2倍;据此解答.
【解答】解:方法一:可以把圆柱形的饮料罐横放,一排6罐,放2层,这样箱子的长等于圆柱底面直径6倍,箱子的宽等于圆柱的高,箱子的高等于圆柱底面直径的2倍;
箱子的长是8×6=48(厘米),宽是12厘米,高是8×2=16(厘米);
方法二:可以竖放,一排6罐,放2层,这样箱子的长等于这个圆柱底面直径的6倍,宽等于圆柱的底面直径,高等于圆柱高的2倍;
箱子的长是8×6=48(厘米),宽是8厘米,高是12×2=24(厘米);
答:从内部量这个箱子的长、宽、高分别是48厘米、12厘米、16厘米或48厘米、8厘米、24厘米.
【点评】此题考查的目的是理解掌握圆柱的特征,并且能够根据圆柱的特征解决有关的实际问题.
19.用丝带捆扎一个圆柱形蛋糕盒(如图),打结用去20cm.捆扎这个蛋糕盒用去丝带多少厘米?
【答案】见试题解答内容
【分析】根据题意,把一个底面直径是50厘米,高是15厘米蛋糕盒用丝带捆扎起来,由图形可知,需要丝带的长度等于这个圆柱底面直径的4倍加上高的4倍再加上打结用的20厘米,据此列式解答.
【解答】解:50×6+15×6+20
=300+90+20
=410(厘米)
答:捆扎这个蛋糕盒用去丝带410厘米.
【点评】此题考查的目的是理解掌握圆柱的特征,并能根据圆柱的特征解决有关的实际问题.
20.将一个圆锥形纸筒沿一边剪开并展开(如图),已知圆锥的底面半径是5cm,它的底面周长是多少厘米?底面积是多少平方厘米?
【答案】底面周长是31.4厘米,底面积是78.5平方厘米。
【分析】首先根据C=2πr,求出底面周长,然后根据S=πr2求出底面积。
【解答】解:3.14×5×2=31.4(厘米)
3.14×52
=3.14×25
=78.5(平方厘米)
答:它的底面周长是31.4厘米,底面积是78.5平方厘米。
【点评】此题主要考查利用公式计算圆锥的底面周长和面积,关键是熟练掌握圆的周长和面积公式。
21世纪教育网(www.21cnjy.com)
1.一个圆柱侧面展开是一个正方形,这个正方形的周长是50.24厘米,这个圆柱的底面半径是多少厘米?
2.如图是一个生日蛋糕的包装盒。这个圆柱形包装盒的底面直径是30cm,高是20cm。像图中这样捆扎,打结处在上底面圆的圆心处,至少需要多少厘米的彩带?(打结处需要35cm的彩带)
3.奶奶过生日,爸爸买了一个大蛋糕。蛋糕盒是圆柱形的,爸爸准备用十字交叉的方法系一条丝带并打一个蝴蝶结(如图),至少需要买多长的丝带?(蝴蝶结需要3.5分米丝带)
4.将一个底面直径是26厘米、高是5厘米的圆锥形木块分成形状、大小完全相同的两个木块后,表面积比原来增加了多少平方厘米?
5.一种圆柱形饮料罐,底面直径是7cm,高是12cm。将20罐这种饮料放入一个长方体纸箱内(如图)。这个纸箱内部的长、宽、高至少是多少厘米?
6.妈妈给小军买了一个生日蛋糕,并用一个圆柱形蛋糕盒包装(如图)。用彩带捆扎这个蛋糕盒,至少需要彩带多少厘米?(打结处彩带大约长30厘米)
7.奶奶过生日,妈妈买了一个大蛋糕.蛋糕盒是圆柱形的,妈妈准备配上十字形的丝带再打上蝴蝶结,需要买多长的丝带?(蝴蝶结需要25cm)
8.如今自带帐篷旅游越来越受人们欢迎。如图,一种近似圆锥形帐篷的底面直径是5m,高是2.4m,这种圆锥形帐篷占地面积是多少?
9.如图,在直角三角形ABC中,以AC所在的直线为轴旋转一周.
(1)可以得到一个什么图形?这个图形的高是多少?
(2)它的底面周长是多少?
10.今天是红红的生日,同学们送给她一个大蛋糕,蛋糕是圆柱形的.服务员阿姨说要配上十字形的丝带才漂亮.你知道至少要多长的丝带才合适吗?(打结处要10 dm)
11.用彩带捆扎一个圆柱形的蛋糕盒(如图),底面直径是40厘米、高是20厘米,打结处用去的彩带长10厘米。扎这个盒子至少用去彩带多少厘米?若要在它的整个侧面贴上商标,商标的面积至少多少平方厘米?
12.奇奇在学习了圆柱的表面积后,做了如下思考:
要计算圆柱的表面积,需要计算圆柱的侧面积加上下两个底面的面积。圆柱的侧面沿高度展开是一个长方形。回顾圆的面积推导过程,圆的面积也可以转化成近似的长方形,那么圆柱的表面积可不可以转化成一个大的长方形的面积呢?
如图是奇奇的操作过程,按照奇奇的方法,请你完成下面的思考过程:
回顾圆的面积推导过程,图1中,黑色小长方形ABMN的宽是圆柱底面的 ,大长方形ACDF的宽等于圆柱的 加圆柱底面的 ,大长方形ACDF的长是圆柱底面的 。
因为长方形的面积=长×宽,所以圆柱的表面积= × 。
13.水运是世界上最省力的木材运输方法,伐木工人将采伐的木材并排捆扎在一起,利用木材的浮力和水流的动力运输木材,从而节约成本。如图,把8根直径约为1米的圆木用铁丝紧紧地并排捆扎在一起,像这样前、后各捆1圈一共要用铁丝多少米?(接头处忽略不计)
14.李念想用一张长方形纸(如图)做侧面围成一个圆柱,你能帮助他从如图的圆中选择合适的圆做底吗?(π值取3.14)
15.如图是爸爸送给源源的生日蛋糕的包装盒。这个圆柱形包装的底面直径是30cm,高是20cm。像图中那样用“十字形”彩带包装,打结处需35cm的彩带,一共需要多少厘米的彩带?
16.转动长方形ABCD.形成右边的两个圆柱,说一说它们分别是以长方形的哪条边为轴旋转形成的?底面半径和高分别是多少?
17.如图,用彩带捆扎一个圆柱形礼盒,打结处用了35厘米长的彩带,礼盒的底面周长是94.2厘米,高是10厘米,求一共用了多长的彩带?
18.一个圆柱形饮料罐的底面直径是8cm,高是12cm,把12罐这种饮料放在长方体箱子里,放两层,从内部量这个箱子的长、宽、高分别是多少?你能写出两种不同的答案吗?
19.用丝带捆扎一个圆柱形蛋糕盒(如图),打结用去20cm.捆扎这个蛋糕盒用去丝带多少厘米?
20.将一个圆锥形纸筒沿一边剪开并展开(如图),已知圆锥的底面半径是5cm,它的底面周长是多少厘米?底面积是多少平方厘米?
圆柱与圆锥
参考答案与试题解析
1.一个圆柱侧面展开是一个正方形,这个正方形的周长是50.24厘米,这个圆柱的底面半径是多少厘米?
【答案】2厘米。
【分析】根据圆柱侧面展开图的特征可知,如果圆柱的侧面沿高展开是一个正方形,那么这个圆柱的底面周长和高相等,根据正方形的周长=边长×4,那么边长=周长÷4,据此求出圆柱的底面周长,再根据圆的周长公式:C=2πr,那么r=C÷π÷2,把数据代入公式解答。
【解答】解:50.24÷4=12.56(厘米)
12.56÷3.14÷2=2(厘米)
答:这个圆柱的底面半径是2厘米。
【点评】此题考查的目的是理解掌握圆柱侧面展开图的特征及应用,正方形的周长公式、圆的周长公式及应用,关键是熟记公式。
2.如图是一个生日蛋糕的包装盒。这个圆柱形包装盒的底面直径是30cm,高是20cm。像图中这样捆扎,打结处在上底面圆的圆心处,至少需要多少厘米的彩带?(打结处需要35cm的彩带)
【答案】235厘米。
【分析】彩带的长为4条直径加上4条高和打结处用去的彩带长,据此即可求解。
【解答】解:30×4+20×4+35
=120+80+35
=235(厘米)
答:一共需要235厘米的彩带。
【点评】此题主要考查利用圆柱的特征来解决实际问题。
3.奶奶过生日,爸爸买了一个大蛋糕。蛋糕盒是圆柱形的,爸爸准备用十字交叉的方法系一条丝带并打一个蝴蝶结(如图),至少需要买多长的丝带?(蝴蝶结需要3.5分米丝带)
【答案】35.5分米。
【分析】通过观察,捆扎这个盒子至少用去丝带4个蛋糕盒底面直径和4个蛋糕盒高,再加上打结用去丝带长3.5分米,由此得解。
【解答】解:5×4+3×4+3.5
=20+12+3.5
=35.5(分米)
答:至少需要买35.5分米长的丝带。
【点评】此题要求学生要有空间想象力,能够想到底面和背面也有和我们现在看到的一样多的丝带。
4.将一个底面直径是26厘米、高是5厘米的圆锥形木块分成形状、大小完全相同的两个木块后,表面积比原来增加了多少平方厘米?
【答案】130平方厘米。
【分析】要把圆锥形木块分成形状、大小完全相同的两个木块,应沿着圆锥的高切开,得到两个切面,切面是两个相同的等腰三角形。切开后,表面积比原来增加的部分为两个等腰三角形的面积。等腰三角形的高是圆锥的高,等腰三角形的底是圆锥的底面直径。根据“三角形的面积=底×高÷2”可求出两个等腰三角形的面积,也就是表面积比原来增加的部分。
【解答】解:26×5÷2×2
=130÷2×2
=65×2
=130(平方厘米)
答:表面积比原来增加了130平方厘米。
【点评】此题考查圆锥的特征。明确切割的方式和切面的特征是解答的关键。
5.一种圆柱形饮料罐,底面直径是7cm,高是12cm。将20罐这种饮料放入一个长方体纸箱内(如图)。这个纸箱内部的长、宽、高至少是多少厘米?
【答案】35厘米,28厘米,12厘米。
【分析】由右图可看出:纸箱的长是5个圆柱形饮料罐的底面直径;纸箱的宽是4个圆柱形饮料罐的底面直径;纸箱的高等于圆柱形饮料罐的高;据此解答。
【解答】解:纸箱的长是:7×5=35(厘米)
纸箱的宽是:7×4=28(厘米)
答:这个纸箱内部的长、宽、高至少是35厘米,28厘米,12厘米。
【点评】解题关键是纸箱的长、宽、高和圆柱形饮料罐的关系。
6.妈妈给小军买了一个生日蛋糕,并用一个圆柱形蛋糕盒包装(如图)。用彩带捆扎这个蛋糕盒,至少需要彩带多少厘米?(打结处彩带大约长30厘米)
【答案】270。
【分析】通过观察图形可知,需要彩带的长度等于这个圆柱的4条直径加上4条高的长度,再加上打结用的30厘米。据此即可得出答案。
【解答】解:40×4+20×4+30
=160+80+30
=240+30
=270(厘米)
答:至少需要彩带270厘米。
【点评】本题考查学生对圆柱特征的掌握和运用。
7.奶奶过生日,妈妈买了一个大蛋糕.蛋糕盒是圆柱形的,妈妈准备配上十字形的丝带再打上蝴蝶结,需要买多长的丝带?(蝴蝶结需要25cm)
【答案】见试题解答内容
【分析】通过观察,捆扎这个盒子至少用去丝带4个蛋糕盒底面直径和4个蛋糕盒高,再加上打结用去丝带长25厘米,由此得解.
【解答】解:45×4+25×4+25
=180+100+25
=305(厘米)
答:需要买305厘米长的丝带.
【点评】此题要求学生要有空间想象力,能够想到底面和背面也有和我们现在看到的一样多的丝带.
8.如今自带帐篷旅游越来越受人们欢迎。如图,一种近似圆锥形帐篷的底面直径是5m,高是2.4m,这种圆锥形帐篷占地面积是多少?
【答案】19.625平方米。
【分析】根据题意,求的是圆锥的底面积,运用圆的面积公式S=πr2,代入数据计算即可。
【解答】解:3.14×(5÷2)2
=3.14×6.25
=19.625(平方米)
答:这种圆锥形帐篷占地面积是19.625平方米。
【点评】此题主要考查圆的面积计算公式的灵活运用,结合题意分析解答即可。
9.如图,在直角三角形ABC中,以AC所在的直线为轴旋转一周.
(1)可以得到一个什么图形?这个图形的高是多少?
(2)它的底面周长是多少?
【答案】见试题解答内容
【分析】(1)直角三角形ABC中,以AC所在的直线为轴旋转一周,可以得到一个圆锥,这个图形的高是原三角形的高,即3cm;
(2)圆锥的底面是个圆,底面半径是原三角形的底,是2cm,所以底面周长是2×2×3.14=12.56厘米.
【解答】解:(1)可以得到一个圆锥,这个图形的高是3cm.
(2)2×2×3.14
=4×3.14
=12.56(cm)
答:它的底面周长是12.56厘米.
【点评】解答此题的关键是掌握圆锥的特征和面动成体的规律.
10.今天是红红的生日,同学们送给她一个大蛋糕,蛋糕是圆柱形的.服务员阿姨说要配上十字形的丝带才漂亮.你知道至少要多长的丝带才合适吗?(打结处要10 dm)
【答案】见试题解答内容
【分析】通过观察,捆扎这个盒子至少用去4个底面直径和4个高长度的和,再加上打结用去丝带的长度10分米,由此得解.
【解答】解:6×4+4×4+10
=24+16+10
=50(分米)
答:至少要50分米的丝带才合适.
【点评】此题要求学生要有空间想象力,能够想到底面和背面也有和我们现在看到的一样多的丝带.
11.用彩带捆扎一个圆柱形的蛋糕盒(如图),底面直径是40厘米、高是20厘米,打结处用去的彩带长10厘米。扎这个盒子至少用去彩带多少厘米?若要在它的整个侧面贴上商标,商标的面积至少多少平方厘米?
【答案】250厘米,2512平方厘米。
【分析】(1)要求扎这个盒子至少用去塑料绳多少厘米,就是求4条直径、4条高和打结用去的绳长的总和。
(2)求商标的面积是多少平方厘米,就是求圆柱形蛋糕盒的侧面积,根据圆柱的侧面积=πdh,解答即可。
【解答】解:彩带的长度:20×4+40×4+10
=80+160+10
=250(厘米)
答:扎这个盒子至少用去彩带250厘米。
商标的面积:3.14×40×20
=125.6×20
=2512(平方厘米)
答:商标的面积至少2512平方厘米。
【点评】解答此题用到的知识点:①圆柱的侧面积的计算方法;②圆柱的特征。
12.奇奇在学习了圆柱的表面积后,做了如下思考:
要计算圆柱的表面积,需要计算圆柱的侧面积加上下两个底面的面积。圆柱的侧面沿高度展开是一个长方形。回顾圆的面积推导过程,圆的面积也可以转化成近似的长方形,那么圆柱的表面积可不可以转化成一个大的长方形的面积呢?
如图是奇奇的操作过程,按照奇奇的方法,请你完成下面的思考过程:
回顾圆的面积推导过程,图1中,黑色小长方形ABMN的宽是圆柱底面的 半径 ,大长方形ACDF的宽等于圆柱的 高 加圆柱底面的 半径 ,大长方形ACDF的长是圆柱底面的 周长 。
因为长方形的面积=长×宽,所以圆柱的表面积= 底面周长 × (高+半径) 。
【答案】见试题解答内容
【分析】利用转化法解答,由图可知:将圆柱的两个底面的圆切分并拼成近似的长方形,拼成的大长方形的长即为圆柱的底面圆周长,宽为圆柱的底面半径加上圆柱的高,圆柱的展开所拼成的大长方形面积即为圆柱表面积,得出圆柱表面积=底面周长×(h+r)。
【解答】解:图1中,黑色小长方形ABMN的宽是圆柱底面的 半径,大长方形ACDF的宽等于圆柱的 高加圆柱底面的 半径,大长方形ACDF的长是圆柱底面的 周长。
因为长方形的面积=长×宽,所以圆柱的表面积=底面周长×(高+半径)。
故答案为:半径,高,半径,周长,底面周长,(高+半径)。
【点评】本题考查了圆柱表面积公式推导的过程。
13.水运是世界上最省力的木材运输方法,伐木工人将采伐的木材并排捆扎在一起,利用木材的浮力和水流的动力运输木材,从而节约成本。如图,把8根直径约为1米的圆木用铁丝紧紧地并排捆扎在一起,像这样前、后各捆1圈一共要用铁丝多少米?(接头处忽略不计)
【答案】34.28米。
【分析】由图可知铁丝紧紧地捆绑一圈,最左边和最右边各一个半圆,上面的铁丝是7个直径,下面的铁丝是7个直径,所以总的长度实际上是由一个圆的周长加上14个直径的长度,前、后各捆1圈是2圈,再乘2即可得解。
【解答】解:3.14×1=3.14(米)
[3.14+1×(7+7)]×2
=(3.14+14)×2
=17.14×2
=34.28(米)
答:像这样前、后各捆1圈一共要用铁丝34.28米。
【点评】此题考查了学生的观察能力以及求圆的周长的方法。
14.李念想用一张长方形纸(如图)做侧面围成一个圆柱,你能帮助他从如图的圆中选择合适的圆做底吗?(π值取3.14)
【答案】②
【分析】根据圆的周长=πd,分别用长方形的长和宽作为圆的周长,计算出直径,在选项中找出符合题意的直径即可。
【解答】解:12.8÷3.14≈4.1(厘米)
15.7÷3.14=5(厘米)
以15.7为底面周长,5厘米为底面直径,即可围成一个圆柱。
答:选择②作为圆柱的底。
【点评】本题考查圆柱的特征以及底面直径的计算。
15.如图是爸爸送给源源的生日蛋糕的包装盒。这个圆柱形包装的底面直径是30cm,高是20cm。像图中那样用“十字形”彩带包装,打结处需35cm的彩带,一共需要多少厘米的彩带?
【答案】235厘米。
【分析】彩带的长为4条直径加上4条高和打结处用去的彩带长,据此即可求解。
【解答】解:30×4+20×4+35
=120+80+35
=235(厘米)
答:一共需要235厘米的彩带。
【点评】此题主要考查利用圆柱的特征来解决实际问题。
16.转动长方形ABCD.形成右边的两个圆柱,说一说它们分别是以长方形的哪条边为轴旋转形成的?底面半径和高分别是多少?
【答案】见试题解答内容
【分析】根据面动成体,转动长方形ABCD,以AB或CD边为轴旋转一周,得到的圆柱高为0.5厘米,底面半径为1厘米,生成圆柱①;以AD或BC为轴旋转一周得到的圆柱高为1厘米,底面半径为0.5厘米,生成圆柱②.
【解答】解:圆柱①是长方形ABCD以AB或CD边为轴旋转一周得到的,底面半径为1厘米,圆柱高为0.5厘米.
圆柱②是长方形ABCD以AD或BC边为轴旋转一周得到的,底面半径为0.5厘米,圆柱高为1厘米.
【点评】一个长方形绕长(或宽)为旋转轴转动一周,将得到一个以长(或宽)为高宽(或长)为底面半径的圆柱.
17.如图,用彩带捆扎一个圆柱形礼盒,打结处用了35厘米长的彩带,礼盒的底面周长是94.2厘米,高是10厘米,求一共用了多长的彩带?
【答案】355厘米。
【分析】根据题意和图形可知,礼盒是圆柱体,底面周长是94.2厘米,高是10厘米,彩带长是圆柱体的8条直径的长度+8条高的长度+接头处用去35厘米,由此解答即可。
【解答】解:94.2÷3.14×8+10×8+35
=240+80+35
=355(厘米)
答:一共用了355厘米的彩带。
【点评】题的解答主要根据圆柱体的特征,它的上下底面是两个完全相同的圆,两个底面之间的距离是它的高。
18.一个圆柱形饮料罐的底面直径是8cm,高是12cm,把12罐这种饮料放在长方体箱子里,放两层,从内部量这个箱子的长、宽、高分别是多少?你能写出两种不同的答案吗?
【答案】见试题解答内容
【分析】根据题意,可以把圆柱形的饮料罐横放,一排6罐,放2层,这样箱子的长等于圆柱底面直径6倍,箱子的宽等于圆柱的高,箱子的高等于圆柱底面直径的2倍;还可以竖放,一排6罐,放2层,这样箱子的长等于这个圆柱底面直径的6倍,宽等于圆柱的底面直径,高等于圆柱高的2倍;据此解答.
【解答】解:方法一:可以把圆柱形的饮料罐横放,一排6罐,放2层,这样箱子的长等于圆柱底面直径6倍,箱子的宽等于圆柱的高,箱子的高等于圆柱底面直径的2倍;
箱子的长是8×6=48(厘米),宽是12厘米,高是8×2=16(厘米);
方法二:可以竖放,一排6罐,放2层,这样箱子的长等于这个圆柱底面直径的6倍,宽等于圆柱的底面直径,高等于圆柱高的2倍;
箱子的长是8×6=48(厘米),宽是8厘米,高是12×2=24(厘米);
答:从内部量这个箱子的长、宽、高分别是48厘米、12厘米、16厘米或48厘米、8厘米、24厘米.
【点评】此题考查的目的是理解掌握圆柱的特征,并且能够根据圆柱的特征解决有关的实际问题.
19.用丝带捆扎一个圆柱形蛋糕盒(如图),打结用去20cm.捆扎这个蛋糕盒用去丝带多少厘米?
【答案】见试题解答内容
【分析】根据题意,把一个底面直径是50厘米,高是15厘米蛋糕盒用丝带捆扎起来,由图形可知,需要丝带的长度等于这个圆柱底面直径的4倍加上高的4倍再加上打结用的20厘米,据此列式解答.
【解答】解:50×6+15×6+20
=300+90+20
=410(厘米)
答:捆扎这个蛋糕盒用去丝带410厘米.
【点评】此题考查的目的是理解掌握圆柱的特征,并能根据圆柱的特征解决有关的实际问题.
20.将一个圆锥形纸筒沿一边剪开并展开(如图),已知圆锥的底面半径是5cm,它的底面周长是多少厘米?底面积是多少平方厘米?
【答案】底面周长是31.4厘米,底面积是78.5平方厘米。
【分析】首先根据C=2πr,求出底面周长,然后根据S=πr2求出底面积。
【解答】解:3.14×5×2=31.4(厘米)
3.14×52
=3.14×25
=78.5(平方厘米)
答:它的底面周长是31.4厘米,底面积是78.5平方厘米。
【点评】此题主要考查利用公式计算圆锥的底面周长和面积,关键是熟练掌握圆的周长和面积公式。
21世纪教育网(www.21cnjy.com)
同课章节目录
