2016春鲁教版数学八下第六章《特殊平行四边形复习课》ppt课件 (共42张PPT)
文档属性
| 名称 | 2016春鲁教版数学八下第六章《特殊平行四边形复习课》ppt课件 (共42张PPT) |

|
|
| 格式 | zip | ||
| 文件大小 | 1.7MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 鲁教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2016-06-05 00:00:00 | ||
图片预览









文档简介
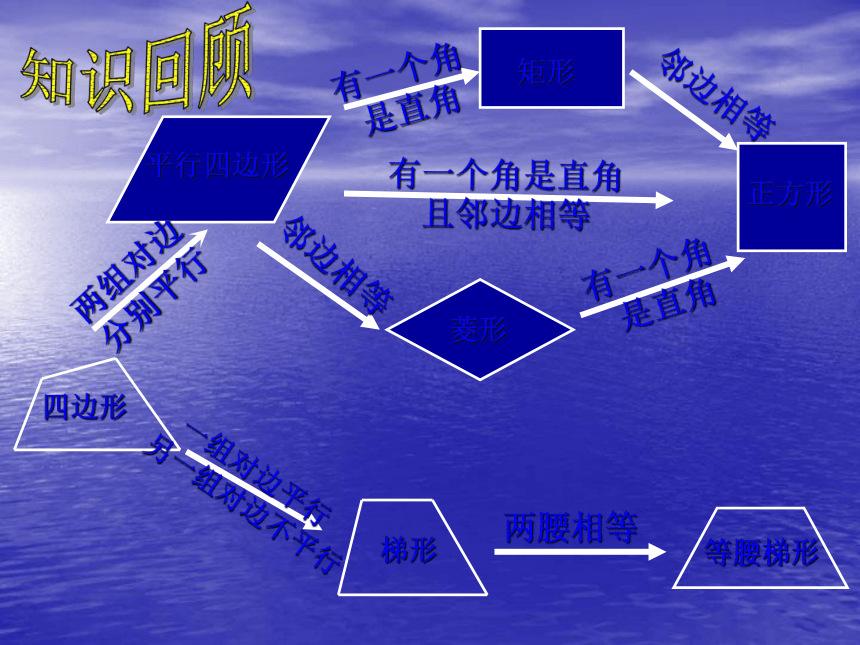
课件42张PPT。复习课特殊的平行四边形知识回顾四边形平行四边形矩形菱形正方形梯形等腰梯形两组对边
分别平行有一个角
是直角邻边相等邻边相等有一个角
是直角 一组对边平行
另一组对边不平行两腰相等 有一个角是直角
且邻边相等平行且相等平行且相等平行
且四边相等平行
且四边相等对角相等
邻角互补四个角
都是直角对角相等
邻角互补四个角
都是直角互相平分互相平分且相等互相垂直平分,且每一条对角线平分一组对角互相垂直平分且相等,每一条对角线平分一组对角中心对称图形中心对称图形
轴对称图形中心对称图形
轴对称图形中心对称图形
轴对称图形二、几种特殊四边形的性质:三、特殊四边形的常用判定方法 平行
四边形(1)两组对边分别平行;(2)两组对边分别相等;(4)对角线互相平分;(5)一组对边平行且相等矩 形 (1)有一个角是直角的平行四边形是矩形;(2)有三个角是直角的四边形是矩形; (3)对角线相等的平行四边形是矩形。 菱 形(1)有一组邻边相等的平行四边形是菱形;(2)四条边都相等的四边形是菱形; (3)对角线互相垂直的平行四边形是菱形。正方形(2)有一组邻边相等的矩形是正方形;(3)有一个角是直角的菱形是正方形。分别相等; (1)有一个角是直角且有一组邻边相等的平行四边形是正方形;1、一组对边平行,另一组对边相等的的四边形是平行四边形。( )
2、两条对角线相等的四边形是矩形。( ) 3、一组邻边相等的的矩形是正方形。( ) 4、对角线互相垂直的四边形是菱形。( ) 5、两条对角线互相平分的四边形是平行四边形。( )√x√判断题xx练一练1、在 ABCD中,已知AB=8,AO=3,∠B=50°
则CD=________,AC=________
∠A=________, ∠D=___________2、在 ABCD中, ∠A+ ∠C= 150°那么
∠A=__________,∠D=_________ 3、在 ABCD中, ∠A:∠B= 4:5,那么
∠B=__________,∠C=_________ 4、请在横线上写出结论,在括号里填理由
∵四边形ABCD是平行四边形
∴_________________( )选择题:1、矩形具有而一般的平行四边形不具有的性质是( )
A、对角相等 B、对角线相 C、对边相等 D、对角线互相平分
2、菱形有而一般的平行四边形不具有的性质是( )
A、对角相等 B、对角线互相平分C、对边平行且相等 D、对角线互相垂直
3.下列性质中,平行四边形不一定具备的是( )
(A)对角相等 (B)邻角互补 (C )对角互补 (D)内角和是360°
(4).下面判定四边形是平行四边形的方法中,错误的是( )。
(A)一组对边平行,另一组对边也平行;(B)一组对角相等,另一组对角也相等
(C )一组对边平行,一组对角相等; (D)一组对边平行,另一组对边相等
(5).能够判定一个四边形是平行四边形的条件是( )
(A)一组对角相等 (B)两条对角线互相平分
(C )两条对角线互相垂直 (D)一对邻角的和为180°
(6)、在△ABC中,AB=AC=6cm,D是BC上一点,且DE∥AC,交AB于E,DF∥AB,交AC于F,则四边形AEDF的周长为( )
1、平行四边形一边长为12cm,那么它的两条
对角线的长度可以是( )
A、8cm和14cm B、10cm 和14cm
C、18cm和20cm D、10cm和34cm
2、四边形的四个内角的度数比是
2:2:3:1,则此四边形是( )
A、任意四边形 B、任意梯形 C、等腰梯形
D、直角梯形 3、平行四边形四个内角的平分线,如果能围成一个四边形,那么这个四边形一定是( )
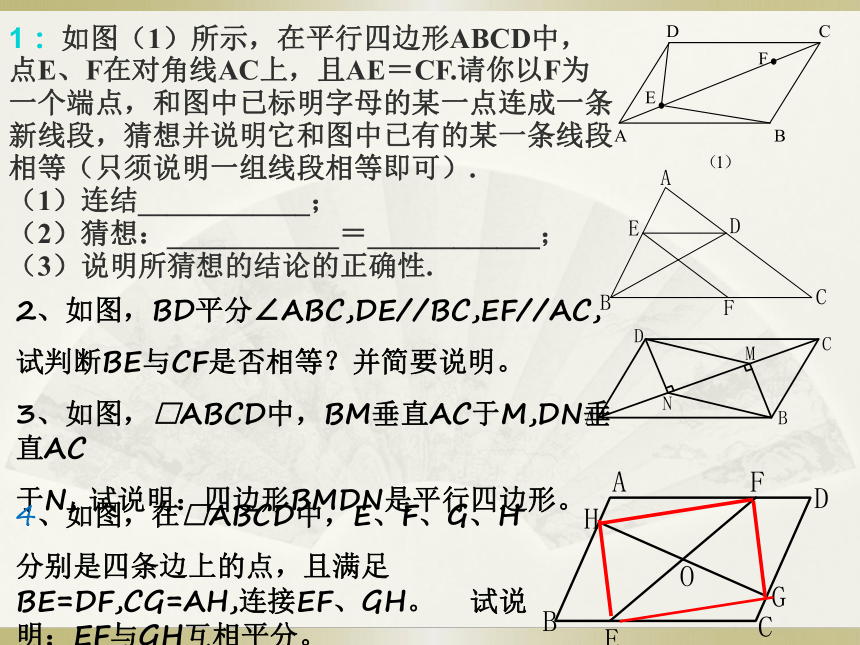
A、矩形 B、菱形 C、正方形 D、等腰梯形 1. 如图所示,平行四边形ABCD的对角线相交于O点,且AB≠BC,过O点作OE⊥AC,交BC于E,如果△ABE的周长为b,则平行四边形ABCD的周长是( )A. b B. 1.5b C. 2b D. 3b2.将两个边长都为3cm,5cm,6cm的三角形纸片拼成平行四边形,这样不同拼法共有_____种3.已知四边形ABCD,从①AB//DC,②AB=DC,③AD//BC,④∠B=∠D中取两个条件加以组合,能推出四边形ABCD是平行四边形的有 _______________________(组合序号)4.若平行四边形一边长为8cm,一条对角线长为6cm,则另一条对角线长X的取值范围是_____________5.M为□ABCD 的边AD上一点,若▲MBC的面积为8cm2,□ABCD的面积为_______6.如图,□ABCD中,AE⊥BC,AF⊥CD,E,F为垂足,已知BE=3cm,AE=4cm,AF=8cm,则□ABCD周长为____cm,面积为_____cm2 1 :如图(1)所示,在平行四边形ABCD中,
点E、F在对角线AC上,且AE=CF.请你以F为
一个端点,和图中已标明字母的某一点连成一条
新线段,猜想并说明它和图中已有的某一条线段
相等(只须说明一组线段相等即可).
(1)连结____________;
(2)猜想:____________=____________;
(3)说明所猜想的结论的正确性.
2、如图,BD平分∠ABC,DE//BC,EF//AC,
试判断BE与CF是否相等?并简要说明。 3、如图,□ABCD中,BM垂直AC于M,DN垂直AC
于N, 试说明:四边形BMDN是平行四边形。4、如图,在□ABCD中,E、F、G、H
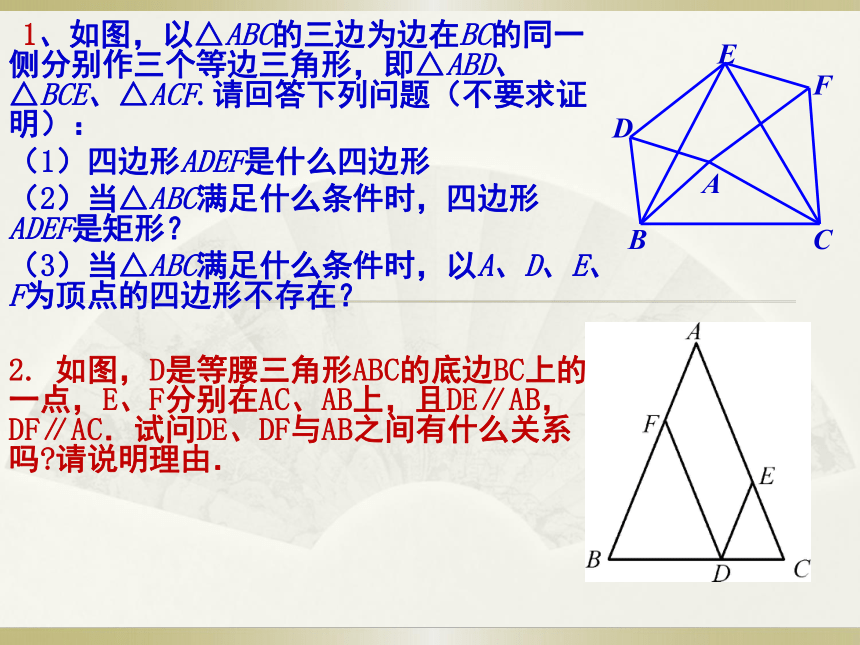
分别是四条边上的点,且满足BE=DF,CG=AH,连接EF、GH。 试说明:EF与GH互相平分。 1、如图,以△ABC的三边为边在BC的同一侧分别作三个等边三角形,即△ABD、△BCE、△ACF.请回答下列问题(不要求证明):
(1)四边形ADEF是什么四边形
(2)当△ABC满足什么条件时,四边形ADEF是矩形?
(3)当△ABC满足什么条件时,以A、D、E、F为顶点的四边形不存在?
2. 如图,D是等腰三角形ABC的底边BC上的一点,E、F分别在AC、AB上,且DE∥AB, DF∥AC.试问DE、DF与AB之间有什么关系吗?请说明理由.
考点一:矩形 例2.如图矩形
ABCD中,AB=3,BC=5,
过对角线交点O作OE⊥AC,
交AD于E,则AE的长是( )例1.如图,矩形ABCD申,对角线AC、BD相交于点0,∠AOB=600,AB=5,则AD的长是( ).
例3.如图,四边形ABCD是矩形,点E在线段CB的延长线上,连接DE交AB于点F,∠AED=2∠CED,点G是DF的中点,若BE=1,AG=4,则AB的长为( ) .2.矩形的判定例3. 如图,四边形ABCD的对角线AC、BD交于点O,BE⊥AC于E,DF⊥AC于F,点O既是AC的中点,又是EF的中点.
(1)求证:△BOE≌△DOF;
(2)若OA= BD,则四边形ABCD是什么特殊四
边形?请说明理由.练习.如图,在△ABC中,AB=AC,D为边BC上一点,以AB,BD为邻边作?ABDE,连接AD,EC.
(1)求证:△ADC≌△ECD;
(2)若BD=CD,求证:四边形ADCE是矩形.3.矩形的折叠问题例4.如图所示,矩形纸片ABCD中,AB=6cm,BC=8cm,现将其沿EF对折,使得点C与点A重合,则AF长为( )练习. )如图2,OABC是一张放在平面直角坐标系中的矩形纸片,O为原点,点A在x轴的正半轴上,点C在y轴的正半轴上,OA=10,OC=8.在OC边上取一点D,将纸片沿AD翻折,使点O落在BC边上的点E处,求D,E两点的坐标. 6、如图,已知矩形纸片ABCD中,AD=9cm,AB=3cm,将其折叠,使点D与点B重合,那么折叠后DE的长和折痕EF的长分别是( )
A、4cm、 cm B、5cm、 cm
C、4cm、 cm D、5cm、 cm
2、把一张长方形的纸条按图那样折叠,若得∠AME=70o ,则∠EMN=( )
A、45o B、50o
C、55o D、60o 3、如图,矩形ABCD沿AE折叠,使D点落在BC边上的F点处,
如果∠BAF=60°,那么∠DAE等于( )
A.15° B.30°
C.45° D.60° 1, 如图,矩形纸片ABCD中,AB=3厘米,BC=4厘米,现将A、C重合,使纸片折叠压平,
设折痕为EF。试确定重叠部分△AEF的面积。1、如图,在矩形ABCD中,AC、BD相交于点O, ∠AOB= 60°,AB=6,则AC=_______2,在矩形ABCD中,AB=10cm,AD=5cm,
E是CD上的一点,且AE=10cm,
则∠CBE= _______3.直角三角形斜边上的高和斜边上的中线分别是5cm和6cm,则它的面积是( )4、如图,在矩形ABCD中,AB=4cm,AD=12cm,P点在AD边上以每秒1 cm的速度从A向D运动,点Q在BC边上,以每秒4 cm的速度从C点出发,在CB间往返运动,二点同时出发,待P点到达D点为止,在这段时间内,线段PQ有( )次平行于AB.
A、1 B、2 C、3 D、44,△ABC中,点O是AC边上的一个动点,过点O作直线M N∥BC,设M N交∠BCA的平分线于点E,交∠BCA的外角
平分线于点F.(1)求证:EO=FO
(2)当点O运动到何处时,四边形AECF是矩形?并证明你的结论.(1)证明
∵ CE 平分∠ ACB
∴ ∠ ACE= ∠ ECB
∵ MN // BC
∴ ∠ ECB= ∠ OEC
∴ ∠ OEC= ∠ ECO
∴ OE=OC
同理OF=OC
∴ OE=OF(2)当O为AC的中点时,
四边形AECF是矩形
∵ OA=OC OE=OF
∴ 四边形AECN是平行四边形
∵ OE=OC=OF
∴ AC=EF
∴ 四边形AECN是矩形考点二:菱形例5.(2012陕西)如图,在菱形ABCD中,对角线AC与BD交于点O,OE⊥AB,垂足为E,若∠ADC=130°,则∠AOE的大小为( )练习:如图,在菱形ABCD中,∠A=60°,E、F分别是AB,AD的中点,DE、BF相交于点G,连接BD,CG.有下列结论:
①∠BGD=120°;②BG+DG=CG;③△BDF≌△CGB;④S△ABD=
其中正确的结论有( )2.菱形的判定例6.如图,矩形ABCD的对角线相交于点O,DE∥AC,CE∥BD.
求证:四边形OCED是菱形.练习:如图,AD是△ABC的角平分线,过点D作DE∥AB,DF∥AC,分别交AC、AB于点E和F.
(1)在图中画出线段DE和DF;
(2)连接EF,则线段AD和EF
互相垂直平分,这是为什么?例、 如图,在△ABC中,∠BAC=90°,AD⊥BC于D,CE平分∠ACB,交AD于G,交AB于E,EF⊥BC于F.求证:四边形AEFG是菱形.3.菱形的面积例7:如图,菱形ABCD的边长为8cm,∠A=60°,DE⊥AB于点E,DF⊥BC于点F,则四边形BEDF的面积为 ( ).练习:如图,已知菱形ABCD的对角线AC、BD的长分别为6cm、8cm,AE⊥BC于点E,则AE的长是( )5. 菱形纸片ABCD中,两条对角线AC= ,BD= 4 。(1)求菱形ABCD的面积;(3) 求∠ADC的度数。 (2)求菱形ABCD的周长;7、已知如图,△ABC中AD平分∠BAC,DE∥AB交AC于F, DF∥AC交AB于E。四边形AFDE是怎样的四边形?说明你的理由。
6.如图,菱形ABCD中,AB=4,∠BAD=60°,E是AB的中点,P是对角线AC上的一个动点,则PE+PB的最小值是 。8.在菱形ABCD中,∠ABC=60°,有一度数为60°的∠MAN绕点A旋转。
(1)若∠MAN的两边AM、AN分别交BC、CD于点E、F,则线段CE、DF的大小关系如何?请证明你的结论
(2)若∠MAN的两边AM、AN分别交BC、CD的延长线于点E、F,则线段CE、DF还有(1)中的结论吗?请说明你的理由考点三:正方形例8如图,正方形ABCD与正三角形AEF的顶点A重合,将△AEF绕顶点A旋转,在旋转过程中,当BE=DF时,∠BAE的大小可以是 ( ).练习:如图,已知正方形ABCD的边长为4,点E、F分别在边AB、BC上,且AE=BF=1,CE、DF交于点O.
下列结论:
①∠DOC=90°,②OC=OE,
③S△ODC=S四边形BEOF中,正确的有( )例9如图,在正方形ABCD中,对角线AC、BD相交于点O,E、F分别在OD、OC上,且DE=CF,连接DF、AE,AE的延长线交DF于点M.
求证:AM⊥DF.7、如图,ABCD是正方形,P是对角线上的一点,引PE⊥BC于E,PF⊥DC于F.
求证:(1)AP=EF;(2)AP⊥EF.8.如图1:正方形ABCD的对角线AC、BD相交于点O,E是AC上的一点,连接EB,过点A作AM⊥BE,垂足M,AM交BD于点F
(1)求证OE=OF
(2)如图2所示,若点E在AC的延长线上,AM⊥EB的延长线于点M,交DB的延长线于点F,其他条件都不变,则结论“OE=OF”还成立吗?如果成立,请给出证明;如果不成立,请说明理由ABCDOFEMABCDFEMO 9.已知正方形ABCD, ME⊥ BD,MF⊥ AC,垂足分别为E、F (1) M是AD上的点,若对角线AC=12cm,求ME+MF的长。 (2)若M是AD上的一个动点,ME+MF的长度是否发生改变? (3)当M点运动到何处时,四边形MFOE的面积最大?11、2002年8月在北京召开的国际数学家大会会标如图所示,它是由四个相同的直角三角形与中间的小正方形拼成的一个大正方形.若大正方形的面积是13,小正方形的面积是1,直角三角形的较长直角边为a,较短直角边为b,则a4+b3的值为( ▲ )
A.35 B.43 C.89 D.9710、如图,在正方形ABCD中,E在BC上,BE=2,CE=1,P在BD上, 则PE+PC的最小值为___________ 12.以△ABC的边AB、AC为边的等边三角形ABD和等边三角形ACE,四边形ADFE是平行四边形.
(1)当∠BAC等于 时,平行四边形ADFE不存在;
(2)当∠BAC等于 时,四边形ADFE是矩形;
(3)当△ABC分别满足什么条件时,平行四边形是菱形、正方形.解:(3) AB=AC时,平行四边形ADFE时菱形。
AB=AC且∠BAC=150°时,平行四边形ADFE是正方形。60°150° 13.如图,在正方形ABCD中 如图(1)AE⊥BF .
AE与BF相等吗?
FABCDEGGABCDEFHABCDEFGHM(1)(2)(3)如图(2)AE⊥HF ,AE与HF相等吗?如图(3)ME⊥HF , ME与HF相等吗?14、如图所示是一块在电脑屏幕上出现矩形色块图,由6个颜色不同的正方形组成,若中间最小的一个正方形边长为1,你能求出这个矩形色块的面积吗?aaa-1a-1a-2a-2a-3a-3a-3由(a-1)+ a
= (a-2)+2(a-3) 得a= 7 故s= 143
15.已知:如图点A’、B’、C’、D’
分别是正方形ABCD的四条边上的点,
并且AA'=BB'=CC'=DD'
求证:四边形A'B'C'D'是正方形16.如图,已知四边形ABCD是边长为2的正方形,以对角线BD为边作正三角形BDE,过E作DA的延长线的垂线EF,垂足为F。
(1)找出图中与EF相等的线段,并证明你的结论;
(2)求AF的长。 18. 如图,有一块矩形纸片ABCD,AB=10,AD=6,将纸片折叠,使AD边落在AB边上,折痕为AE,再将△AED以DE为折痕向右折叠,AE与BC交于点F,则△CEF的面积为( )
(A) 4 (B)6 (C)8 (D)10
20.如图,已知正方形纸片ABCD,M,N分别是AD,BC的中点,把BC向上翻折,使点C恰好落在MN上的P点处,BQ为折痕,则∠PBQ=________度。
17.小许拿了一张正方形的纸片如图甲,沿虚线对折一次得图乙.再对折一次得图丙.然后用剪刀沿图丙中的虚线(虚线与底边平行)剪去一个角.打开后的形状是( ).21. 在一块正方形花坛上,欲修建两条直的小路,使得两条直的小路将花坛分成全等的四部分(不考虑道路宽度),你有几种方法?(至少说出三种)
考点四:三角形的中位线练习:如图,在?ABCD
中,AD=8,点E、F分别是BD、CD
的中点,则EF=( ) .例10如图,AB∥CD,E,F分别为AC,BD的中点,若AB=5,CD=3,则EF的长是( )22.如图,在四边形ABCD中,E、F、G、H分别是边AB、BC、CD、DA的中点,请添加一个条件,使四边形EFGH为菱形,并说明理由。
解:添加的条件__________ AC=BD23.顺次连接任意四边形各边的中点,所构成的四边形以下简称为“中点四边形”。试判断中点四边形EFGH的形状,并说明理由。(1)添加一个条件,使四边形EFGH为菱形;AC ⊥ BDAC=BDAC=BD且AC ⊥ BD(2)添加一个条件,使四边形EFGH为矩形;(3)添加一个条件,使四边形EFGH为正方形;1.矩形的“中点四边形”是 形;
2.菱形的“中点四边形”是 形;
3.正方形的“中点四边形”是 形。
4.等腰梯形的“中点四边形”是 形矩菱正方 那么,特殊平行四边形的“中点四边形”会是怎样的图形呢?菱体会.分享 说能出你这节课的收获和体验
让大家与你分享吗?
分别平行有一个角
是直角邻边相等邻边相等有一个角
是直角 一组对边平行
另一组对边不平行两腰相等 有一个角是直角
且邻边相等平行且相等平行且相等平行
且四边相等平行
且四边相等对角相等
邻角互补四个角
都是直角对角相等
邻角互补四个角
都是直角互相平分互相平分且相等互相垂直平分,且每一条对角线平分一组对角互相垂直平分且相等,每一条对角线平分一组对角中心对称图形中心对称图形
轴对称图形中心对称图形
轴对称图形中心对称图形
轴对称图形二、几种特殊四边形的性质:三、特殊四边形的常用判定方法 平行
四边形(1)两组对边分别平行;(2)两组对边分别相等;(4)对角线互相平分;(5)一组对边平行且相等矩 形 (1)有一个角是直角的平行四边形是矩形;(2)有三个角是直角的四边形是矩形; (3)对角线相等的平行四边形是矩形。 菱 形(1)有一组邻边相等的平行四边形是菱形;(2)四条边都相等的四边形是菱形; (3)对角线互相垂直的平行四边形是菱形。正方形(2)有一组邻边相等的矩形是正方形;(3)有一个角是直角的菱形是正方形。分别相等; (1)有一个角是直角且有一组邻边相等的平行四边形是正方形;1、一组对边平行,另一组对边相等的的四边形是平行四边形。( )
2、两条对角线相等的四边形是矩形。( ) 3、一组邻边相等的的矩形是正方形。( ) 4、对角线互相垂直的四边形是菱形。( ) 5、两条对角线互相平分的四边形是平行四边形。( )√x√判断题xx练一练1、在 ABCD中,已知AB=8,AO=3,∠B=50°
则CD=________,AC=________
∠A=________, ∠D=___________2、在 ABCD中, ∠A+ ∠C= 150°那么
∠A=__________,∠D=_________ 3、在 ABCD中, ∠A:∠B= 4:5,那么
∠B=__________,∠C=_________ 4、请在横线上写出结论,在括号里填理由
∵四边形ABCD是平行四边形
∴_________________( )选择题:1、矩形具有而一般的平行四边形不具有的性质是( )
A、对角相等 B、对角线相 C、对边相等 D、对角线互相平分
2、菱形有而一般的平行四边形不具有的性质是( )
A、对角相等 B、对角线互相平分C、对边平行且相等 D、对角线互相垂直
3.下列性质中,平行四边形不一定具备的是( )
(A)对角相等 (B)邻角互补 (C )对角互补 (D)内角和是360°
(4).下面判定四边形是平行四边形的方法中,错误的是( )。
(A)一组对边平行,另一组对边也平行;(B)一组对角相等,另一组对角也相等
(C )一组对边平行,一组对角相等; (D)一组对边平行,另一组对边相等
(5).能够判定一个四边形是平行四边形的条件是( )
(A)一组对角相等 (B)两条对角线互相平分
(C )两条对角线互相垂直 (D)一对邻角的和为180°
(6)、在△ABC中,AB=AC=6cm,D是BC上一点,且DE∥AC,交AB于E,DF∥AB,交AC于F,则四边形AEDF的周长为( )
1、平行四边形一边长为12cm,那么它的两条
对角线的长度可以是( )
A、8cm和14cm B、10cm 和14cm
C、18cm和20cm D、10cm和34cm
2、四边形的四个内角的度数比是
2:2:3:1,则此四边形是( )
A、任意四边形 B、任意梯形 C、等腰梯形
D、直角梯形 3、平行四边形四个内角的平分线,如果能围成一个四边形,那么这个四边形一定是( )
A、矩形 B、菱形 C、正方形 D、等腰梯形 1. 如图所示,平行四边形ABCD的对角线相交于O点,且AB≠BC,过O点作OE⊥AC,交BC于E,如果△ABE的周长为b,则平行四边形ABCD的周长是( )A. b B. 1.5b C. 2b D. 3b2.将两个边长都为3cm,5cm,6cm的三角形纸片拼成平行四边形,这样不同拼法共有_____种3.已知四边形ABCD,从①AB//DC,②AB=DC,③AD//BC,④∠B=∠D中取两个条件加以组合,能推出四边形ABCD是平行四边形的有 _______________________(组合序号)4.若平行四边形一边长为8cm,一条对角线长为6cm,则另一条对角线长X的取值范围是_____________5.M为□ABCD 的边AD上一点,若▲MBC的面积为8cm2,□ABCD的面积为_______6.如图,□ABCD中,AE⊥BC,AF⊥CD,E,F为垂足,已知BE=3cm,AE=4cm,AF=8cm,则□ABCD周长为____cm,面积为_____cm2 1 :如图(1)所示,在平行四边形ABCD中,
点E、F在对角线AC上,且AE=CF.请你以F为
一个端点,和图中已标明字母的某一点连成一条
新线段,猜想并说明它和图中已有的某一条线段
相等(只须说明一组线段相等即可).
(1)连结____________;
(2)猜想:____________=____________;
(3)说明所猜想的结论的正确性.
2、如图,BD平分∠ABC,DE//BC,EF//AC,
试判断BE与CF是否相等?并简要说明。 3、如图,□ABCD中,BM垂直AC于M,DN垂直AC
于N, 试说明:四边形BMDN是平行四边形。4、如图,在□ABCD中,E、F、G、H
分别是四条边上的点,且满足BE=DF,CG=AH,连接EF、GH。 试说明:EF与GH互相平分。 1、如图,以△ABC的三边为边在BC的同一侧分别作三个等边三角形,即△ABD、△BCE、△ACF.请回答下列问题(不要求证明):
(1)四边形ADEF是什么四边形
(2)当△ABC满足什么条件时,四边形ADEF是矩形?
(3)当△ABC满足什么条件时,以A、D、E、F为顶点的四边形不存在?
2. 如图,D是等腰三角形ABC的底边BC上的一点,E、F分别在AC、AB上,且DE∥AB, DF∥AC.试问DE、DF与AB之间有什么关系吗?请说明理由.
考点一:矩形 例2.如图矩形
ABCD中,AB=3,BC=5,
过对角线交点O作OE⊥AC,
交AD于E,则AE的长是( )例1.如图,矩形ABCD申,对角线AC、BD相交于点0,∠AOB=600,AB=5,则AD的长是( ).
例3.如图,四边形ABCD是矩形,点E在线段CB的延长线上,连接DE交AB于点F,∠AED=2∠CED,点G是DF的中点,若BE=1,AG=4,则AB的长为( ) .2.矩形的判定例3. 如图,四边形ABCD的对角线AC、BD交于点O,BE⊥AC于E,DF⊥AC于F,点O既是AC的中点,又是EF的中点.
(1)求证:△BOE≌△DOF;
(2)若OA= BD,则四边形ABCD是什么特殊四
边形?请说明理由.练习.如图,在△ABC中,AB=AC,D为边BC上一点,以AB,BD为邻边作?ABDE,连接AD,EC.
(1)求证:△ADC≌△ECD;
(2)若BD=CD,求证:四边形ADCE是矩形.3.矩形的折叠问题例4.如图所示,矩形纸片ABCD中,AB=6cm,BC=8cm,现将其沿EF对折,使得点C与点A重合,则AF长为( )练习. )如图2,OABC是一张放在平面直角坐标系中的矩形纸片,O为原点,点A在x轴的正半轴上,点C在y轴的正半轴上,OA=10,OC=8.在OC边上取一点D,将纸片沿AD翻折,使点O落在BC边上的点E处,求D,E两点的坐标. 6、如图,已知矩形纸片ABCD中,AD=9cm,AB=3cm,将其折叠,使点D与点B重合,那么折叠后DE的长和折痕EF的长分别是( )
A、4cm、 cm B、5cm、 cm
C、4cm、 cm D、5cm、 cm
2、把一张长方形的纸条按图那样折叠,若得∠AME=70o ,则∠EMN=( )
A、45o B、50o
C、55o D、60o 3、如图,矩形ABCD沿AE折叠,使D点落在BC边上的F点处,
如果∠BAF=60°,那么∠DAE等于( )
A.15° B.30°
C.45° D.60° 1, 如图,矩形纸片ABCD中,AB=3厘米,BC=4厘米,现将A、C重合,使纸片折叠压平,
设折痕为EF。试确定重叠部分△AEF的面积。1、如图,在矩形ABCD中,AC、BD相交于点O, ∠AOB= 60°,AB=6,则AC=_______2,在矩形ABCD中,AB=10cm,AD=5cm,
E是CD上的一点,且AE=10cm,
则∠CBE= _______3.直角三角形斜边上的高和斜边上的中线分别是5cm和6cm,则它的面积是( )4、如图,在矩形ABCD中,AB=4cm,AD=12cm,P点在AD边上以每秒1 cm的速度从A向D运动,点Q在BC边上,以每秒4 cm的速度从C点出发,在CB间往返运动,二点同时出发,待P点到达D点为止,在这段时间内,线段PQ有( )次平行于AB.
A、1 B、2 C、3 D、44,△ABC中,点O是AC边上的一个动点,过点O作直线M N∥BC,设M N交∠BCA的平分线于点E,交∠BCA的外角
平分线于点F.(1)求证:EO=FO
(2)当点O运动到何处时,四边形AECF是矩形?并证明你的结论.(1)证明
∵ CE 平分∠ ACB
∴ ∠ ACE= ∠ ECB
∵ MN // BC
∴ ∠ ECB= ∠ OEC
∴ ∠ OEC= ∠ ECO
∴ OE=OC
同理OF=OC
∴ OE=OF(2)当O为AC的中点时,
四边形AECF是矩形
∵ OA=OC OE=OF
∴ 四边形AECN是平行四边形
∵ OE=OC=OF
∴ AC=EF
∴ 四边形AECN是矩形考点二:菱形例5.(2012陕西)如图,在菱形ABCD中,对角线AC与BD交于点O,OE⊥AB,垂足为E,若∠ADC=130°,则∠AOE的大小为( )练习:如图,在菱形ABCD中,∠A=60°,E、F分别是AB,AD的中点,DE、BF相交于点G,连接BD,CG.有下列结论:
①∠BGD=120°;②BG+DG=CG;③△BDF≌△CGB;④S△ABD=
其中正确的结论有( )2.菱形的判定例6.如图,矩形ABCD的对角线相交于点O,DE∥AC,CE∥BD.
求证:四边形OCED是菱形.练习:如图,AD是△ABC的角平分线,过点D作DE∥AB,DF∥AC,分别交AC、AB于点E和F.
(1)在图中画出线段DE和DF;
(2)连接EF,则线段AD和EF
互相垂直平分,这是为什么?例、 如图,在△ABC中,∠BAC=90°,AD⊥BC于D,CE平分∠ACB,交AD于G,交AB于E,EF⊥BC于F.求证:四边形AEFG是菱形.3.菱形的面积例7:如图,菱形ABCD的边长为8cm,∠A=60°,DE⊥AB于点E,DF⊥BC于点F,则四边形BEDF的面积为 ( ).练习:如图,已知菱形ABCD的对角线AC、BD的长分别为6cm、8cm,AE⊥BC于点E,则AE的长是( )5. 菱形纸片ABCD中,两条对角线AC= ,BD= 4 。(1)求菱形ABCD的面积;(3) 求∠ADC的度数。 (2)求菱形ABCD的周长;7、已知如图,△ABC中AD平分∠BAC,DE∥AB交AC于F, DF∥AC交AB于E。四边形AFDE是怎样的四边形?说明你的理由。
6.如图,菱形ABCD中,AB=4,∠BAD=60°,E是AB的中点,P是对角线AC上的一个动点,则PE+PB的最小值是 。8.在菱形ABCD中,∠ABC=60°,有一度数为60°的∠MAN绕点A旋转。
(1)若∠MAN的两边AM、AN分别交BC、CD于点E、F,则线段CE、DF的大小关系如何?请证明你的结论
(2)若∠MAN的两边AM、AN分别交BC、CD的延长线于点E、F,则线段CE、DF还有(1)中的结论吗?请说明你的理由考点三:正方形例8如图,正方形ABCD与正三角形AEF的顶点A重合,将△AEF绕顶点A旋转,在旋转过程中,当BE=DF时,∠BAE的大小可以是 ( ).练习:如图,已知正方形ABCD的边长为4,点E、F分别在边AB、BC上,且AE=BF=1,CE、DF交于点O.
下列结论:
①∠DOC=90°,②OC=OE,
③S△ODC=S四边形BEOF中,正确的有( )例9如图,在正方形ABCD中,对角线AC、BD相交于点O,E、F分别在OD、OC上,且DE=CF,连接DF、AE,AE的延长线交DF于点M.
求证:AM⊥DF.7、如图,ABCD是正方形,P是对角线上的一点,引PE⊥BC于E,PF⊥DC于F.
求证:(1)AP=EF;(2)AP⊥EF.8.如图1:正方形ABCD的对角线AC、BD相交于点O,E是AC上的一点,连接EB,过点A作AM⊥BE,垂足M,AM交BD于点F
(1)求证OE=OF
(2)如图2所示,若点E在AC的延长线上,AM⊥EB的延长线于点M,交DB的延长线于点F,其他条件都不变,则结论“OE=OF”还成立吗?如果成立,请给出证明;如果不成立,请说明理由ABCDOFEMABCDFEMO 9.已知正方形ABCD, ME⊥ BD,MF⊥ AC,垂足分别为E、F (1) M是AD上的点,若对角线AC=12cm,求ME+MF的长。 (2)若M是AD上的一个动点,ME+MF的长度是否发生改变? (3)当M点运动到何处时,四边形MFOE的面积最大?11、2002年8月在北京召开的国际数学家大会会标如图所示,它是由四个相同的直角三角形与中间的小正方形拼成的一个大正方形.若大正方形的面积是13,小正方形的面积是1,直角三角形的较长直角边为a,较短直角边为b,则a4+b3的值为( ▲ )
A.35 B.43 C.89 D.9710、如图,在正方形ABCD中,E在BC上,BE=2,CE=1,P在BD上, 则PE+PC的最小值为___________ 12.以△ABC的边AB、AC为边的等边三角形ABD和等边三角形ACE,四边形ADFE是平行四边形.
(1)当∠BAC等于 时,平行四边形ADFE不存在;
(2)当∠BAC等于 时,四边形ADFE是矩形;
(3)当△ABC分别满足什么条件时,平行四边形是菱形、正方形.解:(3) AB=AC时,平行四边形ADFE时菱形。
AB=AC且∠BAC=150°时,平行四边形ADFE是正方形。60°150° 13.如图,在正方形ABCD中 如图(1)AE⊥BF .
AE与BF相等吗?
FABCDEGGABCDEFHABCDEFGHM(1)(2)(3)如图(2)AE⊥HF ,AE与HF相等吗?如图(3)ME⊥HF , ME与HF相等吗?14、如图所示是一块在电脑屏幕上出现矩形色块图,由6个颜色不同的正方形组成,若中间最小的一个正方形边长为1,你能求出这个矩形色块的面积吗?aaa-1a-1a-2a-2a-3a-3a-3由(a-1)+ a
= (a-2)+2(a-3) 得a= 7 故s= 143
15.已知:如图点A’、B’、C’、D’
分别是正方形ABCD的四条边上的点,
并且AA'=BB'=CC'=DD'
求证:四边形A'B'C'D'是正方形16.如图,已知四边形ABCD是边长为2的正方形,以对角线BD为边作正三角形BDE,过E作DA的延长线的垂线EF,垂足为F。
(1)找出图中与EF相等的线段,并证明你的结论;
(2)求AF的长。 18. 如图,有一块矩形纸片ABCD,AB=10,AD=6,将纸片折叠,使AD边落在AB边上,折痕为AE,再将△AED以DE为折痕向右折叠,AE与BC交于点F,则△CEF的面积为( )
(A) 4 (B)6 (C)8 (D)10
20.如图,已知正方形纸片ABCD,M,N分别是AD,BC的中点,把BC向上翻折,使点C恰好落在MN上的P点处,BQ为折痕,则∠PBQ=________度。
17.小许拿了一张正方形的纸片如图甲,沿虚线对折一次得图乙.再对折一次得图丙.然后用剪刀沿图丙中的虚线(虚线与底边平行)剪去一个角.打开后的形状是( ).21. 在一块正方形花坛上,欲修建两条直的小路,使得两条直的小路将花坛分成全等的四部分(不考虑道路宽度),你有几种方法?(至少说出三种)
考点四:三角形的中位线练习:如图,在?ABCD
中,AD=8,点E、F分别是BD、CD
的中点,则EF=( ) .例10如图,AB∥CD,E,F分别为AC,BD的中点,若AB=5,CD=3,则EF的长是( )22.如图,在四边形ABCD中,E、F、G、H分别是边AB、BC、CD、DA的中点,请添加一个条件,使四边形EFGH为菱形,并说明理由。
解:添加的条件__________ AC=BD23.顺次连接任意四边形各边的中点,所构成的四边形以下简称为“中点四边形”。试判断中点四边形EFGH的形状,并说明理由。(1)添加一个条件,使四边形EFGH为菱形;AC ⊥ BDAC=BDAC=BD且AC ⊥ BD(2)添加一个条件,使四边形EFGH为矩形;(3)添加一个条件,使四边形EFGH为正方形;1.矩形的“中点四边形”是 形;
2.菱形的“中点四边形”是 形;
3.正方形的“中点四边形”是 形。
4.等腰梯形的“中点四边形”是 形矩菱正方 那么,特殊平行四边形的“中点四边形”会是怎样的图形呢?菱体会.分享 说能出你这节课的收获和体验
让大家与你分享吗?
