第十八章 平行四边形 单元复习课件(共32张PPT)
文档属性
| 名称 | 第十八章 平行四边形 单元复习课件(共32张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 1.8MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-05-10 00:00:00 | ||
图片预览








文档简介
(共32张PPT)
2025八年级数学下册
第十八章
——平行四边形单元复习
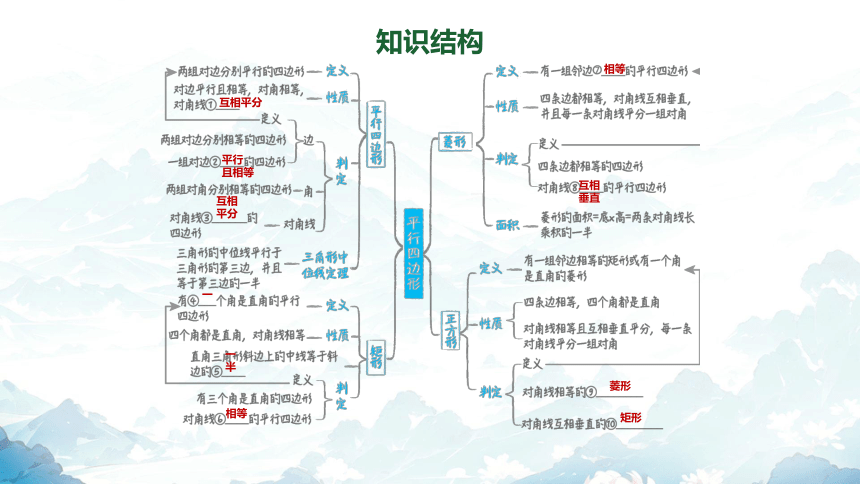
知识结构
互相平分
平行
且相等
互相平分
一
一半
相等
相等
互相垂直
菱形
矩形
达标训练
一、选择题(每题6分,共36分)
1.在中,连接,,,, ,则
的面积是( )
B
A.20 B.24 C.30 D.48
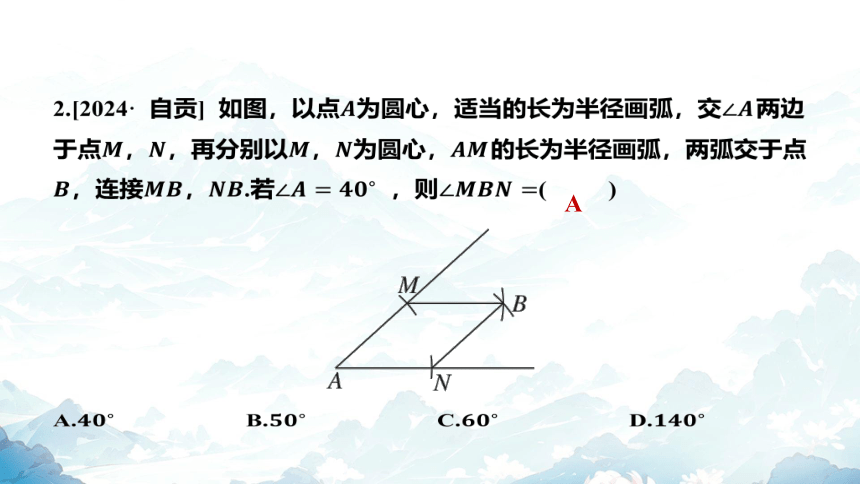
2.[2024· 自贡] 如图,以点为圆心,适当的长为半径画弧,交 两边
于点,,再分别以,为圆心, 的长为半径画弧,两弧交于点
,连接,.若 ,则 ( )
A
A. B. C. D.
(第3题)
3.如图,在四边形 中,
,是对角线的中点, 是
的中点.若,,则 的长为
( )
A
A. B. C. D.
(第4题)
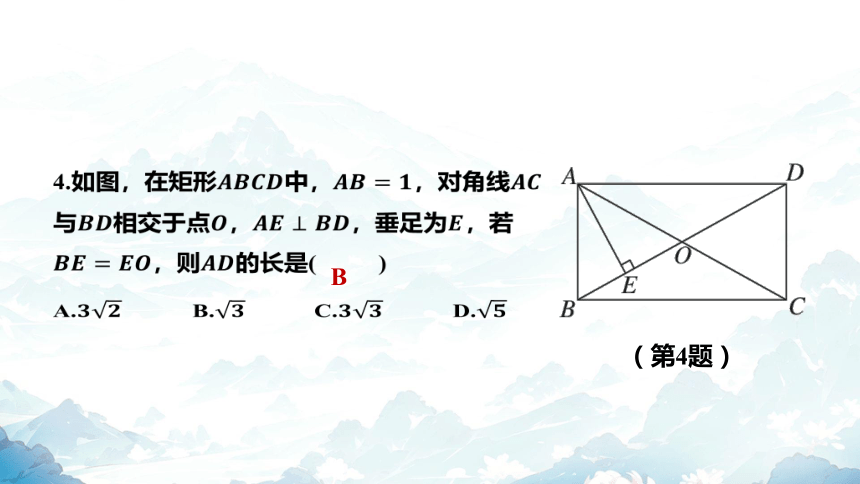
4.如图,在矩形中,,对角线
与相交于点,,垂足为 ,若
,则 的长是( )
B
A. B. C. D.
(第5题)
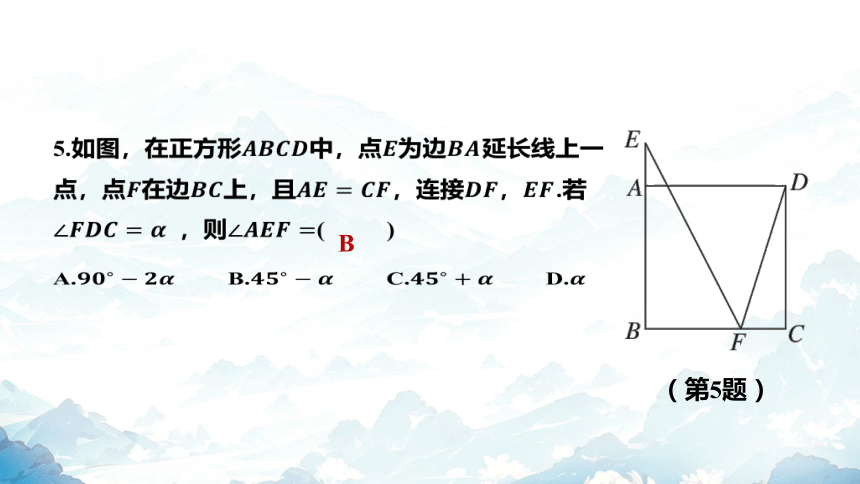
5.如图,在正方形中,点为边 延长线上一
点,点在边上,且,连接, .若
,则 ( )
B
A. B. C. D.
[解析] 点拨:如图,连接,过点作,交 于
点 .
四边形 是正方形,
,, .
又 ,
,
, ,
,
易知 .
, .
,
.
(第6题)
6. 杭州纸伞馆有制
作精美的纸伞,如图,四条长度相
等的伞骨围成菱形 ,伞骨连
接点固定在伞柄顶端,伞圈
能沿着伞柄 滑动.小聪通过测量发
现:当伞完全张开时,伞柄 的中
C
A. B. C. D.
点到伞骨连接点,的距离都等于的一半,若 ,
则 的度数是( )
[解析] 点拨:四边形 是菱形,
, .
, .
由题意得 ,
.
,
,
.
二、填空题(每题6分,共18分)
7.如图,在中,,点在边上,, ,
则当_____时,四边形 是矩形.
(第7题)
8.[2024·郴州月考] 在中,,平分交直线 于
点,,则 的周长为________.
14或26
[解析] 点拨:四边形 是平行四边形,
, .
平分, ,
, .
如图①,当点在线段 上时,
, ,
的周长为 ;
如图②,当点在 的延长线上时,
, ,
的周长为 .
综上所述, 的周长为14或26.
(第9题)
9.[2024·包头] 如图,在菱形 中,
,,是一条对角线, 是
上一点,过点作,垂足为 ,连接
.若,则 的长为_____.
[解析] 点拨:如图,过点作于点 ,
在菱形中, , ,
,
,
, 都是等边三角形,
, ,
易知 .
, ,
,
.
又, ,
, .
在中, ,
.
三、解答题(共46分)
10.(12分)[2024· 陕西] 如图,四边形 是
矩形,点和点在边上,且 .求证:
.
证明: 四边形 是矩形,
, .
,,即 ,
, .
11.(14分)[2024· 湖南] 如图,在四边形中,,点 在边
上,________.请从“;, ”这两组条
件中任选一组作为已知条件,填在横线上(填序号),再解决下列问题:
(1)求证:四边形 为平行四边形;
证明:选择①.
, ,
, 四边形 为平行四边形.
(或选择②.
,, .
, 四边形 为平行四边形.)
(2)若,,,求线段 的长.
解:由(1)知四边形 为平行四边形,
.
, ,
.
12.(20分)如图,在中, ,
延长到点,使.连接 .
(1)求证:四边形 是菱形;
证明:,, .
四边形是平行四边形, .
四边形 是平行四边形.
又, 四边形 是菱形.
(2)连接交于点,若,,则 的长为___.
5
[解析] 点拨:四边形是菱形, .
四边形是平行四边形,, ,
.,, .
在中,由勾股定理可得 .
, .
素质发展
13.综合与实践
顺次连接任意一个四边形的中点得到一个新四边形,我们称这个新四边
形为原四边形的中点四边形.数学兴趣小组通过作图、测量,猜想:原
四边形的对角线对中点四边形的形状有着决定性作用.
以下从对角线的数量关系和位置关系两个方面展开探究.
【探究一】
原四边形对角线关 系 中点四边形形状 _____________________________________________
不相等、不垂直 平行四边形
如图①,在四边形中,,,, 分别是各边的中点.求证:中
点四边形 是平行四边形.
证明:,,,分别是,,, 的中点,
,分别是和 的中位线,
, (____),
.同理可得: .
中点四边形 是平行四边形.
结论:任意四边形的中点四边形是平行四边形.
(1)请你补全上述过程中的证明依据:____________.
从作图、测量结果得出猜想Ⅰ:原四边形的对角线相等时,中点四边形
是菱形.
中位线定理
【探究二】
原四边形对角线关系 中点四边形形状 ____________________________________________
不相等、不垂直 平行四边形
菱形
(2)下面我们结合图②来证明猜想Ⅰ,请你在探究一证明结论的基础上,
写出后续的证明过程.
证明: ,
,
中点四边形 是菱形.
【探究三】
原四边形对角线关系 中点四边形形状 _____________________________________________
不相等、不垂直 平行四边形
___
(3)从作图、测量结果得出猜想Ⅱ:原四边形对角线垂直时,中点四
边形是______.
矩形
(4)下面我们结合图③来证明猜想Ⅱ,请你在探究一证明结论的基础
上,写出后续的证明过程.
证明:由中位线定理易知, .
, ,
,
中点四边形 是矩形.
【归纳总结】
(5)请你根据上述探究过程,补全下面的结论,并在图④中画出对应
的图形.
原四边形对角线关系 中点四边形形状
___ ___
结论:原四边形对角线____________________时,中点四边形是________.
且
正方形
解:画出对应的图形如图所示.(图形不唯一)
2025八年级数学下册
第十八章
——平行四边形单元复习
知识结构
互相平分
平行
且相等
互相平分
一
一半
相等
相等
互相垂直
菱形
矩形
达标训练
一、选择题(每题6分,共36分)
1.在中,连接,,,, ,则
的面积是( )
B
A.20 B.24 C.30 D.48
2.[2024· 自贡] 如图,以点为圆心,适当的长为半径画弧,交 两边
于点,,再分别以,为圆心, 的长为半径画弧,两弧交于点
,连接,.若 ,则 ( )
A
A. B. C. D.
(第3题)
3.如图,在四边形 中,
,是对角线的中点, 是
的中点.若,,则 的长为
( )
A
A. B. C. D.
(第4题)
4.如图,在矩形中,,对角线
与相交于点,,垂足为 ,若
,则 的长是( )
B
A. B. C. D.
(第5题)
5.如图,在正方形中,点为边 延长线上一
点,点在边上,且,连接, .若
,则 ( )
B
A. B. C. D.
[解析] 点拨:如图,连接,过点作,交 于
点 .
四边形 是正方形,
,, .
又 ,
,
, ,
,
易知 .
, .
,
.
(第6题)
6. 杭州纸伞馆有制
作精美的纸伞,如图,四条长度相
等的伞骨围成菱形 ,伞骨连
接点固定在伞柄顶端,伞圈
能沿着伞柄 滑动.小聪通过测量发
现:当伞完全张开时,伞柄 的中
C
A. B. C. D.
点到伞骨连接点,的距离都等于的一半,若 ,
则 的度数是( )
[解析] 点拨:四边形 是菱形,
, .
, .
由题意得 ,
.
,
,
.
二、填空题(每题6分,共18分)
7.如图,在中,,点在边上,, ,
则当_____时,四边形 是矩形.
(第7题)
8.[2024·郴州月考] 在中,,平分交直线 于
点,,则 的周长为________.
14或26
[解析] 点拨:四边形 是平行四边形,
, .
平分, ,
, .
如图①,当点在线段 上时,
, ,
的周长为 ;
如图②,当点在 的延长线上时,
, ,
的周长为 .
综上所述, 的周长为14或26.
(第9题)
9.[2024·包头] 如图,在菱形 中,
,,是一条对角线, 是
上一点,过点作,垂足为 ,连接
.若,则 的长为_____.
[解析] 点拨:如图,过点作于点 ,
在菱形中, , ,
,
,
, 都是等边三角形,
, ,
易知 .
, ,
,
.
又, ,
, .
在中, ,
.
三、解答题(共46分)
10.(12分)[2024· 陕西] 如图,四边形 是
矩形,点和点在边上,且 .求证:
.
证明: 四边形 是矩形,
, .
,,即 ,
, .
11.(14分)[2024· 湖南] 如图,在四边形中,,点 在边
上,________.请从“;, ”这两组条
件中任选一组作为已知条件,填在横线上(填序号),再解决下列问题:
(1)求证:四边形 为平行四边形;
证明:选择①.
, ,
, 四边形 为平行四边形.
(或选择②.
,, .
, 四边形 为平行四边形.)
(2)若,,,求线段 的长.
解:由(1)知四边形 为平行四边形,
.
, ,
.
12.(20分)如图,在中, ,
延长到点,使.连接 .
(1)求证:四边形 是菱形;
证明:,, .
四边形是平行四边形, .
四边形 是平行四边形.
又, 四边形 是菱形.
(2)连接交于点,若,,则 的长为___.
5
[解析] 点拨:四边形是菱形, .
四边形是平行四边形,, ,
.,, .
在中,由勾股定理可得 .
, .
素质发展
13.综合与实践
顺次连接任意一个四边形的中点得到一个新四边形,我们称这个新四边
形为原四边形的中点四边形.数学兴趣小组通过作图、测量,猜想:原
四边形的对角线对中点四边形的形状有着决定性作用.
以下从对角线的数量关系和位置关系两个方面展开探究.
【探究一】
原四边形对角线关 系 中点四边形形状 _____________________________________________
不相等、不垂直 平行四边形
如图①,在四边形中,,,, 分别是各边的中点.求证:中
点四边形 是平行四边形.
证明:,,,分别是,,, 的中点,
,分别是和 的中位线,
, (____),
.同理可得: .
中点四边形 是平行四边形.
结论:任意四边形的中点四边形是平行四边形.
(1)请你补全上述过程中的证明依据:____________.
从作图、测量结果得出猜想Ⅰ:原四边形的对角线相等时,中点四边形
是菱形.
中位线定理
【探究二】
原四边形对角线关系 中点四边形形状 ____________________________________________
不相等、不垂直 平行四边形
菱形
(2)下面我们结合图②来证明猜想Ⅰ,请你在探究一证明结论的基础上,
写出后续的证明过程.
证明: ,
,
中点四边形 是菱形.
【探究三】
原四边形对角线关系 中点四边形形状 _____________________________________________
不相等、不垂直 平行四边形
___
(3)从作图、测量结果得出猜想Ⅱ:原四边形对角线垂直时,中点四
边形是______.
矩形
(4)下面我们结合图③来证明猜想Ⅱ,请你在探究一证明结论的基础
上,写出后续的证明过程.
证明:由中位线定理易知, .
, ,
,
中点四边形 是矩形.
【归纳总结】
(5)请你根据上述探究过程,补全下面的结论,并在图④中画出对应
的图形.
原四边形对角线关系 中点四边形形状
___ ___
结论:原四边形对角线____________________时,中点四边形是________.
且
正方形
解:画出对应的图形如图所示.(图形不唯一)
