第十九章 一次函数 单元复习课件(共27张PPT)
文档属性
| 名称 | 第十九章 一次函数 单元复习课件(共27张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 1.9MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-05-10 21:09:46 | ||
图片预览







文档简介
(共27张PPT)
2025八年级数学下册
第十九章
——一次函数单元复习
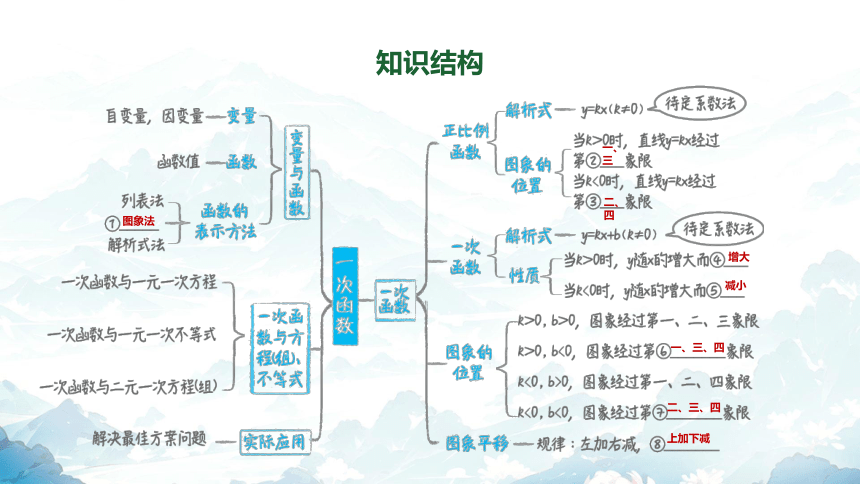
知识结构
图象法
一、
三
二、四
增大
减小
一、三、四
二、三、四
上加下减
达标训练
一、选择题(每题6分,共36分)
1.[2024·北京顺义区一模] 函数自变量 的取值范围是( )
A
A.且 B. C. D.且
2.已知一次函数,若随 的增大而减小,则它的图象
不经过( )
A
A.第一象限 B.第二象限 C.第三象限 D.第四象限
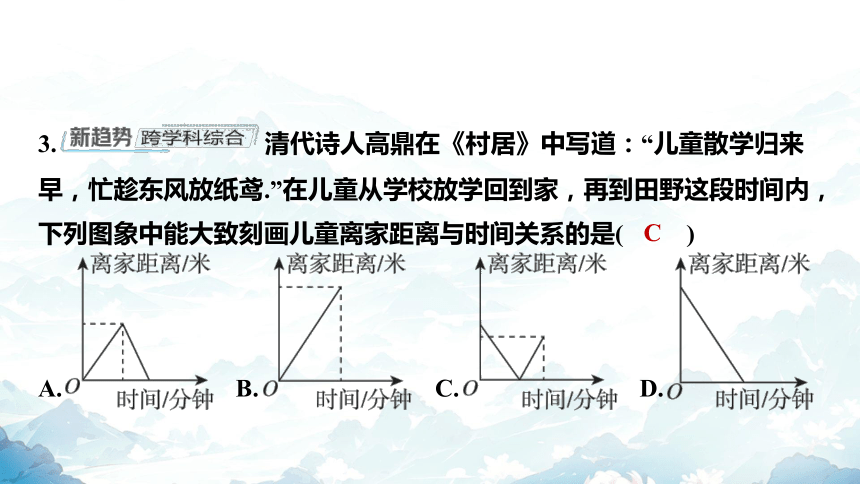
3. 清代诗人高鼎在《村居》中写道:“儿童散学归来
早,忙趁东风放纸鸢.”在儿童从学校放学回到家,再到田野这段时间内,
下列图象中能大致刻画儿童离家距离与时间关系的是( )
C
A. B. C. D.
4.[2024·邢台期末] 将直线 向右平移4个单位长度,平移后的
直线经过点,则 的值是( )
C
A.4 B.5 C.6 D.
5. 古秤是一种人类智慧的产
物,也是华夏文明的瑰宝之一.如图,我们可
以用秤砣到秤纽(秤杆上手提的部分)的水
平距离得出秤钩上所挂物体的重量,称重时,
1 2 3 4 5 6
0.75 1 1.25 1.5 1.75 2
当 为11时,对应的水平距离为( )
B
A. B. C. D.
若秤钩所挂物重为(斤),秤砣到秤纽的水平距离为 .下表中为
若干次称重时所记录的一些数据:
[解析] 点拨:观察表格数据发现与 之间存在一次函数关系,故设
,
将与 分别代入,
得
解得
.
将代入,得 ,
即当为11时,对应的水平距离为 .
(第6题)
6.[2024·广元] 如图①,在
中, ,点从点 出发
沿以 的速度匀速
运动至点,图②是点 运动时,
的面积随时间 变
化的函数图象,则该三角形的斜边
的长为( )
A
A. B. C. D.
[解析] 点拨:由图象可知面积的最大值为 ,
由题意得当点运动到点C时, 的面积最大,
,即 .
由图象可知,当时,,此时点 运动到点B,
.
,
,
.
二、填空题(每题6分,共24分)
7.若一个等腰三角形的顶角度数为度,底角度数为 度,则它们的函数
关系式应是_________________________.
8.如图,一次函数的图象经过点 和点
,一次函数的图象过点,则不等式 的解集
为________.
(第8题)
(第9题)
9.甲车与乙车同时从地出发去往 地,如图,折线
和线段 分别表示甲、乙两车行进过
程中路程与时间的关系,已知甲车中途有事停留
后再继续前往地,两车同时到达 地,则下
列说法:
①乙车的速度为 ;
②甲车再次出发后的速度为 ;
③两车在到达 地前不会相遇;
④甲车再次出发时,两车相距 .
其中正确的有________.(填序号)
②③④
10.如图,直线与轴、轴分别交于点,,点 是直线
上一点,四边形是菱形,则 的长为___.
(第10题)
[解析] 点拨:对于,当时, ;
当时, ,
,,, ,
.
设菱形的对角线交于点,则于点, ,
,
, .
三、解答题(共40分)
11.(12分)[2024·东营] 随着新能源汽车的发展,东营市某公交公司计
划用新能源公交车淘汰“冒黑烟”较严重的燃油公交车.新能源公交车有
型和型两种车型,若购买型公交车3辆, 型公交车1辆,共需260万
元;若购买型公交车2辆, 型公交车3辆,共需360万元.
(1)购买型和 型新能源公交车每辆各需多少万元?
解:设购买型新能源公交车每辆需万元,购买 型新能源公交车每辆
需 万元,
由题意得解得
答:购买型新能源公交车每辆需60万元,购买 型新能源公交车每辆
需80万元.
(2)经调研,某条线路上的型和 型新能源公交车每辆年均载客量分
别为70万人次和100万人次.公司准备购买10辆型、 型两种新能源公交
车,总费用不超过650万元.为保障该线路的年均载客总量最大,请设计
购买方案,并求出年均载客总量的最大值.
解:设购买型新能源公交车辆,则购买型新能源公交车 辆,
由题意得,解得 .
设该线路的年均载客总量为 万人次,则
.
,随 的增大而减小,
,且为整数, 当时, 取得最大值,最大值为
,
此时 ,
购买型新能源公交车8辆, 型新能源公交车2辆时,该线路的年均
载客总量最大,最大值为760万人次.
12.(14分)如图,在平面直角坐标系中,直线
与直线 交于点
,直线交轴于点 .
(1)求直线 的解析式;
解: 直线与直线交于点 ,直
线交轴于点 .
,, ,
,解得 ,
直线的解析式为 .
(2)直接写出当时, 的取值范围;
解:当时, .
(3)若点在轴上,当的面积为9时,求点 的坐标.
解:设 ,
易求得, .
点, ,
,解得或 .
点的坐标为或 .
13.(14分)随着无人机产业的快速发展,无人机航拍逐渐成为摄影创
作的重要方式.某日,学校摄影社团组织灞河景色无人机航拍活动.如
图,在平面直角坐标系中,, 分别表示拍摄某镜头时1号、2号无人机
的飞行高度(米)与飞行时间 (秒)之间的函数关系.
(1)1号无人机飞行的速度是___米/秒,2号无人机
飞行的速度是___米/秒;
6
4
(2)两架无人机飞行多少秒后,1号无人机的高度高于2号无人机?
解:根据题意得, .
令,解得 ,
直线, 交点的横坐标为15,
由图象可得两架无人机飞行15秒后,1号无人机的高度高于2号无人机.
素质发展
14.[2024·北京] 小云有一个圆柱形水杯(记为1号杯),在科
技活动中,小云用所学数学知识和人工智能软件设计了一个
新水杯,并将其制作出来,新水杯(记为2号杯)示意图如图.
当1号杯和2号杯中都有水时,小云分别记录了1号杯的水面高度
(单位:)和2号杯的水面高度(单位: ),部分数据如下:
0 40 100 200 300 400 500
0 2.5 5.0 7.5 10.0 12.5
0 2.8 4.8 7.2 8.9 10.5 11.8
(1)补全表格(结果保留小数点后一位);
解:1.0
[解析] 点拨:由表格可设与的函数关系式为 ,
则,解得 ,
,
当时, .
(2)通过分析数据,发现可以用函数刻画与,与 之间的关系.
在给出的平面直角坐标系中,画出这两个函数的图象;
解:如图.
(3)根据以上数据与函数图象,解决下列问题:
①当1号杯和2号杯中都有 水时,2号杯的水面高度与1号杯的水
面高度的差约为_____ (结果保留小数点后一位);
②在①的条件下,将2号杯中的一部分水倒入1号杯中,当两个水杯的水
面高度相同时,其水面高度约为_____ (结果保留小数点后一位).
2025八年级数学下册
第十九章
——一次函数单元复习
知识结构
图象法
一、
三
二、四
增大
减小
一、三、四
二、三、四
上加下减
达标训练
一、选择题(每题6分,共36分)
1.[2024·北京顺义区一模] 函数自变量 的取值范围是( )
A
A.且 B. C. D.且
2.已知一次函数,若随 的增大而减小,则它的图象
不经过( )
A
A.第一象限 B.第二象限 C.第三象限 D.第四象限
3. 清代诗人高鼎在《村居》中写道:“儿童散学归来
早,忙趁东风放纸鸢.”在儿童从学校放学回到家,再到田野这段时间内,
下列图象中能大致刻画儿童离家距离与时间关系的是( )
C
A. B. C. D.
4.[2024·邢台期末] 将直线 向右平移4个单位长度,平移后的
直线经过点,则 的值是( )
C
A.4 B.5 C.6 D.
5. 古秤是一种人类智慧的产
物,也是华夏文明的瑰宝之一.如图,我们可
以用秤砣到秤纽(秤杆上手提的部分)的水
平距离得出秤钩上所挂物体的重量,称重时,
1 2 3 4 5 6
0.75 1 1.25 1.5 1.75 2
当 为11时,对应的水平距离为( )
B
A. B. C. D.
若秤钩所挂物重为(斤),秤砣到秤纽的水平距离为 .下表中为
若干次称重时所记录的一些数据:
[解析] 点拨:观察表格数据发现与 之间存在一次函数关系,故设
,
将与 分别代入,
得
解得
.
将代入,得 ,
即当为11时,对应的水平距离为 .
(第6题)
6.[2024·广元] 如图①,在
中, ,点从点 出发
沿以 的速度匀速
运动至点,图②是点 运动时,
的面积随时间 变
化的函数图象,则该三角形的斜边
的长为( )
A
A. B. C. D.
[解析] 点拨:由图象可知面积的最大值为 ,
由题意得当点运动到点C时, 的面积最大,
,即 .
由图象可知,当时,,此时点 运动到点B,
.
,
,
.
二、填空题(每题6分,共24分)
7.若一个等腰三角形的顶角度数为度,底角度数为 度,则它们的函数
关系式应是_________________________.
8.如图,一次函数的图象经过点 和点
,一次函数的图象过点,则不等式 的解集
为________.
(第8题)
(第9题)
9.甲车与乙车同时从地出发去往 地,如图,折线
和线段 分别表示甲、乙两车行进过
程中路程与时间的关系,已知甲车中途有事停留
后再继续前往地,两车同时到达 地,则下
列说法:
①乙车的速度为 ;
②甲车再次出发后的速度为 ;
③两车在到达 地前不会相遇;
④甲车再次出发时,两车相距 .
其中正确的有________.(填序号)
②③④
10.如图,直线与轴、轴分别交于点,,点 是直线
上一点,四边形是菱形,则 的长为___.
(第10题)
[解析] 点拨:对于,当时, ;
当时, ,
,,, ,
.
设菱形的对角线交于点,则于点, ,
,
, .
三、解答题(共40分)
11.(12分)[2024·东营] 随着新能源汽车的发展,东营市某公交公司计
划用新能源公交车淘汰“冒黑烟”较严重的燃油公交车.新能源公交车有
型和型两种车型,若购买型公交车3辆, 型公交车1辆,共需260万
元;若购买型公交车2辆, 型公交车3辆,共需360万元.
(1)购买型和 型新能源公交车每辆各需多少万元?
解:设购买型新能源公交车每辆需万元,购买 型新能源公交车每辆
需 万元,
由题意得解得
答:购买型新能源公交车每辆需60万元,购买 型新能源公交车每辆
需80万元.
(2)经调研,某条线路上的型和 型新能源公交车每辆年均载客量分
别为70万人次和100万人次.公司准备购买10辆型、 型两种新能源公交
车,总费用不超过650万元.为保障该线路的年均载客总量最大,请设计
购买方案,并求出年均载客总量的最大值.
解:设购买型新能源公交车辆,则购买型新能源公交车 辆,
由题意得,解得 .
设该线路的年均载客总量为 万人次,则
.
,随 的增大而减小,
,且为整数, 当时, 取得最大值,最大值为
,
此时 ,
购买型新能源公交车8辆, 型新能源公交车2辆时,该线路的年均
载客总量最大,最大值为760万人次.
12.(14分)如图,在平面直角坐标系中,直线
与直线 交于点
,直线交轴于点 .
(1)求直线 的解析式;
解: 直线与直线交于点 ,直
线交轴于点 .
,, ,
,解得 ,
直线的解析式为 .
(2)直接写出当时, 的取值范围;
解:当时, .
(3)若点在轴上,当的面积为9时,求点 的坐标.
解:设 ,
易求得, .
点, ,
,解得或 .
点的坐标为或 .
13.(14分)随着无人机产业的快速发展,无人机航拍逐渐成为摄影创
作的重要方式.某日,学校摄影社团组织灞河景色无人机航拍活动.如
图,在平面直角坐标系中,, 分别表示拍摄某镜头时1号、2号无人机
的飞行高度(米)与飞行时间 (秒)之间的函数关系.
(1)1号无人机飞行的速度是___米/秒,2号无人机
飞行的速度是___米/秒;
6
4
(2)两架无人机飞行多少秒后,1号无人机的高度高于2号无人机?
解:根据题意得, .
令,解得 ,
直线, 交点的横坐标为15,
由图象可得两架无人机飞行15秒后,1号无人机的高度高于2号无人机.
素质发展
14.[2024·北京] 小云有一个圆柱形水杯(记为1号杯),在科
技活动中,小云用所学数学知识和人工智能软件设计了一个
新水杯,并将其制作出来,新水杯(记为2号杯)示意图如图.
当1号杯和2号杯中都有水时,小云分别记录了1号杯的水面高度
(单位:)和2号杯的水面高度(单位: ),部分数据如下:
0 40 100 200 300 400 500
0 2.5 5.0 7.5 10.0 12.5
0 2.8 4.8 7.2 8.9 10.5 11.8
(1)补全表格(结果保留小数点后一位);
解:1.0
[解析] 点拨:由表格可设与的函数关系式为 ,
则,解得 ,
,
当时, .
(2)通过分析数据,发现可以用函数刻画与,与 之间的关系.
在给出的平面直角坐标系中,画出这两个函数的图象;
解:如图.
(3)根据以上数据与函数图象,解决下列问题:
①当1号杯和2号杯中都有 水时,2号杯的水面高度与1号杯的水
面高度的差约为_____ (结果保留小数点后一位);
②在①的条件下,将2号杯中的一部分水倒入1号杯中,当两个水杯的水
面高度相同时,其水面高度约为_____ (结果保留小数点后一位).
