第十七章 勾股定理 单元复习课件(共21张PPT)
文档属性
| 名称 | 第十七章 勾股定理 单元复习课件(共21张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 1.4MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-05-10 00:00:00 | ||
图片预览





文档简介
(共21张PPT)
2025八年级数学下册
第十七章
——勾股定理单元复习
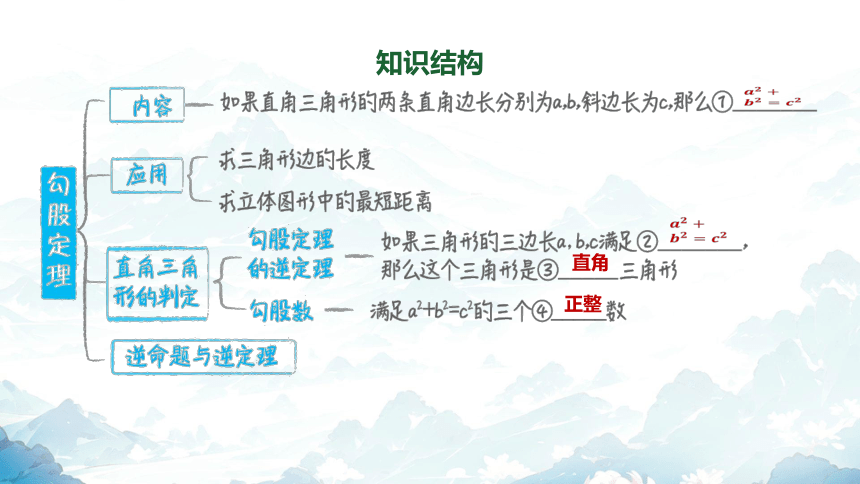
知识结构
直角
正整
达标训练
一、选择题(每题6分,共36分)
1.下列各组数中,不能作为直角三角形的三边长的是( )
D
A.1,2, B.5,4,3 C.17,8,15 D.2,3,4
2.在中, ,,,则 的长为( )
A
A.3 B. C.3或 D.
(第3题)
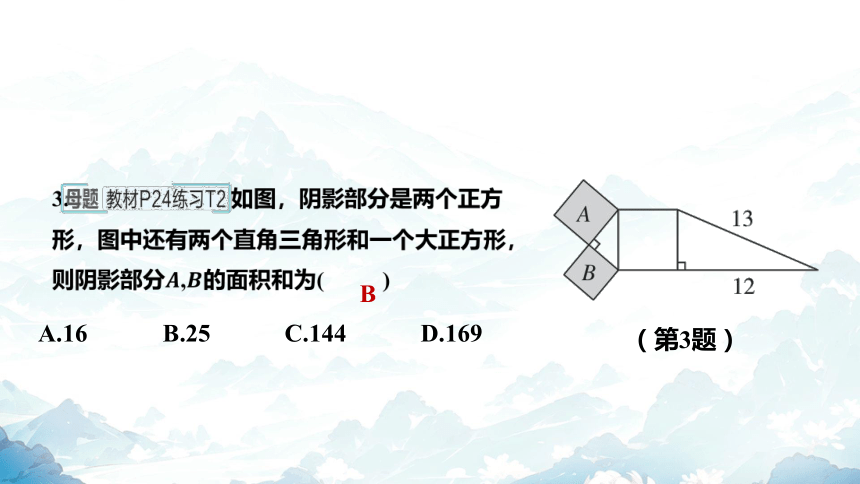
3. 如图,阴影部分是两个正方
形,图中还有两个直角三角形和一个大正方形,
则阴影部分, 的面积和为( )
B
A.16 B.25 C.144 D.169
(第4题)
4.[2024·聊城期末] 如图,数轴上的点, 分别对
应的数是1,2,过点作,以点 为圆
心,长为半径画弧,交于点 ;以数轴原点
(点)为圆心, 长为半径画弧,交数轴于点
,则点 对应的数是( )
D
A. B. C. D.
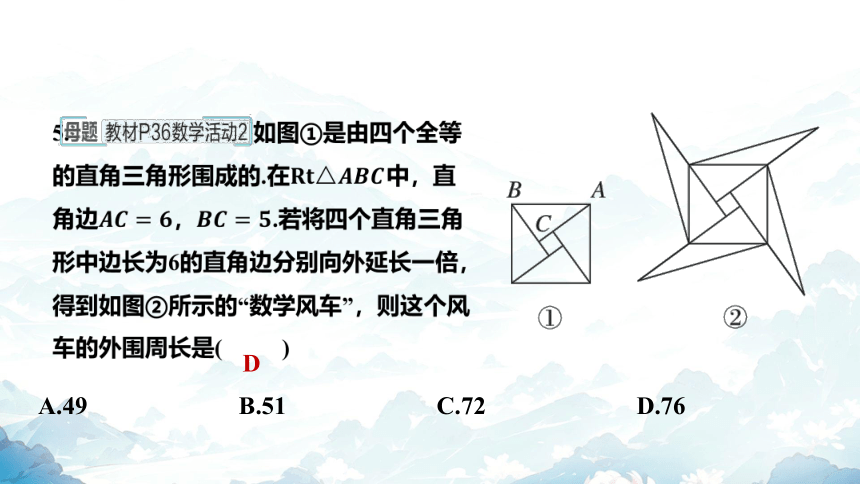
5. 如图①是由四个全等
的直角三角形围成的.在 中,直
角边, .若将四个直角三角
形中边长为6的直角边分别向外延长一倍,
得到如图②所示的“数学风车”,则这个风
车的外围周长是( )
D
A.49 B.51 C.72 D.76
(第6题)
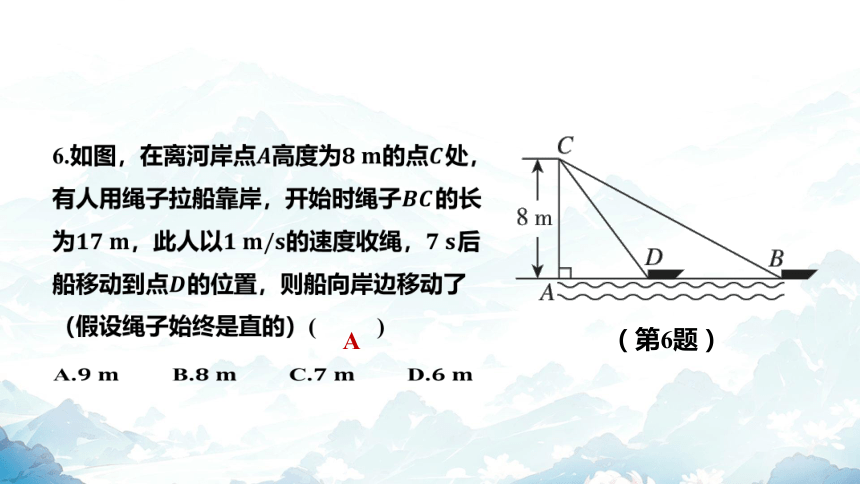
6.如图,在离河岸点高度为的点 处,
有人用绳子拉船靠岸,开始时绳子 的长
为,此人以的速度收绳, 后
船移动到点 的位置,则船向岸边移动了
(假设绳子始终是直的)( )
A
A. B. C. D.
二、填空题(每题6分,共12分)
7.命题“如果,那么 ”的逆命题是____________________
________.
如果,那么
8.如图,已知,,是海上的三座小岛,岛在岛的北偏东 方向
上,距离为12海里,岛在岛的北偏东方向上,距离为13海里,岛 和
岛之间的距离为5海里,则岛在岛 的北偏西_____方向上.
(第8题)
三、解答题(共52分)
9.(15分)如图,在正方形网格中,
每个小正方形的顶点叫做格点,设每
个小正方形的边长均为1.以格点为顶
点分别按下列要求画图.
解:(答案不唯一)
(1)在图①中,画一个,使它的斜边长为 ;
[答案] 如图①, 即为所画.
①
(2)在图②中,画一个等腰三角形,使它的底边长为 ,腰长为5.
[答案] 如图②,等腰三角形 即为所画.
②
10.(15分)某片绿地的形状如图所示,其中 , ,
,垂足分别为,,,,求 的长.
解:如图,延长,交于点 .
在中, , .
又, ,
.
在中, , ,
,
.
11.(22分) 如图, 是等腰直角
三角形,,点在 的斜边上.求证:
.
证明:如图,作,垂足为, .
在中, .
, 易得 .
,
,
, .
素质发展
12.综合与实践
长方体中蕴藏着丰富的数学知识,善
思小组开展了长方体中数学知识的探
究.如图①是底面为正方形 的长
方体盒子,,, .该小组把长方体的两侧
面,剪下来,沿着和 剪开,得到四个全等的直角三
角形,拼成如图②所示的“弦图”.
【探究一】
(1)如图②,若每个直角三角形较小锐角的度数为 ,小正方形
的面积为16,则大正方形 的面积为__________;
[解析] 点拨:小正方形 的面积为16,
.
每个直角三角形较小锐角的度数为 , ,
根据勾股定理得 ,
大正方形的边长为 ,
大正方形的面积为 .
【探究二】
(2)为了使长方体盒子更加美观,现准备在长方体外表面从点到点
粘贴一条彩色条(宽度忽略不计),设所用彩色条的长度为,探究 的
最小值(用含有, 的式子表示),该小组探究如下:将长方体盒子侧
面,展开成图③所示的平面图形,连接,在
中,,即 的最小值为
.上述探究结果是否正确?若不正确,画图并求出 的最小值.
解:不正确.理由如下:
将长方体盒子侧面,上底面 展开成平面图形,
连接 ,如图,
在 中,
.
,
且, ,
,即 ,
的最小值为 .
2025八年级数学下册
第十七章
——勾股定理单元复习
知识结构
直角
正整
达标训练
一、选择题(每题6分,共36分)
1.下列各组数中,不能作为直角三角形的三边长的是( )
D
A.1,2, B.5,4,3 C.17,8,15 D.2,3,4
2.在中, ,,,则 的长为( )
A
A.3 B. C.3或 D.
(第3题)
3. 如图,阴影部分是两个正方
形,图中还有两个直角三角形和一个大正方形,
则阴影部分, 的面积和为( )
B
A.16 B.25 C.144 D.169
(第4题)
4.[2024·聊城期末] 如图,数轴上的点, 分别对
应的数是1,2,过点作,以点 为圆
心,长为半径画弧,交于点 ;以数轴原点
(点)为圆心, 长为半径画弧,交数轴于点
,则点 对应的数是( )
D
A. B. C. D.
5. 如图①是由四个全等
的直角三角形围成的.在 中,直
角边, .若将四个直角三角
形中边长为6的直角边分别向外延长一倍,
得到如图②所示的“数学风车”,则这个风
车的外围周长是( )
D
A.49 B.51 C.72 D.76
(第6题)
6.如图,在离河岸点高度为的点 处,
有人用绳子拉船靠岸,开始时绳子 的长
为,此人以的速度收绳, 后
船移动到点 的位置,则船向岸边移动了
(假设绳子始终是直的)( )
A
A. B. C. D.
二、填空题(每题6分,共12分)
7.命题“如果,那么 ”的逆命题是____________________
________.
如果,那么
8.如图,已知,,是海上的三座小岛,岛在岛的北偏东 方向
上,距离为12海里,岛在岛的北偏东方向上,距离为13海里,岛 和
岛之间的距离为5海里,则岛在岛 的北偏西_____方向上.
(第8题)
三、解答题(共52分)
9.(15分)如图,在正方形网格中,
每个小正方形的顶点叫做格点,设每
个小正方形的边长均为1.以格点为顶
点分别按下列要求画图.
解:(答案不唯一)
(1)在图①中,画一个,使它的斜边长为 ;
[答案] 如图①, 即为所画.
①
(2)在图②中,画一个等腰三角形,使它的底边长为 ,腰长为5.
[答案] 如图②,等腰三角形 即为所画.
②
10.(15分)某片绿地的形状如图所示,其中 , ,
,垂足分别为,,,,求 的长.
解:如图,延长,交于点 .
在中, , .
又, ,
.
在中, , ,
,
.
11.(22分) 如图, 是等腰直角
三角形,,点在 的斜边上.求证:
.
证明:如图,作,垂足为, .
在中, .
, 易得 .
,
,
, .
素质发展
12.综合与实践
长方体中蕴藏着丰富的数学知识,善
思小组开展了长方体中数学知识的探
究.如图①是底面为正方形 的长
方体盒子,,, .该小组把长方体的两侧
面,剪下来,沿着和 剪开,得到四个全等的直角三
角形,拼成如图②所示的“弦图”.
【探究一】
(1)如图②,若每个直角三角形较小锐角的度数为 ,小正方形
的面积为16,则大正方形 的面积为__________;
[解析] 点拨:小正方形 的面积为16,
.
每个直角三角形较小锐角的度数为 , ,
根据勾股定理得 ,
大正方形的边长为 ,
大正方形的面积为 .
【探究二】
(2)为了使长方体盒子更加美观,现准备在长方体外表面从点到点
粘贴一条彩色条(宽度忽略不计),设所用彩色条的长度为,探究 的
最小值(用含有, 的式子表示),该小组探究如下:将长方体盒子侧
面,展开成图③所示的平面图形,连接,在
中,,即 的最小值为
.上述探究结果是否正确?若不正确,画图并求出 的最小值.
解:不正确.理由如下:
将长方体盒子侧面,上底面 展开成平面图形,
连接 ,如图,
在 中,
.
,
且, ,
,即 ,
的最小值为 .
