2016春鲁教版数学八下9.4《探索三角形相似的条件》ppt课件1 (共13张PPT)
文档属性
| 名称 | 2016春鲁教版数学八下9.4《探索三角形相似的条件》ppt课件1 (共13张PPT) |

|
|
| 格式 | zip | ||
| 文件大小 | 304.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 鲁教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2016-06-05 19:46:10 | ||
图片预览




文档简介
课件13张PPT。2018/11/19课首
第九章 相似图形鲁教版 ? 八 年 级《 数 学 ( 下 ) 》9.4探索三角形相似的条件(1)复习:3、三角形全等的判定条件有哪几种?4、你认为三角形相似至少需要哪些条件?5、如果要保证两个三角形相似,至少需要几个角相等呢?2、什么是全等三角形?1、什么是相似多边形?你能给相似三角形下个定义吗?三角对应相等、三边也对应相等的两个三角形全等。SAS、SSS、ASA、AAS、HL三个角分别相等、三边成比例的
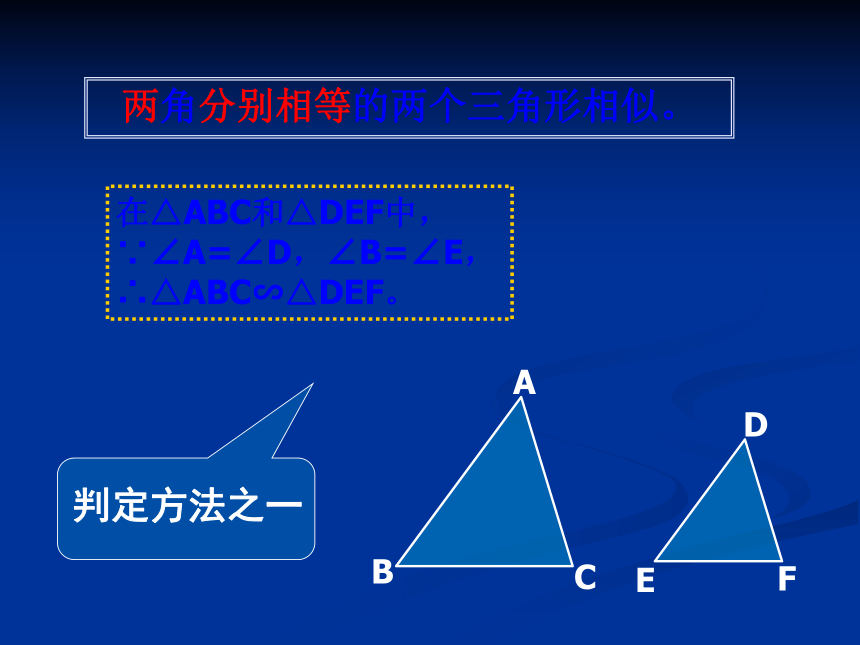
两个三角形叫相似三角形。做一做(1)画一个三角形ABC,使得∠ABC=60°。与同伴交流对比一下,你们所画的三角形相似吗?(2)与同伴合作,一人画三角形ABC,另一人画三角形A′B′C′,使得∠A和∠A ′都等于40。, ∠B 和∠ B′都等于60。。比较你们所画的两个三角形, ∠C 与∠ C′相等吗?对应边的比相等吗?三角形相似吗?不一定。结论:两角分别相等的两个三角形相似。两角分别相等的两个三角形相似。在△ABC和△DEF中,
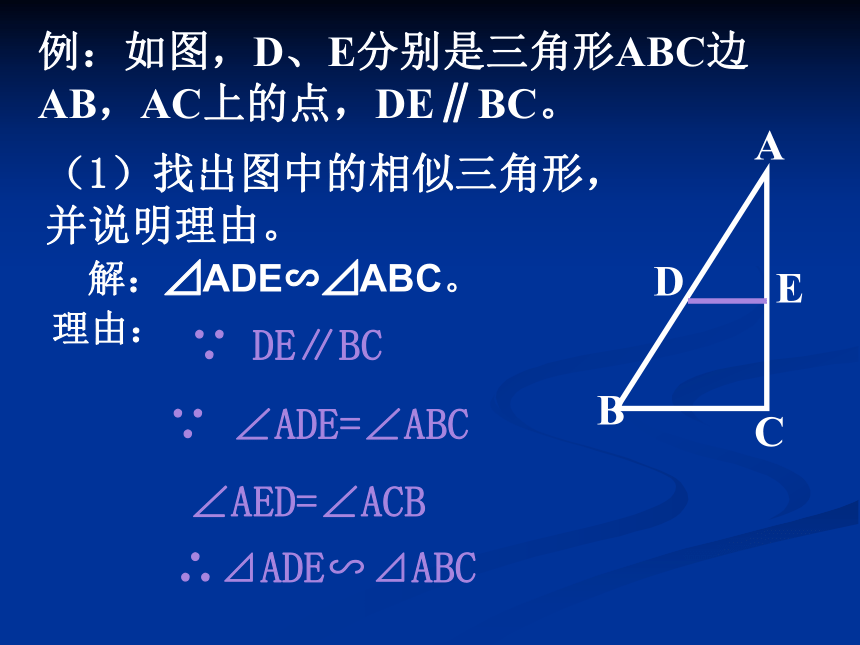
∵∠A=∠D,∠B=∠E,∴△ABC∽△DEF。随堂练习1、有一个锐角相等的两个直角三角形是否相似?为什么?2、顶角相等的两个等腰三角形是否相似?为什么?答:相似。因为一个锐角对应相等,还有一个直角对应相等,即有两个角对应相等,所以这两个三角形相似。答:相似。因为顶角对应相等,由三角形内角和为180。可得两个底角也对应相等,所以这两个三角形相似。3、有一个角相等的两个等腰三角形是否相似?为什么?例:如图,D、E分别是三角形ABC边AB,AC上的点,DE∥BC。(1)找出图中的相似三角形,并说明理由。∵ ∠ADE=∠ABC
∠AED=∠ACB ∴⊿ADE∽⊿ABC∵ DE∥BC解:⊿ADE∽⊿ABC。理由:例:如图,D、E分别是三角形ABC边AB,AC上的点,DE∥BC。(2)写出三组成比例的线段。解:∵ ⊿ADE∽⊿ABC∴例:如图,D、E分别是三角形ABC边AB,AC上的点,DE∥BC。∴ 解:∵∴ ∴ 还可以怎样做?∵ DE∥BC∴ 例:如图,D、E分别是三角形ABC边AB,AC上的点,DE∥BC。
②①④③如图,已知点D,E分别在AB,AC或它们的延长线上,且∠1=∠2,分别指出图中的相似三角形,并写出相应的比例式。△ADE∽△ACB△ADE∽△ABC△ADC∽△ACB△ADE∽△ACB看谁反应快①②③④2.如图,D、E分别是三角形ABC边AB,AC上的点,DE∥BC,AB=7,AD=5,DE=10,求BC的长。
1.如图,在△ABC和△A′B′C′中,已知∠A=50°,∠B=∠B′=60°,∠C′=70°,△ABC与△A′B′C′相似吗?为什么?如果△ABC∽△DEF ,△DEF∽ △MNP
那么,△ABC 与△MNP相似吗?为什么? (1)所有的等腰三角形都相似。( )
(2)所有的等腰直角三角形都相似。( )
(3)所有的等边三角形都相似。( )
(4)所有的直角三角形都相似。( )判断下列说法是否正确?并说明理由。 (5)有一个角是100 °的两个等腰三角形都相似。( )
(6)有一个角是70 °的两个等腰三角形都相似。 ( ) 小试牛刀
第九章 相似图形鲁教版 ? 八 年 级《 数 学 ( 下 ) 》9.4探索三角形相似的条件(1)复习:3、三角形全等的判定条件有哪几种?4、你认为三角形相似至少需要哪些条件?5、如果要保证两个三角形相似,至少需要几个角相等呢?2、什么是全等三角形?1、什么是相似多边形?你能给相似三角形下个定义吗?三角对应相等、三边也对应相等的两个三角形全等。SAS、SSS、ASA、AAS、HL三个角分别相等、三边成比例的
两个三角形叫相似三角形。做一做(1)画一个三角形ABC,使得∠ABC=60°。与同伴交流对比一下,你们所画的三角形相似吗?(2)与同伴合作,一人画三角形ABC,另一人画三角形A′B′C′,使得∠A和∠A ′都等于40。, ∠B 和∠ B′都等于60。。比较你们所画的两个三角形, ∠C 与∠ C′相等吗?对应边的比相等吗?三角形相似吗?不一定。结论:两角分别相等的两个三角形相似。两角分别相等的两个三角形相似。在△ABC和△DEF中,
∵∠A=∠D,∠B=∠E,∴△ABC∽△DEF。随堂练习1、有一个锐角相等的两个直角三角形是否相似?为什么?2、顶角相等的两个等腰三角形是否相似?为什么?答:相似。因为一个锐角对应相等,还有一个直角对应相等,即有两个角对应相等,所以这两个三角形相似。答:相似。因为顶角对应相等,由三角形内角和为180。可得两个底角也对应相等,所以这两个三角形相似。3、有一个角相等的两个等腰三角形是否相似?为什么?例:如图,D、E分别是三角形ABC边AB,AC上的点,DE∥BC。(1)找出图中的相似三角形,并说明理由。∵ ∠ADE=∠ABC
∠AED=∠ACB ∴⊿ADE∽⊿ABC∵ DE∥BC解:⊿ADE∽⊿ABC。理由:例:如图,D、E分别是三角形ABC边AB,AC上的点,DE∥BC。(2)写出三组成比例的线段。解:∵ ⊿ADE∽⊿ABC∴例:如图,D、E分别是三角形ABC边AB,AC上的点,DE∥BC。∴ 解:∵∴ ∴ 还可以怎样做?∵ DE∥BC∴ 例:如图,D、E分别是三角形ABC边AB,AC上的点,DE∥BC。
②①④③如图,已知点D,E分别在AB,AC或它们的延长线上,且∠1=∠2,分别指出图中的相似三角形,并写出相应的比例式。△ADE∽△ACB△ADE∽△ABC△ADC∽△ACB△ADE∽△ACB看谁反应快①②③④2.如图,D、E分别是三角形ABC边AB,AC上的点,DE∥BC,AB=7,AD=5,DE=10,求BC的长。
1.如图,在△ABC和△A′B′C′中,已知∠A=50°,∠B=∠B′=60°,∠C′=70°,△ABC与△A′B′C′相似吗?为什么?如果△ABC∽△DEF ,△DEF∽ △MNP
那么,△ABC 与△MNP相似吗?为什么? (1)所有的等腰三角形都相似。( )
(2)所有的等腰直角三角形都相似。( )
(3)所有的等边三角形都相似。( )
(4)所有的直角三角形都相似。( )判断下列说法是否正确?并说明理由。 (5)有一个角是100 °的两个等腰三角形都相似。( )
(6)有一个角是70 °的两个等腰三角形都相似。 ( ) 小试牛刀
