湖南省永州市祁阳市浯溪二中2025年中考二轮数学专题训练——有关三角形的最值问题(二)(含详解)
文档属性
| 名称 | 湖南省永州市祁阳市浯溪二中2025年中考二轮数学专题训练——有关三角形的最值问题(二)(含详解) |  | |
| 格式 | docx | ||
| 文件大小 | 1.1MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 湘教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-05-08 08:04:49 | ||
图片预览


文档简介
湖南省祁阳市浯溪二中2025年中考二轮数学专题训练——有关三角形的最值问题(二)
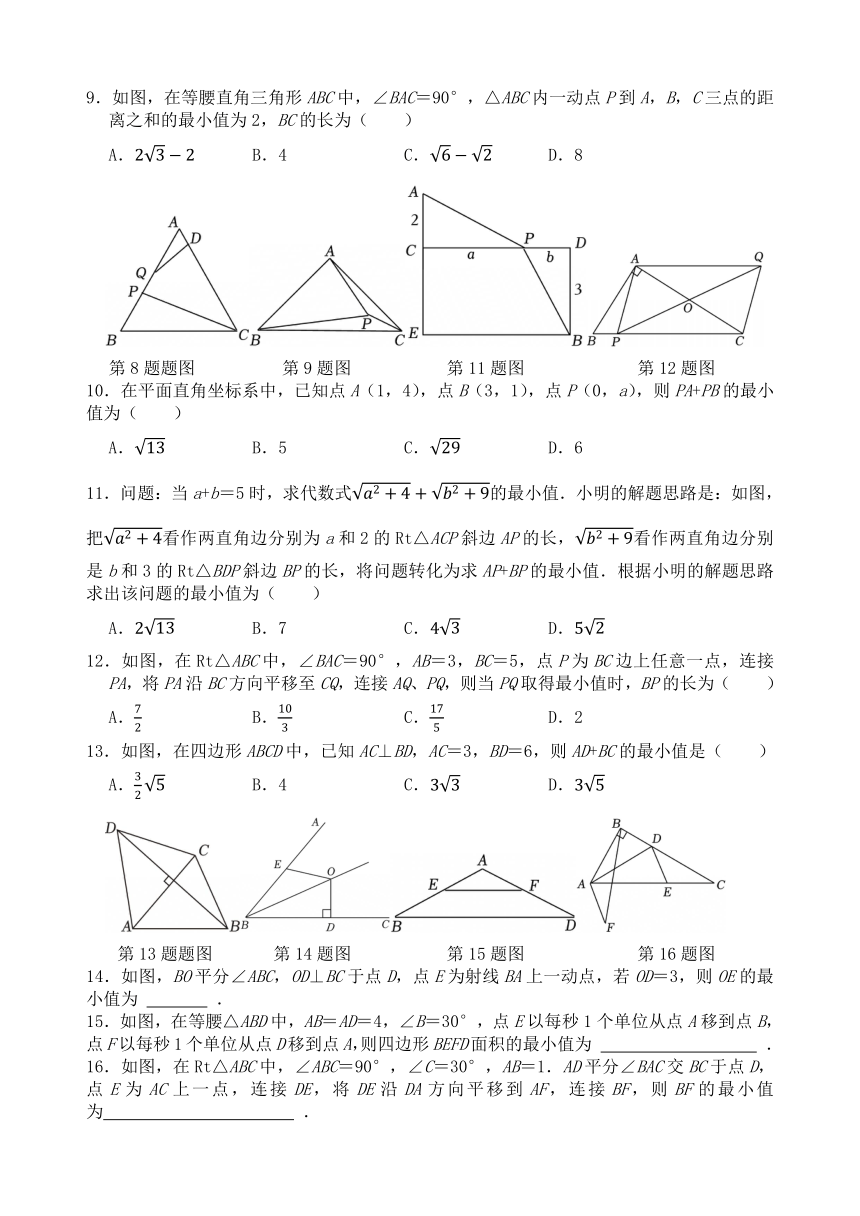
1.如图,在 Rt△ABC中,∠A=90°,BD平分∠ABC,交AC于点D,AB=4,BD=5,若点P是BC边上的动点,则线段DP的最小值为( )
A.2.4 B.3 C.4 D.5
2.如图,在△ABC中,AB=5,BC=10,AC=9,MN为边BC的垂直平分线,点D为直线MN上一动点,则△ABD的周长的最小值为( )
A.10 B.12 C.14 D.15
3.如图,在△ABC中,AB=AC=5,BC=6.若点P在边AC上移动,则BP的最小值是( )
A.3.5 B.4 C.4.5 D.4.8
4.如图,在△ABC中,有一点P在BC边上移动,若AB=AC=13,BC=24,则AP的最小值为( )
A.5 B.6 C.8 D.10
第1题题图 第2题图 第3题图 第4题图
5.如图1,我们把对角线相等的四边形称为对等四边形.如图2,在△ABC中,AB=AC,点P为BC边上一动点,M,N分别为AB,AC边上的动点.已知AB=10,BC=12,若四边形AMPN为对等四边形,则MN的最小值为( )
A.10 B.8 C.6 D.5
第5题题图 第6题图 第7题图
6.已知在△ABC中,AB=AC=4,∠BAC=120°,点D是CA延长线上任意一点,作DE⊥AB于点E,DF⊥BC于点F,连接EF,则EF的最小值为( )
A. B. C. D.
7.如图,等边△ABC的边长为3,过点B的直线l⊥AB,且△ABC与△A'BC'关于直线l对称,D为线段BC'上一动点,则AD+CD的最小值是( )
A.9 B.6 C.5 D.4
8.如图,等边△ABC的边长为3,点D在边AC上,AD,线段PQ在边BA上运动,PQ,有下列结论:①CP与QD可能相等;②△AQD与△BCP可能相似;③四边形PCDQ面积的最大值为;④四边形PCDQ周长的最小值为3.其中,正确结论的个数为( )
A.1 B.2 C.3 D.4
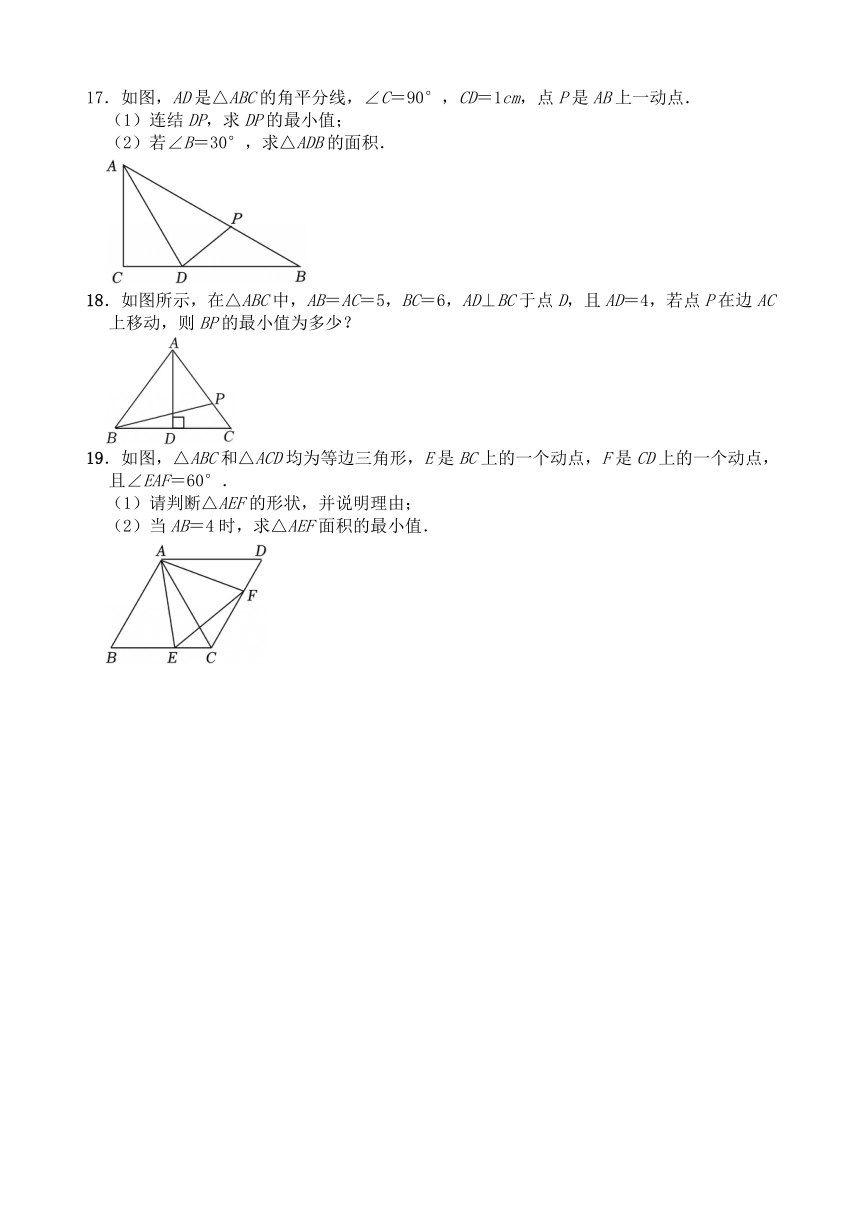
9.如图,在等腰直角三角形ABC中,∠BAC=90°,△ABC内一动点P到A,B,C三点的距离之和的最小值为2,BC的长为( )
A. B.4 C. D.8
第8题题图 第9题图 第11题图 第12题图
10.在平面直角坐标系中,已知点A(1,4),点B(3,1),点P(0,a),则PA+PB的最小值为( )
A. B.5 C. D.6
11.问题:当a+b=5时,求代数式的最小值.小明的解题思路是:如图,把看作两直角边分别为a和2的Rt△ACP斜边AP的长,看作两直角边分别是b和3的Rt△BDP斜边BP的长,将问题转化为求AP+BP的最小值.根据小明的解题思路求出该问题的最小值为( )
A. B.7 C. D.
12.如图,在Rt△ABC中,∠BAC=90°,AB=3,BC=5,点P为BC边上任意一点,连接PA,将PA沿BC方向平移至CQ,连接AQ、PQ,则当PQ取得最小值时,BP的长为( )
A. B. C. D.2
13.如图,在四边形ABCD中,已知AC⊥BD,AC=3,BD=6,则AD+BC的最小值是( )
A. B.4 C. D.
第13题题图 第14题图 第15题图 第16题图
14.如图,BO平分∠ABC,OD⊥BC于点D,点E为射线BA上一动点,若OD=3,则OE的最小值为 .
15.如图,在等腰△ABD中,AB=AD=4,∠B=30°,点E以每秒1个单位从点A移到点B,点F以每秒1个单位从点D移到点A,则四边形BEFD面积的最小值为 .
16.如图,在Rt△ABC中,∠ABC=90°,∠C=30°,AB=1.AD平分∠BAC交BC于点D,点E为AC上一点,连接DE,将DE沿DA方向平移到AF,连接BF,则BF的最小值为 .
17.如图,AD是△ABC的角平分线,∠C=90°,CD=1cm,点P是AB上一动点.
(1)连结DP,求DP的最小值;
(2)若∠B=30°,求△ADB的面积.
18.如图所示,在△ABC中,AB=AC=5,BC=6,AD⊥BC于点D,且AD=4,若点P在边AC上移动,则BP的最小值为多少?
19.如图,△ABC和△ACD均为等边三角形,E是BC上的一个动点,F是CD上的一个动点,且∠EAF=60°.
(1)请判断△AEF的形状,并说明理由;
(2)当AB=4时,求△AEF面积的最小值.
参考答案及解析
题号 1 2 3 4 5 6 7 8 9 10 11 12 13
答案 B C D A B A B C A B D C D
1.B
解析:∵在△ABC中,∠A=90°,AB=4,BD=5,
∴AD3,
过点D作DE⊥BC于点E,由垂线段最短可知当P与E重合时DP最短,
∵BD平分∠ABC交AC于D,
∴DE=AD=3,即线段DP的最小值为3.
2.C
解析:连接DC,如图,
∵AD,CD,AC是△ACD的三条边,
∴AD+DC≥AC,
∵MN为边BC的垂直平分线,AB=5,BC=10,AC=9,
∴DC=BD,
∴△ABD的周长=AB+AD+DB=AB+AD+DC≥AB+AC=5+9=14,
3.D
解析:作AD⊥BC于点D,如图,
∵AB=AC=5,BC=6,
∴BD=CD=3,
∴AD,
∵当BP⊥AC时,BP最小,
∴S△ABC,
∴6×4=5×BP,
解得BP=4.8;
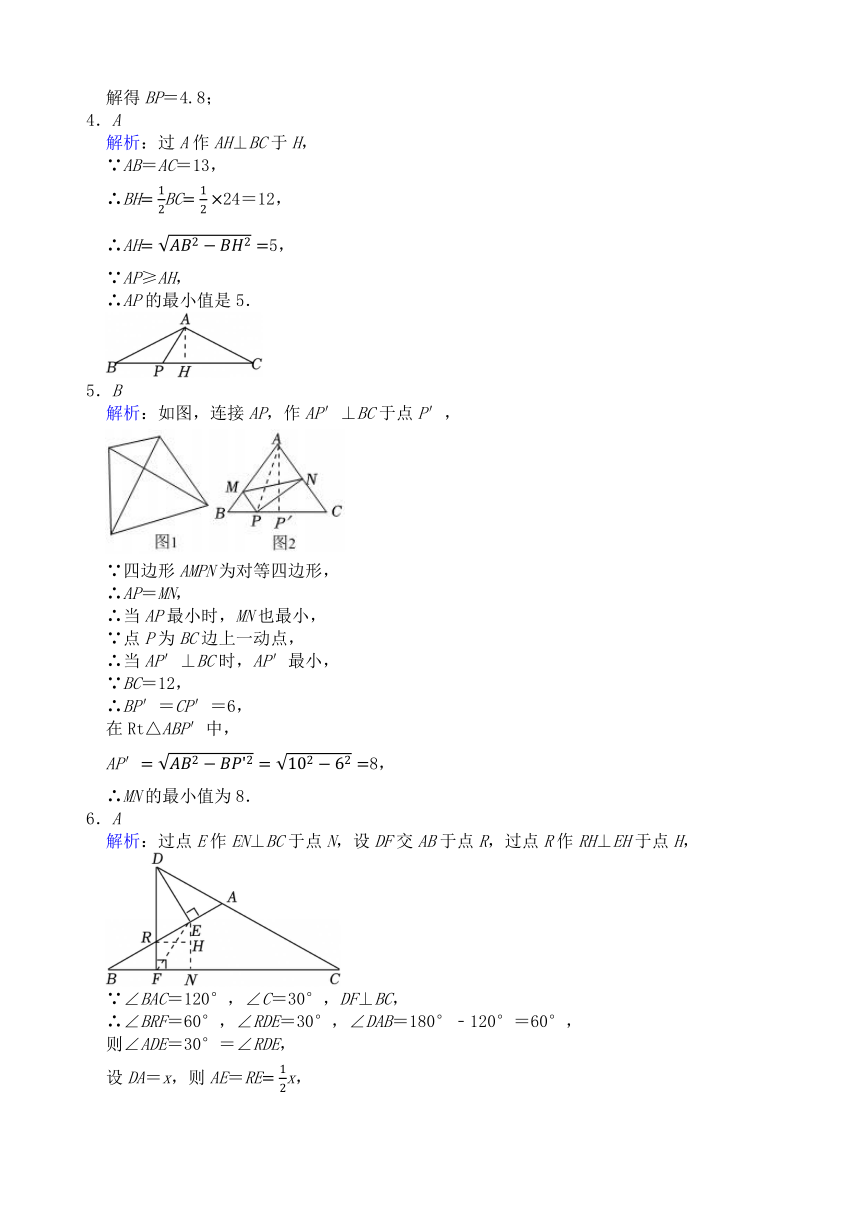
4.A
解析:过A作AH⊥BC于H,
∵AB=AC=13,
∴BHBC24=12,
∴AH5,
∵AP≥AH,
∴AP的最小值是5.
5.B
解析:如图,连接AP,作AP′⊥BC于点P′,
∵四边形AMPN为对等四边形,
∴AP=MN,
∴当AP最小时,MN也最小,
∵点P为BC边上一动点,
∴当AP′⊥BC时,AP′最小,
∵BC=12,
∴BP′=CP′=6,
在Rt△ABP′中,
AP′8,
∴MN的最小值为8.
6.A
解析:过点E作EN⊥BC于点N,设DF交AB于点R,过点R作RH⊥EH于点H,
∵∠BAC=120°,∠C=30°,DF⊥BC,
∴∠BRF=60°,∠RDE=30°,∠DAB=180°﹣120°=60°,
则∠ADE=30°=∠RDE,
设DA=x,则AE=REx,
则BE=AB﹣AE=4x,
在Rt△ERH中,∠ERH=∠B=30°,
则RH=REcos30°x=FN,
则FE2=NE2+FN2=(2)2+(x)2(x﹣2)2+3≥3,
故EF的最小值为,
7.B 解析:如图,连接A′D,
由对称性质可知∠ABC=∠A′BC′=60°,A′B=AB=BC=3,
∴∠CBC′=60°,∴∠CBC′=∠A′BC′,
∵BD=BD,∴△CBD≌△A′BD,
∴CD=A′D,∴AD+CD=A′D+AD,
∴当A、D、A′三点共线时,AD+CD最小,此时AD+CD=A′B+AB=6,
8.C解析:①在△AQD中,AQ+AD>QD,∵,∴AQ+PQ>QD,即AP>QD,当Q点与A点重合时,∴AP≥QD.
在△BCP中,BP+PC>BC,
∵BC=AB,
∴BP+PC>AB,
∴BP+PC>AP+BP,
∴PC>AP,当P点与B点重合时PC=AP=3,∴PC≥AP.
综上,当Q点与A点重合时,PC>AP≥QD;
当P点与B点重合时,PC≥AP>QD;
当P、Q不与A、B重合时,PC>AP>QD;
∴CP与QD不可能相等,故①错误.
②设AQ=x,
∵,AB=3,
∴,
∴0≤x≤2.5.假设△AQD与△BCP相似,
∵∠A=∠B,∴,∴,整理得,2x2﹣5x+3=0,
解得:x1=1,x2=1.5,∵0≤x≤2.5,∴x=1或1.5都符合题意,
∴△AQD与△BCP可能相似,故②正确.
③如图,过P作PE⊥BC于E,过D作DF⊥AB于F,过C点作CG⊥AB于G点.
设AQ=x,则,∴0≤x≤2.5,∵∠B=60°,
∴,∴,∵∠A=60°,,∴,
∴,∵△ABC中,AB=BC=3,∠B=60°,
∴,,
∴S四边形PCDQ=S△ABC﹣S△PBC﹣S△ADQ
,∵S随x的增大而增大,∴当x取最大值2.5时,S的值最大,
∴,故③正确.
④如图,作D点关于直线AB的对称点D1,作D1D2∥AB,且,连接CD2交AB于P点,将P点沿射线PA平移得Q点,连接DQ、D1Q,AD1,
则,QD1=QD,且四边形D1D2PQ是平行四边形,∴PD2=QD1=QD,
则四边形PCDQ的周长=CD+PQ+QD+PC=2.5+0.5+PD2+PC=3+CD2,
此时四边形PCDQ的周长最小.连接AD2,∵∠D1AB=∠DAB=60°,且D1D2∥AB,
∴∠AD1D2=180°﹣∠D1AB=120°,∵,∴,且∠D2AC=90°,∴,
在Rt△D2AC中,,
∴四边形PCDQ的周长的最小值为,故④正确.
9.A 解析:如图,把△APC绕点A逆时针旋转60°得到△AP′C′,连接PP′,BC′,过点C′作C′H⊥BA,
∴∠PAP′=60°,AP=AP′,PC=P′C′,
∴△APP′为等边三角形,
∴AP=PP′,
∴PA+PB+PC=PP′+PB+P′C′,
点C′可看成是线段AC绕A点逆时针旋转60°而得的定点,BC为定长.
当B、P、P′、C′四点在同一直线上时,PA+PB+PC最小.
∴BC′=2,
由旋转性质可知∠PAC=∠P′AC′,AC=AC′,
由条件可知∠BAP+∠PAC=90°,AB=AC′,
∴∠BAP+∠P′AC′=90°,
∴∠BAC′=∠BAP+∠P′AC′+∠PAP′=150°,
∴∠C′AH=30°,设C′H=x,则AB=AC′=2x,,
∴,在Rt△BHC′中,,∴,∴,
∴,
10.B
解析:如图,
作点A关于y轴的对称点A'(﹣1,4),连接A'B,交y轴于点P,
则PA+PB的最小值即线段A'B的长,过点B作BC⊥A'A,
交A'A的延长线于点C,Rt△A'BC中,∵点A'(﹣1,4),点B(3,1),
∴A'C=4,BC=3,由勾股定理得A'B5,
∴PA+PB的最小值为5.
11.D
解析:如图,连接AB,当点A、P、B三点共线时,AP+BP的值最小,
由题意可知,AB5,
即AP+BP的值最小值为5,
12.C解析:由条件可得,
∵四边形APCQ是平行四边形,
∴PO=QO,CO=AO,
∵PQ最短也就是PO最短,
∴过O作BC的垂线OP′,垂足为P′,连接BO,
∵垂线段最短,
∴当点P在点P′处时,PO最小,即PQ最小,
∵S△ABO=S△BOC,即,
∵CO=AO=2,BC=5,AB=3,
∴,∴则PQ的最小值为2.4,∴,
∴,∴当PQ取得最小值时,BP的长为.
13.D 解析:如图,以AC、BC为邻边作平行四边形ACBE,连接DE,
则AC∥BE,BE=AC=3,AE=BC,∴AD+BC=AD+AE≥DE,
∴AD+BC的最小值为DE,∵AC⊥BD,∴BE⊥BD,
∴∠DBE=90°,在Rt△DBE中,由勾股定理得:DE3,
∴AD+BC的最小值为3,故选:D.
14.3.解析:过O点作OF⊥BA于F点,如图,
∵BO平分∠ABC且OD⊥BC,∴OF=OD=3,∵点E为射线BA上一动点,
∴OE的最小值为3.
15.3.
解析:过D作DM⊥BA交BA的延长线于M,过F作FN⊥AM于N,
设E、F运动的时间是t秒(0<t<4),
∴AE=DF=t,∴AF=4﹣t,∵AB=AD=4,∴∠D=∠B=30°,
∴∠DAM=∠B+∠D=60°,∵sin∠DAM=sin60°,
∴DM=2,∵sin∠FAN=sin60°,
∴FN(4﹣t),∴△ABD的面积AB DM4×24,△AEF的面积AE FNt(4﹣t)(t﹣2)2,
∴四边形BEFD面积=△ABD的面积﹣△AEF的面积(t﹣2)2+3,
∴四边形BEFD面积的最小值为3.
16..
解析:根据题意,点E是在线段AC上移动的,则点F的轨迹是在过点F且平行于AC的线段MN上移动,
可作过点F的线段MN∥AC,且MN=AC,
∵在Rt△ABC中,∠ABC=90°,∠C=30°,AB=1.
∴AC=2,BC,
作BF′⊥MN,垂足为F′,AT⊥MN,垂足为T,DQ⊥AC,垂足为Q,
∵AD平分∠BAC交BC于点D,
∴BD=DQ,
设BD=x,则AD=2x,ABx,
∴x,∴BD=DQ,在△DQC和△ATM中,
,∴△DQC≌△ATM(AAS),
∴DQ=AT,∴PF′=DQ=AT,∵BP,
∴BF′=BP+PF′.∴BF的最小值为,
17.解:(1)如图,过点D作DH⊥AB于H,
∵AD是△ABC的角平分线,∠C=90°,DH⊥AB,
∴DH=CD=1cm,
由垂线段最短可知:DP的最小值是1cm;
(2)在Rt△ABC中,∠C=90°,∠B=30°,
则∠BAC=90°﹣30°=60°,BD=2DH=2cm,
∵AD是△ABC的角平分线,
∴∠CAD∠BAC=30°,
∴AD=2CD=2cm,
由勾股定理得:AC22﹣12(cm),
∴S△ADB2(cm2).
18.解:根据垂线段最短,得到BP⊥AC时,BP最短,此时S△ABCBC ADBP AC,
∵BC=6,AD=4,AC=5,∴BP4.8.∴BP的最小值为4.8.
19.解:(1)△AEF是等边三角形.理由如下:
∵△ABC和△ACD均为等边三角形,
∴AB=AC,∠B=∠ACD=∠BAC=60°,
∵∠EAF=60°,
∴∠BAC=∠EAF,
∴∠BAE=∠CAF.
在△ABE与△ACF中,
,
∴△ABE≌△ACF(ASA),
∴AE=AF,
∵∠EAF=60°,
∴△AEF是等边三角形;
(2)由(1)知△AEF是等边三角形,
∴S△AEFAE2,
∴当AE⊥BC时,AE取得最小值,△AEF面积也有最小值,
此时AE=AB sin60°=42,
∴S△AEF(2)2=12.
1.如图,在 Rt△ABC中,∠A=90°,BD平分∠ABC,交AC于点D,AB=4,BD=5,若点P是BC边上的动点,则线段DP的最小值为( )
A.2.4 B.3 C.4 D.5
2.如图,在△ABC中,AB=5,BC=10,AC=9,MN为边BC的垂直平分线,点D为直线MN上一动点,则△ABD的周长的最小值为( )
A.10 B.12 C.14 D.15
3.如图,在△ABC中,AB=AC=5,BC=6.若点P在边AC上移动,则BP的最小值是( )
A.3.5 B.4 C.4.5 D.4.8
4.如图,在△ABC中,有一点P在BC边上移动,若AB=AC=13,BC=24,则AP的最小值为( )
A.5 B.6 C.8 D.10
第1题题图 第2题图 第3题图 第4题图
5.如图1,我们把对角线相等的四边形称为对等四边形.如图2,在△ABC中,AB=AC,点P为BC边上一动点,M,N分别为AB,AC边上的动点.已知AB=10,BC=12,若四边形AMPN为对等四边形,则MN的最小值为( )
A.10 B.8 C.6 D.5
第5题题图 第6题图 第7题图
6.已知在△ABC中,AB=AC=4,∠BAC=120°,点D是CA延长线上任意一点,作DE⊥AB于点E,DF⊥BC于点F,连接EF,则EF的最小值为( )
A. B. C. D.
7.如图,等边△ABC的边长为3,过点B的直线l⊥AB,且△ABC与△A'BC'关于直线l对称,D为线段BC'上一动点,则AD+CD的最小值是( )
A.9 B.6 C.5 D.4
8.如图,等边△ABC的边长为3,点D在边AC上,AD,线段PQ在边BA上运动,PQ,有下列结论:①CP与QD可能相等;②△AQD与△BCP可能相似;③四边形PCDQ面积的最大值为;④四边形PCDQ周长的最小值为3.其中,正确结论的个数为( )
A.1 B.2 C.3 D.4
9.如图,在等腰直角三角形ABC中,∠BAC=90°,△ABC内一动点P到A,B,C三点的距离之和的最小值为2,BC的长为( )
A. B.4 C. D.8
第8题题图 第9题图 第11题图 第12题图
10.在平面直角坐标系中,已知点A(1,4),点B(3,1),点P(0,a),则PA+PB的最小值为( )
A. B.5 C. D.6
11.问题:当a+b=5时,求代数式的最小值.小明的解题思路是:如图,把看作两直角边分别为a和2的Rt△ACP斜边AP的长,看作两直角边分别是b和3的Rt△BDP斜边BP的长,将问题转化为求AP+BP的最小值.根据小明的解题思路求出该问题的最小值为( )
A. B.7 C. D.
12.如图,在Rt△ABC中,∠BAC=90°,AB=3,BC=5,点P为BC边上任意一点,连接PA,将PA沿BC方向平移至CQ,连接AQ、PQ,则当PQ取得最小值时,BP的长为( )
A. B. C. D.2
13.如图,在四边形ABCD中,已知AC⊥BD,AC=3,BD=6,则AD+BC的最小值是( )
A. B.4 C. D.
第13题题图 第14题图 第15题图 第16题图
14.如图,BO平分∠ABC,OD⊥BC于点D,点E为射线BA上一动点,若OD=3,则OE的最小值为 .
15.如图,在等腰△ABD中,AB=AD=4,∠B=30°,点E以每秒1个单位从点A移到点B,点F以每秒1个单位从点D移到点A,则四边形BEFD面积的最小值为 .
16.如图,在Rt△ABC中,∠ABC=90°,∠C=30°,AB=1.AD平分∠BAC交BC于点D,点E为AC上一点,连接DE,将DE沿DA方向平移到AF,连接BF,则BF的最小值为 .
17.如图,AD是△ABC的角平分线,∠C=90°,CD=1cm,点P是AB上一动点.
(1)连结DP,求DP的最小值;
(2)若∠B=30°,求△ADB的面积.
18.如图所示,在△ABC中,AB=AC=5,BC=6,AD⊥BC于点D,且AD=4,若点P在边AC上移动,则BP的最小值为多少?
19.如图,△ABC和△ACD均为等边三角形,E是BC上的一个动点,F是CD上的一个动点,且∠EAF=60°.
(1)请判断△AEF的形状,并说明理由;
(2)当AB=4时,求△AEF面积的最小值.
参考答案及解析
题号 1 2 3 4 5 6 7 8 9 10 11 12 13
答案 B C D A B A B C A B D C D
1.B
解析:∵在△ABC中,∠A=90°,AB=4,BD=5,
∴AD3,
过点D作DE⊥BC于点E,由垂线段最短可知当P与E重合时DP最短,
∵BD平分∠ABC交AC于D,
∴DE=AD=3,即线段DP的最小值为3.
2.C
解析:连接DC,如图,
∵AD,CD,AC是△ACD的三条边,
∴AD+DC≥AC,
∵MN为边BC的垂直平分线,AB=5,BC=10,AC=9,
∴DC=BD,
∴△ABD的周长=AB+AD+DB=AB+AD+DC≥AB+AC=5+9=14,
3.D
解析:作AD⊥BC于点D,如图,
∵AB=AC=5,BC=6,
∴BD=CD=3,
∴AD,
∵当BP⊥AC时,BP最小,
∴S△ABC,
∴6×4=5×BP,
解得BP=4.8;
4.A
解析:过A作AH⊥BC于H,
∵AB=AC=13,
∴BHBC24=12,
∴AH5,
∵AP≥AH,
∴AP的最小值是5.
5.B
解析:如图,连接AP,作AP′⊥BC于点P′,
∵四边形AMPN为对等四边形,
∴AP=MN,
∴当AP最小时,MN也最小,
∵点P为BC边上一动点,
∴当AP′⊥BC时,AP′最小,
∵BC=12,
∴BP′=CP′=6,
在Rt△ABP′中,
AP′8,
∴MN的最小值为8.
6.A
解析:过点E作EN⊥BC于点N,设DF交AB于点R,过点R作RH⊥EH于点H,
∵∠BAC=120°,∠C=30°,DF⊥BC,
∴∠BRF=60°,∠RDE=30°,∠DAB=180°﹣120°=60°,
则∠ADE=30°=∠RDE,
设DA=x,则AE=REx,
则BE=AB﹣AE=4x,
在Rt△ERH中,∠ERH=∠B=30°,
则RH=REcos30°x=FN,
则FE2=NE2+FN2=(2)2+(x)2(x﹣2)2+3≥3,
故EF的最小值为,
7.B 解析:如图,连接A′D,
由对称性质可知∠ABC=∠A′BC′=60°,A′B=AB=BC=3,
∴∠CBC′=60°,∴∠CBC′=∠A′BC′,
∵BD=BD,∴△CBD≌△A′BD,
∴CD=A′D,∴AD+CD=A′D+AD,
∴当A、D、A′三点共线时,AD+CD最小,此时AD+CD=A′B+AB=6,
8.C解析:①在△AQD中,AQ+AD>QD,∵,∴AQ+PQ>QD,即AP>QD,当Q点与A点重合时,∴AP≥QD.
在△BCP中,BP+PC>BC,
∵BC=AB,
∴BP+PC>AB,
∴BP+PC>AP+BP,
∴PC>AP,当P点与B点重合时PC=AP=3,∴PC≥AP.
综上,当Q点与A点重合时,PC>AP≥QD;
当P点与B点重合时,PC≥AP>QD;
当P、Q不与A、B重合时,PC>AP>QD;
∴CP与QD不可能相等,故①错误.
②设AQ=x,
∵,AB=3,
∴,
∴0≤x≤2.5.假设△AQD与△BCP相似,
∵∠A=∠B,∴,∴,整理得,2x2﹣5x+3=0,
解得:x1=1,x2=1.5,∵0≤x≤2.5,∴x=1或1.5都符合题意,
∴△AQD与△BCP可能相似,故②正确.
③如图,过P作PE⊥BC于E,过D作DF⊥AB于F,过C点作CG⊥AB于G点.
设AQ=x,则,∴0≤x≤2.5,∵∠B=60°,
∴,∴,∵∠A=60°,,∴,
∴,∵△ABC中,AB=BC=3,∠B=60°,
∴,,
∴S四边形PCDQ=S△ABC﹣S△PBC﹣S△ADQ
,∵S随x的增大而增大,∴当x取最大值2.5时,S的值最大,
∴,故③正确.
④如图,作D点关于直线AB的对称点D1,作D1D2∥AB,且,连接CD2交AB于P点,将P点沿射线PA平移得Q点,连接DQ、D1Q,AD1,
则,QD1=QD,且四边形D1D2PQ是平行四边形,∴PD2=QD1=QD,
则四边形PCDQ的周长=CD+PQ+QD+PC=2.5+0.5+PD2+PC=3+CD2,
此时四边形PCDQ的周长最小.连接AD2,∵∠D1AB=∠DAB=60°,且D1D2∥AB,
∴∠AD1D2=180°﹣∠D1AB=120°,∵,∴,且∠D2AC=90°,∴,
在Rt△D2AC中,,
∴四边形PCDQ的周长的最小值为,故④正确.
9.A 解析:如图,把△APC绕点A逆时针旋转60°得到△AP′C′,连接PP′,BC′,过点C′作C′H⊥BA,
∴∠PAP′=60°,AP=AP′,PC=P′C′,
∴△APP′为等边三角形,
∴AP=PP′,
∴PA+PB+PC=PP′+PB+P′C′,
点C′可看成是线段AC绕A点逆时针旋转60°而得的定点,BC为定长.
当B、P、P′、C′四点在同一直线上时,PA+PB+PC最小.
∴BC′=2,
由旋转性质可知∠PAC=∠P′AC′,AC=AC′,
由条件可知∠BAP+∠PAC=90°,AB=AC′,
∴∠BAP+∠P′AC′=90°,
∴∠BAC′=∠BAP+∠P′AC′+∠PAP′=150°,
∴∠C′AH=30°,设C′H=x,则AB=AC′=2x,,
∴,在Rt△BHC′中,,∴,∴,
∴,
10.B
解析:如图,
作点A关于y轴的对称点A'(﹣1,4),连接A'B,交y轴于点P,
则PA+PB的最小值即线段A'B的长,过点B作BC⊥A'A,
交A'A的延长线于点C,Rt△A'BC中,∵点A'(﹣1,4),点B(3,1),
∴A'C=4,BC=3,由勾股定理得A'B5,
∴PA+PB的最小值为5.
11.D
解析:如图,连接AB,当点A、P、B三点共线时,AP+BP的值最小,
由题意可知,AB5,
即AP+BP的值最小值为5,
12.C解析:由条件可得,
∵四边形APCQ是平行四边形,
∴PO=QO,CO=AO,
∵PQ最短也就是PO最短,
∴过O作BC的垂线OP′,垂足为P′,连接BO,
∵垂线段最短,
∴当点P在点P′处时,PO最小,即PQ最小,
∵S△ABO=S△BOC,即,
∵CO=AO=2,BC=5,AB=3,
∴,∴则PQ的最小值为2.4,∴,
∴,∴当PQ取得最小值时,BP的长为.
13.D 解析:如图,以AC、BC为邻边作平行四边形ACBE,连接DE,
则AC∥BE,BE=AC=3,AE=BC,∴AD+BC=AD+AE≥DE,
∴AD+BC的最小值为DE,∵AC⊥BD,∴BE⊥BD,
∴∠DBE=90°,在Rt△DBE中,由勾股定理得:DE3,
∴AD+BC的最小值为3,故选:D.
14.3.解析:过O点作OF⊥BA于F点,如图,
∵BO平分∠ABC且OD⊥BC,∴OF=OD=3,∵点E为射线BA上一动点,
∴OE的最小值为3.
15.3.
解析:过D作DM⊥BA交BA的延长线于M,过F作FN⊥AM于N,
设E、F运动的时间是t秒(0<t<4),
∴AE=DF=t,∴AF=4﹣t,∵AB=AD=4,∴∠D=∠B=30°,
∴∠DAM=∠B+∠D=60°,∵sin∠DAM=sin60°,
∴DM=2,∵sin∠FAN=sin60°,
∴FN(4﹣t),∴△ABD的面积AB DM4×24,△AEF的面积AE FNt(4﹣t)(t﹣2)2,
∴四边形BEFD面积=△ABD的面积﹣△AEF的面积(t﹣2)2+3,
∴四边形BEFD面积的最小值为3.
16..
解析:根据题意,点E是在线段AC上移动的,则点F的轨迹是在过点F且平行于AC的线段MN上移动,
可作过点F的线段MN∥AC,且MN=AC,
∵在Rt△ABC中,∠ABC=90°,∠C=30°,AB=1.
∴AC=2,BC,
作BF′⊥MN,垂足为F′,AT⊥MN,垂足为T,DQ⊥AC,垂足为Q,
∵AD平分∠BAC交BC于点D,
∴BD=DQ,
设BD=x,则AD=2x,ABx,
∴x,∴BD=DQ,在△DQC和△ATM中,
,∴△DQC≌△ATM(AAS),
∴DQ=AT,∴PF′=DQ=AT,∵BP,
∴BF′=BP+PF′.∴BF的最小值为,
17.解:(1)如图,过点D作DH⊥AB于H,
∵AD是△ABC的角平分线,∠C=90°,DH⊥AB,
∴DH=CD=1cm,
由垂线段最短可知:DP的最小值是1cm;
(2)在Rt△ABC中,∠C=90°,∠B=30°,
则∠BAC=90°﹣30°=60°,BD=2DH=2cm,
∵AD是△ABC的角平分线,
∴∠CAD∠BAC=30°,
∴AD=2CD=2cm,
由勾股定理得:AC22﹣12(cm),
∴S△ADB2(cm2).
18.解:根据垂线段最短,得到BP⊥AC时,BP最短,此时S△ABCBC ADBP AC,
∵BC=6,AD=4,AC=5,∴BP4.8.∴BP的最小值为4.8.
19.解:(1)△AEF是等边三角形.理由如下:
∵△ABC和△ACD均为等边三角形,
∴AB=AC,∠B=∠ACD=∠BAC=60°,
∵∠EAF=60°,
∴∠BAC=∠EAF,
∴∠BAE=∠CAF.
在△ABE与△ACF中,
,
∴△ABE≌△ACF(ASA),
∴AE=AF,
∵∠EAF=60°,
∴△AEF是等边三角形;
(2)由(1)知△AEF是等边三角形,
∴S△AEFAE2,
∴当AE⊥BC时,AE取得最小值,△AEF面积也有最小值,
此时AE=AB sin60°=42,
∴S△AEF(2)2=12.
同课章节目录
