4.5 第1课时 问题解决策略:特殊化 课件(共18张PPT) 2024--2025学年北师大版七年级数学下册
文档属性
| 名称 | 4.5 第1课时 问题解决策略:特殊化 课件(共18张PPT) 2024--2025学年北师大版七年级数学下册 |  | |
| 格式 | pptx | ||
| 文件大小 | 5.0MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-05-08 08:32:30 | ||
图片预览





文档简介
(共18张PPT)
第四章 三角形
4.5 问题解决策略:特殊化
第1课时 问题解决策略:特殊化
学习目标
(教师展示,1min)
1. 理解特殊化策略在解决数学问题中的重要意义,明确特殊化策略是解决复杂问题的有效手段之一.
2. 会识别出哪些类型的数学问题适合采用特殊化策略来解决,例如几何图形面积计算问题、与图形内点相关的线段关系问题等.
3. 能熟练地将一般性的数学问题转化为特殊情形进行思考,学会在不同特殊情形之间建立联系和转化,培养举一反三的学习能力.
新课导入
希尔伯特
在讨论数学问题时,我相信特殊化比一般化起着更为重要的作用,这种方法是克服数学困难的最重要的杠杆之一.
(师讲述,生感受,1min)
什么是特殊化
举个例子:
三角形的三条中线交于一点
等边三角形的三条中线交于一点
一般性问题
特殊情形
面对一般性的问题时,可以先考虑特殊情形,借助特殊情形下获得的结论或方法解决一般性的问题,这就是特殊化策略。
(师讲述,生感受,1min)
回顾七年级上册我们学过的数轴,点 a 在数轴上的
位置如图所示,你知道怎么快速比较 a,,|a| 的
大小关系吗
a
答:取 a=-0.5,则 a,,| a | 三个数分别
为-0.5,-2,0.5,所以 < a < |a|.
(师讲述,生思考后回答,1min)
【学习任务1】
学生活动1:利用“角边角”判定三角形全等
(师提出问题,生思考,1min)
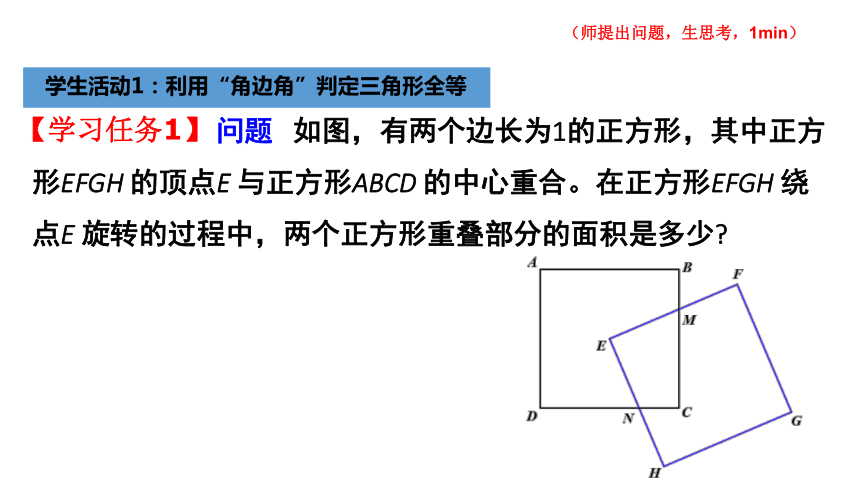
问题 如图,有两个边长为1的正方形,其中正方形EFGH 的顶点E 与正方形ABCD 的中心重合。在正方形EFGH 绕点E 旋转的过程中,两个正方形重叠部分的面积是多少
(师提问,生动手操作,小组讨论后分享,5min)
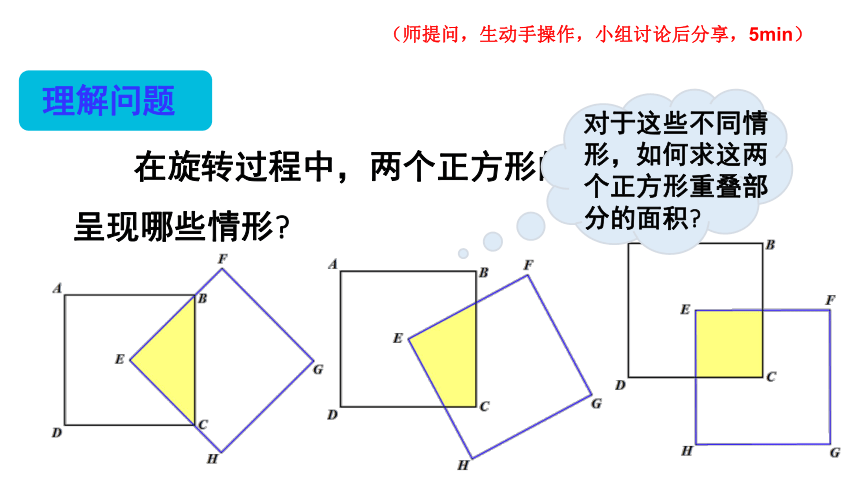
在旋转过程中,两个正方形的重叠部分会呈现哪些情形
理解问题
对于这些不同情形,如何求这两个正方形重叠部分的面积
(师提问,生思考后回答,5min)
拟定计划
哪些特殊情形下,两个正方形重叠部分的面积容易求出
其他情形能转化为容易求解的特殊情形吗?
S重叠=S正方形ABCD =
M
N
△BEM≌△CEN
S重叠=S△BEC =
M
N
P
Q
△EMP≌△ENQ
S重叠=S四边形EQCP =
(师总结板书,生记笔记,2min)
因为某些因素(如形状、位置或数值等)不确定,使得问题有多种情形时、可以限制这个引起变化的因素,考虑最为特殊的情形,采用从特殊情形入手的策略解决问题。
问题思路受阻
发现特殊值(情形)
以特殊值(情形)找到思路
问题得以解决
【评价任务1】
(生独立思考,小组讨论后回答,5min)
【课本P115 】
1.如图,点P是等边三角形ABC 内的任意一点,过点 P向三边作垂线,垂足分别为 D,E,F。小颖从特殊情形入手,认为 AF+BD+CE等于△ABC周长的 。你知道她是怎么做的吗
解:小颖是从以下特殊情形入手:点P为等边三角形ABC三条高的交点,如图所示。
容易得到,△ABD≌ ACD,
所以 BD = CD。
同理可得 AF = BF, AE = CE。
因此,容易得到AF+BD+CE等于△ABC周长的
(生独立思考,举手回答,5min)
2.如图 ,四边形 ABCD 的面积是 16,各边中点分别为 M,N,P,Q,MP与 NQ 相交于点 O,求图中阴影部分的面积。
解:如图,连接OA,OB,OC,OD。
因为 M是AB的中点,
所以 AM = AB
所以 S△OAM = S△OAB
同理可得,
S△OAQ = S△OAD,
S△OCN = S△OBC,
S△OCP = S△OCD。
S阴影 = S△OAM + S△OAQ + S△OCN + S△OCP
= S△OAB + S△OAD + S△OBC + S△OCD
= S四边形ABCD
= ×16 =8
课堂小结
(师引导生回答,2min)
面对一般性的问题时,可以先考虑特殊情形,借助特殊情形下获得的结论或方法解决一般性的问题,这就是特殊化策略。
课堂练习
独立完成(10min)
解:如图,过点 A作BC的垂线交BC于点Q,连接AP,BP,CP.
1. 如图,点 P 是等边三角形 ABC 内的任意一点,过点 P 向三边作垂线,垂足分别为点D,E,F. 小颖从特殊情形入手,认为 PD+PE+PF 等于△ABC 的高,你知道她是怎么做的吗
S△ABC=S△ABP+S△BCP+S△ACP
Q
BC AQ=AB PF+ BC PD+ AC PE
因为 AB=BC=AC,
所以 AQ=PF+PD+PE.
所以 PD+PE+PF 等于△ABC 的高
2.一个三位数除以它的各位数字之和,商最大是多少
解:设这个三位数为 abc ( a、b、c 均为整数,且1≤a≤9,0≤b≤9,0≤c≤9),这个三位数的值是100a + 10b + c,各位数字之和是 a + b + c.
要求商最大,就要让被除数尽可能大,除数尽可能小.
商=.
当这个三位数是 900,
当这个三位数是100,各位数字之和是 1+ 0 + 0 = 1 时,
商为 =100
各位数字之和是9+0+0=9 时,商为 =100;
所以一个三位数除以它的各位数字之和,商最大是100.
第四章 三角形
4.5 问题解决策略:特殊化
第1课时 问题解决策略:特殊化
学习目标
(教师展示,1min)
1. 理解特殊化策略在解决数学问题中的重要意义,明确特殊化策略是解决复杂问题的有效手段之一.
2. 会识别出哪些类型的数学问题适合采用特殊化策略来解决,例如几何图形面积计算问题、与图形内点相关的线段关系问题等.
3. 能熟练地将一般性的数学问题转化为特殊情形进行思考,学会在不同特殊情形之间建立联系和转化,培养举一反三的学习能力.
新课导入
希尔伯特
在讨论数学问题时,我相信特殊化比一般化起着更为重要的作用,这种方法是克服数学困难的最重要的杠杆之一.
(师讲述,生感受,1min)
什么是特殊化
举个例子:
三角形的三条中线交于一点
等边三角形的三条中线交于一点
一般性问题
特殊情形
面对一般性的问题时,可以先考虑特殊情形,借助特殊情形下获得的结论或方法解决一般性的问题,这就是特殊化策略。
(师讲述,生感受,1min)
回顾七年级上册我们学过的数轴,点 a 在数轴上的
位置如图所示,你知道怎么快速比较 a,,|a| 的
大小关系吗
a
答:取 a=-0.5,则 a,,| a | 三个数分别
为-0.5,-2,0.5,所以 < a < |a|.
(师讲述,生思考后回答,1min)
【学习任务1】
学生活动1:利用“角边角”判定三角形全等
(师提出问题,生思考,1min)
问题 如图,有两个边长为1的正方形,其中正方形EFGH 的顶点E 与正方形ABCD 的中心重合。在正方形EFGH 绕点E 旋转的过程中,两个正方形重叠部分的面积是多少
(师提问,生动手操作,小组讨论后分享,5min)
在旋转过程中,两个正方形的重叠部分会呈现哪些情形
理解问题
对于这些不同情形,如何求这两个正方形重叠部分的面积
(师提问,生思考后回答,5min)
拟定计划
哪些特殊情形下,两个正方形重叠部分的面积容易求出
其他情形能转化为容易求解的特殊情形吗?
S重叠=S正方形ABCD =
M
N
△BEM≌△CEN
S重叠=S△BEC =
M
N
P
Q
△EMP≌△ENQ
S重叠=S四边形EQCP =
(师总结板书,生记笔记,2min)
因为某些因素(如形状、位置或数值等)不确定,使得问题有多种情形时、可以限制这个引起变化的因素,考虑最为特殊的情形,采用从特殊情形入手的策略解决问题。
问题思路受阻
发现特殊值(情形)
以特殊值(情形)找到思路
问题得以解决
【评价任务1】
(生独立思考,小组讨论后回答,5min)
【课本P115 】
1.如图,点P是等边三角形ABC 内的任意一点,过点 P向三边作垂线,垂足分别为 D,E,F。小颖从特殊情形入手,认为 AF+BD+CE等于△ABC周长的 。你知道她是怎么做的吗
解:小颖是从以下特殊情形入手:点P为等边三角形ABC三条高的交点,如图所示。
容易得到,△ABD≌ ACD,
所以 BD = CD。
同理可得 AF = BF, AE = CE。
因此,容易得到AF+BD+CE等于△ABC周长的
(生独立思考,举手回答,5min)
2.如图 ,四边形 ABCD 的面积是 16,各边中点分别为 M,N,P,Q,MP与 NQ 相交于点 O,求图中阴影部分的面积。
解:如图,连接OA,OB,OC,OD。
因为 M是AB的中点,
所以 AM = AB
所以 S△OAM = S△OAB
同理可得,
S△OAQ = S△OAD,
S△OCN = S△OBC,
S△OCP = S△OCD。
S阴影 = S△OAM + S△OAQ + S△OCN + S△OCP
= S△OAB + S△OAD + S△OBC + S△OCD
= S四边形ABCD
= ×16 =8
课堂小结
(师引导生回答,2min)
面对一般性的问题时,可以先考虑特殊情形,借助特殊情形下获得的结论或方法解决一般性的问题,这就是特殊化策略。
课堂练习
独立完成(10min)
解:如图,过点 A作BC的垂线交BC于点Q,连接AP,BP,CP.
1. 如图,点 P 是等边三角形 ABC 内的任意一点,过点 P 向三边作垂线,垂足分别为点D,E,F. 小颖从特殊情形入手,认为 PD+PE+PF 等于△ABC 的高,你知道她是怎么做的吗
S△ABC=S△ABP+S△BCP+S△ACP
Q
BC AQ=AB PF+ BC PD+ AC PE
因为 AB=BC=AC,
所以 AQ=PF+PD+PE.
所以 PD+PE+PF 等于△ABC 的高
2.一个三位数除以它的各位数字之和,商最大是多少
解:设这个三位数为 abc ( a、b、c 均为整数,且1≤a≤9,0≤b≤9,0≤c≤9),这个三位数的值是100a + 10b + c,各位数字之和是 a + b + c.
要求商最大,就要让被除数尽可能大,除数尽可能小.
商=.
当这个三位数是 900,
当这个三位数是100,各位数字之和是 1+ 0 + 0 = 1 时,
商为 =100
各位数字之和是9+0+0=9 时,商为 =100;
所以一个三位数除以它的各位数字之和,商最大是100.
同课章节目录
