九年级数学上册人教版第二十四章圆单元测试题(含答案)
文档属性
| 名称 | 九年级数学上册人教版第二十四章圆单元测试题(含答案) |  | |
| 格式 | docx | ||
| 文件大小 | 1.5MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-05-08 16:58:24 | ||
图片预览

文档简介
九年级数学上册人教版第二十四章《圆》单元测试题
一、单选题
1.如图,点A,B,C,D都在上,为的直径,且,若,,则的半径为( )
A.10 B.2 C. D.5
2.如图,是的外接圆,弦交于点,,过点作于点,延长交于点,若,则的长为( )
A. B. C.8 D.
3.如图,ΔABC内接于,是的直径,交于点,.若,则的度数为( )
A. B. C. D.
4.如图,已知四边形内接于,连结,记的度数为,的度数为.若,,则有( )
A. B.
C. D.
5.如图,在正六边形中,连结与,以点为圆心,长为半径画弧.若,则图中阴影部分的面积是( )
A. B. C. D.
6.如图,两个圆为同心圆,大圆的直径与小圆的其中一个交点为,且,大圆的弦切小圆于点.若,则图中阴影部分的面积为( )
A. B.
C. D.
7.如图,四边形内接于,,,,若的长为方程的两个实数根,则线段的长为( )
A. B. C. D.
8.如图,是的直径,点为圆上一点,,是弧的中点,与交于点,若是的中点,则的长为( )
A.9 B.8 C.10 D.11
二、填空题
9.如图,已知切于点A,,点是上异于A,的点,则 .
10.如图,是的直径,是的弦,且.连接,若,则 .
11.如图,是的直径,点,均在上,,若,则的度数为 .
12.如图,在中,是直径,是弦,.过点D作的切线,与的延长线相交于点E.若,则等于 .
13.两个半径相等的半圆按如图所示放置,半圆的圆心落在半圆的圆弧上,半圆的一个直径端点与的圆心重合,若半圆的半径为,则阴影部分的面积是 .
14.如图,在边长为 2 的正六边形中,G为的中点,点Q为正六边形边上任意一点,以为半径的与以为半径的相交时,那么的半径 r 的取值范围是 .
三、解答题
15.如图,ΔABC中,,,平分,点是边上一点,以点为圆心,以为半径作圆,恰好经过点D.
(1)求证:直线是的切线;
(2)若,,求线段的长.
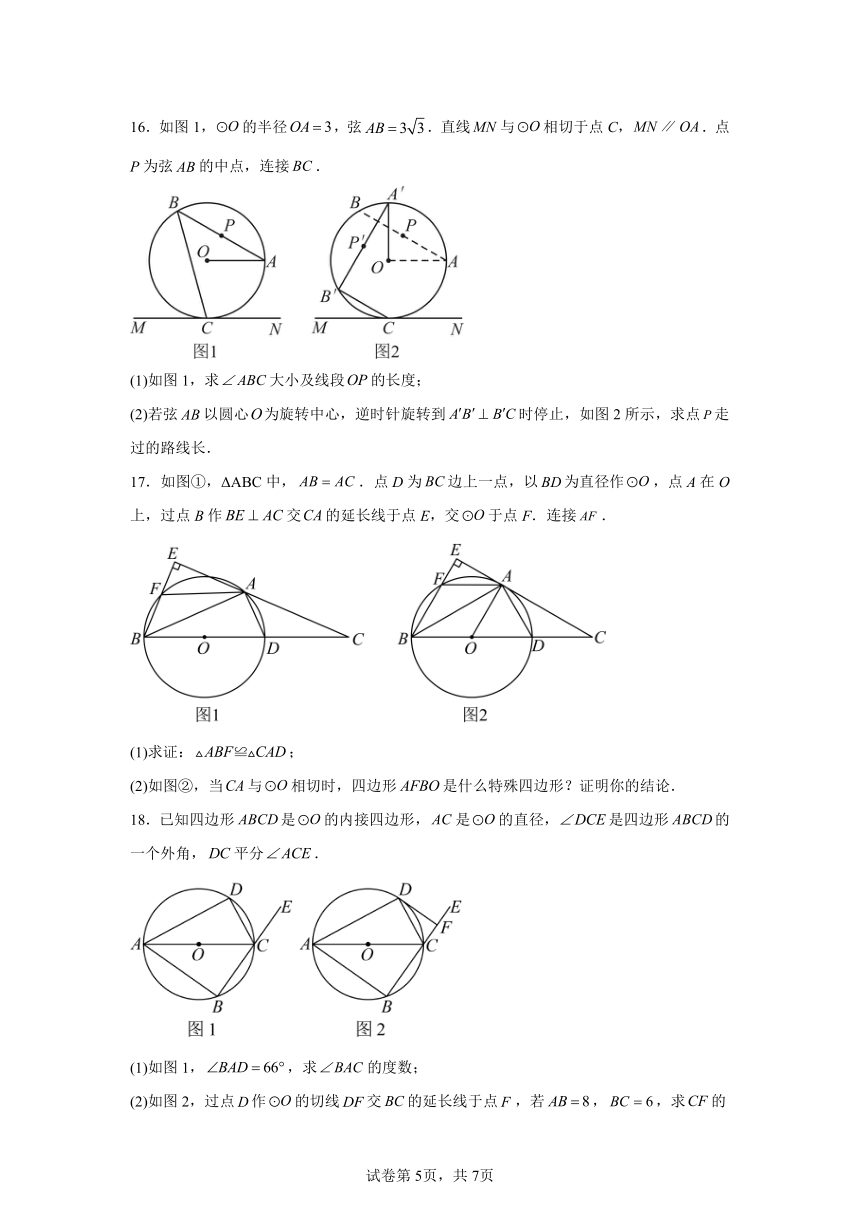
16.如图1,的半径,弦.直线与相切于点C,.点P为弦的中点,连接.
(1)如图1,求大小及线段的长度;
(2)若弦以圆心为旋转中心,逆时针旋转到时停止,如图2所示,求点走过的路线长.
17.如图①,ΔABC中,.点D为边上一点,以为直径作,点A在O上,过点B作交的延长线于点E,交于点F.连接.
(1)求证:;
(2)如图②,当与相切时,四边形是什么特殊四边形?证明你的结论.
18.已知四边形是的内接四边形,是的直径,是四边形的一个外角,平分.
(1)如图1,,求的度数;
(2)如图2,过点作的切线交的延长线于点,若,,求的长.
19.据史料记载,马车的发明者是多年前生活于夏王朝初年的奚仲.马车的发明是中国科技史上的一大创举.如图是古代马车的侧面示意图,是车轮的直径,过圆心O的车架的一端点C着地时,水平地面与车轮相切于点D,连接.
(1)若,求的度数;
(2)若,,求车轮的半径长.
20.如图,是的直径,与相切于点,点是上一点,连接并延长交的延长线于点.连接、相交于点,延长交于点.若平分,且.
(1)求证:是的切线;
(2)若,,求及的长.
21.如图,在ΔABC中,,以为直径的分别交于点D,G,过点D作于点E,交的延长线于点F.
(1)求证:与相切;
(2)当时,求阴影部分的面积.
22.如图1,在中,直径,P是线段延长线上的一点,切于点C,D是上一点,切,连接.
(1)求证:是的切线;
(2)当时(如图2),求的长;
(3)若四边形是菱形(如图2),求弧与线段围成的阴影图形的面积.
试卷第1页,共3页
试卷第1页,共3页
《九年级数学上册人教版第二十四章《圆》单元测试题》参考答案
题号 1 2 3 4 5 6 7 8
答案 D B C C B B B A
9.或
10.
11.
12.36
13.
14.
15.(1)证明:连接.
平分,
,
,
,
,
,
,
直线是的切线;
(2)解:∵,
∴,
在中,,
,
,
,
在中,
,
,
设,则,
,
,
解之得,或(舍去),
.
16.(1)解:连接,,
∵直线与相切于点C,
∴,
,
∵点P为弦的中点
∴垂直平分
;
(2)连接,
∵,
∴为直径,点在线段上.
与圆相切,
.
又,
,即旋转角为.
点走过的路线长为.
17.(1)证明:∵BD为的直径,
∴,
∴,
∵,
∴,
∴,
∵四边形是的内接四边形,
∴,
又∵,
∴;
(2)解:是菱形.
证明:∵,
∴,
∵,
∴,
∴,
∴,
∵与相切,
∴,
∴,
∵,
∴,
∴,
∵,
∴,
∴,
∴四边形是平行四边形,
∵,
∴是菱形.
18.(1)解:是的内接四边形的外角,,
∴.
又平分,
.
是的直径,
.
.
.
(2)如图,连接,过点作于点.
是的直径,
.
在中,,,
.
.
∵,
,
,
,
∵是的切线,是的半径,
∴,
∴.
∵,
∴.
又∵,
∴.
∴.
∴.
∴四边形是矩形.
,
∴.
19.(1)解:如图:连接,
∵地面与车轮相切于点D,
∴,即,
∴,
∴.
(2)解:∵地面与车轮相切于点D,
∴,即,
设车轮的半径为r,则,,
∵,
∴,解得:.
∴车轮的半径长米.
20.(1)证明:如图,连接,
∵与相切于点,
∴,即,
∵平分,
∴,
∵,
∴,
在和中,
,
∴,
∴,
∵,
∴,
∴,
∴,
又∵是的半径,
∴是的切线.
(2)解:如图,连接,
设,
∵,
∴,
由(1)已证:,
∴在中,,即,
解得,
∴,
∴,
由(1)已证:,
∴,
设,则,
在中,,即,
解得,
∴,
∴在中,,
∴,
综上,的长为,的长为.
21.(1)证明:∵,
∴,
∵,
∴
∴,
∴,
∵,
∴,
∵为的半径,
∴与相切.
(2)解:∵,
∴,
∵,
,
,
,
,
,
∴是等边三角形,
,,
,
,
.
22.(1)证明:如图1,连接,则有.
在和中,
∴,
∴,
∵切于点C,
∴,
∴,即,
∴是的切线.
(2)解:如图2,连接 ,由(1)可知, .
当时,四边形为矩形.
又∵,
∴四边形为正方形.
∵,
∴,即
∴,
∴.
(3)解:如图3,连接,设,则,
∵四边形是菱形,
∴.则,
∵是的切线,即.
∴,即.
∴,
∴
∵,
∴,
∴.
答案第1页,共2页
答案第1页,共2页
一、单选题
1.如图,点A,B,C,D都在上,为的直径,且,若,,则的半径为( )
A.10 B.2 C. D.5
2.如图,是的外接圆,弦交于点,,过点作于点,延长交于点,若,则的长为( )
A. B. C.8 D.
3.如图,ΔABC内接于,是的直径,交于点,.若,则的度数为( )
A. B. C. D.
4.如图,已知四边形内接于,连结,记的度数为,的度数为.若,,则有( )
A. B.
C. D.
5.如图,在正六边形中,连结与,以点为圆心,长为半径画弧.若,则图中阴影部分的面积是( )
A. B. C. D.
6.如图,两个圆为同心圆,大圆的直径与小圆的其中一个交点为,且,大圆的弦切小圆于点.若,则图中阴影部分的面积为( )
A. B.
C. D.
7.如图,四边形内接于,,,,若的长为方程的两个实数根,则线段的长为( )
A. B. C. D.
8.如图,是的直径,点为圆上一点,,是弧的中点,与交于点,若是的中点,则的长为( )
A.9 B.8 C.10 D.11
二、填空题
9.如图,已知切于点A,,点是上异于A,的点,则 .
10.如图,是的直径,是的弦,且.连接,若,则 .
11.如图,是的直径,点,均在上,,若,则的度数为 .
12.如图,在中,是直径,是弦,.过点D作的切线,与的延长线相交于点E.若,则等于 .
13.两个半径相等的半圆按如图所示放置,半圆的圆心落在半圆的圆弧上,半圆的一个直径端点与的圆心重合,若半圆的半径为,则阴影部分的面积是 .
14.如图,在边长为 2 的正六边形中,G为的中点,点Q为正六边形边上任意一点,以为半径的与以为半径的相交时,那么的半径 r 的取值范围是 .
三、解答题
15.如图,ΔABC中,,,平分,点是边上一点,以点为圆心,以为半径作圆,恰好经过点D.
(1)求证:直线是的切线;
(2)若,,求线段的长.
16.如图1,的半径,弦.直线与相切于点C,.点P为弦的中点,连接.
(1)如图1,求大小及线段的长度;
(2)若弦以圆心为旋转中心,逆时针旋转到时停止,如图2所示,求点走过的路线长.
17.如图①,ΔABC中,.点D为边上一点,以为直径作,点A在O上,过点B作交的延长线于点E,交于点F.连接.
(1)求证:;
(2)如图②,当与相切时,四边形是什么特殊四边形?证明你的结论.
18.已知四边形是的内接四边形,是的直径,是四边形的一个外角,平分.
(1)如图1,,求的度数;
(2)如图2,过点作的切线交的延长线于点,若,,求的长.
19.据史料记载,马车的发明者是多年前生活于夏王朝初年的奚仲.马车的发明是中国科技史上的一大创举.如图是古代马车的侧面示意图,是车轮的直径,过圆心O的车架的一端点C着地时,水平地面与车轮相切于点D,连接.
(1)若,求的度数;
(2)若,,求车轮的半径长.
20.如图,是的直径,与相切于点,点是上一点,连接并延长交的延长线于点.连接、相交于点,延长交于点.若平分,且.
(1)求证:是的切线;
(2)若,,求及的长.
21.如图,在ΔABC中,,以为直径的分别交于点D,G,过点D作于点E,交的延长线于点F.
(1)求证:与相切;
(2)当时,求阴影部分的面积.
22.如图1,在中,直径,P是线段延长线上的一点,切于点C,D是上一点,切,连接.
(1)求证:是的切线;
(2)当时(如图2),求的长;
(3)若四边形是菱形(如图2),求弧与线段围成的阴影图形的面积.
试卷第1页,共3页
试卷第1页,共3页
《九年级数学上册人教版第二十四章《圆》单元测试题》参考答案
题号 1 2 3 4 5 6 7 8
答案 D B C C B B B A
9.或
10.
11.
12.36
13.
14.
15.(1)证明:连接.
平分,
,
,
,
,
,
,
直线是的切线;
(2)解:∵,
∴,
在中,,
,
,
,
在中,
,
,
设,则,
,
,
解之得,或(舍去),
.
16.(1)解:连接,,
∵直线与相切于点C,
∴,
,
∵点P为弦的中点
∴垂直平分
;
(2)连接,
∵,
∴为直径,点在线段上.
与圆相切,
.
又,
,即旋转角为.
点走过的路线长为.
17.(1)证明:∵BD为的直径,
∴,
∴,
∵,
∴,
∴,
∵四边形是的内接四边形,
∴,
又∵,
∴;
(2)解:是菱形.
证明:∵,
∴,
∵,
∴,
∴,
∴,
∵与相切,
∴,
∴,
∵,
∴,
∴,
∵,
∴,
∴,
∴四边形是平行四边形,
∵,
∴是菱形.
18.(1)解:是的内接四边形的外角,,
∴.
又平分,
.
是的直径,
.
.
.
(2)如图,连接,过点作于点.
是的直径,
.
在中,,,
.
.
∵,
,
,
,
∵是的切线,是的半径,
∴,
∴.
∵,
∴.
又∵,
∴.
∴.
∴.
∴四边形是矩形.
,
∴.
19.(1)解:如图:连接,
∵地面与车轮相切于点D,
∴,即,
∴,
∴.
(2)解:∵地面与车轮相切于点D,
∴,即,
设车轮的半径为r,则,,
∵,
∴,解得:.
∴车轮的半径长米.
20.(1)证明:如图,连接,
∵与相切于点,
∴,即,
∵平分,
∴,
∵,
∴,
在和中,
,
∴,
∴,
∵,
∴,
∴,
∴,
又∵是的半径,
∴是的切线.
(2)解:如图,连接,
设,
∵,
∴,
由(1)已证:,
∴在中,,即,
解得,
∴,
∴,
由(1)已证:,
∴,
设,则,
在中,,即,
解得,
∴,
∴在中,,
∴,
综上,的长为,的长为.
21.(1)证明:∵,
∴,
∵,
∴
∴,
∴,
∵,
∴,
∵为的半径,
∴与相切.
(2)解:∵,
∴,
∵,
,
,
,
,
,
∴是等边三角形,
,,
,
,
.
22.(1)证明:如图1,连接,则有.
在和中,
∴,
∴,
∵切于点C,
∴,
∴,即,
∴是的切线.
(2)解:如图2,连接 ,由(1)可知, .
当时,四边形为矩形.
又∵,
∴四边形为正方形.
∵,
∴,即
∴,
∴.
(3)解:如图3,连接,设,则,
∵四边形是菱形,
∴.则,
∵是的切线,即.
∴,即.
∴,
∴
∵,
∴,
∴.
答案第1页,共2页
答案第1页,共2页
同课章节目录
