第五单元图形的运动(三)(知识梳理+拔高训练)一-2024-2025学年五年级数学下学期培优检测卷(人教版)
文档属性
| 名称 | 第五单元图形的运动(三)(知识梳理+拔高训练)一-2024-2025学年五年级数学下学期培优检测卷(人教版) |

|
|
| 格式 | docx | ||
| 文件大小 | 629.6KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-05-08 00:00:00 | ||
图片预览


文档简介
中小学教育资源及组卷应用平台
第五单元图形的运动(三)(知识梳理+拔高训练)一
知识梳理
知识点01:轴对称
如果一个图形沿着一条直线对折后两部分完全重合,这样的图形叫做轴对称图形,这条直线叫做对称轴。
(1)学过的轴对称平面图形:长(正)方形、圆形、等腰三角形、等边三角形、等腰梯形……
等腰三角形有1条对称轴,等边三角形有3条对称轴,长方形有2条对称轴,正方形有4条对称轴,等腰梯形有 1 条对称轴,任意梯形和平行四边形不是轴对称图形。
(2)圆有无数条对称轴。
(3)对称点到对称轴的距离相等。
(4)轴对称图形的特征和性质:
①对应点到对称轴的距离相等;②对应点的连线与对称轴垂直;③对称轴两边的图形大小、形状完全相同。
(5)对称图形包括轴对称图形和中心对称图形。平行四边形(除菱形)属于中心对称图形。
知识点02:旋转
在平面内,一个图形绕着一个顶点旋转一定的角度得到另一个图形的变化叫做旋转,定点O叫做旋转中心,旋转的角度叫做旋转角,原图形上的一点旋转后成为的另一点成为对应点。
(1)生活中的旋转:电风扇、车轮、纸风车;
(2)旋转要明确绕点,角度和方向;
(3)长方形绕中点旋转180度与原来重合,正方形绕中点旋转90度与原来重合,等边三角形绕中点旋转 120 度与原来重合。
2. 旋转的性质:
(1)图形的旋转是图形上的每一点在平面上绕某个固定点旋转固定角度的位置移动;
(2)其中对应点到旋转中心的距离相等;
(3)旋转前后图形的大小和形状没有改变;
(4)两组对应点分别与旋转中心的连线所成的角相等,都等于旋转角;
(5)旋转中心是唯一不动的点。
3. 对称和旋转的画法:旋转要注意:顺时针、逆时针、度数。
知识点03:平移
平移,是指在同一平面内,将一个图形上的所有点都按照某个直线方向做相同距离的移动,这样的图形运动叫做图形的平移运动,简称平移。
平移不改变图形的形状和大小。图形经过平移,对应线段相等,对应角相等,对应点所连的线段相等。
平移的特征
①平移前后图形的形状、大小不变,只是位置发生改变。
②新图形与原图形的对应点所连的线段平行且相等(或在同一直线上)。
③新图形与原图形的对应线段平行且相等,对应角相等。
拔高训练
一、填空题
1.一场演出9:00开始,12:00结束,会场时钟上的时针从演出开始到结束沿 方向旋转了 度。
2.在钟表的钟面上,从3时到6时,钟面上的时针按( )方向绕轴心旋转了( )°,时针再继续顺时针方向旋转180°,这时钟面上是( )时。
3.“密室逃脱”是最近盛行的一种益智冒险类游戏。乐乐和旭旭只差最后开启密码锁就能成功逃脱,你能帮帮他们吗?
指针先按顺时针方向旋转90°,再按逆时针方向旋转60°,最后按顺时针方向旋转150°。密码是一个( )位数,密码是( )。
4.用做基本图形设计图案,是通过( )得到的;是通过( )得到的。(填“旋转”“平移”或“轴对称”)
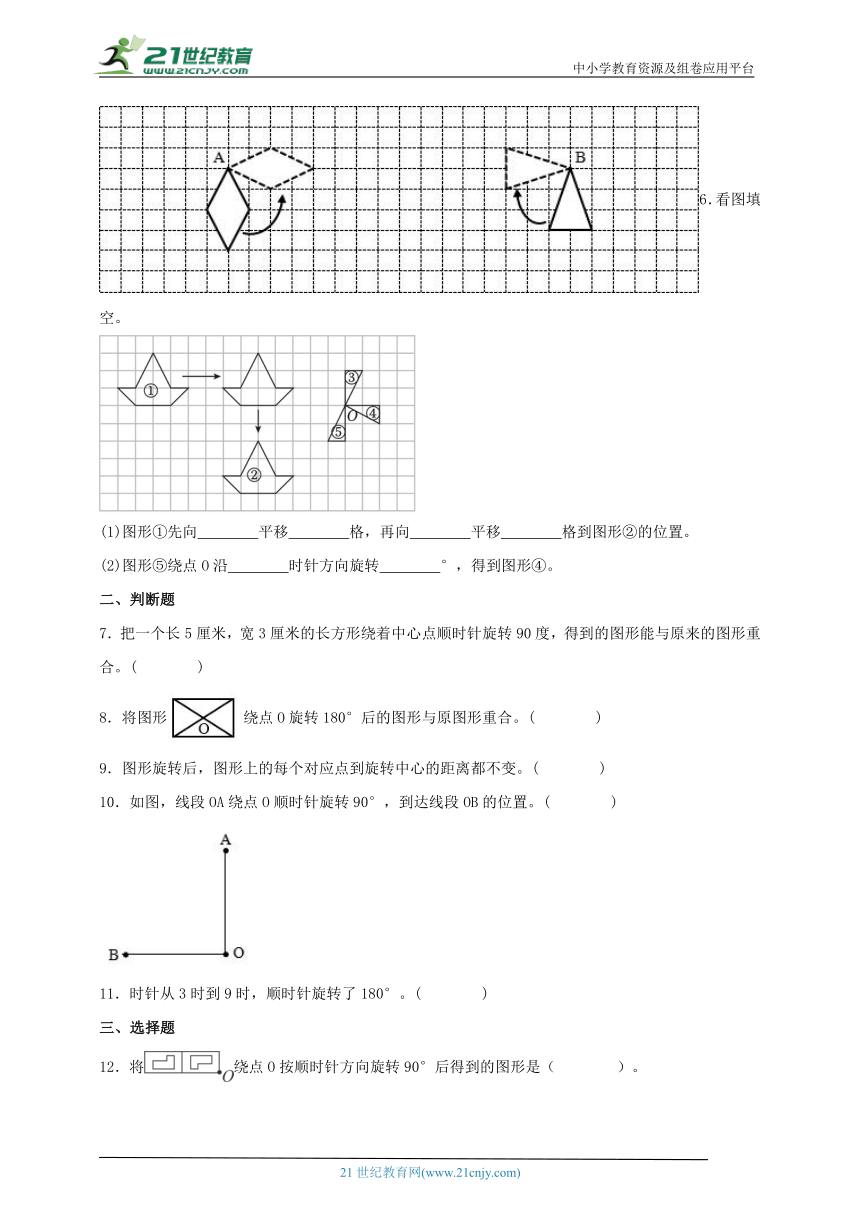
5.下图中的平行四边形绕A点按( )时针方向旋转了( );图中的三角形绕B点按( )时针方向旋转了( )。
6.看图填空。
(1)图形①先向 平移 格,再向 平移 格到图形②的位置。
(2)图形⑤绕点O沿 时针方向旋转 °,得到图形④。
二、判断题
7.把一个长5厘米,宽3厘米的长方形绕着中心点顺时针旋转90度,得到的图形能与原来的图形重合。( )
8.将图形绕点O旋转180°后的图形与原图形重合。( )
9.图形旋转后,图形上的每个对应点到旋转中心的距离都不变。( )
10.如图,线段OA绕点O顺时针旋转90°,到达线段OB的位置。( )
11.时针从3时到9时,顺时针旋转了180°。( )
三、选择题
12.将绕点O按顺时针方向旋转90°后得到的图形是( )。
A. B. C.
13.把图E绕点O顺时针旋转180°,下面旋转正确的是( )。
A.A B.B C.C D.D
14.观察下图。下面说法中,能准确、完整地描述钟面上分针从“1”到“3”的运动过程的是( )。
A.分针绕点O顺时针旋转 B.分针按顺时针方向旋转
C.分针按顺时针方向旋转60° D.分针绕点O顺时针方向旋转60°
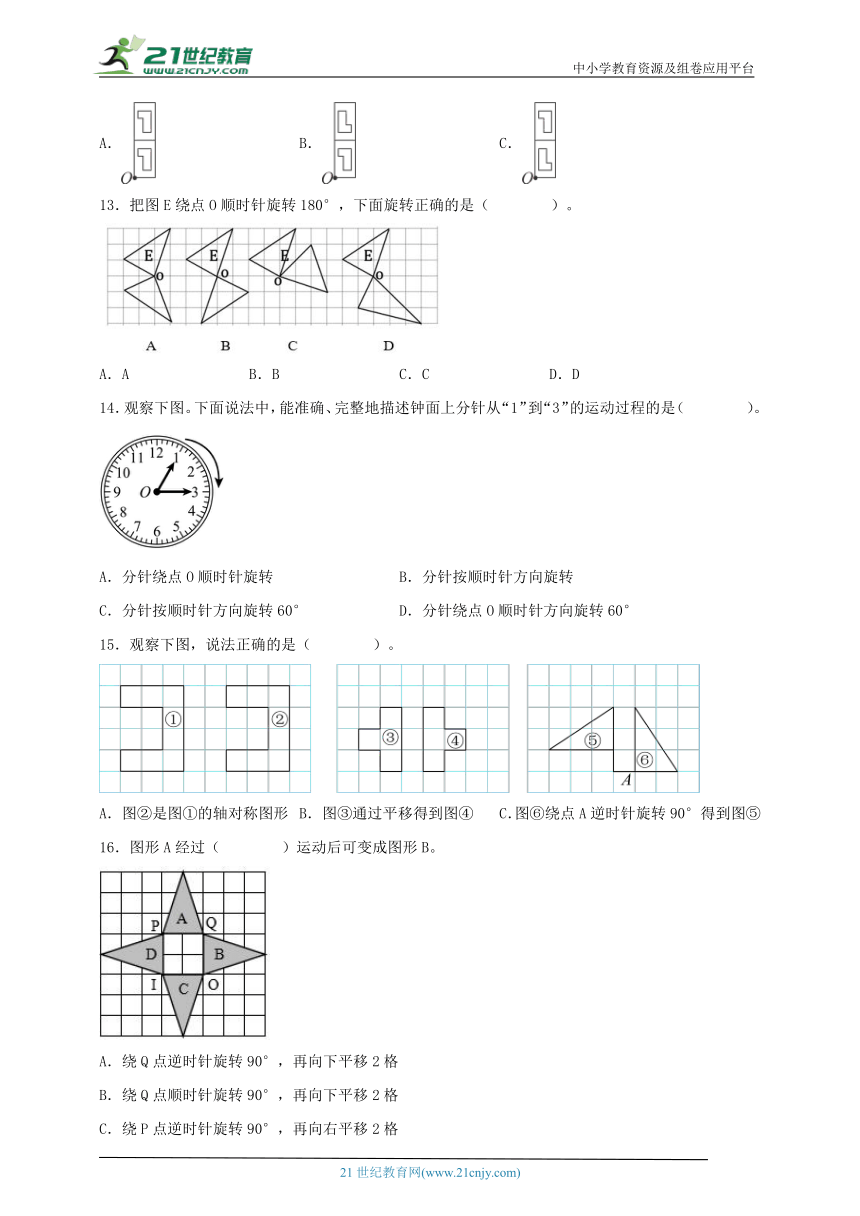
15.观察下图,说法正确的是( )。
A.图②是图①的轴对称图形 B.图③通过平移得到图④ C.图⑥绕点A逆时针旋转90°得到图⑤
16.图形A经过( )运动后可变成图形B。
A.绕Q点逆时针旋转90°,再向下平移2格
B.绕Q点顺时针旋转90°,再向下平移2格
C.绕P点逆时针旋转90°,再向右平移2格
D.绕P点顺时针旋转90°,再向左平移2格
四、作图题
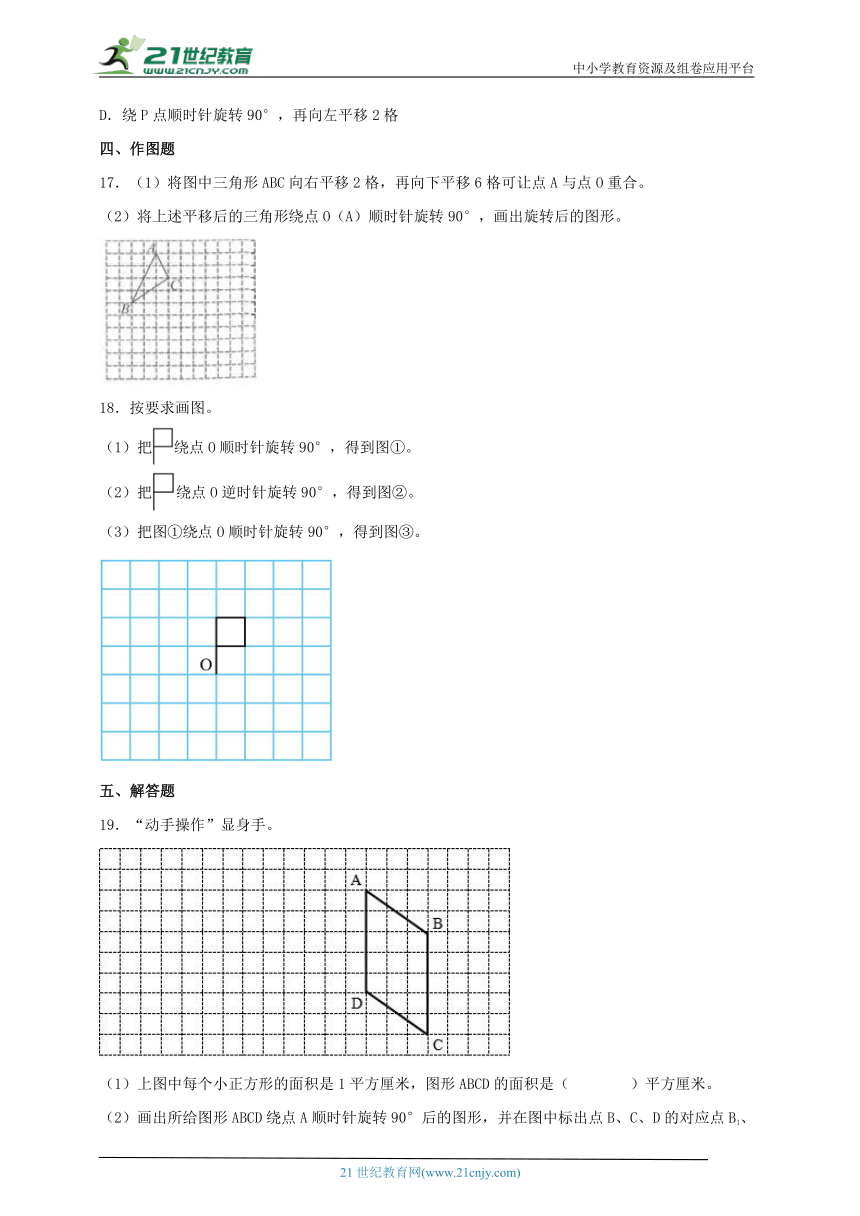
17.(1)将图中三角形ABC向右平移2格,再向下平移6格可让点A与点O重合。
(2)将上述平移后的三角形绕点O(A)顺时针旋转90°,画出旋转后的图形。
18.按要求画图。
(1)把绕点O顺时针旋转90°,得到图①。
(2)把绕点O逆时针旋转90°,得到图②。
(3)把图①绕点O顺时针旋转90°,得到图③。
五、解答题
19.“动手操作”显身手。
(1)上图中每个小正方形的面积是1平方厘米,图形ABCD的面积是( )平方厘米。
(2)画出所给图形ABCD绕点A顺时针旋转90°后的图形,并在图中标出点B、C、D的对应点B1、C1、D1。
20.完成下面问题。
(1)画出图①绕点“O”逆时针旋转90°的图形。
(2)写一写图①如何通过旋转和平移得到图②的。
21.“儿童散学归来早,忙趁东风放纸鸢。”描写的是初春时节,一群活泼可爱的儿童趁着东风放风筝的生动情景。王丽也想做一只风筝,体验一番这种感觉。下面是她在边长为1厘米的方格纸上设计的风筝图。请你帮她完成下。
(1)先画出“风筝”的另一半,使它成为一个轴对称图形。
(2)画出这个“风筝”图绕A点顺时针旋转90后的图形。
(3)这个“风筝”图形的面积是( )。
22.画一画、想一想。
(1)画出图1绕A点顺时针方向旋转90°后的图形。
(2)图1绕A点( )时针方向旋转( )后得到图2。
(3)图1绕A点( )时针方向旋转( )后得到图3。
(4)图中绿色部分占整个图案的( )。灰色部分占整个图案的( )。
23.下图每个小方格的边长都是1厘米。
(1)画出三角形AOB绕点O顺时针旋转后的图形。
(2)上图中有一个长方体展开图,已经标出了三个面,请标出另外三个面。做这个长方体框架至少需要( )厘米长的铁丝,它的体积是( )立方厘米。
参考答案
1.顺时针 90
【分析】沿着时针转动的方向叫做顺时针,逆着在时钟的表盘上,有12个大格,时针走一圈是360°,则每小时时针走一个大格,也就是走30°。9:00开始,12:00结束,经历了3个小时,也就是时针走了3个大格,就是3个30°,用乘法计算。
【详解】12:00-9:00=3(小时)
3×30°=90°
会场时钟上的时针从演出开始到结束沿顺时针方向旋转了90度。
2.顺时针 90 12
【分析】钟面指针转动的方向是顺时针方向;钟面一个大格是30°,旋转的大格数×每个大格度数=旋转度数;旋转度数÷每个大格度数=旋转的大格数,据此确定从6时顺时针方向旋转180°,时针的位置。
【详解】30°×(6-3)
=30°×3
=90°
180°÷30°=6(格)
在钟表的钟面上,从3时到6时,钟面上的时针按顺时针方向绕轴心旋转了90°,时针再继续顺时针方向旋转180°,旋转了6个大格,这时钟面上是12时。
3.三 316
【分析】一个钟面的度数为360°,共分为12份,每一份角度为30°,即相邻两个数的角度为30°,根据题意得到旋转的三个数,据此可得出答案。
【详解】指针开始位置是12点位置,指针先按顺时针方向旋转90°,即指针位置是3;再按逆时针方向旋转60°,即指针位置是1;最后按顺时针方向旋转150°,即指针位置是6。则密码是一个三位数,密码是316。
4.平移 旋转
【分析】
当物体水平方向或竖直方向运动,并且物体的方向不发生改变,这种运动式平移;在平面内,一个图形绕着一个定点旋转一定的角度得到另一个图形的变化就是旋转;如果一个图形沿一条直线折叠,直线两旁的部分能够互相重合,这个图形叫做轴对称图形,据此解答。
【详解】观察图形可知,用做基本图形设计图案,是通过平移得到的;
是通过旋转得到的。
【点睛】解答本题的关键是看基本图形是怎样运动得到图案的。
5.逆 90° 顺 90°
【分析】根据旋转的特征;一个图形绕某点按一定的方向旋转一定的度数,某点的位置不动,其余各部分均绕某点按相同的方向旋转相同的度数,据此解答。
【详解】由图可知:
图中的平行四边形绕A点按逆时针方向旋转了90°;
图中的三角形是绕B点按顺时针方向旋转了90°。
【点睛】本题考查旋转,熟练掌握旋转的三要素:旋转点、旋转方向、旋转角度,是解题的关键。
6.(1) 右 6 下 5
(2) 逆 90
【分析】(1)根据平移的特点,找准方向,数清格数,即可解答;
(2)以点O为旋转点,钟表转动的方向就是顺时针,反之就是逆时针再结合角度解答即可。
【详解】(1)图形①先向右平移6格,再向下平移5格到图形②的位置。
(2)图形⑤绕点O沿逆时针方向旋转90°,得到图形④。
7.×
【分析】根据旋转的特征,将长方形绕中心点顺时针旋转90度,中心点位置不变,其余各部分均绕此点按相同方向旋转相同度数,即可画出旋转后的图形。观察旋转后的图形即可得解。
【详解】
旋转后如图所示:
可见,旋转后的图形与原来的图形不重合。
故答案为:×
【点睛】此题主要考查图形的旋转,准确的作图是完成题目的关键。
8.√
【分析】在平面内,将一个图形绕一点按某个方向转动一个角度,这样的运动叫做图形的旋转;图形旋转的三要素:旋转中心、旋转方向、旋转角度;据此解答。
【详解】
将图形绕点O旋转180°后的图形与原图形重合。
原题说法正确。
故答案为:√
【点睛】掌握旋转的意义是解题的关键,注意这个图形绕点O无论是顺时针旋转180°还是逆时针旋转180°后的图形都能与原图形重合。
9.√
【分析】根据旋转的特征可知,物体或图形旋转后,它们的形状、大小都不改变,只是位置发生了变化。(1)对应点到旋转中心的距离不变;(2)对应点与旋转中心所连线段的夹角等于旋转角。据此解答。
【详解】根据分析得,图形旋转后,图形上的每个对应点到旋转中心的距离都不变。原题的说法是正确的。
故答案为:√
【点睛】此题的解题关键是理解掌握旋转的特征及意义。
10.×
【分析】根据旋转图形的特点,对应点到旋转中心的距离相等,对应点与旋转中心所连线段的夹角等于旋转角,旋转前、后的图形完全相同; 线段OA绕点O顺时针旋转90°后,点O不变,其它各边均绕O点旋转90%后,得的线段是OC,而不是OB,据此判断。
【详解】作图如下:
如图: 线段OA绕点O顺时针旋转90°,到达线段OC的位置,不是线段OB的位置,所以原题干说法错误;
故答案为:×
【点睛】掌握图形的旋转方法是解答本题的关键。
11.√
【分析】钟面指针转动的方向是顺时针方向,钟面一个大格是30°,时针从3时到9时,旋转了(9-3)个大格,每个大格的度数×旋转的大格数=旋转的角度,据此分析。
【详解】30°×(9-3)
=30°×6
=180°
时针从3时到9时,顺时针旋转了180°,说法正确。
故答案为:√
12.B
【分析】根据旋转的特征:物体或图形旋转后,它们的形状、大小都不改变,只是位置发生了变化,据此解答。
【详解】A.图形的形状和位置都发生了改变,不符合旋转的特征,不符合题意;
B.图形的形状、大小都不改变,只是位置发生了变化,符合旋转的特征,符合题意;
C.图形的形状和位置都发生了改变,不符合旋转的特征,不符合题意。
故答案为:B
13.B
【分析】决定旋转后图形的位置的要素:一是旋转中心或轴,二是旋转方向(顺时针或逆时针),三是旋转角度。钟面指针转动的方向是顺时针方向,据此确定旋转方向的角度即可。
【详解】A.图E对称后得到的图形,不符合题意;
B.图E绕点O顺时针旋转180°得到的图形,符合题意;
C.不是图E的旋转图形,不符合题意;
D.不是图E的旋转图形,不符合题意。
故答案为:B
14.D
【分析】整个钟表平均分为12个大格,则每个大格为360°÷12=30°,钟表转动的方向就是顺时针方向,反之是逆时针方向;要准确、完整地描述旋转现象,需要有旋转中心、旋转角度和旋转方向。据此解答即可。
【详解】分针从“1”到“3”共旋转了3-1=2(格)
30°×2=60°
A.分针绕点O顺时针旋转,缺少旋转角度,不完整;
B.分针按顺时针方向旋转,缺少旋转中心和旋转角度,不完整;
C.分针按顺时针方向旋转60°,缺少旋转中心,不完整;
D.分针绕点O顺时针方向旋转60°,准确、完整地描述了从“1”到“3”的运动过程。
故答案为:D
15.C
【分析】根据轴对称图形的意义:如果一个图形沿着一条直线对折后,两部分完全重合,这样的图形叫做轴对称图形,这条直线叫做对称轴;
把一个图形整体沿某一方向移动一定的距离,图形的这种运动,称为平移;
旋转:在平面内,把一个图形围绕某一固定点按顺时针或逆时针方向转动一定的角度的过程,称为旋转。这个点为旋转中心,旋转的角度叫旋转角。
【详解】A.图②是图①通过平移;原题干说法错误;
B.图④是图③的轴对称图形;原题干说法错误;
C.图⑥绕点A逆时针旋转90°得到图⑤;说法正确。
说法正确的是图⑥绕点A逆时针旋转90°得到图⑤。
故答案为:C
16.B
【分析】旋转:在平面内,将一个图形绕一点按某个方向转动一定的角度,这样的运动叫做图形的旋转。这个定点叫做旋转中心,转动的角度叫做旋转角。旋转前后图形的位置和方向改变,形状、大小不变。与时针转动方向相同的是顺时针旋转,反之就是逆时针旋转。
【详解】图形A经过绕Q点顺时针旋转90°,再向下平移2格运动后可变成图形B。
故答案为:B
【点睛】此题考查了旋转的意义及在实际当中的运用。
17.见详解
【分析】(1)根据平移的特征,把三角形ABC的各顶点分别先向右平移2格,再向下平移6格,依次连接即可得到平移后的图形;
(2)根据旋转的特征,平移后的三角形绕点O顺时针旋转90°,点O的位置不动,这个图形的各部分均绕此点按相同方向旋转相同的度数即可画出旋转后的图形。
【详解】如图:
图形①是平移后的图形,图形②是旋转后的图形。
18.见详解
【分析】
(1)根据旋转的特征,把绕点O顺时针旋转90°,点O位置不变,其余各部分均绕此点按相同方向旋转相同度数,即可画出旋转后的图形①。
(2)根据旋转的特征,把绕点O逆时针旋转90°,点O位置不变,其余各部分均绕此点按相同方向旋转相同度数,即可画出旋转后的图形②。
(3)根据旋转的特征,图①绕点O顺时针旋转90°,点O位置不变,其余各部分均绕此点按相同方向旋转相同度数,即可画出旋转后的图形③。
【详解】如图:
19.(1)15
(2)图形见详解
【分析】(1)由题意可知,图中每个小正方形的面积是1平方厘米,则每小格的边长为1厘米,图形ABCD是一个平行四边形,该平行四边形的底为5厘米,高为3厘米,根据平行四边形的面积公式:S=ah,据此计算即可;
(2)将图形ABCD绕点A顺时针旋转90°,点A的位置不动,其余各部分均绕点A按相同方向旋转相同的度数即可,然后标出点B、C、D的对应点B1、C1、D1。
【详解】(1)5×3=15(平方厘米)
则图形ABCD的面积是15平方厘米。
(2)如图所示:
【点睛】本题考查旋转图形,明确作旋转图形的方法是解题的关键。
20.(1)见详解
(2)图①先绕点“0”顺时针旋转90°,再向右平移6格。
【分析】(1)根据旋转的特征,将图①绕点“O”逆时针旋转90°,点O位置不变,其余各部分均绕此点按相同方向旋转相同度数,即可画出旋转后的图形。
(2)在平面内,将一个图形绕一点按某个方向转动一个角度,这样的运动叫做图形的旋转。
在平面内,将一个图形沿着某个方向移动一定的距离,这样的运动叫做图形的平移。
运用旋转和平移的意义及特点,写出图①如何通过旋转和平移得到图②的。
【详解】(1)如图:
(2)图①先绕点“O”顺时针旋转90°,再向右平移6格,即可得到图②。
(答案不唯一)
【点睛】本题考查作旋转后的图形的作图方法以及运用旋转和平移得到指定图形,注意平移和旋转都是图形的位置发生变化而形状、大小不变。
21.(1)见详解;(2)见详解;(3)8平方厘米
【分析】(1)根据轴对称图形的特征,对称点到对称轴的距离相等,对称点的连线垂直于对称轴,在对称轴的另一边画出图形的关键对称点,连结即可。
(2)根据旋转的特征,“风筝”图绕点A顺时针旋转90°,点A的位置不动,这个图形的各部分均绕此点按相同方向旋转相同的度数即可画出旋转后的图形;
(3)观察图可知,“风筝”图由2个底为4厘米,高为2厘米的三角形,根据三角形的面积=底×高÷2,代入数据解答即可。
【详解】(1)轴对称图形如下图;
(2)旋转后的图形如下图;
(3)4×2÷2×2=8(平方厘米)
这个“风筝”图形的面积是8平方厘米。
【点睛】此题是考查作轴对称图形、图形的旋转以及三角形面积公式的灵活应用,作轴对称图形关键是确定对称点(对应点)的位置,图形的旋转注意旋转三要素:旋转中心、旋转方向和旋转角。
22.(1)见详解;(2)逆;90°;(3)顺;180°;(4);
【分析】(1)根据旋转的特征,图1绕点A顺时针旋转90°,点A的位置不动,这个图形的各部分均绕此点按相同方向旋转相同的度数即可画出旋转后的图形;
(2)在平面内,将一个图形绕一个定点按某个方向转动一个角度,这样的运动叫做图形的旋转,旋转方向和钟表的指针旋转方向相同,叫顺时针旋转,旋转方向和钟表的指针旋转方向相反,叫逆时针旋转;据此可知,图1绕A点逆时针方向旋转90度后得到图2。
(3)根据题意可知,图1绕A点顺时针或逆时针方向旋转180度后得到图3。
(4)根据画完的图案可知,绿色三角形占了4个方格,灰色部分占了8个方格。根据求一个数占另一个数的几分之几,用一个数除以另一个数,则用4÷(4+8)即可求出绿色部分占整个图案的几分之几;用8÷(4+8)即可求出灰色部分占整个图案的几分之几。
【详解】(1)如图:
(2)图1绕A点逆时针方向旋转90度后得到图2。
(3)图1绕A点顺时针或逆时针方向旋转180度后得到图3。
(4)已知绿色三角形占了4个方格,灰色部分占了8个方格。
4÷(4+8)
=4÷12
=
8÷(4+8)
=8÷12
=
绿色部分占整个图案的。灰色部分占整个图案的。
【点睛】本题主要考查了图形的旋转和求一个数占另一个数的几分之几,注意旋转三要素:旋转中心、旋转方向和旋转角。
23.(1)图见详解
(2)图见详解;24;6
【分析】(1)把图形的每个点与旋转中心O点连接,再量出题目要求旋转的角度为顺时针90°并旋转线段,最后依次连接这些点,可得到旋转后的图形;
(2)长方体有6个面,一般都是长方形,相对的面完全相同;结合图示观察得到长方体的前面、下面、右面,再根据这三个面的大小,确定另外三个面,并标出后面、上面以及左面;
长方体有12条棱,棱长公式为:(长+宽+高)×4;物体所占空间的大小叫作物体的体积,长方体体积=长×宽×高。每个小方格的边长都是1厘米,观察得到:长方体的长、宽、高分别为:2厘米、1厘米、3厘米,可把数据带入公式,求得它的棱长总和、体积。
【详解】(1)(2)如图:
(2)棱长为:
(3+2+1)×4
=6×4
=24(厘米)
做这个长方体框架至少需要24厘米长的铁丝。
体积为:
3×2×1=6(立方厘米)
它的体积是6立方厘米。
【点睛】综合考查了图形的旋转以及长方体的相关特征和属性,需要明确作旋转图形的规则,以及长方体体积公式、棱长公式的灵活应用。
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
第五单元图形的运动(三)(知识梳理+拔高训练)一
知识梳理
知识点01:轴对称
如果一个图形沿着一条直线对折后两部分完全重合,这样的图形叫做轴对称图形,这条直线叫做对称轴。
(1)学过的轴对称平面图形:长(正)方形、圆形、等腰三角形、等边三角形、等腰梯形……
等腰三角形有1条对称轴,等边三角形有3条对称轴,长方形有2条对称轴,正方形有4条对称轴,等腰梯形有 1 条对称轴,任意梯形和平行四边形不是轴对称图形。
(2)圆有无数条对称轴。
(3)对称点到对称轴的距离相等。
(4)轴对称图形的特征和性质:
①对应点到对称轴的距离相等;②对应点的连线与对称轴垂直;③对称轴两边的图形大小、形状完全相同。
(5)对称图形包括轴对称图形和中心对称图形。平行四边形(除菱形)属于中心对称图形。
知识点02:旋转
在平面内,一个图形绕着一个顶点旋转一定的角度得到另一个图形的变化叫做旋转,定点O叫做旋转中心,旋转的角度叫做旋转角,原图形上的一点旋转后成为的另一点成为对应点。
(1)生活中的旋转:电风扇、车轮、纸风车;
(2)旋转要明确绕点,角度和方向;
(3)长方形绕中点旋转180度与原来重合,正方形绕中点旋转90度与原来重合,等边三角形绕中点旋转 120 度与原来重合。
2. 旋转的性质:
(1)图形的旋转是图形上的每一点在平面上绕某个固定点旋转固定角度的位置移动;
(2)其中对应点到旋转中心的距离相等;
(3)旋转前后图形的大小和形状没有改变;
(4)两组对应点分别与旋转中心的连线所成的角相等,都等于旋转角;
(5)旋转中心是唯一不动的点。
3. 对称和旋转的画法:旋转要注意:顺时针、逆时针、度数。
知识点03:平移
平移,是指在同一平面内,将一个图形上的所有点都按照某个直线方向做相同距离的移动,这样的图形运动叫做图形的平移运动,简称平移。
平移不改变图形的形状和大小。图形经过平移,对应线段相等,对应角相等,对应点所连的线段相等。
平移的特征
①平移前后图形的形状、大小不变,只是位置发生改变。
②新图形与原图形的对应点所连的线段平行且相等(或在同一直线上)。
③新图形与原图形的对应线段平行且相等,对应角相等。
拔高训练
一、填空题
1.一场演出9:00开始,12:00结束,会场时钟上的时针从演出开始到结束沿 方向旋转了 度。
2.在钟表的钟面上,从3时到6时,钟面上的时针按( )方向绕轴心旋转了( )°,时针再继续顺时针方向旋转180°,这时钟面上是( )时。
3.“密室逃脱”是最近盛行的一种益智冒险类游戏。乐乐和旭旭只差最后开启密码锁就能成功逃脱,你能帮帮他们吗?
指针先按顺时针方向旋转90°,再按逆时针方向旋转60°,最后按顺时针方向旋转150°。密码是一个( )位数,密码是( )。
4.用做基本图形设计图案,是通过( )得到的;是通过( )得到的。(填“旋转”“平移”或“轴对称”)
5.下图中的平行四边形绕A点按( )时针方向旋转了( );图中的三角形绕B点按( )时针方向旋转了( )。
6.看图填空。
(1)图形①先向 平移 格,再向 平移 格到图形②的位置。
(2)图形⑤绕点O沿 时针方向旋转 °,得到图形④。
二、判断题
7.把一个长5厘米,宽3厘米的长方形绕着中心点顺时针旋转90度,得到的图形能与原来的图形重合。( )
8.将图形绕点O旋转180°后的图形与原图形重合。( )
9.图形旋转后,图形上的每个对应点到旋转中心的距离都不变。( )
10.如图,线段OA绕点O顺时针旋转90°,到达线段OB的位置。( )
11.时针从3时到9时,顺时针旋转了180°。( )
三、选择题
12.将绕点O按顺时针方向旋转90°后得到的图形是( )。
A. B. C.
13.把图E绕点O顺时针旋转180°,下面旋转正确的是( )。
A.A B.B C.C D.D
14.观察下图。下面说法中,能准确、完整地描述钟面上分针从“1”到“3”的运动过程的是( )。
A.分针绕点O顺时针旋转 B.分针按顺时针方向旋转
C.分针按顺时针方向旋转60° D.分针绕点O顺时针方向旋转60°
15.观察下图,说法正确的是( )。
A.图②是图①的轴对称图形 B.图③通过平移得到图④ C.图⑥绕点A逆时针旋转90°得到图⑤
16.图形A经过( )运动后可变成图形B。
A.绕Q点逆时针旋转90°,再向下平移2格
B.绕Q点顺时针旋转90°,再向下平移2格
C.绕P点逆时针旋转90°,再向右平移2格
D.绕P点顺时针旋转90°,再向左平移2格
四、作图题
17.(1)将图中三角形ABC向右平移2格,再向下平移6格可让点A与点O重合。
(2)将上述平移后的三角形绕点O(A)顺时针旋转90°,画出旋转后的图形。
18.按要求画图。
(1)把绕点O顺时针旋转90°,得到图①。
(2)把绕点O逆时针旋转90°,得到图②。
(3)把图①绕点O顺时针旋转90°,得到图③。
五、解答题
19.“动手操作”显身手。
(1)上图中每个小正方形的面积是1平方厘米,图形ABCD的面积是( )平方厘米。
(2)画出所给图形ABCD绕点A顺时针旋转90°后的图形,并在图中标出点B、C、D的对应点B1、C1、D1。
20.完成下面问题。
(1)画出图①绕点“O”逆时针旋转90°的图形。
(2)写一写图①如何通过旋转和平移得到图②的。
21.“儿童散学归来早,忙趁东风放纸鸢。”描写的是初春时节,一群活泼可爱的儿童趁着东风放风筝的生动情景。王丽也想做一只风筝,体验一番这种感觉。下面是她在边长为1厘米的方格纸上设计的风筝图。请你帮她完成下。
(1)先画出“风筝”的另一半,使它成为一个轴对称图形。
(2)画出这个“风筝”图绕A点顺时针旋转90后的图形。
(3)这个“风筝”图形的面积是( )。
22.画一画、想一想。
(1)画出图1绕A点顺时针方向旋转90°后的图形。
(2)图1绕A点( )时针方向旋转( )后得到图2。
(3)图1绕A点( )时针方向旋转( )后得到图3。
(4)图中绿色部分占整个图案的( )。灰色部分占整个图案的( )。
23.下图每个小方格的边长都是1厘米。
(1)画出三角形AOB绕点O顺时针旋转后的图形。
(2)上图中有一个长方体展开图,已经标出了三个面,请标出另外三个面。做这个长方体框架至少需要( )厘米长的铁丝,它的体积是( )立方厘米。
参考答案
1.顺时针 90
【分析】沿着时针转动的方向叫做顺时针,逆着在时钟的表盘上,有12个大格,时针走一圈是360°,则每小时时针走一个大格,也就是走30°。9:00开始,12:00结束,经历了3个小时,也就是时针走了3个大格,就是3个30°,用乘法计算。
【详解】12:00-9:00=3(小时)
3×30°=90°
会场时钟上的时针从演出开始到结束沿顺时针方向旋转了90度。
2.顺时针 90 12
【分析】钟面指针转动的方向是顺时针方向;钟面一个大格是30°,旋转的大格数×每个大格度数=旋转度数;旋转度数÷每个大格度数=旋转的大格数,据此确定从6时顺时针方向旋转180°,时针的位置。
【详解】30°×(6-3)
=30°×3
=90°
180°÷30°=6(格)
在钟表的钟面上,从3时到6时,钟面上的时针按顺时针方向绕轴心旋转了90°,时针再继续顺时针方向旋转180°,旋转了6个大格,这时钟面上是12时。
3.三 316
【分析】一个钟面的度数为360°,共分为12份,每一份角度为30°,即相邻两个数的角度为30°,根据题意得到旋转的三个数,据此可得出答案。
【详解】指针开始位置是12点位置,指针先按顺时针方向旋转90°,即指针位置是3;再按逆时针方向旋转60°,即指针位置是1;最后按顺时针方向旋转150°,即指针位置是6。则密码是一个三位数,密码是316。
4.平移 旋转
【分析】
当物体水平方向或竖直方向运动,并且物体的方向不发生改变,这种运动式平移;在平面内,一个图形绕着一个定点旋转一定的角度得到另一个图形的变化就是旋转;如果一个图形沿一条直线折叠,直线两旁的部分能够互相重合,这个图形叫做轴对称图形,据此解答。
【详解】观察图形可知,用做基本图形设计图案,是通过平移得到的;
是通过旋转得到的。
【点睛】解答本题的关键是看基本图形是怎样运动得到图案的。
5.逆 90° 顺 90°
【分析】根据旋转的特征;一个图形绕某点按一定的方向旋转一定的度数,某点的位置不动,其余各部分均绕某点按相同的方向旋转相同的度数,据此解答。
【详解】由图可知:
图中的平行四边形绕A点按逆时针方向旋转了90°;
图中的三角形是绕B点按顺时针方向旋转了90°。
【点睛】本题考查旋转,熟练掌握旋转的三要素:旋转点、旋转方向、旋转角度,是解题的关键。
6.(1) 右 6 下 5
(2) 逆 90
【分析】(1)根据平移的特点,找准方向,数清格数,即可解答;
(2)以点O为旋转点,钟表转动的方向就是顺时针,反之就是逆时针再结合角度解答即可。
【详解】(1)图形①先向右平移6格,再向下平移5格到图形②的位置。
(2)图形⑤绕点O沿逆时针方向旋转90°,得到图形④。
7.×
【分析】根据旋转的特征,将长方形绕中心点顺时针旋转90度,中心点位置不变,其余各部分均绕此点按相同方向旋转相同度数,即可画出旋转后的图形。观察旋转后的图形即可得解。
【详解】
旋转后如图所示:
可见,旋转后的图形与原来的图形不重合。
故答案为:×
【点睛】此题主要考查图形的旋转,准确的作图是完成题目的关键。
8.√
【分析】在平面内,将一个图形绕一点按某个方向转动一个角度,这样的运动叫做图形的旋转;图形旋转的三要素:旋转中心、旋转方向、旋转角度;据此解答。
【详解】
将图形绕点O旋转180°后的图形与原图形重合。
原题说法正确。
故答案为:√
【点睛】掌握旋转的意义是解题的关键,注意这个图形绕点O无论是顺时针旋转180°还是逆时针旋转180°后的图形都能与原图形重合。
9.√
【分析】根据旋转的特征可知,物体或图形旋转后,它们的形状、大小都不改变,只是位置发生了变化。(1)对应点到旋转中心的距离不变;(2)对应点与旋转中心所连线段的夹角等于旋转角。据此解答。
【详解】根据分析得,图形旋转后,图形上的每个对应点到旋转中心的距离都不变。原题的说法是正确的。
故答案为:√
【点睛】此题的解题关键是理解掌握旋转的特征及意义。
10.×
【分析】根据旋转图形的特点,对应点到旋转中心的距离相等,对应点与旋转中心所连线段的夹角等于旋转角,旋转前、后的图形完全相同; 线段OA绕点O顺时针旋转90°后,点O不变,其它各边均绕O点旋转90%后,得的线段是OC,而不是OB,据此判断。
【详解】作图如下:
如图: 线段OA绕点O顺时针旋转90°,到达线段OC的位置,不是线段OB的位置,所以原题干说法错误;
故答案为:×
【点睛】掌握图形的旋转方法是解答本题的关键。
11.√
【分析】钟面指针转动的方向是顺时针方向,钟面一个大格是30°,时针从3时到9时,旋转了(9-3)个大格,每个大格的度数×旋转的大格数=旋转的角度,据此分析。
【详解】30°×(9-3)
=30°×6
=180°
时针从3时到9时,顺时针旋转了180°,说法正确。
故答案为:√
12.B
【分析】根据旋转的特征:物体或图形旋转后,它们的形状、大小都不改变,只是位置发生了变化,据此解答。
【详解】A.图形的形状和位置都发生了改变,不符合旋转的特征,不符合题意;
B.图形的形状、大小都不改变,只是位置发生了变化,符合旋转的特征,符合题意;
C.图形的形状和位置都发生了改变,不符合旋转的特征,不符合题意。
故答案为:B
13.B
【分析】决定旋转后图形的位置的要素:一是旋转中心或轴,二是旋转方向(顺时针或逆时针),三是旋转角度。钟面指针转动的方向是顺时针方向,据此确定旋转方向的角度即可。
【详解】A.图E对称后得到的图形,不符合题意;
B.图E绕点O顺时针旋转180°得到的图形,符合题意;
C.不是图E的旋转图形,不符合题意;
D.不是图E的旋转图形,不符合题意。
故答案为:B
14.D
【分析】整个钟表平均分为12个大格,则每个大格为360°÷12=30°,钟表转动的方向就是顺时针方向,反之是逆时针方向;要准确、完整地描述旋转现象,需要有旋转中心、旋转角度和旋转方向。据此解答即可。
【详解】分针从“1”到“3”共旋转了3-1=2(格)
30°×2=60°
A.分针绕点O顺时针旋转,缺少旋转角度,不完整;
B.分针按顺时针方向旋转,缺少旋转中心和旋转角度,不完整;
C.分针按顺时针方向旋转60°,缺少旋转中心,不完整;
D.分针绕点O顺时针方向旋转60°,准确、完整地描述了从“1”到“3”的运动过程。
故答案为:D
15.C
【分析】根据轴对称图形的意义:如果一个图形沿着一条直线对折后,两部分完全重合,这样的图形叫做轴对称图形,这条直线叫做对称轴;
把一个图形整体沿某一方向移动一定的距离,图形的这种运动,称为平移;
旋转:在平面内,把一个图形围绕某一固定点按顺时针或逆时针方向转动一定的角度的过程,称为旋转。这个点为旋转中心,旋转的角度叫旋转角。
【详解】A.图②是图①通过平移;原题干说法错误;
B.图④是图③的轴对称图形;原题干说法错误;
C.图⑥绕点A逆时针旋转90°得到图⑤;说法正确。
说法正确的是图⑥绕点A逆时针旋转90°得到图⑤。
故答案为:C
16.B
【分析】旋转:在平面内,将一个图形绕一点按某个方向转动一定的角度,这样的运动叫做图形的旋转。这个定点叫做旋转中心,转动的角度叫做旋转角。旋转前后图形的位置和方向改变,形状、大小不变。与时针转动方向相同的是顺时针旋转,反之就是逆时针旋转。
【详解】图形A经过绕Q点顺时针旋转90°,再向下平移2格运动后可变成图形B。
故答案为:B
【点睛】此题考查了旋转的意义及在实际当中的运用。
17.见详解
【分析】(1)根据平移的特征,把三角形ABC的各顶点分别先向右平移2格,再向下平移6格,依次连接即可得到平移后的图形;
(2)根据旋转的特征,平移后的三角形绕点O顺时针旋转90°,点O的位置不动,这个图形的各部分均绕此点按相同方向旋转相同的度数即可画出旋转后的图形。
【详解】如图:
图形①是平移后的图形,图形②是旋转后的图形。
18.见详解
【分析】
(1)根据旋转的特征,把绕点O顺时针旋转90°,点O位置不变,其余各部分均绕此点按相同方向旋转相同度数,即可画出旋转后的图形①。
(2)根据旋转的特征,把绕点O逆时针旋转90°,点O位置不变,其余各部分均绕此点按相同方向旋转相同度数,即可画出旋转后的图形②。
(3)根据旋转的特征,图①绕点O顺时针旋转90°,点O位置不变,其余各部分均绕此点按相同方向旋转相同度数,即可画出旋转后的图形③。
【详解】如图:
19.(1)15
(2)图形见详解
【分析】(1)由题意可知,图中每个小正方形的面积是1平方厘米,则每小格的边长为1厘米,图形ABCD是一个平行四边形,该平行四边形的底为5厘米,高为3厘米,根据平行四边形的面积公式:S=ah,据此计算即可;
(2)将图形ABCD绕点A顺时针旋转90°,点A的位置不动,其余各部分均绕点A按相同方向旋转相同的度数即可,然后标出点B、C、D的对应点B1、C1、D1。
【详解】(1)5×3=15(平方厘米)
则图形ABCD的面积是15平方厘米。
(2)如图所示:
【点睛】本题考查旋转图形,明确作旋转图形的方法是解题的关键。
20.(1)见详解
(2)图①先绕点“0”顺时针旋转90°,再向右平移6格。
【分析】(1)根据旋转的特征,将图①绕点“O”逆时针旋转90°,点O位置不变,其余各部分均绕此点按相同方向旋转相同度数,即可画出旋转后的图形。
(2)在平面内,将一个图形绕一点按某个方向转动一个角度,这样的运动叫做图形的旋转。
在平面内,将一个图形沿着某个方向移动一定的距离,这样的运动叫做图形的平移。
运用旋转和平移的意义及特点,写出图①如何通过旋转和平移得到图②的。
【详解】(1)如图:
(2)图①先绕点“O”顺时针旋转90°,再向右平移6格,即可得到图②。
(答案不唯一)
【点睛】本题考查作旋转后的图形的作图方法以及运用旋转和平移得到指定图形,注意平移和旋转都是图形的位置发生变化而形状、大小不变。
21.(1)见详解;(2)见详解;(3)8平方厘米
【分析】(1)根据轴对称图形的特征,对称点到对称轴的距离相等,对称点的连线垂直于对称轴,在对称轴的另一边画出图形的关键对称点,连结即可。
(2)根据旋转的特征,“风筝”图绕点A顺时针旋转90°,点A的位置不动,这个图形的各部分均绕此点按相同方向旋转相同的度数即可画出旋转后的图形;
(3)观察图可知,“风筝”图由2个底为4厘米,高为2厘米的三角形,根据三角形的面积=底×高÷2,代入数据解答即可。
【详解】(1)轴对称图形如下图;
(2)旋转后的图形如下图;
(3)4×2÷2×2=8(平方厘米)
这个“风筝”图形的面积是8平方厘米。
【点睛】此题是考查作轴对称图形、图形的旋转以及三角形面积公式的灵活应用,作轴对称图形关键是确定对称点(对应点)的位置,图形的旋转注意旋转三要素:旋转中心、旋转方向和旋转角。
22.(1)见详解;(2)逆;90°;(3)顺;180°;(4);
【分析】(1)根据旋转的特征,图1绕点A顺时针旋转90°,点A的位置不动,这个图形的各部分均绕此点按相同方向旋转相同的度数即可画出旋转后的图形;
(2)在平面内,将一个图形绕一个定点按某个方向转动一个角度,这样的运动叫做图形的旋转,旋转方向和钟表的指针旋转方向相同,叫顺时针旋转,旋转方向和钟表的指针旋转方向相反,叫逆时针旋转;据此可知,图1绕A点逆时针方向旋转90度后得到图2。
(3)根据题意可知,图1绕A点顺时针或逆时针方向旋转180度后得到图3。
(4)根据画完的图案可知,绿色三角形占了4个方格,灰色部分占了8个方格。根据求一个数占另一个数的几分之几,用一个数除以另一个数,则用4÷(4+8)即可求出绿色部分占整个图案的几分之几;用8÷(4+8)即可求出灰色部分占整个图案的几分之几。
【详解】(1)如图:
(2)图1绕A点逆时针方向旋转90度后得到图2。
(3)图1绕A点顺时针或逆时针方向旋转180度后得到图3。
(4)已知绿色三角形占了4个方格,灰色部分占了8个方格。
4÷(4+8)
=4÷12
=
8÷(4+8)
=8÷12
=
绿色部分占整个图案的。灰色部分占整个图案的。
【点睛】本题主要考查了图形的旋转和求一个数占另一个数的几分之几,注意旋转三要素:旋转中心、旋转方向和旋转角。
23.(1)图见详解
(2)图见详解;24;6
【分析】(1)把图形的每个点与旋转中心O点连接,再量出题目要求旋转的角度为顺时针90°并旋转线段,最后依次连接这些点,可得到旋转后的图形;
(2)长方体有6个面,一般都是长方形,相对的面完全相同;结合图示观察得到长方体的前面、下面、右面,再根据这三个面的大小,确定另外三个面,并标出后面、上面以及左面;
长方体有12条棱,棱长公式为:(长+宽+高)×4;物体所占空间的大小叫作物体的体积,长方体体积=长×宽×高。每个小方格的边长都是1厘米,观察得到:长方体的长、宽、高分别为:2厘米、1厘米、3厘米,可把数据带入公式,求得它的棱长总和、体积。
【详解】(1)(2)如图:
(2)棱长为:
(3+2+1)×4
=6×4
=24(厘米)
做这个长方体框架至少需要24厘米长的铁丝。
体积为:
3×2×1=6(立方厘米)
它的体积是6立方厘米。
【点睛】综合考查了图形的旋转以及长方体的相关特征和属性,需要明确作旋转图形的规则,以及长方体体积公式、棱长公式的灵活应用。
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
