2024-2025学年七年级下学期数学期末考试(浙江舟山市专用)(含答案)
文档属性
| 名称 | 2024-2025学年七年级下学期数学期末考试(浙江舟山市专用)(含答案) |  | |
| 格式 | docx | ||
| 文件大小 | 251.3KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 浙教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-05-08 21:30:40 | ||
图片预览




文档简介
2024保密★启用前
2024-2025学年七年级下册期末测试卷(舟山市专用)
数 学
考试范围:七下全册 考试时间:100分钟 分值:120分
注意事项:
1.答题前填写好自己的姓名、班级、考号等信息
2.请将答案正确填写在答题卡上
一、选择题(本题有10小题,每小题3分,共30分. 每小题只有一个选项是正确的,不选、多选、错选,均不给分)
1.下列方程中,是二元一次方程的是( )
A. B. C. D.
2.如图, 直线 被直线 所截, 下列条件中能判定 的是( )
A. B.
C. D.
3.关于x,y的方程组与有相同的解,则的值为( )
A. B. C. D.
4.某市为美化城市环境,计划在道路两旁种植花卉20万株,由于工作人员的齐心协力,实际每天种植花卉比原计划多,结果提前2天完成任务.设原计划每天种植x万株,则可列方程( )
A. B.
C. D.
5.如图,有型、型、型三种不同的纸板.其中型是边长为的正方形,共有2块;型是长为,宽为的长方形,共有4块:型为边长为的正方形,共有3块.现用这9块纸板去拼出一个大的长方形(不重叠、不留空隙),则下列操作可行的是( )
A.用全部9块纸板 B.拿掉1块型纸板
C.拿掉1块B型纸板 D.加上1块C型纸板
6.红细胞的平均直径为米,这个数据用科学记数法表示为( )
A. B. C. D.
7.若 和 都是关于 的五次多项式,则 是( )
A.关于 的五次多项式
B.关于 的十次多项式
C.关于 的四次多项式
D.关于 的不超过五次的多项式或单项式
8.如图,在中,分别是的角平分线和高线,交于点,则的值为( )
A. B. C. D.
9.81的平方根是( )
A.9 B.±9 C.3 D.±3
10.方程的解是x=( )
A. B. C. D.
二、填空题(本题有6小题,每小题3分,共18分)
11.已知3x+y=2,用关于x的代数式表示y,则y= .
12.已知,是二元一次方程组的解,则的值为 .
13.计算:
14.若关于x,y的二元一次方程有两个解和,则的值为 .
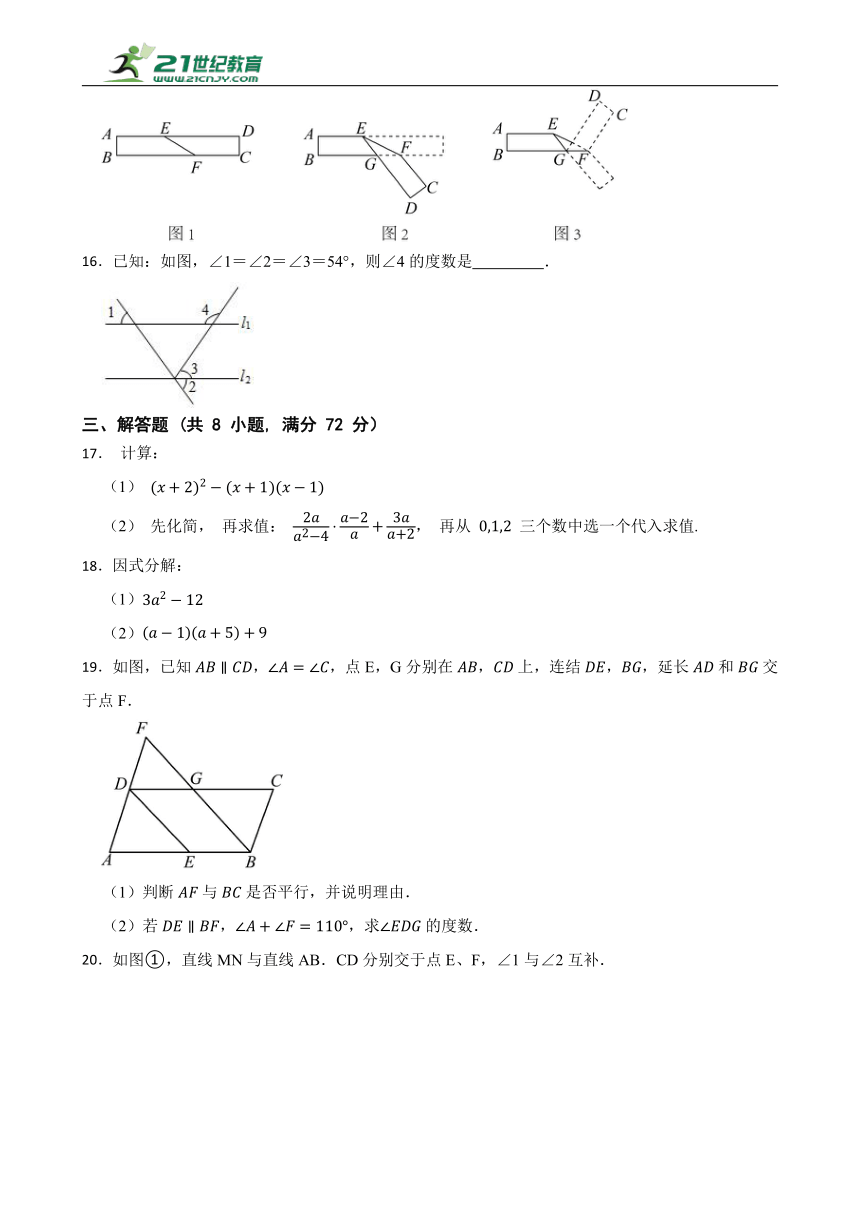
15.如图1,,将长方形纸片ABCD沿直线EF折叠成图2,再沿直线GF折叠成图3,则图3中 .
16.已知:如图,∠1=∠2=∠3=54°,则∠4的度数是 .
三、解答题 (共 8 小题, 满分 72 分)
17. 计算:
(1)
(2) 先化简, 再求值: , 再从 三个数中选一个代入求值.
18.因式分解:
(1)
(2)
19.如图,已知,,点E,G分别在,上,连结,,延长和交于点F.
(1)判断与是否平行,并说明理由.
(2)若,,求的度数.
20.如图①,直线MN与直线AB.CD分别交于点E、F,∠1与∠2互补.
(1)试判断直线AB与直线CD的位置关系,并说明理由;
(2)如图②,∠BEF、∠EFD的角平分线交于点P,EP与CD交于点G,点H是MN上一点,且,求证:;
(3)如图③,在(2)的条件下,连接PH,K是GH上一点使得,作PQ平分∠EPK,求∠HPQ的度数.
21.如图,将一张矩形纸片按如图所示分割成块,其中有两块是边长为的正方形,一块是边长为的正方形.
(1)观察图形,代数式可因式分解为 ;
(2)图中阴影部分面积之和记作,非阴影部分面积之和记作.
用含,的代数式表示,;
若,求的值.
22.(1)知识回顾
①三角形中线性质:三角形的中线能够把三角形面积分成相等的两个部分.
②图形的平移性质:图形的平移不改变图形的形状和大小;一个图形和它经过平移所得的图形中,两组对应点的连线平行(或在同一条直线上)且相等.
(2)知识应用
如图1,把沿着射线BC方向平移到,线段AC与DE交于点.
①若,求的度数.
②若点为AC的中点,的面积为8.
a.求证:点是BC的中点.
b.求的面积.
(3)知识拓展
如图2,把沿着射线BC方向平移到,线段AC与DE交于点,点为EF的中点,DN与MF交于点,若,时,求的面积.
23.阅读材料:我们把多项式及叫做完全平方式.如果一个多项式不是完全平方式,我们常做如下变形:先添加一个适当的项,使式子中出现完全平方式,再减去这个项,使整个式子的值不变,这种方法叫做配方法.配方法是一种重要的解决问题的数学方法,不仅可以将一个看似不能分解的多项式分解因式,还能解决一些与非负数有关的问题或求代数式的最大值,最小值等.
例如:分解因式:;
又例如:求代数式的最小值:∵,
又∵;
∴当时,有最小值,最小值是.
根据阅读材料,利用“配方法”,解决下列问题:
(1)分解因式: .
(2)已知实数,满足,求的值;
(3)当 、 时,多项式的最大值 .
24.为纪念爱国诗人屈原,人们有了端午节吃粽子的习俗.某顾客端午节前在超市购买了40元的豆沙棕和96元的肉棕,已知肉粽单价是豆沙棕单价的2倍,肉棕比豆沙棕多2个.
(1)求豆沙粽和肉棕的单价.
(2)端午节当天,超市为了促销推出降价优惠活动,下表列出了芳芳妈妈、媛媛妈妈的购买数量(单位:个)和付款金额(单位:元):
豆沙粽数量 肉粽数量 付款金额
芳芳妈妈 10 15 135
媛媛妈妈 15 10 115
请根据上表,求豆沙棕和肉粽优惠后的价格.
(3)端午节后,超市为进一步减少库存,将两粽子打包成,两种包装销售,每包都是20个(包装成本忽略不计),每种粽子的销售价格按(1)中的单价五折出售.包装中有个豆沙棕,包装中有个肉棕.活动某天统计发现, 种包装销量为包,B种包装销量为包,A,B两种包装的销售总额为3880元,试求的值.
答案解析部分
1.D
2.D
A、∵∠1与∠4是同旁内角,且∠1+∠4不一定等于180°,∴不能判断a//b,∴A不符合题意;
B、∵∠2与∠3是邻补角,无法判断a//b,∴B不符合题意;
C、∵∠2与∠5是对顶角,无法判断a//b,∴C不符合题意;
D、∵∠4与∠5是内错角,且∠4=∠5,∴a//b,∴D符合题意;
故答案为:D.
利用平行线的判定方法逐项分析判断即可.
3.D
解:∵方程组与有相同的解,
∴与的解相同,
由,解得,
∴,解得,
∴;
故答案为:D.
所谓二元一次方程组的解,就是组成方程组的两个二元一次方程的公共解,由同解方程组可得两个方程组中的四个方程有一个公共解,故将两个方程组中不含参数的两个一次方程组成新的方程组,求出方程组的值,把两个含参方程组成方程组,将所求解代入可得关于字母a、b的方程组,再解方程组求出a、b的值,进而求出代数式的值即可.
4.A
5.B
解:A,全部用上,面积之和是,此式不能进行因式分解,故不能拼成大的长方形。B,拿掉1块A,面积之和是,此式能进行因式分解,故能拼成大的长方形。
C,拿掉1块B,面积之和是,此式不能进行因式分解,故不能拼成大的长方形。
D,加上1块C,面积之和是,此式不能进行因式分解,故不能拼成大的长方形。
故答案为:B.
根据选项条件表示出面积,如果能够进行因式分解则拼接方法可行,否则就不能拼成长方形。
6.B
7.D
解: 若 和 都是关于 的五次多项式,则 是关于 的不超过五次的多项式或单项式 ,
故答案为:D.
再做整式的加减运算时,同类项要合并,根据合并同类项的判断即可.
8.A
9.B
根据平方根的定义进行解答即可.
∵(±9)2=81,
∴81的平方根是±9.
故选B.
本题考查的是平方根的定义,即如果一个数的平方等于a,这个数就叫做a的平方根,也叫做a的二次方根.
10.C
解:∵,,,,
∴原方程可化为:【+++】x=1
即x=1
∴x=.故选C.
由题意易得:,,,,于是可将原方程化简为:x=1,然后系数化为1 即可求解.
11.2-3x
解:根据题意,得y=2-3x.
故答案为:2-3x.
将不含y的项移至等号的右边即可.
12.9
解:把代入方程组,得:,
解得:,
∴;
故答案为:9.
由方程组解的概念可得到关于a、b的二元一次方程组,解方程组可得到a与b的值,则所求代数式的值可求.
13.1
解:由题意可得:
=
=
=
=1
故答案为:1
根据题意将原式变形为,结合平方差公式即可求出答案.
14.6
15.
解:图①中∵,,
∴∠BFE=∠DEF=24°.
∴图2中,,,
∴.
在图3中,∵,
∴,
故答案为:.
根据平行线的性质,得到,,再根据折叠的性质计算出,最后根据即可得到答案.
16.126°
解:如图,
∵∠1=∠2=∠3=54°,
∵∠1=∠5,
∴∠5=∠2,
∴l1∥l2,
∴∠6=∠3,
∴∠4=180°-∠6=180°-54°=126°,
故答案为: 126°.
根据平行线的判定即可得出l1∥l2,然后依据平行线的性质即可求解.
17.(1)解:原式=
=
=
(2)解:
=
=
=
把a=1代入上式得:
故原式的值为.
(1)根据完全平方公式:和公式:进行化简即可.
(2)先把分母中进行分解为:(a+2)(a-2),再进行约分,化成同分母的分式相加,根据同分母分式相加的法则进行计算即可.
18.(1)
(2)
19.(1)解:,理由如下:
,
,
,
,
(2)解:,,
,,
,
,
,
(1)根据平行线的性质可得∠A=∠FDC,推出∠FDC=∠C,根据平行线的判定即可求得;
(2)根据平行线的性质可推出∠FDC+∠ADE=110°,再根据平角定义即可求得.
(1)解:,理由如下:
,
,
,
,
;
(2),,
,,
,
,
,
.
20.(1)解:ABCD,理由如下:
∵∠1与∠2互补,
∴∠1+∠2=180°,
∵∠1+∠BEF=180°
∴∠2=∠BEF
∴AB∥CD;
(2)证明:由(1)知
∴
∵EP平分∠BEF
∴
FP平分∠EFD
∴
∴
∴
∴∠EPF=180°-(∠EFP+∠FEP)=90°,
∴
又
∴;
(3)解:∵
∴
∵PF∥HG,
∴∠FPH=∠PHK,
∴
设,
∵PQ平分∠EPK
∴
又
∴
∴
∴
(1)利用邻补角及题干给出的信息,由同角的补角相等可推出∠2=∠BEF,然后根据同位角相等,两直线平行推出ABCD;
(2)由二直线平行,同旁内角互补得∠BEF+∠EFD=180°;然后根据角平分线的性质可推出∠EFP+∠FEP=90°,由三角形内角和定理证得∠EPF=90°,即EG⊥PF,结合已知条件GH⊥EG,根据同一平面内垂直于同一直线的两条直线互相平行可证PFGH;
(3)由三角形外角性质及已知可推出,由二直线平行,内错角相等得∠FPH=∠PHK,则,
设,,由角平分线的定义及角的构成可得,由垂直的定义得,则,最后根据角的构成,由即可算出答案.
(1)ABCD,
理由如下:
∵∠1与∠2互补,
∴∠1+∠2=180°,
又∵∠1=∠AEF,∠2=∠CFE,
∴∠AEF+∠CFE=180°,
∴AB∥CD;
(2)由(1)知
∴
EP又平分∠BEF
∴
FP平分∠EFD
∴
∴
∴
∴
又
∴;
(3)∵PQ平分∠EPK
∴
又
∴
又
∴
又
∴
∴
∴
∴
∴
21.(1)(2x+y)(x+y)
(2)解:观察图形,得:,;
,
∴3xy-2x2-y2=2x2-xy,
整理,得:4x2-4xy+y2=0
即(2x-y)2=0,
∴2x-y=0,
,
.
(1)解:观察图形得:长方形纸片分为2块是边长为x的正方形,1块是边长为y的正方形,3块是长为y,宽为x的长方形,
∴长方形纸片的面积为:2x2+3xy+y2,
∵长方形纸片的长为:,宽为,
∴长方形纸片的面积为:(2x+y)(x+y),
∴2x2+3xy+y2=(2x+y)(x+y),
∴代数式2x2+3xy+y2因式分解为(2x+y)(x+y);
故答案为:(2x+y)(x+y).
(1)用两种方式计算长方形纸片的面积,即可得到2x2+3xy+y2=(2x+y)(x+y),即可求解;
(2)①根据图形的特征,直接计算即可;②根据,可得4x2-4xy+y2=0,从而得到y=2x,再代入所求的代数式,即可求解.
22.(1)解:平移可得,∠DEF=∠B=60°,∠ACB=∠F=70°,
(2)解:①连结AD,如图所示,
由平移的性质可得:,AD=BE,
,即点是BC中点;
②连结AE,如图所示,
是BC中点,M是AC的中点,
,
(3)解:连结EG,如图所示,
∵N为EF中点,
,,
,
,
,
,
,
,
。
(1)根据平移的性质可得∠DEF=∠B=60°,∠ACB=∠F=70°,再根据三角形内角和定理即可求解;
(2)①由平移可知AD∥BC,AD=BE,根据ASA可证,可得AD=EC,由此即可求证;②E是BC中点,M是AC中点,根据中线的性质可得,,由此即可求解;
(3)连结EG,根据N为EF中点,结合中位线的性质可得,,根据DM:ME=3:1,可得,由面积的和差关系即可求解.
23.(1)
(2)解:∵,
∴,
∴,
∴,
∴,
解得:,
∴;
(3)4;-4;9
解:(1),
故答案为:.
(3) ,
,
,
,
,,
当时, 有最大值9,
,,
故答案为:4;-4;9.
(1)先对多项式进行配方,再利用平方差公式分解多项式.
(2)观察等式,移项后对整式进行配方,再利用完全平方公式的非负性求得a、b的值,进而计算出代数式的值.
(3)先利用完全平方式对多项式进行配方,再通过完全平方式的非负性得到多项式的最大值,进而得到x、y的值.
24.(1)解:设豆沙粽的单价是x元,则肉粽的单价是元,
根据题意得:,
解得:,
经检验,是原方程的解,且符合题意,
,
答:豆沙粽的单价是4元,肉粽的单价是8元
(2)解:设豆沙粽优惠后的单价是a元,肉粽优惠后的单价是b元,
根据题意得:
,
解得,
答:豆沙粽优惠后的单价是3元,肉粽优惠后的单价是7元
(3)解:根据题意得:
整理得:
解得:,,
答:m的值为15或9
(1)设豆沙粽的单价是x元,则肉粽的单价是元, 肉棕个数是;豆沙棕个数是. 等量关系式是肉棕的个数减去豆沙棕的个数=2个.解分式方程求解即可;
(2)设豆沙粽优惠后的单价是a元,肉粽优惠后的单价是b元,根据表中信息列出二元一次方程组,解方程组即可;
(3)根据题意A包装有m个豆沙粽,(20-m)个肉粽,卖出(60-2m)包;B包装有(20-m)个豆沙粽,m个肉粽,卖出(2m+4)包。单价是豆沙粽2元/个,肉粽4元/个,根据两种包装的销售总额为3880元,列出一元二次方程,解方程即可.
(1)解:设豆沙粽的单价是x元,则肉粽的单价是元,
根据题意得:,
解得:,
经检验,是原方程的解,且符合题意,
,
答:豆沙粽的单价是4元,肉粽的单价是8元;
(2)解:设豆沙粽优惠后的单价是a元,肉粽优惠后的单价是b元,
根据题意得:
,
解得,
答:豆沙粽优惠后的单价是3元,肉粽优惠后的单价是7元;
(3)解:根据题意得:
,
整理得:,
解得:,,
答:m的值为15或9.
2024-2025学年七年级下册期末测试卷(舟山市专用)
数 学
考试范围:七下全册 考试时间:100分钟 分值:120分
注意事项:
1.答题前填写好自己的姓名、班级、考号等信息
2.请将答案正确填写在答题卡上
一、选择题(本题有10小题,每小题3分,共30分. 每小题只有一个选项是正确的,不选、多选、错选,均不给分)
1.下列方程中,是二元一次方程的是( )
A. B. C. D.
2.如图, 直线 被直线 所截, 下列条件中能判定 的是( )
A. B.
C. D.
3.关于x,y的方程组与有相同的解,则的值为( )
A. B. C. D.
4.某市为美化城市环境,计划在道路两旁种植花卉20万株,由于工作人员的齐心协力,实际每天种植花卉比原计划多,结果提前2天完成任务.设原计划每天种植x万株,则可列方程( )
A. B.
C. D.
5.如图,有型、型、型三种不同的纸板.其中型是边长为的正方形,共有2块;型是长为,宽为的长方形,共有4块:型为边长为的正方形,共有3块.现用这9块纸板去拼出一个大的长方形(不重叠、不留空隙),则下列操作可行的是( )
A.用全部9块纸板 B.拿掉1块型纸板
C.拿掉1块B型纸板 D.加上1块C型纸板
6.红细胞的平均直径为米,这个数据用科学记数法表示为( )
A. B. C. D.
7.若 和 都是关于 的五次多项式,则 是( )
A.关于 的五次多项式
B.关于 的十次多项式
C.关于 的四次多项式
D.关于 的不超过五次的多项式或单项式
8.如图,在中,分别是的角平分线和高线,交于点,则的值为( )
A. B. C. D.
9.81的平方根是( )
A.9 B.±9 C.3 D.±3
10.方程的解是x=( )
A. B. C. D.
二、填空题(本题有6小题,每小题3分,共18分)
11.已知3x+y=2,用关于x的代数式表示y,则y= .
12.已知,是二元一次方程组的解,则的值为 .
13.计算:
14.若关于x,y的二元一次方程有两个解和,则的值为 .
15.如图1,,将长方形纸片ABCD沿直线EF折叠成图2,再沿直线GF折叠成图3,则图3中 .
16.已知:如图,∠1=∠2=∠3=54°,则∠4的度数是 .
三、解答题 (共 8 小题, 满分 72 分)
17. 计算:
(1)
(2) 先化简, 再求值: , 再从 三个数中选一个代入求值.
18.因式分解:
(1)
(2)
19.如图,已知,,点E,G分别在,上,连结,,延长和交于点F.
(1)判断与是否平行,并说明理由.
(2)若,,求的度数.
20.如图①,直线MN与直线AB.CD分别交于点E、F,∠1与∠2互补.
(1)试判断直线AB与直线CD的位置关系,并说明理由;
(2)如图②,∠BEF、∠EFD的角平分线交于点P,EP与CD交于点G,点H是MN上一点,且,求证:;
(3)如图③,在(2)的条件下,连接PH,K是GH上一点使得,作PQ平分∠EPK,求∠HPQ的度数.
21.如图,将一张矩形纸片按如图所示分割成块,其中有两块是边长为的正方形,一块是边长为的正方形.
(1)观察图形,代数式可因式分解为 ;
(2)图中阴影部分面积之和记作,非阴影部分面积之和记作.
用含,的代数式表示,;
若,求的值.
22.(1)知识回顾
①三角形中线性质:三角形的中线能够把三角形面积分成相等的两个部分.
②图形的平移性质:图形的平移不改变图形的形状和大小;一个图形和它经过平移所得的图形中,两组对应点的连线平行(或在同一条直线上)且相等.
(2)知识应用
如图1,把沿着射线BC方向平移到,线段AC与DE交于点.
①若,求的度数.
②若点为AC的中点,的面积为8.
a.求证:点是BC的中点.
b.求的面积.
(3)知识拓展
如图2,把沿着射线BC方向平移到,线段AC与DE交于点,点为EF的中点,DN与MF交于点,若,时,求的面积.
23.阅读材料:我们把多项式及叫做完全平方式.如果一个多项式不是完全平方式,我们常做如下变形:先添加一个适当的项,使式子中出现完全平方式,再减去这个项,使整个式子的值不变,这种方法叫做配方法.配方法是一种重要的解决问题的数学方法,不仅可以将一个看似不能分解的多项式分解因式,还能解决一些与非负数有关的问题或求代数式的最大值,最小值等.
例如:分解因式:;
又例如:求代数式的最小值:∵,
又∵;
∴当时,有最小值,最小值是.
根据阅读材料,利用“配方法”,解决下列问题:
(1)分解因式: .
(2)已知实数,满足,求的值;
(3)当 、 时,多项式的最大值 .
24.为纪念爱国诗人屈原,人们有了端午节吃粽子的习俗.某顾客端午节前在超市购买了40元的豆沙棕和96元的肉棕,已知肉粽单价是豆沙棕单价的2倍,肉棕比豆沙棕多2个.
(1)求豆沙粽和肉棕的单价.
(2)端午节当天,超市为了促销推出降价优惠活动,下表列出了芳芳妈妈、媛媛妈妈的购买数量(单位:个)和付款金额(单位:元):
豆沙粽数量 肉粽数量 付款金额
芳芳妈妈 10 15 135
媛媛妈妈 15 10 115
请根据上表,求豆沙棕和肉粽优惠后的价格.
(3)端午节后,超市为进一步减少库存,将两粽子打包成,两种包装销售,每包都是20个(包装成本忽略不计),每种粽子的销售价格按(1)中的单价五折出售.包装中有个豆沙棕,包装中有个肉棕.活动某天统计发现, 种包装销量为包,B种包装销量为包,A,B两种包装的销售总额为3880元,试求的值.
答案解析部分
1.D
2.D
A、∵∠1与∠4是同旁内角,且∠1+∠4不一定等于180°,∴不能判断a//b,∴A不符合题意;
B、∵∠2与∠3是邻补角,无法判断a//b,∴B不符合题意;
C、∵∠2与∠5是对顶角,无法判断a//b,∴C不符合题意;
D、∵∠4与∠5是内错角,且∠4=∠5,∴a//b,∴D符合题意;
故答案为:D.
利用平行线的判定方法逐项分析判断即可.
3.D
解:∵方程组与有相同的解,
∴与的解相同,
由,解得,
∴,解得,
∴;
故答案为:D.
所谓二元一次方程组的解,就是组成方程组的两个二元一次方程的公共解,由同解方程组可得两个方程组中的四个方程有一个公共解,故将两个方程组中不含参数的两个一次方程组成新的方程组,求出方程组的值,把两个含参方程组成方程组,将所求解代入可得关于字母a、b的方程组,再解方程组求出a、b的值,进而求出代数式的值即可.
4.A
5.B
解:A,全部用上,面积之和是,此式不能进行因式分解,故不能拼成大的长方形。B,拿掉1块A,面积之和是,此式能进行因式分解,故能拼成大的长方形。
C,拿掉1块B,面积之和是,此式不能进行因式分解,故不能拼成大的长方形。
D,加上1块C,面积之和是,此式不能进行因式分解,故不能拼成大的长方形。
故答案为:B.
根据选项条件表示出面积,如果能够进行因式分解则拼接方法可行,否则就不能拼成长方形。
6.B
7.D
解: 若 和 都是关于 的五次多项式,则 是关于 的不超过五次的多项式或单项式 ,
故答案为:D.
再做整式的加减运算时,同类项要合并,根据合并同类项的判断即可.
8.A
9.B
根据平方根的定义进行解答即可.
∵(±9)2=81,
∴81的平方根是±9.
故选B.
本题考查的是平方根的定义,即如果一个数的平方等于a,这个数就叫做a的平方根,也叫做a的二次方根.
10.C
解:∵,,,,
∴原方程可化为:【+++】x=1
即x=1
∴x=.故选C.
由题意易得:,,,,于是可将原方程化简为:x=1,然后系数化为1 即可求解.
11.2-3x
解:根据题意,得y=2-3x.
故答案为:2-3x.
将不含y的项移至等号的右边即可.
12.9
解:把代入方程组,得:,
解得:,
∴;
故答案为:9.
由方程组解的概念可得到关于a、b的二元一次方程组,解方程组可得到a与b的值,则所求代数式的值可求.
13.1
解:由题意可得:
=
=
=
=1
故答案为:1
根据题意将原式变形为,结合平方差公式即可求出答案.
14.6
15.
解:图①中∵,,
∴∠BFE=∠DEF=24°.
∴图2中,,,
∴.
在图3中,∵,
∴,
故答案为:.
根据平行线的性质,得到,,再根据折叠的性质计算出,最后根据即可得到答案.
16.126°
解:如图,
∵∠1=∠2=∠3=54°,
∵∠1=∠5,
∴∠5=∠2,
∴l1∥l2,
∴∠6=∠3,
∴∠4=180°-∠6=180°-54°=126°,
故答案为: 126°.
根据平行线的判定即可得出l1∥l2,然后依据平行线的性质即可求解.
17.(1)解:原式=
=
=
(2)解:
=
=
=
把a=1代入上式得:
故原式的值为.
(1)根据完全平方公式:和公式:进行化简即可.
(2)先把分母中进行分解为:(a+2)(a-2),再进行约分,化成同分母的分式相加,根据同分母分式相加的法则进行计算即可.
18.(1)
(2)
19.(1)解:,理由如下:
,
,
,
,
(2)解:,,
,,
,
,
,
(1)根据平行线的性质可得∠A=∠FDC,推出∠FDC=∠C,根据平行线的判定即可求得;
(2)根据平行线的性质可推出∠FDC+∠ADE=110°,再根据平角定义即可求得.
(1)解:,理由如下:
,
,
,
,
;
(2),,
,,
,
,
,
.
20.(1)解:ABCD,理由如下:
∵∠1与∠2互补,
∴∠1+∠2=180°,
∵∠1+∠BEF=180°
∴∠2=∠BEF
∴AB∥CD;
(2)证明:由(1)知
∴
∵EP平分∠BEF
∴
FP平分∠EFD
∴
∴
∴
∴∠EPF=180°-(∠EFP+∠FEP)=90°,
∴
又
∴;
(3)解:∵
∴
∵PF∥HG,
∴∠FPH=∠PHK,
∴
设,
∵PQ平分∠EPK
∴
又
∴
∴
∴
(1)利用邻补角及题干给出的信息,由同角的补角相等可推出∠2=∠BEF,然后根据同位角相等,两直线平行推出ABCD;
(2)由二直线平行,同旁内角互补得∠BEF+∠EFD=180°;然后根据角平分线的性质可推出∠EFP+∠FEP=90°,由三角形内角和定理证得∠EPF=90°,即EG⊥PF,结合已知条件GH⊥EG,根据同一平面内垂直于同一直线的两条直线互相平行可证PFGH;
(3)由三角形外角性质及已知可推出,由二直线平行,内错角相等得∠FPH=∠PHK,则,
设,,由角平分线的定义及角的构成可得,由垂直的定义得,则,最后根据角的构成,由即可算出答案.
(1)ABCD,
理由如下:
∵∠1与∠2互补,
∴∠1+∠2=180°,
又∵∠1=∠AEF,∠2=∠CFE,
∴∠AEF+∠CFE=180°,
∴AB∥CD;
(2)由(1)知
∴
EP又平分∠BEF
∴
FP平分∠EFD
∴
∴
∴
∴
又
∴;
(3)∵PQ平分∠EPK
∴
又
∴
又
∴
又
∴
∴
∴
∴
∴
21.(1)(2x+y)(x+y)
(2)解:观察图形,得:,;
,
∴3xy-2x2-y2=2x2-xy,
整理,得:4x2-4xy+y2=0
即(2x-y)2=0,
∴2x-y=0,
,
.
(1)解:观察图形得:长方形纸片分为2块是边长为x的正方形,1块是边长为y的正方形,3块是长为y,宽为x的长方形,
∴长方形纸片的面积为:2x2+3xy+y2,
∵长方形纸片的长为:,宽为,
∴长方形纸片的面积为:(2x+y)(x+y),
∴2x2+3xy+y2=(2x+y)(x+y),
∴代数式2x2+3xy+y2因式分解为(2x+y)(x+y);
故答案为:(2x+y)(x+y).
(1)用两种方式计算长方形纸片的面积,即可得到2x2+3xy+y2=(2x+y)(x+y),即可求解;
(2)①根据图形的特征,直接计算即可;②根据,可得4x2-4xy+y2=0,从而得到y=2x,再代入所求的代数式,即可求解.
22.(1)解:平移可得,∠DEF=∠B=60°,∠ACB=∠F=70°,
(2)解:①连结AD,如图所示,
由平移的性质可得:,AD=BE,
,即点是BC中点;
②连结AE,如图所示,
是BC中点,M是AC的中点,
,
(3)解:连结EG,如图所示,
∵N为EF中点,
,,
,
,
,
,
,
,
。
(1)根据平移的性质可得∠DEF=∠B=60°,∠ACB=∠F=70°,再根据三角形内角和定理即可求解;
(2)①由平移可知AD∥BC,AD=BE,根据ASA可证,可得AD=EC,由此即可求证;②E是BC中点,M是AC中点,根据中线的性质可得,,由此即可求解;
(3)连结EG,根据N为EF中点,结合中位线的性质可得,,根据DM:ME=3:1,可得,由面积的和差关系即可求解.
23.(1)
(2)解:∵,
∴,
∴,
∴,
∴,
解得:,
∴;
(3)4;-4;9
解:(1),
故答案为:.
(3) ,
,
,
,
,,
当时, 有最大值9,
,,
故答案为:4;-4;9.
(1)先对多项式进行配方,再利用平方差公式分解多项式.
(2)观察等式,移项后对整式进行配方,再利用完全平方公式的非负性求得a、b的值,进而计算出代数式的值.
(3)先利用完全平方式对多项式进行配方,再通过完全平方式的非负性得到多项式的最大值,进而得到x、y的值.
24.(1)解:设豆沙粽的单价是x元,则肉粽的单价是元,
根据题意得:,
解得:,
经检验,是原方程的解,且符合题意,
,
答:豆沙粽的单价是4元,肉粽的单价是8元
(2)解:设豆沙粽优惠后的单价是a元,肉粽优惠后的单价是b元,
根据题意得:
,
解得,
答:豆沙粽优惠后的单价是3元,肉粽优惠后的单价是7元
(3)解:根据题意得:
整理得:
解得:,,
答:m的值为15或9
(1)设豆沙粽的单价是x元,则肉粽的单价是元, 肉棕个数是;豆沙棕个数是. 等量关系式是肉棕的个数减去豆沙棕的个数=2个.解分式方程求解即可;
(2)设豆沙粽优惠后的单价是a元,肉粽优惠后的单价是b元,根据表中信息列出二元一次方程组,解方程组即可;
(3)根据题意A包装有m个豆沙粽,(20-m)个肉粽,卖出(60-2m)包;B包装有(20-m)个豆沙粽,m个肉粽,卖出(2m+4)包。单价是豆沙粽2元/个,肉粽4元/个,根据两种包装的销售总额为3880元,列出一元二次方程,解方程即可.
(1)解:设豆沙粽的单价是x元,则肉粽的单价是元,
根据题意得:,
解得:,
经检验,是原方程的解,且符合题意,
,
答:豆沙粽的单价是4元,肉粽的单价是8元;
(2)解:设豆沙粽优惠后的单价是a元,肉粽优惠后的单价是b元,
根据题意得:
,
解得,
答:豆沙粽优惠后的单价是3元,肉粽优惠后的单价是7元;
(3)解:根据题意得:
,
整理得:,
解得:,,
答:m的值为15或9.
同课章节目录
