【期末专项培优】解决问题的策略应用题(含解析)-2024-2025学年五年级下册数学苏教版
文档属性
| 名称 | 【期末专项培优】解决问题的策略应用题(含解析)-2024-2025学年五年级下册数学苏教版 |
|
|
| 格式 | docx | ||
| 文件大小 | 2.5MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 苏教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-05-08 00:00:00 | ||
图片预览


文档简介
解决问题的策略
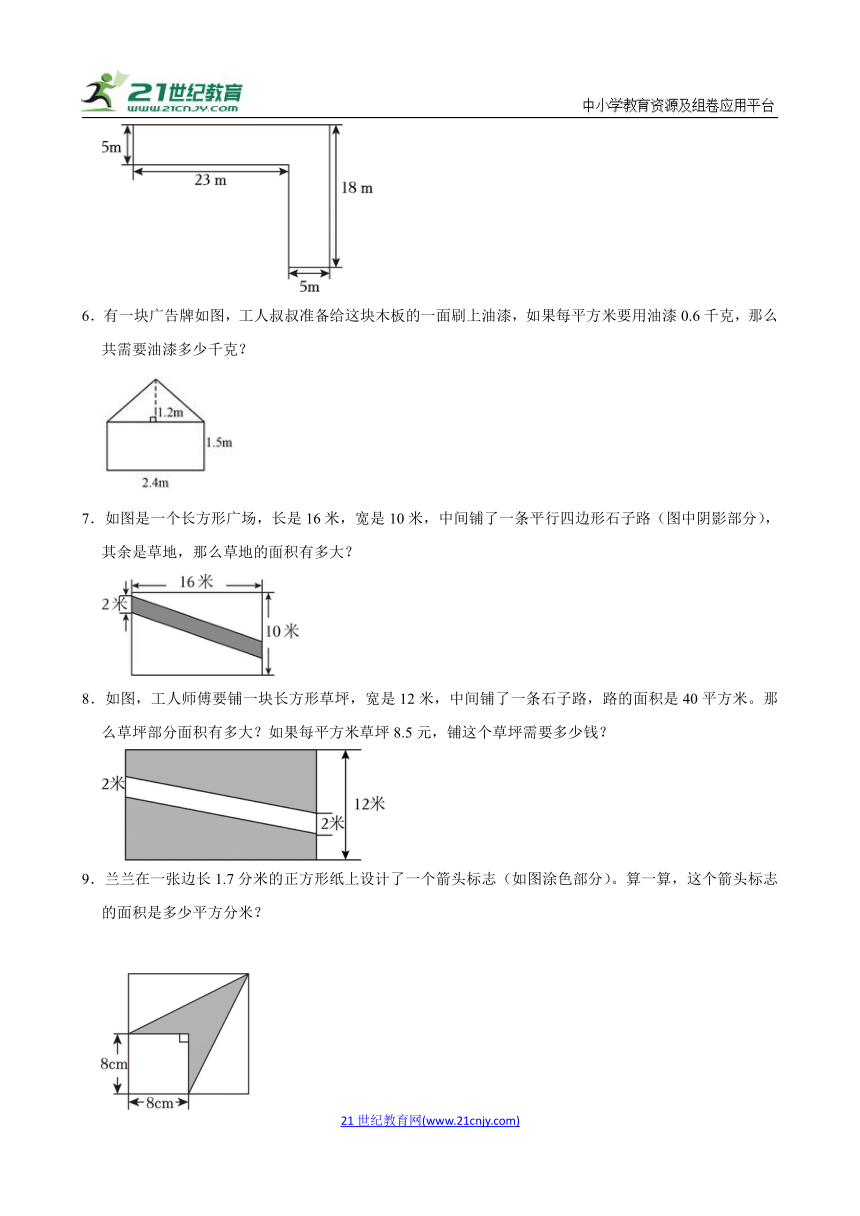
1.(如图)图中是一个苹果园。平均每棵苹果树占地4平方米,园中可种多少棵苹果树?
2.如图,在梯形草坪里辟出一块半圆形地用来种菊花,其余地方植入绿草。绿草占地多少平方米?
3.公园里有一块长40米、宽32米的长方形草坪。草坪中央修建了一个边长是20米的正方形喷泉水池(如图)
(1)铺草坪的面积有多少平方米?
(2)如果用面积是4平方分米的正方形地砖给喷泉水池铺底,共需要多少块地砖?
4.一个运动场如图,两端是半圆形,中间是长方形。
(1)这个运动场的周长是多少米?
(2)这个运动场的面积是多少平方米?(得数保留整数)
5.王伯伯家的一块菜地(如图),这块菜地的面积有多少平方米?
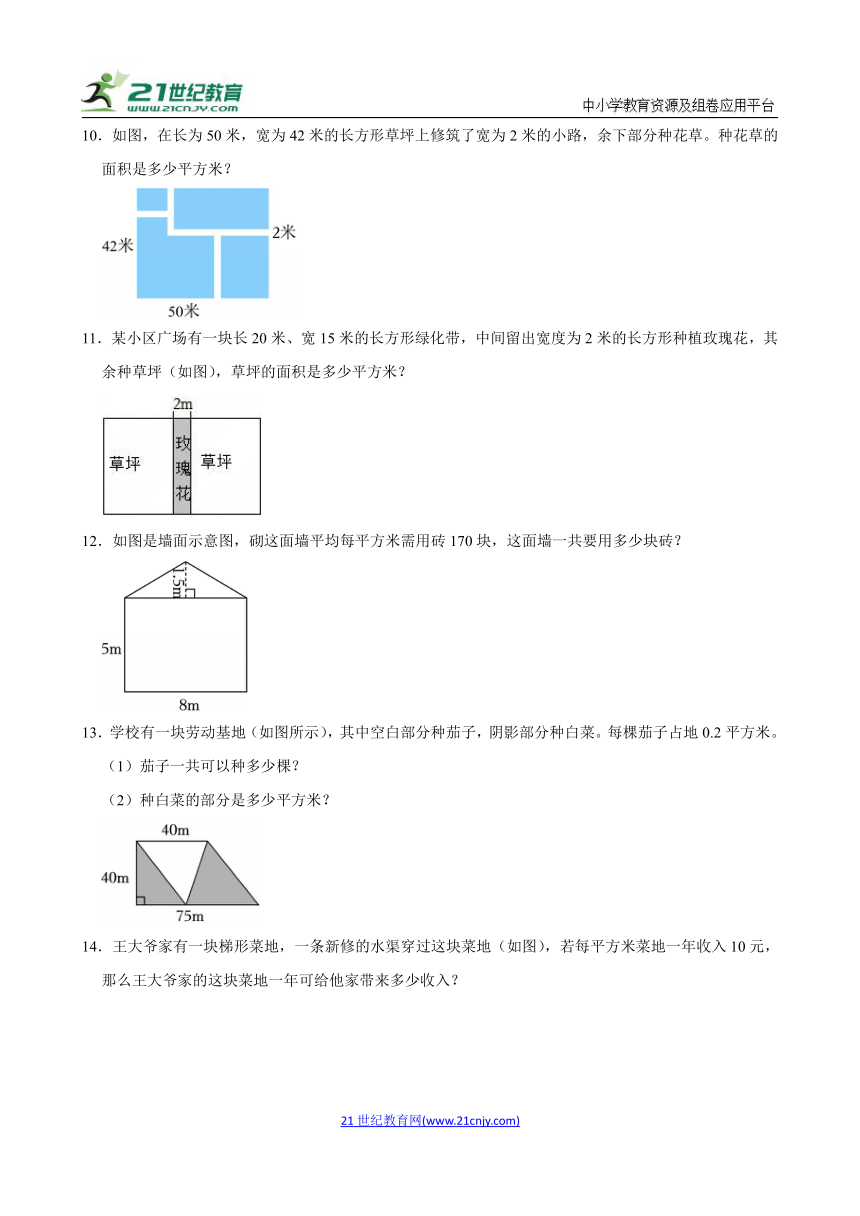
6.有一块广告牌如图,工人叔叔准备给这块木板的一面刷上油漆,如果每平方米要用油漆0.6千克,那么共需要油漆多少千克?
7.如图是一个长方形广场,长是16米,宽是10米,中间铺了一条平行四边形石子路(图中阴影部分),其余是草地,那么草地的面积有多大?
8.如图,工人师傅要铺一块长方形草坪,宽是12米,中间铺了一条石子路,路的面积是40平方米。那么草坪部分面积有多大?如果每平方米草坪8.5元,铺这个草坪需要多少钱?
9.兰兰在一张边长1.7分米的正方形纸上设计了一个箭头标志(如图涂色部分)。算一算,这个箭头标志的面积是多少平方分米?
10.如图,在长为50米,宽为42米的长方形草坪上修筑了宽为2米的小路,余下部分种花草。种花草的面积是多少平方米?
11.某小区广场有一块长20米、宽15米的长方形绿化带,中间留出宽度为2米的长方形种植玫瑰花,其余种草坪(如图),草坪的面积是多少平方米?
12.如图是墙面示意图,砌这面墙平均每平方米需用砖170块,这面墙一共要用多少块砖?
13.学校有一块劳动基地(如图所示),其中空白部分种茄子,阴影部分种白菜。每棵茄子占地0.2平方米。
(1)茄子一共可以种多少棵?
(2)种白菜的部分是多少平方米?
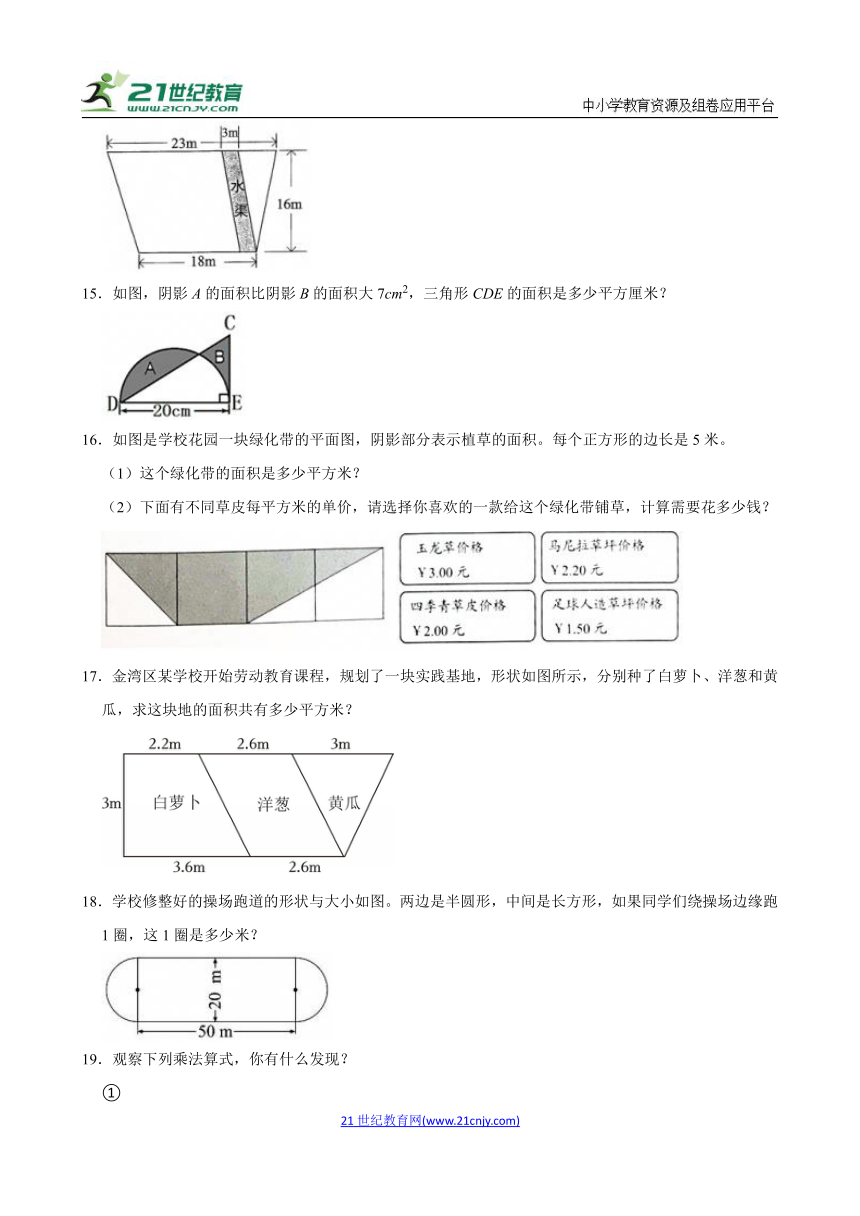
14.王大爷家有一块梯形菜地,一条新修的水渠穿过这块菜地(如图),若每平方米菜地一年收入10元,那么王大爷家的这块菜地一年可给他家带来多少收入?
15.如图,阴影A的面积比阴影B的面积大7cm2,三角形CDE的面积是多少平方厘米?
16.如图是学校花园一块绿化带的平面图,阴影部分表示植草的面积。每个正方形的边长是5米。
(1)这个绿化带的面积是多少平方米?
(2)下面有不同草皮每平方米的单价,请选择你喜欢的一款给这个绿化带铺草,计算需要花多少钱?
17.金湾区某学校开始劳动教育课程,规划了一块实践基地,形状如图所示,分别种了白萝卜、洋葱和黄瓜,求这块地的面积共有多少平方米?
18.学校修整好的操场跑道的形状与大小如图。两边是半圆形,中间是长方形,如果同学们绕操场边缘跑1圈,这1圈是多少米?
19.观察下列乘法算式,你有什么发现?
①
1×2=2
2×2=4
3×2=6
4×2=8
5×2=10
6×2=12
7×2=14
8×2=16
9×2=18
②
1×4=4
2×4=8
3×4=12
4×4=16
5×4=20
6×4=24
7×4=28
8×4=32
9×4=36
③
1×7=7
2×7=14
3×7=21
4×7=28
5×7=35
6×7=42
7×7=49
8×7=56
9×7=63
④
1×9=9
2×9=18
3×9=27
4×9=36
5×9=45
6×9=54
7×9=63
8×9=72
9×9=81
20.阳光小学有一块劳动基地(如图),今年学校计划A地种萝卜,B地种白菜,C地种青椒。
(1)如果种青椒的面积是20平方米,那么种萝卜的面积是多少平方米?
(2)如果每平方米能收白菜27kg,那么B地能收白菜多少千克?
21.如图是王叔叔家的一面墙.如果砌这面墙平均每平方米用砖90块,一共需要用多少块砖?
22.兴滨农业园区有一块梯形稻田,因需要被一条宽2.5米的小路分成两部分(如图)。
(1)修路后,这块稻田的实际面积是多少?
(2)如果一台收割机每分钟能收割210平方米,收割完这块稻田需要多长时间?
23.探索与发现:奇思在乘法口诀表上发现一组有趣的算式,如:
(1)根据上面这组乘法算式的特点,在右边横线上再写一组这样的算式 。
(2)观察上述这两组算式,你发现乘数怎样变化会引起积怎样变化?
(3)奇思发现6×6和5×7之间的规律可以用字母表示出来,下面正确的是 。
A.(a+1)×(a﹣1)=a2+1
B.(a+1)×(a﹣1)=a2
C.(a+1)×(a﹣1)=a2﹣1
D.(a+2)×(a﹣2)=a2+2
(4)根据上面发现的规律,如果2022×2022=4088484,则2021×2023= 。
24.如图是育才小学的运动场。两头是半圆,中间是长75 米。宽60米的长方形,这个运动场的占地面积是多少平方米?
25.今年7月1日起,上海正式实施垃圾分类。如图是可再生资源回收亭的一面墙,它的面积是多少?
26.李大伯家有块平行四边形的空地,现在李大伯要在这块地上种花生和大豆(如图所示)。这块地中,种大豆的面积是多少平方米?
27.乐乐准备粉刷狗屋的前墙(如图中的阴影部分),粉刷的面积一共多少平方米?
28.如图,有一面墙,如果砌墙时每平方米用砖200块,砌这面墙一共要用多少块砖?
29.校园内有一个块半径为8分米的圆形宣传板,要在这块圆形的宣传板上圈出一个最大的正方形用于粘贴学生作品,其他地方作装饰用,请问作装饰的区域面积有多大?
30.如图是教室的一面墙,如果粉刷这面墙每平方米用油漆0.75kg,粉刷这面墙至少要弄油漆多少千克?(得数保留一位小数)
31.如图,一枚半径为1cm的游戏币在边长为6cm的正方形区域内任意移动。在正方形区域内游戏币不能到达的部分的面积是多少平方厘米?
32.花海公园一块长30米,宽20米的向日葵田里铺上了两条宽1米的小路,这块花田种上向日葵的面积是多少平方米?
33.小芳家的客厅里挂了一幅正方形的十字绣作品(如图)圆形绣花部分的直径是1米,这幅十字绣空白部分的面积是多少平方米?
34.如图,边长为6厘米和8厘米的两个正方形拼在一起,则图中空白部分面积是多少平方厘米?
35.如图是由两个正方形拼成的,小正方形的边长是4cm,大正方形的边长是8cm,那么涂色部分的面积是多少平方厘米?
36.学校重新装修时,为每间教室配制了一个工具间(如图)。
(1)这个工具间有多少平方米?
(2)工具间的面积比教室小多少?
37.人民公园有1块梯形空地(如图所示),园内工作人员准备在这块地中划出1块三角形地来种兰花,种兰花的面积是28m2。这块空地的面积是多少?
38.如图,如果将这面墙的两部分都粉刷,每平方米粉刷需要12元。粉刷墙面一共需要多少元钱?
39.友谊公园的中心有一块长方形草坪,草坪里有一条宽1米的曲折小路。草坪的实际面积有多大?
40.一位菜农在如图所示中的梯形菜地中划出一块平行四边形地种青菜。如果剩下的地种萝卜,萝卜地有多少平方米?
41.如图是一块草坪的平面图,这块草坪的面积是多少平方米?
42.如图中阴影长方形ABCD的周长为16厘米(长方形的长、宽均为整数),在它的每条边上各画一个以该边为边长的正方形。已知这四个正方形的面积和是68平方厘米,那么长方形ABCD的面积是平方厘米?
43.一块梯形地中间有一条宽1m的长方形水渠穿过(如图),其他地方种菜。这块地种菜部分的面积是多少平方米?
44.如图,在长方形中有三个大小相等的圆,已知这个长方形的长是18厘米,这个长方形的周长是多少?阴影的面积是多少?
45.一种汽车上用的螺丝垫圈如图所示.这个垫圈的直径是20mm,中间有一个边长为8mm的正方形的孔.这个垫圈的面积是多少平方毫米?
46.有一个运动场(如图),两边是半圆形,中间是长方形。请你计算这个运动场的周长和面积。
47.春暖花开,光明小学“种植基地”(如图,单位:米)迎来了播种季。这块种植基地的面积是多少平方米?
48.为了加强同学们的劳动意识和技能,光华小学开辟出一块劳动实践基地(如图)供同学们进行劳动实践。这块劳动基地的面积是多少平方米?
49.一块稻田的形状如图,如果每公顷施化肥300千克,这块稻田一共需要化肥多少千克?
50.如图,在一张边长是10厘米的正方形纸中,剪去一个长6厘米、宽4厘米的长方形,剩下部分的面积是多少?剩下部分周长是多少?
51.如图是一块长方形草地,长是18米,宽是10米。草地中间有两条交错的小路,一条是长方形,一条是平行四边形。草坪部分面积是多少平方米?
52.曲妍将一张长方形纸的一角如图那样折叠,你能帮她求出涂色部分的面积吗?
(单位:dm)
53.如图:大三角形的空白部分是一个正方形,三角形甲与
三角形乙的面积和是39平方厘米。大三角形ABC的面积是
平方厘米。(提示:可以用拼一拼转化的方法,
也可以用方程。)
54.有一剧场舞台设计如图。舞台的占地面积是多少?要在舞台边缘装上彩灯,至少需要多少米的彩灯线?
55.如图,王大叔把长方形分成了一个三角形地种花菜和一个梯形地种白菜。已知花菜面积比白菜面积少408平方米。求白菜种多少平方米。
56.礼堂的一面外墙有一个双扇门,示意图如下(单位:m)。现在要给墙面贴上小瓷砖,铺满每平方米需要60块砖,贴这面墙大约需要多少块砖?
57.用两张同样大小的正方形白铁皮,边长是1.6m,分别按右面两种方式剪出不同规格的圆片。
(1)两种圆片中每个的周长分别是多少?
(2)剪完图后,哪张白铁皮剩下的废料多?
58.李叔叔准备在这块地里种郁金香(如图),每棵郁金香占地0.25m2,这块地大约可种多少棵郁金香?
59.为了美化校园,学校在一块梯形空地上种植了3种花,同时为了便于同学们观赏,修建了两条2米宽的小路,如图.种花的面积是多少?如果种每平方米花约要25元,那么种花一共需要多少元?
60.王师傅从一张正方形的白铁皮上剪掉一个三角形.求剩下的白铁皮(如图)的面积.
解决问题的策略
参考答案与试题解析
1.(如图)图中是一个苹果园。平均每棵苹果树占地4平方米,园中可种多少棵苹果树?
【答案】17棵。
【分析】根据图示,苹果园的面积等于一个大长方形的面积减去一个底是8米,高是7米的三角形的面积,然后除以4,解答即可。
【解答】解:(5+7)×8﹣8×7÷2
=96﹣28
=68(平方米)
68÷4=17(棵)
答:园中可种17棵苹果树。
【点评】本题考查了组合图形面积计算及实际应用知识,结合题意分析解答即可。
2.如图,在梯形草坪里辟出一块半圆形地用来种菊花,其余地方植入绿草。绿草占地多少平方米?
【答案】343平方米。
【分析】根据图示,绿草占地面积等于梯形面积减去半圆面积,结合题意分析解答即可。
【解答】解:(20+30)×20÷2﹣3.14×(20÷2)2÷2
=500﹣157
=343(平方米)
答:绿草占地343平方米。
【点评】本题考查了组合图形面积计算知识,结合题意分析解答即可。
3.公园里有一块长40米、宽32米的长方形草坪。草坪中央修建了一个边长是20米的正方形喷泉水池(如图)
(1)铺草坪的面积有多少平方米?
(2)如果用面积是4平方分米的正方形地砖给喷泉水池铺底,共需要多少块地砖?
【答案】(1)880平方米;
(2)25块。
【分析】(1)组合图形的面积等于长方形面积减去正方形面积;
(2)用喷泉水池的面积除以每块地砖的面积即可。
【解答】解:(1)40×32﹣20×20
=1280﹣400
=880(平方米)
答:铺草坪的面积有880平方米。
(2)20×20÷(4×4)
=400÷16
=25(块)
答:共需要25块地砖。
【点评】本题主要考查组合图形的面积,关键是把不规则图形转化为归则图形,利用规则图形的面积公式计算。
4.一个运动场如图,两端是半圆形,中间是长方形。
(1)这个运动场的周长是多少米?
(2)这个运动场的面积是多少平方米?(得数保留整数)
【答案】(1)463.76米;(2)13939平方米。
【分析】(1)运动场的周长等于圆的周长加上2条100米的线段,利用圆的周长公式:C=2πr,计算即可。
(2)运动场的面积等于长方形面积加上圆的面积。利用长方形面积公式:S=ab,圆的面积公式:S=πr2,计算即可。
【解答】(1)3.14×42×2+100×2
=263.76+200
=463.76(米)
答:这个运动场的周长是463.76米。
(2)3.14×422+100×42×2
=5538.96+8400
≈13939(平方米)
答:这个运动场的面积是13939平方米。
【点评】本题主要考查组合图形的周长和面积的计算,关键根据图形找出组合图形是由哪些基本图形组成的。
5.王伯伯家的一块菜地(如图),这块菜地的面积有多少平方米?
【答案】205平方米。
【分析】
添加一条辅助线,将图形分成两个长方形,计算出这两块长方形的面积之和即可;
本题需要使用的公式:长方形面积=长×宽。
【解答】解:23×5+18×5
=115+90
=205(平方米)
答:这块菜地的面积有205平方米。
【点评】将组合图形分成两个长方形来计算它的面积是本题的关键,本题可用多种添加辅助线的方法解答。
6.有一块广告牌如图,工人叔叔准备给这块木板的一面刷上油漆,如果每平方米要用油漆0.6千克,那么共需要油漆多少千克?
【答案】3.024千克。
【分析】利用三角形的面积加上长方形的面积,求广告牌的面积,再乘0.6即可求出需要的油漆质量。
【解答】解:2.4×1.2÷2+2.4×1.5
=1.44+3.6
=5.04(平方米)
5.04×0.6=3.024(千克)
答:共需要油漆3.024千克。
【点评】本题属于求组合图形面积的问题,这种类型的题目主要明确组合图形是由哪些基本的图形构成的,然后看是求几种图形的面积和还是求面积差,然后根据面积公式解答即可。
7.如图是一个长方形广场,长是16米,宽是10米,中间铺了一条平行四边形石子路(图中阴影部分),其余是草地,那么草地的面积有多大?
【答案】128平方米。
【分析】根据题意可知,把小路两边的草地通过平移转化为长16米,宽(10﹣2)米的长方形,再根据长方形的面积公式解答即可。
【解答】解:16×(10﹣2)
=16×8
=128(平方米)
答:草地部分面积是128平方米。
【点评】此题主要考查长方形的面积公式的灵活运用,解答关键是明确:小路两边的草地通过平移转化为一个长方形,根据长方形的面积公式解答。
8.如图,工人师傅要铺一块长方形草坪,宽是12米,中间铺了一条石子路,路的面积是40平方米。那么草坪部分面积有多大?如果每平方米草坪8.5元,铺这个草坪需要多少钱?
【答案】200平方米;1700元。
【分析】利用平行四边形面积公式,用路的面积除以2,求平行四边形的高(长方形的宽),再用长方形面积公式:S=ab,计算草坪部分的面积;再乘8.5元求总钱数。
【解答】解:40÷2×(12﹣2)
=20×10
=200(平方米)
200×8.5=1700(元)
答:草坪部分面积有200平方米;铺这个草坪需要1700元。
【点评】本题属于求组合图形面积的问题,这种类型的题目主要明确组合图形是由哪些基本的图形构成的,然后看是求几种图形的面积和还是求面积差,然后根据面积公式解答即可。
9.兰兰在一张边长1.7分米的正方形纸上设计了一个箭头标志(如图涂色部分)。算一算,这个箭头标志的面积是多少平方分米?
【答案】0.72平方分米。
【分析】通过观察图形可知,这个箭头标志的面积等于大正方形的面积减去空白部分两个三角形的面积和小正方形的面积,根据正方形的面积公式:S=a2,三角形的面积公式:S=ah÷2,把数据代入公式解答。
【解答】解:1.7分米=17厘米
17﹣8=9(厘米)
17×17﹣9×17÷2×2﹣8×8
=289﹣153÷2×2﹣64
=289﹣153﹣64
=136﹣64
=72(平方厘米)
72平方厘米=0.72平方分米
答:这个箭头标志的面积是0.72平方分米。
【点评】此题主要考查正方形的面积公式、三角形的面积公式的灵活运用,关键是熟记公式。
10.如图,在长为50米,宽为42米的长方形草坪上修筑了宽为2米的小路,余下部分种花草。种花草的面积是多少平方米?
【答案】1920平方米。
【分析】种花草的面积是长方形草坪的面积去掉小路的面积。小路横拼成长为50米,宽为2米的长方形,竖拼成长为42米,宽为2米的长方形,再加上两条路重叠部分的面积。
【解答】解:50×42﹣(50×2+42×2)+2×2
=2100﹣184+4
=1920(m2)
答:种花草的面积是1920平方米。
故答案为:1920平方米。
【点评】本题考查了学生对长方形面积的掌握,以及学生的观察能力。
11.某小区广场有一块长20米、宽15米的长方形绿化带,中间留出宽度为2米的长方形种植玫瑰花,其余种草坪(如图),草坪的面积是多少平方米?
【答案】270平方米。
【分析】草坪的面积等于长(20﹣2)米、宽15米的长方形的面积,据此解答。
【解答】解:(20﹣2)×15
=18×15
=270(平方米)
答:草坪的面积是270平方米。
【点评】本题主要考查组合图形的面积,关键利用转化思想,把不规则图形转化为规则图形,再计算。
12.如图是墙面示意图,砌这面墙平均每平方米需用砖170块,这面墙一共要用多少块砖?
【答案】7820块。
【分析】先计算图形的面积,图形的面积=长方形的面积+三角形的面积,长方形的面积=长×宽,三角形的面积=底×高÷2;最后用面积乘每平方米需用砖的块数,据此解答。
【解答】解:5×8+8×1.5÷2
=40+6
=46(m2)
46×170= 7820(块)
答:一共要用7820块砖。
【点评】本题考查了长方形、三角形面积公式的灵活运用。
13.学校有一块劳动基地(如图所示),其中空白部分种茄子,阴影部分种白菜。每棵茄子占地0.2平方米。
(1)茄子一共可以种多少棵?
(2)种白菜的部分是多少平方米?
【答案】(1)4000棵;
(2)1500平方米。
【分析】(1)茄子地是一块三角形地,三角形的面积=底×高÷2,据此求出茄子地的面积,再除以每棵茄子的占地面积即可。
(2)三角形的面积=底×高÷2,据此求出阴影部分的面积即可。
【解答】解:(1)40×40÷2÷0.2
=800÷0.2
=4000(棵)
答:茄子一共可以种4000棵。
(2)75×40÷2
=3000÷2
=1500(平方米)
答:种白菜的部分是1500平方米。
【点评】本题考查了三角形面积公式的灵活运用。
14.王大爷家有一块梯形菜地,一条新修的水渠穿过这块菜地(如图),若每平方米菜地一年收入10元,那么王大爷家的这块菜地一年可给他家带来多少收入?
【答案】2800元。
【分析】先求出梯形的面积,其上底是23﹣3=20(米),下底是18﹣3=15(米),高是16米。然后用梯形的面积乘上每平方米菜地的收入10元,即可解题。
【解答】解:梯形面积:
23﹣3=20(米)
18﹣3=15(米)
(20+15)×16÷2
=35×8
=280(平方米)
280×10=2800(元)
答:王大爷家的这块菜地一年可给他家带来2800元收入。
【点评】本题主要考查了组合图形的面积,解题的关键是熟练掌握梯形的面积公式。
15.如图,阴影A的面积比阴影B的面积大7cm2,三角形CDE的面积是多少平方厘米?
【答案】150。
【分析】根据图示可知三角形的面积等于B的面积,加上空白部分的面积;半圆的面积等于阴影A的面积加上空白部分面积,所以三角形CDE的面积等于半圆的面积减去7平方厘米。利用圆的面积公式:S=πr2,计算即可。
【解答】解:3.14×(20÷2)2÷2﹣7
=3.14×100÷2﹣7
=157﹣7
=150(平方厘米)
答:三角形CDE的面积是150平方厘米。
【点评】本题主要考查组合图形的面积,关键是把不规则图形转化为规则图形,计算即可。
16.如图是学校花园一块绿化带的平面图,阴影部分表示植草的面积。每个正方形的边长是5米。
(1)这个绿化带的面积是多少平方米?
(2)下面有不同草皮每平方米的单价,请选择你喜欢的一款给这个绿化带铺草,计算需要花多少钱?
【答案】62.5平方米,187.5元。
【分析】(1)这个绿化带是一个梯形,上底为5×4=20米,下底5米,高5米,利用梯形面积公式即可求出。
(2)选择玉龙草给这个绿化带铺草,利用单价×面积=总价,即可求出(答案不唯一)。
【解答】(1)5×4=20(米)
(20+5)×5÷2=62.5(平方米)
答:这个绿化带的面积是62.5平方米。
(2)选用玉龙草给这个绿化带铺草
62.5×3=187.5(元)
答:选用玉龙草给这个绿化带铺需要187.5元。
【点评】本题考查求梯形面积公式的灵活应用,以及利用梯形面积解决实际问题。
17.金湾区某学校开始劳动教育课程,规划了一块实践基地,形状如图所示,分别种了白萝卜、洋葱和黄瓜,求这块地的面积共有多少平方米?
【答案】21平方米。
【分析】根据图示,白萝卜、洋葱和黄瓜的面积之和是一个上底2.2+2.6+3=7.8(米),下底3.6+2.6=6.2(米),高3米的梯形的面积,根据梯形的面积公式解答即可。
【解答】解:上底:2.2+2.6+3=7.8(米)
下底:3.6+2.6=6.2(米)
面积:(7.8+6.2)×3÷2
=14×3÷2
=21(平方米)
答:这块地的面积共有21平方米。
【点评】本题考查了梯形面积公式的灵活运用知识,结合题意分析解答即可。
18.学校修整好的操场跑道的形状与大小如图。两边是半圆形,中间是长方形,如果同学们绕操场边缘跑1圈,这1圈是多少米?
【答案】162.8米。
【分析】根据题意,可知求出这个运动场的跑道的周长,就可以求出绕运动场的边线跑一圈的路程。由题意可知,两边是圆周长的一半,合起来正好是一个圆的周长,再加上长方形的两个长,就是这个运动场跑道的周长。
【解答】解:3.14×20+50+50
=62.8+100
=162.8(米)
答:这1圈是162.8米。
【点评】此题主要考查圆的周长公式、以及对周长的理解,关键是熟记公式。
19.观察下列乘法算式,你有什么发现?
①
1×2=2
2×2=4
3×2=6
4×2=8
5×2=10
6×2=12
7×2=14
8×2=16
9×2=18
两个数相乘,一个因数不变,另一个因数乘几,积也乘几。
②
1×4=4
2×4=8
3×4=12
4×4=16
5×4=20
6×4=24
7×4=28
8×4=32
9×4=36
两个数相乘,一个因数不变,另一个因数乘几,积也乘几。
③
1×7=7
2×7=14
3×7=21
4×7=28
5×7=35
6×7=42
7×7=49
8×7=56
9×7=63
两个数相乘,一个因数不变,另一个因数乘几,积也乘几。
④
1×9=9
2×9=18
3×9=27
4×9=36
5×9=45
6×9=54
7×9=63
8×9=72
9×9=81
两个数相乘,一个因数不变,另一个因数乘几,积也乘几。
【答案】两个数相乘,一个因数不变,另一个因数乘几,积也乘几。
【分析】根据观察四组算式,第一个因乘几,第二个因数不变,同时积也乘几。
【解答】解:发现:两个数相乘,一个因数不变,另一个因数乘几,积也乘几。
故答案为:两个数相乘,一个因数不变,另一个因数乘几,积也乘几。
【点评】通过观察,分析、归纳发现其中的规律,并应用发现的规律解决问题是应该具备的基本能力。
20.阳光小学有一块劳动基地(如图),今年学校计划A地种萝卜,B地种白菜,C地种青椒。
(1)如果种青椒的面积是20平方米,那么种萝卜的面积是多少平方米?
(2)如果每平方米能收白菜27kg,那么B地能收白菜多少千克?
【答案】(1)48平方米,(2)1296千克。
【分析】对于(1),依据C地青椒的面积和底求出C地的高即A地的高,即三角形高=面积×2÷底,再利用梯形面积=(上底+下底)×高÷2计算即可;
对于(2),先利用平行四边形面积=底×高求出B地面积,再乘27即可解答。
【解答】解:(1)20×2÷5
=40÷5
=8(m)
(3+9)×8÷2
=12×8÷2
=96÷2
=48(m2)
答:种萝卜的面积是48平方米。
(2 )6×8=48(m2)
48×27=1296(kg)
答:B地收白菜1296千克。
【点评】本题主要考查了三角形、梯形、平行四边形面积公式的应用,熟练掌握三角形、梯形、平行四边形面积公式是解答本题的关键。
21.如图是王叔叔家的一面墙.如果砌这面墙平均每平方米用砖90块,一共需要用多少块砖?
【答案】见试题解答内容
【分析】先依据三角形面积公式S=ah÷2和长方形的面积公式S=ab求出这面墙的面积,再乘每平方米需要的砖的块数,问题即可得解.
【解答】解:(6×2÷2+7.5×6)×90
=51×90
=4590(块)
答:一共需要4590块砖.
【点评】本题属于求组合图形面积的问题,这种类型的题目主要明确组合图形是由哪些基本的图形构成的,然后看是求几种图形的面积和还是求面积差,然后根据面积公式解答即可.
22.兴滨农业园区有一块梯形稻田,因需要被一条宽2.5米的小路分成两部分(如图)。
(1)修路后,这块稻田的实际面积是多少?
(2)如果一台收割机每分钟能收割210平方米,收割完这块稻田需要多长时间?
【答案】(1)22200平方米;(2)105.71分钟。
【分析】(1)根据题意,可用梯形的面积公式计算出梯形水稻田的面积,然后再用梯形的面积减去小路的面积即可;
(2)根据题意,可用实际种植的稻田面积除以210进行计算即可。
【解答】解:(1)(125+250)×120÷2﹣2.5×120
=22500﹣300
=22200(平方米)
答:稻田的实际面积是22200平方米。
(2)22200÷210≈105.71(分钟)
答:收割完这块稻田需要105.71分钟。
【点评】此题主要考查的是梯形面积公式和长方形面积公式的灵活应用。
23.探索与发现:奇思在乘法口诀表上发现一组有趣的算式,如:
(1)根据上面这组乘法算式的特点,在右边横线上再写一组这样的算式 7×7=49
6×8=48
5×9=45
4×10=40
3×11=33(答案不唯一) 。
(2)观察上述这两组算式,你发现乘数怎样变化会引起积怎样变化?
(3)奇思发现6×6和5×7之间的规律可以用字母表示出来,下面正确的是 C 。
A.(a+1)×(a﹣1)=a2+1
B.(a+1)×(a﹣1)=a2
C.(a+1)×(a﹣1)=a2﹣1
D.(a+2)×(a﹣2)=a2+2
(4)根据上面发现的规律,如果2022×2022=4088484,则2021×2023= 4088483 。
【答案】(1)7×7=49
6×8=48
5×9=45
4×10=40
3×11=33(答案不唯一)
(2)两个相同的因数相乘,如果一个因数加n,另一个因数减n,积就等于因数的平方减n2。
(3)C;(4)4088483。
【分析】根据算式的规律,可以发现:
6×6和5×7之间的规律可以用字母表示出来:(a+1)×(a﹣1)=a2﹣1;
6×6和4×8之间的规律可以用字母表示出来:(a+2)×(a﹣2)=a2﹣22;
6×6和3×9之间的规律可以用字母表示出来:(a+3)×(a﹣3)=a2﹣32;
据此结合题意解答即,
【解答】解:(1)根据上面这组乘法算式的特点,在右边横线上再写一组这样的算式:
7×7=49
6×8=48
5×9=45
4×10=40
3×11=33(答案不唯一)
(2)观察上述这两组算式,发现:两个相同的因数相乘,如果一个因数加n,另一个因数减n,积就等于因数的平方减n2。
(3)奇思发现6×6和5×7之间的规律可以用字母表示出来,下面正确的是(a+1)×(a﹣1)=a2﹣1,所以选C。
(4)根据上面发现的规律,如果2022×2022=4088484,则:
2021×2023
=2022×2022﹣1
=4088484﹣1
=4088483
故答案为:(1)7×7=49
6×8=48
5×9=45
4×10=40
3×11=33(答案不唯一)
(3)C;(4)4088483。
【点评】本题考查了式的规律知识,结合题意分析解答即可。
24.如图是育才小学的运动场。两头是半圆,中间是长75 米。宽60米的长方形,这个运动场的占地面积是多少平方米?
【答案】7326平方米。
【分析】运动场的占地面积=半径为(60÷2)米的圆的面积+长为75米、宽为60米的长方形的面积,根据圆的面积公式:S=πr ,长方形面积=长×宽,代入数据求解即可。
【解答】解:3.14×(60÷2) +75×60
=2826+4500
=7326(平方米)
答:这个运动场的占地面积是7326平方米。
【点评】本题主要考查组合图形的面积,关键把组合图形转化为规则图形,利用规则图形的面积公式做题。
25.今年7月1日起,上海正式实施垃圾分类。如图是可再生资源回收亭的一面墙,它的面积是多少?
【答案】23。
【分析】根据图示,该回收亭的面积等于一个三角形的面积加上一个长方形的面积,利用三角形面积公式:S=ah÷2,长方形面积:S=ab,计算即可。
【解答】解:4×5+5×1.2÷2
=20+3
=23(平方米)
答:它的面积是23平方米。
【点评】解答求组合图形的面积,关键是观察分析图形是由那几部分组成的,是求各部分的面积和、还是求各部分的面积差,再根据相应的面积公式解答。
26.李大伯家有块平行四边形的空地,现在李大伯要在这块地上种花生和大豆(如图所示)。这块地中,种大豆的面积是多少平方米?
【答案】36.52平方米。
【分析】根据图示,种大豆的面积是三角形的面积,利用三角形面积公式:S=ah÷2,计算即可。
【解答】解:(15.4﹣6.6)×8.3÷2
=8.8×8.3÷2
=36.52(平方米)
答:种大豆的面积是36.52平方米。
【点评】本题主要考查组合图形的面积,关键利用三角形面积公式计算。
27.乐乐准备粉刷狗屋的前墙(如图中的阴影部分),粉刷的面积一共多少平方米?
【答案】2800平方米。
【分析】粉刷的面积等于三角形面积加上大长方形的面积,减去小长方形的面积,利用三角形面积公式:S=ah÷2,长方形面积公式:S=ab计算即可。
【解答】解:50×20÷2+50×70﹣40×30
=500+3500﹣1200
=2800(平方米)
答:粉刷的面积一共2800平方米。
【点评】本题主要考查组合图形的面积,关键是利用规则图形的面积公式计算。
28.如图,有一面墙,如果砌墙时每平方米用砖200块,砌这面墙一共要用多少块砖?
【答案】见试题解答内容
【分析】先求这面墙的面积,墙的面积等于长8米,宽4米的长方形面积加底为8米,高为2米的三角形面积,根据长方形面积计算公式“S=ab”、三角形面积计算公式“S=ah÷2”即可解答.然后再求用砖的块数,用每平米用砖的块数乘墙的面积.
【解答】解:8×4+8×2÷2
=32+8
=40(平方米)
200×40=8000(块)
答:砌这面墙一共要用8000块砖.
【点评】计算不规则图形的面积关键是把不规则图形转化成若干个规则图形,再根据规则图形的面积计算公式解答.
29.校园内有一个块半径为8分米的圆形宣传板,要在这块圆形的宣传板上圈出一个最大的正方形用于粘贴学生作品,其他地方作装饰用,请问作装饰的区域面积有多大?
【答案】72.96平方分米。
【分析】作装饰的区域面积等于圆的面积减去4个三角形的面积。利用圆的面积公式:S=πr ,三角形的面积公式:S=ah÷2,计算即可。
【解答】解:3.14×8 ﹣8×8÷2×4
=200.96﹣128
=72.96(平方分米)
答:作装饰的区域面积有72.96平方分米。
【点评】本题属于求组合图形面积的问题,这种类型的题目主要明确组合图形是由哪些基本的图形构成的,然后看是求几种图形的面积和还是求面积差,然后根据面积公式解答即可。
30.如图是教室的一面墙,如果粉刷这面墙每平方米用油漆0.75kg,粉刷这面墙至少要弄油漆多少千克?(得数保留一位小数)
【答案】18.375千克。
【分析】这面墙的面积=三角形的面积+长方形的面积,三角形面积=底×高÷2,长方形的面积=长×宽,代入公式计算即可求得墙的面积。最后用墙的面积乘0.75,即可求得。
【解答】解:5×1.2÷2+5×4.3
=3+21.5
=24.5(平方米)
24.5×0.75=18.375(千克)
答:粉刷这面墙至少要弄油漆18.375千克。
【点评】本题的关键是求出墙的面积。墙的面积可看作是两个规则图形的面积之和。
31.如图,一枚半径为1cm的游戏币在边长为6cm的正方形区域内任意移动。在正方形区域内游戏币不能到达的部分的面积是多少平方厘米?
【答案】0.86平方厘米。
【分析】游戏币不能到达的部分等于边长是1×2厘米的正方形面积减去半径是1厘米的圆的面积。
【解答】解:(1×2)×(1×2)﹣3.14×1
=4﹣3.14
=0.86(平方厘米)
答:在正方形区域内游戏币不能到达的部分的面积是0.86平方厘米。
【点评】本题属于求组合图形面积的问题,根据正方形和圆点面积公式解答即可。
32.花海公园一块长30米,宽20米的向日葵田里铺上了两条宽1米的小路,这块花田种上向日葵的面积是多少平方米?
【答案】551平方米。
【分析】根据题意,这块花田的实际种植面积就是把这块田的4部分通过上下平移、左右平移得到一个长为(30﹣1)米、宽为(20﹣1)米的长方形的面积,据此列式解答。
【解答】解:(30﹣1)×(20﹣1)
=29×19
=551(平方米)
答:这块花田种上向日葵的面积是551平方米。
【点评】此题主要考查长方形的面积公式的灵活运用,结合题意分析解答即可。
33.小芳家的客厅里挂了一幅正方形的十字绣作品(如图)圆形绣花部分的直径是1米,这幅十字绣空白部分的面积是多少平方米?
【答案】0.215平方米。
【分析】空白部分的面积等于正方形的面积减去圆的面积,根据正方形的面积公式:S=a2,圆的面积公式:S=πr2,把数据代入公式解答。
【解答】解:1×1﹣3.14×(1÷2)2
=1﹣3.14×0.25
=1﹣0.785
=0.215(平方米)
答:这幅十字绣空白部分的面积是0.215平方米。
【点评】此题主要考查正方形的面积公式、圆的面积公式的灵活运用,关键是熟记公式。
34.如图,边长为6厘米和8厘米的两个正方形拼在一起,则图中空白部分面积是多少平方厘米?
【答案】82平方厘米。
【分析】
连接大正方形的对角线,则两个正方形的对角线平行,根据等底等高的三角形面积相等,所以阴影部分面积就等于小正方形面积的一半;由此求出阴影部分的面积,再用两个正方形的面积减去阴影部分的面积就是空白部分的面积,据此解答即可。
【解答】解:(6×6+8×8)﹣6×6÷2
=100﹣18
=82(平方厘米)
答:图中空白部分面积是82平方厘米。
【点评】此题考查组合图形的面积的计算方法,一般都是转化到规则图形中,利用面积公式计算解答。
35.如图是由两个正方形拼成的,小正方形的边长是4cm,大正方形的边长是8cm,那么涂色部分的面积是多少平方厘米?
【答案】24平方厘米。
【分析】阴影部分是上底4厘米、下底8厘米、高4厘米的梯形,利用梯形面积公式:S=(a+b)h÷2,计算即可。
【解答】解:(4+8)×4÷2
=12×4÷2
=24(平方厘米)
答:涂色部分的面积是24平方厘米。
【点评】本题主要考查组合图形的面积,关键利用规则图形的面积公式计算。
36.学校重新装修时,为每间教室配制了一个工具间(如图)。
(1)这个工具间有多少平方米?
(2)工具间的面积比教室小多少?
【答案】(1)6平方米;
(2)42平方米。
【分析】(1)利用三角形面积公式:S=ah÷2,计算工具间的面积;
(2)用教室的面积减去工具间的面积即可。
【解答】解:(1)2×6÷2=6(平方米)
答:这个工具间有6平方米。
(2)8×6﹣6
=48﹣6
=42(平方米)
答:工具间的面积比教室小42平方米。
【点评】本题主要考查平面图形的面积,关键利用长方形面积公式:S=ab,三角形面积公式:S=ah÷2,计算即可。
37.人民公园有1块梯形空地(如图所示),园内工作人员准备在这块地中划出1块三角形地来种兰花,种兰花的面积是28m2。这块空地的面积是多少?
【答案】98m2。
【分析】根据三角形的高=面积×2÷底,求出三角形的高即梯形和平行四边形的高,再确定梯形下底,根据梯形的面积=(上底+下底)×高÷2,列式解答即可。
【解答】解:28×2÷8
=56÷8
=7(米)
(10+8+10)×7÷2
=28×7÷2
=98(平方米)
答:这块空地的面积是98m2。
【点评】关键是掌握梯形和三角形面积公式。
38.如图,如果将这面墙的两部分都粉刷,每平方米粉刷需要12元。粉刷墙面一共需要多少元钱?
【答案】271.2元。
【分析】这面墙的面积等于梯形面积加上长方形面积,再减去小长方形面积;用粉刷面积乘12,计算所需钱数即可。
【解答】解:[(2+6)×1.6÷2+6×3﹣1.2×1.5]×12
=[6.4+18﹣1.8]×12
=22.6×12
=271.2(元)
答:粉刷墙面一共需要271.2元。
【点评】本题主要考查组合图形的面积的计算,关键利用规则图形的面积公式计算。
39.友谊公园的中心有一块长方形草坪,草坪里有一条宽1米的曲折小路。草坪的实际面积有多大?
【答案】99平方米。
【分析】两块草坪可以拼成一块长方形,长方形的长是12﹣1=11(米),长方形的宽是10﹣1=9(米),根据长方形面积=长×宽计算即可出草坪的面积。
【解答】解:(12﹣1)×(10﹣1)
=11×9
=99(平方米)
答:草坪的实际面积是99平方米。
【点评】本题考查组合图形的面积,剪拼法是计算组合图形面积的常用方法。
40.一位菜农在如图所示中的梯形菜地中划出一块平行四边形地种青菜。如果剩下的地种萝卜,萝卜地有多少平方米?
【答案】80平方米。
【分析】从图可知剩下的三角形种植的是萝卜,根据三角形的面积公式 S=ah÷2,即可求出。
【解答】解:30﹣22=8(米)
8×20÷2
=160÷2
=80(平方米)
答:萝卜地有80平方米。
【点评】此题主要考查三角形的面积公式 S=ah÷2的灵活运用,关键是熟记公式。
41.如图是一块草坪的平面图,这块草坪的面积是多少平方米?
【答案】1900平方米。
【分析】草坪的面积等于两个长方形面积的和,利用长方形面积公式:S=ab计算即可。
【解答】解:25×(40+15)+35×15
=1375+525
=1900(平方米)
答:这块草坪的面积是1900平方米。
【点评】本题主要考查组合图形的面积的计算,关键利用规则图形的面积公式计算。
42.如图中阴影长方形ABCD的周长为16厘米(长方形的长、宽均为整数),在它的每条边上各画一个以该边为边长的正方形。已知这四个正方形的面积和是68平方厘米,那么长方形ABCD的面积是平方厘米?
【答案】15平方厘米。
【分析】根据长方形的周长公式“周长=(长+宽)×2”可知,长方形ABCD的周长除以2就是长方形ABCD的长、宽之和,即长+宽=16÷2=8(厘米);根据正方形的面积计算公式“S=a2”,长方形ABCD的长的平方就是一个较大正方形的面积,宽的平方是较小的一个正方形的面积,一个较大正方形面积与一个较小正方形面积之和是四个正方形面积的一半,即68÷2=34(平方厘米)。根据长+宽=8,长2+宽2=34,即可推出长方形的长、宽,再根据长方形的面积计算公式“S=ab”求出长方形ABCD的面积。
【解答】解:长+宽:16÷2=8(厘米)
长2+宽2:68÷2=34(平方厘米)
8=7+1=6+2=5+3=4+4
只有52+32=34
所以长方形ABCD的长为5厘米,宽为3厘米;
面积:5×3=15(平方厘米)
答:长方形ABCD的面积是15平方厘米。
【点评】关键明白长方形的长的平方是一个较大正方形面积,宽的平方是一个较小正方形的面积。而一个大正方形面积与一个小正方形面积是四个正方形面积的一半,即34平方厘米,由长方形的周长可求出长方形的长、宽之和为8厘米,据此即可找出符合题意的长方形的长、宽,进而求出长方形的面积。
43.一块梯形地中间有一条宽1m的长方形水渠穿过(如图),其他地方种菜。这块地种菜部分的面积是多少平方米?
【答案】190平方米。
【分析】由题意可知:菜地的面积=梯形的面积﹣长方形水渠的面积,将数据代入梯形面积公式:S=(a+b)×h÷2、长方形的面积公式:S=ab计算即可。
【解答】解:(30+10)×10÷2﹣1×10
=400÷2﹣1×10
=200﹣10
=190(平方米)
答:这块地种菜部分的面积是190平方米。
【点评】本题主要考查梯形的面积公式,牢记公式是解题的关键。
44.如图,在长方形中有三个大小相等的圆,已知这个长方形的长是18厘米,这个长方形的周长是多少?阴影的面积是多少?
【答案】这个长方形的周长是48厘米;阴影部分的面积是23.22平方厘米。
【分析】根据图示可知,长方形的长等于圆的直径的3倍;长方形的宽等于圆的直径。利用长方形的周长公式:C=(a+b)×2,圆的面积公式:S=πr2,长方形面积公式:S=ab,计算即可。
【解答】解:(18+18÷3)×2
=24×2
=48(厘米)
18×18÷3﹣3.14×(18÷3÷2)2×3
=108﹣84.78
=23.22(平方厘米)
答:这个长方形的周长是48厘米;阴影部分的面积是23.22平方厘米。
【点评】本题主要考查组合图形的面积的计算,关键是把不规则图形转化为规则图形再计算。
45.一种汽车上用的螺丝垫圈如图所示.这个垫圈的直径是20mm,中间有一个边长为8mm的正方形的孔.这个垫圈的面积是多少平方毫米?
【答案】见试题解答内容
【分析】这个垫圈的面积=圆的面积﹣正方形的面积,然后根据圆的面积公式:S=πr2,正方形的面积公式:S=a2,把数据代入公式解答即可.
【解答】解:3.14×(20÷2)2﹣8×8
=314﹣64
=250(平方毫米)
答:这个垫圈的面积是250平方毫米.
【点评】本题属于求组合图形面积的问题,这种类型的题目主要明确组合图形是由哪些基本的图形构成的,然后看是求几种图形的面积和还是求面积差,然后根据面积公式解答即可.
46.有一个运动场(如图),两边是半圆形,中间是长方形。请你计算这个运动场的周长和面积。
【答案】194.2米,2206.5平方米。
【分析】观察图形可知,这个运动场的周长等于直径30米的圆的周长与两条50米的直跑道的长度之和;这个运动场的面积等于直径30米的圆的面积与长50米、宽30米的长方形的面积之和,据此即可解答问题。
【解答】解:3.14×30+50×2
=94.2+100
=194.2(米)
3.14×(30÷2)2+50×30
=706.5+1500
=2206.5(平方米)
答:运动场的周长是194.2米,面积是2206.5平方米。
【点评】解答此题的关键是明确这个图形的周长和面积都包括哪几个部分,再利用公式计算即可解答。
47.春暖花开,光明小学“种植基地”(如图,单位:米)迎来了播种季。这块种植基地的面积是多少平方米?
【答案】1900平方米。
【分析】先分割图形并确定两个长方形的长和宽:观察图形,可以把这个种植基地分割成上下两个长方形,上面长方形的长是47﹣19=28(米),宽是19米;下面长方形的长是53+19=72(米),宽是19(米),根据长方形的面积计算公式分别算出两个长方形的面积,最后把结果加起来就是这个不规则图形的面积,计算时,可运用乘法分配律进行简算。
【解答】解:(47﹣19)×19+(53+19)×19
=28×19+72×19
=19×(28+72)
=19×100
=1900(平方米)
答:这块种植基地的面积是1900平方米。
【点评】本题考查了长方形的面积计算公式的灵活运用。
48.为了加强同学们的劳动意识和技能,光华小学开辟出一块劳动实践基地(如图)供同学们进行劳动实践。这块劳动基地的面积是多少平方米?
【答案】650平方米。
【分析】把所给图示分成两个长方形,利用长方形面积公式:S=ab计算即可。
【解答】解:如图(分法不唯一):
13×24+26×13
=13×(24+26)
=13×50
=650(平方米)
答:这块劳动基地的面积是650平方米。
【点评】本题主要考查不规则图形的面积,关键是把不规则图形转化为规则图形计算。
49.一块稻田的形状如图,如果每公顷施化肥300千克,这块稻田一共需要化肥多少千克?
【答案】1500千克。
【分析】先利用三角形面积公式:S=ah÷2,以及梯形面积公式:S=(a+b)h÷2,求这块稻田的面积,再乘300即可。注意单位要统一。
【解答】解:200×100÷2+(150+250)×200÷2
=10000+400×100
=10000+40000
=50000(平方米)
50000平方米=5公顷
5×300=1500(千克)
答:这块稻田一共需要化肥1500千克。
【点评】本题主要考查组合图形的面积,关键是把不规则图形转化为规则图形,再计算。
50.如图,在一张边长是10厘米的正方形纸中,剪去一个长6厘米、宽4厘米的长方形,剩下部分的面积是多少?剩下部分周长是多少?
【答案】76;48。
【分析】剩余部分的面积等于大正方形的面积减去长方形的面积;剩余部分的周长等于正方形的周长加上长方形的两条宽的长度。长方形面积公式:S=ab、正方形面积公式:S=a2。
【解答】解:面积:
10×10﹣4×6
=100﹣24
=76(平方厘米)
周长:
10×4+4×2
=40+8
=48(厘米)
答:剩下部分的面积是76平方厘米;剩下部分周长是48厘米。
【点评】本题主要考查组合图形的周长和面积,关键是把不规则图形转化为规则图形,再计算。
51.如图是一块长方形草地,长是18米,宽是10米。草地中间有两条交错的小路,一条是长方形,一条是平行四边形。草坪部分面积是多少平方米?
【答案】153平方米。
【分析】求草坪部分的面积,实际上就是求长为(18﹣1)米,宽为(10﹣1)米的长方形的面积,根据长方形的面积=长×宽,代入数据即可求解。
【解答】解:(18﹣1)×(10﹣1)
=17×9
=153(平方米)
答:草坪部分面积是153平方米。
【点评】解答此题的关键是:利用“压缩法”,将小路挤去,即可求出草地部分的面积。
52.曲妍将一张长方形纸的一角如图那样折叠,你能帮她求出涂色部分的面积吗?
(单位:dm)
【答案】见试题解答内容
【分析】根据图形折叠的方法可知,原来长方形的长是7厘米,宽是4厘米,则白色三角形的两条直角边分别是4厘米和7﹣4=3厘米,则图中阴影部分的面积=梯形的面积﹣白色三角形的面积,由此利用梯形和三角形的面积公式即可解答.
【解答】解:(4+7)×4÷2﹣4×(7﹣4)÷2
=11×2﹣4×3÷2
=22﹣6
=16(平方厘米)
答:阴影部分的面积是16平方厘米.
【点评】解答此题的关键是:根据长方形的折叠方法,得出梯形的上下底和高,以及三角形的两条直角边的长度.
53.如图:大三角形的空白部分是一个正方形,三角形甲与
三角形乙的面积和是39平方厘米。大三角形ABC的面积是
75 平方厘米。(提示:可以用拼一拼转化的方法,
也可以用方程。)
【答案】75。
【分析】利用旋转的方法把阴影部分拼成三角形,利用三角形面积公式计算正方形的边长(拼成的三角形的高)。再求三角形ABC的面积即可。
【解答】解:39×2÷(4+9)
=78÷13
=6(厘米)
(4+6)×(9+6)÷2
=10×15÷2
=75(平方厘米)
答:大三角形ABC的面积是75平方厘米。
故答案为:75。
【点评】本题属于求组合图形面积的问题,关键根据三角形面积公式解答即可。
54.有一剧场舞台设计如图。舞台的占地面积是多少?要在舞台边缘装上彩灯,至少需要多少米的彩灯线?
【答案】211.95平方米,65.1米。
【分析】先求大圆半径和小圆半径,再利用环形面积公式计算阴影部分的面积;阴影部分的周长等于大圆周长的一半加上小圆周长的一半,再加上2个9米的长。
【解答】解:(15﹣9)÷2
=6÷2
=3(米)
(15+9)÷2
=24÷2
=12(米)
3.14×122÷2﹣3.14×32÷2
=226.08﹣14.13
=211.95(平方米)
3.14×12+3.14×3+9×2
=37.68+9.42+18
=65.1(米)
答:阴影部分的面积是211.95平方米,至少需要65.1米的彩灯线。
【点评】本题主要考查组合图形的周长和面积,关键是利用圆环面积和圆的周长公式计算。
55.如图,王大叔把长方形分成了一个三角形地种花菜和一个梯形地种白菜。已知花菜面积比白菜面积少408平方米。求白菜种多少平方米。
【答案】684平方米。
【分析】根据图示,花菜面积和白菜面积的和是长方形的面积,利用和差问题公式:(和+差)÷2,计算白菜的种植面积即可。
【解答】解:(40×24+408)÷2
=(960+408)÷2
=1368÷2
=684(平方米)
答:白菜种了684平方米。
【点评】本题主要考查组合图形面积的计算,关键是利用和差问题公式解答。
56.礼堂的一面外墙有一个双扇门,示意图如下(单位:m)。现在要给墙面贴上小瓷砖,铺满每平方米需要60块砖,贴这面墙大约需要多少块砖?
【答案】3660块。
【分析】先用长方形面积加上三角形面积,减去小长方形面积,求铺砖的面积,再乘60,就是需要砖的块数。
【解答】解:6×10+10×1.2÷2﹣2×2.5
=60+6﹣5
=61(平方米)
61×60=3660(块)
答:贴这面墙大约需要3660块砖。
【点评】本题属于求组合图形面积的问题,这种类型的题目主要明确组合图形是由哪些基本的图形构成的,然后看是求几种图形的面积和还是求面积差,然后根据面积公式解答即可。
57.用两张同样大小的正方形白铁皮,边长是1.6m,分别按右面两种方式剪出不同规格的圆片。
(1)两种圆片中每个的周长分别是多少?
(2)剪完图后,哪张白铁皮剩下的废料多?
【答案】(1)5.024米,2.512米。
(2)一样多。
【分析】(1)首先根据题意,分别求出每种圆片的直径分别是多少;然后根据圆的周长=πd(d是圆的直径),求出两种圆片的周长分别是多少即可;
(2)首先根据题意,分别求出每种圆片的半径分别是多少;然后根据圆的面积=πr2(r是圆的半径),求出两种圆片的面积分别是多少;最后再用正方形的面积减去每种圆片的面积,求出剩下的废料的面积分别是多少,再比较大小,判断出哪张白铁皮剩下的废料多些即可。
【解答】解:(1)第一种圆片的周长是:
3.14×1.6=5.024(米)
第二种圆片中每个的周长是:
3.14×(1.6÷2)
=3.14×0.8
=2.512(米)
答:第一种圆片的周长是5.024米,第二种圆片的周长是2.512米。
(2)第一张白铁板剩下的废料的面积是:
1.6×1.6﹣3.14×(1.6÷2)2
=2.56﹣2.0096
=0.5504(平方米)
第二张白铁板剩下的废料的面积是:
1.6×1.6﹣3.14×(1.6÷2÷2)2×4
=2.56﹣2.0096
=0.5504(平方米)
所以两张白铁板剩下的废料一样多。
答:剪完圆后,两张白铁皮剩下的废料一样多。
【点评】此题主要考查了圆与组合图形问题的应用,解答此题的关键是熟练掌握圆的周长、面积公式。
58.李叔叔准备在这块地里种郁金香(如图),每棵郁金香占地0.25m2,这块地大约可种多少棵郁金香?
【答案】见试题解答内容
【分析】
如图:这块地的面积=长方形的面积+三角形的面积,根据三角形的面积=底×高÷2,长方形的面积=长×宽,计算出图形中三角形与长方形的面积和,即可求出这块地的面积;然后用这块地的面积除以每棵郁金香占地的面积,即可求出郁金香的棵数.
【解答】解:15×5+(12﹣5)×(15﹣5)÷2
=75+35
=110(平方米)
110÷0.25=440(棵)
答:这块地大约可种440棵郁金香.
【点评】本题属于求组合图形面积的问题,这种类型的题目主要明确组合图形是由哪些基本的图形构成的,然后看是求几种图形的面积和还是求面积差,然后根据面积公式解答即可.
59.为了美化校园,学校在一块梯形空地上种植了3种花,同时为了便于同学们观赏,修建了两条2米宽的小路,如图.种花的面积是多少?如果种每平方米花约要25元,那么种花一共需要多少元?
【答案】见试题解答内容
【分析】梯形面积减去小路的面积即为种花的面积,梯形的上底下底和高都已知,其面积就可求;小路属于平行四边形,高和底已知,则面积可求;每平方米的花费已知,则总花费就可求.
【解答】解:(12+20)×6÷2﹣2×6×2
=96﹣24
=72(平方米);
72×25=1800(元).
答:种花的面积是72平方米,一共需要1800元.
【点评】本题属于求组合图形面积的问题,这种类型的题目主要明确组合图形是由哪些基本的图形构成的,然后看是求几种图形的面积和还是求面积差,然后根据面积公式解答即可.
60.王师傅从一张正方形的白铁皮上剪掉一个三角形.求剩下的白铁皮(如图)的面积.
【答案】见试题解答内容
【分析】解答方法不唯一.可把这个图形分成一个长12分米,宽6分米的长方形、一个上底为6分米,下底为12分米,高为(12﹣6)分米的梯形.根据长方形面积计算公式“S=ab”、梯形面积计算公式“S=(a+b)h÷2”分别求出长方形、梯形的面积,再把二者相加.
【解答】解:如图
12×6+(6+12)×(12﹣6)÷2
=12×6+18×6÷2
=72+54
=126(dm2)
答:这个图形的面积是126dm2.
【点评】此题解答方法不唯一,也可以用12分米正方形的面积减两直角边都是(12﹣6)分米的直角三角形面积.
21世纪教育网(www.21cnjy.com)
1.(如图)图中是一个苹果园。平均每棵苹果树占地4平方米,园中可种多少棵苹果树?
2.如图,在梯形草坪里辟出一块半圆形地用来种菊花,其余地方植入绿草。绿草占地多少平方米?
3.公园里有一块长40米、宽32米的长方形草坪。草坪中央修建了一个边长是20米的正方形喷泉水池(如图)
(1)铺草坪的面积有多少平方米?
(2)如果用面积是4平方分米的正方形地砖给喷泉水池铺底,共需要多少块地砖?
4.一个运动场如图,两端是半圆形,中间是长方形。
(1)这个运动场的周长是多少米?
(2)这个运动场的面积是多少平方米?(得数保留整数)
5.王伯伯家的一块菜地(如图),这块菜地的面积有多少平方米?
6.有一块广告牌如图,工人叔叔准备给这块木板的一面刷上油漆,如果每平方米要用油漆0.6千克,那么共需要油漆多少千克?
7.如图是一个长方形广场,长是16米,宽是10米,中间铺了一条平行四边形石子路(图中阴影部分),其余是草地,那么草地的面积有多大?
8.如图,工人师傅要铺一块长方形草坪,宽是12米,中间铺了一条石子路,路的面积是40平方米。那么草坪部分面积有多大?如果每平方米草坪8.5元,铺这个草坪需要多少钱?
9.兰兰在一张边长1.7分米的正方形纸上设计了一个箭头标志(如图涂色部分)。算一算,这个箭头标志的面积是多少平方分米?
10.如图,在长为50米,宽为42米的长方形草坪上修筑了宽为2米的小路,余下部分种花草。种花草的面积是多少平方米?
11.某小区广场有一块长20米、宽15米的长方形绿化带,中间留出宽度为2米的长方形种植玫瑰花,其余种草坪(如图),草坪的面积是多少平方米?
12.如图是墙面示意图,砌这面墙平均每平方米需用砖170块,这面墙一共要用多少块砖?
13.学校有一块劳动基地(如图所示),其中空白部分种茄子,阴影部分种白菜。每棵茄子占地0.2平方米。
(1)茄子一共可以种多少棵?
(2)种白菜的部分是多少平方米?
14.王大爷家有一块梯形菜地,一条新修的水渠穿过这块菜地(如图),若每平方米菜地一年收入10元,那么王大爷家的这块菜地一年可给他家带来多少收入?
15.如图,阴影A的面积比阴影B的面积大7cm2,三角形CDE的面积是多少平方厘米?
16.如图是学校花园一块绿化带的平面图,阴影部分表示植草的面积。每个正方形的边长是5米。
(1)这个绿化带的面积是多少平方米?
(2)下面有不同草皮每平方米的单价,请选择你喜欢的一款给这个绿化带铺草,计算需要花多少钱?
17.金湾区某学校开始劳动教育课程,规划了一块实践基地,形状如图所示,分别种了白萝卜、洋葱和黄瓜,求这块地的面积共有多少平方米?
18.学校修整好的操场跑道的形状与大小如图。两边是半圆形,中间是长方形,如果同学们绕操场边缘跑1圈,这1圈是多少米?
19.观察下列乘法算式,你有什么发现?
①
1×2=2
2×2=4
3×2=6
4×2=8
5×2=10
6×2=12
7×2=14
8×2=16
9×2=18
②
1×4=4
2×4=8
3×4=12
4×4=16
5×4=20
6×4=24
7×4=28
8×4=32
9×4=36
③
1×7=7
2×7=14
3×7=21
4×7=28
5×7=35
6×7=42
7×7=49
8×7=56
9×7=63
④
1×9=9
2×9=18
3×9=27
4×9=36
5×9=45
6×9=54
7×9=63
8×9=72
9×9=81
20.阳光小学有一块劳动基地(如图),今年学校计划A地种萝卜,B地种白菜,C地种青椒。
(1)如果种青椒的面积是20平方米,那么种萝卜的面积是多少平方米?
(2)如果每平方米能收白菜27kg,那么B地能收白菜多少千克?
21.如图是王叔叔家的一面墙.如果砌这面墙平均每平方米用砖90块,一共需要用多少块砖?
22.兴滨农业园区有一块梯形稻田,因需要被一条宽2.5米的小路分成两部分(如图)。
(1)修路后,这块稻田的实际面积是多少?
(2)如果一台收割机每分钟能收割210平方米,收割完这块稻田需要多长时间?
23.探索与发现:奇思在乘法口诀表上发现一组有趣的算式,如:
(1)根据上面这组乘法算式的特点,在右边横线上再写一组这样的算式 。
(2)观察上述这两组算式,你发现乘数怎样变化会引起积怎样变化?
(3)奇思发现6×6和5×7之间的规律可以用字母表示出来,下面正确的是 。
A.(a+1)×(a﹣1)=a2+1
B.(a+1)×(a﹣1)=a2
C.(a+1)×(a﹣1)=a2﹣1
D.(a+2)×(a﹣2)=a2+2
(4)根据上面发现的规律,如果2022×2022=4088484,则2021×2023= 。
24.如图是育才小学的运动场。两头是半圆,中间是长75 米。宽60米的长方形,这个运动场的占地面积是多少平方米?
25.今年7月1日起,上海正式实施垃圾分类。如图是可再生资源回收亭的一面墙,它的面积是多少?
26.李大伯家有块平行四边形的空地,现在李大伯要在这块地上种花生和大豆(如图所示)。这块地中,种大豆的面积是多少平方米?
27.乐乐准备粉刷狗屋的前墙(如图中的阴影部分),粉刷的面积一共多少平方米?
28.如图,有一面墙,如果砌墙时每平方米用砖200块,砌这面墙一共要用多少块砖?
29.校园内有一个块半径为8分米的圆形宣传板,要在这块圆形的宣传板上圈出一个最大的正方形用于粘贴学生作品,其他地方作装饰用,请问作装饰的区域面积有多大?
30.如图是教室的一面墙,如果粉刷这面墙每平方米用油漆0.75kg,粉刷这面墙至少要弄油漆多少千克?(得数保留一位小数)
31.如图,一枚半径为1cm的游戏币在边长为6cm的正方形区域内任意移动。在正方形区域内游戏币不能到达的部分的面积是多少平方厘米?
32.花海公园一块长30米,宽20米的向日葵田里铺上了两条宽1米的小路,这块花田种上向日葵的面积是多少平方米?
33.小芳家的客厅里挂了一幅正方形的十字绣作品(如图)圆形绣花部分的直径是1米,这幅十字绣空白部分的面积是多少平方米?
34.如图,边长为6厘米和8厘米的两个正方形拼在一起,则图中空白部分面积是多少平方厘米?
35.如图是由两个正方形拼成的,小正方形的边长是4cm,大正方形的边长是8cm,那么涂色部分的面积是多少平方厘米?
36.学校重新装修时,为每间教室配制了一个工具间(如图)。
(1)这个工具间有多少平方米?
(2)工具间的面积比教室小多少?
37.人民公园有1块梯形空地(如图所示),园内工作人员准备在这块地中划出1块三角形地来种兰花,种兰花的面积是28m2。这块空地的面积是多少?
38.如图,如果将这面墙的两部分都粉刷,每平方米粉刷需要12元。粉刷墙面一共需要多少元钱?
39.友谊公园的中心有一块长方形草坪,草坪里有一条宽1米的曲折小路。草坪的实际面积有多大?
40.一位菜农在如图所示中的梯形菜地中划出一块平行四边形地种青菜。如果剩下的地种萝卜,萝卜地有多少平方米?
41.如图是一块草坪的平面图,这块草坪的面积是多少平方米?
42.如图中阴影长方形ABCD的周长为16厘米(长方形的长、宽均为整数),在它的每条边上各画一个以该边为边长的正方形。已知这四个正方形的面积和是68平方厘米,那么长方形ABCD的面积是平方厘米?
43.一块梯形地中间有一条宽1m的长方形水渠穿过(如图),其他地方种菜。这块地种菜部分的面积是多少平方米?
44.如图,在长方形中有三个大小相等的圆,已知这个长方形的长是18厘米,这个长方形的周长是多少?阴影的面积是多少?
45.一种汽车上用的螺丝垫圈如图所示.这个垫圈的直径是20mm,中间有一个边长为8mm的正方形的孔.这个垫圈的面积是多少平方毫米?
46.有一个运动场(如图),两边是半圆形,中间是长方形。请你计算这个运动场的周长和面积。
47.春暖花开,光明小学“种植基地”(如图,单位:米)迎来了播种季。这块种植基地的面积是多少平方米?
48.为了加强同学们的劳动意识和技能,光华小学开辟出一块劳动实践基地(如图)供同学们进行劳动实践。这块劳动基地的面积是多少平方米?
49.一块稻田的形状如图,如果每公顷施化肥300千克,这块稻田一共需要化肥多少千克?
50.如图,在一张边长是10厘米的正方形纸中,剪去一个长6厘米、宽4厘米的长方形,剩下部分的面积是多少?剩下部分周长是多少?
51.如图是一块长方形草地,长是18米,宽是10米。草地中间有两条交错的小路,一条是长方形,一条是平行四边形。草坪部分面积是多少平方米?
52.曲妍将一张长方形纸的一角如图那样折叠,你能帮她求出涂色部分的面积吗?
(单位:dm)
53.如图:大三角形的空白部分是一个正方形,三角形甲与
三角形乙的面积和是39平方厘米。大三角形ABC的面积是
平方厘米。(提示:可以用拼一拼转化的方法,
也可以用方程。)
54.有一剧场舞台设计如图。舞台的占地面积是多少?要在舞台边缘装上彩灯,至少需要多少米的彩灯线?
55.如图,王大叔把长方形分成了一个三角形地种花菜和一个梯形地种白菜。已知花菜面积比白菜面积少408平方米。求白菜种多少平方米。
56.礼堂的一面外墙有一个双扇门,示意图如下(单位:m)。现在要给墙面贴上小瓷砖,铺满每平方米需要60块砖,贴这面墙大约需要多少块砖?
57.用两张同样大小的正方形白铁皮,边长是1.6m,分别按右面两种方式剪出不同规格的圆片。
(1)两种圆片中每个的周长分别是多少?
(2)剪完图后,哪张白铁皮剩下的废料多?
58.李叔叔准备在这块地里种郁金香(如图),每棵郁金香占地0.25m2,这块地大约可种多少棵郁金香?
59.为了美化校园,学校在一块梯形空地上种植了3种花,同时为了便于同学们观赏,修建了两条2米宽的小路,如图.种花的面积是多少?如果种每平方米花约要25元,那么种花一共需要多少元?
60.王师傅从一张正方形的白铁皮上剪掉一个三角形.求剩下的白铁皮(如图)的面积.
解决问题的策略
参考答案与试题解析
1.(如图)图中是一个苹果园。平均每棵苹果树占地4平方米,园中可种多少棵苹果树?
【答案】17棵。
【分析】根据图示,苹果园的面积等于一个大长方形的面积减去一个底是8米,高是7米的三角形的面积,然后除以4,解答即可。
【解答】解:(5+7)×8﹣8×7÷2
=96﹣28
=68(平方米)
68÷4=17(棵)
答:园中可种17棵苹果树。
【点评】本题考查了组合图形面积计算及实际应用知识,结合题意分析解答即可。
2.如图,在梯形草坪里辟出一块半圆形地用来种菊花,其余地方植入绿草。绿草占地多少平方米?
【答案】343平方米。
【分析】根据图示,绿草占地面积等于梯形面积减去半圆面积,结合题意分析解答即可。
【解答】解:(20+30)×20÷2﹣3.14×(20÷2)2÷2
=500﹣157
=343(平方米)
答:绿草占地343平方米。
【点评】本题考查了组合图形面积计算知识,结合题意分析解答即可。
3.公园里有一块长40米、宽32米的长方形草坪。草坪中央修建了一个边长是20米的正方形喷泉水池(如图)
(1)铺草坪的面积有多少平方米?
(2)如果用面积是4平方分米的正方形地砖给喷泉水池铺底,共需要多少块地砖?
【答案】(1)880平方米;
(2)25块。
【分析】(1)组合图形的面积等于长方形面积减去正方形面积;
(2)用喷泉水池的面积除以每块地砖的面积即可。
【解答】解:(1)40×32﹣20×20
=1280﹣400
=880(平方米)
答:铺草坪的面积有880平方米。
(2)20×20÷(4×4)
=400÷16
=25(块)
答:共需要25块地砖。
【点评】本题主要考查组合图形的面积,关键是把不规则图形转化为归则图形,利用规则图形的面积公式计算。
4.一个运动场如图,两端是半圆形,中间是长方形。
(1)这个运动场的周长是多少米?
(2)这个运动场的面积是多少平方米?(得数保留整数)
【答案】(1)463.76米;(2)13939平方米。
【分析】(1)运动场的周长等于圆的周长加上2条100米的线段,利用圆的周长公式:C=2πr,计算即可。
(2)运动场的面积等于长方形面积加上圆的面积。利用长方形面积公式:S=ab,圆的面积公式:S=πr2,计算即可。
【解答】(1)3.14×42×2+100×2
=263.76+200
=463.76(米)
答:这个运动场的周长是463.76米。
(2)3.14×422+100×42×2
=5538.96+8400
≈13939(平方米)
答:这个运动场的面积是13939平方米。
【点评】本题主要考查组合图形的周长和面积的计算,关键根据图形找出组合图形是由哪些基本图形组成的。
5.王伯伯家的一块菜地(如图),这块菜地的面积有多少平方米?
【答案】205平方米。
【分析】
添加一条辅助线,将图形分成两个长方形,计算出这两块长方形的面积之和即可;
本题需要使用的公式:长方形面积=长×宽。
【解答】解:23×5+18×5
=115+90
=205(平方米)
答:这块菜地的面积有205平方米。
【点评】将组合图形分成两个长方形来计算它的面积是本题的关键,本题可用多种添加辅助线的方法解答。
6.有一块广告牌如图,工人叔叔准备给这块木板的一面刷上油漆,如果每平方米要用油漆0.6千克,那么共需要油漆多少千克?
【答案】3.024千克。
【分析】利用三角形的面积加上长方形的面积,求广告牌的面积,再乘0.6即可求出需要的油漆质量。
【解答】解:2.4×1.2÷2+2.4×1.5
=1.44+3.6
=5.04(平方米)
5.04×0.6=3.024(千克)
答:共需要油漆3.024千克。
【点评】本题属于求组合图形面积的问题,这种类型的题目主要明确组合图形是由哪些基本的图形构成的,然后看是求几种图形的面积和还是求面积差,然后根据面积公式解答即可。
7.如图是一个长方形广场,长是16米,宽是10米,中间铺了一条平行四边形石子路(图中阴影部分),其余是草地,那么草地的面积有多大?
【答案】128平方米。
【分析】根据题意可知,把小路两边的草地通过平移转化为长16米,宽(10﹣2)米的长方形,再根据长方形的面积公式解答即可。
【解答】解:16×(10﹣2)
=16×8
=128(平方米)
答:草地部分面积是128平方米。
【点评】此题主要考查长方形的面积公式的灵活运用,解答关键是明确:小路两边的草地通过平移转化为一个长方形,根据长方形的面积公式解答。
8.如图,工人师傅要铺一块长方形草坪,宽是12米,中间铺了一条石子路,路的面积是40平方米。那么草坪部分面积有多大?如果每平方米草坪8.5元,铺这个草坪需要多少钱?
【答案】200平方米;1700元。
【分析】利用平行四边形面积公式,用路的面积除以2,求平行四边形的高(长方形的宽),再用长方形面积公式:S=ab,计算草坪部分的面积;再乘8.5元求总钱数。
【解答】解:40÷2×(12﹣2)
=20×10
=200(平方米)
200×8.5=1700(元)
答:草坪部分面积有200平方米;铺这个草坪需要1700元。
【点评】本题属于求组合图形面积的问题,这种类型的题目主要明确组合图形是由哪些基本的图形构成的,然后看是求几种图形的面积和还是求面积差,然后根据面积公式解答即可。
9.兰兰在一张边长1.7分米的正方形纸上设计了一个箭头标志(如图涂色部分)。算一算,这个箭头标志的面积是多少平方分米?
【答案】0.72平方分米。
【分析】通过观察图形可知,这个箭头标志的面积等于大正方形的面积减去空白部分两个三角形的面积和小正方形的面积,根据正方形的面积公式:S=a2,三角形的面积公式:S=ah÷2,把数据代入公式解答。
【解答】解:1.7分米=17厘米
17﹣8=9(厘米)
17×17﹣9×17÷2×2﹣8×8
=289﹣153÷2×2﹣64
=289﹣153﹣64
=136﹣64
=72(平方厘米)
72平方厘米=0.72平方分米
答:这个箭头标志的面积是0.72平方分米。
【点评】此题主要考查正方形的面积公式、三角形的面积公式的灵活运用,关键是熟记公式。
10.如图,在长为50米,宽为42米的长方形草坪上修筑了宽为2米的小路,余下部分种花草。种花草的面积是多少平方米?
【答案】1920平方米。
【分析】种花草的面积是长方形草坪的面积去掉小路的面积。小路横拼成长为50米,宽为2米的长方形,竖拼成长为42米,宽为2米的长方形,再加上两条路重叠部分的面积。
【解答】解:50×42﹣(50×2+42×2)+2×2
=2100﹣184+4
=1920(m2)
答:种花草的面积是1920平方米。
故答案为:1920平方米。
【点评】本题考查了学生对长方形面积的掌握,以及学生的观察能力。
11.某小区广场有一块长20米、宽15米的长方形绿化带,中间留出宽度为2米的长方形种植玫瑰花,其余种草坪(如图),草坪的面积是多少平方米?
【答案】270平方米。
【分析】草坪的面积等于长(20﹣2)米、宽15米的长方形的面积,据此解答。
【解答】解:(20﹣2)×15
=18×15
=270(平方米)
答:草坪的面积是270平方米。
【点评】本题主要考查组合图形的面积,关键利用转化思想,把不规则图形转化为规则图形,再计算。
12.如图是墙面示意图,砌这面墙平均每平方米需用砖170块,这面墙一共要用多少块砖?
【答案】7820块。
【分析】先计算图形的面积,图形的面积=长方形的面积+三角形的面积,长方形的面积=长×宽,三角形的面积=底×高÷2;最后用面积乘每平方米需用砖的块数,据此解答。
【解答】解:5×8+8×1.5÷2
=40+6
=46(m2)
46×170= 7820(块)
答:一共要用7820块砖。
【点评】本题考查了长方形、三角形面积公式的灵活运用。
13.学校有一块劳动基地(如图所示),其中空白部分种茄子,阴影部分种白菜。每棵茄子占地0.2平方米。
(1)茄子一共可以种多少棵?
(2)种白菜的部分是多少平方米?
【答案】(1)4000棵;
(2)1500平方米。
【分析】(1)茄子地是一块三角形地,三角形的面积=底×高÷2,据此求出茄子地的面积,再除以每棵茄子的占地面积即可。
(2)三角形的面积=底×高÷2,据此求出阴影部分的面积即可。
【解答】解:(1)40×40÷2÷0.2
=800÷0.2
=4000(棵)
答:茄子一共可以种4000棵。
(2)75×40÷2
=3000÷2
=1500(平方米)
答:种白菜的部分是1500平方米。
【点评】本题考查了三角形面积公式的灵活运用。
14.王大爷家有一块梯形菜地,一条新修的水渠穿过这块菜地(如图),若每平方米菜地一年收入10元,那么王大爷家的这块菜地一年可给他家带来多少收入?
【答案】2800元。
【分析】先求出梯形的面积,其上底是23﹣3=20(米),下底是18﹣3=15(米),高是16米。然后用梯形的面积乘上每平方米菜地的收入10元,即可解题。
【解答】解:梯形面积:
23﹣3=20(米)
18﹣3=15(米)
(20+15)×16÷2
=35×8
=280(平方米)
280×10=2800(元)
答:王大爷家的这块菜地一年可给他家带来2800元收入。
【点评】本题主要考查了组合图形的面积,解题的关键是熟练掌握梯形的面积公式。
15.如图,阴影A的面积比阴影B的面积大7cm2,三角形CDE的面积是多少平方厘米?
【答案】150。
【分析】根据图示可知三角形的面积等于B的面积,加上空白部分的面积;半圆的面积等于阴影A的面积加上空白部分面积,所以三角形CDE的面积等于半圆的面积减去7平方厘米。利用圆的面积公式:S=πr2,计算即可。
【解答】解:3.14×(20÷2)2÷2﹣7
=3.14×100÷2﹣7
=157﹣7
=150(平方厘米)
答:三角形CDE的面积是150平方厘米。
【点评】本题主要考查组合图形的面积,关键是把不规则图形转化为规则图形,计算即可。
16.如图是学校花园一块绿化带的平面图,阴影部分表示植草的面积。每个正方形的边长是5米。
(1)这个绿化带的面积是多少平方米?
(2)下面有不同草皮每平方米的单价,请选择你喜欢的一款给这个绿化带铺草,计算需要花多少钱?
【答案】62.5平方米,187.5元。
【分析】(1)这个绿化带是一个梯形,上底为5×4=20米,下底5米,高5米,利用梯形面积公式即可求出。
(2)选择玉龙草给这个绿化带铺草,利用单价×面积=总价,即可求出(答案不唯一)。
【解答】(1)5×4=20(米)
(20+5)×5÷2=62.5(平方米)
答:这个绿化带的面积是62.5平方米。
(2)选用玉龙草给这个绿化带铺草
62.5×3=187.5(元)
答:选用玉龙草给这个绿化带铺需要187.5元。
【点评】本题考查求梯形面积公式的灵活应用,以及利用梯形面积解决实际问题。
17.金湾区某学校开始劳动教育课程,规划了一块实践基地,形状如图所示,分别种了白萝卜、洋葱和黄瓜,求这块地的面积共有多少平方米?
【答案】21平方米。
【分析】根据图示,白萝卜、洋葱和黄瓜的面积之和是一个上底2.2+2.6+3=7.8(米),下底3.6+2.6=6.2(米),高3米的梯形的面积,根据梯形的面积公式解答即可。
【解答】解:上底:2.2+2.6+3=7.8(米)
下底:3.6+2.6=6.2(米)
面积:(7.8+6.2)×3÷2
=14×3÷2
=21(平方米)
答:这块地的面积共有21平方米。
【点评】本题考查了梯形面积公式的灵活运用知识,结合题意分析解答即可。
18.学校修整好的操场跑道的形状与大小如图。两边是半圆形,中间是长方形,如果同学们绕操场边缘跑1圈,这1圈是多少米?
【答案】162.8米。
【分析】根据题意,可知求出这个运动场的跑道的周长,就可以求出绕运动场的边线跑一圈的路程。由题意可知,两边是圆周长的一半,合起来正好是一个圆的周长,再加上长方形的两个长,就是这个运动场跑道的周长。
【解答】解:3.14×20+50+50
=62.8+100
=162.8(米)
答:这1圈是162.8米。
【点评】此题主要考查圆的周长公式、以及对周长的理解,关键是熟记公式。
19.观察下列乘法算式,你有什么发现?
①
1×2=2
2×2=4
3×2=6
4×2=8
5×2=10
6×2=12
7×2=14
8×2=16
9×2=18
两个数相乘,一个因数不变,另一个因数乘几,积也乘几。
②
1×4=4
2×4=8
3×4=12
4×4=16
5×4=20
6×4=24
7×4=28
8×4=32
9×4=36
两个数相乘,一个因数不变,另一个因数乘几,积也乘几。
③
1×7=7
2×7=14
3×7=21
4×7=28
5×7=35
6×7=42
7×7=49
8×7=56
9×7=63
两个数相乘,一个因数不变,另一个因数乘几,积也乘几。
④
1×9=9
2×9=18
3×9=27
4×9=36
5×9=45
6×9=54
7×9=63
8×9=72
9×9=81
两个数相乘,一个因数不变,另一个因数乘几,积也乘几。
【答案】两个数相乘,一个因数不变,另一个因数乘几,积也乘几。
【分析】根据观察四组算式,第一个因乘几,第二个因数不变,同时积也乘几。
【解答】解:发现:两个数相乘,一个因数不变,另一个因数乘几,积也乘几。
故答案为:两个数相乘,一个因数不变,另一个因数乘几,积也乘几。
【点评】通过观察,分析、归纳发现其中的规律,并应用发现的规律解决问题是应该具备的基本能力。
20.阳光小学有一块劳动基地(如图),今年学校计划A地种萝卜,B地种白菜,C地种青椒。
(1)如果种青椒的面积是20平方米,那么种萝卜的面积是多少平方米?
(2)如果每平方米能收白菜27kg,那么B地能收白菜多少千克?
【答案】(1)48平方米,(2)1296千克。
【分析】对于(1),依据C地青椒的面积和底求出C地的高即A地的高,即三角形高=面积×2÷底,再利用梯形面积=(上底+下底)×高÷2计算即可;
对于(2),先利用平行四边形面积=底×高求出B地面积,再乘27即可解答。
【解答】解:(1)20×2÷5
=40÷5
=8(m)
(3+9)×8÷2
=12×8÷2
=96÷2
=48(m2)
答:种萝卜的面积是48平方米。
(2 )6×8=48(m2)
48×27=1296(kg)
答:B地收白菜1296千克。
【点评】本题主要考查了三角形、梯形、平行四边形面积公式的应用,熟练掌握三角形、梯形、平行四边形面积公式是解答本题的关键。
21.如图是王叔叔家的一面墙.如果砌这面墙平均每平方米用砖90块,一共需要用多少块砖?
【答案】见试题解答内容
【分析】先依据三角形面积公式S=ah÷2和长方形的面积公式S=ab求出这面墙的面积,再乘每平方米需要的砖的块数,问题即可得解.
【解答】解:(6×2÷2+7.5×6)×90
=51×90
=4590(块)
答:一共需要4590块砖.
【点评】本题属于求组合图形面积的问题,这种类型的题目主要明确组合图形是由哪些基本的图形构成的,然后看是求几种图形的面积和还是求面积差,然后根据面积公式解答即可.
22.兴滨农业园区有一块梯形稻田,因需要被一条宽2.5米的小路分成两部分(如图)。
(1)修路后,这块稻田的实际面积是多少?
(2)如果一台收割机每分钟能收割210平方米,收割完这块稻田需要多长时间?
【答案】(1)22200平方米;(2)105.71分钟。
【分析】(1)根据题意,可用梯形的面积公式计算出梯形水稻田的面积,然后再用梯形的面积减去小路的面积即可;
(2)根据题意,可用实际种植的稻田面积除以210进行计算即可。
【解答】解:(1)(125+250)×120÷2﹣2.5×120
=22500﹣300
=22200(平方米)
答:稻田的实际面积是22200平方米。
(2)22200÷210≈105.71(分钟)
答:收割完这块稻田需要105.71分钟。
【点评】此题主要考查的是梯形面积公式和长方形面积公式的灵活应用。
23.探索与发现:奇思在乘法口诀表上发现一组有趣的算式,如:
(1)根据上面这组乘法算式的特点,在右边横线上再写一组这样的算式 7×7=49
6×8=48
5×9=45
4×10=40
3×11=33(答案不唯一) 。
(2)观察上述这两组算式,你发现乘数怎样变化会引起积怎样变化?
(3)奇思发现6×6和5×7之间的规律可以用字母表示出来,下面正确的是 C 。
A.(a+1)×(a﹣1)=a2+1
B.(a+1)×(a﹣1)=a2
C.(a+1)×(a﹣1)=a2﹣1
D.(a+2)×(a﹣2)=a2+2
(4)根据上面发现的规律,如果2022×2022=4088484,则2021×2023= 4088483 。
【答案】(1)7×7=49
6×8=48
5×9=45
4×10=40
3×11=33(答案不唯一)
(2)两个相同的因数相乘,如果一个因数加n,另一个因数减n,积就等于因数的平方减n2。
(3)C;(4)4088483。
【分析】根据算式的规律,可以发现:
6×6和5×7之间的规律可以用字母表示出来:(a+1)×(a﹣1)=a2﹣1;
6×6和4×8之间的规律可以用字母表示出来:(a+2)×(a﹣2)=a2﹣22;
6×6和3×9之间的规律可以用字母表示出来:(a+3)×(a﹣3)=a2﹣32;
据此结合题意解答即,
【解答】解:(1)根据上面这组乘法算式的特点,在右边横线上再写一组这样的算式:
7×7=49
6×8=48
5×9=45
4×10=40
3×11=33(答案不唯一)
(2)观察上述这两组算式,发现:两个相同的因数相乘,如果一个因数加n,另一个因数减n,积就等于因数的平方减n2。
(3)奇思发现6×6和5×7之间的规律可以用字母表示出来,下面正确的是(a+1)×(a﹣1)=a2﹣1,所以选C。
(4)根据上面发现的规律,如果2022×2022=4088484,则:
2021×2023
=2022×2022﹣1
=4088484﹣1
=4088483
故答案为:(1)7×7=49
6×8=48
5×9=45
4×10=40
3×11=33(答案不唯一)
(3)C;(4)4088483。
【点评】本题考查了式的规律知识,结合题意分析解答即可。
24.如图是育才小学的运动场。两头是半圆,中间是长75 米。宽60米的长方形,这个运动场的占地面积是多少平方米?
【答案】7326平方米。
【分析】运动场的占地面积=半径为(60÷2)米的圆的面积+长为75米、宽为60米的长方形的面积,根据圆的面积公式:S=πr ,长方形面积=长×宽,代入数据求解即可。
【解答】解:3.14×(60÷2) +75×60
=2826+4500
=7326(平方米)
答:这个运动场的占地面积是7326平方米。
【点评】本题主要考查组合图形的面积,关键把组合图形转化为规则图形,利用规则图形的面积公式做题。
25.今年7月1日起,上海正式实施垃圾分类。如图是可再生资源回收亭的一面墙,它的面积是多少?
【答案】23。
【分析】根据图示,该回收亭的面积等于一个三角形的面积加上一个长方形的面积,利用三角形面积公式:S=ah÷2,长方形面积:S=ab,计算即可。
【解答】解:4×5+5×1.2÷2
=20+3
=23(平方米)
答:它的面积是23平方米。
【点评】解答求组合图形的面积,关键是观察分析图形是由那几部分组成的,是求各部分的面积和、还是求各部分的面积差,再根据相应的面积公式解答。
26.李大伯家有块平行四边形的空地,现在李大伯要在这块地上种花生和大豆(如图所示)。这块地中,种大豆的面积是多少平方米?
【答案】36.52平方米。
【分析】根据图示,种大豆的面积是三角形的面积,利用三角形面积公式:S=ah÷2,计算即可。
【解答】解:(15.4﹣6.6)×8.3÷2
=8.8×8.3÷2
=36.52(平方米)
答:种大豆的面积是36.52平方米。
【点评】本题主要考查组合图形的面积,关键利用三角形面积公式计算。
27.乐乐准备粉刷狗屋的前墙(如图中的阴影部分),粉刷的面积一共多少平方米?
【答案】2800平方米。
【分析】粉刷的面积等于三角形面积加上大长方形的面积,减去小长方形的面积,利用三角形面积公式:S=ah÷2,长方形面积公式:S=ab计算即可。
【解答】解:50×20÷2+50×70﹣40×30
=500+3500﹣1200
=2800(平方米)
答:粉刷的面积一共2800平方米。
【点评】本题主要考查组合图形的面积,关键是利用规则图形的面积公式计算。
28.如图,有一面墙,如果砌墙时每平方米用砖200块,砌这面墙一共要用多少块砖?
【答案】见试题解答内容
【分析】先求这面墙的面积,墙的面积等于长8米,宽4米的长方形面积加底为8米,高为2米的三角形面积,根据长方形面积计算公式“S=ab”、三角形面积计算公式“S=ah÷2”即可解答.然后再求用砖的块数,用每平米用砖的块数乘墙的面积.
【解答】解:8×4+8×2÷2
=32+8
=40(平方米)
200×40=8000(块)
答:砌这面墙一共要用8000块砖.
【点评】计算不规则图形的面积关键是把不规则图形转化成若干个规则图形,再根据规则图形的面积计算公式解答.
29.校园内有一个块半径为8分米的圆形宣传板,要在这块圆形的宣传板上圈出一个最大的正方形用于粘贴学生作品,其他地方作装饰用,请问作装饰的区域面积有多大?
【答案】72.96平方分米。
【分析】作装饰的区域面积等于圆的面积减去4个三角形的面积。利用圆的面积公式:S=πr ,三角形的面积公式:S=ah÷2,计算即可。
【解答】解:3.14×8 ﹣8×8÷2×4
=200.96﹣128
=72.96(平方分米)
答:作装饰的区域面积有72.96平方分米。
【点评】本题属于求组合图形面积的问题,这种类型的题目主要明确组合图形是由哪些基本的图形构成的,然后看是求几种图形的面积和还是求面积差,然后根据面积公式解答即可。
30.如图是教室的一面墙,如果粉刷这面墙每平方米用油漆0.75kg,粉刷这面墙至少要弄油漆多少千克?(得数保留一位小数)
【答案】18.375千克。
【分析】这面墙的面积=三角形的面积+长方形的面积,三角形面积=底×高÷2,长方形的面积=长×宽,代入公式计算即可求得墙的面积。最后用墙的面积乘0.75,即可求得。
【解答】解:5×1.2÷2+5×4.3
=3+21.5
=24.5(平方米)
24.5×0.75=18.375(千克)
答:粉刷这面墙至少要弄油漆18.375千克。
【点评】本题的关键是求出墙的面积。墙的面积可看作是两个规则图形的面积之和。
31.如图,一枚半径为1cm的游戏币在边长为6cm的正方形区域内任意移动。在正方形区域内游戏币不能到达的部分的面积是多少平方厘米?
【答案】0.86平方厘米。
【分析】游戏币不能到达的部分等于边长是1×2厘米的正方形面积减去半径是1厘米的圆的面积。
【解答】解:(1×2)×(1×2)﹣3.14×1
=4﹣3.14
=0.86(平方厘米)
答:在正方形区域内游戏币不能到达的部分的面积是0.86平方厘米。
【点评】本题属于求组合图形面积的问题,根据正方形和圆点面积公式解答即可。
32.花海公园一块长30米,宽20米的向日葵田里铺上了两条宽1米的小路,这块花田种上向日葵的面积是多少平方米?
【答案】551平方米。
【分析】根据题意,这块花田的实际种植面积就是把这块田的4部分通过上下平移、左右平移得到一个长为(30﹣1)米、宽为(20﹣1)米的长方形的面积,据此列式解答。
【解答】解:(30﹣1)×(20﹣1)
=29×19
=551(平方米)
答:这块花田种上向日葵的面积是551平方米。
【点评】此题主要考查长方形的面积公式的灵活运用,结合题意分析解答即可。
33.小芳家的客厅里挂了一幅正方形的十字绣作品(如图)圆形绣花部分的直径是1米,这幅十字绣空白部分的面积是多少平方米?
【答案】0.215平方米。
【分析】空白部分的面积等于正方形的面积减去圆的面积,根据正方形的面积公式:S=a2,圆的面积公式:S=πr2,把数据代入公式解答。
【解答】解:1×1﹣3.14×(1÷2)2
=1﹣3.14×0.25
=1﹣0.785
=0.215(平方米)
答:这幅十字绣空白部分的面积是0.215平方米。
【点评】此题主要考查正方形的面积公式、圆的面积公式的灵活运用,关键是熟记公式。
34.如图,边长为6厘米和8厘米的两个正方形拼在一起,则图中空白部分面积是多少平方厘米?
【答案】82平方厘米。
【分析】
连接大正方形的对角线,则两个正方形的对角线平行,根据等底等高的三角形面积相等,所以阴影部分面积就等于小正方形面积的一半;由此求出阴影部分的面积,再用两个正方形的面积减去阴影部分的面积就是空白部分的面积,据此解答即可。
【解答】解:(6×6+8×8)﹣6×6÷2
=100﹣18
=82(平方厘米)
答:图中空白部分面积是82平方厘米。
【点评】此题考查组合图形的面积的计算方法,一般都是转化到规则图形中,利用面积公式计算解答。
35.如图是由两个正方形拼成的,小正方形的边长是4cm,大正方形的边长是8cm,那么涂色部分的面积是多少平方厘米?
【答案】24平方厘米。
【分析】阴影部分是上底4厘米、下底8厘米、高4厘米的梯形,利用梯形面积公式:S=(a+b)h÷2,计算即可。
【解答】解:(4+8)×4÷2
=12×4÷2
=24(平方厘米)
答:涂色部分的面积是24平方厘米。
【点评】本题主要考查组合图形的面积,关键利用规则图形的面积公式计算。
36.学校重新装修时,为每间教室配制了一个工具间(如图)。
(1)这个工具间有多少平方米?
(2)工具间的面积比教室小多少?
【答案】(1)6平方米;
(2)42平方米。
【分析】(1)利用三角形面积公式:S=ah÷2,计算工具间的面积;
(2)用教室的面积减去工具间的面积即可。
【解答】解:(1)2×6÷2=6(平方米)
答:这个工具间有6平方米。
(2)8×6﹣6
=48﹣6
=42(平方米)
答:工具间的面积比教室小42平方米。
【点评】本题主要考查平面图形的面积,关键利用长方形面积公式:S=ab,三角形面积公式:S=ah÷2,计算即可。
37.人民公园有1块梯形空地(如图所示),园内工作人员准备在这块地中划出1块三角形地来种兰花,种兰花的面积是28m2。这块空地的面积是多少?
【答案】98m2。
【分析】根据三角形的高=面积×2÷底,求出三角形的高即梯形和平行四边形的高,再确定梯形下底,根据梯形的面积=(上底+下底)×高÷2,列式解答即可。
【解答】解:28×2÷8
=56÷8
=7(米)
(10+8+10)×7÷2
=28×7÷2
=98(平方米)
答:这块空地的面积是98m2。
【点评】关键是掌握梯形和三角形面积公式。
38.如图,如果将这面墙的两部分都粉刷,每平方米粉刷需要12元。粉刷墙面一共需要多少元钱?
【答案】271.2元。
【分析】这面墙的面积等于梯形面积加上长方形面积,再减去小长方形面积;用粉刷面积乘12,计算所需钱数即可。
【解答】解:[(2+6)×1.6÷2+6×3﹣1.2×1.5]×12
=[6.4+18﹣1.8]×12
=22.6×12
=271.2(元)
答:粉刷墙面一共需要271.2元。
【点评】本题主要考查组合图形的面积的计算,关键利用规则图形的面积公式计算。
39.友谊公园的中心有一块长方形草坪,草坪里有一条宽1米的曲折小路。草坪的实际面积有多大?
【答案】99平方米。
【分析】两块草坪可以拼成一块长方形,长方形的长是12﹣1=11(米),长方形的宽是10﹣1=9(米),根据长方形面积=长×宽计算即可出草坪的面积。
【解答】解:(12﹣1)×(10﹣1)
=11×9
=99(平方米)
答:草坪的实际面积是99平方米。
【点评】本题考查组合图形的面积,剪拼法是计算组合图形面积的常用方法。
40.一位菜农在如图所示中的梯形菜地中划出一块平行四边形地种青菜。如果剩下的地种萝卜,萝卜地有多少平方米?
【答案】80平方米。
【分析】从图可知剩下的三角形种植的是萝卜,根据三角形的面积公式 S=ah÷2,即可求出。
【解答】解:30﹣22=8(米)
8×20÷2
=160÷2
=80(平方米)
答:萝卜地有80平方米。
【点评】此题主要考查三角形的面积公式 S=ah÷2的灵活运用,关键是熟记公式。
41.如图是一块草坪的平面图,这块草坪的面积是多少平方米?
【答案】1900平方米。
【分析】草坪的面积等于两个长方形面积的和,利用长方形面积公式:S=ab计算即可。
【解答】解:25×(40+15)+35×15
=1375+525
=1900(平方米)
答:这块草坪的面积是1900平方米。
【点评】本题主要考查组合图形的面积的计算,关键利用规则图形的面积公式计算。
42.如图中阴影长方形ABCD的周长为16厘米(长方形的长、宽均为整数),在它的每条边上各画一个以该边为边长的正方形。已知这四个正方形的面积和是68平方厘米,那么长方形ABCD的面积是平方厘米?
【答案】15平方厘米。
【分析】根据长方形的周长公式“周长=(长+宽)×2”可知,长方形ABCD的周长除以2就是长方形ABCD的长、宽之和,即长+宽=16÷2=8(厘米);根据正方形的面积计算公式“S=a2”,长方形ABCD的长的平方就是一个较大正方形的面积,宽的平方是较小的一个正方形的面积,一个较大正方形面积与一个较小正方形面积之和是四个正方形面积的一半,即68÷2=34(平方厘米)。根据长+宽=8,长2+宽2=34,即可推出长方形的长、宽,再根据长方形的面积计算公式“S=ab”求出长方形ABCD的面积。
【解答】解:长+宽:16÷2=8(厘米)
长2+宽2:68÷2=34(平方厘米)
8=7+1=6+2=5+3=4+4
只有52+32=34
所以长方形ABCD的长为5厘米,宽为3厘米;
面积:5×3=15(平方厘米)
答:长方形ABCD的面积是15平方厘米。
【点评】关键明白长方形的长的平方是一个较大正方形面积,宽的平方是一个较小正方形的面积。而一个大正方形面积与一个小正方形面积是四个正方形面积的一半,即34平方厘米,由长方形的周长可求出长方形的长、宽之和为8厘米,据此即可找出符合题意的长方形的长、宽,进而求出长方形的面积。
43.一块梯形地中间有一条宽1m的长方形水渠穿过(如图),其他地方种菜。这块地种菜部分的面积是多少平方米?
【答案】190平方米。
【分析】由题意可知:菜地的面积=梯形的面积﹣长方形水渠的面积,将数据代入梯形面积公式:S=(a+b)×h÷2、长方形的面积公式:S=ab计算即可。
【解答】解:(30+10)×10÷2﹣1×10
=400÷2﹣1×10
=200﹣10
=190(平方米)
答:这块地种菜部分的面积是190平方米。
【点评】本题主要考查梯形的面积公式,牢记公式是解题的关键。
44.如图,在长方形中有三个大小相等的圆,已知这个长方形的长是18厘米,这个长方形的周长是多少?阴影的面积是多少?
【答案】这个长方形的周长是48厘米;阴影部分的面积是23.22平方厘米。
【分析】根据图示可知,长方形的长等于圆的直径的3倍;长方形的宽等于圆的直径。利用长方形的周长公式:C=(a+b)×2,圆的面积公式:S=πr2,长方形面积公式:S=ab,计算即可。
【解答】解:(18+18÷3)×2
=24×2
=48(厘米)
18×18÷3﹣3.14×(18÷3÷2)2×3
=108﹣84.78
=23.22(平方厘米)
答:这个长方形的周长是48厘米;阴影部分的面积是23.22平方厘米。
【点评】本题主要考查组合图形的面积的计算,关键是把不规则图形转化为规则图形再计算。
45.一种汽车上用的螺丝垫圈如图所示.这个垫圈的直径是20mm,中间有一个边长为8mm的正方形的孔.这个垫圈的面积是多少平方毫米?
【答案】见试题解答内容
【分析】这个垫圈的面积=圆的面积﹣正方形的面积,然后根据圆的面积公式:S=πr2,正方形的面积公式:S=a2,把数据代入公式解答即可.
【解答】解:3.14×(20÷2)2﹣8×8
=314﹣64
=250(平方毫米)
答:这个垫圈的面积是250平方毫米.
【点评】本题属于求组合图形面积的问题,这种类型的题目主要明确组合图形是由哪些基本的图形构成的,然后看是求几种图形的面积和还是求面积差,然后根据面积公式解答即可.
46.有一个运动场(如图),两边是半圆形,中间是长方形。请你计算这个运动场的周长和面积。
【答案】194.2米,2206.5平方米。
【分析】观察图形可知,这个运动场的周长等于直径30米的圆的周长与两条50米的直跑道的长度之和;这个运动场的面积等于直径30米的圆的面积与长50米、宽30米的长方形的面积之和,据此即可解答问题。
【解答】解:3.14×30+50×2
=94.2+100
=194.2(米)
3.14×(30÷2)2+50×30
=706.5+1500
=2206.5(平方米)
答:运动场的周长是194.2米,面积是2206.5平方米。
【点评】解答此题的关键是明确这个图形的周长和面积都包括哪几个部分,再利用公式计算即可解答。
47.春暖花开,光明小学“种植基地”(如图,单位:米)迎来了播种季。这块种植基地的面积是多少平方米?
【答案】1900平方米。
【分析】先分割图形并确定两个长方形的长和宽:观察图形,可以把这个种植基地分割成上下两个长方形,上面长方形的长是47﹣19=28(米),宽是19米;下面长方形的长是53+19=72(米),宽是19(米),根据长方形的面积计算公式分别算出两个长方形的面积,最后把结果加起来就是这个不规则图形的面积,计算时,可运用乘法分配律进行简算。
【解答】解:(47﹣19)×19+(53+19)×19
=28×19+72×19
=19×(28+72)
=19×100
=1900(平方米)
答:这块种植基地的面积是1900平方米。
【点评】本题考查了长方形的面积计算公式的灵活运用。
48.为了加强同学们的劳动意识和技能,光华小学开辟出一块劳动实践基地(如图)供同学们进行劳动实践。这块劳动基地的面积是多少平方米?
【答案】650平方米。
【分析】把所给图示分成两个长方形,利用长方形面积公式:S=ab计算即可。
【解答】解:如图(分法不唯一):
13×24+26×13
=13×(24+26)
=13×50
=650(平方米)
答:这块劳动基地的面积是650平方米。
【点评】本题主要考查不规则图形的面积,关键是把不规则图形转化为规则图形计算。
49.一块稻田的形状如图,如果每公顷施化肥300千克,这块稻田一共需要化肥多少千克?
【答案】1500千克。
【分析】先利用三角形面积公式:S=ah÷2,以及梯形面积公式:S=(a+b)h÷2,求这块稻田的面积,再乘300即可。注意单位要统一。
【解答】解:200×100÷2+(150+250)×200÷2
=10000+400×100
=10000+40000
=50000(平方米)
50000平方米=5公顷
5×300=1500(千克)
答:这块稻田一共需要化肥1500千克。
【点评】本题主要考查组合图形的面积,关键是把不规则图形转化为规则图形,再计算。
50.如图,在一张边长是10厘米的正方形纸中,剪去一个长6厘米、宽4厘米的长方形,剩下部分的面积是多少?剩下部分周长是多少?
【答案】76;48。
【分析】剩余部分的面积等于大正方形的面积减去长方形的面积;剩余部分的周长等于正方形的周长加上长方形的两条宽的长度。长方形面积公式:S=ab、正方形面积公式:S=a2。
【解答】解:面积:
10×10﹣4×6
=100﹣24
=76(平方厘米)
周长:
10×4+4×2
=40+8
=48(厘米)
答:剩下部分的面积是76平方厘米;剩下部分周长是48厘米。
【点评】本题主要考查组合图形的周长和面积,关键是把不规则图形转化为规则图形,再计算。
51.如图是一块长方形草地,长是18米,宽是10米。草地中间有两条交错的小路,一条是长方形,一条是平行四边形。草坪部分面积是多少平方米?
【答案】153平方米。
【分析】求草坪部分的面积,实际上就是求长为(18﹣1)米,宽为(10﹣1)米的长方形的面积,根据长方形的面积=长×宽,代入数据即可求解。
【解答】解:(18﹣1)×(10﹣1)
=17×9
=153(平方米)
答:草坪部分面积是153平方米。
【点评】解答此题的关键是:利用“压缩法”,将小路挤去,即可求出草地部分的面积。
52.曲妍将一张长方形纸的一角如图那样折叠,你能帮她求出涂色部分的面积吗?
(单位:dm)
【答案】见试题解答内容
【分析】根据图形折叠的方法可知,原来长方形的长是7厘米,宽是4厘米,则白色三角形的两条直角边分别是4厘米和7﹣4=3厘米,则图中阴影部分的面积=梯形的面积﹣白色三角形的面积,由此利用梯形和三角形的面积公式即可解答.
【解答】解:(4+7)×4÷2﹣4×(7﹣4)÷2
=11×2﹣4×3÷2
=22﹣6
=16(平方厘米)
答:阴影部分的面积是16平方厘米.
【点评】解答此题的关键是:根据长方形的折叠方法,得出梯形的上下底和高,以及三角形的两条直角边的长度.
53.如图:大三角形的空白部分是一个正方形,三角形甲与
三角形乙的面积和是39平方厘米。大三角形ABC的面积是
75 平方厘米。(提示:可以用拼一拼转化的方法,
也可以用方程。)
【答案】75。
【分析】利用旋转的方法把阴影部分拼成三角形,利用三角形面积公式计算正方形的边长(拼成的三角形的高)。再求三角形ABC的面积即可。
【解答】解:39×2÷(4+9)
=78÷13
=6(厘米)
(4+6)×(9+6)÷2
=10×15÷2
=75(平方厘米)
答:大三角形ABC的面积是75平方厘米。
故答案为:75。
【点评】本题属于求组合图形面积的问题,关键根据三角形面积公式解答即可。
54.有一剧场舞台设计如图。舞台的占地面积是多少?要在舞台边缘装上彩灯,至少需要多少米的彩灯线?
【答案】211.95平方米,65.1米。
【分析】先求大圆半径和小圆半径,再利用环形面积公式计算阴影部分的面积;阴影部分的周长等于大圆周长的一半加上小圆周长的一半,再加上2个9米的长。
【解答】解:(15﹣9)÷2
=6÷2
=3(米)
(15+9)÷2
=24÷2
=12(米)
3.14×122÷2﹣3.14×32÷2
=226.08﹣14.13
=211.95(平方米)
3.14×12+3.14×3+9×2
=37.68+9.42+18
=65.1(米)
答:阴影部分的面积是211.95平方米,至少需要65.1米的彩灯线。
【点评】本题主要考查组合图形的周长和面积,关键是利用圆环面积和圆的周长公式计算。
55.如图,王大叔把长方形分成了一个三角形地种花菜和一个梯形地种白菜。已知花菜面积比白菜面积少408平方米。求白菜种多少平方米。
【答案】684平方米。
【分析】根据图示,花菜面积和白菜面积的和是长方形的面积,利用和差问题公式:(和+差)÷2,计算白菜的种植面积即可。
【解答】解:(40×24+408)÷2
=(960+408)÷2
=1368÷2
=684(平方米)
答:白菜种了684平方米。
【点评】本题主要考查组合图形面积的计算,关键是利用和差问题公式解答。
56.礼堂的一面外墙有一个双扇门,示意图如下(单位:m)。现在要给墙面贴上小瓷砖,铺满每平方米需要60块砖,贴这面墙大约需要多少块砖?
【答案】3660块。
【分析】先用长方形面积加上三角形面积,减去小长方形面积,求铺砖的面积,再乘60,就是需要砖的块数。
【解答】解:6×10+10×1.2÷2﹣2×2.5
=60+6﹣5
=61(平方米)
61×60=3660(块)
答:贴这面墙大约需要3660块砖。
【点评】本题属于求组合图形面积的问题,这种类型的题目主要明确组合图形是由哪些基本的图形构成的,然后看是求几种图形的面积和还是求面积差,然后根据面积公式解答即可。
57.用两张同样大小的正方形白铁皮,边长是1.6m,分别按右面两种方式剪出不同规格的圆片。
(1)两种圆片中每个的周长分别是多少?
(2)剪完图后,哪张白铁皮剩下的废料多?
【答案】(1)5.024米,2.512米。
(2)一样多。
【分析】(1)首先根据题意,分别求出每种圆片的直径分别是多少;然后根据圆的周长=πd(d是圆的直径),求出两种圆片的周长分别是多少即可;
(2)首先根据题意,分别求出每种圆片的半径分别是多少;然后根据圆的面积=πr2(r是圆的半径),求出两种圆片的面积分别是多少;最后再用正方形的面积减去每种圆片的面积,求出剩下的废料的面积分别是多少,再比较大小,判断出哪张白铁皮剩下的废料多些即可。
【解答】解:(1)第一种圆片的周长是:
3.14×1.6=5.024(米)
第二种圆片中每个的周长是:
3.14×(1.6÷2)
=3.14×0.8
=2.512(米)
答:第一种圆片的周长是5.024米,第二种圆片的周长是2.512米。
(2)第一张白铁板剩下的废料的面积是:
1.6×1.6﹣3.14×(1.6÷2)2
=2.56﹣2.0096
=0.5504(平方米)
第二张白铁板剩下的废料的面积是:
1.6×1.6﹣3.14×(1.6÷2÷2)2×4
=2.56﹣2.0096
=0.5504(平方米)
所以两张白铁板剩下的废料一样多。
答:剪完圆后,两张白铁皮剩下的废料一样多。
【点评】此题主要考查了圆与组合图形问题的应用,解答此题的关键是熟练掌握圆的周长、面积公式。
58.李叔叔准备在这块地里种郁金香(如图),每棵郁金香占地0.25m2,这块地大约可种多少棵郁金香?
【答案】见试题解答内容
【分析】
如图:这块地的面积=长方形的面积+三角形的面积,根据三角形的面积=底×高÷2,长方形的面积=长×宽,计算出图形中三角形与长方形的面积和,即可求出这块地的面积;然后用这块地的面积除以每棵郁金香占地的面积,即可求出郁金香的棵数.
【解答】解:15×5+(12﹣5)×(15﹣5)÷2
=75+35
=110(平方米)
110÷0.25=440(棵)
答:这块地大约可种440棵郁金香.
【点评】本题属于求组合图形面积的问题,这种类型的题目主要明确组合图形是由哪些基本的图形构成的,然后看是求几种图形的面积和还是求面积差,然后根据面积公式解答即可.
59.为了美化校园,学校在一块梯形空地上种植了3种花,同时为了便于同学们观赏,修建了两条2米宽的小路,如图.种花的面积是多少?如果种每平方米花约要25元,那么种花一共需要多少元?
【答案】见试题解答内容
【分析】梯形面积减去小路的面积即为种花的面积,梯形的上底下底和高都已知,其面积就可求;小路属于平行四边形,高和底已知,则面积可求;每平方米的花费已知,则总花费就可求.
【解答】解:(12+20)×6÷2﹣2×6×2
=96﹣24
=72(平方米);
72×25=1800(元).
答:种花的面积是72平方米,一共需要1800元.
【点评】本题属于求组合图形面积的问题,这种类型的题目主要明确组合图形是由哪些基本的图形构成的,然后看是求几种图形的面积和还是求面积差,然后根据面积公式解答即可.
60.王师傅从一张正方形的白铁皮上剪掉一个三角形.求剩下的白铁皮(如图)的面积.
【答案】见试题解答内容
【分析】解答方法不唯一.可把这个图形分成一个长12分米,宽6分米的长方形、一个上底为6分米,下底为12分米,高为(12﹣6)分米的梯形.根据长方形面积计算公式“S=ab”、梯形面积计算公式“S=(a+b)h÷2”分别求出长方形、梯形的面积,再把二者相加.
【解答】解:如图
12×6+(6+12)×(12﹣6)÷2
=12×6+18×6÷2
=72+54
=126(dm2)
答:这个图形的面积是126dm2.
【点评】此题解答方法不唯一,也可以用12分米正方形的面积减两直角边都是(12﹣6)分米的直角三角形面积.
21世纪教育网(www.21cnjy.com)
