【期末专项培优】圆柱与圆锥应用题(含解析)-2024-2025学年六年级下册数学北师大版
文档属性
| 名称 | 【期末专项培优】圆柱与圆锥应用题(含解析)-2024-2025学年六年级下册数学北师大版 |

|
|
| 格式 | docx | ||
| 文件大小 | 827.6KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-05-08 00:00:00 | ||
图片预览




文档简介
圆柱与圆锥
1.如图1,这是一个由等底等高的圆柱和圆锥组合而成的计时工具,圆锥内灌满了有颜色水。其中圆锥的高为6厘米,底面半径为3厘米。已知水的流速是1.57立方厘米/分钟。
(1)圆锥内漏完水需要多少时间?
(2)请你在图2中用阴影表示出此时圆柱内的水。
2.用白铁皮制作一个高10分米,底面半径是2分米的圆柱形通风管,至少用铁皮多少平方分米?(得数保留整数)
3.一个圆柱体的侧面积是1cm2,体积是2cm3,它的底面积是多少平方厘米?
4.一个圆锥形沙堆底面周长是12.56米,高是3米,这个圆锥形沙堆的体积是多少?
5.一个无盖的圆柱形铁皮水桶,水桶内存有一些水,水面高度正好是桶高的,淘气将一块体积为628立方厘米的铁块放入水中,完全浸没。这时水面上升了2厘米,水桶正好装满。
(1)这个水桶的高是多少厘米?
(2)做这个水桶需要铁皮多少平方厘米?(铁皮的厚度和接口处忽略不计)
6.一根圆柱形铁棒,底面周长是12.56厘米,长是100厘米,它的体积是多少立方厘米?
7.有一个高8厘米,容积是50毫升的圆柱形容器,装满了水。将一个高6厘米的圆锥形铁块垂直放入水中,有水溢出。把圆锥形铁块从水中取出后,圆柱形容器内水的高度只有6厘米。求圆锥形铁块的体积是多少立方厘米?
8.一根长是20分米,底面直径是8分米的圆柱形木料横放入水中,正好有一半浮在水面上(如图)。
(1)这根木料露出水面部分的面积是多少平方分米?
(2)这根木料没入水中部分的体积是多少立方分米?
9.一个长方体木料,相交于同一个顶点的三条棱长度分别为12分米、8分米、16分米。
(1)这个长方体的体积是多少立方分米?
(2)如果把这个长方体加工成体积最大的圆柱,这个圆柱的体积是多少立方分米?
10.有一个底面直径为20厘米的装有一些水的圆柱形玻璃杯,已知杯中水面距杯口2.24厘米.若将一个半径为9厘米的圆锥形铅锤完全浸入水中,水会溢出314立方厘米.求铅锤的高.
11.一个圆锥体铁块,底面半径是5厘米,高比底面直径少,将这个圆锥体铁块放入到装有水的圆柱形容器中,完全浸没且没有水溢出,已知圆柱从里面量直径是20厘米,铁块放入后水面会上升多少厘米?
12.一个高为4分米的圆柱,把底面分成若干个相等的扇形,再竖直切开拼成一个近似的长方体,表面积增加了16平方分米,圆柱的体积是多少立方分米?(结果保留π)
13.沿着圆柱体的直径自上而下锯成2部分,表面积增加36平方厘米,高与底面直径的比是2:1,这个圆柱的体积是多少?
14.如图,把一个圆柱等分成若干等份,拼成一个近似的长方体,表面积增加了300平方厘米、已知长方体的高是20厘米。长方体的体积是多少?
15.在圆柱体的体积推导过程中,把一个圆柱体平均分成若干等份,然后拼成一个近似的长方体(材料无损耗),拼成的长方体的长是6.28厘米,高是5厘米,这个圆柱体的体积是多少立方厘米?
16.一个圆柱形储气罐,底面直径是16米,高是20米。
(1)它的体积是多少立方米?
(2)现在要在罐的顶面和侧面刷上油漆,如果每千克油漆只能刷4平方米,需要数油漆多少千克?(得数保留整千克)
17.一个圆柱形橡皮泥,底面周长是62.8cm,高是9cm。如果把它捏成底面直径是24cm的圆锥,这个圆锥的高是多少厘米?
18.向阳村要建一个圆柱形储水池.底面半径10米,深3米
(1)这个蓄水池的占地面积多少平方米?
(2)如果给这个蓄水池的四周和池底抹上水泥,抹水泥的面积是多少平方米?
(3)这个蓄水池能蓄水多少立方米?
19.一个圆柱形铁皮水桶(无盖),高15dm,底面直径是高的。做这个水桶大约要用多少铁皮?
20.妙想买了18块圆柱形橡皮泥,每块橡皮泥的底面直径是2cm,高是6cm。
(1)如果把其中一块橡皮泥捏成高是6cm的圆锥,圆锥的底面积是多少?
(2)妙想想用最少的硬纸板做一个长方体盒子(有盖)把18块橡皮泥装进去,做这个长方体盒子需要多少硬纸板?(粘贴处忽略不计)
21.一个圆锥形沙堆,底面半径2米,高1.2米,用这堆沙在10米宽的公路上铺2厘米的路面,能铺多少米?
22.小明把一个底面半径是3厘米的铁圆锥,放在从里面量半径是5厘米的圆柱形透明的玻璃容器内。小明把一瓶装有550毫升的纯净水倒入容器,这时水深正好与圆锥的高相等。圆锥的体积是多少?
23.一个底面周长25.12cm,高9cm的圆柱形钢块熔铸成一个底面直径12cm的圆锥,圆锥的高是多少厘米?
24.如图,一个圆柱高10厘米,如果它的高增加4厘米,那么它的表面积将增加50.24平方厘米,求原来圆柱的体积是多少立方厘米?
25.如果要焊制一个无盖的圆柱形水桶,有以下几种型号的铁皮供搭配选择。
你选择的铁皮型号是 号和 号(填序号),做这个水桶需要多少平方分米的铁皮?能装多少升水?(接口处忽略不计,圆周率取3.14)
26.把一根长5分米的圆钢截成4段后,表面积的总和比原来增加了113.04平方分米.求原来的圆钢的体积.
27.一个高为8分米的圆柱形木桶里,装了半桶水,把水倒出12升后,剩下的水恰好占水桶容积.这个水桶的底面积是多少平方分米?
28.一个圆柱形的汽油桶底面直径是8分米,高5分米.现装满汽油,如果每升汽油重0.85千克,这个油桶的汽油共多少千克?
29.在一个棱长为4厘米的正方体的前后.左右、上下各面的中心位置挖去一个底面半径为1厘米、高为1厘米的圆柱,则挖去后物体的表面积为多少?(圆周率取3.14计算)
30.古希腊著名的数学家阿基米德是历史上最杰出的数学家之一,在他众多的科学发现中,他自己最为满意的是:“圆柱容球定理”。如图,把一个球正好放在一个圆柱形容器中,球的直径与圆柱的高和底面直径相等,此时,球的体积正好是圆柱体积的,球的表面积也正好是圆柱表面积的。请你提一个富有挑战性的问题,并解答(请把此“圆柱容球”图片再画一下)
31.李师傅把一个正方体削成一个最大的圆锥体。正方体的体积是240立方分米,圆锥体的体积是多少立方分米?
32.在一个底面半径5厘米,高18厘米的圆柱形水桶内装满了水,另有一个圆锥形空水桶,它的上口周长为37.68厘米,现在把圆柱形水桶里的水往圆锥形水桶里倒,当圆锥形水桶装满时,圆柱形水桶还剩12厘米高的水,求圆锥形水桶的高。
33.张师傅想用一个底面直径为20厘米、高为40厘米的圆柱体木桩加工工艺品有以下几道工序:
工序1:截取一段圆柱体木桩削成最大的圆锥,使得圆锥的体积是1570立方厘米; 工序2:把圆锥和剩下的圆柱底面相接拼起来,在圆锥部分雕刻上花纹,圆柱部分涂上颜料。
请你帮张师傅算一算:
(1)截取的木桩有多高?
(2)拼接后,涂颜料的面积是多少平方厘米?
34.用一张长314cm、宽157cm的长方形纸围成一个圆柱体,有几种围法?计算一下,看看哪种围法体积大?
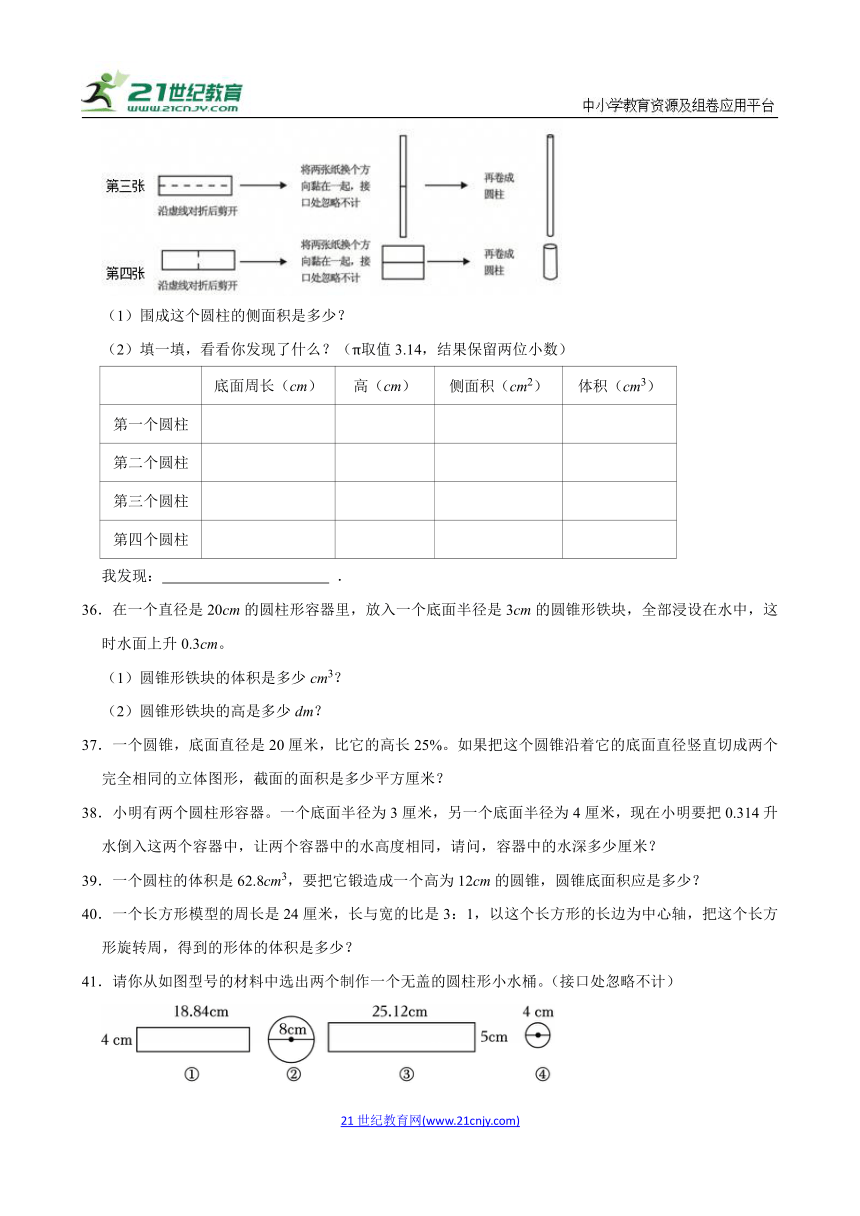
35.欣欣礼品店要用4张长18厘米,宽6厘米的长方形包装纸围成一个圆柱.第一张横着卷成圆柱,第二张竖着卷成圆柱,第三张和第四张围成的圆柱如图所示.
(1)围成这个圆柱的侧面积是多少?
(2)填一填,看看你发现了什么?(π取值3.14,结果保留两位小数)
底面周长(cm) 高(cm) 侧面积(cm2) 体积(cm3)
第一个圆柱
第二个圆柱
第三个圆柱
第四个圆柱
我发现: .
36.在一个直径是20cm的圆柱形容器里,放入一个底面半径是3cm的圆锥形铁块,全部浸设在水中,这时水面上升0.3cm。
(1)圆锥形铁块的体积是多少cm3?
(2)圆锥形铁块的高是多少dm?
37.一个圆锥,底面直径是20厘米,比它的高长25%。如果把这个圆锥沿着它的底面直径竖直切成两个完全相同的立体图形,截面的面积是多少平方厘米?
38.小明有两个圆柱形容器。一个底面半径为3厘米,另一个底面半径为4厘米,现在小明要把0.314升水倒入这两个容器中,让两个容器中的水高度相同,请问,容器中的水深多少厘米?
39.一个圆柱的体积是62.8cm3,要把它锻造成一个高为12cm的圆锥,圆锥底面积应是多少?
40.一个长方形模型的周长是24厘米,长与宽的比是3:1,以这个长方形的长边为中心轴,把这个长方形旋转周,得到的形体的体积是多少?
41.请你从如图型号的材料中选出两个制作一个无盖的圆柱形小水桶。(接口处忽略不计)
(1)选择的型号是 (填序号),这个水桶的底面积是 cm2。
(2)制作这个小水桶,一共需要多少平方厘米的铁皮?
(3)往这个小水桶中注水,水面上升到水桶高的处,这时水桶中水的体积是多少毫升?
42.一只底面半径是10cm的圆柱形瓶中,水深8cm,在瓶中放入长和宽都是8cm、高是15cm的一块长方体铁块,把铁块竖直放在水中,水面上升了几厘米?
43.一个圆柱形容器和一个圆锥形容器等底等高,圆柱形容器内原有12升水,现将圆锥形容器盛满水再全部倒入圆柱形容器,则圆柱形容器内水面上升到处。圆柱形容器的容积是多少?
44.一个圆柱形水桶装满水,把桶里的水倒出后,还剩下12升。水桶的高为5分米,水桶的底面积是多少平方分米?(水桶壁的厚度忽略不计)
45.一个直角三角形,一条直角边长6厘米,另一条直角边长4厘米,以它的较长的直角边为轴旋转一周后形成一个立体图形.求这个旋转后立体图形的体积.
46.一个从里面量底面直径为20cm的圆柱形容器中装有一部分水,在水中浸没一个底面直径为12cm的圆锥形铅锤,这时水面高度是15cm,当把铅锤从容器中取出后,容器中的水面高度下降到13.8cm。这个铅锤的高是多少厘米?
47.一个底面周长是25.12cm,高是18cm的圆柱形玻璃缸中有一些水,把一个底面半径是3cm的圆锥形铁块浸没在水中(水未溢出),缸内水面上升了1.5cm,圆锥形铁块的高是多少?
48.一个圆锥形零件,底面积是170平方厘米,高是12厘米。这个零件的体积是多少立方厘米?
49.广汉市某校六年级一班张敏敏购买了一个底面直径10厘米,高12厘米的圆柱形水杯。为了使水杯更加美观,她在水杯的侧面贴上了一圈彩纸,至少需要多少平方厘米的彩纸(接头处忽略不计)?她先往水杯里倒入628mL水,再把一个高为6厘米的圆锥形玩具,完全浸没在水中,这时水面上升0.8厘米,这个圆锥形玩具的底面积是多少平方厘米?
50.一张长方形铁皮,长18.84dm,宽6dm,用这张铁皮卷成一个圆柱形铁皮水桶的侧面,另配一个底面制成一个最大的水桶。这个铁皮水桶的表面积是多少dm2?水桶的容积是多少?
51.一个圆锥形沙堆,底面周长是25.12米,高1.8米.如果每立方米沙重1.7吨,这堆沙子重多少吨?
52.把一个底面直径20厘米的圆柱切拼成一个近似的长方体,长方体表面积比圆柱表面积多400平方厘米。圆柱的体积是多少立方厘米?
53.将一个底面半径是4厘米,高是9厘米的实心圆柱形铁块,锻造成一个底面半径是8厘米的实心圆锥形铁块,这个圆锥形铁块的高是多少厘米?
54.如图是一个无盖的长方体玻璃容器,水面的高度是8cm。把一个底面半径是4cm的圆锥形铅锤完全浸入水中,水面上升了0.628cm,这个铅锤的高是多少厘米?
55.如图,用一张长165.6厘米的铁皮,剪下一个最大的圆作为圆柱的底面,剩下的部分围在底面上做成一个无盖的铁皮水桶,算一算这个铁皮水桶的容积是多少?(铁皮厚度不计,π取3.14)
56.一种油菜籽榨油机的漏斗是由圆柱和圆锥两部分组成。底面周长是18.84dm,圆柱和圆锥的高都是6dm。每立方分米油菜籽重0.5kg。
(1)这个漏斗最多能装多少千克油菜籽?
(2)如果油菜籽的出油率是45%,一漏斗油菜籽能榨出多少千克菜籽油?
57.一个圆柱形容器从里面量底面直径是20cm,高是10cm,里面水深9cm,现在将一个底面半径是8cm,高是6cm的实心圆锥形铁块完全浸没在水中,这时,圆柱形容器中的水会溢出来吗?如果会溢出,则溢出多少mL?
58.在一个直径是20厘米的圆柱形容器里,放入一个底面半径2厘米的圆锥形铁块,全部浸没在水中,这时水面上升了0.3厘米。这个圆锥形铁块的高是多少厘米?
59.一个圆柱形玻璃杯,内直径为8厘米,内装16厘米深的水,恰好占杯子容量的,杯内还可以加入多少毫升的水?
60.一个圆锥体的体积是15.7立方分米,底面积是3.14平方分米,它的高有多少分米?
圆柱与圆锥
参考答案与试题解析
1.如图1,这是一个由等底等高的圆柱和圆锥组合而成的计时工具,圆锥内灌满了有颜色水。其中圆锥的高为6厘米,底面半径为3厘米。已知水的流速是1.57立方厘米/分钟。
(1)圆锥内漏完水需要多少时间?
(2)请你在图2中用阴影表示出此时圆柱内的水。
【答案】(1)36分钟;
(2)
【分析】(1)根据圆锥的体积公式:Vπr2h,把数据代入公式求出圆锥容器内水的体积,然后根据“包含”除法的意义,用除法解答。
(2)因为等底等等高的圆柱的体积是圆锥体积的3倍,所以当圆柱与圆锥的体积相等,底面积也相等时,圆柱的高是圆锥高的,据此解答即可。
【解答】解:(1)3.14×32×6÷1.57
3.14×9×6÷1.57
=56.52÷1.57
=36(分钟)
答:圆锥内漏完水需要36分钟。
(2)62(厘米)
答:圆柱容器内水深2厘米。
作图如下:
【点评】此题主要考查圆锥体积公式的灵活运用,等底等高的圆柱与圆锥体积之间的关系及应用。
2.用白铁皮制作一个高10分米,底面半径是2分米的圆柱形通风管,至少用铁皮多少平方分米?(得数保留整数)
【答案】见试题解答内容
【分析】求做圆柱形铁皮通风管用多少铁皮,就是求它的侧面积是多少,可直接利用底面周长乘高来解答,然后再选正确答案即可.
【解答】解:3.14×2×2×10
=12.56×10
=125.6
≈126(平方分米)
答:至少用铁皮126平方分米.
【点评】此题是考查求侧面积的实际应用,可利用侧面积公式解答.
3.一个圆柱体的侧面积是1cm2,体积是2cm3,它的底面积是多少平方厘米?
【答案】50.24平方厘米。
【分析】设底面半径为r,高为h,再根据圆柱的侧面积公式:S=πdh,圆柱的体积公式:V=πr2h,列出来两个方程求出半径和高,然后即可得出底面积。
【解答】解:设底面半径为r,高为h
r=4
3.14×4×4=50.24(平方厘米)
答:它的底面积是50.24平方厘米。
【点评】本题考查学生对圆柱表面积和体积公式的掌握和运用。
4.一个圆锥形沙堆底面周长是12.56米,高是3米,这个圆锥形沙堆的体积是多少?
【答案】见试题解答内容
【分析】沙堆的形状是圆锥形的,利用圆锥的体积计算公式解答,即圆锥的体积π(C÷π÷2)2h,把数据代入公式进行解答即可.
【解答】解:3.14×(12.56÷3.14÷2)2×3
3.14×22×3
=3.14×4
=12.56(立方米)
答:这个圆锥沙堆的体积是12.56立方米.
【点评】此题主要考查圆锥的体积计算公式Vπr2h,运用公式计算时不要漏乘.
5.一个无盖的圆柱形铁皮水桶,水桶内存有一些水,水面高度正好是桶高的,淘气将一块体积为628立方厘米的铁块放入水中,完全浸没。这时水面上升了2厘米,水桶正好装满。
(1)这个水桶的高是多少厘米?
(2)做这个水桶需要铁皮多少平方厘米?(铁皮的厚度和接口处忽略不计)
【答案】(1)20厘米;
(2)1570平方厘米。
【分析】(1)把水桶的高看作单位“1”,由题意可知,2厘米相当于水桶高的(1),根据已知一个数的几分之几是多少,求这个数,用除法解答。
(2)根据圆柱的体积公式:V=Sh,那么S=V÷h,据此可以求出水桶的底面积,进而求出水桶的底面半径,再根据圆柱的侧面积公式:S=πdh,圆的面积公式:S=πr2,把数据代入公式解答。
【解答】解:(1)2÷(1)
=2×10
=20(厘米)
答:这个水桶的高是20厘米。
(2)水桶的底面积:628÷2=314(平方厘米)
314÷3.14=100(平方厘米)
因为10的平方是100,所以水桶的底面半径是10厘米,
2×3.14×10×20+314
=62.8×20+314
=1256+314
=1570(平方厘米)
答:做这个水桶需要铁皮1570平方厘米。
【点评】此题主要考查圆柱的体积公式、圆柱的侧面积公式、圆的面积公式的灵活运用,关键是熟记公式。
6.一根圆柱形铁棒,底面周长是12.56厘米,长是100厘米,它的体积是多少立方厘米?
【答案】见试题解答内容
【分析】先根据圆的周长公式求出圆柱形铁棒的底面半径,继而求出圆的面积,再根据圆柱的体积公式V=sh求出它的体积.
【解答】解:12.56÷3.14÷2,
=4÷2,
=2(厘米);
3.14×22×100,
=3.14×4×100,
=3.14×400,
=1256(立方厘米).
答:它的体积是1256立方厘米.
【点评】此题是考查圆柱的体积计算,在利用体积公式V=sh求体积的过程中注意求得圆柱形铁棒的底面半径,从而得到圆柱形铁棒的体积.
7.有一个高8厘米,容积是50毫升的圆柱形容器,装满了水。将一个高6厘米的圆锥形铁块垂直放入水中,有水溢出。把圆锥形铁块从水中取出后,圆柱形容器内水的高度只有6厘米。求圆锥形铁块的体积是多少立方厘米?
【答案】12.5立方厘米。
【分析】首先根据圆柱的体积公式:V=Sh,那么S=V÷h,据此求出圆柱形容器的底面积;圆柱形容器装满了水。将一个高6厘米的圆锥形铁块垂直放入水中,有水溢出。把圆锥形铁块从水中取出后,圆柱形容器内水的高度只有6厘米,溢出水的体积就等于这个圆锥形铁块的体积,据此解答即可。
【解答】解:50毫升=50立方厘米
50÷8=6.25(平方厘米)
8﹣6=2(厘米)
6.25×2
=6.25×2
=12.5(立方厘米)
答:圆锥形铁块的体积12.5立方厘米。
【点评】此题主要考查圆柱体积公式的灵活运用,关键是熟记公式。
8.一根长是20分米,底面直径是8分米的圆柱形木料横放入水中,正好有一半浮在水面上(如图)。
(1)这根木料露出水面部分的面积是多少平方分米?
(2)这根木料没入水中部分的体积是多少立方分米?
【答案】(1)301.44平方米;
(2)502.4立方米。
【分析】(1)根据题意可知,这根木头与水接触面的面积等于这个圆柱表面积的一半,根据圆柱的表面积=侧面积+底面积×2,把数据代入公式求出它的表面积的一半即可。
(2)木头没入水里部分的体积是这个圆柱体积的一半,根据圆柱的体积公式:V=πr2h,把数据代入公式解答。
【解答】解:(1)3.14×8×20÷2+3.14×(8÷2)2
=502.4÷2+3.14×16
=251.2+50.24
=301.44(平方分米)
答:这根木头露出水面部分的面积是301.44平方分米。
(2)3.14×(8÷2)2×20÷2
=3.14×16×20÷2
=50.24×20÷2
=502.4(立方分米)
答:木头没入水里部分的体积是502.4立方分米。
【点评】此题主要考查圆柱的表面积公式、圆柱的体积公式的灵活运用,关键是熟记公式。
9.一个长方体木料,相交于同一个顶点的三条棱长度分别为12分米、8分米、16分米。
(1)这个长方体的体积是多少立方分米?
(2)如果把这个长方体加工成体积最大的圆柱,这个圆柱的体积是多少立方分米?
【答案】(1)1536立方分米
(2)904.32立方分米
【分析】(1)根据长方体的特征,相交于同一点的三条棱,就是长方体的长、宽、高相交于一点,由此可知长方体的长、宽、高的长度;根据长方体的体积公式:长×宽×高,代入数据,求出长方体体积;
(2)把长方体加工成圆柱,有3种方法,①以12分米为直径,高为8分米的圆柱;②以8分米为直径,高为16分米;③以8分米为直径,高为12分米;利用圆柱的体积公式:底面积×高,求出三种加工成的圆柱的体积,再比较大小,求出这个圆柱的最大体积是多少。
【解答】解:(1)12×8×16
=96×16
=1536(立方分米)
答:这个长方体的体积是1536立方分米。
(2)①以12分米为直径,以8分米为高:
体积:3.14×(12÷2)2×8
=3.14×36×8
=113.04×8
=904.32(立方分米)
②以8分米为直径,以16分米为高:
体积:3.14×(8÷2)2×16
=3.14×16×16
=50.24×16
=803.84(立方分米)
③以8分米为直径,高为12厘米:
体积:3.14×(8÷2)2×12
=3.14×16×12
=50.24×12
=602.88(立方分米)
904.32>803.84>602.88
这个圆柱的体积最大是904.32立方分米。
答:这个圆柱的体积是904.32立方分米。
【点评】利用长方体体积公式以及圆柱体积公式进行解答,关键明确长方体内切成最大的圆柱,有三种不同的切法,求最大体积需要求出三者切法的体积,进行比较解答。
10.有一个底面直径为20厘米的装有一些水的圆柱形玻璃杯,已知杯中水面距杯口2.24厘米.若将一个半径为9厘米的圆锥形铅锤完全浸入水中,水会溢出314立方厘米.求铅锤的高.
【答案】见试题解答内容
【分析】根据题意可知:圆柱形玻璃杯内没有水的部分(空的)体积加上放入圆锥形铅锤后溢出水的体积等于这个圆锥形铅锤的体积,根据圆柱的体积公式:V=Sh,求出没有水的体积,再根据圆锥的体积公式:VSh,那么h=VS,把数据代入公式解答.
【解答】解:3.14×(20÷2)2×2.24+314
=3.14×100×2.24+314
=703.36+314
=1017.36(立方厘米),
1017.36(3.14×92)
=1017.36×3÷254.34
=3052.08÷254.34
=12(厘米),
答:铅锤的高是12厘米.
【点评】此题主要考查圆柱、圆锥体积公式的灵活运用,关键是熟记公式.
11.一个圆锥体铁块,底面半径是5厘米,高比底面直径少,将这个圆锥体铁块放入到装有水的圆柱形容器中,完全浸没且没有水溢出,已知圆柱从里面量直径是20厘米,铁块放入后水面会上升多少厘米?
【答案】0.5厘米。
【分析】把圆锥的底面半径看作单位“1”,高比底面直径少,也就是高相当于底面直径的(1),根据一个数乘分数的意义,用乘法求出圆锥的高,再根据圆锥的体积公式:Vr2h,求出圆锥铁块的体积,然后根据圆柱的体积公式:V=πr2h,用圆锥铁块的体积除以圆柱形容器的底面积就是水面上升的高度。
【解答】解:圆锥的高:
5×2×(1)
=10
=6(厘米)
3.14×52×6÷[3.14×(20÷2)2]
3.14×25×6÷[3.14×100]
=157÷314
=0.5(厘米)
答:铁块放入后水面会上升0.5厘米。
【点评】此题主要考查圆锥、圆柱体积公式的灵活运用,关键是熟记公式,重点是求出圆锥的高。
12.一个高为4分米的圆柱,把底面分成若干个相等的扇形,再竖直切开拼成一个近似的长方体,表面积增加了16平方分米,圆柱的体积是多少立方分米?(结果保留π)
【答案】16π立方分米。
【分析】根据圆柱体积公式的推导过程可知,把一个圆柱切拼成一个近似长方体后,体积不变,拼成的近似长方体的表面积把圆柱的表面积增加了两个切面的面积,每个切面的长等于圆柱的高,每个切面的宽等于圆柱的底面半径,已知表面积增加了16平方分米,据此可以求出圆柱的底面半径,再根据圆柱的体积公式:V=πr2h,把数据代入公式解答。
【解答】解:底面半径:
16÷2÷4
=8÷4
=2(分米)
体积:
π×22×4
=π×4×4
=16π(立方分米)
答:圆柱的体积是16π立方分米。
【点评】此题考查的目的是理解掌握圆柱体积公式的推导过程及应用,长方体的表面积、圆柱的表面积的意义及应用。
13.沿着圆柱体的直径自上而下锯成2部分,表面积增加36平方厘米,高与底面直径的比是2:1,这个圆柱的体积是多少?
【答案】42.39立方厘米。
【分析】根据题意可知,把这个圆柱沿底面直径锯成两个半圆柱,表面积增加的两个截面的面积,每个截面的长等于圆柱的高,每个截面的宽等于圆柱的底面直径,已知高与底面直径的比是2:1,据此可以求出高和底面直径,然后根据圆柱的体积公式:V=πr2h,把数据代入公式解答。
【解答】解:36÷2=18(平方厘米)
18=6×3
所以圆柱的高是6厘米,底面直径是3厘米,
3.14×(3÷2)2×6
=3.14×2.25×6
=7.065×6
=42.39(立方厘米)
答:这个圆柱的体积是42.39立方厘米。
【点评】此题主要考查长方形的面积公式、圆柱的体积公式的灵活运用,关键是熟记公式,重点求出圆柱的高和底面直径。
14.如图,把一个圆柱等分成若干等份,拼成一个近似的长方体,表面积增加了300平方厘米、已知长方体的高是20厘米。长方体的体积是多少?
【答案】3532.5立方厘米。
【分析】根据圆柱体积公式的推导过程可知,把一个圆柱切拼成一个近似长方体,拼成的长方体的底面积等于圆柱的底面积,长方体的高等于圆柱的高,拼成的长方体的表面积比圆柱的表面积增加了两个截面的面积,每个切面的长等于圆柱的高,每个切面的宽等于圆柱的底面半径,已知表面积增加了300平方厘米,据此可以求出圆柱的底面半径,再根据圆柱的体积公式:V=πr2h,把数据代入公式解答。
【解答】解:300÷2÷20
=150÷20
=7.5(厘米)
3.14×7.52×20
=3.14×56.25×20
=176.625×20
=3532.5(立方厘米)
答:长方体的体积是3532.5立方厘米。
【点评】此题考查的目的是理解掌握圆柱体积公式的推导过程及应用,关键是求出圆柱的底面半径。
15.在圆柱体的体积推导过程中,把一个圆柱体平均分成若干等份,然后拼成一个近似的长方体(材料无损耗),拼成的长方体的长是6.28厘米,高是5厘米,这个圆柱体的体积是多少立方厘米?
【答案】见试题解答内容
【分析】根据圆柱体积公式的推导过程可知:把一个圆柱体平均分成若干等份,然后拼成一个近似的长方体(材料无损耗),拼成的长方体的长等于圆柱底面周长的一半,长方体的高等于圆柱的高,根据圆的周长公式:C=2πr,求出圆柱的底面半径,再根据圆柱的体积公式:V=πr2h,把数据代入公式解答.
【解答】解:6.28×2÷3.14÷2
=12.56÷3.14÷2
=4÷2
=2(厘米),
3.14×22×5
=3.14×4×5
=62.8(立方厘米),
答:这个圆柱的体积是62.8立方厘米.
【点评】此题主要考查圆的周长公式、圆柱的体积公式的灵活运用,关键是熟记公式.
16.一个圆柱形储气罐,底面直径是16米,高是20米。
(1)它的体积是多少立方米?
(2)现在要在罐的顶面和侧面刷上油漆,如果每千克油漆只能刷4平方米,需要数油漆多少千克?(得数保留整千克)
【答案】(1)4019.2平方米;
(2)302千克。
【分析】(1)根据圆柱的体积公式:V=πr2h,把数据代入公式解答。
(2)根据圆柱的侧面积公式:S=πdh,圆的面积公式:S=πr2,把数据代入公式求出刷油漆的面积,然后根据“包含”除法的意义,用除法解答。
【解答】解:(1)3.14×(16÷2)2×20
=3.14×64×20
=200.96×20
=4019.2(立方米)
答:它的体积是4019.2立方米。
(2)[3.14×16×20+3.14×(16÷2)2]÷4
=[50.24×20+3.14×64]÷4
=[1004.8+200.96]÷4
=1205.76÷4
≈302(千克)
答:需要油漆302千克。
【点评】此题主要考查圆柱的体积公式、圆柱的表面积公式的灵活运用,关键是熟记公式。
17.一个圆柱形橡皮泥,底面周长是62.8cm,高是9cm。如果把它捏成底面直径是24cm的圆锥,这个圆锥的高是多少厘米?
【答案】18.75厘米。
【分析】根据圆柱的体积公式:V=πr2h,圆锥的体积公式:Vr2h,那么h=Vπr2,把数据代入公式解答。
【解答】解:3.14×(62.8÷3.14÷2)2×9[3.14×(24÷2)2]
=3.14×100×9[3.14×144]
=2826×3÷452.16
=8478÷452.16
=18.75(厘米)
答:这个圆锥的高是18.75厘米。
【点评】此题主要考查圆柱、圆锥体积公式的灵活运用,关键是熟记公式。
18.向阳村要建一个圆柱形储水池.底面半径10米,深3米
(1)这个蓄水池的占地面积多少平方米?
(2)如果给这个蓄水池的四周和池底抹上水泥,抹水泥的面积是多少平方米?
(3)这个蓄水池能蓄水多少立方米?
【答案】见试题解答内容
【分析】(1)求这个蓄水池的占地面积也就是求蓄水池的底面积,根据圆的面积公式解答;
(2)抹水泥的面积=圆柱的侧面积+底面积,又因圆柱的侧面积=底面周长×高,圆柱的底面周长和高已知,则可以求出侧面积,底面积已求,于是可以求出抹水泥的面积.
(3)这个蓄水池能蓄水多少立方米,也就是求它容积,根据圆柱的容积公式解答.
【解答】解:(1)3.14×102
=3.14×100
=314(平方米)
答:蓄水池占地314平方米.
(2)3.14×10×2×3+314
=188.4+314
=502.4(平方米)
答:抹水泥的面积是502.4平方米.
(3)314×3=942(立方米)
答:这个蓄水池能蓄水942立方米.
【点评】解答此题主要分清所求物体的形状,转化为求有关图形的体积或面积的问题,把实际问题转化为数学问题,再运用数学知识解决.
19.一个圆柱形铁皮水桶(无盖),高15dm,底面直径是高的。做这个水桶大约要用多少铁皮?
【答案】487dm2。
【分析】无盖的圆柱形铁皮水桶,则计算一个底面积加上侧面积即可,知道底面直径和高的关系,先求出底面直径,再根据公式可求底面积和侧面积,然后相加即可。
【解答】解:圆柱的底面直径:159(dm)
需用铁皮面积:
3.14×9×15+3.14×(9÷2)2
=423.9+63.585
=487.485
≈487(dm2)
答:做这个水桶大约要用487dm2铁皮。
【点评】此题考查了圆柱的表面积的计算方法,计算表面积时注意此题只算一个底面的面积。
20.妙想买了18块圆柱形橡皮泥,每块橡皮泥的底面直径是2cm,高是6cm。
(1)如果把其中一块橡皮泥捏成高是6cm的圆锥,圆锥的底面积是多少?
(2)妙想想用最少的硬纸板做一个长方体盒子(有盖)把18块橡皮泥装进去,做这个长方体盒子需要多少硬纸板?(粘贴处忽略不计)
【答案】(1)9.42平方厘米;
(2)360平方厘米。
【分析】(1)根据圆柱的体积公式:V=πr2h,圆锥的体积公式:VSh,那么S=Vh,把数据代入公式解答。
(2)根据题意,把18个这样的圆柱平均分成3份,每排放6个,放3排。这样长方体盒子的长是圆柱直径的6倍,宽是圆柱底面直径的3倍,盒子的高等于圆柱的高,根据长方体的表面积公式:S=(ab+ah+bh)×2,把数据代入公式解答。
【解答】解:(1)3.14×(2÷2)2×66
=3.14×1×6×3÷6
=9.42(平方厘米)
答:圆锥的底面积是9.42平方厘米。
(2)盒子的长:2×6=12(厘米)
盒子的宽:2×3=6(厘米)
盒子的高是6厘米。
(12×6+12×6+6×6)×2
=(72+72+36)×2
=180×2
=360(平方厘米)
答:做这个长方体盒子需要360平方厘米硬纸板。
【点评】此题主要考查圆柱、圆锥体积公式的灵活运用,长方体表面积公式的灵活运用,关键是熟记公式,重点是确定长方体盒子的长、宽、高。
21.一个圆锥形沙堆,底面半径2米,高1.2米,用这堆沙在10米宽的公路上铺2厘米的路面,能铺多少米?
【答案】见试题解答内容
【分析】先利用圆锥的体积计算公式求出这堆沙的体积,再据沙子的体积不变,代入长方体的体积公式即可求出所铺沙子的长度.
【解答】解:2厘米=0.02米
沙堆的体积:3.14×22×1.2
=3.14×4×0.4
=5.024(立方米)
所铺沙子的长度:5.024÷(10×0.02)
=5.024÷0.2
=25.12(米)
答:能铺25.12米长.
【点评】此题主要考查圆锥和长方体的体积计算方法,关键是明白:沙子的体积不变.
22.小明把一个底面半径是3厘米的铁圆锥,放在从里面量半径是5厘米的圆柱形透明的玻璃容器内。小明把一瓶装有550毫升的纯净水倒入容器,这时水深正好与圆锥的高相等。圆锥的体积是多少?
【答案】75立方厘米。
【分析】根据圆锥的体积公式:Vπr2h,圆柱的体积公式:V=πr2h,圆锥的体积+水的体积=圆柱容器内水高等于圆锥高的体积,设圆锥的高为h厘米,据此列方程求出圆锥的高,然后把数据代入公式求出圆锥的体积。
【解答】解:设圆锥的高为h厘米,
550毫升=550立方厘米
π×32×h+550=π×52h
3πh+550=25πh
25πh﹣3πh=550
22πh=550
h
π×3275(立方厘米)
答:圆锥的体积是75立方厘米。
【点评】此题主要考查圆锥的体积公式、圆柱的体积(容积)公式的灵活运用,关键是熟记公式,重点是求出圆锥的高。
23.一个底面周长25.12cm,高9cm的圆柱形钢块熔铸成一个底面直径12cm的圆锥,圆锥的高是多少厘米?
【答案】12厘米。
【分析】根据体积的意义可知,熔铸前后的体积不变,先根据圆柱的体积公式求出它的体积,再利用圆锥的体积公式求出它的高即可。
【解答】解:3.14×(25.12÷3.14÷2)2×9[3.14×(12÷2)2]
=3.14×16×9[3.14×36]
=452.16×3÷113.04
=1356.48÷113.04
=12(厘米)
答:圆锥的高是12厘米。
【点评】此题主要考查圆柱、圆锥体积公式的灵活运用,关键是熟记公式。
24.如图,一个圆柱高10厘米,如果它的高增加4厘米,那么它的表面积将增加50.24平方厘米,求原来圆柱的体积是多少立方厘米?
【答案】125.6立方厘米。
【分析】用增加的表面积除以增加的高可得到原来圆柱的底面周长,然后再利用圆的周长公式计算出圆柱的底面半径,最后再利用圆柱的体积公式V=Sh计算出圆柱的体积即可。
【解答】解:原来圆柱的底面周长为:50.24÷4=12.56(厘米)
原来圆柱的底面半径为:
12.56÷3.14÷2
=4÷2
=2(厘米)
原来圆柱的体积为:
3.14×22×10
=12.56×10
=125.6(立方厘米)
答:原来圆柱的体积是125.6立方厘米。
【点评】解答此题的关键是确定圆柱的底面半径,然后再利用圆柱的体积公式进行计算即可。
25.如果要焊制一个无盖的圆柱形水桶,有以下几种型号的铁皮供搭配选择。
你选择的铁皮型号是 ① 号和 ③ 号(填序号),做这个水桶需要多少平方分米的铁皮?能装多少升水?(接口处忽略不计,圆周率取3.14)
【答案】答案不唯一。①,③,75.36平方分米。
【分析】根据圆柱侧面展开图的特征,圆柱的侧面沿高展开是一个长方形,这个长方形的长等于圆柱的底面周长,长方形的宽等于圆柱的高,根据圆的周长公式:C=πd,把数据分别代入公式求出两个圆的周长,然后与两个长方形的长进行比较即可,因为水桶无盖,根据圆柱的表面积=侧面积+底面积,把数据代入公式解答。
【解答】解:3.14×4=12.56(分米)
3.14×3=9.42(分米)
可以选择①和③,也可以选择②和④。
我选择①和③。
12.56×5+3.14×(4÷2)2
=62.8+3.14×4
=62.8+12.56
=75.36(平方分米)
答:做这个水桶需要75.36平方分米的铁皮。
故答案为:①,③。
【点评】此题考查的目的是理解掌握圆柱侧面展开图的特点及应用,圆柱的表面积公式及应用。
26.把一根长5分米的圆钢截成4段后,表面积的总和比原来增加了113.04平方分米.求原来的圆钢的体积.
【答案】见试题解答内容
【分析】首先要明确的是:将这根圆钢锯成4段小圆柱后,增加了6个底面,增加的面积已知,于是就可以求出这根圆钢的底面积,从而利用圆柱的体积V=Sh,即可求出这根圆钢的体积.
【解答】解:113.04÷6=18.84(平方分米),
18.84×5=94.2(立方分米).
答:原来的圆钢的体积是94.2立方分米.
【点评】解答此题的关键是明白:将这根圆钢锯成4段小圆柱后,增加了6个底面,求出圆钢的底面积,即可利用圆柱的体积公式求解.
27.一个高为8分米的圆柱形木桶里,装了半桶水,把水倒出12升后,剩下的水恰好占水桶容积.这个水桶的底面积是多少平方分米?
【答案】见试题解答内容
【分析】把水桶的容积看作单位“1”,已知装有半桶水(桶),把水倒出12升后,剩下的水恰好占水桶容积.那么倒出的12升占容积的(),根据已知一个数的几分之几是多少,求这个数,用除法求出水桶的容积(水的体积),然后用水的体积除以水桶的高即可.
【解答】解:12升=12立方分米,
12÷()
=40(立方分米),
40÷8=5(平方分米),
答:这个水桶的底面积是5平方分米.
【点评】此题主要考查圆柱的体积(容积)公式的灵活运用,重点是根据已知一个数的几分之几是多少,求这个数,用除法求出水桶的容积(水的体积),注意:容积单位与体积单位之间的换算.
28.一个圆柱形的汽油桶底面直径是8分米,高5分米.现装满汽油,如果每升汽油重0.85千克,这个油桶的汽油共多少千克?
【答案】见试题解答内容
【分析】首先根据圆柱的体积公式:v=sh,把数据代入公式求出油桶内汽油的体积,然后用汽油的体积乘每升油的质量即可.
【解答】解:1升=1立方分米,
3.14×(8÷2)2×5×0.85
=3.14×16×5×0.85
=50.24×5×0.85
=251.2×0.85
=213.52(千克),
答:这个油桶的汽油共213.52千克.
【点评】此题主要考查圆柱的体积公式在实际生活中的应用,关键是熟记公式.注意:容积单位与体积单位之间的换算.
29.在一个棱长为4厘米的正方体的前后.左右、上下各面的中心位置挖去一个底面半径为1厘米、高为1厘米的圆柱,则挖去后物体的表面积为多少?(圆周率取3.14计算)
【答案】见试题解答内容
【分析】根据题意可知,把这个正方体从前后.左右、上下各面的中心位置挖去一个底面半径为1厘米、高为1厘米的圆柱,挖去后物体的表面积比原来正方体的表面积增加了6个底面半径为1厘米、高为1厘米的圆柱的侧面积,根据正方体的表面积公式:S=6a2,圆柱的侧面积公式:S=2πrh,把数据分别代入公式解答.
【解答】解:4×4×6+2×3.14×1×1×6
=96+6.28×
=96+37.68
=133.68(平方厘米)
答:挖去后物体的表面积为133.68平方厘米.
【点评】此题主要考查正方体的表面积公式、圆柱的侧面积公式的灵活运用,关键是熟记公式.
30.古希腊著名的数学家阿基米德是历史上最杰出的数学家之一,在他众多的科学发现中,他自己最为满意的是:“圆柱容球定理”。如图,把一个球正好放在一个圆柱形容器中,球的直径与圆柱的高和底面直径相等,此时,球的体积正好是圆柱体积的,球的表面积也正好是圆柱表面积的。请你提一个富有挑战性的问题,并解答(请把此“圆柱容球”图片再画一下)
【答案】球的体积是多少立方厘米?113.04立方厘米。
【分析】先画出图形中圆柱的高,提出问题:球的体积是多少立方厘米?再根据球的直径与圆柱的高和底面直径相等,此时球的体积正好是圆柱体积的,利用圆柱的体积公式:V=πr2h,计算圆柱的体积,进而求出球的体积即可。
【解答】解:球的体积是多少立方厘米?
如图:
3.14×(6÷2)2×6
=3.14×9×6
=113.04(立方厘米)
答:图中球的体积是113.04立方厘米。
【点评】本题主要考查球的体积的计算,解题的关键是利用球和圆柱的关系,求出球的体积。
31.李师傅把一个正方体削成一个最大的圆锥体。正方体的体积是240立方分米,圆锥体的体积是多少立方分米?
【答案】62.8立方分米。
【分析】根据题意可知,把一个正方体削成一个最大的圆锥体,这个圆锥的底面直径和高都等于正方体的棱长,首先根据正方体的体积公式:V=a3,圆锥的体积公式:Vπr2h,设正方体的棱长为a分米,把数据代入公式求出圆锥的体积是正方体体积的几分之几,然后根据求一个数的几分之几是多少,用乘法圆锥的体积。
【解答】解:设正方体的棱长为a分米,则圆锥的底面直径和高都是a分米,
圆锥的体积:π×()2×a
πa
(立方分米)
正方体的体积:a×a×a=a3(立方分米)
所以圆锥的体积是正方体体积的:a3
240
=62.8(立方分米)
答:圆锥体的体积是62.8立方分米。
【点评】此题主要考查正方体的体积公式、圆锥的体积公式的灵活运用,关键是明白:把一个正方体削成一个最大的圆锥体,这个圆锥的底面直径和高都等于正方体的棱长,重点是求出圆锥的体积是正方体体积的几分之几,再根据求一个数的几分之几是多少,用乘法解答。
32.在一个底面半径5厘米,高18厘米的圆柱形水桶内装满了水,另有一个圆锥形空水桶,它的上口周长为37.68厘米,现在把圆柱形水桶里的水往圆锥形水桶里倒,当圆锥形水桶装满时,圆柱形水桶还剩12厘米高的水,求圆锥形水桶的高。
【答案】12.5厘米。
【分析】根据圆柱体积=底面积×高,用圆柱形水桶底面积×(水桶的高﹣剩下水的高),求出倒入圆锥形水桶中水的体积,用圆锥底面周长÷圆周率÷2,求出圆锥底面半径,倒入圆锥形水桶中水的体积×3÷圆锥底面积=圆锥形水桶的高,据此列式解答。
【解答】解:3.14×52×(18﹣12)
=3.14×25×6
=78.5×6
=471(立方厘米)
471×3÷[3.14×(37.68÷3.14÷2)2]
=1413÷[3.14×36]
=1413÷113.04
=12.5(厘米)
答:圆锥形水桶的高是12.5厘米。
【点评】此题主要考查圆柱、圆锥的体积(容积)公式的灵活运用,关键是熟记公式。
33.张师傅想用一个底面直径为20厘米、高为40厘米的圆柱体木桩加工工艺品有以下几道工序:
工序1:截取一段圆柱体木桩削成最大的圆锥,使得圆锥的体积是1570立方厘米; 工序2:把圆锥和剩下的圆柱底面相接拼起来,在圆锥部分雕刻上花纹,圆柱部分涂上颜料。
请你帮张师傅算一算:
(1)截取的木桩有多高?
(2)拼接后,涂颜料的面积是多少平方厘米?
【答案】(1)15厘米;
(2)1884平方厘米。
【分析】(1)根据圆锥的体积公式:Vπr2h,那么h=Vπr2,把数据代入公式解答。
(2)用木桩的高减去圆锥的高就是圆柱的高,涂颜料的部分是圆柱的一个底面和侧面,根据圆的面积公式:S=πr2,圆柱的侧面积公式:S=πdh,把数据代入公式解答。
【解答】解:(1)1570[3.14×(20÷2)2]
=1570×3÷[3.14×100]
=4710÷314
=15(厘米)
答:截取的木桩有15厘米高。
(2)3.14×(20÷2)2+3.14×20×(40﹣15)
=3.14×100+3.14×20×25
=314+1570
=1884(平方厘米)
答:涂颜料的面积是1884平方厘米。
【点评】此题主要考查圆锥的体积公式、圆柱的表面积公式的灵活运用,关键是熟记公式。
34.用一张长314cm、宽157cm的长方形纸围成一个圆柱体,有几种围法?计算一下,看看哪种围法体积大?
【答案】见试题解答内容
【分析】根据圆柱侧面展开图的特征,圆柱的侧面展开是一个长方形,这个长方形的长等于圆柱的底面周长,长方形的宽等于圆柱的高,因此,用一张长方形的纸围成一个圆柱有两种围法,其中当围成的圆柱的高等于长方形的宽时,圆柱的体积较大
【解答】解:围成圆柱的高是157厘米,那么圆柱的底面周长就是314厘米,
3.14×(314÷3.14÷2)2×157
=3.14×502×157
=3.14×2500×157
=7850×157
=1232450(立方厘米);
围成圆柱的高是314厘米,那么圆柱的底面周长就是157厘米,
3.14×(157÷3.14÷2)2×314
=3.14×252×314
=3.14×625×314
=1962.5×314
=616225(立方厘米);
1232450立方厘米>616225立方厘米
答:当围成的圆柱的高为157厘米,底面周长是314厘米时,圆柱的体积较大.
【点评】此题考查的目的是理解掌握圆柱侧面展开图的特征,以及圆柱体积公式的灵活运用,关键是熟记公式.
35.欣欣礼品店要用4张长18厘米,宽6厘米的长方形包装纸围成一个圆柱.第一张横着卷成圆柱,第二张竖着卷成圆柱,第三张和第四张围成的圆柱如图所示.
(1)围成这个圆柱的侧面积是多少?
(2)填一填,看看你发现了什么?(π取值3.14,结果保留两位小数)
底面周长(cm) 高(cm) 侧面积(cm2) 体积(cm3)
第一个圆柱
第二个圆柱
第三个圆柱
第四个圆柱
我发现: 当侧面积一定时,越是细长的圆柱体体积越小,越是粗的、矮的圆柱体体积越大(答案不唯一) .
【答案】(1)108;
(2)
底面周长(cm) 高(cm) 侧面积(cm2) 体积(cm3)
第一个圆柱 18 6 108 154.18
第二个圆柱 6 18 108 51.59
第三个圆柱 3 36 108 25.80
第四个圆柱 9 12 108 77.39
我发现:当侧面积一定时,越是细长的圆柱体体积越小,越是粗的、矮的圆柱体体积越大。(答案不唯一)
【分析】(1)根据圆柱侧面展开图的特征,圆柱的侧面沿高展开是一个长方形,这个长方形的长等于圆柱的底面周长,宽等于圆柱的高。所以这4个圆柱的侧面积相等。即都等于每张长方形纸的面积,根据长方形的面积公式:S=ab,把数据代入公式解答。
(2)根据圆柱的体积公式:V=πr2h,把数据代入公式解答。
【解答】解:(1)18×6=108(平方厘米)
答:围成这个圆柱的侧面积都是108平方厘米。
(2)
底面周长(cm) 高(cm) 侧面积(cm2) 体积(cm3)
第一个圆柱 18 6 108 154.18
第二个圆柱 6 18 108 51.59
第三个圆柱 3 36 108 25.80
第四个圆柱 9 12 108 77.39
我发现:当侧面积一定时,越是细长的圆柱体体积越小,越是粗的、矮的圆柱体体积越大。(答案不唯一)
【点评】此题主要考查了圆柱体的侧面积的意义,及在生活中的实际应用。
36.在一个直径是20cm的圆柱形容器里,放入一个底面半径是3cm的圆锥形铁块,全部浸设在水中,这时水面上升0.3cm。
(1)圆锥形铁块的体积是多少cm3?
(2)圆锥形铁块的高是多少dm?
【答案】(1)94.2立方厘米;
(2)1分米。
【分析】(1)根据题意可知,把圆锥放入圆柱形容器中,上升部分水的体积就等于圆锥的体积,根据圆柱的体积公式:V=πr2h,把数据代入公式解答。
(2)根据圆锥的体积公式:Vπr2h,那么h=Vπr2,把数据代入公式解答。
【解答】解:(1)3.14×(20÷2)2×0.3
=3.14×100×0.3
=94.2(立方厘米)
答:圆锥形铁块的体积是94.2立方厘米。
(2)94.2(3.14×32)
=94.2×3÷(3.14×9)
=282.6÷28.26
=10(厘米)
10厘米=1分米
答:圆锥形铁块的高是1分米。
【点评】此题主要考查圆柱、圆锥体积公式的灵活运用,关键是熟记公式。
37.一个圆锥,底面直径是20厘米,比它的高长25%。如果把这个圆锥沿着它的底面直径竖直切成两个完全相同的立体图形,截面的面积是多少平方厘米?
【答案】160平方厘米。
【分析】把圆锥的高看作单位“1”,圆锥的底面直径相当于高的(1+25%),根据已知一个数的百分之几是多少,求这个数,用除法求出高,如果把这个圆锥沿着它的底面直径竖直切成两个完全相同的立体图形,截面是三角形,这个三角形的底等于圆锥的底面直径,三角形的高等于圆锥的高,根据三角形的面积公式:S=ah÷2,把数据代入公式解答。
【解答】解:圆锥的高:
20÷(1+25%)
=20÷1.25
=16(厘米)
20×16÷2
=320÷2
=160(平方厘米)
答:截面的面积是160平方厘米。
【点评】此题考查的目的是理解掌握圆锥的特征,关键是明确:把这个圆锥沿着它的底面直径竖直切成两个完全相同的立体图形,截面是三角形,这个三角形的底等于圆锥的底面直径,三角形的高等于圆锥的高,重点是求出圆锥的高。
38.小明有两个圆柱形容器。一个底面半径为3厘米,另一个底面半径为4厘米,现在小明要把0.314升水倒入这两个容器中,让两个容器中的水高度相同,请问,容器中的水深多少厘米?
【答案】4厘米。
【分析】根据圆柱的容积(体积)公式:V=πr2h,设容器中的水深为x厘米,据此列方程解答。
【解答】解:设容器中的水深为x厘米,
0.314升=314立方厘米
3.14×32×x+3.14×42×x=314
3.14×9×x+3.14×16×x=314
28.26x+50.24x=314
78.5x=314
x=4
答:容器中水深4厘米。
【点评】此题主要考查圆柱的容积(体积)公式的灵活运用,列方程解决问题的方法及应用,关键是熟记公式。
39.一个圆柱的体积是62.8cm3,要把它锻造成一个高为12cm的圆锥,圆锥底面积应是多少?
【答案】见试题解答内容
【分析】圆柱锻造成圆锥,它们的体积相等,根据圆锥的体积公式:VSh,用体积除以再除以高,由此列式解答.
【解答】解:62.812
=62.8×3÷12
=15.7(平方厘米);
答:圆锥的底面积应该是15.7平方厘米.
【点评】此题主要考查圆锥的体积的计算方法,能够根据体积的计算方法解决有关的问题.
40.一个长方形模型的周长是24厘米,长与宽的比是3:1,以这个长方形的长边为中心轴,把这个长方形旋转周,得到的形体的体积是多少?
【答案】见试题解答内容
【分析】长方形的周长除以2求出长与宽的和,再利用按比例分配的方法求出长和宽,以这个长方形的长边为中心轴,把这个长方形旋转一周,得到一个底面半径等于长方形的宽,高等于长方形的长的圆柱体,然后根据圆柱的体积公式:V=sh,把数据代入公式解答,
【解答】解:3+1=4
24÷2=12(厘米)
12(厘米)
123(厘米)
3.14×32×9
=3.14×9×9
=28.26×9
=254.34(立方厘米),
答:得到的两条图形的体积是254.34立方厘米.
【点评】此题主要考查长方形的周长公式、圆柱的体积公式的灵活运用,关键是熟记公式.
41.请你从如图型号的材料中选出两个制作一个无盖的圆柱形小水桶。(接口处忽略不计)
(1)选择的型号是 ②③ (填序号),这个水桶的底面积是 50.24 cm2。
(2)制作这个小水桶,一共需要多少平方厘米的铁皮?
(3)往这个小水桶中注水,水面上升到水桶高的处,这时水桶中水的体积是多少毫升?
【答案】(1)②③,50.24;
(2)175.84平方厘米;
(3)200.96毫升。
【分析】(1)根据圆柱侧面展开图的特征可知,圆柱的侧面沿高展开是一个长方形,这个长方形的长等于圆柱的底面周长,长方形的宽等于圆柱的高,根据圆的周长公式:C=πd,把数据代入公式求出两个圆的周长,然后与长方形的长进行比较即可确定选择的型号,根据圆的面积公式:S=πr2,求出这个水桶的底面积。
(2)制作这个水桶需要铁皮的面积等于长方形的面积加上底面的面积。
(3)根据圆柱的体积(容积)公式:V=Sh,把数据代入公式求出这个水桶容积的即可。
【解答】解:(1)3.14×8=25.12(厘米)
3.14×4=12.56(厘米)
所以选择的型号是②③。
3.14×(8÷2)2
=3.14×16
=50.24(平方厘米)
答:这个水桶的底面积是50.24平方厘米。
(2)25.12×5+50.24
=125.6+50.24
=175.84(平方厘米)
答:一共需要175.84平方厘米的铁皮。
(3)50.24×5
=251.2
=200.96(立方厘米)
200.96立方厘米=200.96毫升
答:这时水桶水的体积是200.96毫升。
故答案为:②③,50.24。
【点评】此题考查的目的是理解掌握圆柱侧面展开图的特征及应用,圆的周长公式、圆的面积公式、圆柱的侧面积公式、圆柱的体积公式及应用,关键是熟记公式。
42.一只底面半径是10cm的圆柱形瓶中,水深8cm,在瓶中放入长和宽都是8cm、高是15cm的一块长方体铁块,把铁块竖直放在水中,水面上升了几厘米?
【答案】2.048厘米。
【分析】根据题意可知,铁块放入前后瓶子内水的体积不变,放入铁块后水的底面积等于圆柱的底面积与铁块底面积的差,根据圆柱的体积公式:V=πr2h,把数据代入公式求出水的体积,然后用水的体积除以放入铁块后水的底面积求出现在水面的高,用现在水面的高减去原来的水深就是水面上升的高度。
【解答】解:3.14×102×8÷(3.14×102﹣8×8)﹣8
=3.14×100×8÷(3.14×100﹣64)﹣8
=314×8÷(314﹣64)﹣8
=2512÷250﹣8
=10.048﹣8
=2.048(厘米)
答:水面上升了2.048厘米。
【点评】此题主要考查圆柱体积公式的灵活运用,关键是抓住水的体积不变,原来的底面积减少了铁块的底面积,求出放入铁块后的水深,进而求出水面上升的高度。
43.一个圆柱形容器和一个圆锥形容器等底等高,圆柱形容器内原有12升水,现将圆锥形容器盛满水再全部倒入圆柱形容器,则圆柱形容器内水面上升到处。圆柱形容器的容积是多少?
【答案】72升。
【分析】因为等底等高的圆柱的体积是圆锥体积的3倍,所以当圆柱与圆锥的体积相等,底面积也相等时,圆柱的高是圆锥高的,由此可以求出圆柱容器内原来水的体积占圆柱容器容积的几分之几,然后根据已知一个数的几分之几是多少,求这个数,用除法解答。
【解答】解:12÷()
=12×6
=72(升)
答:圆柱形容器的容积是72升。
【点评】此题主要考查等底等高的圆柱与圆锥体积之间的关系及应用,关键是求出圆柱容器内原来水的体积占圆柱容器容积的几分之几。
44.一个圆柱形水桶装满水,把桶里的水倒出后,还剩下12升。水桶的高为5分米,水桶的底面积是多少平方分米?(水桶壁的厚度忽略不计)
【答案】7.2平方分米。
【分析】可把这个水桶的容积看作是单位“1”,倒出后剩下的12升就是单位“1”的1,求单位“1”用除法,求它的容积,再除以高,就是水桶的底面积,据此解答。
【解答】解:12升=12立方分米
12÷(1)÷5
=125
=7.2(平方分米)
答:水桶的底面积是7.2平方分米。
【点评】本题的关键是根据分数除法的意义列式求出水桶的容积,再求它的底面积。
45.一个直角三角形,一条直角边长6厘米,另一条直角边长4厘米,以它的较长的直角边为轴旋转一周后形成一个立体图形.求这个旋转后立体图形的体积.
【答案】见试题解答内容
【分析】根据圆锥的定义,一个直角三角形以它的较长的直角边为轴旋转一周后形成一个立体图形,这个立体图形是圆锥,圆锥的底面半径等于三角形的较短的直角边4厘米,高等于较长的直角边6厘米,根据圆锥的体积:vπr2h,把数据代入公式解答即可.
【解答】解:3.14×42×6
3.14×16×6
=100.48(立方厘米)
答:这个立体图形的体积是100.48立方厘米.
【点评】此题考查的目的是理解圆锥的定义,掌握圆锥的体积公式.
46.一个从里面量底面直径为20cm的圆柱形容器中装有一部分水,在水中浸没一个底面直径为12cm的圆锥形铅锤,这时水面高度是15cm,当把铅锤从容器中取出后,容器中的水面高度下降到13.8cm。这个铅锤的高是多少厘米?
【答案】10厘米。
【分析】由题意可知,把圆锥形铅锤从容器中取出后,下降部分水的体积就等于铅锤的体积,根据圆柱的体积公式:V=πr2h,圆锥的体积公式:Vπr2h,那么h=V(πr2),把数据代入公式解答。
【解答】解:3.14×(20÷2)2×(15﹣13.8)[3.14×(12÷2)2]
=3.14×100×1.2×3÷[3.14×36]
=376.8×3÷113.04
=1130.4÷113.04
=10(厘米)
答:这个铅锤的高是10厘米。
【点评】此题主要考查圆柱、圆锥体积公式的灵活运用,关键是熟记公式。
47.一个底面周长是25.12cm,高是18cm的圆柱形玻璃缸中有一些水,把一个底面半径是3cm的圆锥形铁块浸没在水中(水未溢出),缸内水面上升了1.5cm,圆锥形铁块的高是多少?
【答案】8厘米。
【分析】根据题意可知,把圆锥形铁块放入圆柱形玻璃缸中(水未溢出),上升部分水的体积就等于这个圆锥形铁块的体积,根据圆柱的体积公式:V=πr2h,圆锥的体积公式:Vπr2h,那么h=Vπr2,把数据代入公式解答。
【解答】解:3.14×(25.12÷3.14÷2)2×1.5(3.14×32)
=3.14×16×1.5×3÷(3.14×9)
=75.36×3÷28.26
=226.08÷28.26
=8(厘米)
答:圆锥形铁块是高是8厘米。
【点评】此题主要考查圆柱、圆锥体积公式的灵活运用,关键是熟记公式。
48.一个圆锥形零件,底面积是170平方厘米,高是12厘米。这个零件的体积是多少立方厘米?
【答案】见试题解答内容
【分析】根据圆锥的体积公式:vsh,把数据代入公式解答即可.
【解答】解:170×12=680(立方厘米),
答:这个零件的体积是680立方厘米.
【点评】此题主要考查圆锥体积公式的灵活运用,关键是熟记公式.
49.广汉市某校六年级一班张敏敏购买了一个底面直径10厘米,高12厘米的圆柱形水杯。为了使水杯更加美观,她在水杯的侧面贴上了一圈彩纸,至少需要多少平方厘米的彩纸(接头处忽略不计)?她先往水杯里倒入628mL水,再把一个高为6厘米的圆锥形玩具,完全浸没在水中,这时水面上升0.8厘米,这个圆锥形玩具的底面积是多少平方厘米?
【答案】376.8平方厘米,31.4平方厘米。
【分析】根据圆柱的侧面积公式:S=πdh,把数据代入公式求出至少需要彩纸的面积,根据圆柱的体积公式:V=πr2h,把数据代入公式求出圆锥的体积,然后用圆锥的体积除以再除以圆锥的高即可求出圆锥的底面积。
【解答】解:3.14×10×12
=31.4×12
=376.8(平方厘米)
3.14×(10÷2)2×0.86
=3.14×25×0.8×3÷6
=62.8×3÷6
=188.4÷6
=31.4(平方厘米)
答:至少需要376.8平方厘米的彩纸,这个圆锥形玩具的底面积是31.4平方厘米。
【点评】此题主要考查圆柱的侧面积公式、圆柱的体积公式、圆锥的体积公式的灵活运用,关键是熟记公式。
50.一张长方形铁皮,长18.84dm,宽6dm,用这张铁皮卷成一个圆柱形铁皮水桶的侧面,另配一个底面制成一个最大的水桶。这个铁皮水桶的表面积是多少dm2?水桶的容积是多少?
【答案】141.3平方分米,169.56升。
【分析】由题意可知,这个水桶的表面积等于水桶的侧面积加上一个底面的面积,根据圆柱的侧面积公式:S=πdh,圆的面积公式:S=πr2,圆柱的体积(容积)公式:V=Sh,把数据代入公式解答。
【解答】解:18.84×6+3.14×(18.84÷3.14÷2)2
=113.04+3.14×9
=113.04+28.26
=141.3(平方分米)
3.14×(18.84÷3.14÷2)2×6
=3.14×9×6
=28.26×6
=169.56(立方分米)
169.56立方分米=169.56升
答:这个铁皮水桶的表面积是141.3平方分米,桶的容积是169.56升。
【点评】此题主要考查圆柱的体积公式、圆柱的侧面积公式、圆的面积公式的灵活运用,关键是熟记公式。
51.一个圆锥形沙堆,底面周长是25.12米,高1.8米.如果每立方米沙重1.7吨,这堆沙子重多少吨?
【答案】见试题解答内容
【分析】先利用圆的周长公式求出底面半径,进而可以求出圆锥的体积;每立方米的沙重已知,乘总体积数就是这堆沙的总重量.
【解答】解:底面半径:25.12÷(2×3.14)
=25.12÷6.28
=4(米)
沙的总重量:3.14×42×1.8×1.7
=50.24×0.6×1.7
=51.2448(吨);
答:这堆沙子重51.2448吨.
【点评】解答此题的关键是:先求出底面半径,从而求出这堆沙的体积和重量.
52.把一个底面直径20厘米的圆柱切拼成一个近似的长方体,长方体表面积比圆柱表面积多400平方厘米。圆柱的体积是多少立方厘米?
【答案】6280立方厘米。
【分析】根据圆柱体积公式的推导方法可知,把一个圆柱切拼成一个近似长方体,拼成的近似长方体的底面积等于圆柱的底面积,拼成的近似长方体的高等于圆柱的高,拼成的近似长方体的表面积比圆柱的表面积增加了两个切面的面积,每个切面的长等于圆柱的高,每个切面的宽等于圆柱的底面半径,已知拼成的近似长方体的表面积比圆柱的表面积增加了400平方厘米,据此可以求出圆柱的高,然后根据圆柱的体积公式:V=πr2h,把数据代入公式解答。
【解答】解:20÷2=10(厘米)
400÷2÷10
=200÷10
=20(厘米)
3.14×102×20
=3.14×100×20
=314×20
=6280(立方厘米)
答:圆柱的体积是6280立方厘米。
【点评】此题考查的目的是理解掌握圆柱体积公式的推导方法及应用。
53.将一个底面半径是4厘米,高是9厘米的实心圆柱形铁块,锻造成一个底面半径是8厘米的实心圆锥形铁块,这个圆锥形铁块的高是多少厘米?
【答案】6.75厘米。
【分析】根据圆柱的体积公式:V=πr2h,求出铁块的体积,再根据圆锥的体积公式:Vπr2h,那么h=Vπr2,把数据代入公式解答。
【解答】解:3.14×42×9(3.14×82)
=3.14×16×9×3÷(3.14×64)
=452.16×3÷200.96
=1356.48÷200.96
=6.75(厘米)
答:这个圆锥形铁块的高是6.75厘米。
【点评】此题主要考查圆柱、圆锥体积公式的灵活运用,关键是熟记公式。
54.如图是一个无盖的长方体玻璃容器,水面的高度是8cm。把一个底面半径是4cm的圆锥形铅锤完全浸入水中,水面上升了0.628cm,这个铅锤的高是多少厘米?
【答案】6厘米。
【分析】根据题意可知,把这个圆锥形铅锤放入长方体容器中,上升部分水的体积就等于这个铅锤的体积,根据长方体的体积公式:V=abh,圆锥的体积公式:Vπr2h,那么h=V(πr2),把数据代入公式解答。
【解答】解:16×10×0.628(3.14×42)
=160×0.628×3÷(3.14×16)
=100.48×3÷50.24
=301.44÷50.24
=6(厘米)
答:这个铅锤的高是6厘米。
【点评】此题主要考查长方体的体积公式、圆锥的体积公式的灵活运用,关键是熟记公式。
55.如图,用一张长165.6厘米的铁皮,剪下一个最大的圆作为圆柱的底面,剩下的部分围在底面上做成一个无盖的铁皮水桶,算一算这个铁皮水桶的容积是多少?(铁皮厚度不计,π取3.14)
【答案】见试题解答内容
【分析】根据题意可知:铁皮的长等于圆柱的底面周长加上直径,设圆柱的底面直径为x厘米,由题意得:3.14x+x=165.6,解此方程求出圆柱的底面直径,圆柱的高等于底面直径,再根据圆柱的容积(体积)公式:V=sh,把数据代入公式解答.
【解答】解:设圆柱的底面直径为x厘米,由题意得:
3.14x+x=165.6
4.14x=165.6
4.14x÷4.14=165.6÷4.14
x=40.
3.14×(40÷2)2×40
=3.14×400×40
=1256×40
=50240(立方厘米),
答:这个铁皮水桶的容积是50240立方厘米.
【点评】此题考查的目的是理解掌握圆柱展开图的特征,以及圆柱的容积(体积)公式的灵活运用,关键是熟记公式.
56.一种油菜籽榨油机的漏斗是由圆柱和圆锥两部分组成。底面周长是18.84dm,圆柱和圆锥的高都是6dm。每立方分米油菜籽重0.5kg。
(1)这个漏斗最多能装多少千克油菜籽?
(2)如果油菜籽的出油率是45%,一漏斗油菜籽能榨出多少千克菜籽油?
【答案】(1)113.04千克;
(2)50.868千克。
【分析】(1)根据圆柱的体积公式:V=πr2h,圆锥的体积公式:Vπr2h,把数据代入公式求出这个漏斗能装油菜籽的体积,然后再乘每立方米油菜籽的质量即可。
(2)把油菜籽的质量看作单位“1”,根据求一个数的百分之几是多少,用乘法解答。
【解答】解:(1)底面半径:18.84÷3.14÷2=3(分米)
底面积:3.14×32
=3.14×9
=28.26(平方分米)
(28.26×628.26×6)×0.5
=(169.56+56.52)×0.5
=226.08×0.5
=113.04(千克)
答:这个漏斗最多能装113.04千克油菜籽。
(2)113.04×45%=50.868(千克)
答:一漏斗油菜籽能榨出50.868千克菜籽油。
【点评】此题主要考查圆柱的体积公式、圆锥的体积公式的灵活运用,一个数乘百分数的意义及应用,关键是熟记公式。
57.一个圆柱形容器从里面量底面直径是20cm,高是10cm,里面水深9cm,现在将一个底面半径是8cm,高是6cm的实心圆锥形铁块完全浸没在水中,这时,圆柱形容器中的水会溢出来吗?如果会溢出,则溢出多少mL?
【答案】水溢出来,溢出87.92毫升。
【分析】根据题意,如果这个实心圆锥铁块的体积小于或等于圆柱容器无水部分的体积,水就不会溢出,如果圆锥铁块的体积大于圆柱容器无水部分的体积,水就会溢出,溢出水的体积等于圆锥铁块的体积减去圆柱容器无水部分的体积。根据圆柱的体积公式:V=πr2h,圆锥的体积公式;Vπr2h,把数据代入公式解答。
【解答】解:3.14×(20÷2)2×(10﹣9)
=3.14×100×1
=314(立方厘米)
3.14×82×6
3.14×64×6
=401.92(立方厘米)
401.92立方厘米>314立方厘米
所以水会溢出。
401.92﹣314=87.92(立方厘米)
87.92立方厘米=87.92毫升
答:圆柱形容器中的水会溢出来,溢出87.92毫升。
【点评】此题主要考查圆柱的体积公式、圆锥的体积公式的灵活运用,关键是熟记公式。
58.在一个直径是20厘米的圆柱形容器里,放入一个底面半径2厘米的圆锥形铁块,全部浸没在水中,这时水面上升了0.3厘米。这个圆锥形铁块的高是多少厘米?
【答案】22.5厘米。
【分析】根据题意,这个圆锥形铁块的体积就是上升0.3厘米的水的体积,由此可以求出这个圆锥的体积,再利用圆锥的体积公式VSh即可求出这个圆锥的高。
【解答】解:3.14×(20÷2)2×0.3×3÷(3.14×22)
=314×0.9÷12.56
=282.6÷12.56
=22.5(厘米)
答:圆锥形铁块的高是22.5厘米。
【点评】此题考查了圆柱与圆锥的体积公式的灵活应用,这里根据上升的水的体积求得圆锥铁块的体积是本题的关键。
59.一个圆柱形玻璃杯,内直径为8厘米,内装16厘米深的水,恰好占杯子容量的,杯内还可以加入多少毫升的水?
【答案】200.96毫米。
【分析】根据圆柱的体积(容积)公式:V=πr2h,把数据代入公式求出这个杯子能装水的体积,把杯子能装水的体积看作单位“1”,还可以加水的体积相当于杯子容积的(1),根据求一个数的几分之几是多少,用乘法解答。
【解答】解:3.14×(8÷2)2×(16)
=3.14×16×20
=50.24×20
=1004.8(立方厘米)
1004.8立方厘米=1004.8毫米
1004.8×(1)
=1004.8
=200.96(毫米)
答:杯内还可以加入200.96毫米的水。
【点评】此题主要考查圆柱的体积(容积)公式的灵活运用,关键是熟记公式。
60.一个圆锥体的体积是15.7立方分米,底面积是3.14平方分米,它的高有多少分米?
【答案】见试题解答内容
【分析】根据圆锥的体积公式可得:圆锥的高=圆锥的体积×3÷底面积,由此代入数据即可得出答案.
【解答】解:15.7×3÷3.14
=47.1÷3.14
=15(分米)
答:它的高是15分米.
【点评】此题考查了利用圆锥的体积公式V求圆锥的高的计算方法.
21世纪教育网(www.21cnjy.com)
1.如图1,这是一个由等底等高的圆柱和圆锥组合而成的计时工具,圆锥内灌满了有颜色水。其中圆锥的高为6厘米,底面半径为3厘米。已知水的流速是1.57立方厘米/分钟。
(1)圆锥内漏完水需要多少时间?
(2)请你在图2中用阴影表示出此时圆柱内的水。
2.用白铁皮制作一个高10分米,底面半径是2分米的圆柱形通风管,至少用铁皮多少平方分米?(得数保留整数)
3.一个圆柱体的侧面积是1cm2,体积是2cm3,它的底面积是多少平方厘米?
4.一个圆锥形沙堆底面周长是12.56米,高是3米,这个圆锥形沙堆的体积是多少?
5.一个无盖的圆柱形铁皮水桶,水桶内存有一些水,水面高度正好是桶高的,淘气将一块体积为628立方厘米的铁块放入水中,完全浸没。这时水面上升了2厘米,水桶正好装满。
(1)这个水桶的高是多少厘米?
(2)做这个水桶需要铁皮多少平方厘米?(铁皮的厚度和接口处忽略不计)
6.一根圆柱形铁棒,底面周长是12.56厘米,长是100厘米,它的体积是多少立方厘米?
7.有一个高8厘米,容积是50毫升的圆柱形容器,装满了水。将一个高6厘米的圆锥形铁块垂直放入水中,有水溢出。把圆锥形铁块从水中取出后,圆柱形容器内水的高度只有6厘米。求圆锥形铁块的体积是多少立方厘米?
8.一根长是20分米,底面直径是8分米的圆柱形木料横放入水中,正好有一半浮在水面上(如图)。
(1)这根木料露出水面部分的面积是多少平方分米?
(2)这根木料没入水中部分的体积是多少立方分米?
9.一个长方体木料,相交于同一个顶点的三条棱长度分别为12分米、8分米、16分米。
(1)这个长方体的体积是多少立方分米?
(2)如果把这个长方体加工成体积最大的圆柱,这个圆柱的体积是多少立方分米?
10.有一个底面直径为20厘米的装有一些水的圆柱形玻璃杯,已知杯中水面距杯口2.24厘米.若将一个半径为9厘米的圆锥形铅锤完全浸入水中,水会溢出314立方厘米.求铅锤的高.
11.一个圆锥体铁块,底面半径是5厘米,高比底面直径少,将这个圆锥体铁块放入到装有水的圆柱形容器中,完全浸没且没有水溢出,已知圆柱从里面量直径是20厘米,铁块放入后水面会上升多少厘米?
12.一个高为4分米的圆柱,把底面分成若干个相等的扇形,再竖直切开拼成一个近似的长方体,表面积增加了16平方分米,圆柱的体积是多少立方分米?(结果保留π)
13.沿着圆柱体的直径自上而下锯成2部分,表面积增加36平方厘米,高与底面直径的比是2:1,这个圆柱的体积是多少?
14.如图,把一个圆柱等分成若干等份,拼成一个近似的长方体,表面积增加了300平方厘米、已知长方体的高是20厘米。长方体的体积是多少?
15.在圆柱体的体积推导过程中,把一个圆柱体平均分成若干等份,然后拼成一个近似的长方体(材料无损耗),拼成的长方体的长是6.28厘米,高是5厘米,这个圆柱体的体积是多少立方厘米?
16.一个圆柱形储气罐,底面直径是16米,高是20米。
(1)它的体积是多少立方米?
(2)现在要在罐的顶面和侧面刷上油漆,如果每千克油漆只能刷4平方米,需要数油漆多少千克?(得数保留整千克)
17.一个圆柱形橡皮泥,底面周长是62.8cm,高是9cm。如果把它捏成底面直径是24cm的圆锥,这个圆锥的高是多少厘米?
18.向阳村要建一个圆柱形储水池.底面半径10米,深3米
(1)这个蓄水池的占地面积多少平方米?
(2)如果给这个蓄水池的四周和池底抹上水泥,抹水泥的面积是多少平方米?
(3)这个蓄水池能蓄水多少立方米?
19.一个圆柱形铁皮水桶(无盖),高15dm,底面直径是高的。做这个水桶大约要用多少铁皮?
20.妙想买了18块圆柱形橡皮泥,每块橡皮泥的底面直径是2cm,高是6cm。
(1)如果把其中一块橡皮泥捏成高是6cm的圆锥,圆锥的底面积是多少?
(2)妙想想用最少的硬纸板做一个长方体盒子(有盖)把18块橡皮泥装进去,做这个长方体盒子需要多少硬纸板?(粘贴处忽略不计)
21.一个圆锥形沙堆,底面半径2米,高1.2米,用这堆沙在10米宽的公路上铺2厘米的路面,能铺多少米?
22.小明把一个底面半径是3厘米的铁圆锥,放在从里面量半径是5厘米的圆柱形透明的玻璃容器内。小明把一瓶装有550毫升的纯净水倒入容器,这时水深正好与圆锥的高相等。圆锥的体积是多少?
23.一个底面周长25.12cm,高9cm的圆柱形钢块熔铸成一个底面直径12cm的圆锥,圆锥的高是多少厘米?
24.如图,一个圆柱高10厘米,如果它的高增加4厘米,那么它的表面积将增加50.24平方厘米,求原来圆柱的体积是多少立方厘米?
25.如果要焊制一个无盖的圆柱形水桶,有以下几种型号的铁皮供搭配选择。
你选择的铁皮型号是 号和 号(填序号),做这个水桶需要多少平方分米的铁皮?能装多少升水?(接口处忽略不计,圆周率取3.14)
26.把一根长5分米的圆钢截成4段后,表面积的总和比原来增加了113.04平方分米.求原来的圆钢的体积.
27.一个高为8分米的圆柱形木桶里,装了半桶水,把水倒出12升后,剩下的水恰好占水桶容积.这个水桶的底面积是多少平方分米?
28.一个圆柱形的汽油桶底面直径是8分米,高5分米.现装满汽油,如果每升汽油重0.85千克,这个油桶的汽油共多少千克?
29.在一个棱长为4厘米的正方体的前后.左右、上下各面的中心位置挖去一个底面半径为1厘米、高为1厘米的圆柱,则挖去后物体的表面积为多少?(圆周率取3.14计算)
30.古希腊著名的数学家阿基米德是历史上最杰出的数学家之一,在他众多的科学发现中,他自己最为满意的是:“圆柱容球定理”。如图,把一个球正好放在一个圆柱形容器中,球的直径与圆柱的高和底面直径相等,此时,球的体积正好是圆柱体积的,球的表面积也正好是圆柱表面积的。请你提一个富有挑战性的问题,并解答(请把此“圆柱容球”图片再画一下)
31.李师傅把一个正方体削成一个最大的圆锥体。正方体的体积是240立方分米,圆锥体的体积是多少立方分米?
32.在一个底面半径5厘米,高18厘米的圆柱形水桶内装满了水,另有一个圆锥形空水桶,它的上口周长为37.68厘米,现在把圆柱形水桶里的水往圆锥形水桶里倒,当圆锥形水桶装满时,圆柱形水桶还剩12厘米高的水,求圆锥形水桶的高。
33.张师傅想用一个底面直径为20厘米、高为40厘米的圆柱体木桩加工工艺品有以下几道工序:
工序1:截取一段圆柱体木桩削成最大的圆锥,使得圆锥的体积是1570立方厘米; 工序2:把圆锥和剩下的圆柱底面相接拼起来,在圆锥部分雕刻上花纹,圆柱部分涂上颜料。
请你帮张师傅算一算:
(1)截取的木桩有多高?
(2)拼接后,涂颜料的面积是多少平方厘米?
34.用一张长314cm、宽157cm的长方形纸围成一个圆柱体,有几种围法?计算一下,看看哪种围法体积大?
35.欣欣礼品店要用4张长18厘米,宽6厘米的长方形包装纸围成一个圆柱.第一张横着卷成圆柱,第二张竖着卷成圆柱,第三张和第四张围成的圆柱如图所示.
(1)围成这个圆柱的侧面积是多少?
(2)填一填,看看你发现了什么?(π取值3.14,结果保留两位小数)
底面周长(cm) 高(cm) 侧面积(cm2) 体积(cm3)
第一个圆柱
第二个圆柱
第三个圆柱
第四个圆柱
我发现: .
36.在一个直径是20cm的圆柱形容器里,放入一个底面半径是3cm的圆锥形铁块,全部浸设在水中,这时水面上升0.3cm。
(1)圆锥形铁块的体积是多少cm3?
(2)圆锥形铁块的高是多少dm?
37.一个圆锥,底面直径是20厘米,比它的高长25%。如果把这个圆锥沿着它的底面直径竖直切成两个完全相同的立体图形,截面的面积是多少平方厘米?
38.小明有两个圆柱形容器。一个底面半径为3厘米,另一个底面半径为4厘米,现在小明要把0.314升水倒入这两个容器中,让两个容器中的水高度相同,请问,容器中的水深多少厘米?
39.一个圆柱的体积是62.8cm3,要把它锻造成一个高为12cm的圆锥,圆锥底面积应是多少?
40.一个长方形模型的周长是24厘米,长与宽的比是3:1,以这个长方形的长边为中心轴,把这个长方形旋转周,得到的形体的体积是多少?
41.请你从如图型号的材料中选出两个制作一个无盖的圆柱形小水桶。(接口处忽略不计)
(1)选择的型号是 (填序号),这个水桶的底面积是 cm2。
(2)制作这个小水桶,一共需要多少平方厘米的铁皮?
(3)往这个小水桶中注水,水面上升到水桶高的处,这时水桶中水的体积是多少毫升?
42.一只底面半径是10cm的圆柱形瓶中,水深8cm,在瓶中放入长和宽都是8cm、高是15cm的一块长方体铁块,把铁块竖直放在水中,水面上升了几厘米?
43.一个圆柱形容器和一个圆锥形容器等底等高,圆柱形容器内原有12升水,现将圆锥形容器盛满水再全部倒入圆柱形容器,则圆柱形容器内水面上升到处。圆柱形容器的容积是多少?
44.一个圆柱形水桶装满水,把桶里的水倒出后,还剩下12升。水桶的高为5分米,水桶的底面积是多少平方分米?(水桶壁的厚度忽略不计)
45.一个直角三角形,一条直角边长6厘米,另一条直角边长4厘米,以它的较长的直角边为轴旋转一周后形成一个立体图形.求这个旋转后立体图形的体积.
46.一个从里面量底面直径为20cm的圆柱形容器中装有一部分水,在水中浸没一个底面直径为12cm的圆锥形铅锤,这时水面高度是15cm,当把铅锤从容器中取出后,容器中的水面高度下降到13.8cm。这个铅锤的高是多少厘米?
47.一个底面周长是25.12cm,高是18cm的圆柱形玻璃缸中有一些水,把一个底面半径是3cm的圆锥形铁块浸没在水中(水未溢出),缸内水面上升了1.5cm,圆锥形铁块的高是多少?
48.一个圆锥形零件,底面积是170平方厘米,高是12厘米。这个零件的体积是多少立方厘米?
49.广汉市某校六年级一班张敏敏购买了一个底面直径10厘米,高12厘米的圆柱形水杯。为了使水杯更加美观,她在水杯的侧面贴上了一圈彩纸,至少需要多少平方厘米的彩纸(接头处忽略不计)?她先往水杯里倒入628mL水,再把一个高为6厘米的圆锥形玩具,完全浸没在水中,这时水面上升0.8厘米,这个圆锥形玩具的底面积是多少平方厘米?
50.一张长方形铁皮,长18.84dm,宽6dm,用这张铁皮卷成一个圆柱形铁皮水桶的侧面,另配一个底面制成一个最大的水桶。这个铁皮水桶的表面积是多少dm2?水桶的容积是多少?
51.一个圆锥形沙堆,底面周长是25.12米,高1.8米.如果每立方米沙重1.7吨,这堆沙子重多少吨?
52.把一个底面直径20厘米的圆柱切拼成一个近似的长方体,长方体表面积比圆柱表面积多400平方厘米。圆柱的体积是多少立方厘米?
53.将一个底面半径是4厘米,高是9厘米的实心圆柱形铁块,锻造成一个底面半径是8厘米的实心圆锥形铁块,这个圆锥形铁块的高是多少厘米?
54.如图是一个无盖的长方体玻璃容器,水面的高度是8cm。把一个底面半径是4cm的圆锥形铅锤完全浸入水中,水面上升了0.628cm,这个铅锤的高是多少厘米?
55.如图,用一张长165.6厘米的铁皮,剪下一个最大的圆作为圆柱的底面,剩下的部分围在底面上做成一个无盖的铁皮水桶,算一算这个铁皮水桶的容积是多少?(铁皮厚度不计,π取3.14)
56.一种油菜籽榨油机的漏斗是由圆柱和圆锥两部分组成。底面周长是18.84dm,圆柱和圆锥的高都是6dm。每立方分米油菜籽重0.5kg。
(1)这个漏斗最多能装多少千克油菜籽?
(2)如果油菜籽的出油率是45%,一漏斗油菜籽能榨出多少千克菜籽油?
57.一个圆柱形容器从里面量底面直径是20cm,高是10cm,里面水深9cm,现在将一个底面半径是8cm,高是6cm的实心圆锥形铁块完全浸没在水中,这时,圆柱形容器中的水会溢出来吗?如果会溢出,则溢出多少mL?
58.在一个直径是20厘米的圆柱形容器里,放入一个底面半径2厘米的圆锥形铁块,全部浸没在水中,这时水面上升了0.3厘米。这个圆锥形铁块的高是多少厘米?
59.一个圆柱形玻璃杯,内直径为8厘米,内装16厘米深的水,恰好占杯子容量的,杯内还可以加入多少毫升的水?
60.一个圆锥体的体积是15.7立方分米,底面积是3.14平方分米,它的高有多少分米?
圆柱与圆锥
参考答案与试题解析
1.如图1,这是一个由等底等高的圆柱和圆锥组合而成的计时工具,圆锥内灌满了有颜色水。其中圆锥的高为6厘米,底面半径为3厘米。已知水的流速是1.57立方厘米/分钟。
(1)圆锥内漏完水需要多少时间?
(2)请你在图2中用阴影表示出此时圆柱内的水。
【答案】(1)36分钟;
(2)
【分析】(1)根据圆锥的体积公式:Vπr2h,把数据代入公式求出圆锥容器内水的体积,然后根据“包含”除法的意义,用除法解答。
(2)因为等底等等高的圆柱的体积是圆锥体积的3倍,所以当圆柱与圆锥的体积相等,底面积也相等时,圆柱的高是圆锥高的,据此解答即可。
【解答】解:(1)3.14×32×6÷1.57
3.14×9×6÷1.57
=56.52÷1.57
=36(分钟)
答:圆锥内漏完水需要36分钟。
(2)62(厘米)
答:圆柱容器内水深2厘米。
作图如下:
【点评】此题主要考查圆锥体积公式的灵活运用,等底等高的圆柱与圆锥体积之间的关系及应用。
2.用白铁皮制作一个高10分米,底面半径是2分米的圆柱形通风管,至少用铁皮多少平方分米?(得数保留整数)
【答案】见试题解答内容
【分析】求做圆柱形铁皮通风管用多少铁皮,就是求它的侧面积是多少,可直接利用底面周长乘高来解答,然后再选正确答案即可.
【解答】解:3.14×2×2×10
=12.56×10
=125.6
≈126(平方分米)
答:至少用铁皮126平方分米.
【点评】此题是考查求侧面积的实际应用,可利用侧面积公式解答.
3.一个圆柱体的侧面积是1cm2,体积是2cm3,它的底面积是多少平方厘米?
【答案】50.24平方厘米。
【分析】设底面半径为r,高为h,再根据圆柱的侧面积公式:S=πdh,圆柱的体积公式:V=πr2h,列出来两个方程求出半径和高,然后即可得出底面积。
【解答】解:设底面半径为r,高为h
r=4
3.14×4×4=50.24(平方厘米)
答:它的底面积是50.24平方厘米。
【点评】本题考查学生对圆柱表面积和体积公式的掌握和运用。
4.一个圆锥形沙堆底面周长是12.56米,高是3米,这个圆锥形沙堆的体积是多少?
【答案】见试题解答内容
【分析】沙堆的形状是圆锥形的,利用圆锥的体积计算公式解答,即圆锥的体积π(C÷π÷2)2h,把数据代入公式进行解答即可.
【解答】解:3.14×(12.56÷3.14÷2)2×3
3.14×22×3
=3.14×4
=12.56(立方米)
答:这个圆锥沙堆的体积是12.56立方米.
【点评】此题主要考查圆锥的体积计算公式Vπr2h,运用公式计算时不要漏乘.
5.一个无盖的圆柱形铁皮水桶,水桶内存有一些水,水面高度正好是桶高的,淘气将一块体积为628立方厘米的铁块放入水中,完全浸没。这时水面上升了2厘米,水桶正好装满。
(1)这个水桶的高是多少厘米?
(2)做这个水桶需要铁皮多少平方厘米?(铁皮的厚度和接口处忽略不计)
【答案】(1)20厘米;
(2)1570平方厘米。
【分析】(1)把水桶的高看作单位“1”,由题意可知,2厘米相当于水桶高的(1),根据已知一个数的几分之几是多少,求这个数,用除法解答。
(2)根据圆柱的体积公式:V=Sh,那么S=V÷h,据此可以求出水桶的底面积,进而求出水桶的底面半径,再根据圆柱的侧面积公式:S=πdh,圆的面积公式:S=πr2,把数据代入公式解答。
【解答】解:(1)2÷(1)
=2×10
=20(厘米)
答:这个水桶的高是20厘米。
(2)水桶的底面积:628÷2=314(平方厘米)
314÷3.14=100(平方厘米)
因为10的平方是100,所以水桶的底面半径是10厘米,
2×3.14×10×20+314
=62.8×20+314
=1256+314
=1570(平方厘米)
答:做这个水桶需要铁皮1570平方厘米。
【点评】此题主要考查圆柱的体积公式、圆柱的侧面积公式、圆的面积公式的灵活运用,关键是熟记公式。
6.一根圆柱形铁棒,底面周长是12.56厘米,长是100厘米,它的体积是多少立方厘米?
【答案】见试题解答内容
【分析】先根据圆的周长公式求出圆柱形铁棒的底面半径,继而求出圆的面积,再根据圆柱的体积公式V=sh求出它的体积.
【解答】解:12.56÷3.14÷2,
=4÷2,
=2(厘米);
3.14×22×100,
=3.14×4×100,
=3.14×400,
=1256(立方厘米).
答:它的体积是1256立方厘米.
【点评】此题是考查圆柱的体积计算,在利用体积公式V=sh求体积的过程中注意求得圆柱形铁棒的底面半径,从而得到圆柱形铁棒的体积.
7.有一个高8厘米,容积是50毫升的圆柱形容器,装满了水。将一个高6厘米的圆锥形铁块垂直放入水中,有水溢出。把圆锥形铁块从水中取出后,圆柱形容器内水的高度只有6厘米。求圆锥形铁块的体积是多少立方厘米?
【答案】12.5立方厘米。
【分析】首先根据圆柱的体积公式:V=Sh,那么S=V÷h,据此求出圆柱形容器的底面积;圆柱形容器装满了水。将一个高6厘米的圆锥形铁块垂直放入水中,有水溢出。把圆锥形铁块从水中取出后,圆柱形容器内水的高度只有6厘米,溢出水的体积就等于这个圆锥形铁块的体积,据此解答即可。
【解答】解:50毫升=50立方厘米
50÷8=6.25(平方厘米)
8﹣6=2(厘米)
6.25×2
=6.25×2
=12.5(立方厘米)
答:圆锥形铁块的体积12.5立方厘米。
【点评】此题主要考查圆柱体积公式的灵活运用,关键是熟记公式。
8.一根长是20分米,底面直径是8分米的圆柱形木料横放入水中,正好有一半浮在水面上(如图)。
(1)这根木料露出水面部分的面积是多少平方分米?
(2)这根木料没入水中部分的体积是多少立方分米?
【答案】(1)301.44平方米;
(2)502.4立方米。
【分析】(1)根据题意可知,这根木头与水接触面的面积等于这个圆柱表面积的一半,根据圆柱的表面积=侧面积+底面积×2,把数据代入公式求出它的表面积的一半即可。
(2)木头没入水里部分的体积是这个圆柱体积的一半,根据圆柱的体积公式:V=πr2h,把数据代入公式解答。
【解答】解:(1)3.14×8×20÷2+3.14×(8÷2)2
=502.4÷2+3.14×16
=251.2+50.24
=301.44(平方分米)
答:这根木头露出水面部分的面积是301.44平方分米。
(2)3.14×(8÷2)2×20÷2
=3.14×16×20÷2
=50.24×20÷2
=502.4(立方分米)
答:木头没入水里部分的体积是502.4立方分米。
【点评】此题主要考查圆柱的表面积公式、圆柱的体积公式的灵活运用,关键是熟记公式。
9.一个长方体木料,相交于同一个顶点的三条棱长度分别为12分米、8分米、16分米。
(1)这个长方体的体积是多少立方分米?
(2)如果把这个长方体加工成体积最大的圆柱,这个圆柱的体积是多少立方分米?
【答案】(1)1536立方分米
(2)904.32立方分米
【分析】(1)根据长方体的特征,相交于同一点的三条棱,就是长方体的长、宽、高相交于一点,由此可知长方体的长、宽、高的长度;根据长方体的体积公式:长×宽×高,代入数据,求出长方体体积;
(2)把长方体加工成圆柱,有3种方法,①以12分米为直径,高为8分米的圆柱;②以8分米为直径,高为16分米;③以8分米为直径,高为12分米;利用圆柱的体积公式:底面积×高,求出三种加工成的圆柱的体积,再比较大小,求出这个圆柱的最大体积是多少。
【解答】解:(1)12×8×16
=96×16
=1536(立方分米)
答:这个长方体的体积是1536立方分米。
(2)①以12分米为直径,以8分米为高:
体积:3.14×(12÷2)2×8
=3.14×36×8
=113.04×8
=904.32(立方分米)
②以8分米为直径,以16分米为高:
体积:3.14×(8÷2)2×16
=3.14×16×16
=50.24×16
=803.84(立方分米)
③以8分米为直径,高为12厘米:
体积:3.14×(8÷2)2×12
=3.14×16×12
=50.24×12
=602.88(立方分米)
904.32>803.84>602.88
这个圆柱的体积最大是904.32立方分米。
答:这个圆柱的体积是904.32立方分米。
【点评】利用长方体体积公式以及圆柱体积公式进行解答,关键明确长方体内切成最大的圆柱,有三种不同的切法,求最大体积需要求出三者切法的体积,进行比较解答。
10.有一个底面直径为20厘米的装有一些水的圆柱形玻璃杯,已知杯中水面距杯口2.24厘米.若将一个半径为9厘米的圆锥形铅锤完全浸入水中,水会溢出314立方厘米.求铅锤的高.
【答案】见试题解答内容
【分析】根据题意可知:圆柱形玻璃杯内没有水的部分(空的)体积加上放入圆锥形铅锤后溢出水的体积等于这个圆锥形铅锤的体积,根据圆柱的体积公式:V=Sh,求出没有水的体积,再根据圆锥的体积公式:VSh,那么h=VS,把数据代入公式解答.
【解答】解:3.14×(20÷2)2×2.24+314
=3.14×100×2.24+314
=703.36+314
=1017.36(立方厘米),
1017.36(3.14×92)
=1017.36×3÷254.34
=3052.08÷254.34
=12(厘米),
答:铅锤的高是12厘米.
【点评】此题主要考查圆柱、圆锥体积公式的灵活运用,关键是熟记公式.
11.一个圆锥体铁块,底面半径是5厘米,高比底面直径少,将这个圆锥体铁块放入到装有水的圆柱形容器中,完全浸没且没有水溢出,已知圆柱从里面量直径是20厘米,铁块放入后水面会上升多少厘米?
【答案】0.5厘米。
【分析】把圆锥的底面半径看作单位“1”,高比底面直径少,也就是高相当于底面直径的(1),根据一个数乘分数的意义,用乘法求出圆锥的高,再根据圆锥的体积公式:Vr2h,求出圆锥铁块的体积,然后根据圆柱的体积公式:V=πr2h,用圆锥铁块的体积除以圆柱形容器的底面积就是水面上升的高度。
【解答】解:圆锥的高:
5×2×(1)
=10
=6(厘米)
3.14×52×6÷[3.14×(20÷2)2]
3.14×25×6÷[3.14×100]
=157÷314
=0.5(厘米)
答:铁块放入后水面会上升0.5厘米。
【点评】此题主要考查圆锥、圆柱体积公式的灵活运用,关键是熟记公式,重点是求出圆锥的高。
12.一个高为4分米的圆柱,把底面分成若干个相等的扇形,再竖直切开拼成一个近似的长方体,表面积增加了16平方分米,圆柱的体积是多少立方分米?(结果保留π)
【答案】16π立方分米。
【分析】根据圆柱体积公式的推导过程可知,把一个圆柱切拼成一个近似长方体后,体积不变,拼成的近似长方体的表面积把圆柱的表面积增加了两个切面的面积,每个切面的长等于圆柱的高,每个切面的宽等于圆柱的底面半径,已知表面积增加了16平方分米,据此可以求出圆柱的底面半径,再根据圆柱的体积公式:V=πr2h,把数据代入公式解答。
【解答】解:底面半径:
16÷2÷4
=8÷4
=2(分米)
体积:
π×22×4
=π×4×4
=16π(立方分米)
答:圆柱的体积是16π立方分米。
【点评】此题考查的目的是理解掌握圆柱体积公式的推导过程及应用,长方体的表面积、圆柱的表面积的意义及应用。
13.沿着圆柱体的直径自上而下锯成2部分,表面积增加36平方厘米,高与底面直径的比是2:1,这个圆柱的体积是多少?
【答案】42.39立方厘米。
【分析】根据题意可知,把这个圆柱沿底面直径锯成两个半圆柱,表面积增加的两个截面的面积,每个截面的长等于圆柱的高,每个截面的宽等于圆柱的底面直径,已知高与底面直径的比是2:1,据此可以求出高和底面直径,然后根据圆柱的体积公式:V=πr2h,把数据代入公式解答。
【解答】解:36÷2=18(平方厘米)
18=6×3
所以圆柱的高是6厘米,底面直径是3厘米,
3.14×(3÷2)2×6
=3.14×2.25×6
=7.065×6
=42.39(立方厘米)
答:这个圆柱的体积是42.39立方厘米。
【点评】此题主要考查长方形的面积公式、圆柱的体积公式的灵活运用,关键是熟记公式,重点求出圆柱的高和底面直径。
14.如图,把一个圆柱等分成若干等份,拼成一个近似的长方体,表面积增加了300平方厘米、已知长方体的高是20厘米。长方体的体积是多少?
【答案】3532.5立方厘米。
【分析】根据圆柱体积公式的推导过程可知,把一个圆柱切拼成一个近似长方体,拼成的长方体的底面积等于圆柱的底面积,长方体的高等于圆柱的高,拼成的长方体的表面积比圆柱的表面积增加了两个截面的面积,每个切面的长等于圆柱的高,每个切面的宽等于圆柱的底面半径,已知表面积增加了300平方厘米,据此可以求出圆柱的底面半径,再根据圆柱的体积公式:V=πr2h,把数据代入公式解答。
【解答】解:300÷2÷20
=150÷20
=7.5(厘米)
3.14×7.52×20
=3.14×56.25×20
=176.625×20
=3532.5(立方厘米)
答:长方体的体积是3532.5立方厘米。
【点评】此题考查的目的是理解掌握圆柱体积公式的推导过程及应用,关键是求出圆柱的底面半径。
15.在圆柱体的体积推导过程中,把一个圆柱体平均分成若干等份,然后拼成一个近似的长方体(材料无损耗),拼成的长方体的长是6.28厘米,高是5厘米,这个圆柱体的体积是多少立方厘米?
【答案】见试题解答内容
【分析】根据圆柱体积公式的推导过程可知:把一个圆柱体平均分成若干等份,然后拼成一个近似的长方体(材料无损耗),拼成的长方体的长等于圆柱底面周长的一半,长方体的高等于圆柱的高,根据圆的周长公式:C=2πr,求出圆柱的底面半径,再根据圆柱的体积公式:V=πr2h,把数据代入公式解答.
【解答】解:6.28×2÷3.14÷2
=12.56÷3.14÷2
=4÷2
=2(厘米),
3.14×22×5
=3.14×4×5
=62.8(立方厘米),
答:这个圆柱的体积是62.8立方厘米.
【点评】此题主要考查圆的周长公式、圆柱的体积公式的灵活运用,关键是熟记公式.
16.一个圆柱形储气罐,底面直径是16米,高是20米。
(1)它的体积是多少立方米?
(2)现在要在罐的顶面和侧面刷上油漆,如果每千克油漆只能刷4平方米,需要数油漆多少千克?(得数保留整千克)
【答案】(1)4019.2平方米;
(2)302千克。
【分析】(1)根据圆柱的体积公式:V=πr2h,把数据代入公式解答。
(2)根据圆柱的侧面积公式:S=πdh,圆的面积公式:S=πr2,把数据代入公式求出刷油漆的面积,然后根据“包含”除法的意义,用除法解答。
【解答】解:(1)3.14×(16÷2)2×20
=3.14×64×20
=200.96×20
=4019.2(立方米)
答:它的体积是4019.2立方米。
(2)[3.14×16×20+3.14×(16÷2)2]÷4
=[50.24×20+3.14×64]÷4
=[1004.8+200.96]÷4
=1205.76÷4
≈302(千克)
答:需要油漆302千克。
【点评】此题主要考查圆柱的体积公式、圆柱的表面积公式的灵活运用,关键是熟记公式。
17.一个圆柱形橡皮泥,底面周长是62.8cm,高是9cm。如果把它捏成底面直径是24cm的圆锥,这个圆锥的高是多少厘米?
【答案】18.75厘米。
【分析】根据圆柱的体积公式:V=πr2h,圆锥的体积公式:Vr2h,那么h=Vπr2,把数据代入公式解答。
【解答】解:3.14×(62.8÷3.14÷2)2×9[3.14×(24÷2)2]
=3.14×100×9[3.14×144]
=2826×3÷452.16
=8478÷452.16
=18.75(厘米)
答:这个圆锥的高是18.75厘米。
【点评】此题主要考查圆柱、圆锥体积公式的灵活运用,关键是熟记公式。
18.向阳村要建一个圆柱形储水池.底面半径10米,深3米
(1)这个蓄水池的占地面积多少平方米?
(2)如果给这个蓄水池的四周和池底抹上水泥,抹水泥的面积是多少平方米?
(3)这个蓄水池能蓄水多少立方米?
【答案】见试题解答内容
【分析】(1)求这个蓄水池的占地面积也就是求蓄水池的底面积,根据圆的面积公式解答;
(2)抹水泥的面积=圆柱的侧面积+底面积,又因圆柱的侧面积=底面周长×高,圆柱的底面周长和高已知,则可以求出侧面积,底面积已求,于是可以求出抹水泥的面积.
(3)这个蓄水池能蓄水多少立方米,也就是求它容积,根据圆柱的容积公式解答.
【解答】解:(1)3.14×102
=3.14×100
=314(平方米)
答:蓄水池占地314平方米.
(2)3.14×10×2×3+314
=188.4+314
=502.4(平方米)
答:抹水泥的面积是502.4平方米.
(3)314×3=942(立方米)
答:这个蓄水池能蓄水942立方米.
【点评】解答此题主要分清所求物体的形状,转化为求有关图形的体积或面积的问题,把实际问题转化为数学问题,再运用数学知识解决.
19.一个圆柱形铁皮水桶(无盖),高15dm,底面直径是高的。做这个水桶大约要用多少铁皮?
【答案】487dm2。
【分析】无盖的圆柱形铁皮水桶,则计算一个底面积加上侧面积即可,知道底面直径和高的关系,先求出底面直径,再根据公式可求底面积和侧面积,然后相加即可。
【解答】解:圆柱的底面直径:159(dm)
需用铁皮面积:
3.14×9×15+3.14×(9÷2)2
=423.9+63.585
=487.485
≈487(dm2)
答:做这个水桶大约要用487dm2铁皮。
【点评】此题考查了圆柱的表面积的计算方法,计算表面积时注意此题只算一个底面的面积。
20.妙想买了18块圆柱形橡皮泥,每块橡皮泥的底面直径是2cm,高是6cm。
(1)如果把其中一块橡皮泥捏成高是6cm的圆锥,圆锥的底面积是多少?
(2)妙想想用最少的硬纸板做一个长方体盒子(有盖)把18块橡皮泥装进去,做这个长方体盒子需要多少硬纸板?(粘贴处忽略不计)
【答案】(1)9.42平方厘米;
(2)360平方厘米。
【分析】(1)根据圆柱的体积公式:V=πr2h,圆锥的体积公式:VSh,那么S=Vh,把数据代入公式解答。
(2)根据题意,把18个这样的圆柱平均分成3份,每排放6个,放3排。这样长方体盒子的长是圆柱直径的6倍,宽是圆柱底面直径的3倍,盒子的高等于圆柱的高,根据长方体的表面积公式:S=(ab+ah+bh)×2,把数据代入公式解答。
【解答】解:(1)3.14×(2÷2)2×66
=3.14×1×6×3÷6
=9.42(平方厘米)
答:圆锥的底面积是9.42平方厘米。
(2)盒子的长:2×6=12(厘米)
盒子的宽:2×3=6(厘米)
盒子的高是6厘米。
(12×6+12×6+6×6)×2
=(72+72+36)×2
=180×2
=360(平方厘米)
答:做这个长方体盒子需要360平方厘米硬纸板。
【点评】此题主要考查圆柱、圆锥体积公式的灵活运用,长方体表面积公式的灵活运用,关键是熟记公式,重点是确定长方体盒子的长、宽、高。
21.一个圆锥形沙堆,底面半径2米,高1.2米,用这堆沙在10米宽的公路上铺2厘米的路面,能铺多少米?
【答案】见试题解答内容
【分析】先利用圆锥的体积计算公式求出这堆沙的体积,再据沙子的体积不变,代入长方体的体积公式即可求出所铺沙子的长度.
【解答】解:2厘米=0.02米
沙堆的体积:3.14×22×1.2
=3.14×4×0.4
=5.024(立方米)
所铺沙子的长度:5.024÷(10×0.02)
=5.024÷0.2
=25.12(米)
答:能铺25.12米长.
【点评】此题主要考查圆锥和长方体的体积计算方法,关键是明白:沙子的体积不变.
22.小明把一个底面半径是3厘米的铁圆锥,放在从里面量半径是5厘米的圆柱形透明的玻璃容器内。小明把一瓶装有550毫升的纯净水倒入容器,这时水深正好与圆锥的高相等。圆锥的体积是多少?
【答案】75立方厘米。
【分析】根据圆锥的体积公式:Vπr2h,圆柱的体积公式:V=πr2h,圆锥的体积+水的体积=圆柱容器内水高等于圆锥高的体积,设圆锥的高为h厘米,据此列方程求出圆锥的高,然后把数据代入公式求出圆锥的体积。
【解答】解:设圆锥的高为h厘米,
550毫升=550立方厘米
π×32×h+550=π×52h
3πh+550=25πh
25πh﹣3πh=550
22πh=550
h
π×3275(立方厘米)
答:圆锥的体积是75立方厘米。
【点评】此题主要考查圆锥的体积公式、圆柱的体积(容积)公式的灵活运用,关键是熟记公式,重点是求出圆锥的高。
23.一个底面周长25.12cm,高9cm的圆柱形钢块熔铸成一个底面直径12cm的圆锥,圆锥的高是多少厘米?
【答案】12厘米。
【分析】根据体积的意义可知,熔铸前后的体积不变,先根据圆柱的体积公式求出它的体积,再利用圆锥的体积公式求出它的高即可。
【解答】解:3.14×(25.12÷3.14÷2)2×9[3.14×(12÷2)2]
=3.14×16×9[3.14×36]
=452.16×3÷113.04
=1356.48÷113.04
=12(厘米)
答:圆锥的高是12厘米。
【点评】此题主要考查圆柱、圆锥体积公式的灵活运用,关键是熟记公式。
24.如图,一个圆柱高10厘米,如果它的高增加4厘米,那么它的表面积将增加50.24平方厘米,求原来圆柱的体积是多少立方厘米?
【答案】125.6立方厘米。
【分析】用增加的表面积除以增加的高可得到原来圆柱的底面周长,然后再利用圆的周长公式计算出圆柱的底面半径,最后再利用圆柱的体积公式V=Sh计算出圆柱的体积即可。
【解答】解:原来圆柱的底面周长为:50.24÷4=12.56(厘米)
原来圆柱的底面半径为:
12.56÷3.14÷2
=4÷2
=2(厘米)
原来圆柱的体积为:
3.14×22×10
=12.56×10
=125.6(立方厘米)
答:原来圆柱的体积是125.6立方厘米。
【点评】解答此题的关键是确定圆柱的底面半径,然后再利用圆柱的体积公式进行计算即可。
25.如果要焊制一个无盖的圆柱形水桶,有以下几种型号的铁皮供搭配选择。
你选择的铁皮型号是 ① 号和 ③ 号(填序号),做这个水桶需要多少平方分米的铁皮?能装多少升水?(接口处忽略不计,圆周率取3.14)
【答案】答案不唯一。①,③,75.36平方分米。
【分析】根据圆柱侧面展开图的特征,圆柱的侧面沿高展开是一个长方形,这个长方形的长等于圆柱的底面周长,长方形的宽等于圆柱的高,根据圆的周长公式:C=πd,把数据分别代入公式求出两个圆的周长,然后与两个长方形的长进行比较即可,因为水桶无盖,根据圆柱的表面积=侧面积+底面积,把数据代入公式解答。
【解答】解:3.14×4=12.56(分米)
3.14×3=9.42(分米)
可以选择①和③,也可以选择②和④。
我选择①和③。
12.56×5+3.14×(4÷2)2
=62.8+3.14×4
=62.8+12.56
=75.36(平方分米)
答:做这个水桶需要75.36平方分米的铁皮。
故答案为:①,③。
【点评】此题考查的目的是理解掌握圆柱侧面展开图的特点及应用,圆柱的表面积公式及应用。
26.把一根长5分米的圆钢截成4段后,表面积的总和比原来增加了113.04平方分米.求原来的圆钢的体积.
【答案】见试题解答内容
【分析】首先要明确的是:将这根圆钢锯成4段小圆柱后,增加了6个底面,增加的面积已知,于是就可以求出这根圆钢的底面积,从而利用圆柱的体积V=Sh,即可求出这根圆钢的体积.
【解答】解:113.04÷6=18.84(平方分米),
18.84×5=94.2(立方分米).
答:原来的圆钢的体积是94.2立方分米.
【点评】解答此题的关键是明白:将这根圆钢锯成4段小圆柱后,增加了6个底面,求出圆钢的底面积,即可利用圆柱的体积公式求解.
27.一个高为8分米的圆柱形木桶里,装了半桶水,把水倒出12升后,剩下的水恰好占水桶容积.这个水桶的底面积是多少平方分米?
【答案】见试题解答内容
【分析】把水桶的容积看作单位“1”,已知装有半桶水(桶),把水倒出12升后,剩下的水恰好占水桶容积.那么倒出的12升占容积的(),根据已知一个数的几分之几是多少,求这个数,用除法求出水桶的容积(水的体积),然后用水的体积除以水桶的高即可.
【解答】解:12升=12立方分米,
12÷()
=40(立方分米),
40÷8=5(平方分米),
答:这个水桶的底面积是5平方分米.
【点评】此题主要考查圆柱的体积(容积)公式的灵活运用,重点是根据已知一个数的几分之几是多少,求这个数,用除法求出水桶的容积(水的体积),注意:容积单位与体积单位之间的换算.
28.一个圆柱形的汽油桶底面直径是8分米,高5分米.现装满汽油,如果每升汽油重0.85千克,这个油桶的汽油共多少千克?
【答案】见试题解答内容
【分析】首先根据圆柱的体积公式:v=sh,把数据代入公式求出油桶内汽油的体积,然后用汽油的体积乘每升油的质量即可.
【解答】解:1升=1立方分米,
3.14×(8÷2)2×5×0.85
=3.14×16×5×0.85
=50.24×5×0.85
=251.2×0.85
=213.52(千克),
答:这个油桶的汽油共213.52千克.
【点评】此题主要考查圆柱的体积公式在实际生活中的应用,关键是熟记公式.注意:容积单位与体积单位之间的换算.
29.在一个棱长为4厘米的正方体的前后.左右、上下各面的中心位置挖去一个底面半径为1厘米、高为1厘米的圆柱,则挖去后物体的表面积为多少?(圆周率取3.14计算)
【答案】见试题解答内容
【分析】根据题意可知,把这个正方体从前后.左右、上下各面的中心位置挖去一个底面半径为1厘米、高为1厘米的圆柱,挖去后物体的表面积比原来正方体的表面积增加了6个底面半径为1厘米、高为1厘米的圆柱的侧面积,根据正方体的表面积公式:S=6a2,圆柱的侧面积公式:S=2πrh,把数据分别代入公式解答.
【解答】解:4×4×6+2×3.14×1×1×6
=96+6.28×
=96+37.68
=133.68(平方厘米)
答:挖去后物体的表面积为133.68平方厘米.
【点评】此题主要考查正方体的表面积公式、圆柱的侧面积公式的灵活运用,关键是熟记公式.
30.古希腊著名的数学家阿基米德是历史上最杰出的数学家之一,在他众多的科学发现中,他自己最为满意的是:“圆柱容球定理”。如图,把一个球正好放在一个圆柱形容器中,球的直径与圆柱的高和底面直径相等,此时,球的体积正好是圆柱体积的,球的表面积也正好是圆柱表面积的。请你提一个富有挑战性的问题,并解答(请把此“圆柱容球”图片再画一下)
【答案】球的体积是多少立方厘米?113.04立方厘米。
【分析】先画出图形中圆柱的高,提出问题:球的体积是多少立方厘米?再根据球的直径与圆柱的高和底面直径相等,此时球的体积正好是圆柱体积的,利用圆柱的体积公式:V=πr2h,计算圆柱的体积,进而求出球的体积即可。
【解答】解:球的体积是多少立方厘米?
如图:
3.14×(6÷2)2×6
=3.14×9×6
=113.04(立方厘米)
答:图中球的体积是113.04立方厘米。
【点评】本题主要考查球的体积的计算,解题的关键是利用球和圆柱的关系,求出球的体积。
31.李师傅把一个正方体削成一个最大的圆锥体。正方体的体积是240立方分米,圆锥体的体积是多少立方分米?
【答案】62.8立方分米。
【分析】根据题意可知,把一个正方体削成一个最大的圆锥体,这个圆锥的底面直径和高都等于正方体的棱长,首先根据正方体的体积公式:V=a3,圆锥的体积公式:Vπr2h,设正方体的棱长为a分米,把数据代入公式求出圆锥的体积是正方体体积的几分之几,然后根据求一个数的几分之几是多少,用乘法圆锥的体积。
【解答】解:设正方体的棱长为a分米,则圆锥的底面直径和高都是a分米,
圆锥的体积:π×()2×a
πa
(立方分米)
正方体的体积:a×a×a=a3(立方分米)
所以圆锥的体积是正方体体积的:a3
240
=62.8(立方分米)
答:圆锥体的体积是62.8立方分米。
【点评】此题主要考查正方体的体积公式、圆锥的体积公式的灵活运用,关键是明白:把一个正方体削成一个最大的圆锥体,这个圆锥的底面直径和高都等于正方体的棱长,重点是求出圆锥的体积是正方体体积的几分之几,再根据求一个数的几分之几是多少,用乘法解答。
32.在一个底面半径5厘米,高18厘米的圆柱形水桶内装满了水,另有一个圆锥形空水桶,它的上口周长为37.68厘米,现在把圆柱形水桶里的水往圆锥形水桶里倒,当圆锥形水桶装满时,圆柱形水桶还剩12厘米高的水,求圆锥形水桶的高。
【答案】12.5厘米。
【分析】根据圆柱体积=底面积×高,用圆柱形水桶底面积×(水桶的高﹣剩下水的高),求出倒入圆锥形水桶中水的体积,用圆锥底面周长÷圆周率÷2,求出圆锥底面半径,倒入圆锥形水桶中水的体积×3÷圆锥底面积=圆锥形水桶的高,据此列式解答。
【解答】解:3.14×52×(18﹣12)
=3.14×25×6
=78.5×6
=471(立方厘米)
471×3÷[3.14×(37.68÷3.14÷2)2]
=1413÷[3.14×36]
=1413÷113.04
=12.5(厘米)
答:圆锥形水桶的高是12.5厘米。
【点评】此题主要考查圆柱、圆锥的体积(容积)公式的灵活运用,关键是熟记公式。
33.张师傅想用一个底面直径为20厘米、高为40厘米的圆柱体木桩加工工艺品有以下几道工序:
工序1:截取一段圆柱体木桩削成最大的圆锥,使得圆锥的体积是1570立方厘米; 工序2:把圆锥和剩下的圆柱底面相接拼起来,在圆锥部分雕刻上花纹,圆柱部分涂上颜料。
请你帮张师傅算一算:
(1)截取的木桩有多高?
(2)拼接后,涂颜料的面积是多少平方厘米?
【答案】(1)15厘米;
(2)1884平方厘米。
【分析】(1)根据圆锥的体积公式:Vπr2h,那么h=Vπr2,把数据代入公式解答。
(2)用木桩的高减去圆锥的高就是圆柱的高,涂颜料的部分是圆柱的一个底面和侧面,根据圆的面积公式:S=πr2,圆柱的侧面积公式:S=πdh,把数据代入公式解答。
【解答】解:(1)1570[3.14×(20÷2)2]
=1570×3÷[3.14×100]
=4710÷314
=15(厘米)
答:截取的木桩有15厘米高。
(2)3.14×(20÷2)2+3.14×20×(40﹣15)
=3.14×100+3.14×20×25
=314+1570
=1884(平方厘米)
答:涂颜料的面积是1884平方厘米。
【点评】此题主要考查圆锥的体积公式、圆柱的表面积公式的灵活运用,关键是熟记公式。
34.用一张长314cm、宽157cm的长方形纸围成一个圆柱体,有几种围法?计算一下,看看哪种围法体积大?
【答案】见试题解答内容
【分析】根据圆柱侧面展开图的特征,圆柱的侧面展开是一个长方形,这个长方形的长等于圆柱的底面周长,长方形的宽等于圆柱的高,因此,用一张长方形的纸围成一个圆柱有两种围法,其中当围成的圆柱的高等于长方形的宽时,圆柱的体积较大
【解答】解:围成圆柱的高是157厘米,那么圆柱的底面周长就是314厘米,
3.14×(314÷3.14÷2)2×157
=3.14×502×157
=3.14×2500×157
=7850×157
=1232450(立方厘米);
围成圆柱的高是314厘米,那么圆柱的底面周长就是157厘米,
3.14×(157÷3.14÷2)2×314
=3.14×252×314
=3.14×625×314
=1962.5×314
=616225(立方厘米);
1232450立方厘米>616225立方厘米
答:当围成的圆柱的高为157厘米,底面周长是314厘米时,圆柱的体积较大.
【点评】此题考查的目的是理解掌握圆柱侧面展开图的特征,以及圆柱体积公式的灵活运用,关键是熟记公式.
35.欣欣礼品店要用4张长18厘米,宽6厘米的长方形包装纸围成一个圆柱.第一张横着卷成圆柱,第二张竖着卷成圆柱,第三张和第四张围成的圆柱如图所示.
(1)围成这个圆柱的侧面积是多少?
(2)填一填,看看你发现了什么?(π取值3.14,结果保留两位小数)
底面周长(cm) 高(cm) 侧面积(cm2) 体积(cm3)
第一个圆柱
第二个圆柱
第三个圆柱
第四个圆柱
我发现: 当侧面积一定时,越是细长的圆柱体体积越小,越是粗的、矮的圆柱体体积越大(答案不唯一) .
【答案】(1)108;
(2)
底面周长(cm) 高(cm) 侧面积(cm2) 体积(cm3)
第一个圆柱 18 6 108 154.18
第二个圆柱 6 18 108 51.59
第三个圆柱 3 36 108 25.80
第四个圆柱 9 12 108 77.39
我发现:当侧面积一定时,越是细长的圆柱体体积越小,越是粗的、矮的圆柱体体积越大。(答案不唯一)
【分析】(1)根据圆柱侧面展开图的特征,圆柱的侧面沿高展开是一个长方形,这个长方形的长等于圆柱的底面周长,宽等于圆柱的高。所以这4个圆柱的侧面积相等。即都等于每张长方形纸的面积,根据长方形的面积公式:S=ab,把数据代入公式解答。
(2)根据圆柱的体积公式:V=πr2h,把数据代入公式解答。
【解答】解:(1)18×6=108(平方厘米)
答:围成这个圆柱的侧面积都是108平方厘米。
(2)
底面周长(cm) 高(cm) 侧面积(cm2) 体积(cm3)
第一个圆柱 18 6 108 154.18
第二个圆柱 6 18 108 51.59
第三个圆柱 3 36 108 25.80
第四个圆柱 9 12 108 77.39
我发现:当侧面积一定时,越是细长的圆柱体体积越小,越是粗的、矮的圆柱体体积越大。(答案不唯一)
【点评】此题主要考查了圆柱体的侧面积的意义,及在生活中的实际应用。
36.在一个直径是20cm的圆柱形容器里,放入一个底面半径是3cm的圆锥形铁块,全部浸设在水中,这时水面上升0.3cm。
(1)圆锥形铁块的体积是多少cm3?
(2)圆锥形铁块的高是多少dm?
【答案】(1)94.2立方厘米;
(2)1分米。
【分析】(1)根据题意可知,把圆锥放入圆柱形容器中,上升部分水的体积就等于圆锥的体积,根据圆柱的体积公式:V=πr2h,把数据代入公式解答。
(2)根据圆锥的体积公式:Vπr2h,那么h=Vπr2,把数据代入公式解答。
【解答】解:(1)3.14×(20÷2)2×0.3
=3.14×100×0.3
=94.2(立方厘米)
答:圆锥形铁块的体积是94.2立方厘米。
(2)94.2(3.14×32)
=94.2×3÷(3.14×9)
=282.6÷28.26
=10(厘米)
10厘米=1分米
答:圆锥形铁块的高是1分米。
【点评】此题主要考查圆柱、圆锥体积公式的灵活运用,关键是熟记公式。
37.一个圆锥,底面直径是20厘米,比它的高长25%。如果把这个圆锥沿着它的底面直径竖直切成两个完全相同的立体图形,截面的面积是多少平方厘米?
【答案】160平方厘米。
【分析】把圆锥的高看作单位“1”,圆锥的底面直径相当于高的(1+25%),根据已知一个数的百分之几是多少,求这个数,用除法求出高,如果把这个圆锥沿着它的底面直径竖直切成两个完全相同的立体图形,截面是三角形,这个三角形的底等于圆锥的底面直径,三角形的高等于圆锥的高,根据三角形的面积公式:S=ah÷2,把数据代入公式解答。
【解答】解:圆锥的高:
20÷(1+25%)
=20÷1.25
=16(厘米)
20×16÷2
=320÷2
=160(平方厘米)
答:截面的面积是160平方厘米。
【点评】此题考查的目的是理解掌握圆锥的特征,关键是明确:把这个圆锥沿着它的底面直径竖直切成两个完全相同的立体图形,截面是三角形,这个三角形的底等于圆锥的底面直径,三角形的高等于圆锥的高,重点是求出圆锥的高。
38.小明有两个圆柱形容器。一个底面半径为3厘米,另一个底面半径为4厘米,现在小明要把0.314升水倒入这两个容器中,让两个容器中的水高度相同,请问,容器中的水深多少厘米?
【答案】4厘米。
【分析】根据圆柱的容积(体积)公式:V=πr2h,设容器中的水深为x厘米,据此列方程解答。
【解答】解:设容器中的水深为x厘米,
0.314升=314立方厘米
3.14×32×x+3.14×42×x=314
3.14×9×x+3.14×16×x=314
28.26x+50.24x=314
78.5x=314
x=4
答:容器中水深4厘米。
【点评】此题主要考查圆柱的容积(体积)公式的灵活运用,列方程解决问题的方法及应用,关键是熟记公式。
39.一个圆柱的体积是62.8cm3,要把它锻造成一个高为12cm的圆锥,圆锥底面积应是多少?
【答案】见试题解答内容
【分析】圆柱锻造成圆锥,它们的体积相等,根据圆锥的体积公式:VSh,用体积除以再除以高,由此列式解答.
【解答】解:62.812
=62.8×3÷12
=15.7(平方厘米);
答:圆锥的底面积应该是15.7平方厘米.
【点评】此题主要考查圆锥的体积的计算方法,能够根据体积的计算方法解决有关的问题.
40.一个长方形模型的周长是24厘米,长与宽的比是3:1,以这个长方形的长边为中心轴,把这个长方形旋转周,得到的形体的体积是多少?
【答案】见试题解答内容
【分析】长方形的周长除以2求出长与宽的和,再利用按比例分配的方法求出长和宽,以这个长方形的长边为中心轴,把这个长方形旋转一周,得到一个底面半径等于长方形的宽,高等于长方形的长的圆柱体,然后根据圆柱的体积公式:V=sh,把数据代入公式解答,
【解答】解:3+1=4
24÷2=12(厘米)
12(厘米)
123(厘米)
3.14×32×9
=3.14×9×9
=28.26×9
=254.34(立方厘米),
答:得到的两条图形的体积是254.34立方厘米.
【点评】此题主要考查长方形的周长公式、圆柱的体积公式的灵活运用,关键是熟记公式.
41.请你从如图型号的材料中选出两个制作一个无盖的圆柱形小水桶。(接口处忽略不计)
(1)选择的型号是 ②③ (填序号),这个水桶的底面积是 50.24 cm2。
(2)制作这个小水桶,一共需要多少平方厘米的铁皮?
(3)往这个小水桶中注水,水面上升到水桶高的处,这时水桶中水的体积是多少毫升?
【答案】(1)②③,50.24;
(2)175.84平方厘米;
(3)200.96毫升。
【分析】(1)根据圆柱侧面展开图的特征可知,圆柱的侧面沿高展开是一个长方形,这个长方形的长等于圆柱的底面周长,长方形的宽等于圆柱的高,根据圆的周长公式:C=πd,把数据代入公式求出两个圆的周长,然后与长方形的长进行比较即可确定选择的型号,根据圆的面积公式:S=πr2,求出这个水桶的底面积。
(2)制作这个水桶需要铁皮的面积等于长方形的面积加上底面的面积。
(3)根据圆柱的体积(容积)公式:V=Sh,把数据代入公式求出这个水桶容积的即可。
【解答】解:(1)3.14×8=25.12(厘米)
3.14×4=12.56(厘米)
所以选择的型号是②③。
3.14×(8÷2)2
=3.14×16
=50.24(平方厘米)
答:这个水桶的底面积是50.24平方厘米。
(2)25.12×5+50.24
=125.6+50.24
=175.84(平方厘米)
答:一共需要175.84平方厘米的铁皮。
(3)50.24×5
=251.2
=200.96(立方厘米)
200.96立方厘米=200.96毫升
答:这时水桶水的体积是200.96毫升。
故答案为:②③,50.24。
【点评】此题考查的目的是理解掌握圆柱侧面展开图的特征及应用,圆的周长公式、圆的面积公式、圆柱的侧面积公式、圆柱的体积公式及应用,关键是熟记公式。
42.一只底面半径是10cm的圆柱形瓶中,水深8cm,在瓶中放入长和宽都是8cm、高是15cm的一块长方体铁块,把铁块竖直放在水中,水面上升了几厘米?
【答案】2.048厘米。
【分析】根据题意可知,铁块放入前后瓶子内水的体积不变,放入铁块后水的底面积等于圆柱的底面积与铁块底面积的差,根据圆柱的体积公式:V=πr2h,把数据代入公式求出水的体积,然后用水的体积除以放入铁块后水的底面积求出现在水面的高,用现在水面的高减去原来的水深就是水面上升的高度。
【解答】解:3.14×102×8÷(3.14×102﹣8×8)﹣8
=3.14×100×8÷(3.14×100﹣64)﹣8
=314×8÷(314﹣64)﹣8
=2512÷250﹣8
=10.048﹣8
=2.048(厘米)
答:水面上升了2.048厘米。
【点评】此题主要考查圆柱体积公式的灵活运用,关键是抓住水的体积不变,原来的底面积减少了铁块的底面积,求出放入铁块后的水深,进而求出水面上升的高度。
43.一个圆柱形容器和一个圆锥形容器等底等高,圆柱形容器内原有12升水,现将圆锥形容器盛满水再全部倒入圆柱形容器,则圆柱形容器内水面上升到处。圆柱形容器的容积是多少?
【答案】72升。
【分析】因为等底等高的圆柱的体积是圆锥体积的3倍,所以当圆柱与圆锥的体积相等,底面积也相等时,圆柱的高是圆锥高的,由此可以求出圆柱容器内原来水的体积占圆柱容器容积的几分之几,然后根据已知一个数的几分之几是多少,求这个数,用除法解答。
【解答】解:12÷()
=12×6
=72(升)
答:圆柱形容器的容积是72升。
【点评】此题主要考查等底等高的圆柱与圆锥体积之间的关系及应用,关键是求出圆柱容器内原来水的体积占圆柱容器容积的几分之几。
44.一个圆柱形水桶装满水,把桶里的水倒出后,还剩下12升。水桶的高为5分米,水桶的底面积是多少平方分米?(水桶壁的厚度忽略不计)
【答案】7.2平方分米。
【分析】可把这个水桶的容积看作是单位“1”,倒出后剩下的12升就是单位“1”的1,求单位“1”用除法,求它的容积,再除以高,就是水桶的底面积,据此解答。
【解答】解:12升=12立方分米
12÷(1)÷5
=125
=7.2(平方分米)
答:水桶的底面积是7.2平方分米。
【点评】本题的关键是根据分数除法的意义列式求出水桶的容积,再求它的底面积。
45.一个直角三角形,一条直角边长6厘米,另一条直角边长4厘米,以它的较长的直角边为轴旋转一周后形成一个立体图形.求这个旋转后立体图形的体积.
【答案】见试题解答内容
【分析】根据圆锥的定义,一个直角三角形以它的较长的直角边为轴旋转一周后形成一个立体图形,这个立体图形是圆锥,圆锥的底面半径等于三角形的较短的直角边4厘米,高等于较长的直角边6厘米,根据圆锥的体积:vπr2h,把数据代入公式解答即可.
【解答】解:3.14×42×6
3.14×16×6
=100.48(立方厘米)
答:这个立体图形的体积是100.48立方厘米.
【点评】此题考查的目的是理解圆锥的定义,掌握圆锥的体积公式.
46.一个从里面量底面直径为20cm的圆柱形容器中装有一部分水,在水中浸没一个底面直径为12cm的圆锥形铅锤,这时水面高度是15cm,当把铅锤从容器中取出后,容器中的水面高度下降到13.8cm。这个铅锤的高是多少厘米?
【答案】10厘米。
【分析】由题意可知,把圆锥形铅锤从容器中取出后,下降部分水的体积就等于铅锤的体积,根据圆柱的体积公式:V=πr2h,圆锥的体积公式:Vπr2h,那么h=V(πr2),把数据代入公式解答。
【解答】解:3.14×(20÷2)2×(15﹣13.8)[3.14×(12÷2)2]
=3.14×100×1.2×3÷[3.14×36]
=376.8×3÷113.04
=1130.4÷113.04
=10(厘米)
答:这个铅锤的高是10厘米。
【点评】此题主要考查圆柱、圆锥体积公式的灵活运用,关键是熟记公式。
47.一个底面周长是25.12cm,高是18cm的圆柱形玻璃缸中有一些水,把一个底面半径是3cm的圆锥形铁块浸没在水中(水未溢出),缸内水面上升了1.5cm,圆锥形铁块的高是多少?
【答案】8厘米。
【分析】根据题意可知,把圆锥形铁块放入圆柱形玻璃缸中(水未溢出),上升部分水的体积就等于这个圆锥形铁块的体积,根据圆柱的体积公式:V=πr2h,圆锥的体积公式:Vπr2h,那么h=Vπr2,把数据代入公式解答。
【解答】解:3.14×(25.12÷3.14÷2)2×1.5(3.14×32)
=3.14×16×1.5×3÷(3.14×9)
=75.36×3÷28.26
=226.08÷28.26
=8(厘米)
答:圆锥形铁块是高是8厘米。
【点评】此题主要考查圆柱、圆锥体积公式的灵活运用,关键是熟记公式。
48.一个圆锥形零件,底面积是170平方厘米,高是12厘米。这个零件的体积是多少立方厘米?
【答案】见试题解答内容
【分析】根据圆锥的体积公式:vsh,把数据代入公式解答即可.
【解答】解:170×12=680(立方厘米),
答:这个零件的体积是680立方厘米.
【点评】此题主要考查圆锥体积公式的灵活运用,关键是熟记公式.
49.广汉市某校六年级一班张敏敏购买了一个底面直径10厘米,高12厘米的圆柱形水杯。为了使水杯更加美观,她在水杯的侧面贴上了一圈彩纸,至少需要多少平方厘米的彩纸(接头处忽略不计)?她先往水杯里倒入628mL水,再把一个高为6厘米的圆锥形玩具,完全浸没在水中,这时水面上升0.8厘米,这个圆锥形玩具的底面积是多少平方厘米?
【答案】376.8平方厘米,31.4平方厘米。
【分析】根据圆柱的侧面积公式:S=πdh,把数据代入公式求出至少需要彩纸的面积,根据圆柱的体积公式:V=πr2h,把数据代入公式求出圆锥的体积,然后用圆锥的体积除以再除以圆锥的高即可求出圆锥的底面积。
【解答】解:3.14×10×12
=31.4×12
=376.8(平方厘米)
3.14×(10÷2)2×0.86
=3.14×25×0.8×3÷6
=62.8×3÷6
=188.4÷6
=31.4(平方厘米)
答:至少需要376.8平方厘米的彩纸,这个圆锥形玩具的底面积是31.4平方厘米。
【点评】此题主要考查圆柱的侧面积公式、圆柱的体积公式、圆锥的体积公式的灵活运用,关键是熟记公式。
50.一张长方形铁皮,长18.84dm,宽6dm,用这张铁皮卷成一个圆柱形铁皮水桶的侧面,另配一个底面制成一个最大的水桶。这个铁皮水桶的表面积是多少dm2?水桶的容积是多少?
【答案】141.3平方分米,169.56升。
【分析】由题意可知,这个水桶的表面积等于水桶的侧面积加上一个底面的面积,根据圆柱的侧面积公式:S=πdh,圆的面积公式:S=πr2,圆柱的体积(容积)公式:V=Sh,把数据代入公式解答。
【解答】解:18.84×6+3.14×(18.84÷3.14÷2)2
=113.04+3.14×9
=113.04+28.26
=141.3(平方分米)
3.14×(18.84÷3.14÷2)2×6
=3.14×9×6
=28.26×6
=169.56(立方分米)
169.56立方分米=169.56升
答:这个铁皮水桶的表面积是141.3平方分米,桶的容积是169.56升。
【点评】此题主要考查圆柱的体积公式、圆柱的侧面积公式、圆的面积公式的灵活运用,关键是熟记公式。
51.一个圆锥形沙堆,底面周长是25.12米,高1.8米.如果每立方米沙重1.7吨,这堆沙子重多少吨?
【答案】见试题解答内容
【分析】先利用圆的周长公式求出底面半径,进而可以求出圆锥的体积;每立方米的沙重已知,乘总体积数就是这堆沙的总重量.
【解答】解:底面半径:25.12÷(2×3.14)
=25.12÷6.28
=4(米)
沙的总重量:3.14×42×1.8×1.7
=50.24×0.6×1.7
=51.2448(吨);
答:这堆沙子重51.2448吨.
【点评】解答此题的关键是:先求出底面半径,从而求出这堆沙的体积和重量.
52.把一个底面直径20厘米的圆柱切拼成一个近似的长方体,长方体表面积比圆柱表面积多400平方厘米。圆柱的体积是多少立方厘米?
【答案】6280立方厘米。
【分析】根据圆柱体积公式的推导方法可知,把一个圆柱切拼成一个近似长方体,拼成的近似长方体的底面积等于圆柱的底面积,拼成的近似长方体的高等于圆柱的高,拼成的近似长方体的表面积比圆柱的表面积增加了两个切面的面积,每个切面的长等于圆柱的高,每个切面的宽等于圆柱的底面半径,已知拼成的近似长方体的表面积比圆柱的表面积增加了400平方厘米,据此可以求出圆柱的高,然后根据圆柱的体积公式:V=πr2h,把数据代入公式解答。
【解答】解:20÷2=10(厘米)
400÷2÷10
=200÷10
=20(厘米)
3.14×102×20
=3.14×100×20
=314×20
=6280(立方厘米)
答:圆柱的体积是6280立方厘米。
【点评】此题考查的目的是理解掌握圆柱体积公式的推导方法及应用。
53.将一个底面半径是4厘米,高是9厘米的实心圆柱形铁块,锻造成一个底面半径是8厘米的实心圆锥形铁块,这个圆锥形铁块的高是多少厘米?
【答案】6.75厘米。
【分析】根据圆柱的体积公式:V=πr2h,求出铁块的体积,再根据圆锥的体积公式:Vπr2h,那么h=Vπr2,把数据代入公式解答。
【解答】解:3.14×42×9(3.14×82)
=3.14×16×9×3÷(3.14×64)
=452.16×3÷200.96
=1356.48÷200.96
=6.75(厘米)
答:这个圆锥形铁块的高是6.75厘米。
【点评】此题主要考查圆柱、圆锥体积公式的灵活运用,关键是熟记公式。
54.如图是一个无盖的长方体玻璃容器,水面的高度是8cm。把一个底面半径是4cm的圆锥形铅锤完全浸入水中,水面上升了0.628cm,这个铅锤的高是多少厘米?
【答案】6厘米。
【分析】根据题意可知,把这个圆锥形铅锤放入长方体容器中,上升部分水的体积就等于这个铅锤的体积,根据长方体的体积公式:V=abh,圆锥的体积公式:Vπr2h,那么h=V(πr2),把数据代入公式解答。
【解答】解:16×10×0.628(3.14×42)
=160×0.628×3÷(3.14×16)
=100.48×3÷50.24
=301.44÷50.24
=6(厘米)
答:这个铅锤的高是6厘米。
【点评】此题主要考查长方体的体积公式、圆锥的体积公式的灵活运用,关键是熟记公式。
55.如图,用一张长165.6厘米的铁皮,剪下一个最大的圆作为圆柱的底面,剩下的部分围在底面上做成一个无盖的铁皮水桶,算一算这个铁皮水桶的容积是多少?(铁皮厚度不计,π取3.14)
【答案】见试题解答内容
【分析】根据题意可知:铁皮的长等于圆柱的底面周长加上直径,设圆柱的底面直径为x厘米,由题意得:3.14x+x=165.6,解此方程求出圆柱的底面直径,圆柱的高等于底面直径,再根据圆柱的容积(体积)公式:V=sh,把数据代入公式解答.
【解答】解:设圆柱的底面直径为x厘米,由题意得:
3.14x+x=165.6
4.14x=165.6
4.14x÷4.14=165.6÷4.14
x=40.
3.14×(40÷2)2×40
=3.14×400×40
=1256×40
=50240(立方厘米),
答:这个铁皮水桶的容积是50240立方厘米.
【点评】此题考查的目的是理解掌握圆柱展开图的特征,以及圆柱的容积(体积)公式的灵活运用,关键是熟记公式.
56.一种油菜籽榨油机的漏斗是由圆柱和圆锥两部分组成。底面周长是18.84dm,圆柱和圆锥的高都是6dm。每立方分米油菜籽重0.5kg。
(1)这个漏斗最多能装多少千克油菜籽?
(2)如果油菜籽的出油率是45%,一漏斗油菜籽能榨出多少千克菜籽油?
【答案】(1)113.04千克;
(2)50.868千克。
【分析】(1)根据圆柱的体积公式:V=πr2h,圆锥的体积公式:Vπr2h,把数据代入公式求出这个漏斗能装油菜籽的体积,然后再乘每立方米油菜籽的质量即可。
(2)把油菜籽的质量看作单位“1”,根据求一个数的百分之几是多少,用乘法解答。
【解答】解:(1)底面半径:18.84÷3.14÷2=3(分米)
底面积:3.14×32
=3.14×9
=28.26(平方分米)
(28.26×628.26×6)×0.5
=(169.56+56.52)×0.5
=226.08×0.5
=113.04(千克)
答:这个漏斗最多能装113.04千克油菜籽。
(2)113.04×45%=50.868(千克)
答:一漏斗油菜籽能榨出50.868千克菜籽油。
【点评】此题主要考查圆柱的体积公式、圆锥的体积公式的灵活运用,一个数乘百分数的意义及应用,关键是熟记公式。
57.一个圆柱形容器从里面量底面直径是20cm,高是10cm,里面水深9cm,现在将一个底面半径是8cm,高是6cm的实心圆锥形铁块完全浸没在水中,这时,圆柱形容器中的水会溢出来吗?如果会溢出,则溢出多少mL?
【答案】水溢出来,溢出87.92毫升。
【分析】根据题意,如果这个实心圆锥铁块的体积小于或等于圆柱容器无水部分的体积,水就不会溢出,如果圆锥铁块的体积大于圆柱容器无水部分的体积,水就会溢出,溢出水的体积等于圆锥铁块的体积减去圆柱容器无水部分的体积。根据圆柱的体积公式:V=πr2h,圆锥的体积公式;Vπr2h,把数据代入公式解答。
【解答】解:3.14×(20÷2)2×(10﹣9)
=3.14×100×1
=314(立方厘米)
3.14×82×6
3.14×64×6
=401.92(立方厘米)
401.92立方厘米>314立方厘米
所以水会溢出。
401.92﹣314=87.92(立方厘米)
87.92立方厘米=87.92毫升
答:圆柱形容器中的水会溢出来,溢出87.92毫升。
【点评】此题主要考查圆柱的体积公式、圆锥的体积公式的灵活运用,关键是熟记公式。
58.在一个直径是20厘米的圆柱形容器里,放入一个底面半径2厘米的圆锥形铁块,全部浸没在水中,这时水面上升了0.3厘米。这个圆锥形铁块的高是多少厘米?
【答案】22.5厘米。
【分析】根据题意,这个圆锥形铁块的体积就是上升0.3厘米的水的体积,由此可以求出这个圆锥的体积,再利用圆锥的体积公式VSh即可求出这个圆锥的高。
【解答】解:3.14×(20÷2)2×0.3×3÷(3.14×22)
=314×0.9÷12.56
=282.6÷12.56
=22.5(厘米)
答:圆锥形铁块的高是22.5厘米。
【点评】此题考查了圆柱与圆锥的体积公式的灵活应用,这里根据上升的水的体积求得圆锥铁块的体积是本题的关键。
59.一个圆柱形玻璃杯,内直径为8厘米,内装16厘米深的水,恰好占杯子容量的,杯内还可以加入多少毫升的水?
【答案】200.96毫米。
【分析】根据圆柱的体积(容积)公式:V=πr2h,把数据代入公式求出这个杯子能装水的体积,把杯子能装水的体积看作单位“1”,还可以加水的体积相当于杯子容积的(1),根据求一个数的几分之几是多少,用乘法解答。
【解答】解:3.14×(8÷2)2×(16)
=3.14×16×20
=50.24×20
=1004.8(立方厘米)
1004.8立方厘米=1004.8毫米
1004.8×(1)
=1004.8
=200.96(毫米)
答:杯内还可以加入200.96毫米的水。
【点评】此题主要考查圆柱的体积(容积)公式的灵活运用,关键是熟记公式。
60.一个圆锥体的体积是15.7立方分米,底面积是3.14平方分米,它的高有多少分米?
【答案】见试题解答内容
【分析】根据圆锥的体积公式可得:圆锥的高=圆锥的体积×3÷底面积,由此代入数据即可得出答案.
【解答】解:15.7×3÷3.14
=47.1÷3.14
=15(分米)
答:它的高是15分米.
【点评】此题考查了利用圆锥的体积公式V求圆锥的高的计算方法.
21世纪教育网(www.21cnjy.com)
