【期末专项培优】正比例与反比例应用题(含解析)2024-2025学年六年级下册北师大版
文档属性
| 名称 | 【期末专项培优】正比例与反比例应用题(含解析)2024-2025学年六年级下册北师大版 |

|
|
| 格式 | docx | ||
| 文件大小 | 874.5KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-05-08 00:00:00 | ||
图片预览




文档简介
正比例与反比例
1.下表中一共有50个奇数,黑线框出的5个数之和是115;仔细观察后回答问题.
(1)如果框出5个数的和要是235,应该怎么框?(用笔在图中框一框)
(2)一共可以框出多少个大小不同的和?
2.甲、乙两人的钱数之比是3:1,如果甲给乙0.6元,则两人的钱数的比变为2:1;两人共有多少钱?
3.师傅和徒弟加工同一种零件,师傅40分钟加工50个,徒弟20分钟加工18个.
(1)分别写出师傅加工零件个数与时间的比和徒弟加工零件个数与时间的比,并化简.
(2)你还能写出怎样的比?先写出这个比,再化简.
4.小李5分钟做了120道口算题,小王2分钟做了44道口算题.小李和小王每分钟做口算题道数的比是多少?
5.根据下面的条件,你能写出哪些比?
(1)10千克什锦糖中,有花生糖3千克,奶糖2千克,水果糖5千克.
(2)小华5分钟走了350米,小芳6分钟走了360米.
6.农贸公司的香蕉占水果总重量,苹果占总重量的。
(1)写出香蕉、苹果重量的最简比。
(2)如果苹果是32千克,那么香蕉有多少千克?
7.三个连续偶数的和是90,这三个数写成的连比是多少?
8.李老师买了10支钢笔和6个书包,买两种学习用具所花的钱数同样多.
(1)钢笔和书包的单价之比是多少?
(2)如果书包的单价是60元,钢笔的单价是多少元?
(3)你能提出其他数学问题并解答吗?
9.某工厂加工一批零件,每天加工的个数与需要的天数如下表:
每天生产的个数/个 200 300 400 600
需要的天数/天 36 24 18 12
(1)表中有哪两种相关联的量?
(2)写出三组这两种量中相对应的两个数的积,并比较积的大小。这个积表示什么?
(3)每天生产的个数与需要的天数成什么关系?请说明理由。
10.石蜈蚣有几条腿?
11.从A地到B地有150千米.甲车要行10小时,乙车要行15小时.
(1)分别写出甲、乙两车路程与时间的比.
(2)写出甲、乙两车时间的比.
12.在计算一个数与15相乘时,有一种简便的算法﹣﹣“加半添0”法.例如,计算24×15,先用24的一半(即12)与24相加,得36;再在36的末尾添一个0,得360.你能用这种方法计算下面各题吗?
26×15 28×15 32×15 48×15
13.附加题:如表,将每列上、下两个汉字组成一组,如第1组是(亮,实),第2组是(娃,小)……按照这样的规律排列,第30组是什么?
亮 娃 爱 学 习 亮 娃 爱 学 习 亮 娃 爱 ……
实 小 集 团 实 小 集 团 实 小 集 团 实 ……
14.根据甲、乙两车的行程图,回答下面的问题.
(1)甲、乙两车行驶的路程与时间是否成比例?说说理由.
(2)哪一辆汽车的行驶速度快些?
15.王师傅的工作效率比李师傅高10%.在同样的时间里,两人完成的工作量的比是几比几?完成同样的工作量所需的时间比是几比几?
16.某校排练体操,一圈套一圈地围成若干圈,从外向内人数依次减少4.如果围成8圈的最外圈人数比围成4圈的最外圈人数少20人,参加排练的有多少人?
17.两块花布,一块正方形,边长是8分米,一块是长方形,长是10分米,宽是6分米,写出正方形和长方形周长的比、面积的比.
18.用6根同样长的小棒可以摆成一个正六边形(如图①),再接着摆下去(如图②、③、④),图⑧一共需要多少根小棒?
19.A、B两种商品的价格之比为7:2,如果它们的价格分别上涨60元后,价格之比为5:2,这两种商品原来的价格各是多少?
20.一瓶盐水重120克,如果盐有20克,那么盐与水的比是多少?
21.为庆祝六一儿童节,教室前按“红、黄、紫、红、黄、紫……”的顺序摆了26盆花,最后一盆花是什么颜色的?
22.小丽买3本练习本用去3.60元,小冬买5本练习本用去6.00元.
(1)写出小丽用去的钱数和练习本本数的比.
(2)写出小冬用去的钱数和练习本本数的比.
(3)这两个比能组成比例吗?为什么?
23.淘淘家在装修房屋时,买了同样大小的地板砖,铺地面积与所需块数的关系如图.他家的客厅面积是36m2,需要铺多少块这样的地板砖?(用比例解决问题)
24.我们共植树800棵,没有成活的有12棵。写出植树总棵数与活了的棵数的比,并化简。
25.甲数与乙数的比是3:4,乙数与丙数的比是6:7,甲数与丙数的比是多少?甲数、乙数与丙数三个数的比是多少?
26.沿公园的湖边栽树,按照一棵杨树,一棵松树,一棵柳树的顺序栽,一共栽了28棵,最后一棵是什么树?
27.甲、乙两数的和是21,它们的比是3:4,甲、乙两数分别是多少?
28.沿湖边栽树,按照2棵柳树、2棵松树的规律栽.一共栽了37棵,最后一棵栽的是什么树?
29.某地举行庆丰收长桌宴,一张桌子坐6人,两张桌子并起来坐10人,三张桌子并起来坐14人……照这样并下去,参加宴会的共有402人,需要并多少张桌子?
30.同学们去春游,班长给大家分饼干情况如下表.
人数 1 2 3 4 5 6 7
饼干的块数 5 10 15 20 25 30 35
根据表中数据,饼干的块数与人数是不是成正比例?请说明理由.
31.有大小、质地完全相同的红、白、黑三种颜色的珠子共80颗,按1颗红珠子、2颗白珠子、3颗黑珠子的顺序循环排列。三种颜色的珠子各占全部珠子的几分之几?
32.如图所示,这是用火柴棒摆出的一系列三角形图案,按这种方式摆下去,当每边摆上20根火柴棒时(即n=20),需要多少根火柴棒?
33.一本书共352页,小刚已经看了这本书的,萍萍还差44页就看完了.
(1)写出小刚已看页数和未看页数的比.
(2)写出小刚和萍萍已看页数的比.
(3)写出小刚和萍萍未看页数的比.
34.小明用小棒搭房子.搭2间用9根,搭3间用13根.照这样计算,如果搭10间房子,需要用多少根小棒?
35.在六一联欢晚会上,有一个“亲子互动”节目,用火柴棒摆“金鱼”比赛.如图所示,按照下面的规律摆下去.
(1)摆4条“金鱼”需要多少根火柴棒?
(2)用122根火柴棒可以摆多少条“金鱼”?
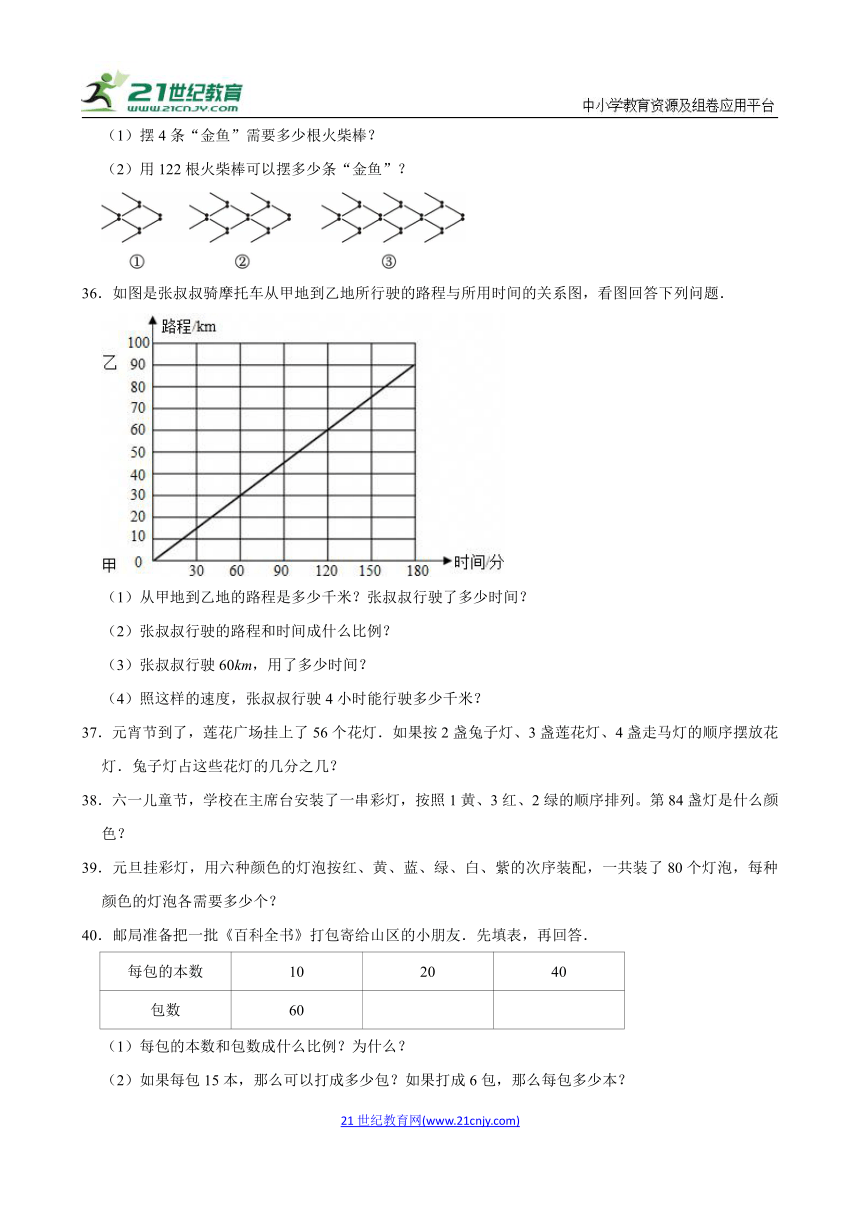
36.如图是张叔叔骑摩托车从甲地到乙地所行驶的路程与所用时间的关系图,看图回答下列问题.
(1)从甲地到乙地的路程是多少千米?张叔叔行驶了多少时间?
(2)张叔叔行驶的路程和时间成什么比例?
(3)张叔叔行驶60km,用了多少时间?
(4)照这样的速度,张叔叔行驶4小时能行驶多少千米?
37.元宵节到了,莲花广场挂上了56个花灯.如果按2盏兔子灯、3盏莲花灯、4盏走马灯的顺序摆放花灯.兔子灯占这些花灯的几分之几?
38.六一儿童节,学校在主席台安装了一串彩灯,按照1黄、3红、2绿的顺序排列。第84盏灯是什么颜色?
39.元旦挂彩灯,用六种颜色的灯泡按红、黄、蓝、绿、白、紫的次序装配,一共装了80个灯泡,每种颜色的灯泡各需要多少个?
40.邮局准备把一批《百科全书》打包寄给山区的小朋友.先填表,再回答.
每包的本数 10 20 40
包数 60
(1)每包的本数和包数成什么比例?为什么?
(2)如果每包15本,那么可以打成多少包?如果打成6包,那么每包多少本?
41.从学校到博物馆,小明步行需要7分钟,小亮步行需要5分钟,小明与小亮的速度比是多少?
42.判断下面每题中的两种量是否成正比例关系,并说明理由.
(1)全班人数一定,出勤人数与缺勤人数;
(2)《光明日报》的单价一定,总价与数量.
43.密码锁的密码是由2、9、8三个数字组成的.密码锁的密码是多少?
44.盒子里放着一串珠子,珠子有黑白两种颜色,它们的排列有一定的规律.请根据排列规律,算出这串珠子共有多少颗?
45.辉辉和同桌合作摆三角形(如图),摆1个三角形用3根小棒,摆2个三角形用5根小棒……请你根据这样的条件,把如表填写完整。
摆1个 摆2个 摆3个 …… 摆6个 …… 摆10个
3根 5根
根 ……
根 ……
根
正比例与反比例
参考答案与试题解析
1.下表中一共有50个奇数,黑线框出的5个数之和是115;仔细观察后回答问题.
(1)如果框出5个数的和要是235,应该怎么框?(用笔在图中框一框)
(2)一共可以框出多少个大小不同的和?
【答案】见试题解答内容
【分析】(!)根据题意发现框出的5个数中横着的每相邻的两个数相差2,竖着每相邻的两个数相差20和框出的5个数的和是中间数的5倍的规律,即可得出框法,从而找到中间的一个数,进而求出其它的四个数即可得出框法;
(2)原来“十”字形框左右平移一共有8个,原来的“十”字形框上下平移一共有3个,一共就有8×3=24(个);
【解答】7解:根据规律框出的5个数的和是中间数的5倍可得:中间数是235÷5=47,其它四个数:47上面是27,下面67,左边是45,右边是49,框法如下:
(2)8×3=24(个);
答:一共可以框出24个大小不同的和.
【点评】解答此题的关键是,根据所给的框法,及表中数的特点,即可找出它们之间的规律,再根据规律作答即可.
2.甲、乙两人的钱数之比是3:1,如果甲给乙0.6元,则两人的钱数的比变为2:1;两人共有多少钱?
【答案】见试题解答内容
【分析】无论甲、乙两人的钱数怎么变,他们的总钱数不变,他们的总钱数原来是4份,现在是3份,可统一为12份,根据比的性质3:1=9:3,2:1=8:4,比由9:3变为8:4是因为甲给了乙0.6元,可知0.6元表示1份,求12份的数,用0.6乘12即可.
【解答】解:3:1=9:3,2:1=8:4,比由9:3变为8:4,是因为甲给了乙0.6元,
可知0.6元表示1份,求12份的数:12×0.6=7.2(元).
答:两人共有7.2元钱.
【点评】此题较难,把比进行转化,然后求出0.6元表示1份,是解答此题的关键.
3.师傅和徒弟加工同一种零件,师傅40分钟加工50个,徒弟20分钟加工18个.
(1)分别写出师傅加工零件个数与时间的比和徒弟加工零件个数与时间的比,并化简.
(2)你还能写出怎样的比?先写出这个比,再化简.
【答案】见试题解答内容
【分析】(1)两个数相除,也叫两个数的比.据此写出即可;把比的前项和后项同时除以它们的最大公因数,化简即可.
(2)写出师傅和徒弟所用时间的比,进而化简即可.
【解答】解:(1)师傅加工零件个数与时间的比:50:40
徒弟加工零件个数与时间的比:18:20
化简:
50:40
=(50÷10):(40÷10)
=5:4
18:20
=(18÷2):(20÷2)
=9:10
(2)师傅和徒弟所用时间的比:40:20
化简:
40:20=(40÷20):(20÷20)=2:1.
【点评】解答此题的关键是明确:两个数相除,也叫两个数的比.
4.小李5分钟做了120道口算题,小王2分钟做了44道口算题.小李和小王每分钟做口算题道数的比是多少?
【答案】见试题解答内容
【分析】首先根据工作效率=工作量÷工作时间,用小李5分钟做的口算题的数量除以5,求出小李平均每分钟做多少;同样用小王2分钟做的口算题的数量除以2,求出小王平均每分钟做多少,再根据比的意义解答.
【解答】解:(120÷5):(44÷2)
=24:22
=12:11
答:小李和小王每分钟做口算题道数的比是12:11.
【点评】此题主要考查了工程问题和比的意义.
5.根据下面的条件,你能写出哪些比?
(1)10千克什锦糖中,有花生糖3千克,奶糖2千克,水果糖5千克.
(2)小华5分钟走了350米,小芳6分钟走了360米.
【答案】见试题解答内容
【分析】两个数相除,也叫两个数的比;根据题意和比的意义可写出各个比,然后化简.
【解答】解:(1)花生糖和奶糖的质量比是3:2,
奶糖和水果糖的质量比是2:5,
水果糖和什锦糖的质量比是5:10=1:2,
花生糖、奶糖、水果糖的质量比是3:2:5.
(2)小华和小芳所走时间的比是5:6,
小华和小芳所走路程的比是350:360=35:36.
【点评】本题主要考查了学生对比的意义的掌握情况.
6.农贸公司的香蕉占水果总重量,苹果占总重量的。
(1)写出香蕉、苹果重量的最简比。
(2)如果苹果是32千克,那么香蕉有多少千克?
【答案】(1)5:8,(2)20千克。
【分析】(1)用香蕉占水果总重量分率比上苹果占水果总重量的分率,化简即可解答;
(2)已知一个数的几分之几是多少,求这个数,用除法解答;求一个数的几分之几,用乘法解答。
【解答】解:(1):
=(20):(20)
=5:8
答:香蕉、苹果重量的最简比是5:8。
(2)32
=80
=20(千克)
答:香蕉有20千克。
【点评】此题考查了比的意义及化简比,分数乘除法的意义及运用。
7.三个连续偶数的和是90,这三个数写成的连比是多少?
【答案】见试题解答内容
【分析】根据偶数的排列规律,相邻的偶数相差2,已知三个连续偶数的和是90,用90除以3即可求出中间的偶数,然后用30﹣2=28、30+2=32求出其它两个即可,这三个数写成的连比是28:30:32,据此解答即可.
【解答】解:90÷3=30
30﹣2=28
30+2=32
所以这三个连续偶数分别是28、30、32.
这三个数写成的连比是28:30:32.
【点评】此题考查的目的是理解掌握偶数的意义及偶数的排列规律,明确:相邻的偶数相差2.
8.李老师买了10支钢笔和6个书包,买两种学习用具所花的钱数同样多.
(1)钢笔和书包的单价之比是多少?
(2)如果书包的单价是60元,钢笔的单价是多少元?
(3)你能提出其他数学问题并解答吗?
【答案】见试题解答内容
【分析】(1)设钢笔的单价为x元、书包的单价为y元,根据“总价=单价×数量”,即可写出钢笔和书包的单价之比.
(2)根据(1)求出的钢笔和书包的单价之比即可求出钢笔的单价.
(3)可提:如果钢笔的单价是36元,书包的单价是多少元?根据(1)求出的钢笔和书包的单价之比即可求出书包的单价.
【解答】解:(1)设钢笔的单价为x元、书包的单价为y元.
10x=6y
x:y=6:10=3:5
答:钢笔和书包的单价之比是3:5.
(2)6036(元)
答:钢笔的单价是36元.
(3)如果钢笔的单价是36元,书包的单价是多少元?
3660(元)
答:书包的单价是60元.
【点评】此题是考查比的意义及化简、比的实际应用等.
9.某工厂加工一批零件,每天加工的个数与需要的天数如下表:
每天生产的个数/个 200 300 400 600
需要的天数/天 36 24 18 12
(1)表中有哪两种相关联的量?
(2)写出三组这两种量中相对应的两个数的积,并比较积的大小。这个积表示什么?
(3)每天生产的个数与需要的天数成什么关系?请说明理由。
【答案】(1)每天生产数量和需要的天数;(2)200×36=7200,300×22=7200,400×18=7200,相等,这批零件的总数;(3)成反比例,每天生产的个数×需要的天数=这批零件的总数(一定)。
【分析】(1)根据题意知:表中有每天生产数量和需要的天数两种量,它们是两种相关联的量,一个量变大,另一个量反而变小,它们的乘积一定,所以每天生产的个数和需要的天数成反比例关系。
(2)200×36=7200,300×22=7200,400×18=7200,600×12=7200,这个积表示这批零件的总数。
(3)因为每天生产的个数×需要的天数=这批零件的总数(一定),所以每天生产的个数与需要的天数成反比例.据此解答。
【解答】解:(1)表中有每天生产数量和需要的天数两种量,因为一个量变大,另一个量反而变小,所以每天生产的个数与需要的天数是相关联的量。
(2)200×36=7200,300×22=7200,400×18=7200,这个积表示这批零件的总数。
(3)因为每天生产的个数×需要的天数=这批零件的总数(一定),所以每天生产的个数与需要的天数成反比例。
【点评】此题属于辨识成正、反比例的量,就看这两个量是对应的比值一定,还是对应的乘积一定,再做判断。
10.石蜈蚣有几条腿?
【答案】见试题解答内容
【分析】根据题意,石蜈蚣腿的数量是个两位数,个位数字是0,十位和个位上的数字之和为3,说明十位上的数字是3,即可得解.
【解答】解:石蜈蚣腿的数量是个两位数,个位数字是0,
十位和个位上的数字之和为3,说明十位上的数字是3﹣0=3,
所以这个两位数是30.
答:石蜈蚣有30条腿.
【点评】此题考查了整数的认识,关键是根据题意求出十位数字.
11.从A地到B地有150千米.甲车要行10小时,乙车要行15小时.
(1)分别写出甲、乙两车路程与时间的比.
(2)写出甲、乙两车时间的比.
【答案】见试题解答内容
【分析】(1)A、B两地的距离已知,甲、乙两车所用的时间已知,根据比的意义即可分别写出甲、乙两车所行路程和时间的比,再化成最简整数比.
(2)甲、乙两车所用的时间已知,根据比的意义即可写出甲、乙两车所用时间的比,再化成最简整数比.
【解答】解:(1)甲车所行路程与时间的比:150:10=15:1
乙车所行路程与时间的比:150:15=10:1
(2)甲、乙两车所用时间的比:10:15=2:3.
【点评】此题是考查比的意义及化简.根据比的意义即可分别写出各比;化简比的关键是找出比的前、后项的最大公因数,然后根据比的基本性质,比的前、后项都除以这个最大公因数.
12.在计算一个数与15相乘时,有一种简便的算法﹣﹣“加半添0”法.例如,计算24×15,先用24的一半(即12)与24相加,得36;再在36的末尾添一个0,得360.你能用这种方法计算下面各题吗?
26×15 28×15 32×15 48×15
【答案】见试题解答内容
【分析】根据巧算的方法:“加半添0”法解答即可.
【解答】解:26÷2+26=39
所以26×15=390
28÷2+28=42
所以28×15=420
32÷2+32=48
所以32×15=480
48÷2+48=72
所以48×15=720
【点评】解答此题的关键是找出算式之间数与数的关系,得出规律,再根据规律解决问题.
13.附加题:如表,将每列上、下两个汉字组成一组,如第1组是(亮,实),第2组是(娃,小)……按照这样的规律排列,第30组是什么?
亮 娃 爱 学 习 亮 娃 爱 学 习 亮 娃 爱 ……
实 小 集 团 实 小 集 团 实 小 集 团 实 ……
【答案】(习,小)。
【分析】第1组5个字一组循环,第2组4个字一组循环,结合有余数除法的计算方法解答即可。
【解答】解:30÷5=6
没有余数,所以第一行的第30个是“习”;
30÷4=7……2
余数是2,所以第二行的第30个是“小”;
答:第30组是(习,小)。
【点评】此题考查了事物的间隔排列规律的灵活应用,这里正确找出事物排列的周期规律是解决此类问题的关键。
14.根据甲、乙两车的行程图,回答下面的问题.
(1)甲、乙两车行驶的路程与时间是否成比例?说说理由.
(2)哪一辆汽车的行驶速度快些?
【答案】见试题解答内容
【分析】(1)此图象的特征:是一条经过原点的直线;从图象中很清晰的看出甲车行驶的路程与行驶时间同时扩大或缩小的变化规律,只要是两种相关联的量变化方向相同,就说明它们对应的比值一定,所以这两种量就成正比例关系;
(2)由图象可知:行驶150千米的路程甲车用的时间少,所以速度较快;据此解答即可.
【解答】解:(1)两辆车子所行的路程和时间成比例,因为是一条直线,所以成正比例;
(2)由图象可知:甲行驶150km,用4.2小时,乙行驶150km,用4.4小时,
4.2<4.4,
路程相同,用的时间越少,速度较快,即甲汽车的行驶速度快些;
【点评】此题主要考查对正比例的意义的运用:两种相关联的量,一种量变化,另一种量也随着变化,但两种量的比值一定,这两种量成正比例.
15.王师傅的工作效率比李师傅高10%.在同样的时间里,两人完成的工作量的比是几比几?完成同样的工作量所需的时间比是几比几?
【答案】见试题解答内容
【分析】把李师傅的工作效率看作单位“1”,那么王师傅的工作效率就是1+10%,根据:工作效率×工作时间=工作总量,可知:工作时间相同,则两人完成工作量的比与工作效率的比成正比;根据:工作时间=工作总量÷工作效率,可知:两人的工作量时间相同,则两人完成工作时间的比与工作效率量的比成反比,由此解答即可.
【解答】解:(1+10%):1
=1.1:10
=11:10;
1:(1+10%)
=1:1.1
=10:11;
答:在同样的时间里,两人完成的工作量的比是11:10;完成同样的工作量所需的时间比是10:11.
【点评】此题主要考查了工程问题的应用,对此类问题要注意把握住基本关系,即:工作量=工作效率×工作时间,工作效率=工作量÷工作时间,工作时间=工作量÷工作效率,解答此题的关键是要明确:工作量一定时,工作效率和工作时间成反比;工作时间一定时,工作量和工作效率成正比.
16.某校排练体操,一圈套一圈地围成若干圈,从外向内人数依次减少4.如果围成8圈的最外圈人数比围成4圈的最外圈人数少20人,参加排练的有多少人?
【答案】见试题解答内容
【分析】无论是围成8圈 还是围成4圈,总人数是不变的.我们把围成8圈的每层从外到内依次叫做8、7、6、5、4、3、2、1层.围成4圈的从外到内,每层分别叫做D、C、B、A层.“围成8圈的最外圈人数比围成4圈的最外圈人数少20人”即8层比D层少20人,因为每层人数依次减少4人,相对应的7层比C层少20人,6层比B层少20人,5层比A层少20人,可以看出8圈的最外边4层一共就比4圈的少了80人,这80人跑哪了?其实就是8圈的最内4层4、3、2、1层的总人数.由此解答.
【解答】解:先求围成8圈时最内4层的人数:
1层+2层+3层+4层=80(人)
再求外4层的人数:
那么5层+6层+7层+8层=80+16×4=144(人)
求总人数:
80+144=224(人)
答:参加排练的有224人.
【点评】方阵问题相关的知识点是:四周的人数=(每边的人数﹣1)×4,每边的人数=四周的人数÷4+1,中实方阵的总人数=每边的人数×每边的人数,空心方阵的总人数=(最外层每边的人数﹣空心方阵的层数)×空心方阵的层数×4.
17.两块花布,一块正方形,边长是8分米,一块是长方形,长是10分米,宽是6分米,写出正方形和长方形周长的比、面积的比.
【答案】见试题解答内容
【分析】根据正方形的周长和长方形的周长计算方法,正方形的面积和长方形的面积的计算方法,先分别求出它们的周长和面积,进而写出它们的周长和面积的比即可.
【解答】解:正方形和长方形的周长比:(8×4):[(10+6)×2]
=32:32
=1:1;
它们的面积比:82:(10×6)
=64:60.
=16:15
答:正方形和长方形的周长比是1:1;面积比是16:15.
【点评】掌握比的意义以及长方形、正方形的面积:长方形的面积=长×宽,正方形的面积=边长×边长,与周长:长方形的周长=(长+宽)×2,正方形周长=边长×4,这些计算方法是解决问题的关键.
18.用6根同样长的小棒可以摆成一个正六边形(如图①),再接着摆下去(如图②、③、④),图⑧一共需要多少根小棒?
【答案】见试题解答内容
【分析】摆1个六边形需要6根小棒,可以写作:5×1+1;摆2个需要11根小棒,可以写作:5×2+1;摆3个需要16根小棒,可以写成:5×3+1;…由此可以推理得出一般规律解答问题.
【解答】解:根据题干分析可得:摆1个六边形需要6根小棒,可以写作:5×1+1;
摆2个需要11根小棒,可以写作:5×2+1;
摆3个需要小棒:5×3+1=16;
摆n个需要小棒:5×n+1=5n+1;
当n=8时,5n+1=5×8+1=41;
答:图⑧一共需要41根小棒.
【点评】根据题干中已知的图形的排列特点及其数量关系,推理得出一般的结论进行解答,是此类问题的关键.
19.A、B两种商品的价格之比为7:2,如果它们的价格分别上涨60元后,价格之比为5:2,这两种商品原来的价格各是多少?
【答案】A原来的价格是315元,B原来的价格各是90元。
【分析】根据题意知道,A、B两种商品的价格差不会变化,由此根据“A、B两种商品的价格之比为7:2,”,知道原来A占价格差的,再根据“价格之比是5:2”知道后来A占价格差的,由此用60除以(),即可求出价格差,进而求出这两种商品原来的价格。
【解答】解:价格差是:
60÷()
=60
=225(元)
A原来的价格是:
225
=225
=315(元)
B原来的价格:315﹣225=90(元)
答:A原来的价格是315元,B原来的价格各是90元。
【点评】解答此题的关键是,根据价格差不变化,将比转化为分率,统一单位“1”,再根据基本的数量关系解决问题。
20.一瓶盐水重120克,如果盐有20克,那么盐与水的比是多少?
【答案】见试题解答内容
【分析】先用“120﹣20”求出盐水中水的质量,进而根据题意,用盐的质量和水的质量相比即可.
【解答】解:20:(120﹣20)
=20:100
=1:5
答:盐与水的质量比是1:5.
【点评】此题考查了比的意义,应明确:盐+水=盐水.
21.为庆祝六一儿童节,教室前按“红、黄、紫、红、黄、紫……”的顺序摆了26盆花,最后一盆花是什么颜色的?
【答案】见试题解答内容
【分析】根据题意,发现这组花的排列规律:每3盆一循环,计算第26盆是第几组循环零几盆,即可判断其颜色.
【解答】解:26÷3=8(组)……2(盆)
所以第28盘花与第2盆一样,是黄色的.
答:最后一盆花是黄色的.
【点评】先找到规律,再根据规律求解.
22.小丽买3本练习本用去3.60元,小冬买5本练习本用去6.00元.
(1)写出小丽用去的钱数和练习本本数的比.
(2)写出小冬用去的钱数和练习本本数的比.
(3)这两个比能组成比例吗?为什么?
【答案】见试题解答内容
【分析】根据题意,分别写出小丽和小冬用去的钱数和练习本本数的比;判断两个比能否组成比例就看两个比的比值是否相等,相等的话就能组成比例.
【解答】解:(1)小丽用去的钱数和练习本本数的比是:3.60:3=6:5;
(2)小冬用去的钱数和练习本本数的比是:6.00:5=6:5;
(3)因为3.6:3,6:5,,比值相等,
所以这两个比能组成比例.
【点评】考查学生对比与比例意义的理解与运用.
23.淘淘家在装修房屋时,买了同样大小的地板砖,铺地面积与所需块数的关系如图.他家的客厅面积是36m2,需要铺多少块这样的地板砖?(用比例解决问题)
【答案】见试题解答内容
【分析】根据图表可知,铺2平方米用8块地板砖,铺6平方米用24块地板砖,8÷2=24÷6=4(一定),那么铺地面积与所需块数成正比例关系;设需要铺x块这样的地板砖,可得36:x=2:8,然后再根据比例的基本性质进行解答.
【解答】解:根据题意与分析可得:铺地面积与所需块数成正比例关系;
设需要铺x块这样的地板砖,根据题意,可得:
36:x=2:8
2x=36×8
2x÷2=36×8÷2
x=144
答:需要铺144块这样的地板砖.
【点评】本题关键是根据图表得出铺地面积与所需块数成正比例关系,然后再根据比例的意义和性质进行解答.
24.我们共植树800棵,没有成活的有12棵。写出植树总棵数与活了的棵数的比,并化简。
【答案】200:197
【分析】根据题目信息和要求首先求出活了多少棵,用植树的棵数减掉没有成活的棵数,就是成活的棵数。再用植树棵数比活了的棵数,进行化简即可。
【解答】解:800﹣12=788(棵)
800:788=(800÷4):(788÷4)=200:197
【点评】此题考查比的意义,关键是求出活了多少棵。
25.甲数与乙数的比是3:4,乙数与丙数的比是6:7,甲数与丙数的比是多少?甲数、乙数与丙数三个数的比是多少?
【答案】见试题解答内容
【分析】首先根据题意,利用比例的基本性质,若乙数=1,则甲数,丙数,进而求出甲数与丙数的比、甲数、乙数与丙数三个数的比,然后根据比的性质,化简成最简整数比即可.
【解答】解:设乙数=1,
由甲数:乙数=3:4,乙数:丙数=6:7,
可得甲数,丙数,
所以甲数:丙数
:
=9:14
甲数:乙数:丙数
:1:
=9:12:14
答:甲数与丙数的比是9:14,甲数、乙数与丙数三个数的比是9:12:14.
【点评】此题主要考查了连比的求法,解答此题的关键是假设其中一个为“1”,然后根据比例的关系表示出其它两个量,再求出它们的比即可.
26.沿公园的湖边栽树,按照一棵杨树,一棵松树,一棵柳树的顺序栽,一共栽了28棵,最后一棵是什么树?
【答案】杨树。
【分析】根据题意,按照一棵杨树,一棵松树,一棵柳树的顺序栽,那么这排树的排列规律是3棵树一个循环周期,据此求出第28棵是第几个循环周期的第几棵即可解答。
【解答】解:1+1+1=3(棵)
28÷3=9(组)……1(棵)
所以第28棵是第9周期的第1棵,是杨树。
答:最后一棵是杨树。
【点评】根据题意得出栽树的规律是解决本题的关键。
27.甲、乙两数的和是21,它们的比是3:4,甲、乙两数分别是多少?
【答案】见试题解答内容
【分析】甲、乙两数的和是21,它们的比是3:4,甲数占了它们和的,乙数占了它们和的,根据求一个数的几分之几是多少的计算方法可列式解答.
【解答】解:219;
2112;
答:甲两数是9;乙数是12.
【点评】本题的关键是根据比与分数的关系,求出甲、乙两数各占了它们和的几分之几,再根据分数乘法的意义列式解答.
28.沿湖边栽树,按照2棵柳树、2棵松树的规律栽.一共栽了37棵,最后一棵栽的是什么树?
【答案】见试题解答内容
【分析】根据题干分析可得,这排树的排列规律是4棵树一个循环周期,分别按照:2棵柳树、2棵松树的顺序栽种,据此求出第37棵是第几个循环周期的第几棵即可解答.
【解答】解:2+2=4(棵)
37÷4=9(组)……1(棵)
所以第37棵是第10周期的第1棵,是柳树.
答:最后一棵栽的是柳树.
【点评】根据题干得出栽树的规律是解决本题的关键.
29.某地举行庆丰收长桌宴,一张桌子坐6人,两张桌子并起来坐10人,三张桌子并起来坐14人……照这样并下去,参加宴会的共有402人,需要并多少张桌子?
【答案】100张。
【分析】根据题意发现:一张桌子坐6人,每多1张桌子就多坐4人,则拼n张桌子,能坐(4n+2)个人;据此逆推即可。
【解答】解:(402﹣2)÷4
=400÷4
=100(张)
答:需要并100张桌子。
【点评】本题考查了图形的变化类题目,认真观察、分析和归纳总结是解决此题的关键。
30.同学们去春游,班长给大家分饼干情况如下表.
人数 1 2 3 4 5 6 7
饼干的块数 5 10 15 20 25 30 35
根据表中数据,饼干的块数与人数是不是成正比例?请说明理由.
【答案】见试题解答内容
【分析】判断两种相关联的量成不成正比例,就看这两种量对应的比值是不是一定,如果是比值一定,就成正比例,根据此进行解答.
【解答】解:5÷1=10÷2=15÷3=20÷4=25÷5=30÷6=35÷7=5(块/人)
已知每人的饼干数是一定的,也就是饼干数和人数的比值是一定的,所以饼干数和人数成正比例.
答:饼干的块数与人数成正比例,因为每人的饼干数是一定的,也就是饼干数和人数的比值是一定的,所以饼干数和人数成正比例.
【点评】此题属于根据正比例的意义,辨识两种相关联的量是否成正比例,就看这两种量对应的比值是否一定,再做出选择.
31.有大小、质地完全相同的红、白、黑三种颜色的珠子共80颗,按1颗红珠子、2颗白珠子、3颗黑珠子的顺序循环排列。三种颜色的珠子各占全部珠子的几分之几?
【答案】红珠子占全部珠子的;白珠子占全部珠子的;黑珠子占全部珠子的。
【分析】1颗红珠子、2颗白珠子、3颗黑珠子循环排列,一个循环有2+1+3=6(颗),共有80÷6=13(个)……2(颗),分别计算各种颜色珠子的颗数,再用除法求各占总数的几分之几即可。
【解答】解:80÷(2+1+3)
=80÷6
=13(组)……2(颗)
1×13+1
=13+1
=14(颗)
2×13+1
=26+1
=27(颗)
3×13=39(颗)
14÷80
27÷80
39÷80
答:红珠子占全部珠子的;白珠子占全部珠子的;黑珠子占全部珠子的。
【点评】解答此题的关键是先求出各有几颗,然后再进一步解答。
32.如图所示,这是用火柴棒摆出的一系列三角形图案,按这种方式摆下去,当每边摆上20根火柴棒时(即n=20),需要多少根火柴棒?
【答案】见试题解答内容
【分析】观察图形可知:前三个图形的火柴棒根数分别是3,9,18根,所以第n个图形的火柴棒根数为:,据此解答即可.
【解答】解:当n=1时,需要3×1=3根;当n=2时,需要3(1+2)=9根;
当n=3时,需要3(1+2+3)=18根,…即结合图形,从水平的角度看,即第几个就是从1加到几,三个角度看是一样的,再乘以3.第n个图形中,需要3(1+2+3+…+n)根.
因此,当n=20时,原式=30×21=630根.
【点评】此题考查了规律性问题.解题时注意由特殊到一般的归纳方法,注意此题的规律为第n个图形中有火柴棒根.
33.一本书共352页,小刚已经看了这本书的,萍萍还差44页就看完了.
(1)写出小刚已看页数和未看页数的比.
(2)写出小刚和萍萍已看页数的比.
(3)写出小刚和萍萍未看页数的比.
【答案】见试题解答内容
【分析】(1)把这本书的总页数看作单位“1”,小刚已经看了这本书的,未看页数是1,进而根据题意求比即可;
(2)把这本书的总页数看作单位“1”,小刚已经看了这本书的,就是求单位“1”的是多少,用乘法计算求出小刚已看的页数,再根据萍萍还差44页就看完,用总页数减去44求出萍萍已看的页数,进而根据题意求比即可;
(3)把这本书的总页数看作单位“1”,小刚已经看了这本书的,未看页数是1,就是求单位“1”的是多少,用乘法计算求出小刚未看的页数,萍萍还差44页就看完;进而根据题意求比即可.
【解答】解:(1):(1)
:
=5:3;
答:写出小刚已看页数和未看页数的比是5:3.
(2)(352):(352﹣44)
=220:308
=5:7;
答:写出小刚和萍萍已看页数的比是5:7.
(2)[352×(1)]:44
=[352]:44
=132:44
=3:1;
答:写出小刚和萍萍未看页数的比3:1.
【点评】此题属于分数乘法应用题中的一个基本类型:求一个数的几分之几是多少,用乘法计算;比的意义.
34.小明用小棒搭房子.搭2间用9根,搭3间用13根.照这样计算,如果搭10间房子,需要用多少根小棒?
【答案】见试题解答内容
【分析】根据搭成的房子间数,和所用小棒的根数,发现规律:搭n间房需要:[5+(n﹣1)×4]=(4n+1)根小棒.
【解答】解:根据图示,
2间房:5+4=9(根)
3间房:5+4+4=13(根)
……
10间房:5+4×(10﹣1)=41(根)
答:搭10间房子,需要用41根小棒.
【点评】本题考查了图形的变化类问题,主要培养学生的观察能力和总结能力.
35.在六一联欢晚会上,有一个“亲子互动”节目,用火柴棒摆“金鱼”比赛.如图所示,按照下面的规律摆下去.
(1)摆4条“金鱼”需要多少根火柴棒?
(2)用122根火柴棒可以摆多少条“金鱼”?
【答案】见试题解答内容
【分析】根据图示可知:摆1条“金鱼”需要火柴棒:8根;摆2条“金鱼”需要火柴棒:8+6=14(根);摆3条“金鱼”需要火柴棒:8+6+6=20(根);……从而得出规律:摆n条“金鱼”需要火柴棒:8+6(n﹣1)=(6n+2)根.据此解答.
【解答】解:摆1条“金鱼”需要火柴棒:8根;
摆2条“金鱼”需要火柴棒:8+6=14(根);
摆3条“金鱼”需要火柴棒:8+6+6=20(根);
……
摆n条“金鱼”需要火柴棒:8+6(n﹣1)=(6n+2)根.
(1)摆4条“金鱼”需要火柴棒:
4×6+2
=24+2
=26(根)
答:摆4条“金鱼”需要26根火柴棒.
(2)6n+2=122
6n=120
n=20
答:用122根火柴棒可以摆20条“金鱼”.
【点评】本题主要考查数与形结合的规律,关键根据所给图示找到这组图形的规律,并运用规律做题.
36.如图是张叔叔骑摩托车从甲地到乙地所行驶的路程与所用时间的关系图,看图回答下列问题.
(1)从甲地到乙地的路程是多少千米?张叔叔行驶了多少时间?
(2)张叔叔行驶的路程和时间成什么比例?
(3)张叔叔行驶60km,用了多少时间?
(4)照这样的速度,张叔叔行驶4小时能行驶多少千米?
【答案】见试题解答内容
【分析】通过观察函数图象可知:
(1)从甲地到乙地的路程是90千米,张叔叔行驶了180÷60=3小时时间;
(2)速度一定,路程和时间成正比关系;
(3)90÷3=30千米/小时
60÷30=2(小时)
(4)照这样的速度,张叔叔行驶4小时能行驶30×4=120千米.
【解答】解:(1)从甲地到乙地的路程是90千米,张叔叔行驶了180÷60=3小时时间;
(2)张叔叔行驶的路程和时间成正比例;
(3)90÷3=30千米/小时
60÷30=2(小时)
答:张叔叔行驶60km,用了2小时.
(4)4×30=120(千米)
答:照这样的速度,张叔叔行驶4小时能行驶120千米.
【点评】解答本题的关键是获取信息.
37.元宵节到了,莲花广场挂上了56个花灯.如果按2盏兔子灯、3盏莲花灯、4盏走马灯的顺序摆放花灯.兔子灯占这些花灯的几分之几?
【答案】见试题解答内容
【分析】根据这组灯的排列顺序可知,每9盏灯1个循环,先求兔子灯有多少盏:56÷9=6(组)……2(盏),6×2+2=14(盏),然后求兔子灯占这些灯总数的分率:14÷56.
【解答】解:这组灯的排列顺序可知,每9盏灯1个循环.
56÷9=6(组)……2(盏)
6×2+2=14(盏)
14÷56
答:兔子灯占这些花灯的.
【点评】此题还可以通过找规律的进行解答,注意解题的关键是发现9个循环一次;用到的知识点:求一个数是另一个数的几分之几,用除法解答.
38.六一儿童节,学校在主席台安装了一串彩灯,按照1黄、3红、2绿的顺序排列。第84盏灯是什么颜色?
【答案】绿色。
【分析】根据按1黄、3红、2绿的顺序排列,可得每个循环有1+2+3=6(盏)灯,用84除以6,求出第84盏彩灯是第几个循环的第几个,进而判断出它的颜色即可。
【解答】解:84÷(1+2+3)
=84÷6
=14
没有余数,所以第84盏灯是绿色。
答:第84盏灯是绿色。
【点评】此题主要考查了事物的间隔规律问题,注意判断出第84盏灯是第几个循环的第几个数即可。
39.元旦挂彩灯,用六种颜色的灯泡按红、黄、蓝、绿、白、紫的次序装配,一共装了80个灯泡,每种颜色的灯泡各需要多少个?
【答案】见试题解答内容
【分析】根据题干分析可得,6盏彩灯一个循环周期,80÷6=13…2,所以80盏彩灯经历了13个循环周期零2个彩灯,每个循环周期都有6种颜色的彩灯各一盏,余下的2盏彩灯是红色和黄色,据此即可解答问题.
【解答】解:80÷6=13…2
所以这80个灯泡是有13个循环周期,余下2盏是红色和黄色,
13+1=14(盏)
答:红颜色的灯泡需要14个,黄颜色的灯泡需要14个,其他蓝、绿、白、紫颜色的彩灯各需要13个.
【点评】根据题干得出灯泡的循环周期是解决此类问题的关键.
40.邮局准备把一批《百科全书》打包寄给山区的小朋友.先填表,再回答.
每包的本数 10 20 40
包数 60
(1)每包的本数和包数成什么比例?为什么?
(2)如果每包15本,那么可以打成多少包?如果打成6包,那么每包多少本?
【答案】见试题解答内容
【分析】(1)总本数=每包的本数×包数,总本数一定,即乘积一定,那么每包的本数和包数成反比例.
(2)先用乘法求出总本数,总本数÷包数=每包的本数,据此解答即可.
【解答】解:
每包的本数 10 20 40
包数 60 30 15
(1)10×60=20×30=40×15=600(本)
总本数=每包的本数×包数,总本数一定,即乘积一定,每包的本数和包数成反比例.
(2)600÷15=40(包)
600÷6=100(本)
答:如果每包15本,那么可以打成40包,如果打成6包,那么每包100本.
【点评】此题属于辨识成正、反比例的量,就看这两个量是对应的比值一定,还是对应的乘积一定,如果对应的比值和乘积都不一定时,这两个量不成比例.
41.从学校到博物馆,小明步行需要7分钟,小亮步行需要5分钟,小明与小亮的速度比是多少?
【答案】见试题解答内容
【分析】把从学校到博物馆的路程看作单位“1”,根据“路程÷时间=速度”分别求出小明与小亮的速度,进而根据题意求比即可.
【解答】解:(1÷7):(1÷5)
:
=5:7;
答:小明与小亮的速度比是5:7.
【点评】解答此题用到的知识点:(1)比的意义;(2)路程、时间和速度三者之间的关系.
42.判断下面每题中的两种量是否成正比例关系,并说明理由.
(1)全班人数一定,出勤人数与缺勤人数;
(2)《光明日报》的单价一定,总价与数量.
【答案】见试题解答内容
【分析】判断两个相关联的量之间成什么比例,就看这两个量是对应的比值一定,还是对应的乘积一定;如果是比值一定,就成正比例;如果是乘积一定,则成反比例.
【解答】解:(1)因为出勤人数+缺勤人数=全班的人数(一定)
所以全班人数一定,出勤人数与缺勤人数不成比例;
(2)因为:总量÷数量=单价(一定),
所以总价和数量成正比例.
【点评】此题属于辨识成正、反比例的量,就看这两个量是对应的比值一定,还是对应的乘积一定,再做判断.
43.密码锁的密码是由2、9、8三个数字组成的.密码锁的密码是多少?
【答案】见试题解答内容
【分析】最大的一位数是9,在2、9、8三个数中,8是轴对称图形,所以密码锁的密码是982.
【解答】解:密码锁的密码是由2、9、8三个数字组成的.密码锁的密码是982.
【点评】解答此题的关键是知道最大的一位数是9和轴对称图形的概念.
44.盒子里放着一串珠子,珠子有黑白两种颜色,它们的排列有一定的规律.请根据排列规律,算出这串珠子共有多少颗?
【答案】见试题解答内容
【分析】根据图示,这组珠子的规律为:1白、1黑;1白2黑;1白、3黑……1白、7黑.所以这串珠子的个数为:1+1+1+2+1+3+1+4+……+1+7=35(颗).
【解答】解:1+1+1+2+1+3+1+4+……+1+7
=1×7+(1+2+3+……+7)
=7
=7+28
=35(颗)
答:这串珠子共有35颗.
【点评】本题主要考查周期现象中的规律,关键发现规律,并运用规律做题.
45.辉辉和同桌合作摆三角形(如图),摆1个三角形用3根小棒,摆2个三角形用5根小棒……请你根据这样的条件,把如表填写完整。
摆1个 摆2个 摆3个 …… 摆6个 …… 摆10个
3根 5根
7 根 ……
13 根 ……
21 根
【答案】7;13;21。
【分析】规律:每增加1个三角形,就增加2根小棒,所以第n个图形要用(2n+1)根小棒。
【解答】解:2×3+1
=6+1
=7(根)
2×6+1
=12+1
=13(根)
2×10+1
=21+1
=21(根)
摆1个 摆2个 摆3个 …… 摆6个 …… 摆10个
3根 5根 7根 …… 13根 …… 21根
故答案为:7;13;21。
【点评】本题考查了图形的变化类问题,主要培养学生的观察能力和总结能力。
21世纪教育网(www.21cnjy.com)
1.下表中一共有50个奇数,黑线框出的5个数之和是115;仔细观察后回答问题.
(1)如果框出5个数的和要是235,应该怎么框?(用笔在图中框一框)
(2)一共可以框出多少个大小不同的和?
2.甲、乙两人的钱数之比是3:1,如果甲给乙0.6元,则两人的钱数的比变为2:1;两人共有多少钱?
3.师傅和徒弟加工同一种零件,师傅40分钟加工50个,徒弟20分钟加工18个.
(1)分别写出师傅加工零件个数与时间的比和徒弟加工零件个数与时间的比,并化简.
(2)你还能写出怎样的比?先写出这个比,再化简.
4.小李5分钟做了120道口算题,小王2分钟做了44道口算题.小李和小王每分钟做口算题道数的比是多少?
5.根据下面的条件,你能写出哪些比?
(1)10千克什锦糖中,有花生糖3千克,奶糖2千克,水果糖5千克.
(2)小华5分钟走了350米,小芳6分钟走了360米.
6.农贸公司的香蕉占水果总重量,苹果占总重量的。
(1)写出香蕉、苹果重量的最简比。
(2)如果苹果是32千克,那么香蕉有多少千克?
7.三个连续偶数的和是90,这三个数写成的连比是多少?
8.李老师买了10支钢笔和6个书包,买两种学习用具所花的钱数同样多.
(1)钢笔和书包的单价之比是多少?
(2)如果书包的单价是60元,钢笔的单价是多少元?
(3)你能提出其他数学问题并解答吗?
9.某工厂加工一批零件,每天加工的个数与需要的天数如下表:
每天生产的个数/个 200 300 400 600
需要的天数/天 36 24 18 12
(1)表中有哪两种相关联的量?
(2)写出三组这两种量中相对应的两个数的积,并比较积的大小。这个积表示什么?
(3)每天生产的个数与需要的天数成什么关系?请说明理由。
10.石蜈蚣有几条腿?
11.从A地到B地有150千米.甲车要行10小时,乙车要行15小时.
(1)分别写出甲、乙两车路程与时间的比.
(2)写出甲、乙两车时间的比.
12.在计算一个数与15相乘时,有一种简便的算法﹣﹣“加半添0”法.例如,计算24×15,先用24的一半(即12)与24相加,得36;再在36的末尾添一个0,得360.你能用这种方法计算下面各题吗?
26×15 28×15 32×15 48×15
13.附加题:如表,将每列上、下两个汉字组成一组,如第1组是(亮,实),第2组是(娃,小)……按照这样的规律排列,第30组是什么?
亮 娃 爱 学 习 亮 娃 爱 学 习 亮 娃 爱 ……
实 小 集 团 实 小 集 团 实 小 集 团 实 ……
14.根据甲、乙两车的行程图,回答下面的问题.
(1)甲、乙两车行驶的路程与时间是否成比例?说说理由.
(2)哪一辆汽车的行驶速度快些?
15.王师傅的工作效率比李师傅高10%.在同样的时间里,两人完成的工作量的比是几比几?完成同样的工作量所需的时间比是几比几?
16.某校排练体操,一圈套一圈地围成若干圈,从外向内人数依次减少4.如果围成8圈的最外圈人数比围成4圈的最外圈人数少20人,参加排练的有多少人?
17.两块花布,一块正方形,边长是8分米,一块是长方形,长是10分米,宽是6分米,写出正方形和长方形周长的比、面积的比.
18.用6根同样长的小棒可以摆成一个正六边形(如图①),再接着摆下去(如图②、③、④),图⑧一共需要多少根小棒?
19.A、B两种商品的价格之比为7:2,如果它们的价格分别上涨60元后,价格之比为5:2,这两种商品原来的价格各是多少?
20.一瓶盐水重120克,如果盐有20克,那么盐与水的比是多少?
21.为庆祝六一儿童节,教室前按“红、黄、紫、红、黄、紫……”的顺序摆了26盆花,最后一盆花是什么颜色的?
22.小丽买3本练习本用去3.60元,小冬买5本练习本用去6.00元.
(1)写出小丽用去的钱数和练习本本数的比.
(2)写出小冬用去的钱数和练习本本数的比.
(3)这两个比能组成比例吗?为什么?
23.淘淘家在装修房屋时,买了同样大小的地板砖,铺地面积与所需块数的关系如图.他家的客厅面积是36m2,需要铺多少块这样的地板砖?(用比例解决问题)
24.我们共植树800棵,没有成活的有12棵。写出植树总棵数与活了的棵数的比,并化简。
25.甲数与乙数的比是3:4,乙数与丙数的比是6:7,甲数与丙数的比是多少?甲数、乙数与丙数三个数的比是多少?
26.沿公园的湖边栽树,按照一棵杨树,一棵松树,一棵柳树的顺序栽,一共栽了28棵,最后一棵是什么树?
27.甲、乙两数的和是21,它们的比是3:4,甲、乙两数分别是多少?
28.沿湖边栽树,按照2棵柳树、2棵松树的规律栽.一共栽了37棵,最后一棵栽的是什么树?
29.某地举行庆丰收长桌宴,一张桌子坐6人,两张桌子并起来坐10人,三张桌子并起来坐14人……照这样并下去,参加宴会的共有402人,需要并多少张桌子?
30.同学们去春游,班长给大家分饼干情况如下表.
人数 1 2 3 4 5 6 7
饼干的块数 5 10 15 20 25 30 35
根据表中数据,饼干的块数与人数是不是成正比例?请说明理由.
31.有大小、质地完全相同的红、白、黑三种颜色的珠子共80颗,按1颗红珠子、2颗白珠子、3颗黑珠子的顺序循环排列。三种颜色的珠子各占全部珠子的几分之几?
32.如图所示,这是用火柴棒摆出的一系列三角形图案,按这种方式摆下去,当每边摆上20根火柴棒时(即n=20),需要多少根火柴棒?
33.一本书共352页,小刚已经看了这本书的,萍萍还差44页就看完了.
(1)写出小刚已看页数和未看页数的比.
(2)写出小刚和萍萍已看页数的比.
(3)写出小刚和萍萍未看页数的比.
34.小明用小棒搭房子.搭2间用9根,搭3间用13根.照这样计算,如果搭10间房子,需要用多少根小棒?
35.在六一联欢晚会上,有一个“亲子互动”节目,用火柴棒摆“金鱼”比赛.如图所示,按照下面的规律摆下去.
(1)摆4条“金鱼”需要多少根火柴棒?
(2)用122根火柴棒可以摆多少条“金鱼”?
36.如图是张叔叔骑摩托车从甲地到乙地所行驶的路程与所用时间的关系图,看图回答下列问题.
(1)从甲地到乙地的路程是多少千米?张叔叔行驶了多少时间?
(2)张叔叔行驶的路程和时间成什么比例?
(3)张叔叔行驶60km,用了多少时间?
(4)照这样的速度,张叔叔行驶4小时能行驶多少千米?
37.元宵节到了,莲花广场挂上了56个花灯.如果按2盏兔子灯、3盏莲花灯、4盏走马灯的顺序摆放花灯.兔子灯占这些花灯的几分之几?
38.六一儿童节,学校在主席台安装了一串彩灯,按照1黄、3红、2绿的顺序排列。第84盏灯是什么颜色?
39.元旦挂彩灯,用六种颜色的灯泡按红、黄、蓝、绿、白、紫的次序装配,一共装了80个灯泡,每种颜色的灯泡各需要多少个?
40.邮局准备把一批《百科全书》打包寄给山区的小朋友.先填表,再回答.
每包的本数 10 20 40
包数 60
(1)每包的本数和包数成什么比例?为什么?
(2)如果每包15本,那么可以打成多少包?如果打成6包,那么每包多少本?
41.从学校到博物馆,小明步行需要7分钟,小亮步行需要5分钟,小明与小亮的速度比是多少?
42.判断下面每题中的两种量是否成正比例关系,并说明理由.
(1)全班人数一定,出勤人数与缺勤人数;
(2)《光明日报》的单价一定,总价与数量.
43.密码锁的密码是由2、9、8三个数字组成的.密码锁的密码是多少?
44.盒子里放着一串珠子,珠子有黑白两种颜色,它们的排列有一定的规律.请根据排列规律,算出这串珠子共有多少颗?
45.辉辉和同桌合作摆三角形(如图),摆1个三角形用3根小棒,摆2个三角形用5根小棒……请你根据这样的条件,把如表填写完整。
摆1个 摆2个 摆3个 …… 摆6个 …… 摆10个
3根 5根
根 ……
根 ……
根
正比例与反比例
参考答案与试题解析
1.下表中一共有50个奇数,黑线框出的5个数之和是115;仔细观察后回答问题.
(1)如果框出5个数的和要是235,应该怎么框?(用笔在图中框一框)
(2)一共可以框出多少个大小不同的和?
【答案】见试题解答内容
【分析】(!)根据题意发现框出的5个数中横着的每相邻的两个数相差2,竖着每相邻的两个数相差20和框出的5个数的和是中间数的5倍的规律,即可得出框法,从而找到中间的一个数,进而求出其它的四个数即可得出框法;
(2)原来“十”字形框左右平移一共有8个,原来的“十”字形框上下平移一共有3个,一共就有8×3=24(个);
【解答】7解:根据规律框出的5个数的和是中间数的5倍可得:中间数是235÷5=47,其它四个数:47上面是27,下面67,左边是45,右边是49,框法如下:
(2)8×3=24(个);
答:一共可以框出24个大小不同的和.
【点评】解答此题的关键是,根据所给的框法,及表中数的特点,即可找出它们之间的规律,再根据规律作答即可.
2.甲、乙两人的钱数之比是3:1,如果甲给乙0.6元,则两人的钱数的比变为2:1;两人共有多少钱?
【答案】见试题解答内容
【分析】无论甲、乙两人的钱数怎么变,他们的总钱数不变,他们的总钱数原来是4份,现在是3份,可统一为12份,根据比的性质3:1=9:3,2:1=8:4,比由9:3变为8:4是因为甲给了乙0.6元,可知0.6元表示1份,求12份的数,用0.6乘12即可.
【解答】解:3:1=9:3,2:1=8:4,比由9:3变为8:4,是因为甲给了乙0.6元,
可知0.6元表示1份,求12份的数:12×0.6=7.2(元).
答:两人共有7.2元钱.
【点评】此题较难,把比进行转化,然后求出0.6元表示1份,是解答此题的关键.
3.师傅和徒弟加工同一种零件,师傅40分钟加工50个,徒弟20分钟加工18个.
(1)分别写出师傅加工零件个数与时间的比和徒弟加工零件个数与时间的比,并化简.
(2)你还能写出怎样的比?先写出这个比,再化简.
【答案】见试题解答内容
【分析】(1)两个数相除,也叫两个数的比.据此写出即可;把比的前项和后项同时除以它们的最大公因数,化简即可.
(2)写出师傅和徒弟所用时间的比,进而化简即可.
【解答】解:(1)师傅加工零件个数与时间的比:50:40
徒弟加工零件个数与时间的比:18:20
化简:
50:40
=(50÷10):(40÷10)
=5:4
18:20
=(18÷2):(20÷2)
=9:10
(2)师傅和徒弟所用时间的比:40:20
化简:
40:20=(40÷20):(20÷20)=2:1.
【点评】解答此题的关键是明确:两个数相除,也叫两个数的比.
4.小李5分钟做了120道口算题,小王2分钟做了44道口算题.小李和小王每分钟做口算题道数的比是多少?
【答案】见试题解答内容
【分析】首先根据工作效率=工作量÷工作时间,用小李5分钟做的口算题的数量除以5,求出小李平均每分钟做多少;同样用小王2分钟做的口算题的数量除以2,求出小王平均每分钟做多少,再根据比的意义解答.
【解答】解:(120÷5):(44÷2)
=24:22
=12:11
答:小李和小王每分钟做口算题道数的比是12:11.
【点评】此题主要考查了工程问题和比的意义.
5.根据下面的条件,你能写出哪些比?
(1)10千克什锦糖中,有花生糖3千克,奶糖2千克,水果糖5千克.
(2)小华5分钟走了350米,小芳6分钟走了360米.
【答案】见试题解答内容
【分析】两个数相除,也叫两个数的比;根据题意和比的意义可写出各个比,然后化简.
【解答】解:(1)花生糖和奶糖的质量比是3:2,
奶糖和水果糖的质量比是2:5,
水果糖和什锦糖的质量比是5:10=1:2,
花生糖、奶糖、水果糖的质量比是3:2:5.
(2)小华和小芳所走时间的比是5:6,
小华和小芳所走路程的比是350:360=35:36.
【点评】本题主要考查了学生对比的意义的掌握情况.
6.农贸公司的香蕉占水果总重量,苹果占总重量的。
(1)写出香蕉、苹果重量的最简比。
(2)如果苹果是32千克,那么香蕉有多少千克?
【答案】(1)5:8,(2)20千克。
【分析】(1)用香蕉占水果总重量分率比上苹果占水果总重量的分率,化简即可解答;
(2)已知一个数的几分之几是多少,求这个数,用除法解答;求一个数的几分之几,用乘法解答。
【解答】解:(1):
=(20):(20)
=5:8
答:香蕉、苹果重量的最简比是5:8。
(2)32
=80
=20(千克)
答:香蕉有20千克。
【点评】此题考查了比的意义及化简比,分数乘除法的意义及运用。
7.三个连续偶数的和是90,这三个数写成的连比是多少?
【答案】见试题解答内容
【分析】根据偶数的排列规律,相邻的偶数相差2,已知三个连续偶数的和是90,用90除以3即可求出中间的偶数,然后用30﹣2=28、30+2=32求出其它两个即可,这三个数写成的连比是28:30:32,据此解答即可.
【解答】解:90÷3=30
30﹣2=28
30+2=32
所以这三个连续偶数分别是28、30、32.
这三个数写成的连比是28:30:32.
【点评】此题考查的目的是理解掌握偶数的意义及偶数的排列规律,明确:相邻的偶数相差2.
8.李老师买了10支钢笔和6个书包,买两种学习用具所花的钱数同样多.
(1)钢笔和书包的单价之比是多少?
(2)如果书包的单价是60元,钢笔的单价是多少元?
(3)你能提出其他数学问题并解答吗?
【答案】见试题解答内容
【分析】(1)设钢笔的单价为x元、书包的单价为y元,根据“总价=单价×数量”,即可写出钢笔和书包的单价之比.
(2)根据(1)求出的钢笔和书包的单价之比即可求出钢笔的单价.
(3)可提:如果钢笔的单价是36元,书包的单价是多少元?根据(1)求出的钢笔和书包的单价之比即可求出书包的单价.
【解答】解:(1)设钢笔的单价为x元、书包的单价为y元.
10x=6y
x:y=6:10=3:5
答:钢笔和书包的单价之比是3:5.
(2)6036(元)
答:钢笔的单价是36元.
(3)如果钢笔的单价是36元,书包的单价是多少元?
3660(元)
答:书包的单价是60元.
【点评】此题是考查比的意义及化简、比的实际应用等.
9.某工厂加工一批零件,每天加工的个数与需要的天数如下表:
每天生产的个数/个 200 300 400 600
需要的天数/天 36 24 18 12
(1)表中有哪两种相关联的量?
(2)写出三组这两种量中相对应的两个数的积,并比较积的大小。这个积表示什么?
(3)每天生产的个数与需要的天数成什么关系?请说明理由。
【答案】(1)每天生产数量和需要的天数;(2)200×36=7200,300×22=7200,400×18=7200,相等,这批零件的总数;(3)成反比例,每天生产的个数×需要的天数=这批零件的总数(一定)。
【分析】(1)根据题意知:表中有每天生产数量和需要的天数两种量,它们是两种相关联的量,一个量变大,另一个量反而变小,它们的乘积一定,所以每天生产的个数和需要的天数成反比例关系。
(2)200×36=7200,300×22=7200,400×18=7200,600×12=7200,这个积表示这批零件的总数。
(3)因为每天生产的个数×需要的天数=这批零件的总数(一定),所以每天生产的个数与需要的天数成反比例.据此解答。
【解答】解:(1)表中有每天生产数量和需要的天数两种量,因为一个量变大,另一个量反而变小,所以每天生产的个数与需要的天数是相关联的量。
(2)200×36=7200,300×22=7200,400×18=7200,这个积表示这批零件的总数。
(3)因为每天生产的个数×需要的天数=这批零件的总数(一定),所以每天生产的个数与需要的天数成反比例。
【点评】此题属于辨识成正、反比例的量,就看这两个量是对应的比值一定,还是对应的乘积一定,再做判断。
10.石蜈蚣有几条腿?
【答案】见试题解答内容
【分析】根据题意,石蜈蚣腿的数量是个两位数,个位数字是0,十位和个位上的数字之和为3,说明十位上的数字是3,即可得解.
【解答】解:石蜈蚣腿的数量是个两位数,个位数字是0,
十位和个位上的数字之和为3,说明十位上的数字是3﹣0=3,
所以这个两位数是30.
答:石蜈蚣有30条腿.
【点评】此题考查了整数的认识,关键是根据题意求出十位数字.
11.从A地到B地有150千米.甲车要行10小时,乙车要行15小时.
(1)分别写出甲、乙两车路程与时间的比.
(2)写出甲、乙两车时间的比.
【答案】见试题解答内容
【分析】(1)A、B两地的距离已知,甲、乙两车所用的时间已知,根据比的意义即可分别写出甲、乙两车所行路程和时间的比,再化成最简整数比.
(2)甲、乙两车所用的时间已知,根据比的意义即可写出甲、乙两车所用时间的比,再化成最简整数比.
【解答】解:(1)甲车所行路程与时间的比:150:10=15:1
乙车所行路程与时间的比:150:15=10:1
(2)甲、乙两车所用时间的比:10:15=2:3.
【点评】此题是考查比的意义及化简.根据比的意义即可分别写出各比;化简比的关键是找出比的前、后项的最大公因数,然后根据比的基本性质,比的前、后项都除以这个最大公因数.
12.在计算一个数与15相乘时,有一种简便的算法﹣﹣“加半添0”法.例如,计算24×15,先用24的一半(即12)与24相加,得36;再在36的末尾添一个0,得360.你能用这种方法计算下面各题吗?
26×15 28×15 32×15 48×15
【答案】见试题解答内容
【分析】根据巧算的方法:“加半添0”法解答即可.
【解答】解:26÷2+26=39
所以26×15=390
28÷2+28=42
所以28×15=420
32÷2+32=48
所以32×15=480
48÷2+48=72
所以48×15=720
【点评】解答此题的关键是找出算式之间数与数的关系,得出规律,再根据规律解决问题.
13.附加题:如表,将每列上、下两个汉字组成一组,如第1组是(亮,实),第2组是(娃,小)……按照这样的规律排列,第30组是什么?
亮 娃 爱 学 习 亮 娃 爱 学 习 亮 娃 爱 ……
实 小 集 团 实 小 集 团 实 小 集 团 实 ……
【答案】(习,小)。
【分析】第1组5个字一组循环,第2组4个字一组循环,结合有余数除法的计算方法解答即可。
【解答】解:30÷5=6
没有余数,所以第一行的第30个是“习”;
30÷4=7……2
余数是2,所以第二行的第30个是“小”;
答:第30组是(习,小)。
【点评】此题考查了事物的间隔排列规律的灵活应用,这里正确找出事物排列的周期规律是解决此类问题的关键。
14.根据甲、乙两车的行程图,回答下面的问题.
(1)甲、乙两车行驶的路程与时间是否成比例?说说理由.
(2)哪一辆汽车的行驶速度快些?
【答案】见试题解答内容
【分析】(1)此图象的特征:是一条经过原点的直线;从图象中很清晰的看出甲车行驶的路程与行驶时间同时扩大或缩小的变化规律,只要是两种相关联的量变化方向相同,就说明它们对应的比值一定,所以这两种量就成正比例关系;
(2)由图象可知:行驶150千米的路程甲车用的时间少,所以速度较快;据此解答即可.
【解答】解:(1)两辆车子所行的路程和时间成比例,因为是一条直线,所以成正比例;
(2)由图象可知:甲行驶150km,用4.2小时,乙行驶150km,用4.4小时,
4.2<4.4,
路程相同,用的时间越少,速度较快,即甲汽车的行驶速度快些;
【点评】此题主要考查对正比例的意义的运用:两种相关联的量,一种量变化,另一种量也随着变化,但两种量的比值一定,这两种量成正比例.
15.王师傅的工作效率比李师傅高10%.在同样的时间里,两人完成的工作量的比是几比几?完成同样的工作量所需的时间比是几比几?
【答案】见试题解答内容
【分析】把李师傅的工作效率看作单位“1”,那么王师傅的工作效率就是1+10%,根据:工作效率×工作时间=工作总量,可知:工作时间相同,则两人完成工作量的比与工作效率的比成正比;根据:工作时间=工作总量÷工作效率,可知:两人的工作量时间相同,则两人完成工作时间的比与工作效率量的比成反比,由此解答即可.
【解答】解:(1+10%):1
=1.1:10
=11:10;
1:(1+10%)
=1:1.1
=10:11;
答:在同样的时间里,两人完成的工作量的比是11:10;完成同样的工作量所需的时间比是10:11.
【点评】此题主要考查了工程问题的应用,对此类问题要注意把握住基本关系,即:工作量=工作效率×工作时间,工作效率=工作量÷工作时间,工作时间=工作量÷工作效率,解答此题的关键是要明确:工作量一定时,工作效率和工作时间成反比;工作时间一定时,工作量和工作效率成正比.
16.某校排练体操,一圈套一圈地围成若干圈,从外向内人数依次减少4.如果围成8圈的最外圈人数比围成4圈的最外圈人数少20人,参加排练的有多少人?
【答案】见试题解答内容
【分析】无论是围成8圈 还是围成4圈,总人数是不变的.我们把围成8圈的每层从外到内依次叫做8、7、6、5、4、3、2、1层.围成4圈的从外到内,每层分别叫做D、C、B、A层.“围成8圈的最外圈人数比围成4圈的最外圈人数少20人”即8层比D层少20人,因为每层人数依次减少4人,相对应的7层比C层少20人,6层比B层少20人,5层比A层少20人,可以看出8圈的最外边4层一共就比4圈的少了80人,这80人跑哪了?其实就是8圈的最内4层4、3、2、1层的总人数.由此解答.
【解答】解:先求围成8圈时最内4层的人数:
1层+2层+3层+4层=80(人)
再求外4层的人数:
那么5层+6层+7层+8层=80+16×4=144(人)
求总人数:
80+144=224(人)
答:参加排练的有224人.
【点评】方阵问题相关的知识点是:四周的人数=(每边的人数﹣1)×4,每边的人数=四周的人数÷4+1,中实方阵的总人数=每边的人数×每边的人数,空心方阵的总人数=(最外层每边的人数﹣空心方阵的层数)×空心方阵的层数×4.
17.两块花布,一块正方形,边长是8分米,一块是长方形,长是10分米,宽是6分米,写出正方形和长方形周长的比、面积的比.
【答案】见试题解答内容
【分析】根据正方形的周长和长方形的周长计算方法,正方形的面积和长方形的面积的计算方法,先分别求出它们的周长和面积,进而写出它们的周长和面积的比即可.
【解答】解:正方形和长方形的周长比:(8×4):[(10+6)×2]
=32:32
=1:1;
它们的面积比:82:(10×6)
=64:60.
=16:15
答:正方形和长方形的周长比是1:1;面积比是16:15.
【点评】掌握比的意义以及长方形、正方形的面积:长方形的面积=长×宽,正方形的面积=边长×边长,与周长:长方形的周长=(长+宽)×2,正方形周长=边长×4,这些计算方法是解决问题的关键.
18.用6根同样长的小棒可以摆成一个正六边形(如图①),再接着摆下去(如图②、③、④),图⑧一共需要多少根小棒?
【答案】见试题解答内容
【分析】摆1个六边形需要6根小棒,可以写作:5×1+1;摆2个需要11根小棒,可以写作:5×2+1;摆3个需要16根小棒,可以写成:5×3+1;…由此可以推理得出一般规律解答问题.
【解答】解:根据题干分析可得:摆1个六边形需要6根小棒,可以写作:5×1+1;
摆2个需要11根小棒,可以写作:5×2+1;
摆3个需要小棒:5×3+1=16;
摆n个需要小棒:5×n+1=5n+1;
当n=8时,5n+1=5×8+1=41;
答:图⑧一共需要41根小棒.
【点评】根据题干中已知的图形的排列特点及其数量关系,推理得出一般的结论进行解答,是此类问题的关键.
19.A、B两种商品的价格之比为7:2,如果它们的价格分别上涨60元后,价格之比为5:2,这两种商品原来的价格各是多少?
【答案】A原来的价格是315元,B原来的价格各是90元。
【分析】根据题意知道,A、B两种商品的价格差不会变化,由此根据“A、B两种商品的价格之比为7:2,”,知道原来A占价格差的,再根据“价格之比是5:2”知道后来A占价格差的,由此用60除以(),即可求出价格差,进而求出这两种商品原来的价格。
【解答】解:价格差是:
60÷()
=60
=225(元)
A原来的价格是:
225
=225
=315(元)
B原来的价格:315﹣225=90(元)
答:A原来的价格是315元,B原来的价格各是90元。
【点评】解答此题的关键是,根据价格差不变化,将比转化为分率,统一单位“1”,再根据基本的数量关系解决问题。
20.一瓶盐水重120克,如果盐有20克,那么盐与水的比是多少?
【答案】见试题解答内容
【分析】先用“120﹣20”求出盐水中水的质量,进而根据题意,用盐的质量和水的质量相比即可.
【解答】解:20:(120﹣20)
=20:100
=1:5
答:盐与水的质量比是1:5.
【点评】此题考查了比的意义,应明确:盐+水=盐水.
21.为庆祝六一儿童节,教室前按“红、黄、紫、红、黄、紫……”的顺序摆了26盆花,最后一盆花是什么颜色的?
【答案】见试题解答内容
【分析】根据题意,发现这组花的排列规律:每3盆一循环,计算第26盆是第几组循环零几盆,即可判断其颜色.
【解答】解:26÷3=8(组)……2(盆)
所以第28盘花与第2盆一样,是黄色的.
答:最后一盆花是黄色的.
【点评】先找到规律,再根据规律求解.
22.小丽买3本练习本用去3.60元,小冬买5本练习本用去6.00元.
(1)写出小丽用去的钱数和练习本本数的比.
(2)写出小冬用去的钱数和练习本本数的比.
(3)这两个比能组成比例吗?为什么?
【答案】见试题解答内容
【分析】根据题意,分别写出小丽和小冬用去的钱数和练习本本数的比;判断两个比能否组成比例就看两个比的比值是否相等,相等的话就能组成比例.
【解答】解:(1)小丽用去的钱数和练习本本数的比是:3.60:3=6:5;
(2)小冬用去的钱数和练习本本数的比是:6.00:5=6:5;
(3)因为3.6:3,6:5,,比值相等,
所以这两个比能组成比例.
【点评】考查学生对比与比例意义的理解与运用.
23.淘淘家在装修房屋时,买了同样大小的地板砖,铺地面积与所需块数的关系如图.他家的客厅面积是36m2,需要铺多少块这样的地板砖?(用比例解决问题)
【答案】见试题解答内容
【分析】根据图表可知,铺2平方米用8块地板砖,铺6平方米用24块地板砖,8÷2=24÷6=4(一定),那么铺地面积与所需块数成正比例关系;设需要铺x块这样的地板砖,可得36:x=2:8,然后再根据比例的基本性质进行解答.
【解答】解:根据题意与分析可得:铺地面积与所需块数成正比例关系;
设需要铺x块这样的地板砖,根据题意,可得:
36:x=2:8
2x=36×8
2x÷2=36×8÷2
x=144
答:需要铺144块这样的地板砖.
【点评】本题关键是根据图表得出铺地面积与所需块数成正比例关系,然后再根据比例的意义和性质进行解答.
24.我们共植树800棵,没有成活的有12棵。写出植树总棵数与活了的棵数的比,并化简。
【答案】200:197
【分析】根据题目信息和要求首先求出活了多少棵,用植树的棵数减掉没有成活的棵数,就是成活的棵数。再用植树棵数比活了的棵数,进行化简即可。
【解答】解:800﹣12=788(棵)
800:788=(800÷4):(788÷4)=200:197
【点评】此题考查比的意义,关键是求出活了多少棵。
25.甲数与乙数的比是3:4,乙数与丙数的比是6:7,甲数与丙数的比是多少?甲数、乙数与丙数三个数的比是多少?
【答案】见试题解答内容
【分析】首先根据题意,利用比例的基本性质,若乙数=1,则甲数,丙数,进而求出甲数与丙数的比、甲数、乙数与丙数三个数的比,然后根据比的性质,化简成最简整数比即可.
【解答】解:设乙数=1,
由甲数:乙数=3:4,乙数:丙数=6:7,
可得甲数,丙数,
所以甲数:丙数
:
=9:14
甲数:乙数:丙数
:1:
=9:12:14
答:甲数与丙数的比是9:14,甲数、乙数与丙数三个数的比是9:12:14.
【点评】此题主要考查了连比的求法,解答此题的关键是假设其中一个为“1”,然后根据比例的关系表示出其它两个量,再求出它们的比即可.
26.沿公园的湖边栽树,按照一棵杨树,一棵松树,一棵柳树的顺序栽,一共栽了28棵,最后一棵是什么树?
【答案】杨树。
【分析】根据题意,按照一棵杨树,一棵松树,一棵柳树的顺序栽,那么这排树的排列规律是3棵树一个循环周期,据此求出第28棵是第几个循环周期的第几棵即可解答。
【解答】解:1+1+1=3(棵)
28÷3=9(组)……1(棵)
所以第28棵是第9周期的第1棵,是杨树。
答:最后一棵是杨树。
【点评】根据题意得出栽树的规律是解决本题的关键。
27.甲、乙两数的和是21,它们的比是3:4,甲、乙两数分别是多少?
【答案】见试题解答内容
【分析】甲、乙两数的和是21,它们的比是3:4,甲数占了它们和的,乙数占了它们和的,根据求一个数的几分之几是多少的计算方法可列式解答.
【解答】解:219;
2112;
答:甲两数是9;乙数是12.
【点评】本题的关键是根据比与分数的关系,求出甲、乙两数各占了它们和的几分之几,再根据分数乘法的意义列式解答.
28.沿湖边栽树,按照2棵柳树、2棵松树的规律栽.一共栽了37棵,最后一棵栽的是什么树?
【答案】见试题解答内容
【分析】根据题干分析可得,这排树的排列规律是4棵树一个循环周期,分别按照:2棵柳树、2棵松树的顺序栽种,据此求出第37棵是第几个循环周期的第几棵即可解答.
【解答】解:2+2=4(棵)
37÷4=9(组)……1(棵)
所以第37棵是第10周期的第1棵,是柳树.
答:最后一棵栽的是柳树.
【点评】根据题干得出栽树的规律是解决本题的关键.
29.某地举行庆丰收长桌宴,一张桌子坐6人,两张桌子并起来坐10人,三张桌子并起来坐14人……照这样并下去,参加宴会的共有402人,需要并多少张桌子?
【答案】100张。
【分析】根据题意发现:一张桌子坐6人,每多1张桌子就多坐4人,则拼n张桌子,能坐(4n+2)个人;据此逆推即可。
【解答】解:(402﹣2)÷4
=400÷4
=100(张)
答:需要并100张桌子。
【点评】本题考查了图形的变化类题目,认真观察、分析和归纳总结是解决此题的关键。
30.同学们去春游,班长给大家分饼干情况如下表.
人数 1 2 3 4 5 6 7
饼干的块数 5 10 15 20 25 30 35
根据表中数据,饼干的块数与人数是不是成正比例?请说明理由.
【答案】见试题解答内容
【分析】判断两种相关联的量成不成正比例,就看这两种量对应的比值是不是一定,如果是比值一定,就成正比例,根据此进行解答.
【解答】解:5÷1=10÷2=15÷3=20÷4=25÷5=30÷6=35÷7=5(块/人)
已知每人的饼干数是一定的,也就是饼干数和人数的比值是一定的,所以饼干数和人数成正比例.
答:饼干的块数与人数成正比例,因为每人的饼干数是一定的,也就是饼干数和人数的比值是一定的,所以饼干数和人数成正比例.
【点评】此题属于根据正比例的意义,辨识两种相关联的量是否成正比例,就看这两种量对应的比值是否一定,再做出选择.
31.有大小、质地完全相同的红、白、黑三种颜色的珠子共80颗,按1颗红珠子、2颗白珠子、3颗黑珠子的顺序循环排列。三种颜色的珠子各占全部珠子的几分之几?
【答案】红珠子占全部珠子的;白珠子占全部珠子的;黑珠子占全部珠子的。
【分析】1颗红珠子、2颗白珠子、3颗黑珠子循环排列,一个循环有2+1+3=6(颗),共有80÷6=13(个)……2(颗),分别计算各种颜色珠子的颗数,再用除法求各占总数的几分之几即可。
【解答】解:80÷(2+1+3)
=80÷6
=13(组)……2(颗)
1×13+1
=13+1
=14(颗)
2×13+1
=26+1
=27(颗)
3×13=39(颗)
14÷80
27÷80
39÷80
答:红珠子占全部珠子的;白珠子占全部珠子的;黑珠子占全部珠子的。
【点评】解答此题的关键是先求出各有几颗,然后再进一步解答。
32.如图所示,这是用火柴棒摆出的一系列三角形图案,按这种方式摆下去,当每边摆上20根火柴棒时(即n=20),需要多少根火柴棒?
【答案】见试题解答内容
【分析】观察图形可知:前三个图形的火柴棒根数分别是3,9,18根,所以第n个图形的火柴棒根数为:,据此解答即可.
【解答】解:当n=1时,需要3×1=3根;当n=2时,需要3(1+2)=9根;
当n=3时,需要3(1+2+3)=18根,…即结合图形,从水平的角度看,即第几个就是从1加到几,三个角度看是一样的,再乘以3.第n个图形中,需要3(1+2+3+…+n)根.
因此,当n=20时,原式=30×21=630根.
【点评】此题考查了规律性问题.解题时注意由特殊到一般的归纳方法,注意此题的规律为第n个图形中有火柴棒根.
33.一本书共352页,小刚已经看了这本书的,萍萍还差44页就看完了.
(1)写出小刚已看页数和未看页数的比.
(2)写出小刚和萍萍已看页数的比.
(3)写出小刚和萍萍未看页数的比.
【答案】见试题解答内容
【分析】(1)把这本书的总页数看作单位“1”,小刚已经看了这本书的,未看页数是1,进而根据题意求比即可;
(2)把这本书的总页数看作单位“1”,小刚已经看了这本书的,就是求单位“1”的是多少,用乘法计算求出小刚已看的页数,再根据萍萍还差44页就看完,用总页数减去44求出萍萍已看的页数,进而根据题意求比即可;
(3)把这本书的总页数看作单位“1”,小刚已经看了这本书的,未看页数是1,就是求单位“1”的是多少,用乘法计算求出小刚未看的页数,萍萍还差44页就看完;进而根据题意求比即可.
【解答】解:(1):(1)
:
=5:3;
答:写出小刚已看页数和未看页数的比是5:3.
(2)(352):(352﹣44)
=220:308
=5:7;
答:写出小刚和萍萍已看页数的比是5:7.
(2)[352×(1)]:44
=[352]:44
=132:44
=3:1;
答:写出小刚和萍萍未看页数的比3:1.
【点评】此题属于分数乘法应用题中的一个基本类型:求一个数的几分之几是多少,用乘法计算;比的意义.
34.小明用小棒搭房子.搭2间用9根,搭3间用13根.照这样计算,如果搭10间房子,需要用多少根小棒?
【答案】见试题解答内容
【分析】根据搭成的房子间数,和所用小棒的根数,发现规律:搭n间房需要:[5+(n﹣1)×4]=(4n+1)根小棒.
【解答】解:根据图示,
2间房:5+4=9(根)
3间房:5+4+4=13(根)
……
10间房:5+4×(10﹣1)=41(根)
答:搭10间房子,需要用41根小棒.
【点评】本题考查了图形的变化类问题,主要培养学生的观察能力和总结能力.
35.在六一联欢晚会上,有一个“亲子互动”节目,用火柴棒摆“金鱼”比赛.如图所示,按照下面的规律摆下去.
(1)摆4条“金鱼”需要多少根火柴棒?
(2)用122根火柴棒可以摆多少条“金鱼”?
【答案】见试题解答内容
【分析】根据图示可知:摆1条“金鱼”需要火柴棒:8根;摆2条“金鱼”需要火柴棒:8+6=14(根);摆3条“金鱼”需要火柴棒:8+6+6=20(根);……从而得出规律:摆n条“金鱼”需要火柴棒:8+6(n﹣1)=(6n+2)根.据此解答.
【解答】解:摆1条“金鱼”需要火柴棒:8根;
摆2条“金鱼”需要火柴棒:8+6=14(根);
摆3条“金鱼”需要火柴棒:8+6+6=20(根);
……
摆n条“金鱼”需要火柴棒:8+6(n﹣1)=(6n+2)根.
(1)摆4条“金鱼”需要火柴棒:
4×6+2
=24+2
=26(根)
答:摆4条“金鱼”需要26根火柴棒.
(2)6n+2=122
6n=120
n=20
答:用122根火柴棒可以摆20条“金鱼”.
【点评】本题主要考查数与形结合的规律,关键根据所给图示找到这组图形的规律,并运用规律做题.
36.如图是张叔叔骑摩托车从甲地到乙地所行驶的路程与所用时间的关系图,看图回答下列问题.
(1)从甲地到乙地的路程是多少千米?张叔叔行驶了多少时间?
(2)张叔叔行驶的路程和时间成什么比例?
(3)张叔叔行驶60km,用了多少时间?
(4)照这样的速度,张叔叔行驶4小时能行驶多少千米?
【答案】见试题解答内容
【分析】通过观察函数图象可知:
(1)从甲地到乙地的路程是90千米,张叔叔行驶了180÷60=3小时时间;
(2)速度一定,路程和时间成正比关系;
(3)90÷3=30千米/小时
60÷30=2(小时)
(4)照这样的速度,张叔叔行驶4小时能行驶30×4=120千米.
【解答】解:(1)从甲地到乙地的路程是90千米,张叔叔行驶了180÷60=3小时时间;
(2)张叔叔行驶的路程和时间成正比例;
(3)90÷3=30千米/小时
60÷30=2(小时)
答:张叔叔行驶60km,用了2小时.
(4)4×30=120(千米)
答:照这样的速度,张叔叔行驶4小时能行驶120千米.
【点评】解答本题的关键是获取信息.
37.元宵节到了,莲花广场挂上了56个花灯.如果按2盏兔子灯、3盏莲花灯、4盏走马灯的顺序摆放花灯.兔子灯占这些花灯的几分之几?
【答案】见试题解答内容
【分析】根据这组灯的排列顺序可知,每9盏灯1个循环,先求兔子灯有多少盏:56÷9=6(组)……2(盏),6×2+2=14(盏),然后求兔子灯占这些灯总数的分率:14÷56.
【解答】解:这组灯的排列顺序可知,每9盏灯1个循环.
56÷9=6(组)……2(盏)
6×2+2=14(盏)
14÷56
答:兔子灯占这些花灯的.
【点评】此题还可以通过找规律的进行解答,注意解题的关键是发现9个循环一次;用到的知识点:求一个数是另一个数的几分之几,用除法解答.
38.六一儿童节,学校在主席台安装了一串彩灯,按照1黄、3红、2绿的顺序排列。第84盏灯是什么颜色?
【答案】绿色。
【分析】根据按1黄、3红、2绿的顺序排列,可得每个循环有1+2+3=6(盏)灯,用84除以6,求出第84盏彩灯是第几个循环的第几个,进而判断出它的颜色即可。
【解答】解:84÷(1+2+3)
=84÷6
=14
没有余数,所以第84盏灯是绿色。
答:第84盏灯是绿色。
【点评】此题主要考查了事物的间隔规律问题,注意判断出第84盏灯是第几个循环的第几个数即可。
39.元旦挂彩灯,用六种颜色的灯泡按红、黄、蓝、绿、白、紫的次序装配,一共装了80个灯泡,每种颜色的灯泡各需要多少个?
【答案】见试题解答内容
【分析】根据题干分析可得,6盏彩灯一个循环周期,80÷6=13…2,所以80盏彩灯经历了13个循环周期零2个彩灯,每个循环周期都有6种颜色的彩灯各一盏,余下的2盏彩灯是红色和黄色,据此即可解答问题.
【解答】解:80÷6=13…2
所以这80个灯泡是有13个循环周期,余下2盏是红色和黄色,
13+1=14(盏)
答:红颜色的灯泡需要14个,黄颜色的灯泡需要14个,其他蓝、绿、白、紫颜色的彩灯各需要13个.
【点评】根据题干得出灯泡的循环周期是解决此类问题的关键.
40.邮局准备把一批《百科全书》打包寄给山区的小朋友.先填表,再回答.
每包的本数 10 20 40
包数 60
(1)每包的本数和包数成什么比例?为什么?
(2)如果每包15本,那么可以打成多少包?如果打成6包,那么每包多少本?
【答案】见试题解答内容
【分析】(1)总本数=每包的本数×包数,总本数一定,即乘积一定,那么每包的本数和包数成反比例.
(2)先用乘法求出总本数,总本数÷包数=每包的本数,据此解答即可.
【解答】解:
每包的本数 10 20 40
包数 60 30 15
(1)10×60=20×30=40×15=600(本)
总本数=每包的本数×包数,总本数一定,即乘积一定,每包的本数和包数成反比例.
(2)600÷15=40(包)
600÷6=100(本)
答:如果每包15本,那么可以打成40包,如果打成6包,那么每包100本.
【点评】此题属于辨识成正、反比例的量,就看这两个量是对应的比值一定,还是对应的乘积一定,如果对应的比值和乘积都不一定时,这两个量不成比例.
41.从学校到博物馆,小明步行需要7分钟,小亮步行需要5分钟,小明与小亮的速度比是多少?
【答案】见试题解答内容
【分析】把从学校到博物馆的路程看作单位“1”,根据“路程÷时间=速度”分别求出小明与小亮的速度,进而根据题意求比即可.
【解答】解:(1÷7):(1÷5)
:
=5:7;
答:小明与小亮的速度比是5:7.
【点评】解答此题用到的知识点:(1)比的意义;(2)路程、时间和速度三者之间的关系.
42.判断下面每题中的两种量是否成正比例关系,并说明理由.
(1)全班人数一定,出勤人数与缺勤人数;
(2)《光明日报》的单价一定,总价与数量.
【答案】见试题解答内容
【分析】判断两个相关联的量之间成什么比例,就看这两个量是对应的比值一定,还是对应的乘积一定;如果是比值一定,就成正比例;如果是乘积一定,则成反比例.
【解答】解:(1)因为出勤人数+缺勤人数=全班的人数(一定)
所以全班人数一定,出勤人数与缺勤人数不成比例;
(2)因为:总量÷数量=单价(一定),
所以总价和数量成正比例.
【点评】此题属于辨识成正、反比例的量,就看这两个量是对应的比值一定,还是对应的乘积一定,再做判断.
43.密码锁的密码是由2、9、8三个数字组成的.密码锁的密码是多少?
【答案】见试题解答内容
【分析】最大的一位数是9,在2、9、8三个数中,8是轴对称图形,所以密码锁的密码是982.
【解答】解:密码锁的密码是由2、9、8三个数字组成的.密码锁的密码是982.
【点评】解答此题的关键是知道最大的一位数是9和轴对称图形的概念.
44.盒子里放着一串珠子,珠子有黑白两种颜色,它们的排列有一定的规律.请根据排列规律,算出这串珠子共有多少颗?
【答案】见试题解答内容
【分析】根据图示,这组珠子的规律为:1白、1黑;1白2黑;1白、3黑……1白、7黑.所以这串珠子的个数为:1+1+1+2+1+3+1+4+……+1+7=35(颗).
【解答】解:1+1+1+2+1+3+1+4+……+1+7
=1×7+(1+2+3+……+7)
=7
=7+28
=35(颗)
答:这串珠子共有35颗.
【点评】本题主要考查周期现象中的规律,关键发现规律,并运用规律做题.
45.辉辉和同桌合作摆三角形(如图),摆1个三角形用3根小棒,摆2个三角形用5根小棒……请你根据这样的条件,把如表填写完整。
摆1个 摆2个 摆3个 …… 摆6个 …… 摆10个
3根 5根
7 根 ……
13 根 ……
21 根
【答案】7;13;21。
【分析】规律:每增加1个三角形,就增加2根小棒,所以第n个图形要用(2n+1)根小棒。
【解答】解:2×3+1
=6+1
=7(根)
2×6+1
=12+1
=13(根)
2×10+1
=21+1
=21(根)
摆1个 摆2个 摆3个 …… 摆6个 …… 摆10个
3根 5根 7根 …… 13根 …… 21根
故答案为:7;13;21。
【点评】本题考查了图形的变化类问题,主要培养学生的观察能力和总结能力。
21世纪教育网(www.21cnjy.com)
