【期末专项培优】长方体和正方体的体积高频易错提高卷(含解析)2024-2025学年五年级下册数学人教版
文档属性
| 名称 | 【期末专项培优】长方体和正方体的体积高频易错提高卷(含解析)2024-2025学年五年级下册数学人教版 |  | |
| 格式 | docx | ||
| 文件大小 | 324.8KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-05-08 22:22:42 | ||
图片预览




文档简介
长方体和正方体的体积
一.选择题(共5小题)
1.(2024秋 栖霞区期末)关于“1毫升水有多少”错误的说法是( )
A.只有很少一点点 B.用滴管大约滴十几滴
C.相当于一瓶眼药水 D.比1升少得多
2.(2024秋 长春期末)学校要粉刷一间教室的四壁和天花板,教室长8米,宽6米,高3米,门窗面积共15平方米,工人师傅想知道需要粉刷的面积是多少平方米?( )
A.120平方米 B.129平方米 C.117平方米 D.144平方米
3.(2024秋 长春期末)一个长方体水箱,从里面量长5分米,宽4分米,高3分米,箱中水面高2分米,把一个棱长2分米的正方体铁块放入水箱,水面会上升多少分米?( )
A.0.4分米 B.0.8分米 C.1.2分米 D.1.4分米
4.(2024秋 长春期末)小新有一块长8厘米、宽6厘米、高4厘米的长方体木块,他想从这块木料中削出一个最大的正方体。他想知道这个正方体的体积是多少立方厘米?( )
A.192立方厘米 B.64立方厘米
C.216立方厘米 D.322立法厘米
5.(2024秋 合肥期末)甲容器的容量是3升,乙容器的容量是3100毫升。则甲容器的容量和乙容器的容量相比,( )
A.甲容器大 B.乙容器大 C.无法比较
二.填空题(共5小题)
6.(2024秋 滨湖区期末)一个长方体木块,高减少4厘米后,就变成了一个正方体,这时表面积比原来少了80平方厘米,原来这个长方体木块的体积是 立方厘米。
7.(2024秋 巢湖市期末)一个长方体,高减少2厘米,就成为一个表面积是216平方厘米的正方体,原来长方体的体积是 立方厘米。
8.(2024秋 建邺区期末)一个长方体木块,从下部和上部分别截去高为3厘米和2厘米的长方体后,变成一个正方体。表面积减少了120平方厘米,则原长方体的体积是 立方厘米。
9.(2024秋 栖霞区期末)科学研究表明,月球上的水可能以冰的形式存在于其地下土壤中,每立方米月球岩石中可提取约6升水,相当于 瓶2升装的纯净水,或相当于 瓶500毫升装的纯净水。
10.(2024秋 桥西区期末)一盒果汁250毫升, 盒这样的果汁是1升。
三.判断题(共5小题)
11.(2024秋 正定县期末)1L水能装满10个容量是100毫升的瓶子。
12.(2024秋 万柏林区期末)在两个杯子中盛满水,盛水多的那个杯子容量大。
13.(2024秋 太原期末)小卓生病咳嗽,妈妈让他每次喝6mL的止咳糖浆。
14.(2024秋 晋源区期末)小卓生病咳嗽,妈妈让他每次喝6L的止咳糖浆。
15.(2024春 琼海期中)两个完全一样的长方体拼成一个新的长方体,跟原来两个长方体的表面积之和及体积之和相比,新长方体的体积变大了,表面积也变大了。
四.计算题(共2小题)
16.(2024春 澄城县期中)计算如图组合图形的表面积和体积。(单位:cm)
17.(2024春 西秀区校级期中)计算长方体表面积、正方体体积。
五.应用题(共6小题)
18.(2024秋 吴江区期末)一个长方体和一个正方体的棱长总和相等。已知长方体的长、宽、高分别是6分米、5分米、4分米。
(1)那么正方体的棱长是多少分米?
(2)长方体的体积是多少立方分米?
19.(2024秋 巢湖市期末)一个长方体油箱长80cm,宽60cm,高40cm,油箱中油面与油箱口的距离为10cm,每升汽油能行驶12.5km,这箱汽油能行驶多少距离?
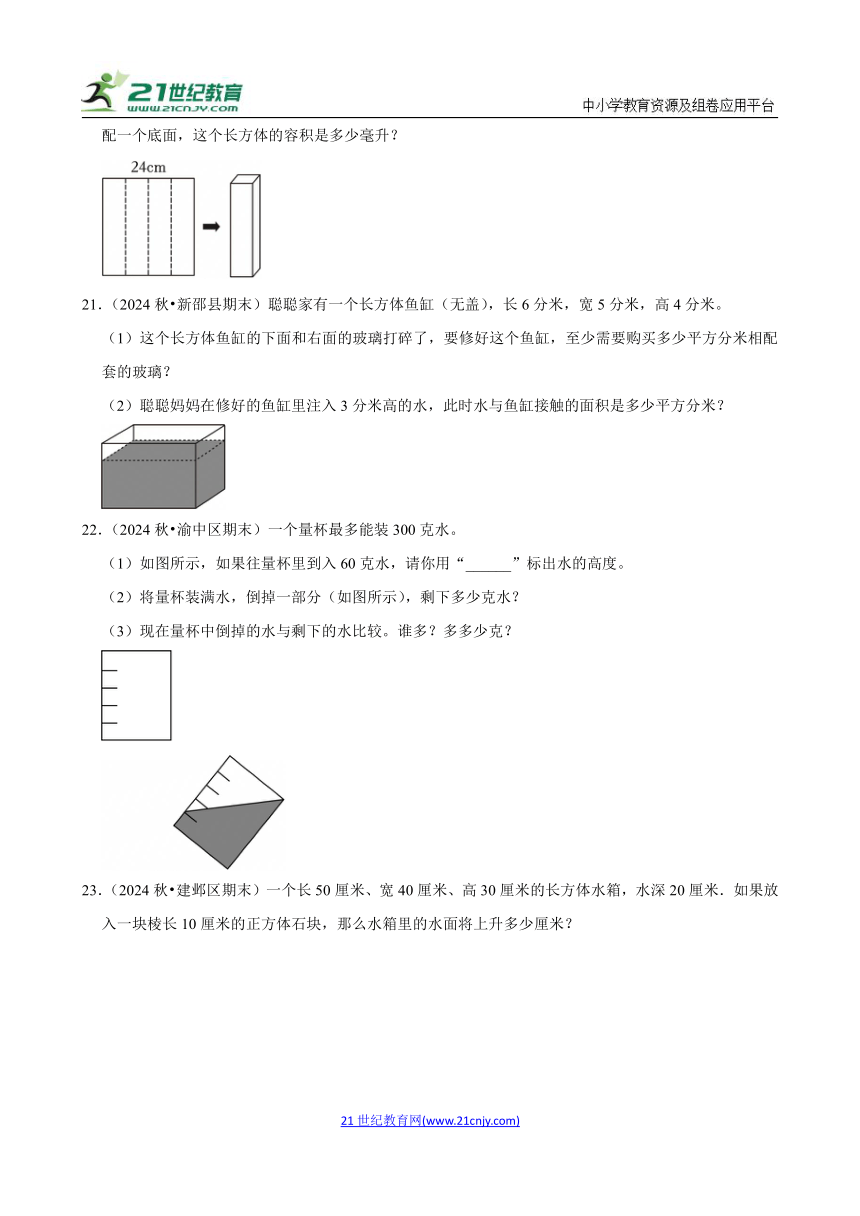
20.(2024秋 天宁区期末)如图,把一张正方形铁皮沿虚线折叠,围成一个长方体的侧面。给这个长方体配一个底面,这个长方体的容积是多少毫升?
21.(2024秋 新邵县期末)聪聪家有一个长方体鱼缸(无盖),长6分米,宽5分米,高4分米。
(1)这个长方体鱼缸的下面和右面的玻璃打碎了,要修好这个鱼缸,至少需要购买多少平方分米相配套的玻璃?
(2)聪聪妈妈在修好的鱼缸里注入3分米高的水,此时水与鱼缸接触的面积是多少平方分米?
22.(2024秋 渝中区期末)一个量杯最多能装300克水。
(1)如图所示,如果往量杯里到入60克水,请你用“______”标出水的高度。
(2)将量杯装满水,倒掉一部分(如图所示),剩下多少克水?
(3)现在量杯中倒掉的水与剩下的水比较。谁多?多多少克?
23.(2024秋 建邺区期末)一个长50厘米、宽40厘米、高30厘米的长方体水箱,水深20厘米.如果放入一块棱长10厘米的正方体石块,那么水箱里的水面将上升多少厘米?
长方体和正方体的体积
参考答案与试题解析
一.选择题(共5小题)
1.(2024秋 栖霞区期末)关于“1毫升水有多少”错误的说法是( )
A.只有很少一点点 B.用滴管大约滴十几滴
C.相当于一瓶眼药水 D.比1升少得多
【考点】体积、容积及其单位.
【专题】综合填空题;应用意识.
【答案】C
【分析】容积单位有升和毫升,其中升是较大的容积单位,毫升是较小的容积单位。根据生活经验,1毫升水用滴管大约能滴十几滴,只有很少一点点,比1升少得多。
【解答】解:A.依据分析可知,1毫升水只有很少一点点,说法正确;
B.依据分析可知,1毫升水用滴管大约能滴十几滴,舒服正确;
C.根据生活经验,一瓶眼药水大约只有5毫升,容量大于5毫升,说法错误;
D.依据分析可知,1毫升水比1升少得多,说法正确。
故选:C。
【点评】此题考查的是容积单位升和毫升的认识,属于基础题,应熟练掌握。
2.(2024秋 长春期末)学校要粉刷一间教室的四壁和天花板,教室长8米,宽6米,高3米,门窗面积共15平方米,工人师傅想知道需要粉刷的面积是多少平方米?( )
A.120平方米 B.129平方米 C.117平方米 D.144平方米
【考点】长方体、正方体表面积与体积计算的应用.
【专题】应用意识.
【答案】C
【分析】根据题意,粉刷教室的四壁和天花板,即粉刷的是长方体的上面、前后面、左右面共5个面;根据“长×宽+长×高×2+宽×高×2”求出这5个面的面积之和,再减去门窗的面积,就是需粉刷的面积。
【解答】解:8×6+8×3×2+6×3×2﹣15
=48+48+36﹣15
=132﹣15
=117(平方米)
答:需要粉刷的面积是117平方米。
故选:C。
【点评】本题考查了长方体表面积计算的应用。
3.(2024秋 长春期末)一个长方体水箱,从里面量长5分米,宽4分米,高3分米,箱中水面高2分米,把一个棱长2分米的正方体铁块放入水箱,水面会上升多少分米?( )
A.0.4分米 B.0.8分米 C.1.2分米 D.1.4分米
【考点】长方体和正方体的体积.
【专题】应用意识.
【答案】A
【分析】水箱中的水面高度=正方体铁块棱长,将正方体铁块放入水箱,铁块完全浸入水中,水面上升的体积就是铁块的体积,根据正方体棱长=棱长×棱长×棱长,求出水面上升的体积,再根据长方体的高=体积÷底面积,即可求出水面上升的高度。
【解答】解:2×2×2÷(5×4)
=8÷20
=0.4(分米)
答:水面会上升0.4分米。
故选:A。
【点评】本题考查了长方体体积计算的应用。
4.(2024秋 长春期末)小新有一块长8厘米、宽6厘米、高4厘米的长方体木块,他想从这块木料中削出一个最大的正方体。他想知道这个正方体的体积是多少立方厘米?( )
A.192立方厘米 B.64立方厘米
C.216立方厘米 D.322立法厘米
【考点】长方体和正方体的体积.
【专题】应用意识.
【答案】B
【分析】根据题意,把一块长方体木料削出一个最大的正方体,那么这个正方体的棱长等于长方体最短的棱;再根据正方体的体积公式V=a3,代入数据计算求出正方体的体积。
【解答】解:4<6<8,即这个最大正方体的棱长是4厘米。
4×4×4=64(立方厘米)
答:这个正方体的体积是64立方厘米。
故选:B。
【点评】本题考查了正方体体积计算的应用。
5.(2024秋 合肥期末)甲容器的容量是3升,乙容器的容量是3100毫升。则甲容器的容量和乙容器的容量相比,( )
A.甲容器大 B.乙容器大 C.无法比较
【考点】体积、容积进率及单位换算.
【专题】应用意识.
【答案】B
【分析】因为升1=1000毫升,那么3升=3000毫升,再根据整数大小比较的方法进行比较即可。
【解答】解:3升=3000毫升
3000毫升<3100毫升
所以乙容器的容量大。
故选:B。
【点评】此题考查的目的是理解掌握容积单位相邻单位之间的进率及换算的方法应用,整数大小比较的方法及应用。
二.填空题(共5小题)
6.(2024秋 滨湖区期末)一个长方体木块,高减少4厘米后,就变成了一个正方体,这时表面积比原来少了80平方厘米,原来这个长方体木块的体积是 225 立方厘米。
【考点】长方体和正方体的体积.
【专题】应用意识.
【答案】225。
【分析】如果高减少4厘米,就变成了一个正方体可知,这个正方体比原长方体表面积减少的4个面是相同的,根据已知表面积减少80平方厘米,可以求出减少面的宽,也就是剩下的正方体的棱长,原来长方体的高比底面边长高3厘米,据此可以求出原长方体的高,再原长方体的体积公式:V=abh,代入数据解答即可。
【解答】解:80÷4÷4
=20÷4
=5(厘米)
5×5×(5+4)
=25×9
=225(立方厘米)
答:原来这个长方体的体积是225立方厘米。
故答案为:225。
【点评】此题主要考查长方体的表面积公式、长方体的体积公式的灵活运用,关键是求出原来长方体的底面边长和高。
7.(2024秋 巢湖市期末)一个长方体,高减少2厘米,就成为一个表面积是216平方厘米的正方体,原来长方体的体积是 288 立方厘米。
【考点】长方体和正方体的体积.
【专题】空间观念.
【答案】288。
【分析】一个长方体,高减少2厘米,就成为一个正方体,说明长方体上下两个面是正方形,正方体表面积÷6=正方体底面积,也是长方体底面积,根据正方形面积=边长×边长,确定正方体棱长,正方体棱长+减少的高=长方体的高,根据长方体体积=底面积×高,即可求出原来长方体的体积。
【解答】解:216÷6=36(平方厘米)
36=6×6
6+2=8(厘米)
36×8=288(立方厘米)
答:原来长方体的体积是288立方厘米。
故答案为:288。
【点评】此题考查正方体表面积、长方体的体积公式的灵活运用。
8.(2024秋 建邺区期末)一个长方体木块,从下部和上部分别截去高为3厘米和2厘米的长方体后,变成一个正方体。表面积减少了120平方厘米,则原长方体的体积是 396 立方厘米。
【考点】长方体和正方体的体积.
【专题】应用意识.
【答案】396。
【分析】从长方体下部和上部分别截去高为3厘米和2厘米的长方体后,便成为一个正方体,则长方体的底面是一个正方形,即截去高为5厘米的长方体后,成为一个正方体;根据表面积减少120厘米可以求出正方体的棱长,然后求出原来长方体的高;最后根据长方体体积=长×宽×高,代入数据计算即可得到原长方体的体积。
【解答】解:原长方体的底面是一个正方形,其棱长是:
120÷4÷(2+3)
=30÷(2+3)
=30÷5
=6(厘米)
原长方体的高是:
6+3+2
=9+2
=11(厘米)
则原长方体的体积是:
6×6×11
=36×11
=396(立方厘米)
答:原长方体的体积是396立方厘米。
故答案为:396。
【点评】此题主要考查长方体的表面积公式、长方体的体积公式的灵活运用,关键是求出长方体的底面边长和高。
9.(2024秋 栖霞区期末)科学研究表明,月球上的水可能以冰的形式存在于其地下土壤中,每立方米月球岩石中可提取约6升水,相当于 3 瓶2升装的纯净水,或相当于 12 瓶500毫升装的纯净水。
【考点】体积、容积及其单位.
【专题】应用题;应用意识.
【答案】3,12。
【分析】用每立方米月球岩石中可提取水的容量除以2升,求出相当于几瓶2升装的纯净水。1升=1000毫升,据此将每立方米月球岩石中可提取水的容量换算成毫升,再用每立方米月球岩石中可提取水的容量除以500毫升,求出相当于几瓶500毫升装的纯净水。
【解答】解:6÷2=3(瓶)
6升=6000毫升
6000÷500=12(瓶)
答:每立方米月球岩石中可提取约6升水,相当于3瓶2升装的纯净水,或相当于12瓶500毫升装的纯净水。
故答案为:3,12。
【点评】本题考查容积单位的换算,关键是熟记升和毫升之间的进率。
10.(2024秋 桥西区期末)一盒果汁250毫升, 4 盒这样的果汁是1升。
【考点】体积、容积进率及单位换算.
【专题】综合填空题;应用意识.
【答案】4。
【分析】根据1升=1000毫升进行填空。
【解答】解:1升=1000毫升
1000÷250=4(盒)
故答案为:4。
【点评】单位之间的换算,大单位换算成小单位要乘它们之间的进率;小单位换算成大单位要除以它们之间的进率。
三.判断题(共5小题)
11.(2024秋 正定县期末)1L水能装满10个容量是100毫升的瓶子。 √
【考点】体积、容积及其单位.
【专题】应用意识.
【答案】√。
【分析】根据体积单位之间的关系:1升=1000毫升,换算单位,判断即可。
【解答】解:1升=1000毫升
1L水能装满10个容量是100毫升的瓶子。原题说法正确。
故答案为:√。
【点评】本题主要考查体积单位的换算。
12.(2024秋 万柏林区期末)在两个杯子中盛满水,盛水多的那个杯子容量大。 √
【考点】体积、容积及其单位.
【专题】应用意识.
【答案】√。
【分析】根据容积是容器所能装物体的体积,解答此题即可。
【解答】解:哪个杯子能盛的水多,我们就说那个杯子的容量大,这句话是正确的。
故答案为:√。
【点评】熟练掌握容积的定义,是解答此题的关键。
13.(2024秋 太原期末)小卓生病咳嗽,妈妈让他每次喝6mL的止咳糖浆。 √
【考点】体积、容积进率及单位换算.
【专题】应用意识.
【答案】√。
【分析】根据容积单位的认识。再结合生活实际进行判断。
【解答】解:儿童每次可以服用5~10毫升,小卓生病咳嗽,妈妈让他每次喝6毫升的止咳糖浆。这个用量是正确的。
故答案为:√。
【点评】此题考查的目的是理解掌握容积单位的认识及应用。
14.(2024秋 晋源区期末)小卓生病咳嗽,妈妈让他每次喝6L的止咳糖浆。 ×
【考点】体积、容积进率及单位换算.
【专题】数感.
【答案】×。
【分析】根据对1升、1毫升实际有多少的认识,结合生活实际,计量小卓生病咳嗽,妈妈让他每次喝止咳糖浆的体积用“毫升”作计量单位。
【解答】解:小卓生病咳嗽,妈妈让他每次喝m6L的止咳糖浆。
原题说法错误。
故答案为:×。
【点评】此题考查根据情景选择合适的计量单位,要注意联系生活实际、计量单位和数据的大小,灵活选择。
15.(2024春 琼海期中)两个完全一样的长方体拼成一个新的长方体,跟原来两个长方体的表面积之和及体积之和相比,新长方体的体积变大了,表面积也变大了。 ×
【考点】长方体和正方体的体积.
【专题】应用意识.
【答案】×。
【分析】根据长方体表面积的意义、长方体体积的意义可知,两个完全一样的长方体拼成一个新的长方体,跟原来两个长方体的表面积之和及体积之和相比,新长方体的体积不变,表面积变小了。据此判断。
【解答】解:两个完全一样的长方体拼成一个新的长方体,跟原来两个长方体的表面积之和及体积之和相比,新长方体的体积不变,表面积变小了。
因此题干中的结论是错误的。
故答案为:×。
【点评】此题考查的目的是理解掌握长方体表面积的意义、体积的意义及应用。
四.计算题(共2小题)
16.(2024春 澄城县期中)计算如图组合图形的表面积和体积。(单位:cm)
【考点】长方体和正方体的体积;长方体和正方体的表面积.
【专题】应用意识.
【答案】238平方厘米,199立方厘米。
【分析】由于正方体与长方体粘合在一起,求这个组合图形的表面积时上面的正方体只求4个侧面的面积,下面的长方体求出表面积,然后合并起来;这个组合图形的体积等于正方体与长方体的体积和。
【解答】解:4×4×4+(9×5+9×3+5×3)×2
=16×4+(45+27+15)×2
=64+87×2
=64+174
=238(平方厘米)
4×4×4+9×5×3
=64+135
=199(立方厘米)
答:这个组合图形的表面积是238平方厘米,体积是199立方厘米。
【点评】此题主要考查正方体、长方体的表面积公式、体积公式的灵活运用,关键是熟记公式。
17.(2024春 西秀区校级期中)计算长方体表面积、正方体体积。
【考点】长方体和正方体的体积;长方体和正方体的表面积.
【专题】应用意识.
【答案】202,343。
【分析】根据长方体的表面积公式:S=(ab+ah+bh)×2,正方体的体积公式:V=a3,把数据代入公式解答。
【解答】,解:(9×4+9×5+4×5)×2
=(36+45+20)×2
=101×2
=202
7×7×7
=49×7
=343
答:长方体的表面积是202,正方体的体积是343。
【点评】此题主要考查长方体的表面积公式、正方体的体积公式的灵活运用,关键是熟记公式。
五.应用题(共6小题)
18.(2024秋 吴江区期末)一个长方体和一个正方体的棱长总和相等。已知长方体的长、宽、高分别是6分米、5分米、4分米。
(1)那么正方体的棱长是多少分米?
(2)长方体的体积是多少立方分米?
【考点】长方体和正方体的体积;正方体的特征.
【专题】应用题;应用意识.
【答案】(1)5分米;(2)120立方分米。
【分析】(1)已知长方体的长、宽、高分别是6分米、5分米、4分米,根据长方体的棱长总和=(长+宽+高)×4,据此求出长方体的棱长总和;已知一个长方体和一个正方体的棱长总和相等,根据正方体的棱长总和=棱长×12,可知正方体的棱长=棱长总和÷12,据此求出正方体的棱长;
(2)根据长方体的体积=长×宽×高,代入数据计算即可求出这个长方体的体积。
【解答】解:(1)(6+5+4)×4÷12
=15×4÷12
=60÷12
=5(分米)
答:正方体的棱长是5分米。
(2)6×5×4
=30×4
=120(立方分米)
答:长方体的体积是120立方分米。
【点评】本题考查的是长方体、正方体棱长知识的运用和长方体体积计算公式的运用。
19.(2024秋 巢湖市期末)一个长方体油箱长80cm,宽60cm,高40cm,油箱中油面与油箱口的距离为10cm,每升汽油能行驶12.5km,这箱汽油能行驶多少距离?
【考点】长方体、正方体表面积与体积计算的应用.
【专题】运算能力.
【答案】1800千米。
【分析】油箱中油面与油箱口的距离为10cm,则油箱中油的高度是40﹣10=30(厘米),再把80厘米、60厘米和30厘米都化成分米。根据长方体的体积公式:V=abh,代入数据求出油箱中油的体积;用1升油可行的千米数乘油的体积,就是这箱油能行驶的千米数,列式解答即可。
【解答】解:80厘米=8分米、60厘米=6分米
40﹣10=30(厘米)
30厘米=3分米
8×6×3
=48×3
=144(立方分米)
144立方分米=144升
144×12.5=1800(千米)
答:这箱汽油能行驶1800千米距离。
【点评】此题主要考查长方体体积的实际应用;关键是先求出油的体积,再用乘法解答,注意单位换算。
20.(2024秋 天宁区期末)如图,把一张正方形铁皮沿虚线折叠,围成一个长方体的侧面。给这个长方体配一个底面,这个长方体的容积是多少毫升?
【考点】长方体和正方体的体积.
【专题】应用意识.
【答案】864毫升。
【分析】通过观察图形可知,这个长方体的底面周长和高都是24厘米,根据正方形的周长公式:C=4a,那么a=C÷4,据此求出底面边长,再根据长方体的体积(容积)公式:V=abh,把数据代入公式解答。
【解答】解:24÷4=6(厘米)
6×6×24
=36×24
=864(立方厘米)
864立方厘米=864毫升
答:这个长方体的容积是864毫升。
【点评】此题主要考查正方形的周长公式、长方体的体积公式的灵活运用,关键是熟记公式。
21.(2024秋 新邵县期末)聪聪家有一个长方体鱼缸(无盖),长6分米,宽5分米,高4分米。
(1)这个长方体鱼缸的下面和右面的玻璃打碎了,要修好这个鱼缸,至少需要购买多少平方分米相配套的玻璃?
(2)聪聪妈妈在修好的鱼缸里注入3分米高的水,此时水与鱼缸接触的面积是多少平方分米?
【考点】长方体、正方体表面积与体积计算的应用;长方体和正方体的表面积.
【专题】应用意识.
【答案】(1)50平方分米;
(2)96平方分米。
【分析】(1)根据题意可知,打碎下面玻璃长是6分米,宽是5分米,右侧玻璃的长是5分米,宽是4分米,可用长方形的面积公式S=长×宽进行解答即可;
(2)要求水与鱼缸的接触面积是多少平方分米,即求出长6分米,宽5分米,高3分米的长方体五个面积是多少即可得解,根据长方体面积公式(S=ab+2ah+2bh),将数据代入即可得出答案。
【解答】解:(1)6×5+5×4
=30+20
=50(平方分米)
答:至少需要购买50平方分米相配套的玻璃。
(2)6×5+2×6×3+2×5×3
=30+36+30
=96(平方分米)
答:水与鱼缸接触的面积是96平方分米。
【点评】本题考查学生对长方形面积公式和长方体面积公式的掌握和运用。
22.(2024秋 渝中区期末)一个量杯最多能装300克水。
(1)如图所示,如果往量杯里到入60克水,请你用“______”标出水的高度。
(2)将量杯装满水,倒掉一部分(如图所示),剩下多少克水?
(3)现在量杯中倒掉的水与剩下的水比较。谁多?多多少克?
【考点】体积、容积及其单位.
【专题】应用意识.
【答案】(1)
(2)180克;
(3)剩下的水,60克。
【分析】(1)量杯装满水300克,60克水占量杯总容量的,即,据此解答;
(2)根据图示可知:剩下的水占量杯总容量的加上(1)的,据此计算出剩下多少克水即可;
(3)先用300克减去(2)的结果,求出剩下的水的克数,再求出倒掉的水的克数,比较多少后求差几颗。
【解答】解:(1)60÷300
(2)(1)
300180(克)
答:剩下180克水。
(3)300﹣180=120(克)
180克>120克
180﹣120=60(克)
答:剩下的水多,多60克。
【点评】本题考查了利用求一个数是另一个数的几分之几及分数与整数四则混合运算解决问题,需准确识图,正确分析题目中的数量关系。
23.(2024秋 建邺区期末)一个长50厘米、宽40厘米、高30厘米的长方体水箱,水深20厘米.如果放入一块棱长10厘米的正方体石块,那么水箱里的水面将上升多少厘米?
【考点】长方体和正方体的体积.
【专题】立体图形的认识与计算.
【答案】见试题解答内容
【分析】首先根据正方体的体积公式:V=a3,求出正方体石块的体积,然后用石块的体积除以长方体的底面积即可.
【解答】解:10×10×10÷(50×40)
=1000÷2000
=0.5(厘米),
答:水箱里的水面将上升0.5厘米.
【点评】此题主要考查正方体、长方体的体积公式的灵活运用,关键是熟记公式.
21世纪教育网(www.21cnjy.com)
一.选择题(共5小题)
1.(2024秋 栖霞区期末)关于“1毫升水有多少”错误的说法是( )
A.只有很少一点点 B.用滴管大约滴十几滴
C.相当于一瓶眼药水 D.比1升少得多
2.(2024秋 长春期末)学校要粉刷一间教室的四壁和天花板,教室长8米,宽6米,高3米,门窗面积共15平方米,工人师傅想知道需要粉刷的面积是多少平方米?( )
A.120平方米 B.129平方米 C.117平方米 D.144平方米
3.(2024秋 长春期末)一个长方体水箱,从里面量长5分米,宽4分米,高3分米,箱中水面高2分米,把一个棱长2分米的正方体铁块放入水箱,水面会上升多少分米?( )
A.0.4分米 B.0.8分米 C.1.2分米 D.1.4分米
4.(2024秋 长春期末)小新有一块长8厘米、宽6厘米、高4厘米的长方体木块,他想从这块木料中削出一个最大的正方体。他想知道这个正方体的体积是多少立方厘米?( )
A.192立方厘米 B.64立方厘米
C.216立方厘米 D.322立法厘米
5.(2024秋 合肥期末)甲容器的容量是3升,乙容器的容量是3100毫升。则甲容器的容量和乙容器的容量相比,( )
A.甲容器大 B.乙容器大 C.无法比较
二.填空题(共5小题)
6.(2024秋 滨湖区期末)一个长方体木块,高减少4厘米后,就变成了一个正方体,这时表面积比原来少了80平方厘米,原来这个长方体木块的体积是 立方厘米。
7.(2024秋 巢湖市期末)一个长方体,高减少2厘米,就成为一个表面积是216平方厘米的正方体,原来长方体的体积是 立方厘米。
8.(2024秋 建邺区期末)一个长方体木块,从下部和上部分别截去高为3厘米和2厘米的长方体后,变成一个正方体。表面积减少了120平方厘米,则原长方体的体积是 立方厘米。
9.(2024秋 栖霞区期末)科学研究表明,月球上的水可能以冰的形式存在于其地下土壤中,每立方米月球岩石中可提取约6升水,相当于 瓶2升装的纯净水,或相当于 瓶500毫升装的纯净水。
10.(2024秋 桥西区期末)一盒果汁250毫升, 盒这样的果汁是1升。
三.判断题(共5小题)
11.(2024秋 正定县期末)1L水能装满10个容量是100毫升的瓶子。
12.(2024秋 万柏林区期末)在两个杯子中盛满水,盛水多的那个杯子容量大。
13.(2024秋 太原期末)小卓生病咳嗽,妈妈让他每次喝6mL的止咳糖浆。
14.(2024秋 晋源区期末)小卓生病咳嗽,妈妈让他每次喝6L的止咳糖浆。
15.(2024春 琼海期中)两个完全一样的长方体拼成一个新的长方体,跟原来两个长方体的表面积之和及体积之和相比,新长方体的体积变大了,表面积也变大了。
四.计算题(共2小题)
16.(2024春 澄城县期中)计算如图组合图形的表面积和体积。(单位:cm)
17.(2024春 西秀区校级期中)计算长方体表面积、正方体体积。
五.应用题(共6小题)
18.(2024秋 吴江区期末)一个长方体和一个正方体的棱长总和相等。已知长方体的长、宽、高分别是6分米、5分米、4分米。
(1)那么正方体的棱长是多少分米?
(2)长方体的体积是多少立方分米?
19.(2024秋 巢湖市期末)一个长方体油箱长80cm,宽60cm,高40cm,油箱中油面与油箱口的距离为10cm,每升汽油能行驶12.5km,这箱汽油能行驶多少距离?
20.(2024秋 天宁区期末)如图,把一张正方形铁皮沿虚线折叠,围成一个长方体的侧面。给这个长方体配一个底面,这个长方体的容积是多少毫升?
21.(2024秋 新邵县期末)聪聪家有一个长方体鱼缸(无盖),长6分米,宽5分米,高4分米。
(1)这个长方体鱼缸的下面和右面的玻璃打碎了,要修好这个鱼缸,至少需要购买多少平方分米相配套的玻璃?
(2)聪聪妈妈在修好的鱼缸里注入3分米高的水,此时水与鱼缸接触的面积是多少平方分米?
22.(2024秋 渝中区期末)一个量杯最多能装300克水。
(1)如图所示,如果往量杯里到入60克水,请你用“______”标出水的高度。
(2)将量杯装满水,倒掉一部分(如图所示),剩下多少克水?
(3)现在量杯中倒掉的水与剩下的水比较。谁多?多多少克?
23.(2024秋 建邺区期末)一个长50厘米、宽40厘米、高30厘米的长方体水箱,水深20厘米.如果放入一块棱长10厘米的正方体石块,那么水箱里的水面将上升多少厘米?
长方体和正方体的体积
参考答案与试题解析
一.选择题(共5小题)
1.(2024秋 栖霞区期末)关于“1毫升水有多少”错误的说法是( )
A.只有很少一点点 B.用滴管大约滴十几滴
C.相当于一瓶眼药水 D.比1升少得多
【考点】体积、容积及其单位.
【专题】综合填空题;应用意识.
【答案】C
【分析】容积单位有升和毫升,其中升是较大的容积单位,毫升是较小的容积单位。根据生活经验,1毫升水用滴管大约能滴十几滴,只有很少一点点,比1升少得多。
【解答】解:A.依据分析可知,1毫升水只有很少一点点,说法正确;
B.依据分析可知,1毫升水用滴管大约能滴十几滴,舒服正确;
C.根据生活经验,一瓶眼药水大约只有5毫升,容量大于5毫升,说法错误;
D.依据分析可知,1毫升水比1升少得多,说法正确。
故选:C。
【点评】此题考查的是容积单位升和毫升的认识,属于基础题,应熟练掌握。
2.(2024秋 长春期末)学校要粉刷一间教室的四壁和天花板,教室长8米,宽6米,高3米,门窗面积共15平方米,工人师傅想知道需要粉刷的面积是多少平方米?( )
A.120平方米 B.129平方米 C.117平方米 D.144平方米
【考点】长方体、正方体表面积与体积计算的应用.
【专题】应用意识.
【答案】C
【分析】根据题意,粉刷教室的四壁和天花板,即粉刷的是长方体的上面、前后面、左右面共5个面;根据“长×宽+长×高×2+宽×高×2”求出这5个面的面积之和,再减去门窗的面积,就是需粉刷的面积。
【解答】解:8×6+8×3×2+6×3×2﹣15
=48+48+36﹣15
=132﹣15
=117(平方米)
答:需要粉刷的面积是117平方米。
故选:C。
【点评】本题考查了长方体表面积计算的应用。
3.(2024秋 长春期末)一个长方体水箱,从里面量长5分米,宽4分米,高3分米,箱中水面高2分米,把一个棱长2分米的正方体铁块放入水箱,水面会上升多少分米?( )
A.0.4分米 B.0.8分米 C.1.2分米 D.1.4分米
【考点】长方体和正方体的体积.
【专题】应用意识.
【答案】A
【分析】水箱中的水面高度=正方体铁块棱长,将正方体铁块放入水箱,铁块完全浸入水中,水面上升的体积就是铁块的体积,根据正方体棱长=棱长×棱长×棱长,求出水面上升的体积,再根据长方体的高=体积÷底面积,即可求出水面上升的高度。
【解答】解:2×2×2÷(5×4)
=8÷20
=0.4(分米)
答:水面会上升0.4分米。
故选:A。
【点评】本题考查了长方体体积计算的应用。
4.(2024秋 长春期末)小新有一块长8厘米、宽6厘米、高4厘米的长方体木块,他想从这块木料中削出一个最大的正方体。他想知道这个正方体的体积是多少立方厘米?( )
A.192立方厘米 B.64立方厘米
C.216立方厘米 D.322立法厘米
【考点】长方体和正方体的体积.
【专题】应用意识.
【答案】B
【分析】根据题意,把一块长方体木料削出一个最大的正方体,那么这个正方体的棱长等于长方体最短的棱;再根据正方体的体积公式V=a3,代入数据计算求出正方体的体积。
【解答】解:4<6<8,即这个最大正方体的棱长是4厘米。
4×4×4=64(立方厘米)
答:这个正方体的体积是64立方厘米。
故选:B。
【点评】本题考查了正方体体积计算的应用。
5.(2024秋 合肥期末)甲容器的容量是3升,乙容器的容量是3100毫升。则甲容器的容量和乙容器的容量相比,( )
A.甲容器大 B.乙容器大 C.无法比较
【考点】体积、容积进率及单位换算.
【专题】应用意识.
【答案】B
【分析】因为升1=1000毫升,那么3升=3000毫升,再根据整数大小比较的方法进行比较即可。
【解答】解:3升=3000毫升
3000毫升<3100毫升
所以乙容器的容量大。
故选:B。
【点评】此题考查的目的是理解掌握容积单位相邻单位之间的进率及换算的方法应用,整数大小比较的方法及应用。
二.填空题(共5小题)
6.(2024秋 滨湖区期末)一个长方体木块,高减少4厘米后,就变成了一个正方体,这时表面积比原来少了80平方厘米,原来这个长方体木块的体积是 225 立方厘米。
【考点】长方体和正方体的体积.
【专题】应用意识.
【答案】225。
【分析】如果高减少4厘米,就变成了一个正方体可知,这个正方体比原长方体表面积减少的4个面是相同的,根据已知表面积减少80平方厘米,可以求出减少面的宽,也就是剩下的正方体的棱长,原来长方体的高比底面边长高3厘米,据此可以求出原长方体的高,再原长方体的体积公式:V=abh,代入数据解答即可。
【解答】解:80÷4÷4
=20÷4
=5(厘米)
5×5×(5+4)
=25×9
=225(立方厘米)
答:原来这个长方体的体积是225立方厘米。
故答案为:225。
【点评】此题主要考查长方体的表面积公式、长方体的体积公式的灵活运用,关键是求出原来长方体的底面边长和高。
7.(2024秋 巢湖市期末)一个长方体,高减少2厘米,就成为一个表面积是216平方厘米的正方体,原来长方体的体积是 288 立方厘米。
【考点】长方体和正方体的体积.
【专题】空间观念.
【答案】288。
【分析】一个长方体,高减少2厘米,就成为一个正方体,说明长方体上下两个面是正方形,正方体表面积÷6=正方体底面积,也是长方体底面积,根据正方形面积=边长×边长,确定正方体棱长,正方体棱长+减少的高=长方体的高,根据长方体体积=底面积×高,即可求出原来长方体的体积。
【解答】解:216÷6=36(平方厘米)
36=6×6
6+2=8(厘米)
36×8=288(立方厘米)
答:原来长方体的体积是288立方厘米。
故答案为:288。
【点评】此题考查正方体表面积、长方体的体积公式的灵活运用。
8.(2024秋 建邺区期末)一个长方体木块,从下部和上部分别截去高为3厘米和2厘米的长方体后,变成一个正方体。表面积减少了120平方厘米,则原长方体的体积是 396 立方厘米。
【考点】长方体和正方体的体积.
【专题】应用意识.
【答案】396。
【分析】从长方体下部和上部分别截去高为3厘米和2厘米的长方体后,便成为一个正方体,则长方体的底面是一个正方形,即截去高为5厘米的长方体后,成为一个正方体;根据表面积减少120厘米可以求出正方体的棱长,然后求出原来长方体的高;最后根据长方体体积=长×宽×高,代入数据计算即可得到原长方体的体积。
【解答】解:原长方体的底面是一个正方形,其棱长是:
120÷4÷(2+3)
=30÷(2+3)
=30÷5
=6(厘米)
原长方体的高是:
6+3+2
=9+2
=11(厘米)
则原长方体的体积是:
6×6×11
=36×11
=396(立方厘米)
答:原长方体的体积是396立方厘米。
故答案为:396。
【点评】此题主要考查长方体的表面积公式、长方体的体积公式的灵活运用,关键是求出长方体的底面边长和高。
9.(2024秋 栖霞区期末)科学研究表明,月球上的水可能以冰的形式存在于其地下土壤中,每立方米月球岩石中可提取约6升水,相当于 3 瓶2升装的纯净水,或相当于 12 瓶500毫升装的纯净水。
【考点】体积、容积及其单位.
【专题】应用题;应用意识.
【答案】3,12。
【分析】用每立方米月球岩石中可提取水的容量除以2升,求出相当于几瓶2升装的纯净水。1升=1000毫升,据此将每立方米月球岩石中可提取水的容量换算成毫升,再用每立方米月球岩石中可提取水的容量除以500毫升,求出相当于几瓶500毫升装的纯净水。
【解答】解:6÷2=3(瓶)
6升=6000毫升
6000÷500=12(瓶)
答:每立方米月球岩石中可提取约6升水,相当于3瓶2升装的纯净水,或相当于12瓶500毫升装的纯净水。
故答案为:3,12。
【点评】本题考查容积单位的换算,关键是熟记升和毫升之间的进率。
10.(2024秋 桥西区期末)一盒果汁250毫升, 4 盒这样的果汁是1升。
【考点】体积、容积进率及单位换算.
【专题】综合填空题;应用意识.
【答案】4。
【分析】根据1升=1000毫升进行填空。
【解答】解:1升=1000毫升
1000÷250=4(盒)
故答案为:4。
【点评】单位之间的换算,大单位换算成小单位要乘它们之间的进率;小单位换算成大单位要除以它们之间的进率。
三.判断题(共5小题)
11.(2024秋 正定县期末)1L水能装满10个容量是100毫升的瓶子。 √
【考点】体积、容积及其单位.
【专题】应用意识.
【答案】√。
【分析】根据体积单位之间的关系:1升=1000毫升,换算单位,判断即可。
【解答】解:1升=1000毫升
1L水能装满10个容量是100毫升的瓶子。原题说法正确。
故答案为:√。
【点评】本题主要考查体积单位的换算。
12.(2024秋 万柏林区期末)在两个杯子中盛满水,盛水多的那个杯子容量大。 √
【考点】体积、容积及其单位.
【专题】应用意识.
【答案】√。
【分析】根据容积是容器所能装物体的体积,解答此题即可。
【解答】解:哪个杯子能盛的水多,我们就说那个杯子的容量大,这句话是正确的。
故答案为:√。
【点评】熟练掌握容积的定义,是解答此题的关键。
13.(2024秋 太原期末)小卓生病咳嗽,妈妈让他每次喝6mL的止咳糖浆。 √
【考点】体积、容积进率及单位换算.
【专题】应用意识.
【答案】√。
【分析】根据容积单位的认识。再结合生活实际进行判断。
【解答】解:儿童每次可以服用5~10毫升,小卓生病咳嗽,妈妈让他每次喝6毫升的止咳糖浆。这个用量是正确的。
故答案为:√。
【点评】此题考查的目的是理解掌握容积单位的认识及应用。
14.(2024秋 晋源区期末)小卓生病咳嗽,妈妈让他每次喝6L的止咳糖浆。 ×
【考点】体积、容积进率及单位换算.
【专题】数感.
【答案】×。
【分析】根据对1升、1毫升实际有多少的认识,结合生活实际,计量小卓生病咳嗽,妈妈让他每次喝止咳糖浆的体积用“毫升”作计量单位。
【解答】解:小卓生病咳嗽,妈妈让他每次喝m6L的止咳糖浆。
原题说法错误。
故答案为:×。
【点评】此题考查根据情景选择合适的计量单位,要注意联系生活实际、计量单位和数据的大小,灵活选择。
15.(2024春 琼海期中)两个完全一样的长方体拼成一个新的长方体,跟原来两个长方体的表面积之和及体积之和相比,新长方体的体积变大了,表面积也变大了。 ×
【考点】长方体和正方体的体积.
【专题】应用意识.
【答案】×。
【分析】根据长方体表面积的意义、长方体体积的意义可知,两个完全一样的长方体拼成一个新的长方体,跟原来两个长方体的表面积之和及体积之和相比,新长方体的体积不变,表面积变小了。据此判断。
【解答】解:两个完全一样的长方体拼成一个新的长方体,跟原来两个长方体的表面积之和及体积之和相比,新长方体的体积不变,表面积变小了。
因此题干中的结论是错误的。
故答案为:×。
【点评】此题考查的目的是理解掌握长方体表面积的意义、体积的意义及应用。
四.计算题(共2小题)
16.(2024春 澄城县期中)计算如图组合图形的表面积和体积。(单位:cm)
【考点】长方体和正方体的体积;长方体和正方体的表面积.
【专题】应用意识.
【答案】238平方厘米,199立方厘米。
【分析】由于正方体与长方体粘合在一起,求这个组合图形的表面积时上面的正方体只求4个侧面的面积,下面的长方体求出表面积,然后合并起来;这个组合图形的体积等于正方体与长方体的体积和。
【解答】解:4×4×4+(9×5+9×3+5×3)×2
=16×4+(45+27+15)×2
=64+87×2
=64+174
=238(平方厘米)
4×4×4+9×5×3
=64+135
=199(立方厘米)
答:这个组合图形的表面积是238平方厘米,体积是199立方厘米。
【点评】此题主要考查正方体、长方体的表面积公式、体积公式的灵活运用,关键是熟记公式。
17.(2024春 西秀区校级期中)计算长方体表面积、正方体体积。
【考点】长方体和正方体的体积;长方体和正方体的表面积.
【专题】应用意识.
【答案】202,343。
【分析】根据长方体的表面积公式:S=(ab+ah+bh)×2,正方体的体积公式:V=a3,把数据代入公式解答。
【解答】,解:(9×4+9×5+4×5)×2
=(36+45+20)×2
=101×2
=202
7×7×7
=49×7
=343
答:长方体的表面积是202,正方体的体积是343。
【点评】此题主要考查长方体的表面积公式、正方体的体积公式的灵活运用,关键是熟记公式。
五.应用题(共6小题)
18.(2024秋 吴江区期末)一个长方体和一个正方体的棱长总和相等。已知长方体的长、宽、高分别是6分米、5分米、4分米。
(1)那么正方体的棱长是多少分米?
(2)长方体的体积是多少立方分米?
【考点】长方体和正方体的体积;正方体的特征.
【专题】应用题;应用意识.
【答案】(1)5分米;(2)120立方分米。
【分析】(1)已知长方体的长、宽、高分别是6分米、5分米、4分米,根据长方体的棱长总和=(长+宽+高)×4,据此求出长方体的棱长总和;已知一个长方体和一个正方体的棱长总和相等,根据正方体的棱长总和=棱长×12,可知正方体的棱长=棱长总和÷12,据此求出正方体的棱长;
(2)根据长方体的体积=长×宽×高,代入数据计算即可求出这个长方体的体积。
【解答】解:(1)(6+5+4)×4÷12
=15×4÷12
=60÷12
=5(分米)
答:正方体的棱长是5分米。
(2)6×5×4
=30×4
=120(立方分米)
答:长方体的体积是120立方分米。
【点评】本题考查的是长方体、正方体棱长知识的运用和长方体体积计算公式的运用。
19.(2024秋 巢湖市期末)一个长方体油箱长80cm,宽60cm,高40cm,油箱中油面与油箱口的距离为10cm,每升汽油能行驶12.5km,这箱汽油能行驶多少距离?
【考点】长方体、正方体表面积与体积计算的应用.
【专题】运算能力.
【答案】1800千米。
【分析】油箱中油面与油箱口的距离为10cm,则油箱中油的高度是40﹣10=30(厘米),再把80厘米、60厘米和30厘米都化成分米。根据长方体的体积公式:V=abh,代入数据求出油箱中油的体积;用1升油可行的千米数乘油的体积,就是这箱油能行驶的千米数,列式解答即可。
【解答】解:80厘米=8分米、60厘米=6分米
40﹣10=30(厘米)
30厘米=3分米
8×6×3
=48×3
=144(立方分米)
144立方分米=144升
144×12.5=1800(千米)
答:这箱汽油能行驶1800千米距离。
【点评】此题主要考查长方体体积的实际应用;关键是先求出油的体积,再用乘法解答,注意单位换算。
20.(2024秋 天宁区期末)如图,把一张正方形铁皮沿虚线折叠,围成一个长方体的侧面。给这个长方体配一个底面,这个长方体的容积是多少毫升?
【考点】长方体和正方体的体积.
【专题】应用意识.
【答案】864毫升。
【分析】通过观察图形可知,这个长方体的底面周长和高都是24厘米,根据正方形的周长公式:C=4a,那么a=C÷4,据此求出底面边长,再根据长方体的体积(容积)公式:V=abh,把数据代入公式解答。
【解答】解:24÷4=6(厘米)
6×6×24
=36×24
=864(立方厘米)
864立方厘米=864毫升
答:这个长方体的容积是864毫升。
【点评】此题主要考查正方形的周长公式、长方体的体积公式的灵活运用,关键是熟记公式。
21.(2024秋 新邵县期末)聪聪家有一个长方体鱼缸(无盖),长6分米,宽5分米,高4分米。
(1)这个长方体鱼缸的下面和右面的玻璃打碎了,要修好这个鱼缸,至少需要购买多少平方分米相配套的玻璃?
(2)聪聪妈妈在修好的鱼缸里注入3分米高的水,此时水与鱼缸接触的面积是多少平方分米?
【考点】长方体、正方体表面积与体积计算的应用;长方体和正方体的表面积.
【专题】应用意识.
【答案】(1)50平方分米;
(2)96平方分米。
【分析】(1)根据题意可知,打碎下面玻璃长是6分米,宽是5分米,右侧玻璃的长是5分米,宽是4分米,可用长方形的面积公式S=长×宽进行解答即可;
(2)要求水与鱼缸的接触面积是多少平方分米,即求出长6分米,宽5分米,高3分米的长方体五个面积是多少即可得解,根据长方体面积公式(S=ab+2ah+2bh),将数据代入即可得出答案。
【解答】解:(1)6×5+5×4
=30+20
=50(平方分米)
答:至少需要购买50平方分米相配套的玻璃。
(2)6×5+2×6×3+2×5×3
=30+36+30
=96(平方分米)
答:水与鱼缸接触的面积是96平方分米。
【点评】本题考查学生对长方形面积公式和长方体面积公式的掌握和运用。
22.(2024秋 渝中区期末)一个量杯最多能装300克水。
(1)如图所示,如果往量杯里到入60克水,请你用“______”标出水的高度。
(2)将量杯装满水,倒掉一部分(如图所示),剩下多少克水?
(3)现在量杯中倒掉的水与剩下的水比较。谁多?多多少克?
【考点】体积、容积及其单位.
【专题】应用意识.
【答案】(1)
(2)180克;
(3)剩下的水,60克。
【分析】(1)量杯装满水300克,60克水占量杯总容量的,即,据此解答;
(2)根据图示可知:剩下的水占量杯总容量的加上(1)的,据此计算出剩下多少克水即可;
(3)先用300克减去(2)的结果,求出剩下的水的克数,再求出倒掉的水的克数,比较多少后求差几颗。
【解答】解:(1)60÷300
(2)(1)
300180(克)
答:剩下180克水。
(3)300﹣180=120(克)
180克>120克
180﹣120=60(克)
答:剩下的水多,多60克。
【点评】本题考查了利用求一个数是另一个数的几分之几及分数与整数四则混合运算解决问题,需准确识图,正确分析题目中的数量关系。
23.(2024秋 建邺区期末)一个长50厘米、宽40厘米、高30厘米的长方体水箱,水深20厘米.如果放入一块棱长10厘米的正方体石块,那么水箱里的水面将上升多少厘米?
【考点】长方体和正方体的体积.
【专题】立体图形的认识与计算.
【答案】见试题解答内容
【分析】首先根据正方体的体积公式:V=a3,求出正方体石块的体积,然后用石块的体积除以长方体的底面积即可.
【解答】解:10×10×10÷(50×40)
=1000÷2000
=0.5(厘米),
答:水箱里的水面将上升0.5厘米.
【点评】此题主要考查正方体、长方体的体积公式的灵活运用,关键是熟记公式.
21世纪教育网(www.21cnjy.com)
