第十九章 一次函数 中档突破专项练习(含答案) 2024-2025学年人教版八年级数学下册
文档属性
| 名称 | 第十九章 一次函数 中档突破专项练习(含答案) 2024-2025学年人教版八年级数学下册 | 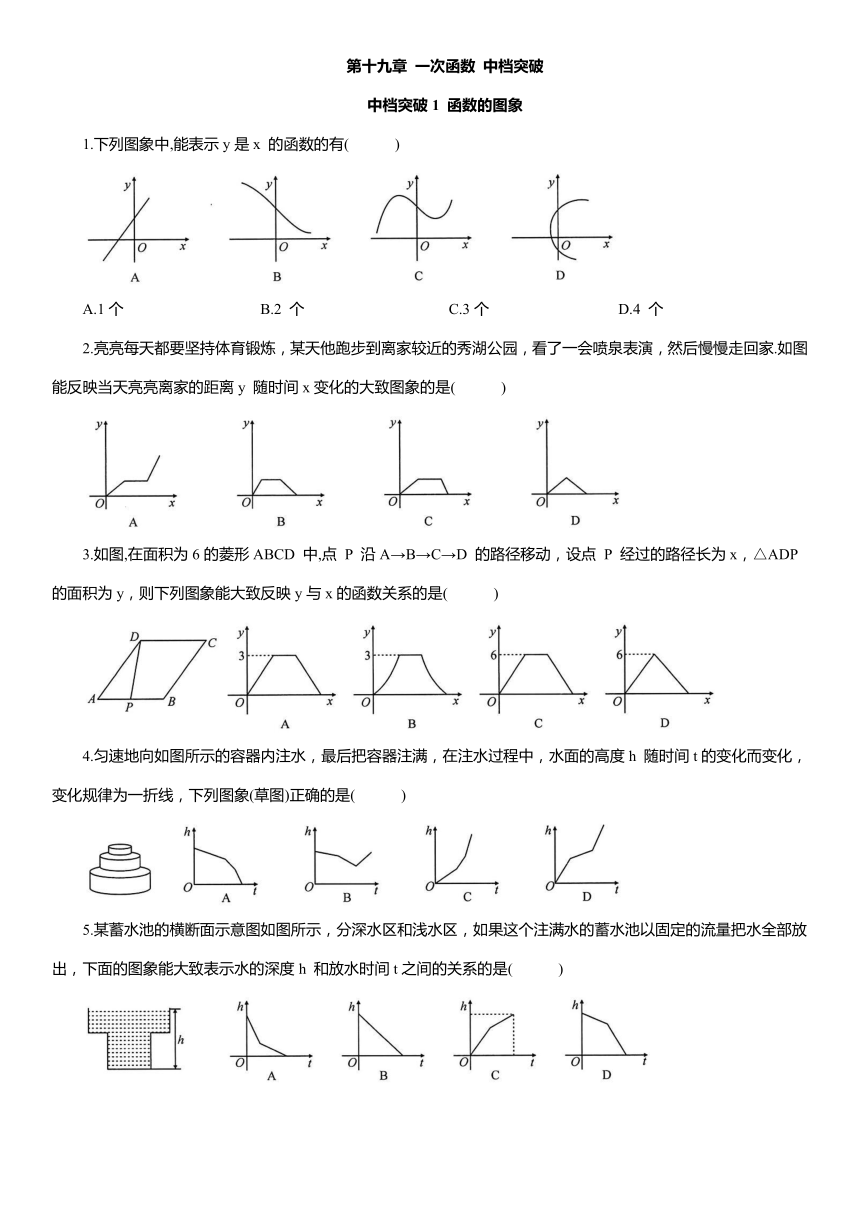 | |
| 格式 | docx | ||
| 文件大小 | 540.7KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-05-09 09:57:44 | ||
图片预览





文档简介
第十九章 一次函数 中档突破
中档突破1 函数的图象
1.下列图象中,能表示y是x 的函数的有( )
A.1个 B.2 个 C.3个 D.4 个
2.亮亮每天都要坚持体育锻炼,某天他跑步到离家较近的秀湖公园,看了一会喷泉表演,然后慢慢走回家.如图能反映当天亮亮离家的距离y 随时间x变化的大致图象的是( )
3.如图,在面积为6的菱形ABCD 中,点 P 沿A→B→C→D 的路径移动,设点 P 经过的路径长为x,△ADP 的面积为y,则下列图象能大致反映y与x的函数关系的是( )
4.匀速地向如图所示的容器内注水,最后把容器注满,在注水过程中,水面的高度h 随时间t的变化而变化,变化规律为一折线,下列图象(草图)正确的是( )
5.某蓄水池的横断面示意图如图所示,分深水区和浅水区,如果这个注满水的蓄水池以固定的流量把水全部放出,下面的图象能大致表示水的深度h 和放水时间t之间的关系的是( )
中档突破2 一次函数的图象和性质
1.在平面直角坐标系中,一次函数 的图象可能是( )
2.若一次函数y=(2m+1)x+m-3的图象不经过第二象限,则m的取值范围是( )
B. m<3
3.是一次函数y= kx+b(k<0)图象上的两点,则y 与y 的大小关系是( )
D.不能确定
4.一次函数y=2x+n的图象上有三个点A(-3,a),B(1,b),C(-1,c),据此可以判断a,b,c的大小关系为( )
A. a5.若点A(x ,-3),B(x ,-4),C(x ,1)不在一次函数 1)x+4的图象上,则:x ,x ,x 的大小关系是( )
6.若一次函数y=kx+2的y随x的增大而减小,则该函数图象可能经过的点的坐标是( )
A.(2,5) B.(1,1) C.(-1,-2) D.(-2,0)
7.在平面直角坐标系中,过点(-1,-2)的直线l 经过一、二、三象限,若点(0,a),(1,b),(c,-1)都在直线l上,则下列判断正确的是( )
A. a<0 B. b<-2 C. c>-1 D. b中档突破3 一次函数解析式及应用
一、求一次函数解析式
1.已知 且 与x成正比例,y 与x-2成正比例.当x=2时,y=7;当x=1时,y=0.
(1)求y与x之间的函数关系式;
(2)计算x=4时,y的值.
2.如图,直线y=3x+3分别交x轴,y轴于点A,B.
(1)当0(2)点 在直线 y=3x+3上.
①直接写出 n 的值为 ;
②过点 C作CD⊥AB 交x轴于点D,求直线CD 的解析式.
二、利用一次函数解析式求值
3.在平面直角坐标系中,已知点A(a,1),B(b,-2)均在直线y=-2x+m 上,则a-b的值为( )
B.-3 C.3 D.4
4.已知直线y= ax+b与直线y=x+3交于点 B(--3,n),则代数式 的值为( )
A.3 B.2 C.1 D.0
中档突破4 一次函数与图形变换
一、平移
1.直线y=—2x+1向下平移5个单位长度后的对应直线的解析式是
2.将直线y=2x+3向左平移2个单位长度后的对应直线的解析式为( )
A. y=2(x-2)+3B. y=2(x+2)+3 C. y=2x+5 D. y=2x+1
3.把直线y=-x+3向上平移m个单位长度后,与直线y=2x+4的交点在第一象限,则m 的取值范围是( )
A.11 D. m<4
二、对称
4.如图,在平面直角坐标系中,已知直线 与x轴,y轴分别交于A,B 两点,C是 y轴正半轴上一点,把△ABC 沿直线 AC 折叠,使点 B 刚好落在x 轴负半轴上,则点 C 的坐标是( )
B.(0, C.(0,3) D.(0,4)
5.如图,已知直线l的解析式是 ,与x轴,y轴分别交于点A,B.
(1)直接写出将直线l向左平移2个单位长度得到的直线l 的解析式为 ;直接写出直线l关于x 轴对称的直线l 的解析式为 ;
(2)在(1)的条件下,求直线l与直线l 的距离.
中档突破5 一次函数与实际问题(一)图象信息
一、行程问题
1.甲、乙两人沿同一直线同时出发去往 B 地,运动过程中甲、乙两人离 B 地的距离y(km)与出发时间x(h)的关系如图所示,下列说法错误的是( )
A.甲、乙两人在出发后2 h第一次相遇 B.甲的速度是 16 km/h
C.甲到达 B 地时两人相距50 km D.出发时乙在甲前方20 km
2.小王骑车从甲地到乙地,小李骑车从乙地到甲地,小王的速度小于小李的速度,两人同时出发,沿同一条公路匀速前进.图中的折线表示两人之间的距离y(km)与小王的行驶时间x(h)之间的函数关系,下列结论错误的是( )
A.小王骑车的速度为10 km/h B.小李骑车的速度为20 km/h
C. a 的值为15 D.走完全程,小李用时是小王的
3.甲、乙两车同时从A,B 两地出发,相向而行,甲车到达 B 地后立即返回A 地,两车离A 地的距离y(单位:km)与所用时间x(单位:min)之间的函数关系如图所示(粗线表示乙车,细线表示甲车),则甲、乙两车在途中两次相遇的间隔时间为( )
A.9 min B.10 min C.11 min D.12 min
二、工程问题
4.某社区有一块空地需要绿化,某绿化组承担了此项任务,绿化组工作一段时间后,提高了工作效率.该绿化组完成的绿化面积S(单位: )与工作时间t(单位:h)之间的函数关系如图所示,则该绿化组提高工作效率前每小时完成的绿化面积是( )
三、租车问题
5.某公司准备与汽车租赁公司签订租车合同,以每月用车路程xkm计算,甲汽车租赁公司每月收取的租赁费为y 元,乙汽车租赁公司每月收取的租赁费为y 元,若y ,y 与x之间的函数关系如图所示,其中x=0对应的函数值为月固定租赁费,则下列判断错误的是( )
A.当月用车路程为1 800km时,选甲汽车租赁公司比较合算
B.当月用车路程为2 000 km时,两家汽车租赁公司租赁费用相同
C.当月用车路程为2 300 km时,选乙汽车租赁公司比较合算
D.除去月固定租赁费,甲租赁公司每公里收取的费用比乙租赁公司少
四、销售问题
6.某农资门市部连续8天调进一批化肥进行销售,在开始调进化肥的第7天开始销售.若进货期间每天调入化肥的吨数与销售期间每天销售化肥的吨数都保持不变,这个门市部的化肥存量S(单位:吨)与时间t(单位:天)之间的函数关系如图所示,则该门市部这次化肥销售活动(从开始进货到销售完毕)所用时间为 天.
五、进出水管问题
7.一个容器有进水管和出水管,每分钟的进水量和出水量是两个常数.从某时刻开始 4 min内只进水不出水,从第4 min 到第 24 min 内既进水又出水,从第24 min开始只出水不进水,容器内水量y(单位:L)与时间x(单位:min)之间的关系如图所示,则图中a 的值是( )
A.32 B.34 C.36 D.38
中档突破6 一次函数与实际问题(二)表格信息
1.有一个装有水的容器,如图所示,注水之前容器内有少量水,现向容器内注水,并同时开始计时,在注水过程中,水面高度匀速增加,则容器注满水之前,将容器内的水面高度y(cm)与时间x(s)记录于下表,则★的值是( )
x/秒 5 10 25 30
y/ cm 11 12 15
A.16 B.17 C.18 D.19
2.物理课上,于老师让同学们做这样的实验:在放水的盆中放入质地均匀的木块B,再在其上方放置不同质量的铁块A.已知木块 B 全程保持漂浮状态,通过测量木块B 浮在水面上的高度h(mm)与铁块A 的质量x(g),可得它们之间满足一次函数关系.据此可以判断下表中记录错误的数据是( )
实验次数 一 二 三 四
铁块 A 质量x/g 25 50 75 100
高度 h/ mm 40 30 15 10
A.第一次的数据 B.第二次的数据 C.第三次的数据 D.第四次的数据
3.杆秤是我国传统的计重工具.如图,可以用秤砣到秤纽的水平距离,来得出秤钩上所挂物体的质量.称重时,若秤砣到秤纽的水平距离为x(单位:cm)时,秤钩所挂物重为y(单位:kg),则y是x的一次函数.下表记录了四次称重的数据,其中只有一组数据记录错误,它是( )
A.第1组 B.第2 组 C.第3组 D.第4组
组数 1 2 3 4
x/ cm 1 2 4 7
y/ kg 0.80 1.05 1.65 2.30
中档突破7 一次函数与方程(组)、不等式
1.直线. 和 如图所示,则关于x的不等式 的解集是 .
2.如图,在平面直角坐标系xOy 中,若直线 -2x+a 与直线. 相交于点 P(1,-3),则关于x的不等式-2x+a< bx-4的解集是 .
3.在平面直角坐标系xOy中,一次函数 y= kx和y=mx+n的图象如图所示,则关于x的一元一次不等式(k-m)x-n>0的解集是 .
4.如图,直线 经过点(2,4),当 kx+b>2x时,x 的取值范围是 .
5.如图,直线y=3x和y= kx+2相交于点 P(a,6),则关于x的不等式(3-k)x≤2的解集为 .
6.一次函数 与 的图象如图所示,则0< mx+n<-x+a 的解集为( )
A. x>3 B. x<2 C.2中档突破8 一次函数与实际问题(三)方案设计
类型一 费用最少问题
1.2022年新洲区计划对邾城街文昌大道长2400米的污水管网进行改造.经投标,由甲、乙两个工程队来完成,若甲队每天能完成长度是乙队每天能完成长度的2倍,并且独立完成长度为400米管网改造所用的时间,甲队比乙队少5天.
(1)求甲、乙两工程队每天能完成管网改造的长度;
(2)设甲工程队施工x天,乙工程队施工y天,刚好完成改造任务(两工程队都必须参加,且工作天数都为整数).求y关于x的函数关系式,并写出自变量x的范围;
(3)若甲队每天施工费用为0.6万元,乙队每天施工费用为0.25万元,且甲乙两队施工的总天数不超过40天,则如何安排甲、乙两队施工的天数,才能使施工总费用最低 并求出最低费用.
2.A 城有肥料200t,B 城有肥料300t.现要把这些肥料全部运往C,D
两乡,C乡需要肥料240t,D乡需要肥料260t,其运往C,D两乡的运费如下表:设从 A 城运往C 乡的肥料为 xt,从A 城运往两乡的总运费为y 元,从B 城运往两乡的总运费为y 元
(1)分别写出y ,y 与x之间的函数关系式(不要求写自变量的取值范围);
(2)试比较A,B两城总运费的大小;
两城/两乡 C(元/t) D(元/t)
A 20 24
B 15 17
(3)若B 城的总运费不得超过4800元,怎样调运使两城总费用的和最少 并求出最小值.
类型二 利润最大问题
3.某商店销售一种产品,该产品成本价为6元/件,售价为8元/件,销售人员将该产品一个月(30天)销售情况记录绘成如下图象,图中的折线ODE表示日销量y(件)与销售时间x(天)之间的函数关系,若线段DE 表示的函数关系中,时间每增加1天,日销量减少5件.
(1)第25天的日销量是 件,这天销售利润是 元;
(2)求y与x之间的函数关系式,并写出x的取值范围;
(3)日销售利润不低于640元的天数共有多少天 销售期间日销售最大利润是多少元
类型三 方案最佳问题
4.某商场电饭煲的销售价为每台1 100元,豆浆机的销售价为每台1000元,每台电饭煲的进价比每台豆浆机的进价多200元,商场用10 000元购进电饭煲的数量与用8 000元购进豆浆机的数量相等.
(1)求每台电饭煲与豆浆机的进价分别是多少
(2)现在商场准备一次购进这两种家电共100台,设购进电饭煲x台,这100 台家电的销售总利润为y元,要求购进豆浆机数量不超过电饭煲数量的2倍,总利润不低于16 400元,请分析合理的方案共有多少种 并确定获利最大的方案以及最大利润;
(3)实际进货时,厂家对电饭煲出厂价下调k(0类型四含参类问题
5.武汉某文化公司向市场投放A 型和B 型商品共200件进行试销,A型商品成本价140元/件,B型商品成本价 120元/件,要求两种商品的总成本价不超过26400元,已知A 型商品的售价为200元/件,B 型商品的售价为170元/件,全部售出且获得的利润不低于10 800元.设该公司投放A 型商品x件,销售这批商品的利润为y 元.
(1)求y 与x之间的函数解析式,并求出x的取值范围;
(2)要使这批商品的利润最大,该公司应该向市场投放多少件 A 型商品 最大利润是多少
(3)该公司决定在试销活动中每售出一件A 型商品,就从一件 A 型商品的利润中捐献慈善资金a(a>0)元,当该公司售完这200件商品并捐献资金后获得的最大收益为10 960元时,求a 的值.
6.某商场购进A,B 两种服装共100件,已知购进这100件服装的费用不得超过7 500元,且其中A 种服装不少于65件,它们的进价和售价如表.
其中购进A 种服装为x件,如果购进的A,B两种服装全部销售完,根据表中信息,解答下列问题.
(1)求获取总利润y 元与购进A 种服装x件的函数关系式,并写出x的取值范围;
服装 进价(元/件) 售价(元/件)
A 80 120
B 60 90
(2)该商场对A 种服装以每件优惠a(07.某茶叶店准备从茶农处采购甲、乙两种不同品质的茶叶,已知采购2斤甲型茶叶和1斤乙型茶叶共需要550元;采购3斤甲型茶叶和2斤乙型茶叶共需要900元.
(1)甲、乙两种型号的茶叶每斤分别是多少元
(2)该茶叶店准备用不超过3 500元的资金采购甲、乙两种型号的茶叶共20斤,其中购进甲种型号的茶叶的斤数不少于购进乙种茶叶的 ,采购的斤数需为整数,那么该茶店有哪几种采购方案
(3)在(2)的条件下,已知该茶叶店销售甲型茶叶1斤可获利 )元,销售乙型茶叶1斤可获利4m 元,若20斤茶叶全部售出的最大利润为792元,请直接写出m 的值为 .
8.某商店销售A 型和B 型两种电脑,每台A 型电脑的利润为400元,每台B 型电脑的利润为500元.该商店计划一次性购买两种型号的电脑共100台,且B 型电脑的进货量不超过A 型电脑的2倍,设购进A 型电脑x台,这100台电脑的销售总利润为y元.
(1)直接写出 y 与x 的函数关系式;
(2)该商店购进A 型,B型电脑各多少台,才能使销售总利润最大,最大利润是多少
(3)实际进货时,电脑厂家对A 型电脑的出厂价下调 元,B型电脑的出厂价不变,且限定商店最多购进 A 型电脑60台,若商店保持同种电脑售价不变,怎样进货可使销售完100台电脑的总利润最大
9.某商店销售10台A 型电脑和20台 B 型电脑的利润为4 000元,销售 20台 A 型电脑和10台 B 型电脑的利润为3 500元.
(1)求每台A 型电脑和B 型电脑的销售利润;
(2)该商店计划一次购进两种型号的电脑共100台,其中B 型电脑的进货量不超过A 型电脑的2倍,设购进A 型电脑x台,这100台电脑的销售总利润为 y元.
①求y关于x的函数关系式;
②该商店购进A 型、B型电脑各多少台,才能使销售总利润最大
(3)实际进货时,厂家对A 型电脑出厂价下调m(010.A 城有肥料200t,B 城有肥料300 t,现要把这些肥料全部运往C,D两乡,从A 城往C,D两乡运肥料的费用分别为20元/t和25元/t;从B 城往C,D 两乡运肥料的费用分别为15元/t和24元/t.现C乡需要肥料240t,D乡需要肥料260t,设A城运往C乡的肥料为 xt,运往C乡肥料的总运费为y ,运往D乡肥料的总运费为y .
(1)写出y 关于x的函数关系式以及y 关于x的函数关系式,并指出自变量的取值范围;
(2)怎么样调度使得该过程的总运费最少 并求出最少的运输费以及最少的运输方案;
(3)由于从B 城到D 乡开辟了一条新的公路,使B 城到D 乡的运输费每吨减少了 8)元,如何调度才能使总运费最少 最少运输费是多少(用含a的式子表达)
中档突破9 一次函数与线段问题
类型一 线段长
1.直线y= kx+b经过A(—2,0),B(0,4)两点,C点的坐标为(0,-1).
(1)求 k 和b的值;
(2)E 为线段AB 上一点,F 为直线AC 上一点,
①如图1,若EF∥BC,求点 E 的坐标;
②如图2,若EF∥AO,请直接写出点 E 的坐标.
2.如图,直线 与x轴交于点A,与y 轴交于点B,与直线 y=x交于点E,点 E 的横坐标为3.
(1)求点 A 的坐标;
(2)在x轴上有一点 P(m,0),过点 P 作x轴的垂线,与直线 交于点C,与直线y=x交于点D.若CD=5,求m 的值.
类型二 线段关系
3.如图,直线 交x轴于点A,交y轴于点B,与直线y=x-2交于点 D(3,m).
(1)求 k,m的值;
(2)已知点 P(n,n),过点 P 作垂直于y 轴的直线与直线 交于点 M,过点 P 作垂直于x轴的直线与直线. 交于点 N(P与 N 不重合).若 ,求n 的值.
4.如图,直线 与x轴,y轴分别交于点A,B,与函数 的图象交于点M(1,2).
(1)直接写出k,b的值和不等式 的解集;
(2)在x轴上有一点 P,过点 P 作x轴的垂线,分别交函数 和 的图象于点C,D.若 求点 P 的坐标.
中档突破10 一次函数与面积问题
类型一 根据坐标求面积
1.已知一次函数 的图象经过点( 和 且与x轴交于点A,与y 轴交于点 B.
(1)求这个函数的解析式,并在图中直接画出图象;
(2)已知点 P(m,n)在线段AB 上,点 C(3,5),求. 的面积(用含 m 的式子表示).
2.已知一次函数. 的图象经过点(1,4)和( 且交x轴于点A,交 y轴于点B.
(1)求这个函数的解析式;
(2)求 的面积;
(3)已知点 ,点 N(0,2),点 P(m,n)在线段 AB 上,设 的面积为S,请直接写出S 关于m 的函数关系式以及自变量m 的取值范围: .
类型二 根据面积求坐标或参数值
3.如图,直线AB 与x轴交于点A(2,0),与y轴交于点.
(1)求直线 AB 的解析式;
(2)若直线AB 上的点C 在第一象限,且 求点 C 的坐标.
4.已知一次函数. 的图象交x轴于点A(4,0),交y轴于点B(0,2).
(1)求这个一次函数的解析式;
(2)若在第一象限有一点 C(2,m),且 的面积为4,求m 的值.
5.点 P(x,y)在第一象限,且. 点 A(3,0),设 的面积为S.
(1)用含x 的式子表示S,并写出x的取值范围;
(2)在如图网格中建立直角坐标系,并画出函数S 的图象;
(3)当△OPA 面积是5时,求点 P 的坐标.
类型三 面积与分类讨论
6.如图,在平面直角坐标系中,点A(2,2), ,直线 AB 交 y 轴于点C.
(1)求直线 AB 的解析式和点 C 的坐标;
(2)在直线 OA 上有一点 P,使得 的面积为4,求点 P 的坐标.
7.如图,在平面直角坐标系中,点
(1)求直线 AB 的解析式;
(2)已知点 在直线 AB 的下方, 的面积为10,求m 的值.
类型四 根据面积关系求值
8.直线 与 x 轴交于点A,与y 轴交于点 B,已知点 点 P 在x 轴上,
(1)求 A,B 两点的坐标;
(2)求点 P 的坐标.
9.如图,在平面直角坐标系xOy 中,直线 交x轴于点C,交y轴于点D,点A,B 的坐标分别为(1,0),(0,2),直线AB 与直线CD 相交于点 P.
(1)直线 AB 的解析式为 ;
(2)点 P 的坐标为 ,连接OP,则
(3)若直线 CD 上存在一点E,使得 的面积是 的面积的4 倍,求点 E 的坐标.
中档突破11 一次函数与角度问题
类型一 一次函数与45 度角
1.如图,直线 交x轴于点 A,交 y 轴于点 B,点 P在直线 AB 上.
(1)若AP=2BP,求点 P 的坐标;
(2)若 求点 P 的坐标.
2.如图,在平面直角坐标系中,直线 与x轴,y 轴分别交于点B,A,C 为OA 上一点,且 ,E 是线段BC 上一点,连接AE 并延长交OB 于点D,若 求OD 的长.
类型二 一次函数与角度关系
3.如图,直线. 与直线 交于点C,它们与y轴分别交于A,B两点.
(1)求 A,B,C三点的坐标;
(2)点 P 在x轴上,使 ,求点 P 的坐标.
4.如图1,在平面直角坐标系中,点A(0,4),B(—2,0),C是x轴正半轴上一点,且
(1)求点 C 的坐标;
(2)如图2,在x轴正半轴上有一点 P,使 求点 P 的坐标;
(3)如图3,E是y轴上点A 下方一动点,将线段EC 绕点E 逆时针旋转一个小于 的角到EF,且有 ,求OF 的最小值.
第十九章 一次函数
中档突破1 函数的图象
1. C 2. B 3. A
4. C 解:最下面的容器最粗,第二个容器较粗,那么每个阶段的函数图象水面高度h 随时间t的增大而增长,用时较短,故选 C.
5. D
中档突破2 一次函数的图象和性质
1. B 解:当k>0时,图象经过二、三、四象限;当k<0时,图象经过一、二、三象限,故选 B.
2. D 解:根据题意,得2m+1>0且m-3≤0,解得 m≤3.故选 D.
3. A 解:∵k<0,∴y随x的增大而减小,∵--1<2,∴y >y .故选 A.
4. A 解:∵k=2>0,∴y随x的增大而增大,∵--3<-1<1,∴a5. B 解: ∴y随x的增大而减小,∵--4<-3<1, 故选 B.
6. B 解:将 A,B,C,D四个选项的坐标分别代入y=kx+2,计算k值,只有B得到k=-1<0,故选 B.
7. C 解:由题意可画出大致图象,由图可知,0中档突破3 一次函数解析式及应用
1.解:(1)设 把x=2,y=7和x=1,y=0代入,得 解得∴y与x之间的函数关系式为y=7x-7.(2)把x=4代入y=7x-7,得y=7×4-7=21.
2.解:(1)-1(2)①把 代入y=3x+3,得 解得n=1;
②过点C作CH⊥x轴于点 H.由y=3x+3,得A(-1,0),又∵n=1,∴CH=OA=1,可得△AOB≌△CHD,
∴DH=OB=3,∴D( ,0),又 由待定系数法可求得直线 CD 的解析式为
3. A 解:∵点 A(a,1),B(b,-2)均在直线 y=-2x+m上,∴-2a+m=1①,-2b+m=-2②,
由②-①,得2a--2b=-3,∴a-b=- 故选 A.
4. D 解:∵点B(-3,n)在直线y=x+3上,∴-3+3=n,∴n=0,∴B(-3,0),代入y= ax+b,得-3a+b=0, 故选 D.
中档突破4 一次函数与图形变换
1. y=-2x-4 2. B 3. C
4. B 解:易求A(4,0),B(0,3),即OA=4,OB=3,∵AB 沿直线AC 折叠,使点 B 刚好落在x轴上, 设CO=n,则 在 Rt△B'OC 中, 解得 点C 的坐标为(o, ).
5.解:
(2)过点O作OH⊥l于点 H,
在 Rt△OAB 中,
OA=2,OB=4,
∴直线l与直线l 的距离为
中档突破5 一次函数与实际问题(一)图象信息
1. C 解:由题意,得出发时乙在甲前方20km,故D正确;v甲=80÷5=16(km/h),故B正确;
vz=60÷10=6(km/h),(80-60)÷(16-6)=2(h),即甲、乙两人在出发后2 h第一次相遇,故A 正确;甲到达 B 地时两人相距60-6×5=30(km),故 C 错误.故选 C.
2. D 解:小王骑车的速度为30÷3=10(km/h),故选项A正确;小李骑车的速度为30÷1-10=20(km/h),故选项B正确;a=10×(30÷20)=15,故选项 C正确;走完全程,小李所用的时间为30÷20=1.5(h),小王所用的时间为3h,故走完全程,小李所用的时间是小王的 故选项 D错误.故选 D.
3. A 解:设 A,B 两地的距离为S km,
则甲车的速度为 乙车的速度为 甲、乙两车在途中第一次相遇的时间为 设甲、乙两车在途中第二次相遇的时间为 a min,则 解得a=18,∴18-9=9(min),即甲、乙两车在途中两次相遇的间隔时间为9 min.故选 A.
4. B 解:当t≥2时,由(4,1 000),(5,1 300),得 S=300t-200,即工作2h,该绿化组完成的绿化面积是 400 m .
∴提高工作效率前每小时完成的绿化面积是
故选 B.
5. D 解:当月用车路程为1800 km时,yy ,C说法正确;y 的图象倾斜程度更大,即甲租赁公司每公里收取的费用比乙租赁公司多,D说法错误,故选 D.
6.11
7. C 解:由图象可知,进水的速度为20÷4=5(L/ min),出水的速度为5-(35-20)÷(16-4)=3.75(L/ min),第24分钟时的水量为20+(5-3.75)×(24-4)=45(L),a=24+45÷3.75=36.故选 C.
中档突破6 一次函数与实际问题(二)表格信息
1. A 解:由(5,11),(10,12),得该一次函数解析式为 10.当x=30时, 即★的值是16.故选 A.
2. C 解:设h=kx+b(k≠0),假设第一次和第二次数据都是正确的,则 解得
∴h=-0.4x+50,当x=75时,h=-0.4×75+50=20,这与表格中的数据不符;当x=100时,
h=-0.4×100+50=10,这与表格中的数据相符,假设成立,故第三次数据是错误的.故选 C.
3. C 解:设y= kx+b,把x=1,y=0.80,x=2,y=1.05代入,求得y=0.25x+0.55,
当x=4时,y=0.25×4+0.55=1.55,
∴第3组数据不在这条直线上,
当x=7时,y=0.25×7+0.55=2.30,
∴第4组数据在这条直线上,故选 C.
中档突破7 一次函数与方程(组)、不等式
1. x<-1 解:根据图象,可知关于x的不等式. b的解集是x<-1,故答案为x<-1.
2. x>1 解:当x>1时,函数y=-2x+a的图象都在y=bx-4的图象下方,所以不等式-2x+a< bx-4的解集为x>1.故答案为x>1.
3. x>1 解:由(k-m)x-n>0,得 kx> mx+n.根据图象可知两函数的交点为(1,2),所以关于x的一元一次不等式 kx>mx+n的解集是x>1,即关于x的一元一次不等式(k-m)x-n>0的解集是x>1,故答案为x>1.
4. x<2 解:∵直线y= kx+b(k<0)经过点(2,4),直线y=2x也经过(2,4),由图象可得,当 kx+b>2x时,x的取值范围是x<2,故答案为x<2.
5. x≤2 解析:把 P(a,6)代入y=3x,得6=3a,解得a=2.观察图象可知,当3x≤kx+2时,x≤2,∴(3-k)x≤2的解集为x≤2.
6. C 解:由图可得,当0< mx+n时,x>2;
当 mx+n<-x+a时,x<3,
∴不等式组0< mx+n<-x+a的解集为2中档突破8 一次函数与实际问题(三)方案设计
类型一 费用最少问题
1.解:(1)设乙工程队每天能完成管网改造的长度为a 米,则甲工程队每天能完成管网改造的长度为2a 米,
根据题意,得 解得a=40.经检验,a=40是原方程的解,且符合题意,则40×2=80(米),
答:甲、乙两工程队每天能完成管网改造的长度分别是80米,40米;
(2)根据题意,得80x+40y=2400,
即 y=-2x+60,1≤x≤29,且x为整数;
(3)由题意,得x+y≤40,
∴--2x+60+x≤40,解得x≥20.
设施工总费用为 ω元,由题意,得ω=0.6x+0.25y=0.6x+0.25(-2x+60)=0.1x+15.
∵0.1>0,∴ω随x的增大而增大,当x=20时,ω最小=0.1×20+15=17(万元),此时y=20.
答:安排甲队施工20天,乙队施工20天,才能使施工总费用最低,最低费用为17万元.
2.解:(1)根据题意,得y =20x+24(200-x)=-4x+4800,y =15(240-x)+17(300-240+x)=2x+4620.
(2)若 ,则-4x+4800=2x+4620,解得x=30,A,B两城总费用一样;
若y解得x>30,A城总费用比B 城总费用小;
若 ,则-4x+4800>2x+4620,
解得0(3)依题意,得y =2x+4620≤4800,解得x≤90,
设两城总费用为y,则.
∵--2<0,∴y随x的增大而减小,
∴当x=90时,y有最小值9240.
答:当从A 城调往C乡肥料90t,调往 D 乡肥料110t,从B城调往C乡肥料 150t,调往 D 乡肥料150t时,两城总费用的和最少,最小值为9240元.
类型二 利润最大问题
3.解:(1)340-(25-22)×5=325(件),(8-6)×325=650(元),故答案为325,650;
(2)设直线OD 的函数关系式为y=kx,
将(17,340)代入y= kx,得340=17k,解得k=20.
∴直线OD 的函数关系式为y=20x,
设直线 DE 的解析式为y= mx+n;
将(22,340),(25,325)代入 y= mx+n,
得 解得
∴直线 DE 的函数关系式为y=-5x+450.
联立 解得
∴点 D 的坐标为(18,360).∴y与x之间的函数关系式为
(3)640÷(8-6)=320(件),当y=320时,由20x=320或-5x+450=320,解得x=16或x=26,
∴26-16+1=11(天),
∴日销售利润不低于640元的天数共有11天,
∵折线 ODE 的最高点 D 的坐标为(18,360),360×2=720(元).
∴当x=18时,日销售利润最大,最大利润为720元.
类型三 方案最佳问题
4.解:(1)设每台豆浆机的进价为 m 元,则每台电饭煲的进价(m+200)元,由题意,得 解得m=800,经检验,m=800是原分式方程的解,且符合题意,∴m+200=1000(元).
答:每台豆浆机的进价为800元,每台电饭煲的进价1000元;
(2)由题意得y=(1100-1000)x+(1000-800)(100-x)=-100x+20000,
∵x为正整数,∴x=34,35,36.
∴共有3种方案,即①电饭煲34台,豆浆机66台;
②电饭煲35台,豆浆机65台;
③电饭煲36 台,豆浆机 64台;
∵y=-100x+20000,-100<0,
∴y随x的增大而减小,∴当x=34时,y有最大值,最大值为-100×34+20000=16600(元).
答:当购进电饭煲34台,豆浆机66台获利最大,最大利润为16 600元;
(3)设厂家对电饭煲出厂价下调k(0∴y =(1100-1000+k)x+(1000-800)(100-x)=(k-100)x+20000,
①当100∴x=36时,y 取得最大值,
即购进电饭煲36台,豆浆机64台,总利润最大;
②当0∴x=34时,y 取得最大值,
即购进电饭煲34台,豆浆机66台,总利润最大;
③当k=100时,无论采取哪种方案,y 恒为20000元.
类型四 含参类问题
5.解:(1)根据题意,得 y=(200--140)x+(170-120)×(200-x),即y=10x+10000,
∵两种商品的总成本价不超过26400元,全部售出且获得的利润不低于10 800元,
解得80≤x≤120.
答:y与x 之间的函数解析式为y=10x+10 000,x 的取值范围是80≤x≤120且x为整数;
(2)由(1)可知y=10x+10000(80≤x≤120),∵10>0,∴y 随x的增大而增大,当x=120时,y最大=10×120+10 000=11 200(元).
答:该公司应该向市场投放120件A 型商品,最大利润为11 200元;
(3)根据题意,可知一共捐出 ax元,∴y=10x+10000-ax=(10-a)x+10000,当10-a<0时,
y=(10-a)x+10000的最大值小于10 000,不符合最大收益为10960元,∴这种情况不成立;
当10-a=0即a=10时,y=10000元,不符合最大收益为10 960元,∴这种情况不成立;
当10-a>0时,y随x的增大而增大,当x=120,y取最大值,∴120(10-a)+10000=10 960,∴a=2.
综上所述,a的值为2.
6.解:(1)∵80x+60(100-x)≤7500,解得x≤75,∴y=40x+30(100-x)=10x+3000(65≤x≤75且x为整数);
(2)∵y=(40-a)x+30(100-x)=(10-a)x+3000,方案1:当00,y随x的增大而增大,所以当x=75时,y有最大值,则购进A 种服装75件,B种服装25件;
方案2:当a=10时,所有方案获利相同,所以按哪种方案进货都可以;
方案3:当107.解:(1)设甲种茶叶每斤是x元,乙种茶叶每斤是 y元,根据题意,得 解得
答:甲种茶叶每斤是200元,乙种茶叶每斤是150元;
(2)设购买乙种茶叶a斤,则购买甲种茶叶(20-a)斤,根据题意,得 解得 10≤a≤12,∵a为整数,∴a=10,11,12.
故该茶叶店有3种采购方案,
方案一:购买甲种茶叶10斤,乙种茶叶10斤;
方案二:购买甲种茶叶9斤,乙种茶叶11斤;
方案三:购买甲种茶叶8斤,乙种茶叶12斤.
(3)设茶叶全部售出的利润为ω元,根据题意,得ω=3m(20-a)+4ma= ma+60m,∵m>0,∴w随a的增大而增大,∴当a=12时w有最大值,即12m+60m=792,解得m=11.
8.解:(1)由题意,得y=400x+500(100-x)=-100x+50000;
(2)∵100-x≤2x,∴x≥
∵y=-100x+50000,-100<0,
∴y随x的增大而减小,
∵x为整数,∴x=34时,y最大=46 600.
答:该商店购进A 型34台,B型电脑66台,才能使销售总利润最大,最大利润是46 600元;
(3)由题意,得.y=(400+m)x+500(100-x),
即 且x为整数.
①当0即商店购进34 台A 型电脑和66台 B 型电脑的销售利润最大;
②m=100时,m-100=0,y=50000,即商店购进 A 型电脑数量满足 的整数时,均获得最大利润;
③当1000,y随x的增大而增大,∴当x=60时,y取得最大值.即商店购进60台A 型电脑和40台 B 型电脑的销售利润最大.
9.解:(1)设每台A 型电脑的销售利润为a 元,每台 B 型电脑的销售利润为b元.根据题意,得
解得
答:每台A 型电脑的销售利润为100元,每台 B 型电脑的销售利润为150元;
(2)①根据题意,得y=100x+150(100-x),
即y=-50x+15 000;
②根据题意,得100-x≤2x,解得
∵y=-50x+15000,-50<0,
∴y随x的增大而减小,∵x为正整数,
∴当x=34时,y取最大值,则100-x=66.即商店购进34台 A 型电脑和66台B 型电脑的销售总利润最大;
(3)根据题意,得y=(100+m)x+150(100-x),即
①当0②m=50时,m-50=0,y=15 000,即商店购进A 型电脑数量满足 的整数时,均获得最大总利润;
③当500,y 随x的增大而增大,∴当x=70时,y 取得最大值.即商店购进70台A 型电脑和 30台 B 型电脑的销售总利润最大.
10.解:(1)根据题意,得y =20x+15(240-x)=5x+3600,y =25(200-x)+24(x+60)=-x+6440,0≤x≤200;
(2)设总运费为y元,根据题意,得y与x之间的函数关系为:y=5x+3600+(-x+6440)=4x+10040,
∵4>0,∴y随x的增大而增大,
∴当x=0时,y最小=10 040,
∴从A 城运往C 乡O t,运往 D 乡 200 t,从 B 城运往C乡240t,运往 D 乡60t,此时总运费最少,总运费最小值是10 040元;
(3)根据题意可知,改善后的总运费为 y=20x+15(240-x)+25(200-x)+(24-a)(x+60),
整理,得y=(4-a)x+10040-60a,
解得0≤x≤200.
①当4-a>0,即2≤a<4时,y随x的增大而增大,
∴当x=0时,y最小=10 040-60a;
②当4-a<0,即4∴当x=200时,y最小=10 840-260a;
③当4-a=0,即a=4时,无论x取何值,
y的值恒为10 040-60×4=9 800.
综上所述,当2≤a<4时,从A 城运往C乡0t ,运往D乡200t,从B 城运往C乡240t,运往D 乡60t,此时总运费最少,y最小=10040-60a;
当4当a=4时,从A 城运往C 乡的肥料满足0≤x≤200的整数时,运输总费用恒为9 800元.
中档突破9 一次函数与线段问题
类型一 线段长
1.解:(1)根据题意,得 解得
(2)设直线AC 的解析式为y= mx-1,把A(-2,0)代入,得-2m-1=0,解得
∴直线 AC 的解析式为
①若 EF∥BC,设E(x,2x+4),∵EF=3,∴F(x,2x+1),把 F 的坐标代入 得 解得
②若EF∥AO,设E(x,2x+4),
∵EF=3,∴F(x-3,2x+4),
把点 F 的坐标代入 得 3)-1,解得
2.解:(1)∵点 E 在直线y=x上,且横坐标为3,∴E(3,3),把 E(3,3)代入 中,得b=4,
令 y=0,得x=12,∴点A 的坐标为(12,0);
(2)∵P(m,0),∴点C 的坐标为 D(m,x 解得 或
类型二 线段关系
3.解:(1)把 D(3,m)代入 y=x-2,得m=3-2=1,
∴点 D 的坐标为(3,1),
把D(3,1)代入y= kx+7,得3k+7=1,∴k=-2,m=1;
(2)由(1)得直线 AB 的解析式为y=-2x+7,当y=n时,x-2=n,x=n+2,∴点M 的坐标为(n+2,n),当x=n时,y=-2n+7,
∴点 N 的坐标为(n,-2n+7),
∵点 P(n,n),∴PM=2,PN=|3n-7|,
∵PN=2PM,∴|3n-7|=4,∴n=1或
4.解:(1)把 M(1,2)代入 y=kx,得k=2;把M(1,2)代入 得 b,解得
当y=0时, 解得x=5,则A(5,0),所以不等式 的解集为1≤x≤5;(2)当x=0时, 则B(o, ), 设P(m,0),则 D(m,2m),∵2CD=OB, 解得 或 ,∴点 P 的坐标为.P( ,o)或( ,o).
中档突破10 一次函数与面积问题
类型一 根据坐标求面积
1.解:(1)∵一次函数y= kx+b的图象经过点(-1,6)和(3, 解得该函数的解析式为y=-2x+4;
(2)令x=0,则y=-2×0+4=4,令y=0,则0=-2x+4,∴x=2,∴A(2,0),B(0,4),设直线BC:y= ax+4,把C(3,5)代入,得5=3a+4,解得
2.解:(1)∵一次函数y= kx+b的图象经过点(1,4)和(-1,8),
解得这个函数的解析式为y=-2x+6;
(2)令x=0,则y=-2×0+6=6,令y=0,则0=-2x+6,
∴x=3,∴A(3,0)和B(0,6),
(3)∵点 P(m,n)在线段 AB 上,∴n=-2m+6,过点 M作MH⊥y 轴于点 H,过点 P 作 PQ⊥MH 于点 Q,则MH=6,NH=4,PQ=-2m+8,
∴S=-4m+12(0≤m<3).
类型二 根据面积求坐标或参数值
3.解:(1)设直线AB 的解析式为y= kx+b,
∵直线 AB 经过点A(2,0),B(0,-4),
解得
∴直线AB 的解析式为y=2x-4;
(2)设点C 的坐标为(m,n), 10,解得m=5.将m=5代入y=2x-4,得n=2×5-4=6.∴点C 的坐标是(5,6).
4.解:(1)把 A(4,0),B(0,2)代入 y = kx+b,得 解得
∴该一次函数解析式为
(2)把x=2代入一次函数解析式,得y=-1+2=1, 即|m-1|=2,解得m=3或m=-1(舍去),则m的值为3.
5.解:(1)∵点 A 的坐标为(3,0).∴OA=3,∵x+y=4,∴y=4-x,
即
画出函数 S 的图象如图;
(3)∵△OPA 面积是5, 解得 ∴点 P 的坐标为(
类型三 面积与分类讨论
6.解:(1)设直线 AB 的解析式为y= kx+b,把A(2,2),B(-4,0)分别代入,得 解得
∴直线 AB 的解析式为 当x=0时,
∴点C 的坐标为((○, );
(2)易得直线OA 的解析式为y=x,过点 P 作 PQ∥y轴交直线AB 于点Q,设 P(t,t),则
∵△BCP 的面积为4,
即
∴t=-1或t=5,∴P(-1,-1)或(5,5).
7.解:(1)设直线 AB 的解析式为y= kx+b,∵A(-2,0),B(1,4),
解得
(2)方法一:在x轴上取点M(3,0),∵A(-2,0),B(1,4),∴△ABM 的面积为10,过点 M 作直线l∥ AB,设
∵△ABC的面积为10,∴C(m,2-m)在直线l上, 即
方法二:思路如下:∵C(m,2-m),
∴点C 在直线:y=--x+2上,过点 C 作CM∥y轴交直线AB 于点 M,由S△ABC = S△ACM - S△BCM = 10,得 10= 解得
类型四 根据面积关系求值
8.解:(1)令y=0,则 令x=0,则y=2;∴点 A 的坐标为(4,0),点 B 的坐标为(0,2);
(2)①当点 P 在点A 的左侧时,
∵S△PAB=S△ABC,∴PC∥AB,
设直线 PC 的解析式为
则 解得
此时P(-3,0);
②当点 P 在点A 的右侧时,
由①,得
∴PA=7,此时P(11,0),
∴点 P 的坐标为(-3.0)或(11,0).
9.解:(1)y=-2x+2;(2)(2,-2),1;
(3)过P,E两点分别作 PG⊥y轴于点G,EF⊥y轴于点 F,∵直线l的解析式为y=2x-6,∴D(0,-6),
设E(m,2m-6),
∵P(2,-2),∴PG=2,
∵点 B 坐标为(0,2),∴BD=2-(-6)=8,
∵△BPE 的面积是△APO 的面积的4倍,
∴S△BPE=4①点 E 在点 D,P 之间,如图1,
∴m=1,∴2m-6=-4,∴E(1,-4);
②点E 在DP 的延长线上,如图2,
∴m=3,∴2m-6=0,∴E(3,0),
综上所述,E(1,-4)或(3,0).
中档突破11 一次函数与角度问题
类型一 一次函数与45 度角
1.解:(1)点 P 的坐标为 或(4,4);
①作∠AOB 的平分线交 AB 于点 P ,用角平分线结论可知AO: BO=2:1=AP : BP ,
用y=-x与 可求点 P 的坐标;
②当AB=BP 时,用全等可求 P 的坐标;
(2)过点O作OD⊥OP 交AB 于点 D,过点 D,P 作x轴的垂线,设点 利用三垂直全等可推出点D的坐标为 将点 D 的坐标代入直线AB中可求出 ,则点 P 的坐标为(
2.解:过点 A 作AP∥BC,作 DP⊥AD,两线交于点 P,作PH⊥x轴于点 H.
∵直线 与x轴,y 轴分别交于点B,A,
∴B(8,0),A(0,6),∴OA=6,OB=8,
∵C为OA 上一点,且OC=2,
∴C(0,2),∴直线 BC 的解析式为
∵∠AEC=45°,∴△ADP 为等腰 Rt△,可证△AOD≌△DHP,∴OD=HP,设 D(t,0).
∴P(t+6,t),∵直线AP 的解析式为
解得
类型二 一次函数与角度关系
3.解:(1)对于y=x+7,令x=0,则y=7,故点A(0,7),同理可得,点 B(0,-2),
联立 解得 故点C(-3,4);
(2)在 y轴的正半轴上取点B'(0,2),则 连接 PB',
∴PB=PB',则∠
故 ,设点P(x,0),则 解得 ,故点 P的坐标为 或
4.解:(1)设点C(a,0),则 ∴a=3,∴C(3,0);
(2)过点 B 作BD⊥AB 交AP 的延长线于点D,则△ABD是等腰直角三角形.过点 D 作 DM⊥x轴于点 M,则△BDM≌△ABO,
∴DM=BO=2,BM=AO=4,
∴OM=BM--BO=2,∴D(2,-2).
由待定系数法求得
(3)作点 C 关于y轴的对称点C',连接AC',C'E,则 射线 EF 交AC'于点 H,
∵∠CEF+2∠OAC=180°,∴∠HEC+∠C'AC=180°,
又
∴∠C'HE=∠ACE=∠AC'E,
∴EH=EC',又∵EC'=EF,
∴EH=EF,∴点 F 与H 重合.
∴点 F 在AC'上.∴当OF⊥AC'时,OF 有最小值,最小值为2.4.
中档突破1 函数的图象
1.下列图象中,能表示y是x 的函数的有( )
A.1个 B.2 个 C.3个 D.4 个
2.亮亮每天都要坚持体育锻炼,某天他跑步到离家较近的秀湖公园,看了一会喷泉表演,然后慢慢走回家.如图能反映当天亮亮离家的距离y 随时间x变化的大致图象的是( )
3.如图,在面积为6的菱形ABCD 中,点 P 沿A→B→C→D 的路径移动,设点 P 经过的路径长为x,△ADP 的面积为y,则下列图象能大致反映y与x的函数关系的是( )
4.匀速地向如图所示的容器内注水,最后把容器注满,在注水过程中,水面的高度h 随时间t的变化而变化,变化规律为一折线,下列图象(草图)正确的是( )
5.某蓄水池的横断面示意图如图所示,分深水区和浅水区,如果这个注满水的蓄水池以固定的流量把水全部放出,下面的图象能大致表示水的深度h 和放水时间t之间的关系的是( )
中档突破2 一次函数的图象和性质
1.在平面直角坐标系中,一次函数 的图象可能是( )
2.若一次函数y=(2m+1)x+m-3的图象不经过第二象限,则m的取值范围是( )
B. m<3
3.是一次函数y= kx+b(k<0)图象上的两点,则y 与y 的大小关系是( )
D.不能确定
4.一次函数y=2x+n的图象上有三个点A(-3,a),B(1,b),C(-1,c),据此可以判断a,b,c的大小关系为( )
A. a
6.若一次函数y=kx+2的y随x的增大而减小,则该函数图象可能经过的点的坐标是( )
A.(2,5) B.(1,1) C.(-1,-2) D.(-2,0)
7.在平面直角坐标系中,过点(-1,-2)的直线l 经过一、二、三象限,若点(0,a),(1,b),(c,-1)都在直线l上,则下列判断正确的是( )
A. a<0 B. b<-2 C. c>-1 D. b
一、求一次函数解析式
1.已知 且 与x成正比例,y 与x-2成正比例.当x=2时,y=7;当x=1时,y=0.
(1)求y与x之间的函数关系式;
(2)计算x=4时,y的值.
2.如图,直线y=3x+3分别交x轴,y轴于点A,B.
(1)当0
①直接写出 n 的值为 ;
②过点 C作CD⊥AB 交x轴于点D,求直线CD 的解析式.
二、利用一次函数解析式求值
3.在平面直角坐标系中,已知点A(a,1),B(b,-2)均在直线y=-2x+m 上,则a-b的值为( )
B.-3 C.3 D.4
4.已知直线y= ax+b与直线y=x+3交于点 B(--3,n),则代数式 的值为( )
A.3 B.2 C.1 D.0
中档突破4 一次函数与图形变换
一、平移
1.直线y=—2x+1向下平移5个单位长度后的对应直线的解析式是
2.将直线y=2x+3向左平移2个单位长度后的对应直线的解析式为( )
A. y=2(x-2)+3B. y=2(x+2)+3 C. y=2x+5 D. y=2x+1
3.把直线y=-x+3向上平移m个单位长度后,与直线y=2x+4的交点在第一象限,则m 的取值范围是( )
A.1
二、对称
4.如图,在平面直角坐标系中,已知直线 与x轴,y轴分别交于A,B 两点,C是 y轴正半轴上一点,把△ABC 沿直线 AC 折叠,使点 B 刚好落在x 轴负半轴上,则点 C 的坐标是( )
B.(0, C.(0,3) D.(0,4)
5.如图,已知直线l的解析式是 ,与x轴,y轴分别交于点A,B.
(1)直接写出将直线l向左平移2个单位长度得到的直线l 的解析式为 ;直接写出直线l关于x 轴对称的直线l 的解析式为 ;
(2)在(1)的条件下,求直线l与直线l 的距离.
中档突破5 一次函数与实际问题(一)图象信息
一、行程问题
1.甲、乙两人沿同一直线同时出发去往 B 地,运动过程中甲、乙两人离 B 地的距离y(km)与出发时间x(h)的关系如图所示,下列说法错误的是( )
A.甲、乙两人在出发后2 h第一次相遇 B.甲的速度是 16 km/h
C.甲到达 B 地时两人相距50 km D.出发时乙在甲前方20 km
2.小王骑车从甲地到乙地,小李骑车从乙地到甲地,小王的速度小于小李的速度,两人同时出发,沿同一条公路匀速前进.图中的折线表示两人之间的距离y(km)与小王的行驶时间x(h)之间的函数关系,下列结论错误的是( )
A.小王骑车的速度为10 km/h B.小李骑车的速度为20 km/h
C. a 的值为15 D.走完全程,小李用时是小王的
3.甲、乙两车同时从A,B 两地出发,相向而行,甲车到达 B 地后立即返回A 地,两车离A 地的距离y(单位:km)与所用时间x(单位:min)之间的函数关系如图所示(粗线表示乙车,细线表示甲车),则甲、乙两车在途中两次相遇的间隔时间为( )
A.9 min B.10 min C.11 min D.12 min
二、工程问题
4.某社区有一块空地需要绿化,某绿化组承担了此项任务,绿化组工作一段时间后,提高了工作效率.该绿化组完成的绿化面积S(单位: )与工作时间t(单位:h)之间的函数关系如图所示,则该绿化组提高工作效率前每小时完成的绿化面积是( )
三、租车问题
5.某公司准备与汽车租赁公司签订租车合同,以每月用车路程xkm计算,甲汽车租赁公司每月收取的租赁费为y 元,乙汽车租赁公司每月收取的租赁费为y 元,若y ,y 与x之间的函数关系如图所示,其中x=0对应的函数值为月固定租赁费,则下列判断错误的是( )
A.当月用车路程为1 800km时,选甲汽车租赁公司比较合算
B.当月用车路程为2 000 km时,两家汽车租赁公司租赁费用相同
C.当月用车路程为2 300 km时,选乙汽车租赁公司比较合算
D.除去月固定租赁费,甲租赁公司每公里收取的费用比乙租赁公司少
四、销售问题
6.某农资门市部连续8天调进一批化肥进行销售,在开始调进化肥的第7天开始销售.若进货期间每天调入化肥的吨数与销售期间每天销售化肥的吨数都保持不变,这个门市部的化肥存量S(单位:吨)与时间t(单位:天)之间的函数关系如图所示,则该门市部这次化肥销售活动(从开始进货到销售完毕)所用时间为 天.
五、进出水管问题
7.一个容器有进水管和出水管,每分钟的进水量和出水量是两个常数.从某时刻开始 4 min内只进水不出水,从第4 min 到第 24 min 内既进水又出水,从第24 min开始只出水不进水,容器内水量y(单位:L)与时间x(单位:min)之间的关系如图所示,则图中a 的值是( )
A.32 B.34 C.36 D.38
中档突破6 一次函数与实际问题(二)表格信息
1.有一个装有水的容器,如图所示,注水之前容器内有少量水,现向容器内注水,并同时开始计时,在注水过程中,水面高度匀速增加,则容器注满水之前,将容器内的水面高度y(cm)与时间x(s)记录于下表,则★的值是( )
x/秒 5 10 25 30
y/ cm 11 12 15
A.16 B.17 C.18 D.19
2.物理课上,于老师让同学们做这样的实验:在放水的盆中放入质地均匀的木块B,再在其上方放置不同质量的铁块A.已知木块 B 全程保持漂浮状态,通过测量木块B 浮在水面上的高度h(mm)与铁块A 的质量x(g),可得它们之间满足一次函数关系.据此可以判断下表中记录错误的数据是( )
实验次数 一 二 三 四
铁块 A 质量x/g 25 50 75 100
高度 h/ mm 40 30 15 10
A.第一次的数据 B.第二次的数据 C.第三次的数据 D.第四次的数据
3.杆秤是我国传统的计重工具.如图,可以用秤砣到秤纽的水平距离,来得出秤钩上所挂物体的质量.称重时,若秤砣到秤纽的水平距离为x(单位:cm)时,秤钩所挂物重为y(单位:kg),则y是x的一次函数.下表记录了四次称重的数据,其中只有一组数据记录错误,它是( )
A.第1组 B.第2 组 C.第3组 D.第4组
组数 1 2 3 4
x/ cm 1 2 4 7
y/ kg 0.80 1.05 1.65 2.30
中档突破7 一次函数与方程(组)、不等式
1.直线. 和 如图所示,则关于x的不等式 的解集是 .
2.如图,在平面直角坐标系xOy 中,若直线 -2x+a 与直线. 相交于点 P(1,-3),则关于x的不等式-2x+a< bx-4的解集是 .
3.在平面直角坐标系xOy中,一次函数 y= kx和y=mx+n的图象如图所示,则关于x的一元一次不等式(k-m)x-n>0的解集是 .
4.如图,直线 经过点(2,4),当 kx+b>2x时,x 的取值范围是 .
5.如图,直线y=3x和y= kx+2相交于点 P(a,6),则关于x的不等式(3-k)x≤2的解集为 .
6.一次函数 与 的图象如图所示,则0< mx+n<-x+a 的解集为( )
A. x>3 B. x<2 C.2
类型一 费用最少问题
1.2022年新洲区计划对邾城街文昌大道长2400米的污水管网进行改造.经投标,由甲、乙两个工程队来完成,若甲队每天能完成长度是乙队每天能完成长度的2倍,并且独立完成长度为400米管网改造所用的时间,甲队比乙队少5天.
(1)求甲、乙两工程队每天能完成管网改造的长度;
(2)设甲工程队施工x天,乙工程队施工y天,刚好完成改造任务(两工程队都必须参加,且工作天数都为整数).求y关于x的函数关系式,并写出自变量x的范围;
(3)若甲队每天施工费用为0.6万元,乙队每天施工费用为0.25万元,且甲乙两队施工的总天数不超过40天,则如何安排甲、乙两队施工的天数,才能使施工总费用最低 并求出最低费用.
2.A 城有肥料200t,B 城有肥料300t.现要把这些肥料全部运往C,D
两乡,C乡需要肥料240t,D乡需要肥料260t,其运往C,D两乡的运费如下表:设从 A 城运往C 乡的肥料为 xt,从A 城运往两乡的总运费为y 元,从B 城运往两乡的总运费为y 元
(1)分别写出y ,y 与x之间的函数关系式(不要求写自变量的取值范围);
(2)试比较A,B两城总运费的大小;
两城/两乡 C(元/t) D(元/t)
A 20 24
B 15 17
(3)若B 城的总运费不得超过4800元,怎样调运使两城总费用的和最少 并求出最小值.
类型二 利润最大问题
3.某商店销售一种产品,该产品成本价为6元/件,售价为8元/件,销售人员将该产品一个月(30天)销售情况记录绘成如下图象,图中的折线ODE表示日销量y(件)与销售时间x(天)之间的函数关系,若线段DE 表示的函数关系中,时间每增加1天,日销量减少5件.
(1)第25天的日销量是 件,这天销售利润是 元;
(2)求y与x之间的函数关系式,并写出x的取值范围;
(3)日销售利润不低于640元的天数共有多少天 销售期间日销售最大利润是多少元
类型三 方案最佳问题
4.某商场电饭煲的销售价为每台1 100元,豆浆机的销售价为每台1000元,每台电饭煲的进价比每台豆浆机的进价多200元,商场用10 000元购进电饭煲的数量与用8 000元购进豆浆机的数量相等.
(1)求每台电饭煲与豆浆机的进价分别是多少
(2)现在商场准备一次购进这两种家电共100台,设购进电饭煲x台,这100 台家电的销售总利润为y元,要求购进豆浆机数量不超过电饭煲数量的2倍,总利润不低于16 400元,请分析合理的方案共有多少种 并确定获利最大的方案以及最大利润;
(3)实际进货时,厂家对电饭煲出厂价下调k(0
5.武汉某文化公司向市场投放A 型和B 型商品共200件进行试销,A型商品成本价140元/件,B型商品成本价 120元/件,要求两种商品的总成本价不超过26400元,已知A 型商品的售价为200元/件,B 型商品的售价为170元/件,全部售出且获得的利润不低于10 800元.设该公司投放A 型商品x件,销售这批商品的利润为y 元.
(1)求y 与x之间的函数解析式,并求出x的取值范围;
(2)要使这批商品的利润最大,该公司应该向市场投放多少件 A 型商品 最大利润是多少
(3)该公司决定在试销活动中每售出一件A 型商品,就从一件 A 型商品的利润中捐献慈善资金a(a>0)元,当该公司售完这200件商品并捐献资金后获得的最大收益为10 960元时,求a 的值.
6.某商场购进A,B 两种服装共100件,已知购进这100件服装的费用不得超过7 500元,且其中A 种服装不少于65件,它们的进价和售价如表.
其中购进A 种服装为x件,如果购进的A,B两种服装全部销售完,根据表中信息,解答下列问题.
(1)求获取总利润y 元与购进A 种服装x件的函数关系式,并写出x的取值范围;
服装 进价(元/件) 售价(元/件)
A 80 120
B 60 90
(2)该商场对A 种服装以每件优惠a(0
(1)甲、乙两种型号的茶叶每斤分别是多少元
(2)该茶叶店准备用不超过3 500元的资金采购甲、乙两种型号的茶叶共20斤,其中购进甲种型号的茶叶的斤数不少于购进乙种茶叶的 ,采购的斤数需为整数,那么该茶店有哪几种采购方案
(3)在(2)的条件下,已知该茶叶店销售甲型茶叶1斤可获利 )元,销售乙型茶叶1斤可获利4m 元,若20斤茶叶全部售出的最大利润为792元,请直接写出m 的值为 .
8.某商店销售A 型和B 型两种电脑,每台A 型电脑的利润为400元,每台B 型电脑的利润为500元.该商店计划一次性购买两种型号的电脑共100台,且B 型电脑的进货量不超过A 型电脑的2倍,设购进A 型电脑x台,这100台电脑的销售总利润为y元.
(1)直接写出 y 与x 的函数关系式;
(2)该商店购进A 型,B型电脑各多少台,才能使销售总利润最大,最大利润是多少
(3)实际进货时,电脑厂家对A 型电脑的出厂价下调 元,B型电脑的出厂价不变,且限定商店最多购进 A 型电脑60台,若商店保持同种电脑售价不变,怎样进货可使销售完100台电脑的总利润最大
9.某商店销售10台A 型电脑和20台 B 型电脑的利润为4 000元,销售 20台 A 型电脑和10台 B 型电脑的利润为3 500元.
(1)求每台A 型电脑和B 型电脑的销售利润;
(2)该商店计划一次购进两种型号的电脑共100台,其中B 型电脑的进货量不超过A 型电脑的2倍,设购进A 型电脑x台,这100台电脑的销售总利润为 y元.
①求y关于x的函数关系式;
②该商店购进A 型、B型电脑各多少台,才能使销售总利润最大
(3)实际进货时,厂家对A 型电脑出厂价下调m(0
(1)写出y 关于x的函数关系式以及y 关于x的函数关系式,并指出自变量的取值范围;
(2)怎么样调度使得该过程的总运费最少 并求出最少的运输费以及最少的运输方案;
(3)由于从B 城到D 乡开辟了一条新的公路,使B 城到D 乡的运输费每吨减少了 8)元,如何调度才能使总运费最少 最少运输费是多少(用含a的式子表达)
中档突破9 一次函数与线段问题
类型一 线段长
1.直线y= kx+b经过A(—2,0),B(0,4)两点,C点的坐标为(0,-1).
(1)求 k 和b的值;
(2)E 为线段AB 上一点,F 为直线AC 上一点,
①如图1,若EF∥BC,求点 E 的坐标;
②如图2,若EF∥AO,请直接写出点 E 的坐标.
2.如图,直线 与x轴交于点A,与y 轴交于点B,与直线 y=x交于点E,点 E 的横坐标为3.
(1)求点 A 的坐标;
(2)在x轴上有一点 P(m,0),过点 P 作x轴的垂线,与直线 交于点C,与直线y=x交于点D.若CD=5,求m 的值.
类型二 线段关系
3.如图,直线 交x轴于点A,交y轴于点B,与直线y=x-2交于点 D(3,m).
(1)求 k,m的值;
(2)已知点 P(n,n),过点 P 作垂直于y 轴的直线与直线 交于点 M,过点 P 作垂直于x轴的直线与直线. 交于点 N(P与 N 不重合).若 ,求n 的值.
4.如图,直线 与x轴,y轴分别交于点A,B,与函数 的图象交于点M(1,2).
(1)直接写出k,b的值和不等式 的解集;
(2)在x轴上有一点 P,过点 P 作x轴的垂线,分别交函数 和 的图象于点C,D.若 求点 P 的坐标.
中档突破10 一次函数与面积问题
类型一 根据坐标求面积
1.已知一次函数 的图象经过点( 和 且与x轴交于点A,与y 轴交于点 B.
(1)求这个函数的解析式,并在图中直接画出图象;
(2)已知点 P(m,n)在线段AB 上,点 C(3,5),求. 的面积(用含 m 的式子表示).
2.已知一次函数. 的图象经过点(1,4)和( 且交x轴于点A,交 y轴于点B.
(1)求这个函数的解析式;
(2)求 的面积;
(3)已知点 ,点 N(0,2),点 P(m,n)在线段 AB 上,设 的面积为S,请直接写出S 关于m 的函数关系式以及自变量m 的取值范围: .
类型二 根据面积求坐标或参数值
3.如图,直线AB 与x轴交于点A(2,0),与y轴交于点.
(1)求直线 AB 的解析式;
(2)若直线AB 上的点C 在第一象限,且 求点 C 的坐标.
4.已知一次函数. 的图象交x轴于点A(4,0),交y轴于点B(0,2).
(1)求这个一次函数的解析式;
(2)若在第一象限有一点 C(2,m),且 的面积为4,求m 的值.
5.点 P(x,y)在第一象限,且. 点 A(3,0),设 的面积为S.
(1)用含x 的式子表示S,并写出x的取值范围;
(2)在如图网格中建立直角坐标系,并画出函数S 的图象;
(3)当△OPA 面积是5时,求点 P 的坐标.
类型三 面积与分类讨论
6.如图,在平面直角坐标系中,点A(2,2), ,直线 AB 交 y 轴于点C.
(1)求直线 AB 的解析式和点 C 的坐标;
(2)在直线 OA 上有一点 P,使得 的面积为4,求点 P 的坐标.
7.如图,在平面直角坐标系中,点
(1)求直线 AB 的解析式;
(2)已知点 在直线 AB 的下方, 的面积为10,求m 的值.
类型四 根据面积关系求值
8.直线 与 x 轴交于点A,与y 轴交于点 B,已知点 点 P 在x 轴上,
(1)求 A,B 两点的坐标;
(2)求点 P 的坐标.
9.如图,在平面直角坐标系xOy 中,直线 交x轴于点C,交y轴于点D,点A,B 的坐标分别为(1,0),(0,2),直线AB 与直线CD 相交于点 P.
(1)直线 AB 的解析式为 ;
(2)点 P 的坐标为 ,连接OP,则
(3)若直线 CD 上存在一点E,使得 的面积是 的面积的4 倍,求点 E 的坐标.
中档突破11 一次函数与角度问题
类型一 一次函数与45 度角
1.如图,直线 交x轴于点 A,交 y 轴于点 B,点 P在直线 AB 上.
(1)若AP=2BP,求点 P 的坐标;
(2)若 求点 P 的坐标.
2.如图,在平面直角坐标系中,直线 与x轴,y 轴分别交于点B,A,C 为OA 上一点,且 ,E 是线段BC 上一点,连接AE 并延长交OB 于点D,若 求OD 的长.
类型二 一次函数与角度关系
3.如图,直线. 与直线 交于点C,它们与y轴分别交于A,B两点.
(1)求 A,B,C三点的坐标;
(2)点 P 在x轴上,使 ,求点 P 的坐标.
4.如图1,在平面直角坐标系中,点A(0,4),B(—2,0),C是x轴正半轴上一点,且
(1)求点 C 的坐标;
(2)如图2,在x轴正半轴上有一点 P,使 求点 P 的坐标;
(3)如图3,E是y轴上点A 下方一动点,将线段EC 绕点E 逆时针旋转一个小于 的角到EF,且有 ,求OF 的最小值.
第十九章 一次函数
中档突破1 函数的图象
1. C 2. B 3. A
4. C 解:最下面的容器最粗,第二个容器较粗,那么每个阶段的函数图象水面高度h 随时间t的增大而增长,用时较短,故选 C.
5. D
中档突破2 一次函数的图象和性质
1. B 解:当k>0时,图象经过二、三、四象限;当k<0时,图象经过一、二、三象限,故选 B.
2. D 解:根据题意,得2m+1>0且m-3≤0,解得 m≤3.故选 D.
3. A 解:∵k<0,∴y随x的增大而减小,∵--1<2,∴y >y .故选 A.
4. A 解:∵k=2>0,∴y随x的增大而增大,∵--3<-1<1,∴a
6. B 解:将 A,B,C,D四个选项的坐标分别代入y=kx+2,计算k值,只有B得到k=-1<0,故选 B.
7. C 解:由题意可画出大致图象,由图可知,0
1.解:(1)设 把x=2,y=7和x=1,y=0代入,得 解得∴y与x之间的函数关系式为y=7x-7.(2)把x=4代入y=7x-7,得y=7×4-7=21.
2.解:(1)-1
②过点C作CH⊥x轴于点 H.由y=3x+3,得A(-1,0),又∵n=1,∴CH=OA=1,可得△AOB≌△CHD,
∴DH=OB=3,∴D( ,0),又 由待定系数法可求得直线 CD 的解析式为
3. A 解:∵点 A(a,1),B(b,-2)均在直线 y=-2x+m上,∴-2a+m=1①,-2b+m=-2②,
由②-①,得2a--2b=-3,∴a-b=- 故选 A.
4. D 解:∵点B(-3,n)在直线y=x+3上,∴-3+3=n,∴n=0,∴B(-3,0),代入y= ax+b,得-3a+b=0, 故选 D.
中档突破4 一次函数与图形变换
1. y=-2x-4 2. B 3. C
4. B 解:易求A(4,0),B(0,3),即OA=4,OB=3,∵AB 沿直线AC 折叠,使点 B 刚好落在x轴上, 设CO=n,则 在 Rt△B'OC 中, 解得 点C 的坐标为(o, ).
5.解:
(2)过点O作OH⊥l于点 H,
在 Rt△OAB 中,
OA=2,OB=4,
∴直线l与直线l 的距离为
中档突破5 一次函数与实际问题(一)图象信息
1. C 解:由题意,得出发时乙在甲前方20km,故D正确;v甲=80÷5=16(km/h),故B正确;
vz=60÷10=6(km/h),(80-60)÷(16-6)=2(h),即甲、乙两人在出发后2 h第一次相遇,故A 正确;甲到达 B 地时两人相距60-6×5=30(km),故 C 错误.故选 C.
2. D 解:小王骑车的速度为30÷3=10(km/h),故选项A正确;小李骑车的速度为30÷1-10=20(km/h),故选项B正确;a=10×(30÷20)=15,故选项 C正确;走完全程,小李所用的时间为30÷20=1.5(h),小王所用的时间为3h,故走完全程,小李所用的时间是小王的 故选项 D错误.故选 D.
3. A 解:设 A,B 两地的距离为S km,
则甲车的速度为 乙车的速度为 甲、乙两车在途中第一次相遇的时间为 设甲、乙两车在途中第二次相遇的时间为 a min,则 解得a=18,∴18-9=9(min),即甲、乙两车在途中两次相遇的间隔时间为9 min.故选 A.
4. B 解:当t≥2时,由(4,1 000),(5,1 300),得 S=300t-200,即工作2h,该绿化组完成的绿化面积是 400 m .
∴提高工作效率前每小时完成的绿化面积是
故选 B.
5. D 解:当月用车路程为1800 km时,y
6.11
7. C 解:由图象可知,进水的速度为20÷4=5(L/ min),出水的速度为5-(35-20)÷(16-4)=3.75(L/ min),第24分钟时的水量为20+(5-3.75)×(24-4)=45(L),a=24+45÷3.75=36.故选 C.
中档突破6 一次函数与实际问题(二)表格信息
1. A 解:由(5,11),(10,12),得该一次函数解析式为 10.当x=30时, 即★的值是16.故选 A.
2. C 解:设h=kx+b(k≠0),假设第一次和第二次数据都是正确的,则 解得
∴h=-0.4x+50,当x=75时,h=-0.4×75+50=20,这与表格中的数据不符;当x=100时,
h=-0.4×100+50=10,这与表格中的数据相符,假设成立,故第三次数据是错误的.故选 C.
3. C 解:设y= kx+b,把x=1,y=0.80,x=2,y=1.05代入,求得y=0.25x+0.55,
当x=4时,y=0.25×4+0.55=1.55,
∴第3组数据不在这条直线上,
当x=7时,y=0.25×7+0.55=2.30,
∴第4组数据在这条直线上,故选 C.
中档突破7 一次函数与方程(组)、不等式
1. x<-1 解:根据图象,可知关于x的不等式. b的解集是x<-1,故答案为x<-1.
2. x>1 解:当x>1时,函数y=-2x+a的图象都在y=bx-4的图象下方,所以不等式-2x+a< bx-4的解集为x>1.故答案为x>1.
3. x>1 解:由(k-m)x-n>0,得 kx> mx+n.根据图象可知两函数的交点为(1,2),所以关于x的一元一次不等式 kx>mx+n的解集是x>1,即关于x的一元一次不等式(k-m)x-n>0的解集是x>1,故答案为x>1.
4. x<2 解:∵直线y= kx+b(k<0)经过点(2,4),直线y=2x也经过(2,4),由图象可得,当 kx+b>2x时,x的取值范围是x<2,故答案为x<2.
5. x≤2 解析:把 P(a,6)代入y=3x,得6=3a,解得a=2.观察图象可知,当3x≤kx+2时,x≤2,∴(3-k)x≤2的解集为x≤2.
6. C 解:由图可得,当0< mx+n时,x>2;
当 mx+n<-x+a时,x<3,
∴不等式组0< mx+n<-x+a的解集为2
类型一 费用最少问题
1.解:(1)设乙工程队每天能完成管网改造的长度为a 米,则甲工程队每天能完成管网改造的长度为2a 米,
根据题意,得 解得a=40.经检验,a=40是原方程的解,且符合题意,则40×2=80(米),
答:甲、乙两工程队每天能完成管网改造的长度分别是80米,40米;
(2)根据题意,得80x+40y=2400,
即 y=-2x+60,1≤x≤29,且x为整数;
(3)由题意,得x+y≤40,
∴--2x+60+x≤40,解得x≥20.
设施工总费用为 ω元,由题意,得ω=0.6x+0.25y=0.6x+0.25(-2x+60)=0.1x+15.
∵0.1>0,∴ω随x的增大而增大,当x=20时,ω最小=0.1×20+15=17(万元),此时y=20.
答:安排甲队施工20天,乙队施工20天,才能使施工总费用最低,最低费用为17万元.
2.解:(1)根据题意,得y =20x+24(200-x)=-4x+4800,y =15(240-x)+17(300-240+x)=2x+4620.
(2)若 ,则-4x+4800=2x+4620,解得x=30,A,B两城总费用一样;
若y
若 ,则-4x+4800>2x+4620,
解得0
设两城总费用为y,则.
∵--2<0,∴y随x的增大而减小,
∴当x=90时,y有最小值9240.
答:当从A 城调往C乡肥料90t,调往 D 乡肥料110t,从B城调往C乡肥料 150t,调往 D 乡肥料150t时,两城总费用的和最少,最小值为9240元.
类型二 利润最大问题
3.解:(1)340-(25-22)×5=325(件),(8-6)×325=650(元),故答案为325,650;
(2)设直线OD 的函数关系式为y=kx,
将(17,340)代入y= kx,得340=17k,解得k=20.
∴直线OD 的函数关系式为y=20x,
设直线 DE 的解析式为y= mx+n;
将(22,340),(25,325)代入 y= mx+n,
得 解得
∴直线 DE 的函数关系式为y=-5x+450.
联立 解得
∴点 D 的坐标为(18,360).∴y与x之间的函数关系式为
(3)640÷(8-6)=320(件),当y=320时,由20x=320或-5x+450=320,解得x=16或x=26,
∴26-16+1=11(天),
∴日销售利润不低于640元的天数共有11天,
∵折线 ODE 的最高点 D 的坐标为(18,360),360×2=720(元).
∴当x=18时,日销售利润最大,最大利润为720元.
类型三 方案最佳问题
4.解:(1)设每台豆浆机的进价为 m 元,则每台电饭煲的进价(m+200)元,由题意,得 解得m=800,经检验,m=800是原分式方程的解,且符合题意,∴m+200=1000(元).
答:每台豆浆机的进价为800元,每台电饭煲的进价1000元;
(2)由题意得y=(1100-1000)x+(1000-800)(100-x)=-100x+20000,
∵x为正整数,∴x=34,35,36.
∴共有3种方案,即①电饭煲34台,豆浆机66台;
②电饭煲35台,豆浆机65台;
③电饭煲36 台,豆浆机 64台;
∵y=-100x+20000,-100<0,
∴y随x的增大而减小,∴当x=34时,y有最大值,最大值为-100×34+20000=16600(元).
答:当购进电饭煲34台,豆浆机66台获利最大,最大利润为16 600元;
(3)设厂家对电饭煲出厂价下调k(0
①当100
即购进电饭煲36台,豆浆机64台,总利润最大;
②当0
即购进电饭煲34台,豆浆机66台,总利润最大;
③当k=100时,无论采取哪种方案,y 恒为20000元.
类型四 含参类问题
5.解:(1)根据题意,得 y=(200--140)x+(170-120)×(200-x),即y=10x+10000,
∵两种商品的总成本价不超过26400元,全部售出且获得的利润不低于10 800元,
解得80≤x≤120.
答:y与x 之间的函数解析式为y=10x+10 000,x 的取值范围是80≤x≤120且x为整数;
(2)由(1)可知y=10x+10000(80≤x≤120),∵10>0,∴y 随x的增大而增大,当x=120时,y最大=10×120+10 000=11 200(元).
答:该公司应该向市场投放120件A 型商品,最大利润为11 200元;
(3)根据题意,可知一共捐出 ax元,∴y=10x+10000-ax=(10-a)x+10000,当10-a<0时,
y=(10-a)x+10000的最大值小于10 000,不符合最大收益为10960元,∴这种情况不成立;
当10-a=0即a=10时,y=10000元,不符合最大收益为10 960元,∴这种情况不成立;
当10-a>0时,y随x的增大而增大,当x=120,y取最大值,∴120(10-a)+10000=10 960,∴a=2.
综上所述,a的值为2.
6.解:(1)∵80x+60(100-x)≤7500,解得x≤75,∴y=40x+30(100-x)=10x+3000(65≤x≤75且x为整数);
(2)∵y=(40-a)x+30(100-x)=(10-a)x+3000,方案1:当0
方案2:当a=10时,所有方案获利相同,所以按哪种方案进货都可以;
方案3:当10
答:甲种茶叶每斤是200元,乙种茶叶每斤是150元;
(2)设购买乙种茶叶a斤,则购买甲种茶叶(20-a)斤,根据题意,得 解得 10≤a≤12,∵a为整数,∴a=10,11,12.
故该茶叶店有3种采购方案,
方案一:购买甲种茶叶10斤,乙种茶叶10斤;
方案二:购买甲种茶叶9斤,乙种茶叶11斤;
方案三:购买甲种茶叶8斤,乙种茶叶12斤.
(3)设茶叶全部售出的利润为ω元,根据题意,得ω=3m(20-a)+4ma= ma+60m,∵m>0,∴w随a的增大而增大,∴当a=12时w有最大值,即12m+60m=792,解得m=11.
8.解:(1)由题意,得y=400x+500(100-x)=-100x+50000;
(2)∵100-x≤2x,∴x≥
∵y=-100x+50000,-100<0,
∴y随x的增大而减小,
∵x为整数,∴x=34时,y最大=46 600.
答:该商店购进A 型34台,B型电脑66台,才能使销售总利润最大,最大利润是46 600元;
(3)由题意,得.y=(400+m)x+500(100-x),
即 且x为整数.
①当0
②m=100时,m-100=0,y=50000,即商店购进 A 型电脑数量满足 的整数时,均获得最大利润;
③当100
9.解:(1)设每台A 型电脑的销售利润为a 元,每台 B 型电脑的销售利润为b元.根据题意,得
解得
答:每台A 型电脑的销售利润为100元,每台 B 型电脑的销售利润为150元;
(2)①根据题意,得y=100x+150(100-x),
即y=-50x+15 000;
②根据题意,得100-x≤2x,解得
∵y=-50x+15000,-50<0,
∴y随x的增大而减小,∵x为正整数,
∴当x=34时,y取最大值,则100-x=66.即商店购进34台 A 型电脑和66台B 型电脑的销售总利润最大;
(3)根据题意,得y=(100+m)x+150(100-x),即
①当0
③当50
10.解:(1)根据题意,得y =20x+15(240-x)=5x+3600,y =25(200-x)+24(x+60)=-x+6440,0≤x≤200;
(2)设总运费为y元,根据题意,得y与x之间的函数关系为:y=5x+3600+(-x+6440)=4x+10040,
∵4>0,∴y随x的增大而增大,
∴当x=0时,y最小=10 040,
∴从A 城运往C 乡O t,运往 D 乡 200 t,从 B 城运往C乡240t,运往 D 乡60t,此时总运费最少,总运费最小值是10 040元;
(3)根据题意可知,改善后的总运费为 y=20x+15(240-x)+25(200-x)+(24-a)(x+60),
整理,得y=(4-a)x+10040-60a,
解得0≤x≤200.
①当4-a>0,即2≤a<4时,y随x的增大而增大,
∴当x=0时,y最小=10 040-60a;
②当4-a<0,即4
③当4-a=0,即a=4时,无论x取何值,
y的值恒为10 040-60×4=9 800.
综上所述,当2≤a<4时,从A 城运往C乡0t ,运往D乡200t,从B 城运往C乡240t,运往D 乡60t,此时总运费最少,y最小=10040-60a;
当4
中档突破9 一次函数与线段问题
类型一 线段长
1.解:(1)根据题意,得 解得
(2)设直线AC 的解析式为y= mx-1,把A(-2,0)代入,得-2m-1=0,解得
∴直线 AC 的解析式为
①若 EF∥BC,设E(x,2x+4),∵EF=3,∴F(x,2x+1),把 F 的坐标代入 得 解得
②若EF∥AO,设E(x,2x+4),
∵EF=3,∴F(x-3,2x+4),
把点 F 的坐标代入 得 3)-1,解得
2.解:(1)∵点 E 在直线y=x上,且横坐标为3,∴E(3,3),把 E(3,3)代入 中,得b=4,
令 y=0,得x=12,∴点A 的坐标为(12,0);
(2)∵P(m,0),∴点C 的坐标为 D(m,x 解得 或
类型二 线段关系
3.解:(1)把 D(3,m)代入 y=x-2,得m=3-2=1,
∴点 D 的坐标为(3,1),
把D(3,1)代入y= kx+7,得3k+7=1,∴k=-2,m=1;
(2)由(1)得直线 AB 的解析式为y=-2x+7,当y=n时,x-2=n,x=n+2,∴点M 的坐标为(n+2,n),当x=n时,y=-2n+7,
∴点 N 的坐标为(n,-2n+7),
∵点 P(n,n),∴PM=2,PN=|3n-7|,
∵PN=2PM,∴|3n-7|=4,∴n=1或
4.解:(1)把 M(1,2)代入 y=kx,得k=2;把M(1,2)代入 得 b,解得
当y=0时, 解得x=5,则A(5,0),所以不等式 的解集为1≤x≤5;(2)当x=0时, 则B(o, ), 设P(m,0),则 D(m,2m),∵2CD=OB, 解得 或 ,∴点 P 的坐标为.P( ,o)或( ,o).
中档突破10 一次函数与面积问题
类型一 根据坐标求面积
1.解:(1)∵一次函数y= kx+b的图象经过点(-1,6)和(3, 解得该函数的解析式为y=-2x+4;
(2)令x=0,则y=-2×0+4=4,令y=0,则0=-2x+4,∴x=2,∴A(2,0),B(0,4),设直线BC:y= ax+4,把C(3,5)代入,得5=3a+4,解得
2.解:(1)∵一次函数y= kx+b的图象经过点(1,4)和(-1,8),
解得这个函数的解析式为y=-2x+6;
(2)令x=0,则y=-2×0+6=6,令y=0,则0=-2x+6,
∴x=3,∴A(3,0)和B(0,6),
(3)∵点 P(m,n)在线段 AB 上,∴n=-2m+6,过点 M作MH⊥y 轴于点 H,过点 P 作 PQ⊥MH 于点 Q,则MH=6,NH=4,PQ=-2m+8,
∴S=-4m+12(0≤m<3).
类型二 根据面积求坐标或参数值
3.解:(1)设直线AB 的解析式为y= kx+b,
∵直线 AB 经过点A(2,0),B(0,-4),
解得
∴直线AB 的解析式为y=2x-4;
(2)设点C 的坐标为(m,n), 10,解得m=5.将m=5代入y=2x-4,得n=2×5-4=6.∴点C 的坐标是(5,6).
4.解:(1)把 A(4,0),B(0,2)代入 y = kx+b,得 解得
∴该一次函数解析式为
(2)把x=2代入一次函数解析式,得y=-1+2=1, 即|m-1|=2,解得m=3或m=-1(舍去),则m的值为3.
5.解:(1)∵点 A 的坐标为(3,0).∴OA=3,∵x+y=4,∴y=4-x,
即
画出函数 S 的图象如图;
(3)∵△OPA 面积是5, 解得 ∴点 P 的坐标为(
类型三 面积与分类讨论
6.解:(1)设直线 AB 的解析式为y= kx+b,把A(2,2),B(-4,0)分别代入,得 解得
∴直线 AB 的解析式为 当x=0时,
∴点C 的坐标为((○, );
(2)易得直线OA 的解析式为y=x,过点 P 作 PQ∥y轴交直线AB 于点Q,设 P(t,t),则
∵△BCP 的面积为4,
即
∴t=-1或t=5,∴P(-1,-1)或(5,5).
7.解:(1)设直线 AB 的解析式为y= kx+b,∵A(-2,0),B(1,4),
解得
(2)方法一:在x轴上取点M(3,0),∵A(-2,0),B(1,4),∴△ABM 的面积为10,过点 M 作直线l∥ AB,设
∵△ABC的面积为10,∴C(m,2-m)在直线l上, 即
方法二:思路如下:∵C(m,2-m),
∴点C 在直线:y=--x+2上,过点 C 作CM∥y轴交直线AB 于点 M,由S△ABC = S△ACM - S△BCM = 10,得 10= 解得
类型四 根据面积关系求值
8.解:(1)令y=0,则 令x=0,则y=2;∴点 A 的坐标为(4,0),点 B 的坐标为(0,2);
(2)①当点 P 在点A 的左侧时,
∵S△PAB=S△ABC,∴PC∥AB,
设直线 PC 的解析式为
则 解得
此时P(-3,0);
②当点 P 在点A 的右侧时,
由①,得
∴PA=7,此时P(11,0),
∴点 P 的坐标为(-3.0)或(11,0).
9.解:(1)y=-2x+2;(2)(2,-2),1;
(3)过P,E两点分别作 PG⊥y轴于点G,EF⊥y轴于点 F,∵直线l的解析式为y=2x-6,∴D(0,-6),
设E(m,2m-6),
∵P(2,-2),∴PG=2,
∵点 B 坐标为(0,2),∴BD=2-(-6)=8,
∵△BPE 的面积是△APO 的面积的4倍,
∴S△BPE=4
∴m=1,∴2m-6=-4,∴E(1,-4);
②点E 在DP 的延长线上,如图2,
∴m=3,∴2m-6=0,∴E(3,0),
综上所述,E(1,-4)或(3,0).
中档突破11 一次函数与角度问题
类型一 一次函数与45 度角
1.解:(1)点 P 的坐标为 或(4,4);
①作∠AOB 的平分线交 AB 于点 P ,用角平分线结论可知AO: BO=2:1=AP : BP ,
用y=-x与 可求点 P 的坐标;
②当AB=BP 时,用全等可求 P 的坐标;
(2)过点O作OD⊥OP 交AB 于点 D,过点 D,P 作x轴的垂线,设点 利用三垂直全等可推出点D的坐标为 将点 D 的坐标代入直线AB中可求出 ,则点 P 的坐标为(
2.解:过点 A 作AP∥BC,作 DP⊥AD,两线交于点 P,作PH⊥x轴于点 H.
∵直线 与x轴,y 轴分别交于点B,A,
∴B(8,0),A(0,6),∴OA=6,OB=8,
∵C为OA 上一点,且OC=2,
∴C(0,2),∴直线 BC 的解析式为
∵∠AEC=45°,∴△ADP 为等腰 Rt△,可证△AOD≌△DHP,∴OD=HP,设 D(t,0).
∴P(t+6,t),∵直线AP 的解析式为
解得
类型二 一次函数与角度关系
3.解:(1)对于y=x+7,令x=0,则y=7,故点A(0,7),同理可得,点 B(0,-2),
联立 解得 故点C(-3,4);
(2)在 y轴的正半轴上取点B'(0,2),则 连接 PB',
∴PB=PB',则∠
故 ,设点P(x,0),则 解得 ,故点 P的坐标为 或
4.解:(1)设点C(a,0),则 ∴a=3,∴C(3,0);
(2)过点 B 作BD⊥AB 交AP 的延长线于点D,则△ABD是等腰直角三角形.过点 D 作 DM⊥x轴于点 M,则△BDM≌△ABO,
∴DM=BO=2,BM=AO=4,
∴OM=BM--BO=2,∴D(2,-2).
由待定系数法求得
(3)作点 C 关于y轴的对称点C',连接AC',C'E,则 射线 EF 交AC'于点 H,
∵∠CEF+2∠OAC=180°,∴∠HEC+∠C'AC=180°,
又
∴∠C'HE=∠ACE=∠AC'E,
∴EH=EC',又∵EC'=EF,
∴EH=EF,∴点 F 与H 重合.
∴点 F 在AC'上.∴当OF⊥AC'时,OF 有最小值,最小值为2.4.
