第十九章 一次函数选填题压轴突破(含详解)2024-2025学年人教版八年级数学下册
文档属性
| 名称 | 第十九章 一次函数选填题压轴突破(含详解)2024-2025学年人教版八年级数学下册 |
|
|
| 格式 | docx | ||
| 文件大小 | 212.4KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-05-09 00:00:00 | ||
图片预览





文档简介
第十九章 一次函数选填题压轴突破
压轴突破1 一次函数与动态函数图象问题
一、由图形变动判定函数图象
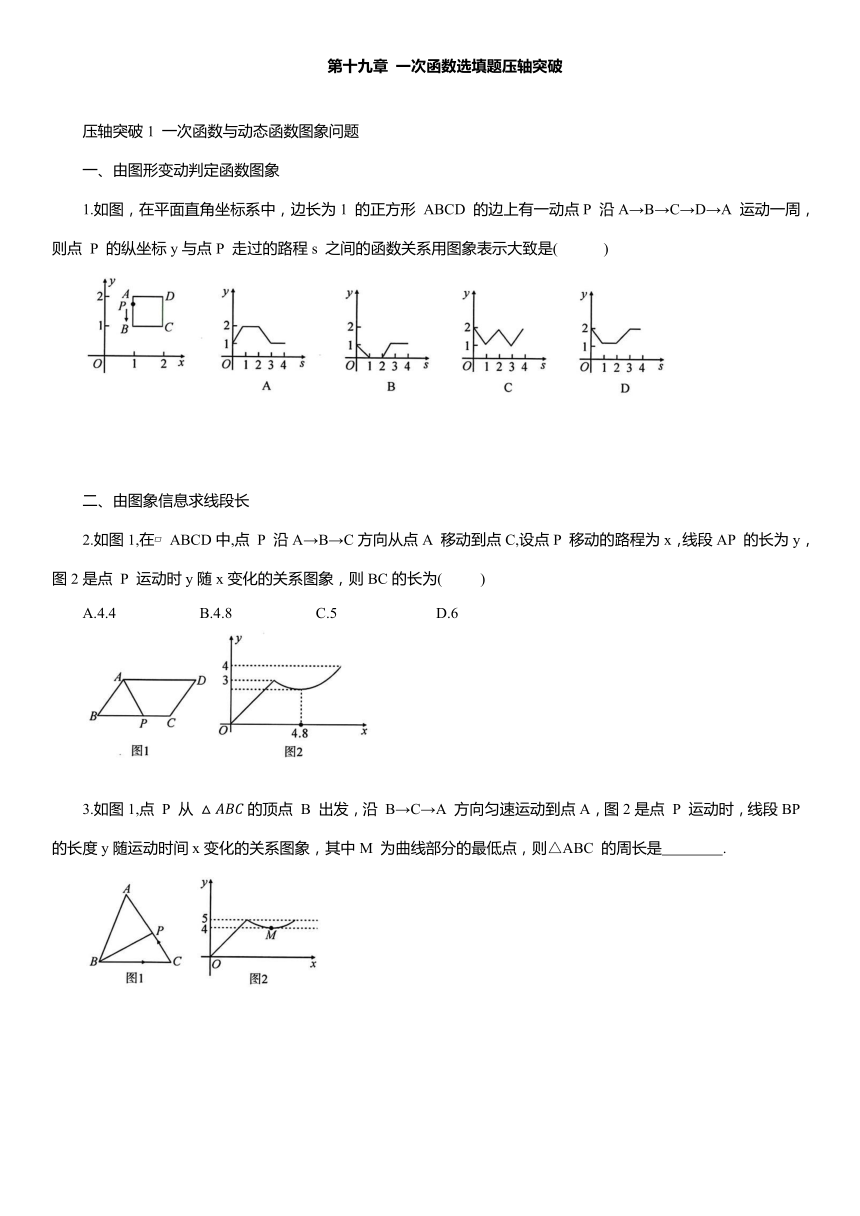
1.如图,在平面直角坐标系中,边长为1 的正方形 ABCD 的边上有一动点P 沿A→B→C→D→A 运动一周,则点 P 的纵坐标y与点P 走过的路程s 之间的函数关系用图象表示大致是( )
二、由图象信息求线段长
2.如图1,在 ABCD中,点 P 沿A→B→C方向从点A 移动到点C,设点P 移动的路程为x,线段AP 的长为y,图2是点 P 运动时y随x变化的关系图象,则BC的长为( )
A.4.4 B.4.8 C.5 D.6
3.如图1,点 P 从 的顶点 B 出发,沿 B→C→A 方向匀速运动到点A,图2是点 P 运动时,线段BP 的长度y随运动时间x变化的关系图象,其中M 为曲线部分的最低点,则△ABC 的周长是 .
三、结合图形与图象信息求参数值
4.如图1,点 F 从菱形ABCD 的顶点A 出发,沿 A→D→B 以1 cm/s的速度匀速运动到点 B,图2 是点 F 运动时, 的面积, 随运动时间x(s)变化的关系图象,则a 的值为( )
A.5 B.4
5.如图1,将正方形ABCD 置于平面直角坐标系中,其中AD 边在x轴上,其余各边均与坐标轴平行,直线L:y=x-3沿x轴的负方向以每秒1个单位的速度平移,在平移的过程中,该直线被正方形ABCD 的边所截得的线段长为m,平移的时间为t(秒),m与t的函数图象如图2所示,则图2中a 的值为( )
A.7 B.9 C.12 D.13
四、由图象信息求图形面积
6.如图1,在平面直角坐标系中,平行四边形ABCD 在第一象限,且BC∥x轴.直线y=x从原点O出发,沿x轴正方向平移,在平移过程中,直线被平行四边形ABCD的边截得的线段长度n与直线在x轴上平移的距离m的函数图象如图2所示,则平行四边形ABCD的面积为( )
A.3 C.6
压轴突破2 一次函数与多结论问题
1.在平面直角坐标系xOy中,已知直线y= kx+k+2(k是常数,且k≠0)上两点A(x ,y )和 则下列结论:
①若 则k<0;
②直线 AB 向右平移1个单位长度后得到的直线解析式为y=kx+2;
③若直线 AB 不经过第三象限,则-2④若原点O 到直线AB 的距离最大时,则直线 AB 的解析式为 其中结论正确的是 (填序号).
2.下列结论:①若 在直线 上,且 则 ②若直线y= kx+b经过第一、二、三象限,则k>0,b>0;③若一次函数 的图象交 y轴于点A(0,3),则m=±1.其中正确结论的个数是( )
A.0 B.1 C.2 D.3
3.已知一次函数: 5的图象上两点 和B(x ,y ).下列结论:①若( 则m<1;②图象经过定点(2,3);③原点O到直线AB 的距离的最大值为5.其中结论正确的是 (填序号).
4.已知函数. 图象上的两点. 下列结论:①当x=a时,函数有最小值b;②当x>a 时,y随x增大而减小;③若 且 则 其中正确的结论是 (填序号).
5.一次函数. (k,b为常数,且 中的x与y的部分对应值如下表:
x -1 2
y n 0
下列结论:①方程 的解为 ②若 则k·b>0;③若关于x 的一元一次不等式( 的解集为 则 ④当直线. 与 的函数图象只有一个公共点时,k的所有取值范围为 或 .中一定正确的是 (填写正确结论的序号).
6.一次函数. 与 的图象如图所示.下列说法:
①函数 中y 随x的增大而减小;②函数 的图象经过第一、二、四象限;
③不等式 的解集是. 其中结论正确的是 (填序号).
7.如图,已知一次函数 与正比例函数 的图象交于点P.下列四个结论:(:①k>0;②b>0;③当x<0时, ④当 时, 其中结论正确的是 (填序号).
压轴突破3 一次函数与数形结合问题
1.函数. ,当m≤x≤4时,对应 y的取值范围为-2≤y≤3,则 m 的取值范围为 ( )
A. m=-1 B.m≤-1 C.-6≤m≤-1 D.-1≤m<4
2.已知函数 和 当 时,x的取值范围是( )
或
3.把a,b,c三个数中最大那个数记为 max{a,b,c},如 max{3,4,5}=5, max{3,5,5}=5, max{x,x+1,x+2}=x+2.在平面直角坐标系xOy 中,若直线 与函数 的图象有且只有2个交点,则k 的取值范围是 .
4.已知函数y=|x-2a|(a为常数),当1≤x≤3时,y有最小值为5,则a 的值为( )
A.3或-1 B.3 或4 C.-2或-1 D.-2或4
压轴突破4 一次函数与定点、定值问题
1.一次函数y= ax+b(a,b是常数,且a≠0),若2a+b+3=0,则这个一次函数的图象必经过的点是( )
A.(-1,-5) B.(2,-3) D.(1,2)
2.如图,在平面直角坐标系xOy中,点 A 的坐标为(9,6),AB⊥y轴,垂足为B,点P 从原点O 出发向x轴正方向运动,同时,点Q 从点A 出发向点B 运动,当点Q 到达点B 时,点P,Q同时停止运动,若点 P 与点Q 的速度之比为1:2,则下列说法正确的是( )
A.线段 PQ 始终经过点(2,3) B.线段 PQ 始终经过点(3,2)
C.线段 PQ 始终经过点(2,2) D.线段 PQ 不可能始终经过某一定点
3.直线y=x+n与直线y= mx+3n(m是常数,m≠0且m≠1)交于点A,当n的值发生变化时,点A 到直线 的距离总是一个定值,则m 的值是( )
A.3 B.2 C. D.
已知在平面直角坐标系中,A(3,2),点C 在x轴上,当k变化时,一次函数y=(k-3)x+k的图象都经过一定点B,则CA+CB 的最小值为 .
压轴突破5 一次函数与最值问题
1.如图,已知直线AB 分别交坐标轴于A(2,0),B(0,—6)两点,直线上任意一点 P(x,y),设点 P 到x轴和y轴的距离分别是m和n,则m+n的最小值为( )
A.2 B.3 C.5 D.6
2.如图,在平面直角坐标系中,已知A(10,0),P 为线段OA 上任意一点.在直线 上取点E,使 ,延长PE 至点F,使. ,分别取OE,AF 的中点 M,N,连接MN,则 MN 的最小值是( )
A.4.8 B.5 C.5.4 D.6
3.如图,直线 与x轴,y 轴分别交于点A 和点 B,C,D分别为线段AB,OB 的中点,P为OA 上一动点,当 PC+PD 的值最小时,点 P 的坐标为( )
A.(-3,0) B.(-6,0)
第十九章 一次函数
压轴突破1 一次函数与动态函数图象问题
1. D 解:由于点 P 是在正方形的边上移动,所以点 P 的纵坐标y与点P 走过的路程s 之间的函数关系用图象表示为D.故选 D.
2. C 解:如图1,过点 A 作AE⊥BC 于点 E,连接AC,由图2得,当点 P 与点 B 重合时,AP=AB=3,当 P 与E 重合时,AB+BP=4.8,∴BP=BE=1.8,∴AE= √AB -BE =2.4,当点 P 到达点 C 时,AP = AC =4,∴EC =√AC -AE =3.2,∴BC=BE+EC=1.8+3.2=5.故选 C.
3.16 解:根据图象可知点 P 在 BC 上运动时,此时 BP 不断增大,由图象可知:点P 从B 向C 运动时,BP 的最大值为5,即BC=5,由于M 是曲线部分的最低点,∴此时BP最小,即BP⊥AC时,BP=4,∴由勾股定理,得 PC=3,由于图象的曲线部分是轴对称图形,曲线右端点纵坐标为5,∴AB=BC=5,∴此时 PA=PC=3(三线合一),∴AC=6,∴△ABC 的周长为5+5+6=16,故答案为16.
4. D 解:过点 D 作 DE⊥BC 于点E.由图象可知,点 F 由点A 到点 D 用时为a s,
∴DE=4;当点 F 从点 D 到点B 时,用时5s,
∴EC=a-3,DC=a,在 Rt△DEC中 解得 故选 D.
5. D 解:设直线 L 与x轴交于点M,令 y=x-3=0,则x=3,即点M(3,0),由图2,知. ,则正方形 AB-CD的边长为6,从图2看,MA=1,则点 A(2,0),故点 D的坐标为(-4,0),当直线 L 过点C 时,设直线 L'交x轴于点N,对应的时间为a,由直线 L 和x轴的夹角为45°,则当直线 L 在L'的位置时,ND=CD=6,点 N(-10,0),则a=10+3=13,故选 D.
6. B 解:如图,过点 B 作BM⊥AD 于点M,分别过点 B,D 作直线y=x的平行线,交 AD 于点 E.如图3所示,由图象和题意可得AE=6-4=2,DE=7-6=1,BE=2,∴AD=2+1=3,∵直线BE平行于直线y= ∴平行四边形 ABCD 的面积为AD 故选 B.
压轴突破2 一次函数与多结论问题
1.①②④ 解:( 故①正确;②直线AB 向右平移1个单位长度后的直线解析式为y=k(x-1)+k+2= kx+2,故②正确;
③∵y= kx+k+2=k(x+1)+2,∴直线 AB 经过点(--1,2),当直线 AB 经过原点时,k=-2,∴若直线 AB不经过第三象限,则-2≤k<0,故③不正确;
④设直线 AB 经过定点C(-1,2),交y轴于点D(0,t),则OC⊥AB,由( 得 t ,解得t= ,∴D(0, ),∴直线 AB 的解析式为y= 故④正确.故答案为①②④.
2. B 解:①∵k<0,∴y随x的增大而减小,
又∵P (x ,y ),P (x ,y )在直线y= kx+b(k<0)上,且 ∴①不正确;
②当直线y= kx+b经过第一、二、三象限时,k>0,b>0,∴②正确;
③∵一次函数 的图象交 y轴于点A(0,3), 解得m=-1,∴结论③不正确.
∴正确的结论只有1个.故选 B.
3.①② 解:由 可知一次函数y=(m-1)x-2m+5中,y 随x的增大而减小,
∴m-1<0,即 m<1,故①正确;把x=2代入y=(m-1)x-2m+5得,y=2(m-1)-2m+5=3,
∴图象经过定点(2,3),故②正确;∵一次函数y=(m-1)x-2m+5的图象经过定点(2,3),∴原点O到直线AB的距离的最大值为原点到点(2,3)的距离,∴最大值为 故③错误.故答案为①②.
4.①③ 解:在函数y=|x-a|+b中,
∵|x-a|≥0,当x=a时,y取得最小值b,故①选项符合题意;由①可知,当x>a时,y随着x增大而增大,故②选项不符合题意; 且 x ,∵当x=a时,y取得最小值b,∴y >y ,故③选项符合题意.故答案为①③.
5.①③ 解:根据表格数据可知当x=2时,y=0,∴方程 kx+b=0(k≠0)的解为x=2,故①正确;若n>0,则函数y随x的增大而减小,∴k<0,b>0,∴k·b<0,故②错误;∵关于x的一元一次不等式(k--1)x+b>0 的解集为 ∴直线y=kx+b与直线y=x的交点坐标为 直线 y、= kx+b 过点(2,0),解得 一次函数为 代入(-1,n)得 故③正确;
∵直线y= kx+b经过点(2,0),
∴当直线y=kx+b与y=|x|的函数图象只有一个公共点时,k的所有取值范围为k≤-1或k>1,故④错误,故答案为①③.
6.①③④ 解:由图象可得:对于函数. 来说,y随x的增大而减小,故①正确;
由于a<0,d<0,所以函数y= ax+d 的图象经过第二、三、四象限,故②错误;
由图象可得当x<3时,一次函数 的图象在 的图象上方,
∴ax+b> cx+d 的解集是x<3,故③正确;
∵一次函数 与 的图象的交点的横坐标为3,∴3a+b=3c+d,∴3a-3c=d-b, 故④正确.故答案①③④.
7.②③④ 解:∵正比例函数的图象经过第二、四象限,
∴k<0,故①错误;
∵一次函数的图象与 y轴的正半轴相交,
∴b>0,故②正确;
∵当x<0时,正比例函数的图象在第二象限,
∴y >0,故③正确;
∵当x<-2时,正比例函数的图象在一次函数的图象上方,
∴当x<-2时, kx>x+b,故④正确.故答案为②③④.
压轴突破3 一次函数与数形结合问题
1. C 解:画出函数y=|x+1|-2的图象如图所示.把y=3代入y=|x+1|-2,得3=|x+1|-2,解得x=4 或-6,把y=-2代入y=|x+1|-2,得-2=|x+1|-2,解得x=-1,当m≤x≤4时,对应y的取值范围为-2≤y≤3,由图象可知-6≤m≤-1.故选 C.
2. B 解:∵当 x≥0 时,直线 与 的交点为 当x<0时,直线 与 的交点为 由图象可知:当y或 解:当x>2时,-x}=x,当x<-1时,y= 当--1≤x≤2时, 如图,当直线 经过点(2,2)时, 当直线 与直线y=x平行时,k=0,∴0< 时,有两个交点;当直线 经过点(--1,1)时, 当直线 与直线 y=-x平行时, 时,有两个交点.综上所述 或
4. D 解:分两种情况:①当x≥2a时,y=x-2a,∵k=1>0,∴当1≤x≤3时,y随x的增大而增大,即当x=1时,y=5,则5=1-2a,a=-2;
②当x<2a时,y=-x+2a,∵k=-1<0,∴当1≤x≤3时,y随x的增大而减小,即当x=3时,y=5,则5=-3+2a,a=4,∴a=-2或4,故选 D.
压轴突破4 一次函数与定点、定值问题
1. B 解:∵2a+b+3=0,∴b=-2a-3,
即y= ax-2a-3=a(x-2)-3,当x=2时,y=-3,
∴该一次函数的图象经过点(2,-3),
∴B选项正确.故选 B.
2. B 解:当OP=t时,点 P 的坐标为(t,0),点 Q 的坐标为(9-2t,6),设直线 PQ 的解析式为y= kx+b(k≠0),将P (t, 0), Q (9 - 2t, 6) 代 入 y = kx + b,得 解得 直线 PQ 的解析式为 当y-2=0时,x=3,∴线段 PQ 始终经过(3,2),故选 B.
3. C 解:联立 得 即点 A 在直线 上,∵点 A 到直线 的距离总是一个定值,∴直线 与直线 平行, 故选 C.
4. 解:y= kx-3x+k=(x+1)k-3x,∵当k变化时,一次函数的图象都过一定点,∴x+1=0,∴x=-1,∴y=3,∴B(-1,3),∴点 B 关于x轴的对称点 ,连接AB'交x轴于点C,此时CA+CB 最小,即 AB',分别过点A,B'作x,y轴的垂线交于点D,∴D(3,-3),∴B'D=3-(-1)=4,AD=2-(-3)=5, 故答案为
压轴突破5 一次函数与最值问题
1. A 解:由A(2,0),B(0,-6),得直线AB 的解析式为y=3x-6,∵P(x,y)是直线AB上任意一点,∴m=|3x-6|,n=|x|,∴m+n=|3x-6|+|x|.①当点 P(x,y)满足x≥2时,m+n=4x-6≥2;②当点 P(x,y)满足02. A 解:连接 PM,PN,设AF 交直线 EM 于点J,连接 PJ.易得四边形PMJN 是矩形,
∴MN=PJ,∴当 JP⊥OA 时, PJ 的值最小,此时MN 的值最小.
∵AF⊥OM,A(10,0),直线OM 的解析式为
∴直线 AF 的解析式为
F 军彳
∴PJ 的最小值为 ,即MN 的最小值为 .故选 A.
3. C 解:作点 D 关于x轴对称的点 D',连接CD'交x轴于点 P,
此时PC+PD 的值最小,令 中x=0,则y=4,∴点 B 为(0,4);令 中y=0,
则 解得x=-6,∴点 A 为(-6,0).
∵C,D 分别为线段AB,OB 的中点,
∴点C(-3,2),点 D(0,2).
∵点 D'和点 D 关于x轴对称,∴点 D'为(0,-2).
设直线CD'的解析式为y= kx+b,
∵直线CD'经过点C(-3,2),D'(0,-2),
解得
∴直线 CD'的解析式为
令 y=0,则 解得
∴点 P 为
压轴突破1 一次函数与动态函数图象问题
一、由图形变动判定函数图象
1.如图,在平面直角坐标系中,边长为1 的正方形 ABCD 的边上有一动点P 沿A→B→C→D→A 运动一周,则点 P 的纵坐标y与点P 走过的路程s 之间的函数关系用图象表示大致是( )
二、由图象信息求线段长
2.如图1,在 ABCD中,点 P 沿A→B→C方向从点A 移动到点C,设点P 移动的路程为x,线段AP 的长为y,图2是点 P 运动时y随x变化的关系图象,则BC的长为( )
A.4.4 B.4.8 C.5 D.6
3.如图1,点 P 从 的顶点 B 出发,沿 B→C→A 方向匀速运动到点A,图2是点 P 运动时,线段BP 的长度y随运动时间x变化的关系图象,其中M 为曲线部分的最低点,则△ABC 的周长是 .
三、结合图形与图象信息求参数值
4.如图1,点 F 从菱形ABCD 的顶点A 出发,沿 A→D→B 以1 cm/s的速度匀速运动到点 B,图2 是点 F 运动时, 的面积, 随运动时间x(s)变化的关系图象,则a 的值为( )
A.5 B.4
5.如图1,将正方形ABCD 置于平面直角坐标系中,其中AD 边在x轴上,其余各边均与坐标轴平行,直线L:y=x-3沿x轴的负方向以每秒1个单位的速度平移,在平移的过程中,该直线被正方形ABCD 的边所截得的线段长为m,平移的时间为t(秒),m与t的函数图象如图2所示,则图2中a 的值为( )
A.7 B.9 C.12 D.13
四、由图象信息求图形面积
6.如图1,在平面直角坐标系中,平行四边形ABCD 在第一象限,且BC∥x轴.直线y=x从原点O出发,沿x轴正方向平移,在平移过程中,直线被平行四边形ABCD的边截得的线段长度n与直线在x轴上平移的距离m的函数图象如图2所示,则平行四边形ABCD的面积为( )
A.3 C.6
压轴突破2 一次函数与多结论问题
1.在平面直角坐标系xOy中,已知直线y= kx+k+2(k是常数,且k≠0)上两点A(x ,y )和 则下列结论:
①若 则k<0;
②直线 AB 向右平移1个单位长度后得到的直线解析式为y=kx+2;
③若直线 AB 不经过第三象限,则-2
2.下列结论:①若 在直线 上,且 则 ②若直线y= kx+b经过第一、二、三象限,则k>0,b>0;③若一次函数 的图象交 y轴于点A(0,3),则m=±1.其中正确结论的个数是( )
A.0 B.1 C.2 D.3
3.已知一次函数: 5的图象上两点 和B(x ,y ).下列结论:①若( 则m<1;②图象经过定点(2,3);③原点O到直线AB 的距离的最大值为5.其中结论正确的是 (填序号).
4.已知函数. 图象上的两点. 下列结论:①当x=a时,函数有最小值b;②当x>a 时,y随x增大而减小;③若 且 则 其中正确的结论是 (填序号).
5.一次函数. (k,b为常数,且 中的x与y的部分对应值如下表:
x -1 2
y n 0
下列结论:①方程 的解为 ②若 则k·b>0;③若关于x 的一元一次不等式( 的解集为 则 ④当直线. 与 的函数图象只有一个公共点时,k的所有取值范围为 或 .中一定正确的是 (填写正确结论的序号).
6.一次函数. 与 的图象如图所示.下列说法:
①函数 中y 随x的增大而减小;②函数 的图象经过第一、二、四象限;
③不等式 的解集是. 其中结论正确的是 (填序号).
7.如图,已知一次函数 与正比例函数 的图象交于点P.下列四个结论:(:①k>0;②b>0;③当x<0时, ④当 时, 其中结论正确的是 (填序号).
压轴突破3 一次函数与数形结合问题
1.函数. ,当m≤x≤4时,对应 y的取值范围为-2≤y≤3,则 m 的取值范围为 ( )
A. m=-1 B.m≤-1 C.-6≤m≤-1 D.-1≤m<4
2.已知函数 和 当 时,x的取值范围是( )
或
3.把a,b,c三个数中最大那个数记为 max{a,b,c},如 max{3,4,5}=5, max{3,5,5}=5, max{x,x+1,x+2}=x+2.在平面直角坐标系xOy 中,若直线 与函数 的图象有且只有2个交点,则k 的取值范围是 .
4.已知函数y=|x-2a|(a为常数),当1≤x≤3时,y有最小值为5,则a 的值为( )
A.3或-1 B.3 或4 C.-2或-1 D.-2或4
压轴突破4 一次函数与定点、定值问题
1.一次函数y= ax+b(a,b是常数,且a≠0),若2a+b+3=0,则这个一次函数的图象必经过的点是( )
A.(-1,-5) B.(2,-3) D.(1,2)
2.如图,在平面直角坐标系xOy中,点 A 的坐标为(9,6),AB⊥y轴,垂足为B,点P 从原点O 出发向x轴正方向运动,同时,点Q 从点A 出发向点B 运动,当点Q 到达点B 时,点P,Q同时停止运动,若点 P 与点Q 的速度之比为1:2,则下列说法正确的是( )
A.线段 PQ 始终经过点(2,3) B.线段 PQ 始终经过点(3,2)
C.线段 PQ 始终经过点(2,2) D.线段 PQ 不可能始终经过某一定点
3.直线y=x+n与直线y= mx+3n(m是常数,m≠0且m≠1)交于点A,当n的值发生变化时,点A 到直线 的距离总是一个定值,则m 的值是( )
A.3 B.2 C. D.
已知在平面直角坐标系中,A(3,2),点C 在x轴上,当k变化时,一次函数y=(k-3)x+k的图象都经过一定点B,则CA+CB 的最小值为 .
压轴突破5 一次函数与最值问题
1.如图,已知直线AB 分别交坐标轴于A(2,0),B(0,—6)两点,直线上任意一点 P(x,y),设点 P 到x轴和y轴的距离分别是m和n,则m+n的最小值为( )
A.2 B.3 C.5 D.6
2.如图,在平面直角坐标系中,已知A(10,0),P 为线段OA 上任意一点.在直线 上取点E,使 ,延长PE 至点F,使. ,分别取OE,AF 的中点 M,N,连接MN,则 MN 的最小值是( )
A.4.8 B.5 C.5.4 D.6
3.如图,直线 与x轴,y 轴分别交于点A 和点 B,C,D分别为线段AB,OB 的中点,P为OA 上一动点,当 PC+PD 的值最小时,点 P 的坐标为( )
A.(-3,0) B.(-6,0)
第十九章 一次函数
压轴突破1 一次函数与动态函数图象问题
1. D 解:由于点 P 是在正方形的边上移动,所以点 P 的纵坐标y与点P 走过的路程s 之间的函数关系用图象表示为D.故选 D.
2. C 解:如图1,过点 A 作AE⊥BC 于点 E,连接AC,由图2得,当点 P 与点 B 重合时,AP=AB=3,当 P 与E 重合时,AB+BP=4.8,∴BP=BE=1.8,∴AE= √AB -BE =2.4,当点 P 到达点 C 时,AP = AC =4,∴EC =√AC -AE =3.2,∴BC=BE+EC=1.8+3.2=5.故选 C.
3.16 解:根据图象可知点 P 在 BC 上运动时,此时 BP 不断增大,由图象可知:点P 从B 向C 运动时,BP 的最大值为5,即BC=5,由于M 是曲线部分的最低点,∴此时BP最小,即BP⊥AC时,BP=4,∴由勾股定理,得 PC=3,由于图象的曲线部分是轴对称图形,曲线右端点纵坐标为5,∴AB=BC=5,∴此时 PA=PC=3(三线合一),∴AC=6,∴△ABC 的周长为5+5+6=16,故答案为16.
4. D 解:过点 D 作 DE⊥BC 于点E.由图象可知,点 F 由点A 到点 D 用时为a s,
∴DE=4;当点 F 从点 D 到点B 时,用时5s,
∴EC=a-3,DC=a,在 Rt△DEC中 解得 故选 D.
5. D 解:设直线 L 与x轴交于点M,令 y=x-3=0,则x=3,即点M(3,0),由图2,知. ,则正方形 AB-CD的边长为6,从图2看,MA=1,则点 A(2,0),故点 D的坐标为(-4,0),当直线 L 过点C 时,设直线 L'交x轴于点N,对应的时间为a,由直线 L 和x轴的夹角为45°,则当直线 L 在L'的位置时,ND=CD=6,点 N(-10,0),则a=10+3=13,故选 D.
6. B 解:如图,过点 B 作BM⊥AD 于点M,分别过点 B,D 作直线y=x的平行线,交 AD 于点 E.如图3所示,由图象和题意可得AE=6-4=2,DE=7-6=1,BE=2,∴AD=2+1=3,∵直线BE平行于直线y= ∴平行四边形 ABCD 的面积为AD 故选 B.
压轴突破2 一次函数与多结论问题
1.①②④ 解:( 故①正确;②直线AB 向右平移1个单位长度后的直线解析式为y=k(x-1)+k+2= kx+2,故②正确;
③∵y= kx+k+2=k(x+1)+2,∴直线 AB 经过点(--1,2),当直线 AB 经过原点时,k=-2,∴若直线 AB不经过第三象限,则-2≤k<0,故③不正确;
④设直线 AB 经过定点C(-1,2),交y轴于点D(0,t),则OC⊥AB,由( 得 t ,解得t= ,∴D(0, ),∴直线 AB 的解析式为y= 故④正确.故答案为①②④.
2. B 解:①∵k<0,∴y随x的增大而减小,
又∵P (x ,y ),P (x ,y )在直线y= kx+b(k<0)上,且 ∴①不正确;
②当直线y= kx+b经过第一、二、三象限时,k>0,b>0,∴②正确;
③∵一次函数 的图象交 y轴于点A(0,3), 解得m=-1,∴结论③不正确.
∴正确的结论只有1个.故选 B.
3.①② 解:由 可知一次函数y=(m-1)x-2m+5中,y 随x的增大而减小,
∴m-1<0,即 m<1,故①正确;把x=2代入y=(m-1)x-2m+5得,y=2(m-1)-2m+5=3,
∴图象经过定点(2,3),故②正确;∵一次函数y=(m-1)x-2m+5的图象经过定点(2,3),∴原点O到直线AB的距离的最大值为原点到点(2,3)的距离,∴最大值为 故③错误.故答案为①②.
4.①③ 解:在函数y=|x-a|+b中,
∵|x-a|≥0,当x=a时,y取得最小值b,故①选项符合题意;由①可知,当x>a时,y随着x增大而增大,故②选项不符合题意; 且 x ,∵当x=a时,y取得最小值b,∴y >y ,故③选项符合题意.故答案为①③.
5.①③ 解:根据表格数据可知当x=2时,y=0,∴方程 kx+b=0(k≠0)的解为x=2,故①正确;若n>0,则函数y随x的增大而减小,∴k<0,b>0,∴k·b<0,故②错误;∵关于x的一元一次不等式(k--1)x+b>0 的解集为 ∴直线y=kx+b与直线y=x的交点坐标为 直线 y、= kx+b 过点(2,0),解得 一次函数为 代入(-1,n)得 故③正确;
∵直线y= kx+b经过点(2,0),
∴当直线y=kx+b与y=|x|的函数图象只有一个公共点时,k的所有取值范围为k≤-1或k>1,故④错误,故答案为①③.
6.①③④ 解:由图象可得:对于函数. 来说,y随x的增大而减小,故①正确;
由于a<0,d<0,所以函数y= ax+d 的图象经过第二、三、四象限,故②错误;
由图象可得当x<3时,一次函数 的图象在 的图象上方,
∴ax+b> cx+d 的解集是x<3,故③正确;
∵一次函数 与 的图象的交点的横坐标为3,∴3a+b=3c+d,∴3a-3c=d-b, 故④正确.故答案①③④.
7.②③④ 解:∵正比例函数的图象经过第二、四象限,
∴k<0,故①错误;
∵一次函数的图象与 y轴的正半轴相交,
∴b>0,故②正确;
∵当x<0时,正比例函数的图象在第二象限,
∴y >0,故③正确;
∵当x<-2时,正比例函数的图象在一次函数的图象上方,
∴当x<-2时, kx>x+b,故④正确.故答案为②③④.
压轴突破3 一次函数与数形结合问题
1. C 解:画出函数y=|x+1|-2的图象如图所示.把y=3代入y=|x+1|-2,得3=|x+1|-2,解得x=4 或-6,把y=-2代入y=|x+1|-2,得-2=|x+1|-2,解得x=-1,当m≤x≤4时,对应y的取值范围为-2≤y≤3,由图象可知-6≤m≤-1.故选 C.
2. B 解:∵当 x≥0 时,直线 与 的交点为 当x<0时,直线 与 的交点为 由图象可知:当y
4. D 解:分两种情况:①当x≥2a时,y=x-2a,∵k=1>0,∴当1≤x≤3时,y随x的增大而增大,即当x=1时,y=5,则5=1-2a,a=-2;
②当x<2a时,y=-x+2a,∵k=-1<0,∴当1≤x≤3时,y随x的增大而减小,即当x=3时,y=5,则5=-3+2a,a=4,∴a=-2或4,故选 D.
压轴突破4 一次函数与定点、定值问题
1. B 解:∵2a+b+3=0,∴b=-2a-3,
即y= ax-2a-3=a(x-2)-3,当x=2时,y=-3,
∴该一次函数的图象经过点(2,-3),
∴B选项正确.故选 B.
2. B 解:当OP=t时,点 P 的坐标为(t,0),点 Q 的坐标为(9-2t,6),设直线 PQ 的解析式为y= kx+b(k≠0),将P (t, 0), Q (9 - 2t, 6) 代 入 y = kx + b,得 解得 直线 PQ 的解析式为 当y-2=0时,x=3,∴线段 PQ 始终经过(3,2),故选 B.
3. C 解:联立 得 即点 A 在直线 上,∵点 A 到直线 的距离总是一个定值,∴直线 与直线 平行, 故选 C.
4. 解:y= kx-3x+k=(x+1)k-3x,∵当k变化时,一次函数的图象都过一定点,∴x+1=0,∴x=-1,∴y=3,∴B(-1,3),∴点 B 关于x轴的对称点 ,连接AB'交x轴于点C,此时CA+CB 最小,即 AB',分别过点A,B'作x,y轴的垂线交于点D,∴D(3,-3),∴B'D=3-(-1)=4,AD=2-(-3)=5, 故答案为
压轴突破5 一次函数与最值问题
1. A 解:由A(2,0),B(0,-6),得直线AB 的解析式为y=3x-6,∵P(x,y)是直线AB上任意一点,∴m=|3x-6|,n=|x|,∴m+n=|3x-6|+|x|.①当点 P(x,y)满足x≥2时,m+n=4x-6≥2;②当点 P(x,y)满足0
∴MN=PJ,∴当 JP⊥OA 时, PJ 的值最小,此时MN 的值最小.
∵AF⊥OM,A(10,0),直线OM 的解析式为
∴直线 AF 的解析式为
F 军彳
∴PJ 的最小值为 ,即MN 的最小值为 .故选 A.
3. C 解:作点 D 关于x轴对称的点 D',连接CD'交x轴于点 P,
此时PC+PD 的值最小,令 中x=0,则y=4,∴点 B 为(0,4);令 中y=0,
则 解得x=-6,∴点 A 为(-6,0).
∵C,D 分别为线段AB,OB 的中点,
∴点C(-3,2),点 D(0,2).
∵点 D'和点 D 关于x轴对称,∴点 D'为(0,-2).
设直线CD'的解析式为y= kx+b,
∵直线CD'经过点C(-3,2),D'(0,-2),
解得
∴直线 CD'的解析式为
令 y=0,则 解得
∴点 P 为
