第十七章 勾股定理选填题压轴突破 (含详解)2024-2025学年人教版八年级数学下册
文档属性
| 名称 | 第十七章 勾股定理选填题压轴突破 (含详解)2024-2025学年人教版八年级数学下册 |  | |
| 格式 | docx | ||
| 文件大小 | 388.2KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-05-09 10:15:16 | ||
图片预览


文档简介
第十七章 勾股定理选填题压轴突破
压轴突破1 构造直角三角形,运用勾股定理
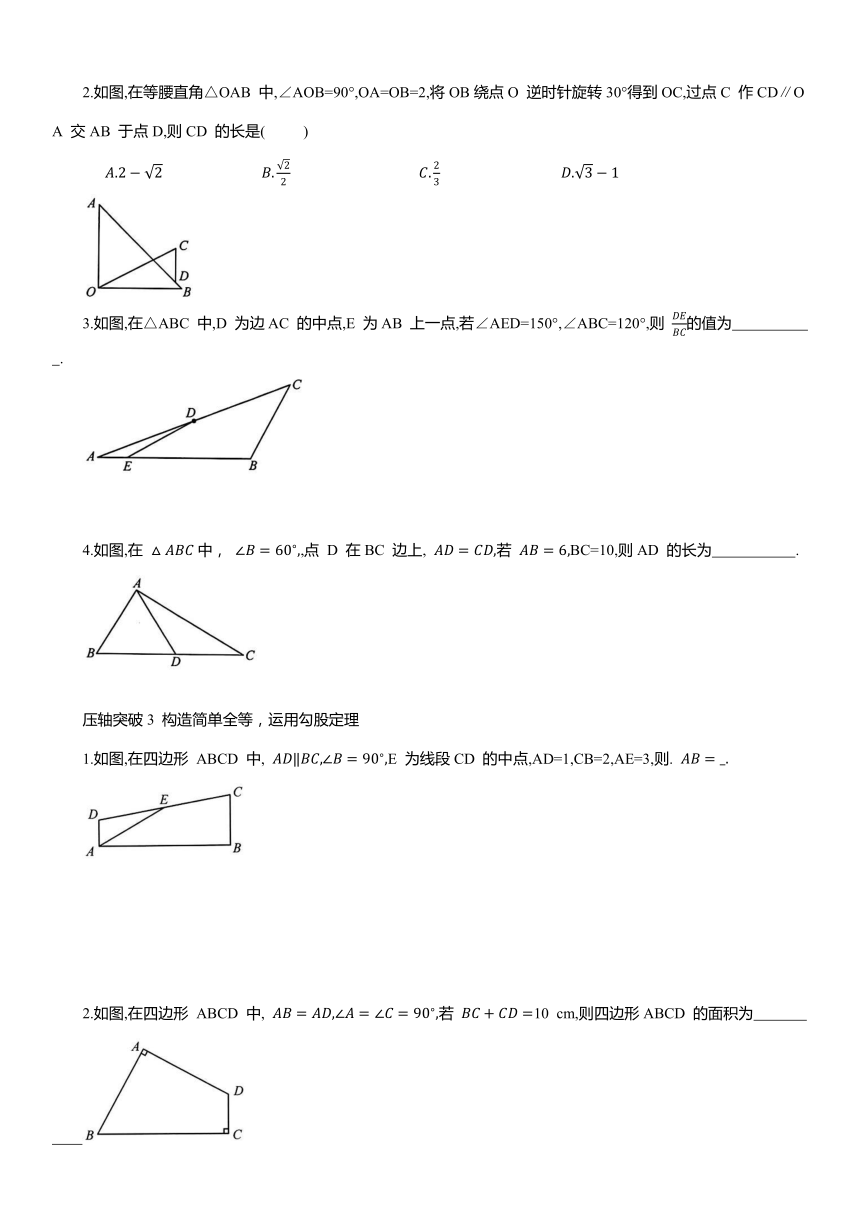
1.如图, .延长CB 交AD于点E,则△CDE 的面积为 .
2.如图,在△ABC 中,AB=AC=10,BC=16,若∠BAD=3∠DAC,则 CD 的长为 .
3.如图,在△ABC 中, ,点 D 在 BC 的延长线上,且∠ADC=30°.若AB=2,则CD 的长为( )
A.1 B.
4.如图,在四边形 ABCD 中, 连接 BD,则 BD 的长为 .
压轴突破2 构造含特殊角的直角三角形,运用勾股定理
1.如图,在等边. 中,D 为BC 边上一点, 则 的值是 .
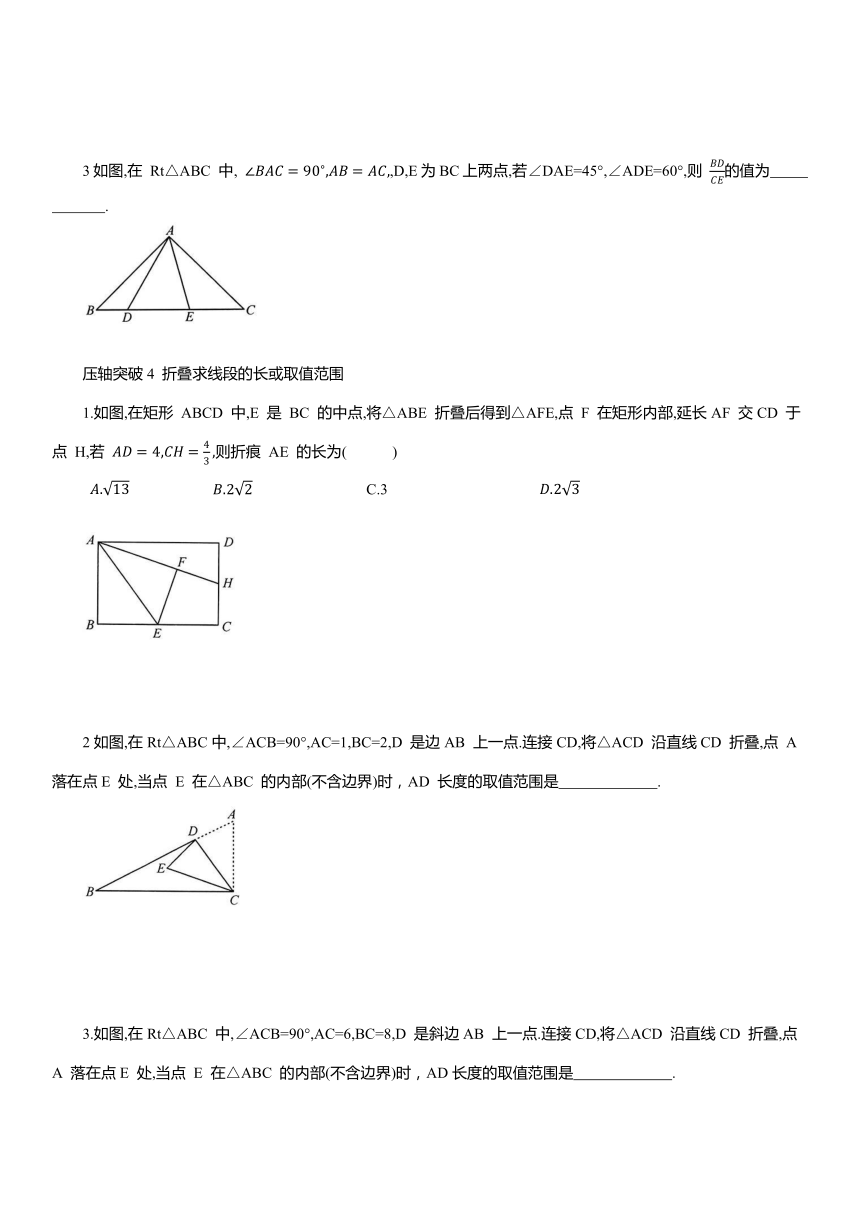
2.如图,在等腰直角△OAB 中,∠AOB=90°,OA=OB=2,将OB绕点O 逆时针旋转30°得到OC,过点C 作CD∥OA 交AB 于点D,则CD 的长是( )
3.如图,在△ABC 中,D 为边AC 的中点,E 为AB 上一点,若∠AED=150°,∠ABC=120°,则 的值为 .
4.如图,在 中, ,点 D 在BC 边上, 若 BC=10,则AD 的长为 .
压轴突破3 构造简单全等,运用勾股定理
1.如图,在四边形 ABCD 中, E 为线段CD 的中点,AD=1,CB=2,AE=3,则.
2.如图,在四边形 ABCD 中, 若 10 cm,则四边形ABCD 的面积为
3如图,在 Rt△ABC 中, ,D,E为BC上两点,若∠DAE=45°,∠ADE=60°,则 的值为 .
压轴突破4 折叠求线段的长或取值范围
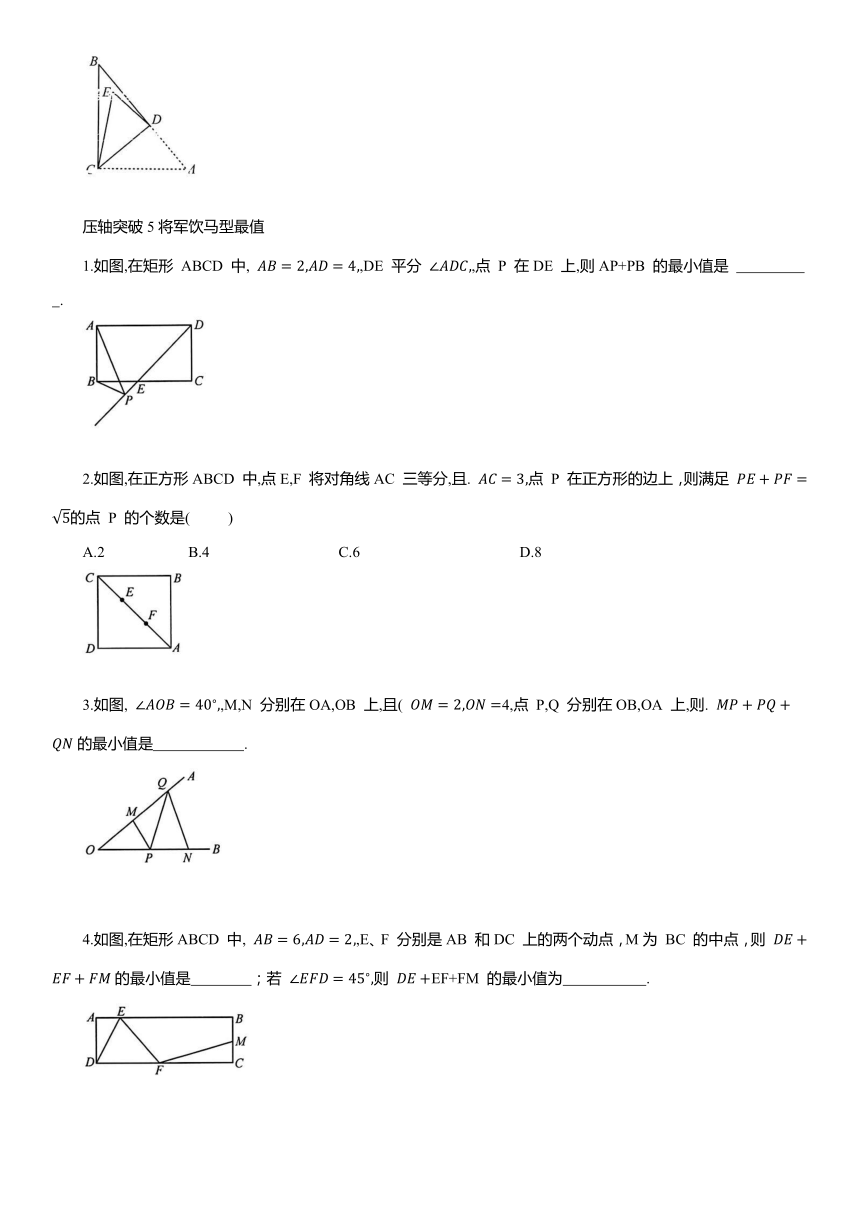
1.如图,在矩形 ABCD 中,E 是 BC 的中点,将△ABE 折叠后得到△AFE,点 F 在矩形内部,延长AF 交CD 于点 H,若 则折痕 AE 的长为( )
C.3
2如图,在Rt△ABC中,∠ACB=90°,AC=1,BC=2,D 是边AB 上一点.连接CD,将△ACD 沿直线CD 折叠,点 A 落在点E 处,当点 E 在△ABC 的内部(不含边界)时,AD 长度的取值范围是 .
3.如图,在Rt△ABC 中,∠ACB=90°,AC=6,BC=8,D 是斜边AB 上一点.连接CD,将△ACD 沿直线CD 折叠,点 A 落在点E 处,当点 E 在△ABC 的内部(不含边界)时,AD长度的取值范围是 .
压轴突破5将军饮马型最值
1.如图,在矩形 ABCD 中, ,DE 平分 ,点 P 在DE 上,则AP+PB 的最小值是 .
2.如图,在正方形ABCD 中,点E,F 将对角线AC 三等分,且. 点 P 在正方形的边上,则满足 的点 P 的个数是( )
A.2 B.4 C.6 D.8
3.如图, ,M,N 分别在OA,OB 上,且( 4,点 P,Q 分别在OB,OA 上,则. 的最小值是 .
4.如图,在矩形ABCD 中, ,E、F 分别是AB 和DC 上的两个动点,M为 BC 的中点,则 的最小值是 ;若 则 EF+FM 的最小值为 .
压轴突破6 构造全等求最值
1.如图,在四边形 ABCD 中, 45°,则 BD 的最大值为 .
2.正方形 ABCD 的边长为10,E 是正方形外一动点, P 为AB 的中点.当点 E 运动时,线段 PE 的取值范围为 .
E
3.如图,在 中, P 是 内一点,若AP+BP+CP 的最小值为 ,则BC 的长度为 .
B
4.如图,在 中, O是 内一点,则点O到 三个顶点的距离之和的最小值是 .
压轴突破7 勾股定理与全等构造
1.如图,在 中, ,分别以CD,DE 为边在 外部作正方形 ABCD 和正方形 DEFG,若 则
2.如图,在四边形 ABCD 中, 若 则 BD 的长为( )
A.5 C.6
3.如图,在四边形ABCD中, 5,AD=7,则 BC 的长为 ,AC 的长为 .
4.在四边形 ABCD 中, ,若BC=5,DC=3,则AC的长为 .
5.如图,在等腰直角△CAB 中,CA=CB,点M,N 在直线AB 上,且∠MCN=135°,BM=8,AN=10,则MN 的长为 .
6.如图,在等腰直角△ACB 中,CA=CB,∠ACB=90°,∠ECF=45°,点 E,F 在AB 上,AM⊥AB,BN⊥AB,AM,BN分别交直线CE,CF 于点 M,N,若AM=2,BN=5,则 MN 的长为 .
7.如图,在四边形 ABCD 中,∠B=∠C=90°,E 为边BC 上一点,连接AE,DE,△ADE 是等边三角形,若 则 的值为 .
8.如图,在△ABC 中,∠B=45°,点 D 在BC 上,CE⊥AD 于点E,交AB 于点F,FC=AD,若AF=6,BC=8,则AC 的长是( )
A.5 -1 B.5 C.3
第十七章 勾股定理
压轴突破1 构造直角三角形,运用勾股定理
解:连接AC,∵∠ABC=90°,AB=BC=1,
∴△ACD 是直角三角形,∠CAD=90°,
2.5 解:过点 A 作AE⊥BC于点E,过点 D 作DF⊥AC 于点F,
∵AB=AC=10,BC=16,∴CE=8,
设∠CAD=x,则∠BAD=3x,
∵AE⊥BC,AB=AC,∴∠BAE=∠CAE=2x,
∴∠EAD=∠DAC,
∴DE=DF,设CD=a,则DE=8-a,
解得a=5,即CD=5.
3. C 解:过点 A 作AM⊥BC 于点M,可得AM=BM=CM= ,利用∠ADC=30°,求得
解:连接AC,∵∠ABC=90°,AB=BC=1, 即AC +CD =AD ,∴∠ACD=90°,
过点 D 作DE⊥BC 交BC 的延长线于点E,
∵∠BCD=135°,∴∠DCE=45°,
∵DE⊥BE,∴∠DCE=∠EDC=45°,∴CE=DE,
∵CD=2 ,∴CE=DE=2,
∴BE=BC+CE=3.
压轴突破2 构造含特殊角的直角三角形,运用勾股定理
解:过点 D 作 DN⊥BC 交AC 于点N,
∵△ABC 是等边三角形,∴∠C=∠BAC=60°,
∴∠DNC=30°.设CD=a,
则CN=2CD=2a,DN= a,
∴∠ADN=∠DNC-∠DAC=15°,
2. D 解:延长CD 交OB 于点 E,
∵∠AOB=90°,CD∥OA,∴∠CEO=90°.
∵OB=OC=2,∠COE=30°,∴CE=1,OE=
∵△OAB 是等腰直角三角形,∴∠B=45°.
∵∠CEB=90°,∴△DEB 是等腰直角三角形.
3. 解:过点 C 作CM⊥AB 交AB 的延长线于点 M,取AM 的中点N,连接 DN,则
∴DN⊥AB.设 DN=x,则CM=2x,
∵∠AED=150°,∠ABC=120°,
∴∠DEN=30°,∠CBM=60°,
4. 解:过点A作AE⊥BC于点E,
∵∠B=60°,∠AEB=90°,∴BE= AB=3,
设AD=CD=x,则 DE=7-x,在 Rt△AED 中,AE + 即 解得
压轴突破3 构造简单全等,运用勾股定理
1.3 解:延长AE,BC 交于点 F,易得△AED≌△FEC.∴AF=6,BF=3,∴AB=3
2.25 解:过点 A 作AE⊥BC 于点E,AF⊥CD 交CD 的延长线于点F,
∴△ABE≌△ADF,∴BE=DF,AE=AF,
∵∠AEC=∠C=∠F=90°,
∴四边形AECF 为正方形,∴CE=CF,
∵BC+CD=EC+CF=2EC=10,
3. 解:∵AB=AC,∠BAC=90°,
∴∠B=∠ACB=45°,
∵∠DAE=45°,∠ADE=60°,
将△ABD 绕点A 逆时针旋转90°得到△ACF,连接 EF,则AF=AD,CF=BD,∠CAF=∠BAD,
∠ACF=∠B=45°,∴∠ECF=∠ACB+∠ACF=90°,∵∠DAE=45°,∴∠FAE=∠CAF+∠CAE=∠BAD+∠CAE=45°,∴∠FAE=∠DAE,
∴∠AEF=∠AED=75°,
故答案为
压轴突破4 折叠求线段的长或取值范围
1. A 解:连接EH,则△EFH≌△ECH,∴CH=FH=
解得.x=3,
解:∵∠ACB=90°,AC=1,BC=2, 当点 E 落在AB 上时,如图,由折叠得∠ADC=∠EDC=90°,
当点 E 落在BC 上时,如图,
过点 D 作 DH⊥AC 于点 H,DG⊥BC于点 G,则DH=DG,
∵DH⊥AC,∴∠HDC=∠HCD=45°,∴CH=DH,由面积法可求 当点 E 在△ABC 的内部(不含边界)时,AD 长度的取值范围是 故答案为
解:∵∠ACB=90°,AC=6,BC=8, 如图,当点 E 落在AB 上时,由面积法可求 由勾股定理,得AD= 如图,当点 E 落在 BC 上时,过点 D作DH⊥AC,垂足为 H,∴∠DHA=∠DHC=90°,由折叠得 是等腰直角三角形,∴DH=CH,过点 D 作DG⊥BC 于点G,由面积法可求 ∴当点 E 在△ABC 的内部(不含边界)时,AD 长度的取值范围是 故答案为
解:延长DC至点A',使 连接A'B,则
∵DE 平分∠ADC,∴∠ADP=∠A'DP,
∴△ADP≌△A'DP,∴AP=A'P,
: ,
∴AP+PB 的最小值是2
2. B 解:作点 F 关于AD 的对称点M,连接 EM 交AD 于点P,连接 PF,AM,则 PE+PF=PE+PM=EM,∵CE=EF=AF=1,∴AM=AF=1,
∵∠EAM=90°,∴EM= 同理,在正方形其他各边上各有一个点 P,使.
∴满足条件的点 P 有4个.
3.2 解:分别作 M,N 关于OB,OA 的对称点 M',N',过点 M'作 M'C⊥N'O 交 N'O的延长线于点 C,连接 OM',PM',QN',M'N'分别交OA,Q',P',∴MP+PQ+OB 于点( M'N',当且仅当点 P 与点 P',点Q 与点 Q'重合时取等号. 由 题 意, 知 ∠M'ON' = 120°, ∴ ∠M'OC = 60°,∵OM=2,ON=4,∴OM'=2,ON'=4,∴OC=1,M'C= 即 MP +PQ+QN 的最小值是2
4.解:作点 D 关于AB 的对称点 D’,作点 M 关于CD 的对称点 M',连接 D'M',D'E,FM',则 DE+EF+FM=D'E+EF+FM',∴当D',E,F,M'在同一条直线上时,所求的DE+EF+FM 最小,最小值即为 D'M'的长.过点 M'作AD 的垂线,交AD 的延长线于点H,. 故答案为
过点 E 作 EP⊥CD 于点 P,∵∠EFD=45°,
∴EP=PF=BC=2,∴EF=2 ,则 DE+EF+FM=DE+FM+2 ,∴求. 的最小值,即先求DE+FM 的最小值.作∠ADF 的平分线 DG 交AB 于点G,则. ,连接GF,可证△GDF≌△EFD,∴GF=DE,作点 M 关于 DC 的对称点 M',连接 FM',GM',则
当G,F,M'三点共线时,DE+FM 的最小值为 ∴DE+EF+FM 的最小值为
压轴突破6 构造全等求最值
解:以AD 为直角边,点A 为直角顶点向外作等腰 Rt△ADE,连接 CE,DE,则 易得△ABD≌△ACE,可得 BD =CE.在△CDE 中,DE+DC≥CE,所以 BD 的最大值为:
解:过点D 作 DF⊥DE,交 AE 于点 F,则△DEF 为等腰直角三角形,连接EC,AC,取 AC 的中点 O,连接PO,OE,
∵△DEF 为等腰直角三角形,∴DF=DE,
∵∠ADF+∠FDC=∠CDE+∠FDC,
∴∠ADF=∠CDE,
在△ADF 与△CDE 中,
∴△ADF≌△CDE(SAS),
∴∠AFD=∠CED=135°,∴∠AEC=90°,
∵正方形边长为10,∴
∴OE-PO≤PE≤PO+OE,
故答案为
解:将△ABP绕 点A顺时针旋转 60°得到△AMG.连接PG,CM,则 AB = AC = AM,MG=PB,AG=AP,∠GAP=60°,∴△GAP 是等边三角形,∴PA=PG,∴PA +PB + PC = CP +PG+GM,∴当点 M,G,P,C 共线时,PA+PB+PC的值最小,最小值为线段CM 的长,
∵AP+BP+CP 的最小值为4
∴CM=4 ,∵∠BAM=60°,∠BAC=30°,
∴∠MAC=90°,∴AM=AC=4,过点 B 作BN⊥AC 于点N.则 故答案为
解:连接 OM,ON,OG,分别以 OM,NM 为边向左构造等边△MOE 和等边△MNF,则 △MON ≌ △MEF,∴ON=EF.连接FG,此时OM+ON+OG=OE+EF+OG≥FG.当点 E,O 落在FG 上时取得最小值,即 FG 的长,过点G 作GH⊥FM 交FM 的延长线于点 H,可得等腰Rt△MGH,∴MH=GH=4,∴FG=√FH +GH =
压轴突破7 勾股定理与全等构造
1.10 解:过点G作GH⊥AD,交AD 的延长线于点 H, 可证△DGH≌△DEC,∴CE=GH=2,
2. C 解:在AD 上方,以点 A 为直角顶点作等腰直角△ADE,连接CE,
易证△ABD≌△ACE,
∴BD=CE,DE=4
∵∠ABC=∠ACB=∠ADC=45°,∴∠EDC=90°,
3.解:方法一:连接BD,过点 B 作BE⊥AD 于点E,则AE=BE=4,∵AD=7,∴DE=3,
∴BD=CD=5,∴∠CBD=∠BCD=45°,
∴△BCD 为等腰直角三角形,
过点C作CF⊥AD 于点F,则△BDE≌△DCF,∴DF=BE=4,
方法二:同方法一可证得△BCD 为等腰直角三角形.过点D向下作DE⊥AD 且DE=AD,连接AE,则△ADC≌△EDB,∴AC=BE.∵AE=7 ,AB=4 ,∠BAE=
解:以D C为 边向上作等边△DCE,连接BE,BD.
∵AB=AD,∠BAD=60°,∴△DAB 为等边三角形,
∴DB=DA,∠ADC=∠BDE,DC=DE,
∴△ADC≌△BDE,∴BE=AC,
∵∠BCE=∠BCD+∠DCE=90°,∴在 Rt△BCE 中,
解:以点C为 旋转中心,将△CAN逆时针旋转90°得到△CBD,连接 DM,则可证明△MCD≌△MCN,MD=MN,∵MB=8,AN =BD=10,∴MN=MD=
解:将△ACM绕点C顺时针旋转90°得到△CBF',则∠ 易得△MCN≌△F'CN,∴MN = NF'= √NB +BF = 故.MN 的长为
7. 解:延长CB 至点F,使∠AFB=60°,延长 BC 至点 H,使∠DHC=60°,
∵△ADE 为等边三角形,
∴∠AED=60°,AE=ED,由一线三等角模型可得,
△AEF≌△EDH(AAS),
∴AF=EH,EF=DH.设AB=2a,CD=3a,
8. D 解:过点 F 作 FM⊥BC 于点M,过点 A 作AN⊥BC于点N,则△ADN≌△CFM,
∴FM=DN=BM=x,AN=CM=8-x=BN,
∴DN=NC=x,∴AD=AC.
压轴突破1 构造直角三角形,运用勾股定理
1.如图, .延长CB 交AD于点E,则△CDE 的面积为 .
2.如图,在△ABC 中,AB=AC=10,BC=16,若∠BAD=3∠DAC,则 CD 的长为 .
3.如图,在△ABC 中, ,点 D 在 BC 的延长线上,且∠ADC=30°.若AB=2,则CD 的长为( )
A.1 B.
4.如图,在四边形 ABCD 中, 连接 BD,则 BD 的长为 .
压轴突破2 构造含特殊角的直角三角形,运用勾股定理
1.如图,在等边. 中,D 为BC 边上一点, 则 的值是 .
2.如图,在等腰直角△OAB 中,∠AOB=90°,OA=OB=2,将OB绕点O 逆时针旋转30°得到OC,过点C 作CD∥OA 交AB 于点D,则CD 的长是( )
3.如图,在△ABC 中,D 为边AC 的中点,E 为AB 上一点,若∠AED=150°,∠ABC=120°,则 的值为 .
4.如图,在 中, ,点 D 在BC 边上, 若 BC=10,则AD 的长为 .
压轴突破3 构造简单全等,运用勾股定理
1.如图,在四边形 ABCD 中, E 为线段CD 的中点,AD=1,CB=2,AE=3,则.
2.如图,在四边形 ABCD 中, 若 10 cm,则四边形ABCD 的面积为
3如图,在 Rt△ABC 中, ,D,E为BC上两点,若∠DAE=45°,∠ADE=60°,则 的值为 .
压轴突破4 折叠求线段的长或取值范围
1.如图,在矩形 ABCD 中,E 是 BC 的中点,将△ABE 折叠后得到△AFE,点 F 在矩形内部,延长AF 交CD 于点 H,若 则折痕 AE 的长为( )
C.3
2如图,在Rt△ABC中,∠ACB=90°,AC=1,BC=2,D 是边AB 上一点.连接CD,将△ACD 沿直线CD 折叠,点 A 落在点E 处,当点 E 在△ABC 的内部(不含边界)时,AD 长度的取值范围是 .
3.如图,在Rt△ABC 中,∠ACB=90°,AC=6,BC=8,D 是斜边AB 上一点.连接CD,将△ACD 沿直线CD 折叠,点 A 落在点E 处,当点 E 在△ABC 的内部(不含边界)时,AD长度的取值范围是 .
压轴突破5将军饮马型最值
1.如图,在矩形 ABCD 中, ,DE 平分 ,点 P 在DE 上,则AP+PB 的最小值是 .
2.如图,在正方形ABCD 中,点E,F 将对角线AC 三等分,且. 点 P 在正方形的边上,则满足 的点 P 的个数是( )
A.2 B.4 C.6 D.8
3.如图, ,M,N 分别在OA,OB 上,且( 4,点 P,Q 分别在OB,OA 上,则. 的最小值是 .
4.如图,在矩形ABCD 中, ,E、F 分别是AB 和DC 上的两个动点,M为 BC 的中点,则 的最小值是 ;若 则 EF+FM 的最小值为 .
压轴突破6 构造全等求最值
1.如图,在四边形 ABCD 中, 45°,则 BD 的最大值为 .
2.正方形 ABCD 的边长为10,E 是正方形外一动点, P 为AB 的中点.当点 E 运动时,线段 PE 的取值范围为 .
E
3.如图,在 中, P 是 内一点,若AP+BP+CP 的最小值为 ,则BC 的长度为 .
B
4.如图,在 中, O是 内一点,则点O到 三个顶点的距离之和的最小值是 .
压轴突破7 勾股定理与全等构造
1.如图,在 中, ,分别以CD,DE 为边在 外部作正方形 ABCD 和正方形 DEFG,若 则
2.如图,在四边形 ABCD 中, 若 则 BD 的长为( )
A.5 C.6
3.如图,在四边形ABCD中, 5,AD=7,则 BC 的长为 ,AC 的长为 .
4.在四边形 ABCD 中, ,若BC=5,DC=3,则AC的长为 .
5.如图,在等腰直角△CAB 中,CA=CB,点M,N 在直线AB 上,且∠MCN=135°,BM=8,AN=10,则MN 的长为 .
6.如图,在等腰直角△ACB 中,CA=CB,∠ACB=90°,∠ECF=45°,点 E,F 在AB 上,AM⊥AB,BN⊥AB,AM,BN分别交直线CE,CF 于点 M,N,若AM=2,BN=5,则 MN 的长为 .
7.如图,在四边形 ABCD 中,∠B=∠C=90°,E 为边BC 上一点,连接AE,DE,△ADE 是等边三角形,若 则 的值为 .
8.如图,在△ABC 中,∠B=45°,点 D 在BC 上,CE⊥AD 于点E,交AB 于点F,FC=AD,若AF=6,BC=8,则AC 的长是( )
A.5 -1 B.5 C.3
第十七章 勾股定理
压轴突破1 构造直角三角形,运用勾股定理
解:连接AC,∵∠ABC=90°,AB=BC=1,
∴△ACD 是直角三角形,∠CAD=90°,
2.5 解:过点 A 作AE⊥BC于点E,过点 D 作DF⊥AC 于点F,
∵AB=AC=10,BC=16,∴CE=8,
设∠CAD=x,则∠BAD=3x,
∵AE⊥BC,AB=AC,∴∠BAE=∠CAE=2x,
∴∠EAD=∠DAC,
∴DE=DF,设CD=a,则DE=8-a,
解得a=5,即CD=5.
3. C 解:过点 A 作AM⊥BC 于点M,可得AM=BM=CM= ,利用∠ADC=30°,求得
解:连接AC,∵∠ABC=90°,AB=BC=1, 即AC +CD =AD ,∴∠ACD=90°,
过点 D 作DE⊥BC 交BC 的延长线于点E,
∵∠BCD=135°,∴∠DCE=45°,
∵DE⊥BE,∴∠DCE=∠EDC=45°,∴CE=DE,
∵CD=2 ,∴CE=DE=2,
∴BE=BC+CE=3.
压轴突破2 构造含特殊角的直角三角形,运用勾股定理
解:过点 D 作 DN⊥BC 交AC 于点N,
∵△ABC 是等边三角形,∴∠C=∠BAC=60°,
∴∠DNC=30°.设CD=a,
则CN=2CD=2a,DN= a,
∴∠ADN=∠DNC-∠DAC=15°,
2. D 解:延长CD 交OB 于点 E,
∵∠AOB=90°,CD∥OA,∴∠CEO=90°.
∵OB=OC=2,∠COE=30°,∴CE=1,OE=
∵△OAB 是等腰直角三角形,∴∠B=45°.
∵∠CEB=90°,∴△DEB 是等腰直角三角形.
3. 解:过点 C 作CM⊥AB 交AB 的延长线于点 M,取AM 的中点N,连接 DN,则
∴DN⊥AB.设 DN=x,则CM=2x,
∵∠AED=150°,∠ABC=120°,
∴∠DEN=30°,∠CBM=60°,
4. 解:过点A作AE⊥BC于点E,
∵∠B=60°,∠AEB=90°,∴BE= AB=3,
设AD=CD=x,则 DE=7-x,在 Rt△AED 中,AE + 即 解得
压轴突破3 构造简单全等,运用勾股定理
1.3 解:延长AE,BC 交于点 F,易得△AED≌△FEC.∴AF=6,BF=3,∴AB=3
2.25 解:过点 A 作AE⊥BC 于点E,AF⊥CD 交CD 的延长线于点F,
∴△ABE≌△ADF,∴BE=DF,AE=AF,
∵∠AEC=∠C=∠F=90°,
∴四边形AECF 为正方形,∴CE=CF,
∵BC+CD=EC+CF=2EC=10,
3. 解:∵AB=AC,∠BAC=90°,
∴∠B=∠ACB=45°,
∵∠DAE=45°,∠ADE=60°,
将△ABD 绕点A 逆时针旋转90°得到△ACF,连接 EF,则AF=AD,CF=BD,∠CAF=∠BAD,
∠ACF=∠B=45°,∴∠ECF=∠ACB+∠ACF=90°,∵∠DAE=45°,∴∠FAE=∠CAF+∠CAE=∠BAD+∠CAE=45°,∴∠FAE=∠DAE,
∴∠AEF=∠AED=75°,
故答案为
压轴突破4 折叠求线段的长或取值范围
1. A 解:连接EH,则△EFH≌△ECH,∴CH=FH=
解得.x=3,
解:∵∠ACB=90°,AC=1,BC=2, 当点 E 落在AB 上时,如图,由折叠得∠ADC=∠EDC=90°,
当点 E 落在BC 上时,如图,
过点 D 作 DH⊥AC 于点 H,DG⊥BC于点 G,则DH=DG,
∵DH⊥AC,∴∠HDC=∠HCD=45°,∴CH=DH,由面积法可求 当点 E 在△ABC 的内部(不含边界)时,AD 长度的取值范围是 故答案为
解:∵∠ACB=90°,AC=6,BC=8, 如图,当点 E 落在AB 上时,由面积法可求 由勾股定理,得AD= 如图,当点 E 落在 BC 上时,过点 D作DH⊥AC,垂足为 H,∴∠DHA=∠DHC=90°,由折叠得 是等腰直角三角形,∴DH=CH,过点 D 作DG⊥BC 于点G,由面积法可求 ∴当点 E 在△ABC 的内部(不含边界)时,AD 长度的取值范围是 故答案为
解:延长DC至点A',使 连接A'B,则
∵DE 平分∠ADC,∴∠ADP=∠A'DP,
∴△ADP≌△A'DP,∴AP=A'P,
: ,
∴AP+PB 的最小值是2
2. B 解:作点 F 关于AD 的对称点M,连接 EM 交AD 于点P,连接 PF,AM,则 PE+PF=PE+PM=EM,∵CE=EF=AF=1,∴AM=AF=1,
∵∠EAM=90°,∴EM= 同理,在正方形其他各边上各有一个点 P,使.
∴满足条件的点 P 有4个.
3.2 解:分别作 M,N 关于OB,OA 的对称点 M',N',过点 M'作 M'C⊥N'O 交 N'O的延长线于点 C,连接 OM',PM',QN',M'N'分别交OA,Q',P',∴MP+PQ+OB 于点( M'N',当且仅当点 P 与点 P',点Q 与点 Q'重合时取等号. 由 题 意, 知 ∠M'ON' = 120°, ∴ ∠M'OC = 60°,∵OM=2,ON=4,∴OM'=2,ON'=4,∴OC=1,M'C= 即 MP +PQ+QN 的最小值是2
4.解:作点 D 关于AB 的对称点 D’,作点 M 关于CD 的对称点 M',连接 D'M',D'E,FM',则 DE+EF+FM=D'E+EF+FM',∴当D',E,F,M'在同一条直线上时,所求的DE+EF+FM 最小,最小值即为 D'M'的长.过点 M'作AD 的垂线,交AD 的延长线于点H,. 故答案为
过点 E 作 EP⊥CD 于点 P,∵∠EFD=45°,
∴EP=PF=BC=2,∴EF=2 ,则 DE+EF+FM=DE+FM+2 ,∴求. 的最小值,即先求DE+FM 的最小值.作∠ADF 的平分线 DG 交AB 于点G,则. ,连接GF,可证△GDF≌△EFD,∴GF=DE,作点 M 关于 DC 的对称点 M',连接 FM',GM',则
当G,F,M'三点共线时,DE+FM 的最小值为 ∴DE+EF+FM 的最小值为
压轴突破6 构造全等求最值
解:以AD 为直角边,点A 为直角顶点向外作等腰 Rt△ADE,连接 CE,DE,则 易得△ABD≌△ACE,可得 BD =CE.在△CDE 中,DE+DC≥CE,所以 BD 的最大值为:
解:过点D 作 DF⊥DE,交 AE 于点 F,则△DEF 为等腰直角三角形,连接EC,AC,取 AC 的中点 O,连接PO,OE,
∵△DEF 为等腰直角三角形,∴DF=DE,
∵∠ADF+∠FDC=∠CDE+∠FDC,
∴∠ADF=∠CDE,
在△ADF 与△CDE 中,
∴△ADF≌△CDE(SAS),
∴∠AFD=∠CED=135°,∴∠AEC=90°,
∵正方形边长为10,∴
∴OE-PO≤PE≤PO+OE,
故答案为
解:将△ABP绕 点A顺时针旋转 60°得到△AMG.连接PG,CM,则 AB = AC = AM,MG=PB,AG=AP,∠GAP=60°,∴△GAP 是等边三角形,∴PA=PG,∴PA +PB + PC = CP +PG+GM,∴当点 M,G,P,C 共线时,PA+PB+PC的值最小,最小值为线段CM 的长,
∵AP+BP+CP 的最小值为4
∴CM=4 ,∵∠BAM=60°,∠BAC=30°,
∴∠MAC=90°,∴AM=AC=4,过点 B 作BN⊥AC 于点N.则 故答案为
解:连接 OM,ON,OG,分别以 OM,NM 为边向左构造等边△MOE 和等边△MNF,则 △MON ≌ △MEF,∴ON=EF.连接FG,此时OM+ON+OG=OE+EF+OG≥FG.当点 E,O 落在FG 上时取得最小值,即 FG 的长,过点G 作GH⊥FM 交FM 的延长线于点 H,可得等腰Rt△MGH,∴MH=GH=4,∴FG=√FH +GH =
压轴突破7 勾股定理与全等构造
1.10 解:过点G作GH⊥AD,交AD 的延长线于点 H, 可证△DGH≌△DEC,∴CE=GH=2,
2. C 解:在AD 上方,以点 A 为直角顶点作等腰直角△ADE,连接CE,
易证△ABD≌△ACE,
∴BD=CE,DE=4
∵∠ABC=∠ACB=∠ADC=45°,∴∠EDC=90°,
3.解:方法一:连接BD,过点 B 作BE⊥AD 于点E,则AE=BE=4,∵AD=7,∴DE=3,
∴BD=CD=5,∴∠CBD=∠BCD=45°,
∴△BCD 为等腰直角三角形,
过点C作CF⊥AD 于点F,则△BDE≌△DCF,∴DF=BE=4,
方法二:同方法一可证得△BCD 为等腰直角三角形.过点D向下作DE⊥AD 且DE=AD,连接AE,则△ADC≌△EDB,∴AC=BE.∵AE=7 ,AB=4 ,∠BAE=
解:以D C为 边向上作等边△DCE,连接BE,BD.
∵AB=AD,∠BAD=60°,∴△DAB 为等边三角形,
∴DB=DA,∠ADC=∠BDE,DC=DE,
∴△ADC≌△BDE,∴BE=AC,
∵∠BCE=∠BCD+∠DCE=90°,∴在 Rt△BCE 中,
解:以点C为 旋转中心,将△CAN逆时针旋转90°得到△CBD,连接 DM,则可证明△MCD≌△MCN,MD=MN,∵MB=8,AN =BD=10,∴MN=MD=
解:将△ACM绕点C顺时针旋转90°得到△CBF',则∠ 易得△MCN≌△F'CN,∴MN = NF'= √NB +BF = 故.MN 的长为
7. 解:延长CB 至点F,使∠AFB=60°,延长 BC 至点 H,使∠DHC=60°,
∵△ADE 为等边三角形,
∴∠AED=60°,AE=ED,由一线三等角模型可得,
△AEF≌△EDH(AAS),
∴AF=EH,EF=DH.设AB=2a,CD=3a,
8. D 解:过点 F 作 FM⊥BC 于点M,过点 A 作AN⊥BC于点N,则△ADN≌△CFM,
∴FM=DN=BM=x,AN=CM=8-x=BN,
∴DN=NC=x,∴AD=AC.
