湖南省长沙市2025年中考数学考前练习卷(一)(含解析)
文档属性
| 名称 | 湖南省长沙市2025年中考数学考前练习卷(一)(含解析) |  | |
| 格式 | docx | ||
| 文件大小 | 1.5MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 通用版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-05-10 09:37:15 | ||
图片预览




文档简介
中小学教育资源及组卷应用平台
湖南省长沙市2025年中考数学考前练习卷(一)
温馨提示:
1.答题前,请考生先将自己的姓名、准考证号填写清楚,并认真核对条形码上的姓名、准考证号、考室和座位号;
2.必须在答题卡上答题,在草稿纸、试题卷上答题无效;
3.答题时,请考生注意各大题题号后面的答题提示;
4.请勿折叠答题卡,保持字体工整、笔迹清晰、卡面清洁;
5.答题卡上不得使用涂改液、涂改胶和贴纸;
6.本学科试卷共25个小题,考试时量120分钟,满分120分.
一、选择题:本题共10小题,每小题3分,共30分.在每小题给出的四个选项中,只有一项是符合题目要求的.
1.下列各数中,不是无理数的是( )
A. B. C. D.
2.下列图形中,既是轴对称图形又是中心对称图形的是( )
A. B.
C. D.
3.下列计算正确的是( )
A. B.
C. D.
4.以下列各组数为边,能组成三角形的是( )
A.1,2,3 B.4,3,5 C.15,7,7 D.6,8,18
5.澳门官方公布的最新数据显示,截至12月7日,2024年澳门累计入境旅客达3254.5万人次.澳门旅游业相关人士预测,全年入境旅客量有望突破3300万人次.3254.5万用科学记数法表示正确的是( )
A. B. C. D.
6.如图,,,,则的度数为( )
A. B. C. D.
7.如图是根据某早餐店1日至5日每天的用水量(单位:吨)绘制成的折线统计图.下列结论正确的是( )
A.平均数是5 B.众数是6 C.中位数是10 D.方差是8
8.一次函数的图象经过第二、三、四象限,则的取值范围是( )
A. B. C. D.
9.如图,在中,,,,是它的内切圆,用剪刀沿的切线剪一个,则的周长为( )
A.4 B.6 C.8 D.10
10.从,,,,中任取两数作为,,使抛物线的开口向上,对称轴在轴左侧的概率为( )
A. B. C. D.
二、填空题:本题共6小题,每小题3分,共18分.
11.分解因式: .
12.如图,平分,于点,点为射线上一动点,若,则的最小值为 .
13.不等式组的解集是 .
14.现有分别标有汉字“喜”“乐”“安”“宁”的四张卡片,它们除汉字外完全相同,若把四张卡片背面朝上,洗匀后放在桌面上,然后随机抽出一张,不放回,再随机抽出一张,两次抽出的卡片上的汉字恰好是“安”“宁”的概率是 .
15.在一定条件下,乐器中弦振动的频率f与弦长l成反比例关系,即(k为常数,).若某乐器的弦长l为米,振动频率f为200赫兹,则k的值为 .
16.勾股定理最早出现在商高的《周髀算经》:“勾广三,股修四,经隅五”,我国古代把直角三角形的直角边中较小者称为“勾”,另一长直角边称为“股”,把斜边称为“弦”.观察下列勾股数: ;…,这类勾股数的特点是:勾为奇数,弦与股相差为1.柏拉图研究了勾为偶数,弦与股相差为2的一类勾股数,如: …,若此类勾股数的勾为 ,则其弦是 .
三、解答题:本题共9小题,共72分,解答应写出文字说明、证明过程或演算步骤.
17.计算:
18.先化简,再求值:,其中,.
19.如图,在中,,分别以点和点为圆心,大于的长为半径作弧,两弧交于两点,连接直线,交于点,交于点.
(1)求证:直线垂直平分线段;
(2)若,连接,求的度数.
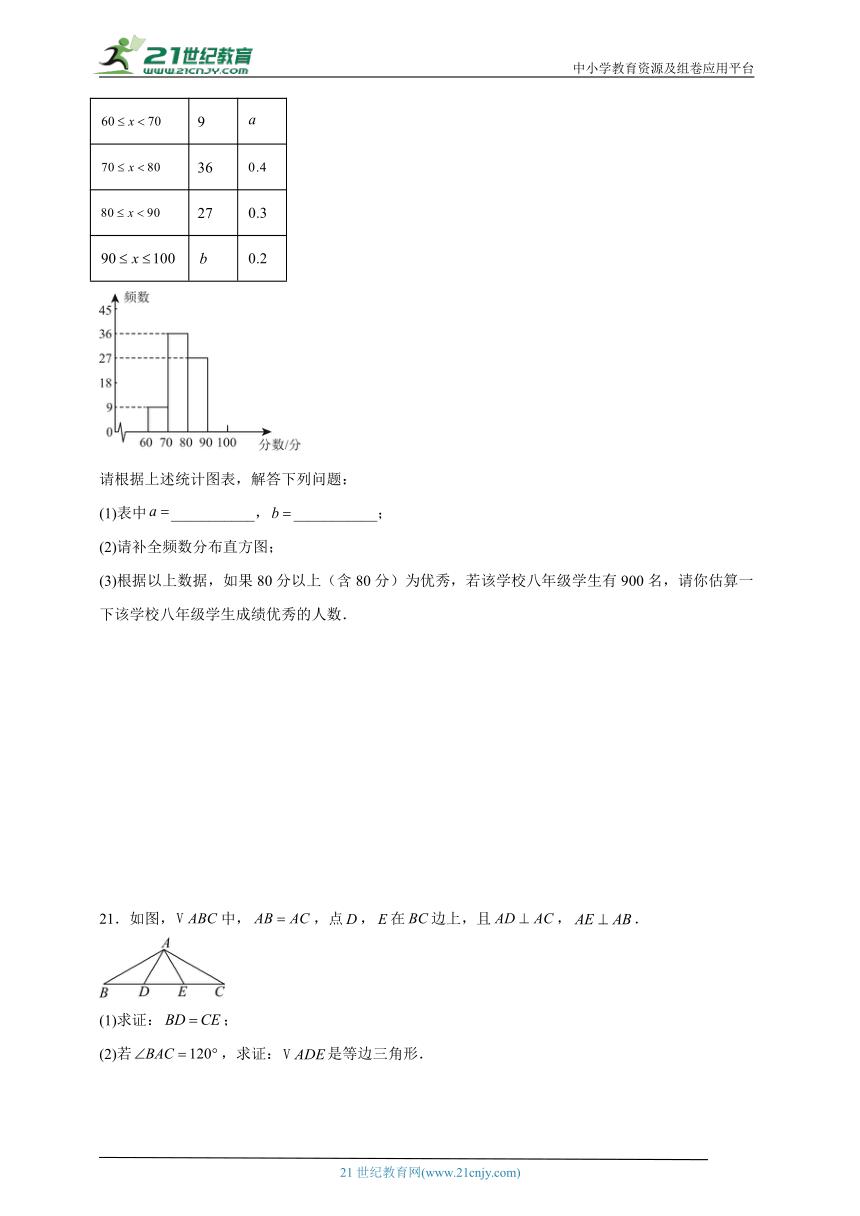
20.2025年1月23日,中共中央、国务院、中央军委给神舟十八号航天员叶光富颁发“二级航天功勋奖章”,授予李聪、李广苏“英雄航天员”荣誉称号并颁发“三级航天功勋奖章”.神舟十八号载人飞行任务的圆满成功,标志着中国航天事业在实现高水平科技自立自强的新征程中迈出关键一步.此次任务不仅提升我国综合国力和中华民族凝聚力,更进一步增强了全体中华儿女的民族自信心和自豪感,对激励全党全军全国各族人民团结奋进、砥砺前行具有重要意义.某校为了解本校学生对航天知识的了解情况,对八年级学生进行了航天知识测试,测试成绩全部合格,现随机选取了部分学生的成绩,整理并制作成了如下不完整的图表:
分数段 频数 频率
9
36
27
请根据上述统计图表,解答下列问题:
(1)表中___________,___________;
(2)请补全频数分布直方图;
(3)根据以上数据,如果80分以上(含80分)为优秀,若该学校八年级学生有900名,请你估算一下该学校八年级学生成绩优秀的人数.
21.如图,中,,点,在边上,且,.
(1)求证:;
(2)若,求证:是等边三角形.
22.2024年巴黎奥运会将于7月26日至8月11日举行,某经销店调查发现:与吉祥物相关的A,B两款纪念品深受青少年喜爱.已知购进3个A款比购进2个B款多用120元;购进1个A款和2个B款共用200元.
(1)分别求出A,B两款纪念品的进货单价;
(2)该商店决定购进这两款纪念品共70个,其总费用不超过5000元,则至少应购买B款纪念品多少个?
23.如图,在中,点为的中点,过点作,延长到点使,连接,.
(1)求证:四边形是矩形;
(2)若,求的长.
24.对凸四边形我们进行约定:若四边形对角线既不垂直也不相等,叫做“线无垂等”四边形;若四边形对角线垂直但不相等,叫做“线垂不等”四边形;若四边形对角线相等但不垂直,叫做“线等不垂”四边形;若四边形对角线既相等又垂直,叫做“线垂且等”四边形.
(1)判断下列说法是否正确(正确的请在题后括号内打“”,错误的打“”).
所有的平行四边形都是“线无垂等”四边形;( )
邻边相等的矩形是“线垂且等”四边形;( )
依次连接“线垂不等”四边形各边中点,构成的四边形是“线等不垂”四边形.( )
(2)如图,在中,,于点,分别为的中点.
四边形为“___________”四边形(从约定的四种类型中选一种填入);
若和的面积分别为和,求四边形的面积;
(3)如图,在中,已知是的弦,作,,分别交于点和点,连接.
求证:四边形是“线垂且等”四边形;
如图,已知且对角线与交于点,若的半径为,到的距离为,求弦的长度.
25.已知抛物线的对称轴为直线,抛物线与轴交于点A,B(点在点的左侧),点为抛物线的顶点.
(1)求点和点的坐标;
(2)若在上的最大值为9,求此时的面积;
(3)已知点为抛物线上点,之间的动点(点不与点,重合),点为线段上一定点(点不与点A,B重合),过点作轴的垂线,直线分别交射线,于点,若时,在点运动的过程中,的值始终为8,求点的坐标及的值.
《湖南省长沙市2025年中考数学考前练习卷(一)》参考答案
题号 1 2 3 4 5 6 7 8 9 10
答案 A C B B D C D C B B
1.A
【分析】本题考查了无理数即无限不循环小数,正确理解定义是解题的关键.
根据无理数的定义去甄别即可.
【详解】解:A、是有理数,故该项正确,符合题意;
B、是无理数,故该项错误,不符合题意;
C、是无理数,故该项错误,不符合题意;
D、是无理数,故该项错误,不符合题意;
故选A.
2.C
【分析】本题主要考查轴对称图形和中心对称图形;根据轴对称图形和中心对称图形的定义逐一判断即可.
【详解】解:A是轴对称图形,不是中心对称图形,不符合题意;
B是轴对称图形,不是中心对称图形,不符合题意;
C既是轴对称图形又是中心对称图形,符合题意;
D不是轴对称图形,是中心对称图形,不符合题意;
故选:C.
3.B
【分析】本题考查了整式的混合运算,掌握合并同类项,同底数幂的除法,单项式乘以多项式,完全平方公式是解题的关键.
根据合并同类项、同底数幂的除法、单项式乘以多项式、完全平方公式的运算法则,逐项计算判断即可.
【详解】解:A.,原选项计算错误,不符合题意;
B.,原选项计算正确,符合题意;
C.,原选项计算错误,不符合题意;
D.,原选项计算错误,不符合题意.
故选:B.
4.B
【分析】本题主要考查三角形的三边关系 ;根据三角形的两边之和大于第三边, 两边之差小于第三边判断即可.
【详解】解:A.,不符合题意;
B.,符合题意;
C.,不符合题意;
D.,不符合题意;
故选:B.
5.D
【分析】本题主要考查了科学记数法,科学记数法的表现形式为的形式,其中,n为整数,确定n的值时,要看把原数变成a时,小数点移动了多少位,n的绝对值与小数点移动的位数相同,当原数绝对值大于等于10时,n是正数,当原数绝对值小于1时n是负数;由此进行求解即可得到答案.
【详解】解:3254.5万用科学记数法表示,
故选:D.
6.C
【分析】本题考查平行线的性质,垂直的定义,熟练掌握平行线的性质是解题的关键.
根据垂直得到,即可求出,然后根据平行线的性质求出即可.
【详解】解:∵,
∴,
又∵,
∴,
又∵,
∴,
故选:C.
7.D
【分析】根据题目要求算出平均数、众数、中位数、方差,再作出选择即可.
【详解】解:A、平均数为,故选项错误,不符合题意;
B、众数为,,,,,故选项错误,不符合题意;
C、从小到大排列为,,,,,中位数是,故选项错误,不符合题意;
D、方差,故选项正确,符合题意;
故选∶D.
【点睛】本题考查平均数、众数、中位数、方差的算法,熟练掌握平均数、众数、中位数、方差的算法是解题的关键.
8.C
【分析】本题主要考查了一次函数的图象,根据一次函数的图象经过的象限得到,,求出m的取值范围即可.
【详解】解:∵一次函数的图象经过第二、三、四象限,
∴,
解得,
故选:C.
9.B
【分析】本题考查了三角形的内切圆与内心,勾股定理,切线的性质,解决本题的关键是掌握切线的性质.设的内切圆切三边于点,连接,由切线长定理可知,根据是的切线,可得,,根据勾股定理可得,得四边形是正方形,再求出内切圆的半径为,进而可得的周长.
【详解】解:如图,设的内切圆切三边于点、、,连接、、,
由切线长定理可知,,,
∵是的切线,
∴,,
∵,,,
∴,
∴,
则四边形是正方形,
∵是的内切圆,
∴内切圆的半径,
∴,
∴,
∴,
∴的周长为:.
故选:B.
10.B
【分析】本题考查了列表法与树状图法,二次函数的性质,概率公式,首先根据题意得到,,然后利用列表法即可列举出所有各种可能的情况,然后利用概率公式即可求解.
【详解】解:∵抛物线的开口向上,对称轴在y轴左侧,
∴,,
∴;
列表如下:
∴共有20种等可能结果,其中使抛物线的开口向上,对称轴在y轴左侧的有2种结果,
∴使抛物线的开口向上,对称轴在y轴左侧的概率为.
故选:B.
11.
【分析】本题考查了分解因式,掌握因式分解的方法是解题关键.提公因式分解因式即可.
【详解】解:,
故答案为:.
12.3
【分析】本题考查了角平分线的性质:角的平分线上的点到角的两边的距离相等.也考查了垂线段最短.过O点作于H点,如图,先根据角平分线的性质得到,然后根据垂线段最短解决问题.
【详解】解:过O点作于H点,如图,
平分,
,
∵点E为射线上一动点,
∴的最小值为的长,
即的最小值为3.
故答案为:3.
13.
【分析】本题考查解不等式组,解题的关键在于准确解出每个不等式,找到公共的解集.先解第一个不等式,再解第二个不等式,然后根据“同大取大,同小取小,大小小大中间找,大大小小找不到”这个规律求出不等式组的解集便可.
【详解】解:解不等式①,得,
解不等式②,得,
因此,原不等式组的解集为,
故答案为:.
14.
【分析】此题考查了用列表法或树状图法求概率,熟练掌握概率所求情况数与总情况数之比是解题关键.画树状图列出所有等可能结果,从中找到符合条件的结果数,再根据概率公式求解即可.
【详解】解:“喜”“乐”“安”“宁”的四张卡片分别用、、、表示,
画树状图如图所示:
由树状图可知,共有12种等可能的结果,其中两次抽出的卡片上的汉字恰好是“安”“宁”有2种,
两次抽出的卡片上的汉字恰好是“安”“宁”概率是,
故答案为:.
15.160
【分析】本题考查了待定系数法求反比例函数解析式,把,代入求解即可.
【详解】解:把,代入,得,
解得,
故答案为:160.
16.
【分析】根据规律可得,如果a,b,c是符合同样规律的一组勾股数,(m为偶数且),根据所给的二组数找规律可得结论.
【详解】根据规律可得,如果a,b,c是符合同样规律的一组勾股数, (m为偶数且 ),则另一条直角边 ,弦 .
则弦为,
故答案为:.
【点睛】此题主要考查了勾股数的定义,数字类的规律问题,得出规律是解题关键.
17.4
【分析】本题考查实数的运算,特殊角三角函数值,零指数幂,负整数指数幂,先计算负整数指数幂,特殊角的三角函数值,零指数幂,化简绝对值,再加减即可.
【详解】解:
.
18.,.
【分析】本题考查了多项式乘以多项式,完全平方公式,合并同类项,熟练掌握运算法则是解题的关键.
先通过多项式乘以多项式法则,完全平方公式进行化简,然后由合并同类项法则化成最简,再把,代入求值即可.
【详解】解:
,
当,时,
原式
.
19.(1)见解析
(2)
【分析】本题考查作图—复杂作图,线段的垂直平分线的性质.
(1)根据线段的垂直平分线的作法证明即可;
(2)由垂直平分线的性质得,进而得,即可求解.
【详解】(1)证明:连接,,,,
由作图可知,
∴M,N在线段的垂直平分线上,
∴直线垂直平分线段;
(2)解:∵直线垂直平分线段,点D是直线和的交点,即点D在直线上,
∴,
∵,
∴,
∴,
∵,
∴.
20.(1)
(2)见解析
(3)估计该学校八年级学生成绩优秀的人数为450人
【分析】本题主要考查了频数分布表,频数分布直方图,用样本估计总体,正确读懂统计图和统计图是解题的关键.
(1)用的频数除以其频率求出样本容量,进而求出a、b的值即可;
(2)根据(1)所求补全统计图即可;
(3)用900乘以样本中80分以上(含80分)的频率即可得到答案.
【详解】(1)解:∵样本容量为,
∴;
(2)解:补全频数分布直方图如图所示:
(3)解:(人),
答:估计该学校八年级学生成绩优秀的人数为450人.
21.(1)见解析
(2)见解析
【分析】本题考查了全等三角形的判定和性质,等边三角形的判定,三角形内角和定理.
(1)证明得,进而得,即可得出结论;
(2)先由等腰三角形的性质得,再由三角形内角和定理得,即可得出结论.
【详解】(1)证明:∵,,
∴,
∵,
∴,
在和中,
,
∴,
∴,
∴,
∴;
(2)解:∵,,
∴,
在和中,
∵,
∴,即,
∴是等边三角形.
22.(1)A款纪念品的进货单价为80元,则B款纪念品的进货单价为60元
(2)至少应购买B款纪念品30个
【分析】本题考查二元一次方程组的应用、一元一次不等式的应用,(1)设A款纪念品的进货单价为x元,则B款纪念品的进货单价为y元,根据题意列二元一次方程组求解即可;
(2)设购买B款纪念品a个,则购买A款纪念品个,根据题意列一元一次不等式求得a的取值范围,即可求解.
【详解】(1)解:设A款纪念品的进货单价为x元,则B款纪念品的进货单价为y元,
由题意得,,
解得,
答:A款纪念品的进货单价为80元,则B款纪念品的进货单价为60元.
(2)解:设购买B款纪念品a个,则购买A款纪念品个,
由题意得,,
解得,,
答:至少应购买B款纪念品30个.
23.(1)证明见解析
(2)
【分析】()利用平行四边形的性质可证四边形是平行四边形,进而由即可求证;
()由()可得,即得,,进而由得,利用勾股定理得,最后根据直角三角形的性质即可求解.
【详解】(1)证明:∵四边形是平行四边形,
∴,,
∴,
∵,
∴,
即,
∴,
∴四边形是平行四边形,
又∵,
∴,
∴四边形是矩形;
(2)解:由()可知,,,,
∵,,
∴,
∴,
∵,
∴,
∴,
在中,由勾股定理得,,
∵是的中点,,
∴.
【点睛】本题考查了平行四边形的判定和性质,矩形的判定和性质,勾股定理,直角三角形的性质,三角函数,掌握以上知识点是解题的关键.
24.(1);;
(2)线等不垂;;
(3)见解析;.
【分析】()根据题中定义即可判断;
()如图,连接,,交于点,由中位线定理得,,根据直角三角形斜边上的中线性质,,,由,则有,从而即可判断;
根据三角形中线的定义和面积和差即可求解;
()连接,,与相交于点,再根据“线垂且等”四边形的定义即可求证;
过点作于点,证明,则,即,再根据到的距离为,即,设,则,然后代入求出,再证明,则,故,最后用勾股定理即可求解.
【详解】(1)解:所有的平行四边形都是“线无垂等”四边形,此说法错误;
邻边相等的矩形是“线垂且等”四边形,此说法正确;
依次连接“线垂不等”四边形各边中点,构成的四边形是“线等不垂”四边形,此说法正确;
故答案为:,,;
(2)如图,连接,,交于点,
∵分别为的中点,
∴,,
∵,
∴,
∵分别为的中点,
∴,
∴,,
∵,
∴,
∴,
∴,
∴四边形为“线等不垂”四边形,
故答案为:线等不垂;
∵,,
∴,
∵分别为的中点,
∴,
∵,
∴,
∴;
(3)证明:如图,连接,,与相交于点,
∵,,
∴,
∴,,
∴,即,
∵,,
∴,
又∵,,
∴,
∴,
∴四边形是“线垂且等”四边形;
解:如图,∵,,
∴,
由知,,
∴,
过点作于点,
∴,
∵,,
∴,
∴,
∴,
∴,
∵到的距离为,即,
设,则,
∴,
解得或(舍去),
∴,,
∵,,
∴,
∵,
∴,
∴,
∴,
∴,
在中,,,
∴.
【点睛】此题考查了全等三角形的判定和性质、勾股定理、圆周角定理,相似三角形的判定与性质,中位线定理,直角三角形斜边上的中线性质,解一元二次方程、等腰直角三角形的判定和性质等知识,熟练掌握知识点的应用是解题的关键.
25.(1),
(2)或27
(3),
【分析】(1)首先根据对称轴得到,求出抛物线,然后令得到,然后求解即可;
(2)首先得到,,然后分两种情况讨论:当时和当时,然后分别根据二次函数的性质求解即可;
(3)设点,点,分别表示出直线和解析式,然后表示出,然后根据题意得到,进而求解即可.
【详解】(1)∵抛物线的对称轴为直线
∴,
∴,
∴抛物线,
令可得,
解得,,
∴,;
(2)由(1)得,
∵,
∴
当时,开口向上,
∴时,y取最大值,
∴,
解得,
∴
此时顶点
∴的面积为;
当时,开口向下,
∴时,y取最大值,
此时点,的面积为;
综上,的面积为或27.
(3)设点,点,
∵,
∴设直线的解析式为
∴
解得
∴直线的解析式;
同理直线的解析式为
当时,,
∴
∴
∵点P运动的过程中的值始终为定值8,即不受t的影响,
∴,
解得,
∴,
∴,
解得.
【点睛】此题考查了二次函数的图象和性质,二次函数和x轴交点问题以及线段问题,熟练掌握二次函数的图象与性质是解答本题的关键.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
湖南省长沙市2025年中考数学考前练习卷(一)
温馨提示:
1.答题前,请考生先将自己的姓名、准考证号填写清楚,并认真核对条形码上的姓名、准考证号、考室和座位号;
2.必须在答题卡上答题,在草稿纸、试题卷上答题无效;
3.答题时,请考生注意各大题题号后面的答题提示;
4.请勿折叠答题卡,保持字体工整、笔迹清晰、卡面清洁;
5.答题卡上不得使用涂改液、涂改胶和贴纸;
6.本学科试卷共25个小题,考试时量120分钟,满分120分.
一、选择题:本题共10小题,每小题3分,共30分.在每小题给出的四个选项中,只有一项是符合题目要求的.
1.下列各数中,不是无理数的是( )
A. B. C. D.
2.下列图形中,既是轴对称图形又是中心对称图形的是( )
A. B.
C. D.
3.下列计算正确的是( )
A. B.
C. D.
4.以下列各组数为边,能组成三角形的是( )
A.1,2,3 B.4,3,5 C.15,7,7 D.6,8,18
5.澳门官方公布的最新数据显示,截至12月7日,2024年澳门累计入境旅客达3254.5万人次.澳门旅游业相关人士预测,全年入境旅客量有望突破3300万人次.3254.5万用科学记数法表示正确的是( )
A. B. C. D.
6.如图,,,,则的度数为( )
A. B. C. D.
7.如图是根据某早餐店1日至5日每天的用水量(单位:吨)绘制成的折线统计图.下列结论正确的是( )
A.平均数是5 B.众数是6 C.中位数是10 D.方差是8
8.一次函数的图象经过第二、三、四象限,则的取值范围是( )
A. B. C. D.
9.如图,在中,,,,是它的内切圆,用剪刀沿的切线剪一个,则的周长为( )
A.4 B.6 C.8 D.10
10.从,,,,中任取两数作为,,使抛物线的开口向上,对称轴在轴左侧的概率为( )
A. B. C. D.
二、填空题:本题共6小题,每小题3分,共18分.
11.分解因式: .
12.如图,平分,于点,点为射线上一动点,若,则的最小值为 .
13.不等式组的解集是 .
14.现有分别标有汉字“喜”“乐”“安”“宁”的四张卡片,它们除汉字外完全相同,若把四张卡片背面朝上,洗匀后放在桌面上,然后随机抽出一张,不放回,再随机抽出一张,两次抽出的卡片上的汉字恰好是“安”“宁”的概率是 .
15.在一定条件下,乐器中弦振动的频率f与弦长l成反比例关系,即(k为常数,).若某乐器的弦长l为米,振动频率f为200赫兹,则k的值为 .
16.勾股定理最早出现在商高的《周髀算经》:“勾广三,股修四,经隅五”,我国古代把直角三角形的直角边中较小者称为“勾”,另一长直角边称为“股”,把斜边称为“弦”.观察下列勾股数: ;…,这类勾股数的特点是:勾为奇数,弦与股相差为1.柏拉图研究了勾为偶数,弦与股相差为2的一类勾股数,如: …,若此类勾股数的勾为 ,则其弦是 .
三、解答题:本题共9小题,共72分,解答应写出文字说明、证明过程或演算步骤.
17.计算:
18.先化简,再求值:,其中,.
19.如图,在中,,分别以点和点为圆心,大于的长为半径作弧,两弧交于两点,连接直线,交于点,交于点.
(1)求证:直线垂直平分线段;
(2)若,连接,求的度数.
20.2025年1月23日,中共中央、国务院、中央军委给神舟十八号航天员叶光富颁发“二级航天功勋奖章”,授予李聪、李广苏“英雄航天员”荣誉称号并颁发“三级航天功勋奖章”.神舟十八号载人飞行任务的圆满成功,标志着中国航天事业在实现高水平科技自立自强的新征程中迈出关键一步.此次任务不仅提升我国综合国力和中华民族凝聚力,更进一步增强了全体中华儿女的民族自信心和自豪感,对激励全党全军全国各族人民团结奋进、砥砺前行具有重要意义.某校为了解本校学生对航天知识的了解情况,对八年级学生进行了航天知识测试,测试成绩全部合格,现随机选取了部分学生的成绩,整理并制作成了如下不完整的图表:
分数段 频数 频率
9
36
27
请根据上述统计图表,解答下列问题:
(1)表中___________,___________;
(2)请补全频数分布直方图;
(3)根据以上数据,如果80分以上(含80分)为优秀,若该学校八年级学生有900名,请你估算一下该学校八年级学生成绩优秀的人数.
21.如图,中,,点,在边上,且,.
(1)求证:;
(2)若,求证:是等边三角形.
22.2024年巴黎奥运会将于7月26日至8月11日举行,某经销店调查发现:与吉祥物相关的A,B两款纪念品深受青少年喜爱.已知购进3个A款比购进2个B款多用120元;购进1个A款和2个B款共用200元.
(1)分别求出A,B两款纪念品的进货单价;
(2)该商店决定购进这两款纪念品共70个,其总费用不超过5000元,则至少应购买B款纪念品多少个?
23.如图,在中,点为的中点,过点作,延长到点使,连接,.
(1)求证:四边形是矩形;
(2)若,求的长.
24.对凸四边形我们进行约定:若四边形对角线既不垂直也不相等,叫做“线无垂等”四边形;若四边形对角线垂直但不相等,叫做“线垂不等”四边形;若四边形对角线相等但不垂直,叫做“线等不垂”四边形;若四边形对角线既相等又垂直,叫做“线垂且等”四边形.
(1)判断下列说法是否正确(正确的请在题后括号内打“”,错误的打“”).
所有的平行四边形都是“线无垂等”四边形;( )
邻边相等的矩形是“线垂且等”四边形;( )
依次连接“线垂不等”四边形各边中点,构成的四边形是“线等不垂”四边形.( )
(2)如图,在中,,于点,分别为的中点.
四边形为“___________”四边形(从约定的四种类型中选一种填入);
若和的面积分别为和,求四边形的面积;
(3)如图,在中,已知是的弦,作,,分别交于点和点,连接.
求证:四边形是“线垂且等”四边形;
如图,已知且对角线与交于点,若的半径为,到的距离为,求弦的长度.
25.已知抛物线的对称轴为直线,抛物线与轴交于点A,B(点在点的左侧),点为抛物线的顶点.
(1)求点和点的坐标;
(2)若在上的最大值为9,求此时的面积;
(3)已知点为抛物线上点,之间的动点(点不与点,重合),点为线段上一定点(点不与点A,B重合),过点作轴的垂线,直线分别交射线,于点,若时,在点运动的过程中,的值始终为8,求点的坐标及的值.
《湖南省长沙市2025年中考数学考前练习卷(一)》参考答案
题号 1 2 3 4 5 6 7 8 9 10
答案 A C B B D C D C B B
1.A
【分析】本题考查了无理数即无限不循环小数,正确理解定义是解题的关键.
根据无理数的定义去甄别即可.
【详解】解:A、是有理数,故该项正确,符合题意;
B、是无理数,故该项错误,不符合题意;
C、是无理数,故该项错误,不符合题意;
D、是无理数,故该项错误,不符合题意;
故选A.
2.C
【分析】本题主要考查轴对称图形和中心对称图形;根据轴对称图形和中心对称图形的定义逐一判断即可.
【详解】解:A是轴对称图形,不是中心对称图形,不符合题意;
B是轴对称图形,不是中心对称图形,不符合题意;
C既是轴对称图形又是中心对称图形,符合题意;
D不是轴对称图形,是中心对称图形,不符合题意;
故选:C.
3.B
【分析】本题考查了整式的混合运算,掌握合并同类项,同底数幂的除法,单项式乘以多项式,完全平方公式是解题的关键.
根据合并同类项、同底数幂的除法、单项式乘以多项式、完全平方公式的运算法则,逐项计算判断即可.
【详解】解:A.,原选项计算错误,不符合题意;
B.,原选项计算正确,符合题意;
C.,原选项计算错误,不符合题意;
D.,原选项计算错误,不符合题意.
故选:B.
4.B
【分析】本题主要考查三角形的三边关系 ;根据三角形的两边之和大于第三边, 两边之差小于第三边判断即可.
【详解】解:A.,不符合题意;
B.,符合题意;
C.,不符合题意;
D.,不符合题意;
故选:B.
5.D
【分析】本题主要考查了科学记数法,科学记数法的表现形式为的形式,其中,n为整数,确定n的值时,要看把原数变成a时,小数点移动了多少位,n的绝对值与小数点移动的位数相同,当原数绝对值大于等于10时,n是正数,当原数绝对值小于1时n是负数;由此进行求解即可得到答案.
【详解】解:3254.5万用科学记数法表示,
故选:D.
6.C
【分析】本题考查平行线的性质,垂直的定义,熟练掌握平行线的性质是解题的关键.
根据垂直得到,即可求出,然后根据平行线的性质求出即可.
【详解】解:∵,
∴,
又∵,
∴,
又∵,
∴,
故选:C.
7.D
【分析】根据题目要求算出平均数、众数、中位数、方差,再作出选择即可.
【详解】解:A、平均数为,故选项错误,不符合题意;
B、众数为,,,,,故选项错误,不符合题意;
C、从小到大排列为,,,,,中位数是,故选项错误,不符合题意;
D、方差,故选项正确,符合题意;
故选∶D.
【点睛】本题考查平均数、众数、中位数、方差的算法,熟练掌握平均数、众数、中位数、方差的算法是解题的关键.
8.C
【分析】本题主要考查了一次函数的图象,根据一次函数的图象经过的象限得到,,求出m的取值范围即可.
【详解】解:∵一次函数的图象经过第二、三、四象限,
∴,
解得,
故选:C.
9.B
【分析】本题考查了三角形的内切圆与内心,勾股定理,切线的性质,解决本题的关键是掌握切线的性质.设的内切圆切三边于点,连接,由切线长定理可知,根据是的切线,可得,,根据勾股定理可得,得四边形是正方形,再求出内切圆的半径为,进而可得的周长.
【详解】解:如图,设的内切圆切三边于点、、,连接、、,
由切线长定理可知,,,
∵是的切线,
∴,,
∵,,,
∴,
∴,
则四边形是正方形,
∵是的内切圆,
∴内切圆的半径,
∴,
∴,
∴,
∴的周长为:.
故选:B.
10.B
【分析】本题考查了列表法与树状图法,二次函数的性质,概率公式,首先根据题意得到,,然后利用列表法即可列举出所有各种可能的情况,然后利用概率公式即可求解.
【详解】解:∵抛物线的开口向上,对称轴在y轴左侧,
∴,,
∴;
列表如下:
∴共有20种等可能结果,其中使抛物线的开口向上,对称轴在y轴左侧的有2种结果,
∴使抛物线的开口向上,对称轴在y轴左侧的概率为.
故选:B.
11.
【分析】本题考查了分解因式,掌握因式分解的方法是解题关键.提公因式分解因式即可.
【详解】解:,
故答案为:.
12.3
【分析】本题考查了角平分线的性质:角的平分线上的点到角的两边的距离相等.也考查了垂线段最短.过O点作于H点,如图,先根据角平分线的性质得到,然后根据垂线段最短解决问题.
【详解】解:过O点作于H点,如图,
平分,
,
∵点E为射线上一动点,
∴的最小值为的长,
即的最小值为3.
故答案为:3.
13.
【分析】本题考查解不等式组,解题的关键在于准确解出每个不等式,找到公共的解集.先解第一个不等式,再解第二个不等式,然后根据“同大取大,同小取小,大小小大中间找,大大小小找不到”这个规律求出不等式组的解集便可.
【详解】解:解不等式①,得,
解不等式②,得,
因此,原不等式组的解集为,
故答案为:.
14.
【分析】此题考查了用列表法或树状图法求概率,熟练掌握概率所求情况数与总情况数之比是解题关键.画树状图列出所有等可能结果,从中找到符合条件的结果数,再根据概率公式求解即可.
【详解】解:“喜”“乐”“安”“宁”的四张卡片分别用、、、表示,
画树状图如图所示:
由树状图可知,共有12种等可能的结果,其中两次抽出的卡片上的汉字恰好是“安”“宁”有2种,
两次抽出的卡片上的汉字恰好是“安”“宁”概率是,
故答案为:.
15.160
【分析】本题考查了待定系数法求反比例函数解析式,把,代入求解即可.
【详解】解:把,代入,得,
解得,
故答案为:160.
16.
【分析】根据规律可得,如果a,b,c是符合同样规律的一组勾股数,(m为偶数且),根据所给的二组数找规律可得结论.
【详解】根据规律可得,如果a,b,c是符合同样规律的一组勾股数, (m为偶数且 ),则另一条直角边 ,弦 .
则弦为,
故答案为:.
【点睛】此题主要考查了勾股数的定义,数字类的规律问题,得出规律是解题关键.
17.4
【分析】本题考查实数的运算,特殊角三角函数值,零指数幂,负整数指数幂,先计算负整数指数幂,特殊角的三角函数值,零指数幂,化简绝对值,再加减即可.
【详解】解:
.
18.,.
【分析】本题考查了多项式乘以多项式,完全平方公式,合并同类项,熟练掌握运算法则是解题的关键.
先通过多项式乘以多项式法则,完全平方公式进行化简,然后由合并同类项法则化成最简,再把,代入求值即可.
【详解】解:
,
当,时,
原式
.
19.(1)见解析
(2)
【分析】本题考查作图—复杂作图,线段的垂直平分线的性质.
(1)根据线段的垂直平分线的作法证明即可;
(2)由垂直平分线的性质得,进而得,即可求解.
【详解】(1)证明:连接,,,,
由作图可知,
∴M,N在线段的垂直平分线上,
∴直线垂直平分线段;
(2)解:∵直线垂直平分线段,点D是直线和的交点,即点D在直线上,
∴,
∵,
∴,
∴,
∵,
∴.
20.(1)
(2)见解析
(3)估计该学校八年级学生成绩优秀的人数为450人
【分析】本题主要考查了频数分布表,频数分布直方图,用样本估计总体,正确读懂统计图和统计图是解题的关键.
(1)用的频数除以其频率求出样本容量,进而求出a、b的值即可;
(2)根据(1)所求补全统计图即可;
(3)用900乘以样本中80分以上(含80分)的频率即可得到答案.
【详解】(1)解:∵样本容量为,
∴;
(2)解:补全频数分布直方图如图所示:
(3)解:(人),
答:估计该学校八年级学生成绩优秀的人数为450人.
21.(1)见解析
(2)见解析
【分析】本题考查了全等三角形的判定和性质,等边三角形的判定,三角形内角和定理.
(1)证明得,进而得,即可得出结论;
(2)先由等腰三角形的性质得,再由三角形内角和定理得,即可得出结论.
【详解】(1)证明:∵,,
∴,
∵,
∴,
在和中,
,
∴,
∴,
∴,
∴;
(2)解:∵,,
∴,
在和中,
∵,
∴,即,
∴是等边三角形.
22.(1)A款纪念品的进货单价为80元,则B款纪念品的进货单价为60元
(2)至少应购买B款纪念品30个
【分析】本题考查二元一次方程组的应用、一元一次不等式的应用,(1)设A款纪念品的进货单价为x元,则B款纪念品的进货单价为y元,根据题意列二元一次方程组求解即可;
(2)设购买B款纪念品a个,则购买A款纪念品个,根据题意列一元一次不等式求得a的取值范围,即可求解.
【详解】(1)解:设A款纪念品的进货单价为x元,则B款纪念品的进货单价为y元,
由题意得,,
解得,
答:A款纪念品的进货单价为80元,则B款纪念品的进货单价为60元.
(2)解:设购买B款纪念品a个,则购买A款纪念品个,
由题意得,,
解得,,
答:至少应购买B款纪念品30个.
23.(1)证明见解析
(2)
【分析】()利用平行四边形的性质可证四边形是平行四边形,进而由即可求证;
()由()可得,即得,,进而由得,利用勾股定理得,最后根据直角三角形的性质即可求解.
【详解】(1)证明:∵四边形是平行四边形,
∴,,
∴,
∵,
∴,
即,
∴,
∴四边形是平行四边形,
又∵,
∴,
∴四边形是矩形;
(2)解:由()可知,,,,
∵,,
∴,
∴,
∵,
∴,
∴,
在中,由勾股定理得,,
∵是的中点,,
∴.
【点睛】本题考查了平行四边形的判定和性质,矩形的判定和性质,勾股定理,直角三角形的性质,三角函数,掌握以上知识点是解题的关键.
24.(1);;
(2)线等不垂;;
(3)见解析;.
【分析】()根据题中定义即可判断;
()如图,连接,,交于点,由中位线定理得,,根据直角三角形斜边上的中线性质,,,由,则有,从而即可判断;
根据三角形中线的定义和面积和差即可求解;
()连接,,与相交于点,再根据“线垂且等”四边形的定义即可求证;
过点作于点,证明,则,即,再根据到的距离为,即,设,则,然后代入求出,再证明,则,故,最后用勾股定理即可求解.
【详解】(1)解:所有的平行四边形都是“线无垂等”四边形,此说法错误;
邻边相等的矩形是“线垂且等”四边形,此说法正确;
依次连接“线垂不等”四边形各边中点,构成的四边形是“线等不垂”四边形,此说法正确;
故答案为:,,;
(2)如图,连接,,交于点,
∵分别为的中点,
∴,,
∵,
∴,
∵分别为的中点,
∴,
∴,,
∵,
∴,
∴,
∴,
∴四边形为“线等不垂”四边形,
故答案为:线等不垂;
∵,,
∴,
∵分别为的中点,
∴,
∵,
∴,
∴;
(3)证明:如图,连接,,与相交于点,
∵,,
∴,
∴,,
∴,即,
∵,,
∴,
又∵,,
∴,
∴,
∴四边形是“线垂且等”四边形;
解:如图,∵,,
∴,
由知,,
∴,
过点作于点,
∴,
∵,,
∴,
∴,
∴,
∴,
∵到的距离为,即,
设,则,
∴,
解得或(舍去),
∴,,
∵,,
∴,
∵,
∴,
∴,
∴,
∴,
在中,,,
∴.
【点睛】此题考查了全等三角形的判定和性质、勾股定理、圆周角定理,相似三角形的判定与性质,中位线定理,直角三角形斜边上的中线性质,解一元二次方程、等腰直角三角形的判定和性质等知识,熟练掌握知识点的应用是解题的关键.
25.(1),
(2)或27
(3),
【分析】(1)首先根据对称轴得到,求出抛物线,然后令得到,然后求解即可;
(2)首先得到,,然后分两种情况讨论:当时和当时,然后分别根据二次函数的性质求解即可;
(3)设点,点,分别表示出直线和解析式,然后表示出,然后根据题意得到,进而求解即可.
【详解】(1)∵抛物线的对称轴为直线
∴,
∴,
∴抛物线,
令可得,
解得,,
∴,;
(2)由(1)得,
∵,
∴
当时,开口向上,
∴时,y取最大值,
∴,
解得,
∴
此时顶点
∴的面积为;
当时,开口向下,
∴时,y取最大值,
此时点,的面积为;
综上,的面积为或27.
(3)设点,点,
∵,
∴设直线的解析式为
∴
解得
∴直线的解析式;
同理直线的解析式为
当时,,
∴
∴
∵点P运动的过程中的值始终为定值8,即不受t的影响,
∴,
解得,
∴,
∴,
解得.
【点睛】此题考查了二次函数的图象和性质,二次函数和x轴交点问题以及线段问题,熟练掌握二次函数的图象与性质是解答本题的关键.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
同课章节目录
