江苏省南京市2025年中考数学考前练习卷(三)(含解析)
文档属性
| 名称 | 江苏省南京市2025年中考数学考前练习卷(三)(含解析) |  | |
| 格式 | docx | ||
| 文件大小 | 2.1MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 通用版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-05-10 09:41:14 | ||
图片预览



文档简介
中小学教育资源及组卷应用平台
江苏省南京市2025年中考数学考前练习卷(三)
注意事项:
1.全卷满分120分.考试时间为120分钟.考生答题全部答在答题卡上,答在本试卷上无效.
2.请认真核对监考教师在答题卡上所粘贴条形码的姓名、考试证号是否与本人相符合,再将自己的姓名、考试证号用0.5毫米黑色墨水签字笔填写在答题卡及本试卷上.
3.答选择题必须用2B铅笔将答题卡上对应的答案标号涂黑.如需改动,请用橡皮擦干净后,再选涂其他答案.答非选择题必须用0.5毫米黑色墨水签字笔写在答题卡上的指定位置,在其他位置答题一律无效.
4.作图必须用2B铅笔作答,并请加黑加粗,描写清楚.
一、选择题(本大题共6小题,每小题2分,共12分.在每小题所给出的四个选项中,恰有一项是符合题目要求的,请将正确选项前的字母代号填涂在答题卡相应位置上)
1.蛇年新春,五湖四海的游客竞相奔赴南京过大年.春节期间,秦淮区接待游客量超过500万人次,约占全市三分之一,旅游总收入突破50亿元,超全市四分之一,均创历史新高.将500万和50亿用科学记数法分别表示为( )
A., B., C., D.,
2.已知圆锥底面圆的半径为2,母线长为3,则该圆锥侧面展开图的面积是( )
A. B. C. D.
3.若式子在实数范围内有意义,则a,b的取值范围分别是( )
A., B., C., D.,
4.若代数式,,则M和N的大小关系是( )
A. B. C. D.与a的值有关
5.已知关于x的方程的两个不相等的实数根分别是p,q,那么的值是( )
A. B.0 C.1 D.2
6.将两组全等的正方形按如图所示的位置摆放.在两个涂色的三角形中,较大的和较小的面积的比是( )
A. B. C. D.
二、填空题(本大题共10小题,每小题2分,共20分.请把答案填写在答题卡相应位置上)
7.16的算术平方根是 .
8.计算:= .
9.化简= .
10.若,则的值为 .
11.若一元二次方程的两根为m,n,则的值为 .
12.若数据10,9,a,12,9的平均数是10,则这组数据的方差是
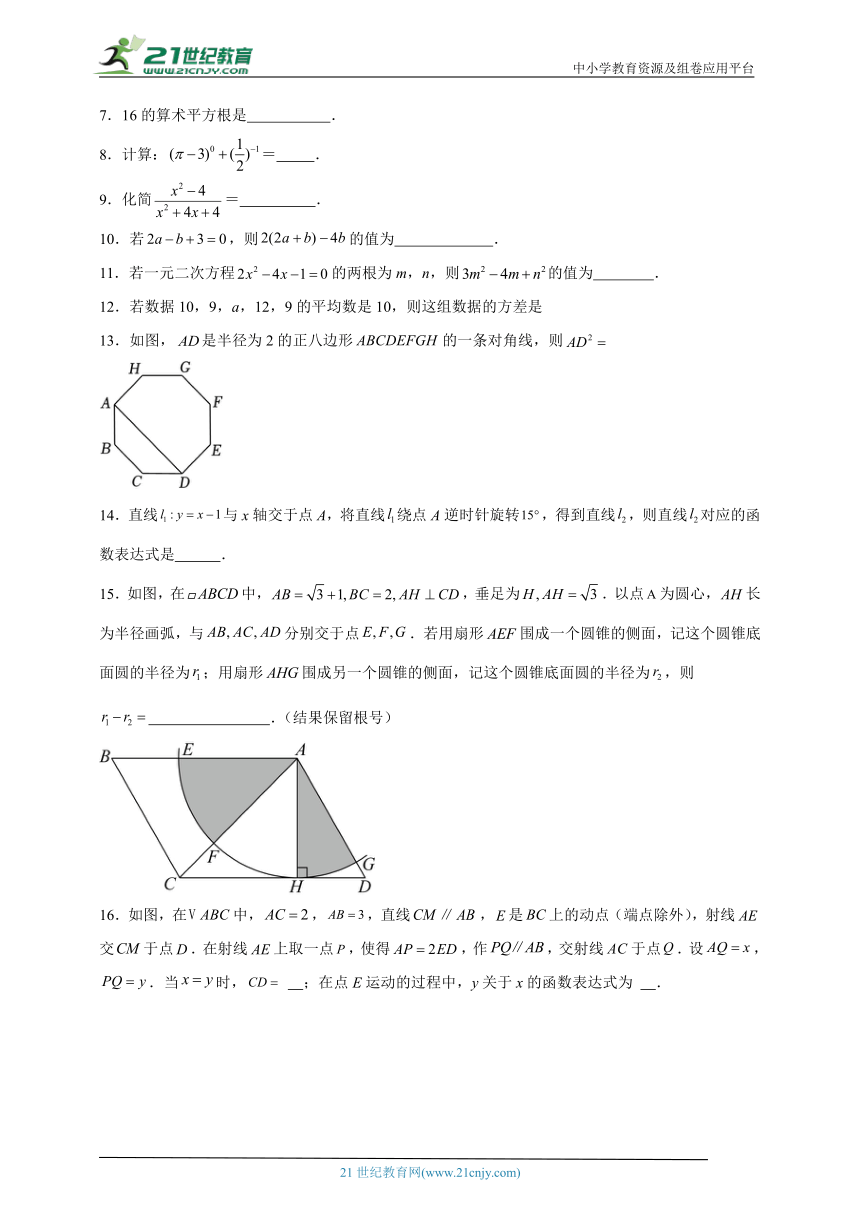
13.如图,是半径为2的正八边形的一条对角线,则
14.直线与x轴交于点A,将直线绕点A逆时针旋转,得到直线,则直线对应的函数表达式是 .
15.如图,在中,,垂足为.以点为圆心,长为半径画弧,与分别交于点.若用扇形围成一个圆锥的侧面,记这个圆锥底面圆的半径为;用扇形围成另一个圆锥的侧面,记这个圆锥底面圆的半径为,则 .(结果保留根号)
16.如图,在中,,,直线,是上的动点(端点除外),射线交于点.在射线上取一点,使得,作,交射线于点.设,.当时, ;在点E运动的过程中,y关于x的函数表达式为 .
三、解答题(本大题共11小题,共88分.请在答题卡指定区域内作答,解答时应写出文字说明、证明过程或演算步骤)
17.解不等式组并写出该不等式组的最大整数解.
18.计算:.
19.为了改善生态环境,防止水土流失,某村计划在荒坡上种树960棵,由于青年志愿者支援,实际每天种树的棵树是原计划的倍,结果提前4天完成任务,原计划每天种树多少棵?
20.如图,菱形的对角线,相交于点,是边的中点,连接,过点,作的垂线,垂足分别为,.
(1)求证:四边形是矩形;
(2)若,,求四边形的面积.
21.甲口袋中有2个红球、1个白球、乙口袋中有1个红球、1个白球,这些球除颜色外无其他差别.分别从每个口袋中随机摸出1个球,设摸出的2个球都是红球的概率为.
(1)求的值;
(2)在乙口袋中再放入个红球,若的值为,则的值为__________.
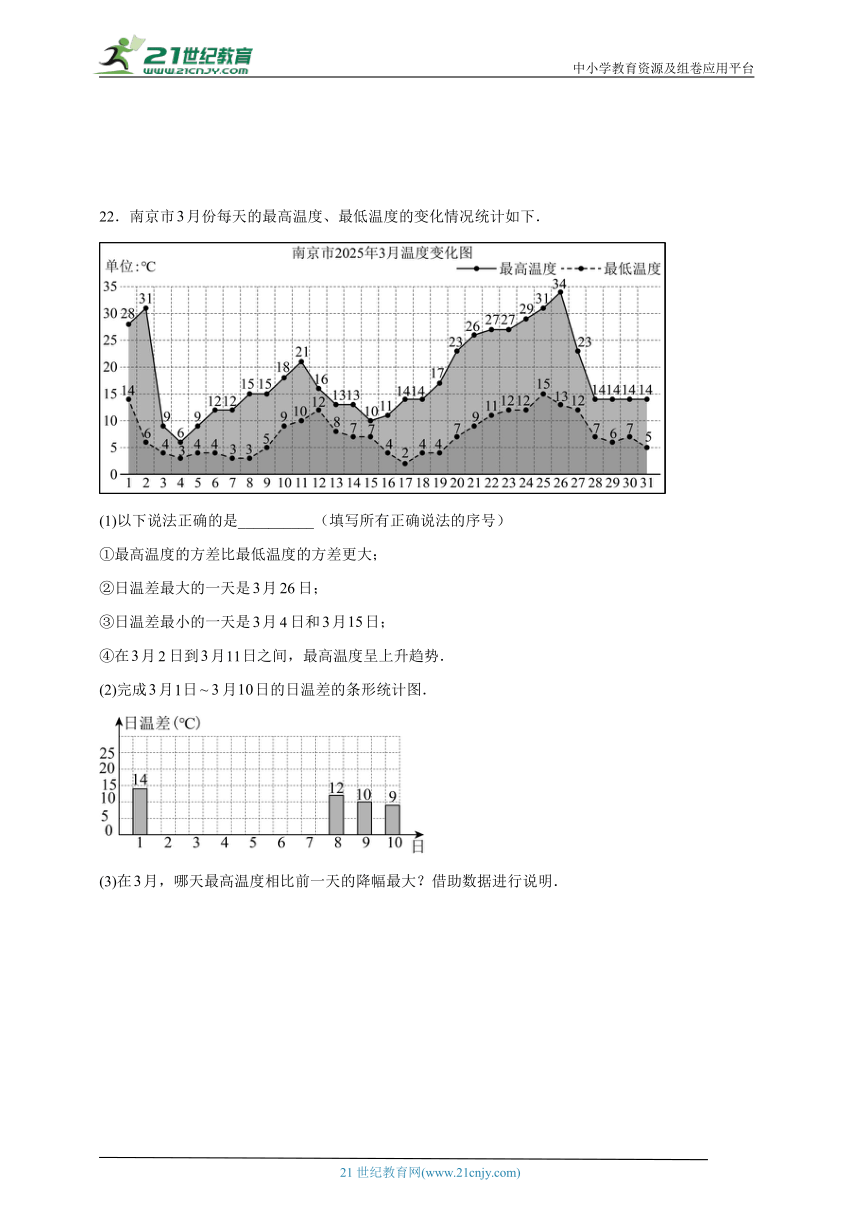
22.南京市月份每天的最高温度、最低温度的变化情况统计如下.
(1)以下说法正确的是__________(填写所有正确说法的序号)
①最高温度的方差比最低温度的方差更大;
②日温差最大的一天是月日;
③日温差最小的一天是月日和月日;
④在月日到月日之间,最高温度呈上升趋势.
(2)完成月日月日的日温差的条形统计图.
(3)在月,哪天最高温度相比前一天的降幅最大?借助数据进行说明.
23.如图,在中,,是的外接圆;是的直径,与交于点,在的延长线上取点,使平分.
(1)求证:是的切线;
(2)若,,求的长.
24.如图,小明乘高铁从南向北匀速行驶,速度为.小明在处通过窗口看到远处两棵树(记为和),此时在小明的北偏东方向,在小明的北偏东方向.后,小明到达处,此时和恰好都在自己的南偏东方向.求两棵树之间的距离.(参考数据:,.)
25.已知二次函数的图象为.
(1)用表示图象的顶点坐标;
(2)证明:当时,图象与轴有两个交点;
(3)记一次函数(是常数,,)的图象为线段,若图象与线段恰有一个公共点,直接写出的取值范围.
26.尺规作图:求作一个等腰三角形,使它分别满足以下要求:
()底边长为,底边上的高长为;
()腰上的高长为,底边上的高长为.
要求:保留作图的痕迹,写出必要的文字说明.
27.立竿见影.
如图①,在平地上竖立一根直竿,太阳每天东升西落,直竿在阳光下的影子随之变化.研究表明,南京地区的影端轨迹(直竿影子顶端的轨迹)在春分日、秋分日是正东西向的直线,在其它时候是双曲线的一支,日期与轨迹形状的对应情况如图②所示.在老师指导下,鼓楼区的几位同学在学校进行了如下探索.
(1)某一天甲同学在操场上观测到竿影顶端的3处标记点,位置如图①所示,则他的这次观测大约在__________季节.(填“春夏”或“秋冬”)
(2)月日,乙同学从到每隔标记一次影端的位置.
①当天的影端轨迹最接近图②中的哪条线?
②他选用了两处标记点确定出正东西方向,请指出他确定方向的方案和道理.
(3)如图③,丙同学在实验室中用灯光模拟出“在春分日,直竿的影端轨迹为正东西向的直线”,丁同学提出:在地平面上放置一个三棱柱形状的木斜坡,其下沿紧挨着竿底且指向北偏西方向(俯视图如图④所示),影端轨迹有何变化?
①在图④中用粗线画出落在坡面上的影端轨迹;
②已知到直线的距离为,斜坡坡角为,春分日正午时分太阳光线与地平面的夹角约为,此时影端落在斜坡上的处,求到地平面的距离(精确到).
(参考数据:,.)
《江苏省南京市2025年中考数学考前练习卷(三)》参考答案
题号 1 2 3 4 5 6
答案 C C B C A A
1.C
【分析】本题考查了科学记数法的表示方法,科学记数法的表现形式为的形式,其中为整数,确定的值时,要看把原数变成时,小数点移动了多少位,的绝对值与小数点移动的位数相同,当原数绝对值大于等于 10 时,是非负数,当原数绝对值小于 1 时,是负数,表示时关键是要正确确定的值以及的值.
【详解】解:用科学记数法可将数据500万表示为,
用科学记数法可将数据50亿表示为,
故选:C.
2.C
【分析】本题主要考查了圆锥的计算,熟知圆锥的侧面积公式是解题的关键.
根据圆锥的侧面积公式即可解决问题.
【详解】解:由题知,
因为圆锥底面圆的半径为2,母线长为3,
所以圆锥侧面展开图的面积是.
故选:C.
3.B
【分析】本题主要考查了二次根式、分式有意义的条件,掌握二次根式有意义的条件为被开方数大于等于零、分式有意义的条件为分母不等于零成为解题的关键.
直接根据二次根式、分式有意义的条件即可解答.
【详解】解:∵式子在实数范围内有意义,
∴,.
故选B.
4.C
【分析】此题考查了整式的加减,以及非负数的性质,把M与N代入中计算,判断差的正负即可得到结果.
【详解】解:∵,,
∴
,
∵,
∴,
∴.
故选:C.
5.A
【分析】本题考查一元二次方程根与系数的关系,熟练掌握一元二次方程根与系数的关系为,是解题的关键.根据题意得到,即可求解.
【详解】解:方程有两个不相等的实数根分别是p,q,
,,
当时,成立,此时,即,不符合题意,
,
又,
∴,
,
故选:A.
6.A
【分析】本题考查了等腰直角三角形的性质,勾股定理,面积,正方形的性质,根据题意可得,,是等腰直角三角形,,设,则,然后代入求解即可,掌握知识点的应用是解题的关键.
【详解】解:如图,根据题意可得,,是等腰直角三角形,,点到距离与点到距离相等,则,
∴四边形是菱形,
∴,
设,
∴根据勾股定理得,,
∴,
∴,
∴,
∴较大的和较小的面积的比是,
故选:.
7.4
【详解】解:∵
∴16的平方根为4和-4,
∴16的算术平方根为4,
故答案为:4
8.3
【分析】根据零指数幂和负指数幂的意义计算.
【详解】解:,
故答案为:3.
【点睛】本题考查了整数指数幂的运算,熟练掌握零指数幂和负指数幂的意义是解题关键.
9.
【分析】先把分子分母分解因式化为:再约分即可.
【详解】解:
故答案为:
【点睛】本题考查的是分式的约分,熟练的把分子分母分解因式,再约去公因式是解本题的关键.
10.
【分析】由,可得,根据,计算求解即可.
【详解】解:由,可得,
∴,
故答案为:.
【点睛】本题考查了代数式求值.解题的关键在于正确的运算.
11.6
【分析】本题考查了根与系数的关系及利用完全平方公式求解,若是一元二次方程的两根时,,熟练掌握一元二次方程根与系数的关系是解题关键.
根据根与系数的关系得,,再把变形为,然后利用整体代入的方法计算,再利用完全平方公式求解即可.
【详解】解:∵一元二次方程的两个根为,,
∴,
∴
故答案为:6.
12.1.2
【分析】先由平均数的公式计算出a的值,再根据方差的公式计算即可.
【详解】解:∵数据10,9,a,12,9的平均数是10,
∴(10+9+a+12+9)÷5=10,
解得:a=10,
∴这组数据的方差是15[(10 10) +(9 10) +(10 10) +(12 10) +(9 10) ]=1.2
故选B.
【点睛】本题考查方差和平均数,方差反映了一组数据的波动大小,方差越大,波动性越大,反之也成立.
13.
【分析】本题考查了正多边形与圆,勾股定理,熟练掌握勾股定理是解题的关键.
设正八边形的中心为O,连接,由正八边形,得到,求得,过D作于H,根据勾股定理即可得到结论.
【详解】解:设正八边形的中心为O,
连接AE,OD,
∵正八边形,
∴,
∵,
∴,
∴,
过D作于H,
∵,
∴,
∴,
∴,
∴,
故答案为:.
14.
【分析】根据题意可求得与坐标轴的交点A和点B,可得,结合旋转得到,则,求得,即得点C坐标,利用待定系数法即可求得直线的解析式.
【详解】解:依题意画出旋转前的函数图象和旋转后的函数图象,如图所示∶
设与y轴的交点为点B,
令,得;令,即,
∴, ,
∴,,
即
∵直线绕点A逆时针旋转,得到直线,
∴,,
∴,
则点,
设直线的解析式为,则
,解得,
那么,直线的解析式为,
故答案为:.
【点睛】本题主要考查一次函数与坐标轴的交点、直线的旋转、解直角三角形以及待定系数法求一次函数解析式,解题的关键是找到旋转后对应的直角边长.
15./
【分析】由,,,,,,,,求解,,证明,可得,再分别计算圆锥的底面半径即可.
【详解】解:∵在中,,,
∴,,
∵,,
∴,,
∴,
∵,
∴,
∴,,
解得:,,
∴;
故答案为:
【点睛】本题考查的是平行四边形的性质,勾股定理的应用,锐角三角函数的应用,扇形的弧长的计算,圆锥的底面半径的计算,熟记圆锥的侧面展开图的扇形弧长等于底面圆的周长是解本题的关键.
16. 2
【分析】本题考查了相似三角形的判定和性质,解题的关键是掌握相似三角形对应边成比例.易得,则,得出,代入数据即可求出;根据,得出,设,则,通过证明,得出,则,进而得出,结合,可得,代入各个数据,即可得出 关于的函数表达式.
【详解】解:∵,,
∴,
∴,
∴,即,
∵,
∴;
∵,
∴,即,
整理得:,
设,
∵,
∴,
∵,
∴,
∴,即,
整理得:,
∴,
∵,
∴,即,
整理得:,
故答案为:2;.
17.,最大整数解为
【分析】本题考查了解一元一次不等式组,一元一次不等式组的整数解,先求出不等式组的解集,进而根据不等式组的解集即可求解,正确求出不等式组的解集是解题的关键.
【详解】解:,
由①得,,
由②得,,
∴不等式组的解集为,
∴不等式组的最大整数解为.
18.
【分析】本题考查分式的混合运算,先将括号内分式通分,分子因式分解,变分式除法为乘法,最后约分化简即可.
【详解】解:
.
19.原计划每天种树60棵.
【详解】试题分析:设原计划每天种树x棵,则实际每天种树为x棵,根据实际比原计划提前4天完成任务,列方程求解.
试题解析:设原计划每天种树x棵,则实际每天种树为x棵,
由题意得,,
解得:x=60,
经检验,x=60是原方程的解,且符合题意.
答:原计划每天种树60棵.
考点:分式方程的应用.
20.(1)见解析
(2)6
【分析】本题考查菱形的性质,矩形的判定和性质,三角形中位线的性质,勾股定理,能够综合应用上述知识点是解题的关键.
(1)由菱形的性质可得,进而可得是的中位线,推出,依次证明四边形是平行四边形、矩形即可;
(2)菱形的性质及勾股定理求出菱形的边长,设,利用勾股定理解和求出,进而可得,最后根据矩形面积公式即可求解.
【详解】(1)证明:菱形的对角线,相交于点,
,,
是边的中点,
,
是的中位线,
,,
,,
,,
四边形是平行四边形,
又,
四边形是矩形;
(2)解:菱形中,,
,,,
,
,
设,则,
在中,,
在中,,
由(1)知是矩形,
解得,即
,
矩形的面积为:.
21.(1)
(2)2
【分析】本题主要考查了运用列表法概率的应用,掌握运用列表法概率成为解题的关键.
(1)先根据题意列表求得所有等可能结果数以及满足题意的结果数,然后运用概率公式求解即可;
(2)先根据题意列表求得所有等可能结果数以及满足题意的结果数,然后运用概率公式列方程求解即可.
【详解】(1)解:根据题意列表如下:
甲乙 红 红 白
红 红,红 红,红 红,白
白 白,红 白,红 白,白
由列表可知:共有6种等可能结果,其中摸出的2个球都是红球的结果数为2,
所以摸出的2个球都是红球的概率为.
(2)解:列表如下:
甲乙 红 红 白
红 红,红 红,红 红,白
白 白,红 白,红 白,白
红1 红1,红 红1,红 红1,白
… … … …
红a 红a,红 红a ,红 红a,白
由列表可知:共有种等可能结果,其中摸出的2个球都是红球的结果数为,
所以摸出的2个球都是红球的概率为,
∴,
解得,
经检验是原方程的解,且符合题意,
∴,
故答案为:2.
22.(1)①③
(2)补图见解析
(3)月日最高温度相比前一天的降幅最大,理由见解析
【分析】()根据折线统计图逐项判断即可求解;
()分别求出月日月日的温差,再补全条形统计图即可;
()根据折线统计图解答即可;
本题考查了折线统计图,看懂统计图是解题的关键.
【详解】(1)解:由图可知,最高温度的波动较最低温度的波动大,
∴最高温度的方差比最低温度的方差更大,故①正确;
日温差最大的一天是月日,故②错误;
日温差最小的一天是月日和月日,故③正确;
在月日到月日之间,最高温度先下降,再上升,故④错误;
∴说法正确的是①③,
故答案为:①③;
(2)解:补图如下:
(3)解:月日最高温度相比前一天的降幅最大,理由如下:由图可知,月日的最高温度为,月日的最高温度为,降温,降幅最大.
23.(1)证明见解析
(2)
【分析】()由圆周角定理可得,进而可得,即得,即可求证;
()由已知得,再由得,代入计算即可求解.
【详解】(1)证明:∵是的直径,
∴,
∴,
∵,
∴,
∵平分,
∴,
∵,
∴,
∴,
∴,
∴,
即,
∴是的切线;
(2)解:∵,,
∴,
由()知,,,
∴,
即,
又∵,
∴,
∴,
即,
解得.
【点睛】本题考查了圆周角定理,等腰三角形的性质,切线的判定,相似三角形的判定和性质,掌握以上知识点是解题的关键.
24.100m
【分析】本题考查了解直角三角形的应用,勾股定理,解题的关键是正确构造直角三角形.
过点分别作,,垂足为点,先求出,解,可设,由勾股定理得,确定为等腰直角三角形,则,由,求出,则即可求解,解 设,,解可得,由,求出,即可求解,最后由即可求解.
【详解】解:过点分别作,,垂足为点,
由题意得,,
∵在中,,
∴设,
∴,
∵,,
∴为等腰直角三角形,
∴,
∴,
解得:,
∴,
∵在中,,
∴设,
同理可得:,
∵在中,,
∴,
∴,
解得:,
∴,
∴,
答:两棵树之间的距离为.
25.(1);
(2)见解析;
(3)当或或时,图象与线段恰有一个公共点.
【分析】本题主要考查了一次函数的图象与性质、二次函数的图象与性质,解决本题的关键是根据根据一次函数与二次函数的性质确定函数图象的交点.
把二次函数的解析式化成顶点坐标式,即可得到图象的顶点坐标为;
当时,可得:,利用一元二次方程根与系数的关系可证当时,图象与轴有两个交点;
根据一次函数的解析式可知点的坐标为,点的坐标为,由可知,,所以本题要分当时,当时,当时,三种情况讨论.
【详解】(1)解:整理,
可得:,
图象的顶点坐标为;
(2)解:当时,
可得:,
,
整理得:,
当时,,
方程有两个不相等的实数根,
图象与轴有两个交点;
(3)解:当时,,
当时,,
设点的坐标为,点的坐标为,
由可知,,
即时,图象开口向上并且与轴有一个交点,
如下图所示,
此时,,
图象与轴交点的坐标是,
点恰好在图象上,
当时,点的坐标为,
线段恰好与图象有一个交点;
如下图所示,
当时,,
图象开口向上并且与轴没有交点,
如果线段恰好与图象有一个交点,
则点在轴上方,
,即,
当时,,
线段恰好与图象有一个交点,
,
解得:;
如下图所示,
当时,
若,则有,
解得:或,
即当时,图象过点,
即图象与线段有一个交点;
综上所述,当或或时,图象与线段恰有一个公共点.
26.()画图见解析;()画图见解析
【分析】()在射线上截取线段,作线段的垂直平分线,垂足为点,并截取,连接,则即为所求;
()在直线上取点,过点作且使得,以点为圆心,为半径画圆,再以为直径画圆,两圆相交于点,连接并延长,分别交直线于点,连接,过点作于,由是直径可得,即得,即得到,进而由相似三角形的性质可得,故即为所求;
本题考查了作垂线,圆周角定理,相似三角形的判定和性质等,掌握基本作图技能是解题的关键.
【详解】解:()如图所示,即为所求;
()如图所示,即为所求.
27.(1)秋冬
(2)①;②见解析
(3)①见解析;②
【分析】本题考查了反比例函数的应用、解直角三角形的应用、几何体的俯视图,理解题意是解题的关键.
(1)根据题意,结合图①和图②即可得出答案;
(2)①根据月日在春分日和夏至日之间,结合图②即可得出答案;②观察图②可知双曲线为轴对称图形,对称轴为过点的正南北向的直线,故选择相距正午等时间的两处标记点,即可解答;
(3)①由题意得,直竿的影端轨迹为正东西向的直线,则影端轨迹的俯视图也是正东西向的直线,据此即可在图④中画出落在坡面上的影端轨迹;②设点到直线的垂足为点,则,由影端轨迹可得,三点共线,作于点,由题意得,,再利用解直角三角形的知识即可求解.
【详解】(1)解:由图①可知,竿影顶端的标记点在和标记点的东北方向,
结合图②可知,他的这次观测大约在秋冬季节.
故答案为:秋冬.
(2)解:①月日在春分日和夏至日之间,
结合图②可知,当天的影端轨迹最接近图②中的;
②方案:选用相距正午等时间(如上午和下午)的两处标记点,
道理:由图②可知,双曲线是轴对称图形,对称轴为过点的正南北向的直线;选用相距正午等时间的两处标记点,则两处标记点关于双曲线的对称轴对称,连接两处标记点即可确定出正东西方向.
(3)解:①如图所示,落在坡面上的影端轨迹即为所求:
②设点到直线的垂足为点,则,
由影端轨迹可得,三点共线,
如图,作于点,则,
由题意得,,,
在中,,
,
设,则,
在中,,
,
,
,即,
解得:,
答:到地平面的距离为.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
江苏省南京市2025年中考数学考前练习卷(三)
注意事项:
1.全卷满分120分.考试时间为120分钟.考生答题全部答在答题卡上,答在本试卷上无效.
2.请认真核对监考教师在答题卡上所粘贴条形码的姓名、考试证号是否与本人相符合,再将自己的姓名、考试证号用0.5毫米黑色墨水签字笔填写在答题卡及本试卷上.
3.答选择题必须用2B铅笔将答题卡上对应的答案标号涂黑.如需改动,请用橡皮擦干净后,再选涂其他答案.答非选择题必须用0.5毫米黑色墨水签字笔写在答题卡上的指定位置,在其他位置答题一律无效.
4.作图必须用2B铅笔作答,并请加黑加粗,描写清楚.
一、选择题(本大题共6小题,每小题2分,共12分.在每小题所给出的四个选项中,恰有一项是符合题目要求的,请将正确选项前的字母代号填涂在答题卡相应位置上)
1.蛇年新春,五湖四海的游客竞相奔赴南京过大年.春节期间,秦淮区接待游客量超过500万人次,约占全市三分之一,旅游总收入突破50亿元,超全市四分之一,均创历史新高.将500万和50亿用科学记数法分别表示为( )
A., B., C., D.,
2.已知圆锥底面圆的半径为2,母线长为3,则该圆锥侧面展开图的面积是( )
A. B. C. D.
3.若式子在实数范围内有意义,则a,b的取值范围分别是( )
A., B., C., D.,
4.若代数式,,则M和N的大小关系是( )
A. B. C. D.与a的值有关
5.已知关于x的方程的两个不相等的实数根分别是p,q,那么的值是( )
A. B.0 C.1 D.2
6.将两组全等的正方形按如图所示的位置摆放.在两个涂色的三角形中,较大的和较小的面积的比是( )
A. B. C. D.
二、填空题(本大题共10小题,每小题2分,共20分.请把答案填写在答题卡相应位置上)
7.16的算术平方根是 .
8.计算:= .
9.化简= .
10.若,则的值为 .
11.若一元二次方程的两根为m,n,则的值为 .
12.若数据10,9,a,12,9的平均数是10,则这组数据的方差是
13.如图,是半径为2的正八边形的一条对角线,则
14.直线与x轴交于点A,将直线绕点A逆时针旋转,得到直线,则直线对应的函数表达式是 .
15.如图,在中,,垂足为.以点为圆心,长为半径画弧,与分别交于点.若用扇形围成一个圆锥的侧面,记这个圆锥底面圆的半径为;用扇形围成另一个圆锥的侧面,记这个圆锥底面圆的半径为,则 .(结果保留根号)
16.如图,在中,,,直线,是上的动点(端点除外),射线交于点.在射线上取一点,使得,作,交射线于点.设,.当时, ;在点E运动的过程中,y关于x的函数表达式为 .
三、解答题(本大题共11小题,共88分.请在答题卡指定区域内作答,解答时应写出文字说明、证明过程或演算步骤)
17.解不等式组并写出该不等式组的最大整数解.
18.计算:.
19.为了改善生态环境,防止水土流失,某村计划在荒坡上种树960棵,由于青年志愿者支援,实际每天种树的棵树是原计划的倍,结果提前4天完成任务,原计划每天种树多少棵?
20.如图,菱形的对角线,相交于点,是边的中点,连接,过点,作的垂线,垂足分别为,.
(1)求证:四边形是矩形;
(2)若,,求四边形的面积.
21.甲口袋中有2个红球、1个白球、乙口袋中有1个红球、1个白球,这些球除颜色外无其他差别.分别从每个口袋中随机摸出1个球,设摸出的2个球都是红球的概率为.
(1)求的值;
(2)在乙口袋中再放入个红球,若的值为,则的值为__________.
22.南京市月份每天的最高温度、最低温度的变化情况统计如下.
(1)以下说法正确的是__________(填写所有正确说法的序号)
①最高温度的方差比最低温度的方差更大;
②日温差最大的一天是月日;
③日温差最小的一天是月日和月日;
④在月日到月日之间,最高温度呈上升趋势.
(2)完成月日月日的日温差的条形统计图.
(3)在月,哪天最高温度相比前一天的降幅最大?借助数据进行说明.
23.如图,在中,,是的外接圆;是的直径,与交于点,在的延长线上取点,使平分.
(1)求证:是的切线;
(2)若,,求的长.
24.如图,小明乘高铁从南向北匀速行驶,速度为.小明在处通过窗口看到远处两棵树(记为和),此时在小明的北偏东方向,在小明的北偏东方向.后,小明到达处,此时和恰好都在自己的南偏东方向.求两棵树之间的距离.(参考数据:,.)
25.已知二次函数的图象为.
(1)用表示图象的顶点坐标;
(2)证明:当时,图象与轴有两个交点;
(3)记一次函数(是常数,,)的图象为线段,若图象与线段恰有一个公共点,直接写出的取值范围.
26.尺规作图:求作一个等腰三角形,使它分别满足以下要求:
()底边长为,底边上的高长为;
()腰上的高长为,底边上的高长为.
要求:保留作图的痕迹,写出必要的文字说明.
27.立竿见影.
如图①,在平地上竖立一根直竿,太阳每天东升西落,直竿在阳光下的影子随之变化.研究表明,南京地区的影端轨迹(直竿影子顶端的轨迹)在春分日、秋分日是正东西向的直线,在其它时候是双曲线的一支,日期与轨迹形状的对应情况如图②所示.在老师指导下,鼓楼区的几位同学在学校进行了如下探索.
(1)某一天甲同学在操场上观测到竿影顶端的3处标记点,位置如图①所示,则他的这次观测大约在__________季节.(填“春夏”或“秋冬”)
(2)月日,乙同学从到每隔标记一次影端的位置.
①当天的影端轨迹最接近图②中的哪条线?
②他选用了两处标记点确定出正东西方向,请指出他确定方向的方案和道理.
(3)如图③,丙同学在实验室中用灯光模拟出“在春分日,直竿的影端轨迹为正东西向的直线”,丁同学提出:在地平面上放置一个三棱柱形状的木斜坡,其下沿紧挨着竿底且指向北偏西方向(俯视图如图④所示),影端轨迹有何变化?
①在图④中用粗线画出落在坡面上的影端轨迹;
②已知到直线的距离为,斜坡坡角为,春分日正午时分太阳光线与地平面的夹角约为,此时影端落在斜坡上的处,求到地平面的距离(精确到).
(参考数据:,.)
《江苏省南京市2025年中考数学考前练习卷(三)》参考答案
题号 1 2 3 4 5 6
答案 C C B C A A
1.C
【分析】本题考查了科学记数法的表示方法,科学记数法的表现形式为的形式,其中为整数,确定的值时,要看把原数变成时,小数点移动了多少位,的绝对值与小数点移动的位数相同,当原数绝对值大于等于 10 时,是非负数,当原数绝对值小于 1 时,是负数,表示时关键是要正确确定的值以及的值.
【详解】解:用科学记数法可将数据500万表示为,
用科学记数法可将数据50亿表示为,
故选:C.
2.C
【分析】本题主要考查了圆锥的计算,熟知圆锥的侧面积公式是解题的关键.
根据圆锥的侧面积公式即可解决问题.
【详解】解:由题知,
因为圆锥底面圆的半径为2,母线长为3,
所以圆锥侧面展开图的面积是.
故选:C.
3.B
【分析】本题主要考查了二次根式、分式有意义的条件,掌握二次根式有意义的条件为被开方数大于等于零、分式有意义的条件为分母不等于零成为解题的关键.
直接根据二次根式、分式有意义的条件即可解答.
【详解】解:∵式子在实数范围内有意义,
∴,.
故选B.
4.C
【分析】此题考查了整式的加减,以及非负数的性质,把M与N代入中计算,判断差的正负即可得到结果.
【详解】解:∵,,
∴
,
∵,
∴,
∴.
故选:C.
5.A
【分析】本题考查一元二次方程根与系数的关系,熟练掌握一元二次方程根与系数的关系为,是解题的关键.根据题意得到,即可求解.
【详解】解:方程有两个不相等的实数根分别是p,q,
,,
当时,成立,此时,即,不符合题意,
,
又,
∴,
,
故选:A.
6.A
【分析】本题考查了等腰直角三角形的性质,勾股定理,面积,正方形的性质,根据题意可得,,是等腰直角三角形,,设,则,然后代入求解即可,掌握知识点的应用是解题的关键.
【详解】解:如图,根据题意可得,,是等腰直角三角形,,点到距离与点到距离相等,则,
∴四边形是菱形,
∴,
设,
∴根据勾股定理得,,
∴,
∴,
∴,
∴较大的和较小的面积的比是,
故选:.
7.4
【详解】解:∵
∴16的平方根为4和-4,
∴16的算术平方根为4,
故答案为:4
8.3
【分析】根据零指数幂和负指数幂的意义计算.
【详解】解:,
故答案为:3.
【点睛】本题考查了整数指数幂的运算,熟练掌握零指数幂和负指数幂的意义是解题关键.
9.
【分析】先把分子分母分解因式化为:再约分即可.
【详解】解:
故答案为:
【点睛】本题考查的是分式的约分,熟练的把分子分母分解因式,再约去公因式是解本题的关键.
10.
【分析】由,可得,根据,计算求解即可.
【详解】解:由,可得,
∴,
故答案为:.
【点睛】本题考查了代数式求值.解题的关键在于正确的运算.
11.6
【分析】本题考查了根与系数的关系及利用完全平方公式求解,若是一元二次方程的两根时,,熟练掌握一元二次方程根与系数的关系是解题关键.
根据根与系数的关系得,,再把变形为,然后利用整体代入的方法计算,再利用完全平方公式求解即可.
【详解】解:∵一元二次方程的两个根为,,
∴,
∴
故答案为:6.
12.1.2
【分析】先由平均数的公式计算出a的值,再根据方差的公式计算即可.
【详解】解:∵数据10,9,a,12,9的平均数是10,
∴(10+9+a+12+9)÷5=10,
解得:a=10,
∴这组数据的方差是15[(10 10) +(9 10) +(10 10) +(12 10) +(9 10) ]=1.2
故选B.
【点睛】本题考查方差和平均数,方差反映了一组数据的波动大小,方差越大,波动性越大,反之也成立.
13.
【分析】本题考查了正多边形与圆,勾股定理,熟练掌握勾股定理是解题的关键.
设正八边形的中心为O,连接,由正八边形,得到,求得,过D作于H,根据勾股定理即可得到结论.
【详解】解:设正八边形的中心为O,
连接AE,OD,
∵正八边形,
∴,
∵,
∴,
∴,
过D作于H,
∵,
∴,
∴,
∴,
∴,
故答案为:.
14.
【分析】根据题意可求得与坐标轴的交点A和点B,可得,结合旋转得到,则,求得,即得点C坐标,利用待定系数法即可求得直线的解析式.
【详解】解:依题意画出旋转前的函数图象和旋转后的函数图象,如图所示∶
设与y轴的交点为点B,
令,得;令,即,
∴, ,
∴,,
即
∵直线绕点A逆时针旋转,得到直线,
∴,,
∴,
则点,
设直线的解析式为,则
,解得,
那么,直线的解析式为,
故答案为:.
【点睛】本题主要考查一次函数与坐标轴的交点、直线的旋转、解直角三角形以及待定系数法求一次函数解析式,解题的关键是找到旋转后对应的直角边长.
15./
【分析】由,,,,,,,,求解,,证明,可得,再分别计算圆锥的底面半径即可.
【详解】解:∵在中,,,
∴,,
∵,,
∴,,
∴,
∵,
∴,
∴,,
解得:,,
∴;
故答案为:
【点睛】本题考查的是平行四边形的性质,勾股定理的应用,锐角三角函数的应用,扇形的弧长的计算,圆锥的底面半径的计算,熟记圆锥的侧面展开图的扇形弧长等于底面圆的周长是解本题的关键.
16. 2
【分析】本题考查了相似三角形的判定和性质,解题的关键是掌握相似三角形对应边成比例.易得,则,得出,代入数据即可求出;根据,得出,设,则,通过证明,得出,则,进而得出,结合,可得,代入各个数据,即可得出 关于的函数表达式.
【详解】解:∵,,
∴,
∴,
∴,即,
∵,
∴;
∵,
∴,即,
整理得:,
设,
∵,
∴,
∵,
∴,
∴,即,
整理得:,
∴,
∵,
∴,即,
整理得:,
故答案为:2;.
17.,最大整数解为
【分析】本题考查了解一元一次不等式组,一元一次不等式组的整数解,先求出不等式组的解集,进而根据不等式组的解集即可求解,正确求出不等式组的解集是解题的关键.
【详解】解:,
由①得,,
由②得,,
∴不等式组的解集为,
∴不等式组的最大整数解为.
18.
【分析】本题考查分式的混合运算,先将括号内分式通分,分子因式分解,变分式除法为乘法,最后约分化简即可.
【详解】解:
.
19.原计划每天种树60棵.
【详解】试题分析:设原计划每天种树x棵,则实际每天种树为x棵,根据实际比原计划提前4天完成任务,列方程求解.
试题解析:设原计划每天种树x棵,则实际每天种树为x棵,
由题意得,,
解得:x=60,
经检验,x=60是原方程的解,且符合题意.
答:原计划每天种树60棵.
考点:分式方程的应用.
20.(1)见解析
(2)6
【分析】本题考查菱形的性质,矩形的判定和性质,三角形中位线的性质,勾股定理,能够综合应用上述知识点是解题的关键.
(1)由菱形的性质可得,进而可得是的中位线,推出,依次证明四边形是平行四边形、矩形即可;
(2)菱形的性质及勾股定理求出菱形的边长,设,利用勾股定理解和求出,进而可得,最后根据矩形面积公式即可求解.
【详解】(1)证明:菱形的对角线,相交于点,
,,
是边的中点,
,
是的中位线,
,,
,,
,,
四边形是平行四边形,
又,
四边形是矩形;
(2)解:菱形中,,
,,,
,
,
设,则,
在中,,
在中,,
由(1)知是矩形,
解得,即
,
矩形的面积为:.
21.(1)
(2)2
【分析】本题主要考查了运用列表法概率的应用,掌握运用列表法概率成为解题的关键.
(1)先根据题意列表求得所有等可能结果数以及满足题意的结果数,然后运用概率公式求解即可;
(2)先根据题意列表求得所有等可能结果数以及满足题意的结果数,然后运用概率公式列方程求解即可.
【详解】(1)解:根据题意列表如下:
甲乙 红 红 白
红 红,红 红,红 红,白
白 白,红 白,红 白,白
由列表可知:共有6种等可能结果,其中摸出的2个球都是红球的结果数为2,
所以摸出的2个球都是红球的概率为.
(2)解:列表如下:
甲乙 红 红 白
红 红,红 红,红 红,白
白 白,红 白,红 白,白
红1 红1,红 红1,红 红1,白
… … … …
红a 红a,红 红a ,红 红a,白
由列表可知:共有种等可能结果,其中摸出的2个球都是红球的结果数为,
所以摸出的2个球都是红球的概率为,
∴,
解得,
经检验是原方程的解,且符合题意,
∴,
故答案为:2.
22.(1)①③
(2)补图见解析
(3)月日最高温度相比前一天的降幅最大,理由见解析
【分析】()根据折线统计图逐项判断即可求解;
()分别求出月日月日的温差,再补全条形统计图即可;
()根据折线统计图解答即可;
本题考查了折线统计图,看懂统计图是解题的关键.
【详解】(1)解:由图可知,最高温度的波动较最低温度的波动大,
∴最高温度的方差比最低温度的方差更大,故①正确;
日温差最大的一天是月日,故②错误;
日温差最小的一天是月日和月日,故③正确;
在月日到月日之间,最高温度先下降,再上升,故④错误;
∴说法正确的是①③,
故答案为:①③;
(2)解:补图如下:
(3)解:月日最高温度相比前一天的降幅最大,理由如下:由图可知,月日的最高温度为,月日的最高温度为,降温,降幅最大.
23.(1)证明见解析
(2)
【分析】()由圆周角定理可得,进而可得,即得,即可求证;
()由已知得,再由得,代入计算即可求解.
【详解】(1)证明:∵是的直径,
∴,
∴,
∵,
∴,
∵平分,
∴,
∵,
∴,
∴,
∴,
∴,
即,
∴是的切线;
(2)解:∵,,
∴,
由()知,,,
∴,
即,
又∵,
∴,
∴,
即,
解得.
【点睛】本题考查了圆周角定理,等腰三角形的性质,切线的判定,相似三角形的判定和性质,掌握以上知识点是解题的关键.
24.100m
【分析】本题考查了解直角三角形的应用,勾股定理,解题的关键是正确构造直角三角形.
过点分别作,,垂足为点,先求出,解,可设,由勾股定理得,确定为等腰直角三角形,则,由,求出,则即可求解,解 设,,解可得,由,求出,即可求解,最后由即可求解.
【详解】解:过点分别作,,垂足为点,
由题意得,,
∵在中,,
∴设,
∴,
∵,,
∴为等腰直角三角形,
∴,
∴,
解得:,
∴,
∵在中,,
∴设,
同理可得:,
∵在中,,
∴,
∴,
解得:,
∴,
∴,
答:两棵树之间的距离为.
25.(1);
(2)见解析;
(3)当或或时,图象与线段恰有一个公共点.
【分析】本题主要考查了一次函数的图象与性质、二次函数的图象与性质,解决本题的关键是根据根据一次函数与二次函数的性质确定函数图象的交点.
把二次函数的解析式化成顶点坐标式,即可得到图象的顶点坐标为;
当时,可得:,利用一元二次方程根与系数的关系可证当时,图象与轴有两个交点;
根据一次函数的解析式可知点的坐标为,点的坐标为,由可知,,所以本题要分当时,当时,当时,三种情况讨论.
【详解】(1)解:整理,
可得:,
图象的顶点坐标为;
(2)解:当时,
可得:,
,
整理得:,
当时,,
方程有两个不相等的实数根,
图象与轴有两个交点;
(3)解:当时,,
当时,,
设点的坐标为,点的坐标为,
由可知,,
即时,图象开口向上并且与轴有一个交点,
如下图所示,
此时,,
图象与轴交点的坐标是,
点恰好在图象上,
当时,点的坐标为,
线段恰好与图象有一个交点;
如下图所示,
当时,,
图象开口向上并且与轴没有交点,
如果线段恰好与图象有一个交点,
则点在轴上方,
,即,
当时,,
线段恰好与图象有一个交点,
,
解得:;
如下图所示,
当时,
若,则有,
解得:或,
即当时,图象过点,
即图象与线段有一个交点;
综上所述,当或或时,图象与线段恰有一个公共点.
26.()画图见解析;()画图见解析
【分析】()在射线上截取线段,作线段的垂直平分线,垂足为点,并截取,连接,则即为所求;
()在直线上取点,过点作且使得,以点为圆心,为半径画圆,再以为直径画圆,两圆相交于点,连接并延长,分别交直线于点,连接,过点作于,由是直径可得,即得,即得到,进而由相似三角形的性质可得,故即为所求;
本题考查了作垂线,圆周角定理,相似三角形的判定和性质等,掌握基本作图技能是解题的关键.
【详解】解:()如图所示,即为所求;
()如图所示,即为所求.
27.(1)秋冬
(2)①;②见解析
(3)①见解析;②
【分析】本题考查了反比例函数的应用、解直角三角形的应用、几何体的俯视图,理解题意是解题的关键.
(1)根据题意,结合图①和图②即可得出答案;
(2)①根据月日在春分日和夏至日之间,结合图②即可得出答案;②观察图②可知双曲线为轴对称图形,对称轴为过点的正南北向的直线,故选择相距正午等时间的两处标记点,即可解答;
(3)①由题意得,直竿的影端轨迹为正东西向的直线,则影端轨迹的俯视图也是正东西向的直线,据此即可在图④中画出落在坡面上的影端轨迹;②设点到直线的垂足为点,则,由影端轨迹可得,三点共线,作于点,由题意得,,再利用解直角三角形的知识即可求解.
【详解】(1)解:由图①可知,竿影顶端的标记点在和标记点的东北方向,
结合图②可知,他的这次观测大约在秋冬季节.
故答案为:秋冬.
(2)解:①月日在春分日和夏至日之间,
结合图②可知,当天的影端轨迹最接近图②中的;
②方案:选用相距正午等时间(如上午和下午)的两处标记点,
道理:由图②可知,双曲线是轴对称图形,对称轴为过点的正南北向的直线;选用相距正午等时间的两处标记点,则两处标记点关于双曲线的对称轴对称,连接两处标记点即可确定出正东西方向.
(3)解:①如图所示,落在坡面上的影端轨迹即为所求:
②设点到直线的垂足为点,则,
由影端轨迹可得,三点共线,
如图,作于点,则,
由题意得,,,
在中,,
,
设,则,
在中,,
,
,
,即,
解得:,
答:到地平面的距离为.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
同课章节目录
