17.1 勾股定理 同步练习题 (含答案)人教版八年级数学下册
文档属性
| 名称 | 17.1 勾股定理 同步练习题 (含答案)人教版八年级数学下册 |  | |
| 格式 | docx | ||
| 文件大小 | 887.2KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-05-09 09:56:18 | ||
图片预览




文档简介
勾股定理 同步练习题
知识点梳理
1.定义:直角三角形两直角边的平方和等于斜边的平方.如果直角三角形的两直角边长分别为,斜边长为,那么.
在我国又称商高定理,在外国则叫毕达哥拉斯定理,或百牛定理.
2、要点诠释:
(1)勾股定理揭示了一个直角三角形三边之间的数量关系.
(2)利用勾股定理,当设定一条直角边长为未知数后,根据题目已知的线段长可以建立方程求解,这样就将数与形有机地结合起来,达到了解决问题的目的.
(3)理解勾股定理的一些变式: ,,
一、单选题
1.下列各组数中是勾股数的是( )
A.,, B.1,2,3 C.,, D.9,40,41
2.在直角中,,如果,那么的长度为( ).
A. B. C. D.
3.如图,在△ABC中,∠BAC=90°,BC=5,以AB,AC为边作正方形,这两个正方形的面积和为( )
A.5 B.9 C.16 D.25
4.在平面直角坐标系中,点在第三象限,点到轴的距离为3,到原点的距离为5,则点的坐标为 ( )
A. B. C. D.
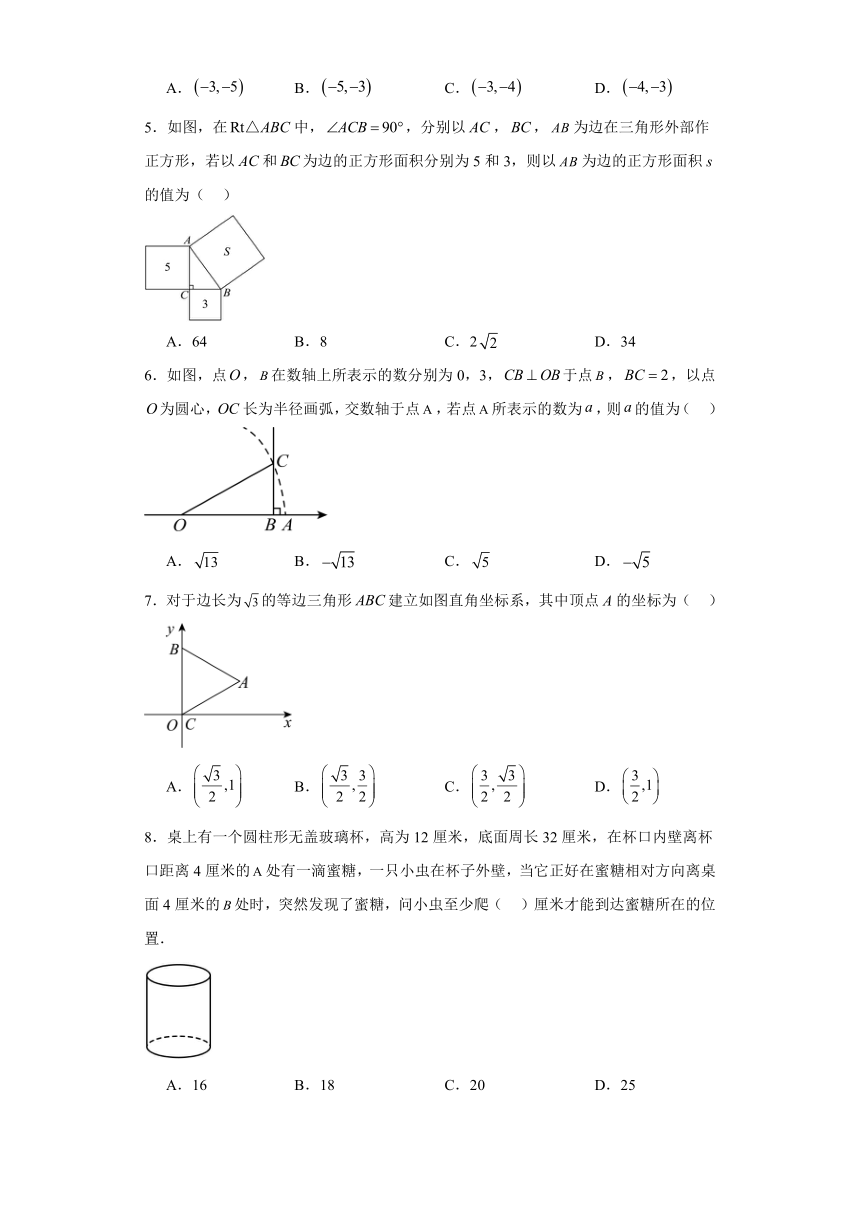
5.如图,在中,,分别以,,为边在三角形外部作正方形,若以和为边的正方形面积分别为5和3,则以为边的正方形面积s的值为( )
A.64 B.8 C.2 D.34
6.如图,点,在数轴上所表示的数分别为0,3,于点,,以点为圆心,长为半径画弧,交数轴于点,若点所表示的数为,则的值为( )
A. B. C. D.
7.对于边长为的等边三角形建立如图直角坐标系,其中顶点A的坐标为( )
A. B. C. D.
8.桌上有一个圆柱形无盖玻璃杯,高为12厘米,底面周长32厘米,在杯口内壁离杯口距离4厘米的处有一滴蜜糖,一只小虫在杯子外壁,当它正好在蜜糖相对方向离桌面4厘米的处时,突然发现了蜜糖,问小虫至少爬( )厘米才能到达蜜糖所在的位置.
A.16 B.18 C.20 D.25
二、填空题
9.若一个三角形的三边长为,则使此三角形是直角三角形的的值是 .
10.点和点的距离为 .
11.如图,在中,,,是的中点,在斜边上有一动点.从点出发,沿着的方向以每秒1cm的速度运动,当点运动到点时,停止运动.设动点的运动时间为s,连接,若为等腰直角三角形,则的值为 .
12.在平面直角坐标系中,点A,点的坐标分别为,.若是以为顶角的等腰三角形,点在轴上,则点的坐标为 .
13.如图,高速公路的同一侧有A,B两城镇,它们到高速公路所在直线的距离分别为,,.要在高速公路上C,D之间建一个出口P,使A,B两城镇到P的距离之和最小,则这个最短距离为 .
三、解答题
14.如图,在中,,是边上的高.
(1)若点是的中点,求证:;
(2)若,,求的长.
15.如图,方格纸中的每个小方格都是边长为1个单位的正方形.
(1)画出等腰直角三角形,点在方格纸上的格点上,;
(2)画出等腰三角形,点在方格纸上的格点上,的面积为6,连接,直接写出的长.
16.如图,点D在的边上,交于点F,.
(1)求证:.
(2)若.
①求的度数(用含m的代数式表示).
②当时,求的长.
17.“赵爽弦图”巧妙地利用面积关系证明了勾股定理,是我国古代数学的骄傲!如图,“赵爽弦图”是由四个全等的直角三角形和一个小正方形拼成的一个大正方形.设直角三角形较长直角边长为a,较短直角边长为b,斜边为c.
(1)请利用“赵爽弦图”证明:;
(2)若大正方形的面积为20,小正方形面积为4,求其中一个直角三角形的面积.
18.如图,在中,,,点为边上一点,且,点和点关于直线对称,连接.
(1)当时,的形状为_____________;
(2)当时,的形状为______________,试用等式表示和之间的数量关系,并说明理由.(提示:可连接;
(3)若可沿的方向平移后与重合,则此时的度数为_______°,此时可看作是绕点逆时针旋转______°得到的.
参考答案:
1.D
2.D
3.C
4.D
5.B
6.A
7.C
8.C
9.或4
10.3
11.或/或
12.或/或
13.
14.(1)证明:点是的中点,是边上的高.
垂直平分,
,
,
,
是等边三角形,
;
(2)解:设,则,
,
是边上的高,
,
在中,,
即,
解得或(舍去),
.
15.(1)解:根据题意得:,
是以,为腰,以为斜边的等腰直角三角形,
,
解得:,
,且点在方格纸上的格点上,
等腰直角三角形如图所示:
(2)解:依题意,,
①取,连接,如图所示,
,
取的中点N,过点N作,交于点G,
根据格点的特点,
点G为的中点,连接,
,
,
,
,
故不符合题意,
②取连接,如图所示,
,,
取的中点Q,作交于点G,
根据格点的特点,,
点G为的中点,连接,
,
,
,
,
符合题意,符号题意,且点F在格点上,
连接,
,
③以为底,作的垂直平分线,如图所示,
不符合题意,
等腰三角形如图所示,
.
16.(1)证明:,
,
,
,
又∵,
,
在和中,
,
,
.
(2)解:①设,
∵,
∴,
∴,
∵,
∴,
∴,
∵,
∴,
∴,
解得:,
∴
;
②过点A作于点M,如图所示:
∵,
∴,
∴,
∵,,
∴,
∴,,
∴,
∴.
17.(1)解:直角三角形较长直角边长为a,较短直角边长为b,斜边为c,
小正方形的面积四个直角三角形的面积大正方形的面积,
,
,
;
(2)解:由题意可得:,
即,
,
故一个直角三角形的面积为.
18.(1)解:,,,
,,
,
,
点和点关于直线对称,
垂直平分,
,
,
,
是等边三角形,
故答案为:等边三角形.
(2),
理由:,
,
,
,
,
是等腰直角三角形,
,
连接,则,
,
是等边三角形,
,
故答案为:等腰直角三角形.
(3)如图2,连接,
可沿的方向平移后与重合,
,,
,,
,
,
,
,
,
,,
,
,
此时可看作是绕点逆时针旋转得到的,
故答案为:72,108.
知识点梳理
1.定义:直角三角形两直角边的平方和等于斜边的平方.如果直角三角形的两直角边长分别为,斜边长为,那么.
在我国又称商高定理,在外国则叫毕达哥拉斯定理,或百牛定理.
2、要点诠释:
(1)勾股定理揭示了一个直角三角形三边之间的数量关系.
(2)利用勾股定理,当设定一条直角边长为未知数后,根据题目已知的线段长可以建立方程求解,这样就将数与形有机地结合起来,达到了解决问题的目的.
(3)理解勾股定理的一些变式: ,,
一、单选题
1.下列各组数中是勾股数的是( )
A.,, B.1,2,3 C.,, D.9,40,41
2.在直角中,,如果,那么的长度为( ).
A. B. C. D.
3.如图,在△ABC中,∠BAC=90°,BC=5,以AB,AC为边作正方形,这两个正方形的面积和为( )
A.5 B.9 C.16 D.25
4.在平面直角坐标系中,点在第三象限,点到轴的距离为3,到原点的距离为5,则点的坐标为 ( )
A. B. C. D.
5.如图,在中,,分别以,,为边在三角形外部作正方形,若以和为边的正方形面积分别为5和3,则以为边的正方形面积s的值为( )
A.64 B.8 C.2 D.34
6.如图,点,在数轴上所表示的数分别为0,3,于点,,以点为圆心,长为半径画弧,交数轴于点,若点所表示的数为,则的值为( )
A. B. C. D.
7.对于边长为的等边三角形建立如图直角坐标系,其中顶点A的坐标为( )
A. B. C. D.
8.桌上有一个圆柱形无盖玻璃杯,高为12厘米,底面周长32厘米,在杯口内壁离杯口距离4厘米的处有一滴蜜糖,一只小虫在杯子外壁,当它正好在蜜糖相对方向离桌面4厘米的处时,突然发现了蜜糖,问小虫至少爬( )厘米才能到达蜜糖所在的位置.
A.16 B.18 C.20 D.25
二、填空题
9.若一个三角形的三边长为,则使此三角形是直角三角形的的值是 .
10.点和点的距离为 .
11.如图,在中,,,是的中点,在斜边上有一动点.从点出发,沿着的方向以每秒1cm的速度运动,当点运动到点时,停止运动.设动点的运动时间为s,连接,若为等腰直角三角形,则的值为 .
12.在平面直角坐标系中,点A,点的坐标分别为,.若是以为顶角的等腰三角形,点在轴上,则点的坐标为 .
13.如图,高速公路的同一侧有A,B两城镇,它们到高速公路所在直线的距离分别为,,.要在高速公路上C,D之间建一个出口P,使A,B两城镇到P的距离之和最小,则这个最短距离为 .
三、解答题
14.如图,在中,,是边上的高.
(1)若点是的中点,求证:;
(2)若,,求的长.
15.如图,方格纸中的每个小方格都是边长为1个单位的正方形.
(1)画出等腰直角三角形,点在方格纸上的格点上,;
(2)画出等腰三角形,点在方格纸上的格点上,的面积为6,连接,直接写出的长.
16.如图,点D在的边上,交于点F,.
(1)求证:.
(2)若.
①求的度数(用含m的代数式表示).
②当时,求的长.
17.“赵爽弦图”巧妙地利用面积关系证明了勾股定理,是我国古代数学的骄傲!如图,“赵爽弦图”是由四个全等的直角三角形和一个小正方形拼成的一个大正方形.设直角三角形较长直角边长为a,较短直角边长为b,斜边为c.
(1)请利用“赵爽弦图”证明:;
(2)若大正方形的面积为20,小正方形面积为4,求其中一个直角三角形的面积.
18.如图,在中,,,点为边上一点,且,点和点关于直线对称,连接.
(1)当时,的形状为_____________;
(2)当时,的形状为______________,试用等式表示和之间的数量关系,并说明理由.(提示:可连接;
(3)若可沿的方向平移后与重合,则此时的度数为_______°,此时可看作是绕点逆时针旋转______°得到的.
参考答案:
1.D
2.D
3.C
4.D
5.B
6.A
7.C
8.C
9.或4
10.3
11.或/或
12.或/或
13.
14.(1)证明:点是的中点,是边上的高.
垂直平分,
,
,
,
是等边三角形,
;
(2)解:设,则,
,
是边上的高,
,
在中,,
即,
解得或(舍去),
.
15.(1)解:根据题意得:,
是以,为腰,以为斜边的等腰直角三角形,
,
解得:,
,且点在方格纸上的格点上,
等腰直角三角形如图所示:
(2)解:依题意,,
①取,连接,如图所示,
,
取的中点N,过点N作,交于点G,
根据格点的特点,
点G为的中点,连接,
,
,
,
,
故不符合题意,
②取连接,如图所示,
,,
取的中点Q,作交于点G,
根据格点的特点,,
点G为的中点,连接,
,
,
,
,
符合题意,符号题意,且点F在格点上,
连接,
,
③以为底,作的垂直平分线,如图所示,
不符合题意,
等腰三角形如图所示,
.
16.(1)证明:,
,
,
,
又∵,
,
在和中,
,
,
.
(2)解:①设,
∵,
∴,
∴,
∵,
∴,
∴,
∵,
∴,
∴,
解得:,
∴
;
②过点A作于点M,如图所示:
∵,
∴,
∴,
∵,,
∴,
∴,,
∴,
∴.
17.(1)解:直角三角形较长直角边长为a,较短直角边长为b,斜边为c,
小正方形的面积四个直角三角形的面积大正方形的面积,
,
,
;
(2)解:由题意可得:,
即,
,
故一个直角三角形的面积为.
18.(1)解:,,,
,,
,
,
点和点关于直线对称,
垂直平分,
,
,
,
是等边三角形,
故答案为:等边三角形.
(2),
理由:,
,
,
,
,
是等腰直角三角形,
,
连接,则,
,
是等边三角形,
,
故答案为:等腰直角三角形.
(3)如图2,连接,
可沿的方向平移后与重合,
,,
,,
,
,
,
,
,
,,
,
,
此时可看作是绕点逆时针旋转得到的,
故答案为:72,108.
