【期末专项培优】圆柱的体积高频易错提高卷(含解析)2024-2025学年六年级下册数学北师大版
文档属性
| 名称 | 【期末专项培优】圆柱的体积高频易错提高卷(含解析)2024-2025学年六年级下册数学北师大版 |  | |
| 格式 | docx | ||
| 文件大小 | 395.9KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-05-09 08:39:29 | ||
图片预览



文档简介
期末专项培优:圆柱的体积
一.选择题(共5小题)
1.(2024春?巨野县期中)一个圆柱和一个圆锥等底等高,它们体积差是20立方厘米,圆柱的体积是( )立方厘米。
A.40 B.30 C.20 D.15
2.(2024?历城区)一个瓶子里装有一些水,把瓶盖拧紧倒置放平(如图),根据图中的数据可以计算出瓶中水的体积占瓶子容积的( )
A.29 B.23 C.14 D.13
3.(2024?岚山区)一个圆柱的底面半径扩大到原来的3倍,高不变,体积扩大到原来的( )
A.3倍 B.6倍 C.9倍 D.27倍
4.(2024?即墨区)如图,分别以长方形的长和宽所在直线为轴旋转一周,形成两个立体图形。这两个立体图形的体积( )
A.图①形成的体积大 B.图②形成的体积大
C.一样大 D.不确定哪个大
5.(2024?隆昌市)一个圆柱的高扩大到原来的2倍,底面周长缩小到原来的12,它的体积( )
A.大小不变 B.扩大到原来的2倍
C.缩小到原来的12 D.无法确定
二.填空题(共5小题)
6.(2024春?湖里区期中)一根长3米的圆木,截成三段后,表面积增加80平方厘米,这根圆木原来的体积是 立方分米。
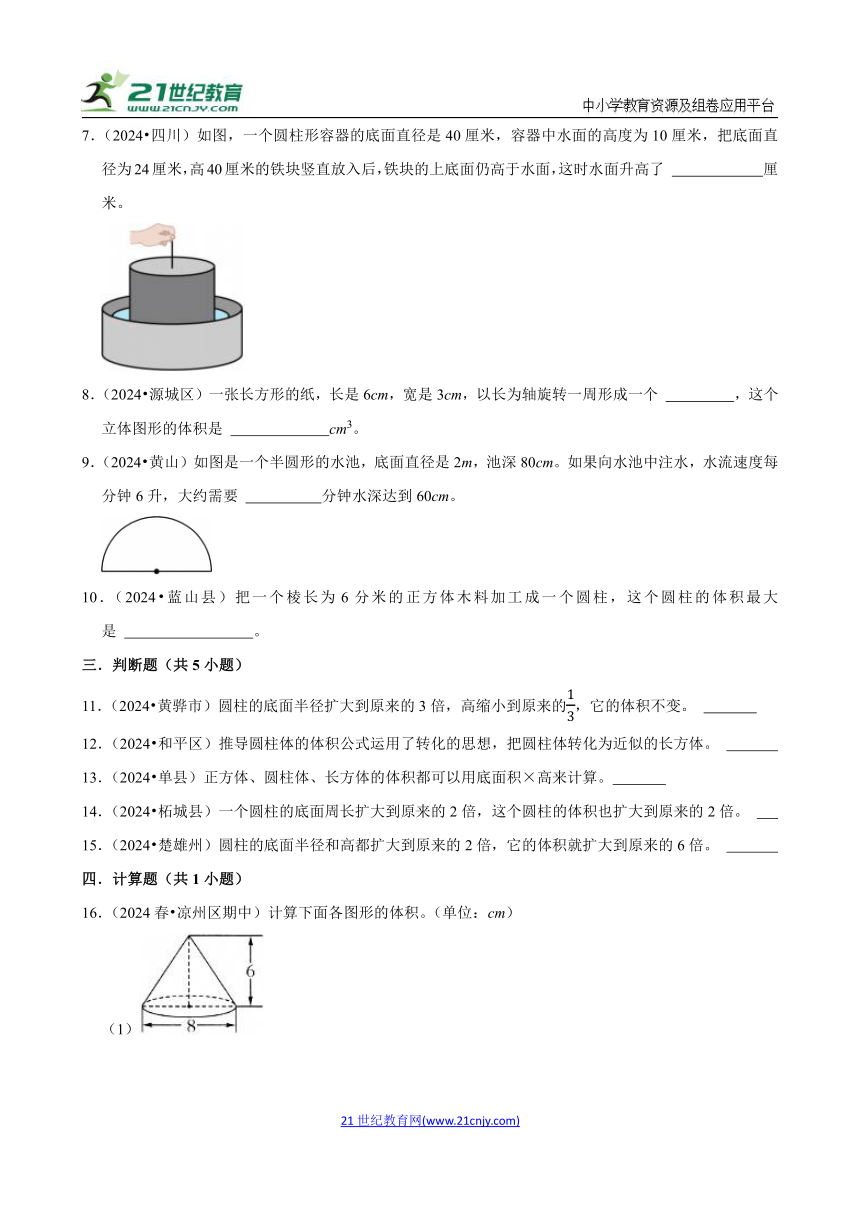
7.(2024?四川)如图,一个圆柱形容器的底面直径是40厘米,容器中水面的高度为10厘米,把底面直径为24厘米,高40厘米的铁块竖直放入后,铁块的上底面仍高于水面,这时水面升高了 厘米。
8.(2024?源城区)一张长方形的纸,长是6cm,宽是3cm,以长为轴旋转一周形成一个 ,这个立体图形的体积是 cm3。
9.(2024?黄山)如图是一个半圆形的水池,底面直径是2m,池深80cm。如果向水池中注水,水流速度每分钟6升,大约需要 分钟水深达到60cm。
10.(2024?蓝山县)把一个棱长为6分米的正方体木料加工成一个圆柱,这个圆柱的体积最大是 。
三.判断题(共5小题)
11.(2024?黄骅市)圆柱的底面半径扩大到原来的3倍,高缩小到原来的13,它的体积不变。
12.(2024?和平区)推导圆柱体的体积公式运用了转化的思想,把圆柱体转化为近似的长方体。
13.(2024?单县)正方体、圆柱体、长方体的体积都可以用底面积×高来计算。
14.(2024?柘城县)一个圆柱的底面周长扩大到原来的2倍,这个圆柱的体积也扩大到原来的2倍。
15.(2024?楚雄州)圆柱的底面半径和高都扩大到原来的2倍,它的体积就扩大到原来的6倍。
四.计算题(共1小题)
16.(2024春?凉州区期中)计算下面各图形的体积。(单位:cm)
(1)
(2)
五.应用题(共4小题)
17.(2024?邻水县)一个底面直径是8分米,高是7.5分米的圆柱形水桶里装有4分米高的水,现放入一个石块,石块全部没入水中,水面上升了2分米,这个石块的体积是多少立方分米?(水桶厚度忽略不计)
18.(2024?乾县)一个从里面量底面直径是40厘米的圆柱形容器中装有一些水,将一个高是15厘米,底面半径是10厘米的实心圆锥形铁块完全浸没在水中(水未溢出)。当铁块从水中取出后,容器中的水面下降了几厘米?
19.(2024?宛城区)有一个高12cm、容积为600mL的圆柱形容器A,里面装满了水,现把长18cm的圆柱B垂直放入,使B的底面和A的底面接触,这时一部分水从容器中溢出。当把B从A中拿走后,A中水的高度只有8cm。求圆柱B的体积。
20.(2024?沈丘县)北京时间2023年10月26日,“神十七”发射成功。当它升空后,会与“天和核心舱”端口进行对接,形成一条长约10dm,直径约8dm的圆形通道,这是航天员进入空间站的“生命通道”。这个“生命通道”的容积约是多少?
六.解答题(共2小题)
21.(2024春?高明区期末)菲菲家有一个玻璃瓶,下部主体是一个长方体,顶部是不规则的形状(如图①)。菲菲想知道这个瓶子的容积,于是她做了如下的操作实验:(单位:cm)
a.给瓶子注入一些水并测量出水位数据(见图②,瓶子厚度忽略不计,下同)
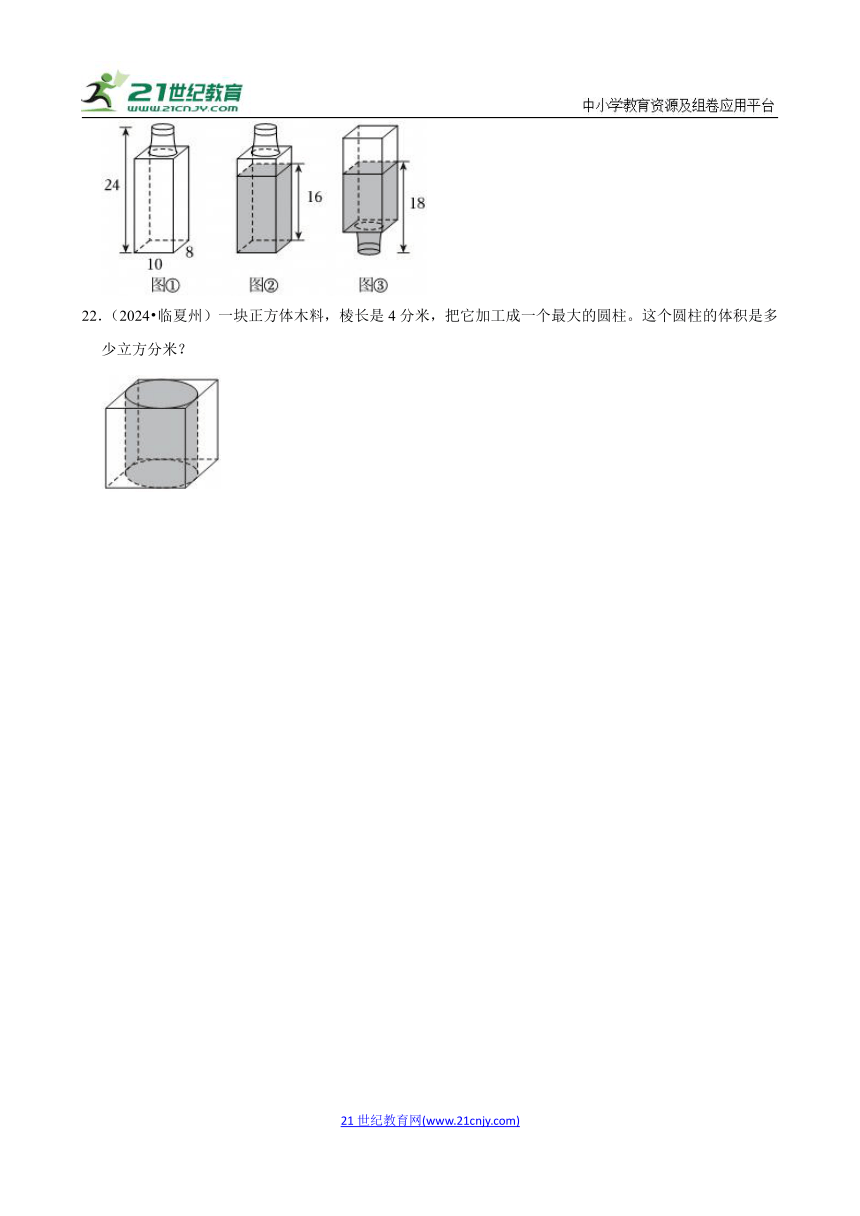
b.将瓶盖拧严实后把瓶子倒着放,再量出这时的水位高度(见图③)根据以上信息,请你帮菲菲算出:
(1)现在瓶子里水的体积是多少毫升?
(2)这个瓶子的容积是多少毫升?
22.(2024?临夏州)一块正方体木料,棱长是4分米,把它加工成一个最大的圆柱。这个圆柱的体积是多少立方分米?
期末专项培优:圆柱的体积
参考答案与试题解析
一.选择题(共5小题)
1.(2024春?巨野县期中)一个圆柱和一个圆锥等底等高,它们体积差是20立方厘米,圆柱的体积是( )立方厘米。
A.40 B.30 C.20 D.15
【考点】圆柱的体积.
【专题】空间与图形.
【答案】B
【分析】等底等高的圆柱的体积是圆锥体积的3倍,因此它们的体积差除以2就是圆锥的体积,用圆锥的体积乘3就是圆柱的体积。
【解答】解:20÷2=10(立方厘米)
10×3=30(立方厘米)
答:圆柱的体积是30立方厘米。
故选:B。
【点评】本题考查的目的是使学生理解掌握:等底等高的圆柱与圆锥之间的体积关系,即等底等高的圆柱是圆锥体积的3倍。据此关系可以解决有关的实际问题即可。
2.(2024?历城区)一个瓶子里装有一些水,把瓶盖拧紧倒置放平(如图),根据图中的数据可以计算出瓶中水的体积占瓶子容积的( )
A.29 B.23 C.14 D.13
【考点】圆柱的体积.
【专题】应用意识.
【答案】C
【分析】根据题意,瓶子容积可以看作是正放时水的体积+倒放时无水部分圆柱的体积,这两部分合起来正好是一个圆柱,这部分圆柱的高包括两部分,水的高度+无水圆柱的高度,底面积相同,可以求出水的高度占圆柱高度的几分之几,也就是瓶中水的体积占瓶子容积的几分之几。据此解答即可。
【解答】解:6÷(18+6)
=6÷24
=14
答;瓶中水的体积占瓶子容积的14。
故选:C。
【点评】本题考查圆柱的体积。
3.(2024?岚山区)一个圆柱的底面半径扩大到原来的3倍,高不变,体积扩大到原来的( )
A.3倍 B.6倍 C.9倍 D.27倍
【考点】圆柱的体积.
【专题】应用题;应用意识.
【答案】C
【分析】圆柱的体积=底面积×高,圆柱的高不变,设圆柱底面半径为r,高为h,原来的体积为V,扩大后的体积为V1,则扩大后的半径为3r,代入圆柱的体积公式,从而可以求出它的体积扩大的倍数。
【解答】解:原来的体积:V=πr2h
扩大后的体积:V1=π(3r)2h=9πr2h
体积扩大:9πr2h÷πr2h=9
答:它的体积扩大为原来的9倍。
故选:C。
【点评】此题主要考查圆柱体的体积计算公式的灵活应用。
4.(2024?即墨区)如图,分别以长方形的长和宽所在直线为轴旋转一周,形成两个立体图形。这两个立体图形的体积( )
A.图①形成的体积大 B.图②形成的体积大
C.一样大 D.不确定哪个大
【考点】圆柱的体积.
【专题】空间观念;应用意识.
【答案】B
【分析】以长为轴旋转一周,得到一个底面半径为3厘米,高为5厘米的圆柱体,以宽为轴旋转一周,得到一个底面半径为5厘米,高为3厘米的圆柱体利用圆柱的体积公式:V=πr2h进行解答即可。
【解答】解:3.14×32×5
=3.14×9×5
=28.26×3
=141.3(立方厘米)
3.14×53×3
=3.14×25×3
=78.5×3
=235.5(立方厘米)
235.5>141.3
答:图②形成的体积大。
故选:B。
【点评】本题是考查将一个简单图形绕一轴旋转一周所组成的图形是什么图形,二是考查圆柱的体积计算。关键是弄清旋转得到的圆柱的底面半径和高。
5.(2024?隆昌市)一个圆柱的高扩大到原来的2倍,底面周长缩小到原来的12,它的体积( )
A.大小不变 B.扩大到原来的2倍
C.缩小到原来的12 D.无法确定
【考点】圆柱的体积.
【专题】立体图形的认识与计算;几何直观.
【答案】C
【分析】圆柱的体积=底面积×高,底面周长缩小到原来的12,则半径也缩小到原来的12,因为底面积=πr2,所以此时底面积缩小为原来的14,据此解答。
【解答】解:底面周长缩小到原来的12,则半径也缩小到原来的12,因为底面积=πr2,所以此时底面积缩小为原来的14,所以高扩大到原来的2倍,它的底面周长缩小到原来的12,体积缩小为原来的2×14=12。
故选:C。
【点评】熟练掌握周长缩小到原来几分之几,面积就缩小到原来的几分之几的平方是解题的关键。
二.填空题(共5小题)
6.(2024春?湖里区期中)一根长3米的圆木,截成三段后,表面积增加80平方厘米,这根圆木原来的体积是 6 立方分米。
【考点】圆柱的体积.
【专题】应用意识.
【答案】6。
【分析】表面积增加80平方厘米,即增加4个圆木底面积,用80除以4即可求出圆木的底面积,再用底面积乘高即可求出圆木的体积。
【解答】解:3米=30分米
80÷4=20(平方厘米)
20平方厘米=0.2平方分米
0.2×30=6(立方分米)
答:这根圆木原来的体积是6立方分米。
故答案为:6。
【点评】本题考查了圆柱体积计算的应用。
7.(2024?四川)如图,一个圆柱形容器的底面直径是40厘米,容器中水面的高度为10厘米,把底面直径为24厘米,高40厘米的铁块竖直放入后,铁块的上底面仍高于水面,这时水面升高了 5.625 厘米。
【考点】圆柱的体积.
【专题】应用题;几何直观;应用意识.
【答案】5.625。
【分析】根据圆柱的体积V=πr2h可以求出容器内水的体积;放进去底面半径24厘米的圆柱体铁块后,铁块的上底面仍高于水面,说明这时候水的体积没变,但是水箱的底面积变小了,利用h=V÷S,从而可以求出水此时的高度,最后用现在的水面高度减去原来的水面高度,由此解决问题。
【解答】解:根据圆柱的体积V=πr2h可得:
3.14×(40÷2)2
=3.14×400
=1256(平方厘米)
1256×10=12560(立方厘米)
3.14×(24÷2)2
=3.14×144
=452.16(平方厘米)
1256﹣452.16=803.84(平方厘米)
12560÷803.84=15.625(厘米)
15.625﹣10=5.625(厘米)
答:这时水面升高5.625厘米。
故答案为:5.625。
【点评】抓住前后水的体积不变,原来底面积减少了圆柱体铁块的底面积部分,利用圆柱的体积公式即可求得底面积减少后的水深,由此即可解决问题。
8.(2024?源城区)一张长方形的纸,长是6cm,宽是3cm,以长为轴旋转一周形成一个 圆柱 ,这个立体图形的体积是 169.56 cm3。
【考点】圆柱的体积.
【专题】立体图形的认识与计算;几何直观.
【答案】圆柱,169.56。
【分析】一张长方形的纸以长为轴旋转一周得到一个圆柱体,圆柱的底面半径是长方形的宽,高是长方形的长,据此利用圆柱的体积公式:V=πr2h,代入数据计算解答。
【解答】解:一张长方形的纸,长是6cm,宽是3cm,以长为轴旋转一周形成一个圆柱;
3.14×3×3×6
=3.14×54
=169.56(立方厘米)
答:这个立体图形的体积是169.56cm3。
故答案为:圆柱,169.56。
【点评】本题考查了圆柱体积公式的应用。
9.(2024?黄山)如图是一个半圆形的水池,底面直径是2m,池深80cm。如果向水池中注水,水流速度每分钟6升,大约需要 157 分钟水深达到60cm。
【考点】圆柱的体积.
【专题】几何直观.
【答案】157。
【分析】根据题意,首先求出半径是2÷2=1(米),高是60厘米的圆柱一半的体积,然后除以6升,解答即可。
【解答】解:半径是:2÷2=1(米)
1米=10分米
高是:60厘米=6分米
6升=6立方分米
3.14×102×6÷2÷6
=942÷6
=157(分钟)
答:大约需要157分钟水深达到60厘米。
故答案为:157。
【点评】本题考查了圆柱体积公式的灵活运用,结合题意分析解答即可。
10.(2024?蓝山县)把一个棱长为6分米的正方体木料加工成一个圆柱,这个圆柱的体积最大是 169.56立方分米 。
【考点】圆柱的体积.
【专题】应用意识.
【答案】169.56立方分米。
【分析】把一个正方体木料加工成一个最大的圆柱体,这个圆柱的底面直径和高都等于正方体的棱长,根据圆柱的体积公式:V=πr2h,把数据代入公式解答。
【解答】解:3.14×(6÷2)2×6
=3.14×9×6
=28.26×6
=169.56(立方分米)
答:这个圆柱的体积最大是169.56立方分米。
故答案为:169.56立方分米。
【点评】此题主要考查圆柱体积公式的灵活运用,关键是熟记公式。
三.判断题(共5小题)
11.(2024?黄骅市)圆柱的底面半径扩大到原来的3倍,高缩小到原来的13,它的体积不变。 ×
【考点】圆柱的体积.
【专题】立体图形的认识与计算;几何直观.
【答案】×
【分析】根据圆柱的体积=底面积×高计算解答。
【解答】解:.3×3×13=3,则体积扩大到原来的3倍,故错误。
故答案为:×。
【点评】本题考查了圆柱体积公式的应用。
12.(2024?和平区)推导圆柱体的体积公式运用了转化的思想,把圆柱体转化为近似的长方体。 √
【考点】圆柱的体积.
【专题】推理能力;应用意识.
【答案】√
【分析】根据圆柱体积公式的推导过程可知,把圆柱剪拼成近似长方体,虽然形状变了,但是体积不变,根据长方体的体积公式推导出圆柱的体积公式。据此判断。
【解答】解:由分析得:推导圆柱体的体积公式运用了转化的思想,把圆柱体转化为近似的长方体。这种说法是正确的。
故答案为:√。
【点评】此题考查的目的是理解掌握圆柱体积公式的推导方法及应用。
13.(2024?单县)正方体、圆柱体、长方体的体积都可以用底面积×高来计算。 √
【考点】圆柱的体积;长方体和正方体的体积.
【专题】空间观念;应用意识.
【答案】√
【分析】根据正方体和长方体的统一体积公式:V=Sh,圆柱的体积公式:V=Sh,据此判断即可。
【解答】解:正方体、圆柱体、长方体的体积都可以用底面积×高来计算。此说法正确。
故答案为:√。
【点评】此题考查的目的是理解掌握正方体、长方体、圆柱的体积公式及应用。
14.(2024?柘城县)一个圆柱的底面周长扩大到原来的2倍,这个圆柱的体积也扩大到原来的2倍。 ×
【考点】圆柱的体积.
【专题】立体图形的认识与计算;几何直观.
【答案】×
【分析】圆柱的体积为V=πr2h,影响圆柱体积大小的因素还和高有关,一个圆柱的底面周长扩大到原来的2倍,说明底面半径扩大了原来的2倍,那么底面积就扩大原来的22倍,高不变的情况下,体积也扩大原来的22倍,据此解答。
【解答】解:一个圆柱的底面周长扩大到原来的2倍,高不变的情况下,这个圆柱的体积扩大到原来的4倍,原题说法错误。
故答案为:×。
【点评】本题考查了圆柱体积公式的应用。
15.(2024?楚雄州)圆柱的底面半径和高都扩大到原来的2倍,它的体积就扩大到原来的6倍。 ×
【考点】圆柱的体积.
【专题】数据分析观念.
【答案】×
【分析】根据圆柱的体积公式:V=Sh,圆柱的底面半径扩大到原来的2倍,底面积扩大到原来的4倍,高扩大到原来的2倍,再根据因数与积的变化规律,积扩大的倍数等于因数扩大倍数的乘积。据此解答。
【解答】解:圆柱的底面半径扩大到原来的2倍,底面积就扩大到原来的4倍,高扩大到原来2倍,那么它的体积扩大到原来的4×2=8倍。
故答案为:×。
【点评】此题主要根据圆柱的体积公式和因数与积的变化规律解决问题。
四.计算题(共1小题)
16.(2024春?凉州区期中)计算下面各图形的体积。(单位:cm)
(1)
(2)
【考点】圆柱的体积;表外乘除混合.
【专题】应用题;应用意识.
【答案】(1)100.48cm3;(2)2009.6cm3。
【分析】(1)根据圆锥体积=13×底面积×高,然后代入数据计算;
(2)根据圆柱的体积=底面积×高列式计算即可。
【解答】解:(1)13×3.14×(8÷2)2×6
=2×3.14×16
=6.28×16
=100.48(cm3)
(2)3.14×[(10÷2)2﹣(6÷2)2]×40
=3.14×16×40
=59.24×40
=2009.6(cm3)
【点评】解答此题要运用分数除法的意义以及圆柱的体积公式。
五.应用题(共4小题)
17.(2024?邻水县)一个底面直径是8分米,高是7.5分米的圆柱形水桶里装有4分米高的水,现放入一个石块,石块全部没入水中,水面上升了2分米,这个石块的体积是多少立方分米?(水桶厚度忽略不计)
【考点】圆柱的体积.
【专题】应用题;应用意识.
【答案】100.48立方分米。
【分析】从题意可知:石块的体积=圆柱形水桶的底面积×水面上升的高度,根据圆柱的底面积:S=πr2,代入数据计算,求出底面积,再乘上升高度2分米,即可求出石块的体积。
【解答】解:3.14×(8÷2)2
=3.14×42
=3.14×16
=50.24(平方分米)
50.24×2=100.48(立方分米)
答:这个石块的体积是100.48立方分米。
【点评】解答本题的关键是知道上升的水的体积等于石块的体积。
18.(2024?乾县)一个从里面量底面直径是40厘米的圆柱形容器中装有一些水,将一个高是15厘米,底面半径是10厘米的实心圆锥形铁块完全浸没在水中(水未溢出)。当铁块从水中取出后,容器中的水面下降了几厘米?
【考点】圆柱的体积.
【专题】应用意识.
【答案】1.25厘米。
【分析】根据圆锥的体积公式:V=13πr2,圆柱的体积公式:V=πr2h,把数据代入公式求出圆锥形铁块的体积,然后用圆锥形铁块的体积除以圆柱形容器的底面积即可。
【解答】解:13×3.14×102×15÷[3.14×(40÷2)2]
=13×3.14×100×15÷[3.14×400]
=1570÷1256
=1.25(厘米)
答:当铁块从水中取出后,容器中的水面下降了1.25厘米。
【点评】此题主要考查圆锥的体积公式、圆柱的体积公式的灵活运用,关键是熟记公式。
19.(2024?宛城区)有一个高12cm、容积为600mL的圆柱形容器A,里面装满了水,现把长18cm的圆柱B垂直放入,使B的底面和A的底面接触,这时一部分水从容器中溢出。当把B从A中拿走后,A中水的高度只有8cm。求圆柱B的体积。
【考点】圆柱的体积.
【专题】空间观念;应用意识.
【答案】300cm3。
【分析】圆柱形容器A高12cm,容积为600mL,根据圆柱的体积公式:V=Sh,可求出圆柱形容器A的底面积,圆柱B放入后,溢出水的体积就是圆柱B在水中的体积,用底面积乘水面下降的高度可求出溢出水的体积,再除以圆柱B在水中的高,可求出圆柱B的底面积,最后乘圆柱B的高,可求出圆柱B的体积。
【解答】解:600mL=600cm3
600÷12=50(cm2)
50×(12﹣8)÷12×18
=200÷12×18
=300(cm3)
答:圆柱B的体积是300cm3。
【点评】本题主要考查圆柱体积公式的应用。解题关键是明确溢出水的体积就是圆柱B在水中的体积。
20.(2024?沈丘县)北京时间2023年10月26日,“神十七”发射成功。当它升空后,会与“天和核心舱”端口进行对接,形成一条长约10dm,直径约8dm的圆形通道,这是航天员进入空间站的“生命通道”。这个“生命通道”的容积约是多少?
【考点】圆柱的体积.
【专题】应用意识.
【答案】502.4立方分米。
【分析】根据圆柱的容积公式:V=πr2h,把数据代入公式解答。
【解答】解:3.14×(8÷2)2×10
=3.14×16×10
=50.24×10
=502.4(立方分米)
答:这个“生命通道”的容积约是502.4立方分米。
【点评】此题主要考查圆柱容积公式的灵活运用,关键是熟记公式。
六.解答题(共2小题)
21.(2024春?高明区期末)菲菲家有一个玻璃瓶,下部主体是一个长方体,顶部是不规则的形状(如图①)。菲菲想知道这个瓶子的容积,于是她做了如下的操作实验:(单位:cm)
a.给瓶子注入一些水并测量出水位数据(见图②,瓶子厚度忽略不计,下同)
b.将瓶盖拧严实后把瓶子倒着放,再量出这时的水位高度(见图③)根据以上信息,请你帮菲菲算出:
(1)现在瓶子里水的体积是多少毫升?
(2)这个瓶子的容积是多少毫升?
【考点】圆柱的体积;长方体和正方体的体积.
【专题】操作型;立体图形的认识与计算;几何直观.
【答案】(1)1280毫升。
(2)1760毫升。
【分析】(1)根据长方体的长是10厘米,宽是8厘米,水面的高是16厘米,用长×宽×高计算出现在瓶子里水的体积是多少毫升。
(2)这个瓶子的容积=瓶子里水的体积+瓶子倒着放空白部分的体积。
【解答】解:(1)10×8×16
=80×16
=1280(立方厘米)
=1280(毫升)
答:现在瓶子里水的体积是1280毫升。
(2)1280+10×8×(24﹣18)
=1280+10×8×6
=1280+480
=1760(毫升)
答:这个瓶子的容积是1760毫升。
【点评】本题考查了长方体的体积计算。
22.(2024?临夏州)一块正方体木料,棱长是4分米,把它加工成一个最大的圆柱。这个圆柱的体积是多少立方分米?
【考点】圆柱的体积;长方体和正方体的体积.
【专题】应用意识.
【答案】50.24立方分米。
【分析】根据正方体的特征、圆柱的特征可知,把一块正方体木料削成一个最大的圆柱,也就是削成的圆柱的底面直径和高都等于正方体的棱长,根据圆柱的体积公式:V=πr2h,把数据代入公式解答。
【解答】解:3.14×(4÷2)2×4
=3.14×4×4
=12.56×4
=50.24(立方分米)
答:这个圆柱的体积是50.24立方分米。
【点评】此题主要考查圆柱体积公式的灵活运用,关键是熟记公式。
一.选择题(共5小题)
1.(2024春?巨野县期中)一个圆柱和一个圆锥等底等高,它们体积差是20立方厘米,圆柱的体积是( )立方厘米。
A.40 B.30 C.20 D.15
2.(2024?历城区)一个瓶子里装有一些水,把瓶盖拧紧倒置放平(如图),根据图中的数据可以计算出瓶中水的体积占瓶子容积的( )
A.29 B.23 C.14 D.13
3.(2024?岚山区)一个圆柱的底面半径扩大到原来的3倍,高不变,体积扩大到原来的( )
A.3倍 B.6倍 C.9倍 D.27倍
4.(2024?即墨区)如图,分别以长方形的长和宽所在直线为轴旋转一周,形成两个立体图形。这两个立体图形的体积( )
A.图①形成的体积大 B.图②形成的体积大
C.一样大 D.不确定哪个大
5.(2024?隆昌市)一个圆柱的高扩大到原来的2倍,底面周长缩小到原来的12,它的体积( )
A.大小不变 B.扩大到原来的2倍
C.缩小到原来的12 D.无法确定
二.填空题(共5小题)
6.(2024春?湖里区期中)一根长3米的圆木,截成三段后,表面积增加80平方厘米,这根圆木原来的体积是 立方分米。
7.(2024?四川)如图,一个圆柱形容器的底面直径是40厘米,容器中水面的高度为10厘米,把底面直径为24厘米,高40厘米的铁块竖直放入后,铁块的上底面仍高于水面,这时水面升高了 厘米。
8.(2024?源城区)一张长方形的纸,长是6cm,宽是3cm,以长为轴旋转一周形成一个 ,这个立体图形的体积是 cm3。
9.(2024?黄山)如图是一个半圆形的水池,底面直径是2m,池深80cm。如果向水池中注水,水流速度每分钟6升,大约需要 分钟水深达到60cm。
10.(2024?蓝山县)把一个棱长为6分米的正方体木料加工成一个圆柱,这个圆柱的体积最大是 。
三.判断题(共5小题)
11.(2024?黄骅市)圆柱的底面半径扩大到原来的3倍,高缩小到原来的13,它的体积不变。
12.(2024?和平区)推导圆柱体的体积公式运用了转化的思想,把圆柱体转化为近似的长方体。
13.(2024?单县)正方体、圆柱体、长方体的体积都可以用底面积×高来计算。
14.(2024?柘城县)一个圆柱的底面周长扩大到原来的2倍,这个圆柱的体积也扩大到原来的2倍。
15.(2024?楚雄州)圆柱的底面半径和高都扩大到原来的2倍,它的体积就扩大到原来的6倍。
四.计算题(共1小题)
16.(2024春?凉州区期中)计算下面各图形的体积。(单位:cm)
(1)
(2)
五.应用题(共4小题)
17.(2024?邻水县)一个底面直径是8分米,高是7.5分米的圆柱形水桶里装有4分米高的水,现放入一个石块,石块全部没入水中,水面上升了2分米,这个石块的体积是多少立方分米?(水桶厚度忽略不计)
18.(2024?乾县)一个从里面量底面直径是40厘米的圆柱形容器中装有一些水,将一个高是15厘米,底面半径是10厘米的实心圆锥形铁块完全浸没在水中(水未溢出)。当铁块从水中取出后,容器中的水面下降了几厘米?
19.(2024?宛城区)有一个高12cm、容积为600mL的圆柱形容器A,里面装满了水,现把长18cm的圆柱B垂直放入,使B的底面和A的底面接触,这时一部分水从容器中溢出。当把B从A中拿走后,A中水的高度只有8cm。求圆柱B的体积。
20.(2024?沈丘县)北京时间2023年10月26日,“神十七”发射成功。当它升空后,会与“天和核心舱”端口进行对接,形成一条长约10dm,直径约8dm的圆形通道,这是航天员进入空间站的“生命通道”。这个“生命通道”的容积约是多少?
六.解答题(共2小题)
21.(2024春?高明区期末)菲菲家有一个玻璃瓶,下部主体是一个长方体,顶部是不规则的形状(如图①)。菲菲想知道这个瓶子的容积,于是她做了如下的操作实验:(单位:cm)
a.给瓶子注入一些水并测量出水位数据(见图②,瓶子厚度忽略不计,下同)
b.将瓶盖拧严实后把瓶子倒着放,再量出这时的水位高度(见图③)根据以上信息,请你帮菲菲算出:
(1)现在瓶子里水的体积是多少毫升?
(2)这个瓶子的容积是多少毫升?
22.(2024?临夏州)一块正方体木料,棱长是4分米,把它加工成一个最大的圆柱。这个圆柱的体积是多少立方分米?
期末专项培优:圆柱的体积
参考答案与试题解析
一.选择题(共5小题)
1.(2024春?巨野县期中)一个圆柱和一个圆锥等底等高,它们体积差是20立方厘米,圆柱的体积是( )立方厘米。
A.40 B.30 C.20 D.15
【考点】圆柱的体积.
【专题】空间与图形.
【答案】B
【分析】等底等高的圆柱的体积是圆锥体积的3倍,因此它们的体积差除以2就是圆锥的体积,用圆锥的体积乘3就是圆柱的体积。
【解答】解:20÷2=10(立方厘米)
10×3=30(立方厘米)
答:圆柱的体积是30立方厘米。
故选:B。
【点评】本题考查的目的是使学生理解掌握:等底等高的圆柱与圆锥之间的体积关系,即等底等高的圆柱是圆锥体积的3倍。据此关系可以解决有关的实际问题即可。
2.(2024?历城区)一个瓶子里装有一些水,把瓶盖拧紧倒置放平(如图),根据图中的数据可以计算出瓶中水的体积占瓶子容积的( )
A.29 B.23 C.14 D.13
【考点】圆柱的体积.
【专题】应用意识.
【答案】C
【分析】根据题意,瓶子容积可以看作是正放时水的体积+倒放时无水部分圆柱的体积,这两部分合起来正好是一个圆柱,这部分圆柱的高包括两部分,水的高度+无水圆柱的高度,底面积相同,可以求出水的高度占圆柱高度的几分之几,也就是瓶中水的体积占瓶子容积的几分之几。据此解答即可。
【解答】解:6÷(18+6)
=6÷24
=14
答;瓶中水的体积占瓶子容积的14。
故选:C。
【点评】本题考查圆柱的体积。
3.(2024?岚山区)一个圆柱的底面半径扩大到原来的3倍,高不变,体积扩大到原来的( )
A.3倍 B.6倍 C.9倍 D.27倍
【考点】圆柱的体积.
【专题】应用题;应用意识.
【答案】C
【分析】圆柱的体积=底面积×高,圆柱的高不变,设圆柱底面半径为r,高为h,原来的体积为V,扩大后的体积为V1,则扩大后的半径为3r,代入圆柱的体积公式,从而可以求出它的体积扩大的倍数。
【解答】解:原来的体积:V=πr2h
扩大后的体积:V1=π(3r)2h=9πr2h
体积扩大:9πr2h÷πr2h=9
答:它的体积扩大为原来的9倍。
故选:C。
【点评】此题主要考查圆柱体的体积计算公式的灵活应用。
4.(2024?即墨区)如图,分别以长方形的长和宽所在直线为轴旋转一周,形成两个立体图形。这两个立体图形的体积( )
A.图①形成的体积大 B.图②形成的体积大
C.一样大 D.不确定哪个大
【考点】圆柱的体积.
【专题】空间观念;应用意识.
【答案】B
【分析】以长为轴旋转一周,得到一个底面半径为3厘米,高为5厘米的圆柱体,以宽为轴旋转一周,得到一个底面半径为5厘米,高为3厘米的圆柱体利用圆柱的体积公式:V=πr2h进行解答即可。
【解答】解:3.14×32×5
=3.14×9×5
=28.26×3
=141.3(立方厘米)
3.14×53×3
=3.14×25×3
=78.5×3
=235.5(立方厘米)
235.5>141.3
答:图②形成的体积大。
故选:B。
【点评】本题是考查将一个简单图形绕一轴旋转一周所组成的图形是什么图形,二是考查圆柱的体积计算。关键是弄清旋转得到的圆柱的底面半径和高。
5.(2024?隆昌市)一个圆柱的高扩大到原来的2倍,底面周长缩小到原来的12,它的体积( )
A.大小不变 B.扩大到原来的2倍
C.缩小到原来的12 D.无法确定
【考点】圆柱的体积.
【专题】立体图形的认识与计算;几何直观.
【答案】C
【分析】圆柱的体积=底面积×高,底面周长缩小到原来的12,则半径也缩小到原来的12,因为底面积=πr2,所以此时底面积缩小为原来的14,据此解答。
【解答】解:底面周长缩小到原来的12,则半径也缩小到原来的12,因为底面积=πr2,所以此时底面积缩小为原来的14,所以高扩大到原来的2倍,它的底面周长缩小到原来的12,体积缩小为原来的2×14=12。
故选:C。
【点评】熟练掌握周长缩小到原来几分之几,面积就缩小到原来的几分之几的平方是解题的关键。
二.填空题(共5小题)
6.(2024春?湖里区期中)一根长3米的圆木,截成三段后,表面积增加80平方厘米,这根圆木原来的体积是 6 立方分米。
【考点】圆柱的体积.
【专题】应用意识.
【答案】6。
【分析】表面积增加80平方厘米,即增加4个圆木底面积,用80除以4即可求出圆木的底面积,再用底面积乘高即可求出圆木的体积。
【解答】解:3米=30分米
80÷4=20(平方厘米)
20平方厘米=0.2平方分米
0.2×30=6(立方分米)
答:这根圆木原来的体积是6立方分米。
故答案为:6。
【点评】本题考查了圆柱体积计算的应用。
7.(2024?四川)如图,一个圆柱形容器的底面直径是40厘米,容器中水面的高度为10厘米,把底面直径为24厘米,高40厘米的铁块竖直放入后,铁块的上底面仍高于水面,这时水面升高了 5.625 厘米。
【考点】圆柱的体积.
【专题】应用题;几何直观;应用意识.
【答案】5.625。
【分析】根据圆柱的体积V=πr2h可以求出容器内水的体积;放进去底面半径24厘米的圆柱体铁块后,铁块的上底面仍高于水面,说明这时候水的体积没变,但是水箱的底面积变小了,利用h=V÷S,从而可以求出水此时的高度,最后用现在的水面高度减去原来的水面高度,由此解决问题。
【解答】解:根据圆柱的体积V=πr2h可得:
3.14×(40÷2)2
=3.14×400
=1256(平方厘米)
1256×10=12560(立方厘米)
3.14×(24÷2)2
=3.14×144
=452.16(平方厘米)
1256﹣452.16=803.84(平方厘米)
12560÷803.84=15.625(厘米)
15.625﹣10=5.625(厘米)
答:这时水面升高5.625厘米。
故答案为:5.625。
【点评】抓住前后水的体积不变,原来底面积减少了圆柱体铁块的底面积部分,利用圆柱的体积公式即可求得底面积减少后的水深,由此即可解决问题。
8.(2024?源城区)一张长方形的纸,长是6cm,宽是3cm,以长为轴旋转一周形成一个 圆柱 ,这个立体图形的体积是 169.56 cm3。
【考点】圆柱的体积.
【专题】立体图形的认识与计算;几何直观.
【答案】圆柱,169.56。
【分析】一张长方形的纸以长为轴旋转一周得到一个圆柱体,圆柱的底面半径是长方形的宽,高是长方形的长,据此利用圆柱的体积公式:V=πr2h,代入数据计算解答。
【解答】解:一张长方形的纸,长是6cm,宽是3cm,以长为轴旋转一周形成一个圆柱;
3.14×3×3×6
=3.14×54
=169.56(立方厘米)
答:这个立体图形的体积是169.56cm3。
故答案为:圆柱,169.56。
【点评】本题考查了圆柱体积公式的应用。
9.(2024?黄山)如图是一个半圆形的水池,底面直径是2m,池深80cm。如果向水池中注水,水流速度每分钟6升,大约需要 157 分钟水深达到60cm。
【考点】圆柱的体积.
【专题】几何直观.
【答案】157。
【分析】根据题意,首先求出半径是2÷2=1(米),高是60厘米的圆柱一半的体积,然后除以6升,解答即可。
【解答】解:半径是:2÷2=1(米)
1米=10分米
高是:60厘米=6分米
6升=6立方分米
3.14×102×6÷2÷6
=942÷6
=157(分钟)
答:大约需要157分钟水深达到60厘米。
故答案为:157。
【点评】本题考查了圆柱体积公式的灵活运用,结合题意分析解答即可。
10.(2024?蓝山县)把一个棱长为6分米的正方体木料加工成一个圆柱,这个圆柱的体积最大是 169.56立方分米 。
【考点】圆柱的体积.
【专题】应用意识.
【答案】169.56立方分米。
【分析】把一个正方体木料加工成一个最大的圆柱体,这个圆柱的底面直径和高都等于正方体的棱长,根据圆柱的体积公式:V=πr2h,把数据代入公式解答。
【解答】解:3.14×(6÷2)2×6
=3.14×9×6
=28.26×6
=169.56(立方分米)
答:这个圆柱的体积最大是169.56立方分米。
故答案为:169.56立方分米。
【点评】此题主要考查圆柱体积公式的灵活运用,关键是熟记公式。
三.判断题(共5小题)
11.(2024?黄骅市)圆柱的底面半径扩大到原来的3倍,高缩小到原来的13,它的体积不变。 ×
【考点】圆柱的体积.
【专题】立体图形的认识与计算;几何直观.
【答案】×
【分析】根据圆柱的体积=底面积×高计算解答。
【解答】解:.3×3×13=3,则体积扩大到原来的3倍,故错误。
故答案为:×。
【点评】本题考查了圆柱体积公式的应用。
12.(2024?和平区)推导圆柱体的体积公式运用了转化的思想,把圆柱体转化为近似的长方体。 √
【考点】圆柱的体积.
【专题】推理能力;应用意识.
【答案】√
【分析】根据圆柱体积公式的推导过程可知,把圆柱剪拼成近似长方体,虽然形状变了,但是体积不变,根据长方体的体积公式推导出圆柱的体积公式。据此判断。
【解答】解:由分析得:推导圆柱体的体积公式运用了转化的思想,把圆柱体转化为近似的长方体。这种说法是正确的。
故答案为:√。
【点评】此题考查的目的是理解掌握圆柱体积公式的推导方法及应用。
13.(2024?单县)正方体、圆柱体、长方体的体积都可以用底面积×高来计算。 √
【考点】圆柱的体积;长方体和正方体的体积.
【专题】空间观念;应用意识.
【答案】√
【分析】根据正方体和长方体的统一体积公式:V=Sh,圆柱的体积公式:V=Sh,据此判断即可。
【解答】解:正方体、圆柱体、长方体的体积都可以用底面积×高来计算。此说法正确。
故答案为:√。
【点评】此题考查的目的是理解掌握正方体、长方体、圆柱的体积公式及应用。
14.(2024?柘城县)一个圆柱的底面周长扩大到原来的2倍,这个圆柱的体积也扩大到原来的2倍。 ×
【考点】圆柱的体积.
【专题】立体图形的认识与计算;几何直观.
【答案】×
【分析】圆柱的体积为V=πr2h,影响圆柱体积大小的因素还和高有关,一个圆柱的底面周长扩大到原来的2倍,说明底面半径扩大了原来的2倍,那么底面积就扩大原来的22倍,高不变的情况下,体积也扩大原来的22倍,据此解答。
【解答】解:一个圆柱的底面周长扩大到原来的2倍,高不变的情况下,这个圆柱的体积扩大到原来的4倍,原题说法错误。
故答案为:×。
【点评】本题考查了圆柱体积公式的应用。
15.(2024?楚雄州)圆柱的底面半径和高都扩大到原来的2倍,它的体积就扩大到原来的6倍。 ×
【考点】圆柱的体积.
【专题】数据分析观念.
【答案】×
【分析】根据圆柱的体积公式:V=Sh,圆柱的底面半径扩大到原来的2倍,底面积扩大到原来的4倍,高扩大到原来的2倍,再根据因数与积的变化规律,积扩大的倍数等于因数扩大倍数的乘积。据此解答。
【解答】解:圆柱的底面半径扩大到原来的2倍,底面积就扩大到原来的4倍,高扩大到原来2倍,那么它的体积扩大到原来的4×2=8倍。
故答案为:×。
【点评】此题主要根据圆柱的体积公式和因数与积的变化规律解决问题。
四.计算题(共1小题)
16.(2024春?凉州区期中)计算下面各图形的体积。(单位:cm)
(1)
(2)
【考点】圆柱的体积;表外乘除混合.
【专题】应用题;应用意识.
【答案】(1)100.48cm3;(2)2009.6cm3。
【分析】(1)根据圆锥体积=13×底面积×高,然后代入数据计算;
(2)根据圆柱的体积=底面积×高列式计算即可。
【解答】解:(1)13×3.14×(8÷2)2×6
=2×3.14×16
=6.28×16
=100.48(cm3)
(2)3.14×[(10÷2)2﹣(6÷2)2]×40
=3.14×16×40
=59.24×40
=2009.6(cm3)
【点评】解答此题要运用分数除法的意义以及圆柱的体积公式。
五.应用题(共4小题)
17.(2024?邻水县)一个底面直径是8分米,高是7.5分米的圆柱形水桶里装有4分米高的水,现放入一个石块,石块全部没入水中,水面上升了2分米,这个石块的体积是多少立方分米?(水桶厚度忽略不计)
【考点】圆柱的体积.
【专题】应用题;应用意识.
【答案】100.48立方分米。
【分析】从题意可知:石块的体积=圆柱形水桶的底面积×水面上升的高度,根据圆柱的底面积:S=πr2,代入数据计算,求出底面积,再乘上升高度2分米,即可求出石块的体积。
【解答】解:3.14×(8÷2)2
=3.14×42
=3.14×16
=50.24(平方分米)
50.24×2=100.48(立方分米)
答:这个石块的体积是100.48立方分米。
【点评】解答本题的关键是知道上升的水的体积等于石块的体积。
18.(2024?乾县)一个从里面量底面直径是40厘米的圆柱形容器中装有一些水,将一个高是15厘米,底面半径是10厘米的实心圆锥形铁块完全浸没在水中(水未溢出)。当铁块从水中取出后,容器中的水面下降了几厘米?
【考点】圆柱的体积.
【专题】应用意识.
【答案】1.25厘米。
【分析】根据圆锥的体积公式:V=13πr2,圆柱的体积公式:V=πr2h,把数据代入公式求出圆锥形铁块的体积,然后用圆锥形铁块的体积除以圆柱形容器的底面积即可。
【解答】解:13×3.14×102×15÷[3.14×(40÷2)2]
=13×3.14×100×15÷[3.14×400]
=1570÷1256
=1.25(厘米)
答:当铁块从水中取出后,容器中的水面下降了1.25厘米。
【点评】此题主要考查圆锥的体积公式、圆柱的体积公式的灵活运用,关键是熟记公式。
19.(2024?宛城区)有一个高12cm、容积为600mL的圆柱形容器A,里面装满了水,现把长18cm的圆柱B垂直放入,使B的底面和A的底面接触,这时一部分水从容器中溢出。当把B从A中拿走后,A中水的高度只有8cm。求圆柱B的体积。
【考点】圆柱的体积.
【专题】空间观念;应用意识.
【答案】300cm3。
【分析】圆柱形容器A高12cm,容积为600mL,根据圆柱的体积公式:V=Sh,可求出圆柱形容器A的底面积,圆柱B放入后,溢出水的体积就是圆柱B在水中的体积,用底面积乘水面下降的高度可求出溢出水的体积,再除以圆柱B在水中的高,可求出圆柱B的底面积,最后乘圆柱B的高,可求出圆柱B的体积。
【解答】解:600mL=600cm3
600÷12=50(cm2)
50×(12﹣8)÷12×18
=200÷12×18
=300(cm3)
答:圆柱B的体积是300cm3。
【点评】本题主要考查圆柱体积公式的应用。解题关键是明确溢出水的体积就是圆柱B在水中的体积。
20.(2024?沈丘县)北京时间2023年10月26日,“神十七”发射成功。当它升空后,会与“天和核心舱”端口进行对接,形成一条长约10dm,直径约8dm的圆形通道,这是航天员进入空间站的“生命通道”。这个“生命通道”的容积约是多少?
【考点】圆柱的体积.
【专题】应用意识.
【答案】502.4立方分米。
【分析】根据圆柱的容积公式:V=πr2h,把数据代入公式解答。
【解答】解:3.14×(8÷2)2×10
=3.14×16×10
=50.24×10
=502.4(立方分米)
答:这个“生命通道”的容积约是502.4立方分米。
【点评】此题主要考查圆柱容积公式的灵活运用,关键是熟记公式。
六.解答题(共2小题)
21.(2024春?高明区期末)菲菲家有一个玻璃瓶,下部主体是一个长方体,顶部是不规则的形状(如图①)。菲菲想知道这个瓶子的容积,于是她做了如下的操作实验:(单位:cm)
a.给瓶子注入一些水并测量出水位数据(见图②,瓶子厚度忽略不计,下同)
b.将瓶盖拧严实后把瓶子倒着放,再量出这时的水位高度(见图③)根据以上信息,请你帮菲菲算出:
(1)现在瓶子里水的体积是多少毫升?
(2)这个瓶子的容积是多少毫升?
【考点】圆柱的体积;长方体和正方体的体积.
【专题】操作型;立体图形的认识与计算;几何直观.
【答案】(1)1280毫升。
(2)1760毫升。
【分析】(1)根据长方体的长是10厘米,宽是8厘米,水面的高是16厘米,用长×宽×高计算出现在瓶子里水的体积是多少毫升。
(2)这个瓶子的容积=瓶子里水的体积+瓶子倒着放空白部分的体积。
【解答】解:(1)10×8×16
=80×16
=1280(立方厘米)
=1280(毫升)
答:现在瓶子里水的体积是1280毫升。
(2)1280+10×8×(24﹣18)
=1280+10×8×6
=1280+480
=1760(毫升)
答:这个瓶子的容积是1760毫升。
【点评】本题考查了长方体的体积计算。
22.(2024?临夏州)一块正方体木料,棱长是4分米,把它加工成一个最大的圆柱。这个圆柱的体积是多少立方分米?
【考点】圆柱的体积;长方体和正方体的体积.
【专题】应用意识.
【答案】50.24立方分米。
【分析】根据正方体的特征、圆柱的特征可知,把一块正方体木料削成一个最大的圆柱,也就是削成的圆柱的底面直径和高都等于正方体的棱长,根据圆柱的体积公式:V=πr2h,把数据代入公式解答。
【解答】解:3.14×(4÷2)2×4
=3.14×4×4
=12.56×4
=50.24(立方分米)
答:这个圆柱的体积是50.24立方分米。
【点评】此题主要考查圆柱体积公式的灵活运用,关键是熟记公式。
