【期末专项培优】图形的放大和缩小高频易错提高卷(含解析)2024-2025学年六年级下册数学北师大版
文档属性
| 名称 | 【期末专项培优】图形的放大和缩小高频易错提高卷(含解析)2024-2025学年六年级下册数学北师大版 |

|
|
| 格式 | docx | ||
| 文件大小 | 940.1KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-05-09 08:48:51 | ||
图片预览




文档简介
期末专项培优:图形的放大和缩小
一.选择题(共5小题)
1.(2024春 滨海县期中)将一个周长为16厘米的正方形变换成面积为64平方厘米的正方形。实际是按( )的比放大的。
A.2:1 B.3:1 C.4:1 D.6:1
2.(2024春 凉州区期中)一个长方形的长是4分米,宽是3分米,把它按3:1扩大,得到图形的面积是( )平方分米。
A.36 B.108 C.42
3.(2024 山阳县)如图的图形是按一定比例缩小的,则x=( )
A.10 B.8 C.7.5
4.(2024 河北)把一个长为6厘米,宽为4厘米的长方形按1:2的比缩小后,长方形的面积是( )平方厘米。
A.6 B.24 C.12
5.(2024 广汉市)一个长方形,长和宽分别为10cm和8cm,按照1:2的比例缩小,所得到的新的长方形的长和宽分别为( )
A.4cm、5cm B.5cm、4cm C.16cm、20cm D.20cm、16cm
二.填空题(共5小题)
6.(2024春 平川区校级期中)如果把一个正方形按4:1放大,放大后正方形与放大前正方形的面积比是 。
7.(2024春 潮州期中)一个长方形长4cm,宽3cm,按3:1的比放大后得到图形的面积是 cm2。
8.(2024春 东莞市期中)将一个长3cm,宽2cm的长方形按2:1放大画在图纸上,这个长方形的周长是 cm,面积是 cm2。
9.(2024春 绵阳期中)一个长5cm,宽3cm的长方形按3:1放大,放大后的长方形的面积是 cm2;放大前与放大后面积的比是 。
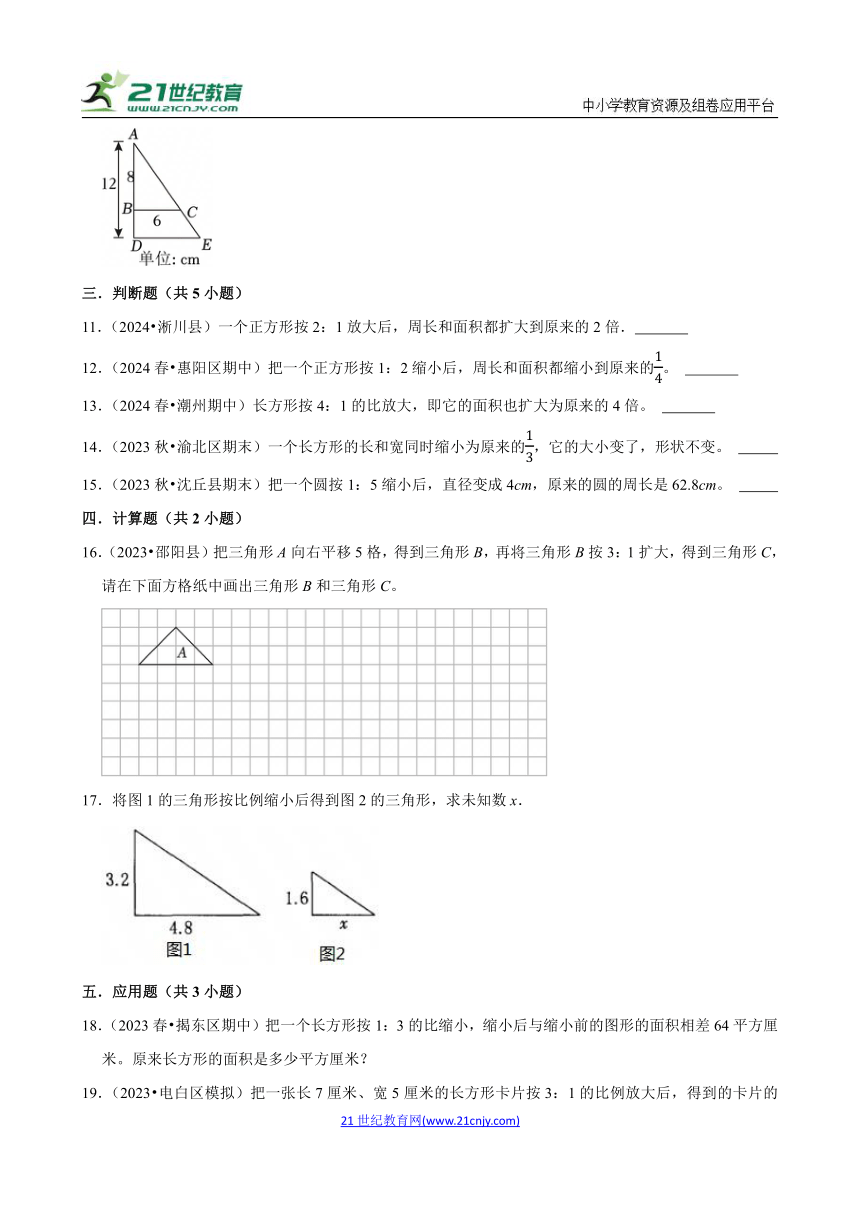
10.(2024 杭州)如图,将三角形ABC按比例放大成三角形ADE。已知AC=10cm,那么CE= cm。
三.判断题(共5小题)
11.(2024 淅川县)一个正方形按2:1放大后,周长和面积都扩大到原来的2倍.
12.(2024春 惠阳区期中)把一个正方形按1:2缩小后,周长和面积都缩小到原来的。
13.(2024春 潮州期中)长方形按4:1的比放大,即它的面积也扩大为原来的4倍。
14.(2023秋 渝北区期末)一个长方形的长和宽同时缩小为原来的,它的大小变了,形状不变。
15.(2023秋 沈丘县期末)把一个圆按1:5缩小后,直径变成4cm,原来的圆的周长是62.8cm。
四.计算题(共2小题)
16.(2023 邵阳县)把三角形A向右平移5格,得到三角形B,再将三角形B按3:1扩大,得到三角形C,请在下面方格纸中画出三角形B和三角形C。
17.将图1的三角形按比例缩小后得到图2的三角形,求未知数x.
五.应用题(共3小题)
18.(2023春 揭东区期中)把一个长方形按1:3的比缩小,缩小后与缩小前的图形的面积相差64平方厘米。原来长方形的面积是多少平方厘米?
19.(2023 电白区模拟)把一张长7厘米、宽5厘米的长方形卡片按3:1的比例放大后,得到的卡片的面积是多少平方厘米?
20.(2021 钦北区)李明在电脑上把一张长6厘米,宽4厘米的照片按比例放大,放大后照片的长是13.5厘米,宽是多少厘米?
六.解答题(共2小题)
21.(2024 播州区模拟)画一画.
(1)将三角形A的各条边按4:1放大,得到三角形B.
(2)将三角形B的各条边按1:2缩小,得到三角形C.
22.(2024 北川县)如图方格纸中小正方形的边长是1cm,按要求完成下面各题。
(1)圆O的圆心O点所在的位置用数对表示是( , )。画出将圆O向右平移4格后的图形。
(2)画出三角形ABC按2:1放大后的图形。原来三角形ABC的面积是放大后图形面积的 %。
期末专项培优:图形的放大和缩小
参考答案与试题解析
一.选择题(共5小题)
1.(2024春 滨海县期中)将一个周长为16厘米的正方形变换成面积为64平方厘米的正方形。实际是按( )的比放大的。
A.2:1 B.3:1 C.4:1 D.6:1
【考点】图形的放大与缩小.
【专题】比和比例应用题;应用意识.
【答案】A
【分析】根据正方形的周长=边长×4,正方形的边长=周长÷4,周长为16厘米的正方形,边长=16÷4=4(厘米);正方形的面积=边长×边长,面积为64平方厘米的正方形,边长是8厘米;将一个边长是4厘米的正方形变换成边长是8厘米的正方形,8:4=2:1,实际是按2:1的比放大的。
【解答】解:变换前正方形的边长:16÷4=4(厘米)
8×8=64(平方厘米)
所以变换后正方形的边长是8厘米。
8:4=2:1
答:实际是按2:1的比放大的。
故选:A。
【点评】掌握正方形的周长、面积公式是解题关键。
2.(2024春 凉州区期中)一个长方形的长是4分米,宽是3分米,把它按3:1扩大,得到图形的面积是( )平方分米。
A.36 B.108 C.42
【考点】图形的放大与缩小.
【专题】综合题;数据分析观念.
【答案】B
【分析】根据图形放大与缩小的意义,长4分米,宽3分米的长方形按3:1放大后,长是(4×3)分米,宽是(3×3)分米。根据长方形的面积计算公式“S=ab”即可求出放大后长方形的面积。
【解答】解:(4×3)×(3×3)
=12×9
=108(平方分米)
答:得到的长方形的面积是108平方分米。
故选:B。
【点评】长方形按3:1放大,即把长方形放大到原来的3倍,一个图形放大的倍数,是指对应边放大的倍数。
3.(2024 山阳县)如图的图形是按一定比例缩小的,则x=( )
A.10 B.8 C.7.5
【考点】图形的放大与缩小.
【专题】综合判断题;运算能力.
【答案】C
【分析】由于图形是按一定的比例缩小的,所以原来长比现在的长的比值和原来宽比现在的宽的比值相等,所以根据图中数据列比例解答即可。
【解答】解:根据题意,
5:4=x:6
4x=30
x=30÷4
x=7.5
故选:C。
【点评】本题主要是考查图形的放大和缩小的意义,根据图中数据列比例解答即可。
4.(2024 河北)把一个长为6厘米,宽为4厘米的长方形按1:2的比缩小后,长方形的面积是( )平方厘米。
A.6 B.24 C.12
【考点】图形的放大与缩小.
【专题】几何直观.
【答案】A
【分析】根据图形放大与缩小的意义,一个长6厘米、宽4厘米的长方形,按1:2缩小后长是(6÷2)厘米,宽是(4÷2)厘米,根据长方形的面积计算公式“S=ab”即可求出缩小后的面积。
【解答】解:(6÷2)×(4÷2)
=3×2
=6(平方厘米)
答:缩小后长方形的面积是6平方厘米。
故选:A。
【点评】本题考查了图形放大或缩小知识,结合题意分析解答即可。
5.(2024 广汉市)一个长方形,长和宽分别为10cm和8cm,按照1:2的比例缩小,所得到的新的长方形的长和宽分别为( )
A.4cm、5cm B.5cm、4cm C.16cm、20cm D.20cm、16cm
【考点】图形的放大与缩小.
【专题】图形与变换;应用意识.
【答案】B
【分析】用10和8分别乘,即可解答。
【解答】解:105(cm)
84(cm)
答:所得到的新的长方形的长和宽分别为5cm、4cm。
故选:B。
【点评】本题考查的是图形的放大与缩小,掌握方法是解答关键。
二.填空题(共5小题)
6.(2024春 平川区校级期中)如果把一个正方形按4:1放大,放大后正方形与放大前正方形的面积比是 16:1 。
【考点】图形的放大与缩小.
【专题】空间与图形.
【答案】16:1。
【分析】把一个正方形按4:l的比放大,则边长扩大到原来的4倍。正方形的面积=边长×边长,则正方形的面积扩大到原来的4×4=16倍,据此解答。
【解答】解:4×4=16
答:一个正方形按4:l的比放大,面积放大到原来的16倍,则放大后与放大前图形的面积比是16:1。
故答案为:16:1。
【点评】掌握图形放大和缩小的方法是解题的关键。
7.(2024春 潮州期中)一个长方形长4cm,宽3cm,按3:1的比放大后得到图形的面积是 108 cm2。
【考点】图形的放大与缩小.
【专题】空间与图形.
【答案】108。
【分析】一个长方形长4cm,宽3cm,按3:1的比放大后得到的图形,长和宽会放大到原来的3倍,据此分别放大后的长和宽,再求出面积即可。
【解答】解:4×3=12(厘米)
3×3=9(厘米)
12×9=108(平方厘米)
答:按3:1的比放大后得到图形的面积是108cm2。
故答案为:108。
【点评】掌握图形放大的特征是解题的关键。
8.(2024春 东莞市期中)将一个长3cm,宽2cm的长方形按2:1放大画在图纸上,这个长方形的周长是 20 cm,面积是 24 cm2。
【考点】图形的放大与缩小;长方形的周长;长方形、正方形的面积.
【专题】空间与图形.
【答案】20;24。
【分析】长方形按2:1放大,也就是把长方形的长和宽扩大到原来的2倍,求出放大后长方形的长和宽,再计算即可。
【解答】解:3×2=6(厘米)
2×2=4(厘米)
(6+4)×2=20(厘米)
6×4=24(平方厘米)
答:这个长方形的周长是20cm,面积是24cm2。
故答案为:20;24。
【点评】掌握图形放大和缩小的方法是解题的关键。
9.(2024春 绵阳期中)一个长5cm,宽3cm的长方形按3:1放大,放大后的长方形的面积是 135 cm2;放大前与放大后面积的比是 1:9 。
【考点】图形的放大与缩小.
【专题】空间与图形.
【答案】135;1:9。
【分析】长方形按3:1放大后,长和宽都扩大到原来的3倍,分别计算出变化前后的面积,再进行解答即可。
【解答】解:5×3=15(平方厘米)
(5×3)×(3×3)
=15×9
=135(平方厘米)
15:135=15:135=1:9
答:放大后的长方形的面积是135cm2;放大前与放大后面积的比是1:9。
故答案为:135;1:9。
【点评】明确长方形按3:1放大后,长和宽是都扩大到原来的3倍是解答本题的关键。
10.(2024 杭州)如图,将三角形ABC按比例放大成三角形ADE。已知AC=10cm,那么CE= 5 cm。
【考点】图形的放大与缩小.
【专题】应用意识.
【答案】5。
【分析】读题发现:已知三角形ABC的三条边的长度,按比例算出CE长度即可。
【解答】解:设CE的长度为xcm,则:
8:(12﹣8)=10:x
8:4=10:x
8x=4×10
8x=40
8x÷8=40÷8
x=5
故答案为:5。
【点评】本题考查了图形的放大、比的意义的应用问题,解答本题的关键或突破口在于清楚:AB与BD的长度比等于AC与CE的长度比,据此写出比例再算出结果即可。
三.判断题(共5小题)
11.(2024 淅川县)一个正方形按2:1放大后,周长和面积都扩大到原来的2倍. ×
【考点】图形的放大与缩小.
【专题】综合判断题;比和比例.
【答案】×
【分析】设这个正方形原来的边长为1,根据图形放大与缩小的意义,按2:1放大后的正方形的边长为2,分别求出原正方形周长、面积和放大后的正方形周长、面积,再看放大后的正方形的周长、面积是否分别是原正方形周长、面积的2倍.
【解答】解:设原正方形的边长为1
其周长是1×2=2
面积是1×1=1
按2:1放大后的正方形的边长为2
其周长是2×2=4
面积是2×2=4
4÷2=2
4÷1=4
即周长放大到原来的2倍,面积放大到原来的4倍,故原题说法错误;
故答案为:×.
【点评】图形放大或缩小的倍数是指对应边放大或缩小的倍数,周长也放大或缩小这个倍数,面积放大或缩小这个倍数的平方倍.
12.(2024春 惠阳区期中)把一个正方形按1:2缩小后,周长和面积都缩小到原来的。 ×
【考点】图形的放大与缩小.
【专题】空间与图形;几何直观.
【答案】×。
【分析】把一个正方形按1:2缩小后,周长缩小到原来的,面积缩小到原来的。
【解答】解:把一个正方形按1:2缩小后,周长缩小到原来的,面积缩小到原来的;原题说法错误。
故答案为:×。
【点评】掌握图形放大和缩小的方法是解题的关键。
13.(2024春 潮州期中)长方形按4:1的比放大,即它的面积也扩大为原来的4倍。 ×
【考点】图形的放大与缩小.
【专题】空间与图形.
【答案】×。
【分析】根据图形放大的意义,放大后的图形是原图形对应线段长的4倍,也就是长和宽分别扩大到原来的4倍,面积扩大到原来的4×4=16倍,据此解答。
【解答】解:长方形按4:1的比放大,即它的面积也扩大为原来的16倍,原题说法错误。
故答案为:×。
【点评】掌握图形放大的特征是解题的关键。
14.(2023秋 渝北区期末)一个长方形的长和宽同时缩小为原来的,它的大小变了,形状不变。 √
【考点】图形的放大与缩小.
【专题】应用意识.
【答案】√。
【分析】根据图形放大或缩小的意义,一个长方形的长和宽同时缩小为原来的,改变的是这个长方形的大小,而形状不变。
【解答】解:个长方形的长和宽同时缩小为原来的,它的大小变了,形状不变。
原题说法正确。
故答案为:√。
【点评】此题考查了图形放大或缩小的意义。一个图形放大或缩小,改变的是大小,形状不变。
15.(2023秋 沈丘县期末)把一个圆按1:5缩小后,直径变成4cm,原来的圆的周长是62.8cm。 √
【考点】图形的放大与缩小.
【专题】计算题;应用意识.
【答案】√
【分析】因为把一个圆按1:5缩小后,直径变成4cm,那么原来的直径,用“4×5”解答,再求出原来的圆的周长即可判断。
【解答】解:4×5=20(厘米)
3.14×20=62.8(厘米)
原来的圆的周长是62.8cm。说法正确。
故答案为:√。
【点评】求出原来的圆的直径是解答本题的关键。
四.计算题(共2小题)
16.(2023 邵阳县)把三角形A向右平移5格,得到三角形B,再将三角形B按3:1扩大,得到三角形C,请在下面方格纸中画出三角形B和三角形C。
【考点】图形的放大与缩小.
【专题】几何直观.
【答案】
【分析】根据平移的方法把三角形A的各个顶点向右平移5格,然后依次连接得到三角形B,再根据图形放大的方法,将三角形B的底和高分别扩大到原来的3倍,形状不变,即可画出按3:1扩大的三角形C。
【解答】解:如图:
【点评】本题考查了平移和图形的放大知识,结合题意分析解答即可。
17.将图1的三角形按比例缩小后得到图2的三角形,求未知数x.
【考点】图形的放大与缩小.
【专题】图形与变换;应用意识.
【答案】见试题解答内容
【分析】根据题意可知,缩小后的三角形与原三角形对应边成比例,所以设未知边为x,列比例为:1.6:x=3.2:4.8,利用比例的基本性质解比例即可.
【解答】解:设未知边为x,
1.6:x=3.2:4.8
3.2 x=1.6×4.8
x=2.4
答:未知数为2.4.
【点评】本题主要考查图形的放大与缩小,关键利用放大或缩小后的图形与原图形对应边成比例做题.
五.应用题(共3小题)
18.(2023春 揭东区期中)把一个长方形按1:3的比缩小,缩小后与缩小前的图形的面积相差64平方厘米。原来长方形的面积是多少平方厘米?
【考点】图形的放大与缩小.
【专题】应用意识.
【答案】72平方厘米。
【分析】一个图形按1:3缩小后,缩小后的图形的面积与缩小前图形的面积的比是(1×1):(3×3)=1:9;由此解答即可.
【解答】解:缩小后的图形的面积与缩小前图形的面积的比是(1×1):(3×3)=1:9
64÷(9﹣1)×9
=64÷8×9
=72(平方厘米)
答:原来长方形的面积是72平方厘米。
【点评】本题是考查图形的放大与缩小,一个图形放大或缩小n倍,它的面积将放大或缩小n2倍。
19.(2023 电白区模拟)把一张长7厘米、宽5厘米的长方形卡片按3:1的比例放大后,得到的卡片的面积是多少平方厘米?
【考点】图形的放大与缩小.
【专题】比和比例.
【答案】见试题解答内容
【分析】一个长7厘米、宽5厘米的长方形按3:1放大,即将这个长方形的长和宽同时扩大3倍,根据长方形的面积公式可知得到的图形的面积是:(7×3)×(5×3)=315(平方厘米).
【解答】解:(7×3)×(5×3)
=21×15
=315(平方厘米)
答:得到的卡片的面积是315平方厘米.
【点评】本题主要考查图形的放大或缩小,关键根据长方形的面积公式完成本题.
20.(2021 钦北区)李明在电脑上把一张长6厘米,宽4厘米的照片按比例放大,放大后照片的长是13.5厘米,宽是多少厘米?
【考点】图形的放大与缩小.
【专题】图形与变换;空间观念.
【答案】9厘米。
【分析】由题意可知:放大前后的长及放大前后的宽的比是一定的,即放大前后的对应的边成正比例,由此列出比例解决问题。
【解答】解:设放大后照片的宽应是x厘米,
6:13.5=4:x
6x=54
x=9
答:宽是9厘米。
【点评】解答此题关键是明确按比例放大长与长的比等于宽与宽的比。
六.解答题(共2小题)
21.(2024 播州区模拟)画一画.
(1)将三角形A的各条边按4:1放大,得到三角形B.
(2)将三角形B的各条边按1:2缩小,得到三角形C.
【考点】图形的放大与缩小.
【专题】图形与变换.
【答案】见试题解答内容
【分析】三角形A的两条直角边是2格,放大后两条直角边8格.据此画出图形B.
将B按1:2缩小后直角边变为4格,据此画出图形C.
【解答】解:所画图形如下:
【点评】本题考查图形的放大与缩小.
22.(2024 北川县)如图方格纸中小正方形的边长是1cm,按要求完成下面各题。
(1)圆O的圆心O点所在的位置用数对表示是( 3 , 8 )。画出将圆O向右平移4格后的图形。
(2)画出三角形ABC按2:1放大后的图形。原来三角形ABC的面积是放大后图形面积的 25 %。
【考点】图形的放大与缩小;数对与位置.
【专题】空间观念;几何直观.
【答案】(1)3,8;(2)25。
【分析】(1)用数对表示位置时,先表示第几列,再表示第几行,可知圆O的圆心O点所在的位置用数对表示是(3,8)。然后根据平移的方法,画出将圆O向右平移4格后的图形即可。
(2)根据图形放大的方法,画出三角形ABC按2:1放大到原来2倍后的图形即可。然后根据三角形的面积=底×高÷2,分别求出原来三角形ABC的面积和放大后图形面积,结合百分数的意义解答即可。
【解答】解:(1)圆O的圆心O点所在的位置用数对表示是(3,8)。画出将圆O向右平移4格后的图形。如图:
(2)画出三角形ABC按2:1放大后的图形。如图:
(3×2÷2)÷(6×4÷2)
=3÷12
=25%
答:原来三角形ABC的面积是放大后图形面积的25%。
故答案为:3,8;25。
【点评】本题考查了图形的平移、图形的放大、数对表示位置以及百分数的意义,结合题意分析解答即可。
21世纪教育网(www.21cnjy.com)
一.选择题(共5小题)
1.(2024春 滨海县期中)将一个周长为16厘米的正方形变换成面积为64平方厘米的正方形。实际是按( )的比放大的。
A.2:1 B.3:1 C.4:1 D.6:1
2.(2024春 凉州区期中)一个长方形的长是4分米,宽是3分米,把它按3:1扩大,得到图形的面积是( )平方分米。
A.36 B.108 C.42
3.(2024 山阳县)如图的图形是按一定比例缩小的,则x=( )
A.10 B.8 C.7.5
4.(2024 河北)把一个长为6厘米,宽为4厘米的长方形按1:2的比缩小后,长方形的面积是( )平方厘米。
A.6 B.24 C.12
5.(2024 广汉市)一个长方形,长和宽分别为10cm和8cm,按照1:2的比例缩小,所得到的新的长方形的长和宽分别为( )
A.4cm、5cm B.5cm、4cm C.16cm、20cm D.20cm、16cm
二.填空题(共5小题)
6.(2024春 平川区校级期中)如果把一个正方形按4:1放大,放大后正方形与放大前正方形的面积比是 。
7.(2024春 潮州期中)一个长方形长4cm,宽3cm,按3:1的比放大后得到图形的面积是 cm2。
8.(2024春 东莞市期中)将一个长3cm,宽2cm的长方形按2:1放大画在图纸上,这个长方形的周长是 cm,面积是 cm2。
9.(2024春 绵阳期中)一个长5cm,宽3cm的长方形按3:1放大,放大后的长方形的面积是 cm2;放大前与放大后面积的比是 。
10.(2024 杭州)如图,将三角形ABC按比例放大成三角形ADE。已知AC=10cm,那么CE= cm。
三.判断题(共5小题)
11.(2024 淅川县)一个正方形按2:1放大后,周长和面积都扩大到原来的2倍.
12.(2024春 惠阳区期中)把一个正方形按1:2缩小后,周长和面积都缩小到原来的。
13.(2024春 潮州期中)长方形按4:1的比放大,即它的面积也扩大为原来的4倍。
14.(2023秋 渝北区期末)一个长方形的长和宽同时缩小为原来的,它的大小变了,形状不变。
15.(2023秋 沈丘县期末)把一个圆按1:5缩小后,直径变成4cm,原来的圆的周长是62.8cm。
四.计算题(共2小题)
16.(2023 邵阳县)把三角形A向右平移5格,得到三角形B,再将三角形B按3:1扩大,得到三角形C,请在下面方格纸中画出三角形B和三角形C。
17.将图1的三角形按比例缩小后得到图2的三角形,求未知数x.
五.应用题(共3小题)
18.(2023春 揭东区期中)把一个长方形按1:3的比缩小,缩小后与缩小前的图形的面积相差64平方厘米。原来长方形的面积是多少平方厘米?
19.(2023 电白区模拟)把一张长7厘米、宽5厘米的长方形卡片按3:1的比例放大后,得到的卡片的面积是多少平方厘米?
20.(2021 钦北区)李明在电脑上把一张长6厘米,宽4厘米的照片按比例放大,放大后照片的长是13.5厘米,宽是多少厘米?
六.解答题(共2小题)
21.(2024 播州区模拟)画一画.
(1)将三角形A的各条边按4:1放大,得到三角形B.
(2)将三角形B的各条边按1:2缩小,得到三角形C.
22.(2024 北川县)如图方格纸中小正方形的边长是1cm,按要求完成下面各题。
(1)圆O的圆心O点所在的位置用数对表示是( , )。画出将圆O向右平移4格后的图形。
(2)画出三角形ABC按2:1放大后的图形。原来三角形ABC的面积是放大后图形面积的 %。
期末专项培优:图形的放大和缩小
参考答案与试题解析
一.选择题(共5小题)
1.(2024春 滨海县期中)将一个周长为16厘米的正方形变换成面积为64平方厘米的正方形。实际是按( )的比放大的。
A.2:1 B.3:1 C.4:1 D.6:1
【考点】图形的放大与缩小.
【专题】比和比例应用题;应用意识.
【答案】A
【分析】根据正方形的周长=边长×4,正方形的边长=周长÷4,周长为16厘米的正方形,边长=16÷4=4(厘米);正方形的面积=边长×边长,面积为64平方厘米的正方形,边长是8厘米;将一个边长是4厘米的正方形变换成边长是8厘米的正方形,8:4=2:1,实际是按2:1的比放大的。
【解答】解:变换前正方形的边长:16÷4=4(厘米)
8×8=64(平方厘米)
所以变换后正方形的边长是8厘米。
8:4=2:1
答:实际是按2:1的比放大的。
故选:A。
【点评】掌握正方形的周长、面积公式是解题关键。
2.(2024春 凉州区期中)一个长方形的长是4分米,宽是3分米,把它按3:1扩大,得到图形的面积是( )平方分米。
A.36 B.108 C.42
【考点】图形的放大与缩小.
【专题】综合题;数据分析观念.
【答案】B
【分析】根据图形放大与缩小的意义,长4分米,宽3分米的长方形按3:1放大后,长是(4×3)分米,宽是(3×3)分米。根据长方形的面积计算公式“S=ab”即可求出放大后长方形的面积。
【解答】解:(4×3)×(3×3)
=12×9
=108(平方分米)
答:得到的长方形的面积是108平方分米。
故选:B。
【点评】长方形按3:1放大,即把长方形放大到原来的3倍,一个图形放大的倍数,是指对应边放大的倍数。
3.(2024 山阳县)如图的图形是按一定比例缩小的,则x=( )
A.10 B.8 C.7.5
【考点】图形的放大与缩小.
【专题】综合判断题;运算能力.
【答案】C
【分析】由于图形是按一定的比例缩小的,所以原来长比现在的长的比值和原来宽比现在的宽的比值相等,所以根据图中数据列比例解答即可。
【解答】解:根据题意,
5:4=x:6
4x=30
x=30÷4
x=7.5
故选:C。
【点评】本题主要是考查图形的放大和缩小的意义,根据图中数据列比例解答即可。
4.(2024 河北)把一个长为6厘米,宽为4厘米的长方形按1:2的比缩小后,长方形的面积是( )平方厘米。
A.6 B.24 C.12
【考点】图形的放大与缩小.
【专题】几何直观.
【答案】A
【分析】根据图形放大与缩小的意义,一个长6厘米、宽4厘米的长方形,按1:2缩小后长是(6÷2)厘米,宽是(4÷2)厘米,根据长方形的面积计算公式“S=ab”即可求出缩小后的面积。
【解答】解:(6÷2)×(4÷2)
=3×2
=6(平方厘米)
答:缩小后长方形的面积是6平方厘米。
故选:A。
【点评】本题考查了图形放大或缩小知识,结合题意分析解答即可。
5.(2024 广汉市)一个长方形,长和宽分别为10cm和8cm,按照1:2的比例缩小,所得到的新的长方形的长和宽分别为( )
A.4cm、5cm B.5cm、4cm C.16cm、20cm D.20cm、16cm
【考点】图形的放大与缩小.
【专题】图形与变换;应用意识.
【答案】B
【分析】用10和8分别乘,即可解答。
【解答】解:105(cm)
84(cm)
答:所得到的新的长方形的长和宽分别为5cm、4cm。
故选:B。
【点评】本题考查的是图形的放大与缩小,掌握方法是解答关键。
二.填空题(共5小题)
6.(2024春 平川区校级期中)如果把一个正方形按4:1放大,放大后正方形与放大前正方形的面积比是 16:1 。
【考点】图形的放大与缩小.
【专题】空间与图形.
【答案】16:1。
【分析】把一个正方形按4:l的比放大,则边长扩大到原来的4倍。正方形的面积=边长×边长,则正方形的面积扩大到原来的4×4=16倍,据此解答。
【解答】解:4×4=16
答:一个正方形按4:l的比放大,面积放大到原来的16倍,则放大后与放大前图形的面积比是16:1。
故答案为:16:1。
【点评】掌握图形放大和缩小的方法是解题的关键。
7.(2024春 潮州期中)一个长方形长4cm,宽3cm,按3:1的比放大后得到图形的面积是 108 cm2。
【考点】图形的放大与缩小.
【专题】空间与图形.
【答案】108。
【分析】一个长方形长4cm,宽3cm,按3:1的比放大后得到的图形,长和宽会放大到原来的3倍,据此分别放大后的长和宽,再求出面积即可。
【解答】解:4×3=12(厘米)
3×3=9(厘米)
12×9=108(平方厘米)
答:按3:1的比放大后得到图形的面积是108cm2。
故答案为:108。
【点评】掌握图形放大的特征是解题的关键。
8.(2024春 东莞市期中)将一个长3cm,宽2cm的长方形按2:1放大画在图纸上,这个长方形的周长是 20 cm,面积是 24 cm2。
【考点】图形的放大与缩小;长方形的周长;长方形、正方形的面积.
【专题】空间与图形.
【答案】20;24。
【分析】长方形按2:1放大,也就是把长方形的长和宽扩大到原来的2倍,求出放大后长方形的长和宽,再计算即可。
【解答】解:3×2=6(厘米)
2×2=4(厘米)
(6+4)×2=20(厘米)
6×4=24(平方厘米)
答:这个长方形的周长是20cm,面积是24cm2。
故答案为:20;24。
【点评】掌握图形放大和缩小的方法是解题的关键。
9.(2024春 绵阳期中)一个长5cm,宽3cm的长方形按3:1放大,放大后的长方形的面积是 135 cm2;放大前与放大后面积的比是 1:9 。
【考点】图形的放大与缩小.
【专题】空间与图形.
【答案】135;1:9。
【分析】长方形按3:1放大后,长和宽都扩大到原来的3倍,分别计算出变化前后的面积,再进行解答即可。
【解答】解:5×3=15(平方厘米)
(5×3)×(3×3)
=15×9
=135(平方厘米)
15:135=15:135=1:9
答:放大后的长方形的面积是135cm2;放大前与放大后面积的比是1:9。
故答案为:135;1:9。
【点评】明确长方形按3:1放大后,长和宽是都扩大到原来的3倍是解答本题的关键。
10.(2024 杭州)如图,将三角形ABC按比例放大成三角形ADE。已知AC=10cm,那么CE= 5 cm。
【考点】图形的放大与缩小.
【专题】应用意识.
【答案】5。
【分析】读题发现:已知三角形ABC的三条边的长度,按比例算出CE长度即可。
【解答】解:设CE的长度为xcm,则:
8:(12﹣8)=10:x
8:4=10:x
8x=4×10
8x=40
8x÷8=40÷8
x=5
故答案为:5。
【点评】本题考查了图形的放大、比的意义的应用问题,解答本题的关键或突破口在于清楚:AB与BD的长度比等于AC与CE的长度比,据此写出比例再算出结果即可。
三.判断题(共5小题)
11.(2024 淅川县)一个正方形按2:1放大后,周长和面积都扩大到原来的2倍. ×
【考点】图形的放大与缩小.
【专题】综合判断题;比和比例.
【答案】×
【分析】设这个正方形原来的边长为1,根据图形放大与缩小的意义,按2:1放大后的正方形的边长为2,分别求出原正方形周长、面积和放大后的正方形周长、面积,再看放大后的正方形的周长、面积是否分别是原正方形周长、面积的2倍.
【解答】解:设原正方形的边长为1
其周长是1×2=2
面积是1×1=1
按2:1放大后的正方形的边长为2
其周长是2×2=4
面积是2×2=4
4÷2=2
4÷1=4
即周长放大到原来的2倍,面积放大到原来的4倍,故原题说法错误;
故答案为:×.
【点评】图形放大或缩小的倍数是指对应边放大或缩小的倍数,周长也放大或缩小这个倍数,面积放大或缩小这个倍数的平方倍.
12.(2024春 惠阳区期中)把一个正方形按1:2缩小后,周长和面积都缩小到原来的。 ×
【考点】图形的放大与缩小.
【专题】空间与图形;几何直观.
【答案】×。
【分析】把一个正方形按1:2缩小后,周长缩小到原来的,面积缩小到原来的。
【解答】解:把一个正方形按1:2缩小后,周长缩小到原来的,面积缩小到原来的;原题说法错误。
故答案为:×。
【点评】掌握图形放大和缩小的方法是解题的关键。
13.(2024春 潮州期中)长方形按4:1的比放大,即它的面积也扩大为原来的4倍。 ×
【考点】图形的放大与缩小.
【专题】空间与图形.
【答案】×。
【分析】根据图形放大的意义,放大后的图形是原图形对应线段长的4倍,也就是长和宽分别扩大到原来的4倍,面积扩大到原来的4×4=16倍,据此解答。
【解答】解:长方形按4:1的比放大,即它的面积也扩大为原来的16倍,原题说法错误。
故答案为:×。
【点评】掌握图形放大的特征是解题的关键。
14.(2023秋 渝北区期末)一个长方形的长和宽同时缩小为原来的,它的大小变了,形状不变。 √
【考点】图形的放大与缩小.
【专题】应用意识.
【答案】√。
【分析】根据图形放大或缩小的意义,一个长方形的长和宽同时缩小为原来的,改变的是这个长方形的大小,而形状不变。
【解答】解:个长方形的长和宽同时缩小为原来的,它的大小变了,形状不变。
原题说法正确。
故答案为:√。
【点评】此题考查了图形放大或缩小的意义。一个图形放大或缩小,改变的是大小,形状不变。
15.(2023秋 沈丘县期末)把一个圆按1:5缩小后,直径变成4cm,原来的圆的周长是62.8cm。 √
【考点】图形的放大与缩小.
【专题】计算题;应用意识.
【答案】√
【分析】因为把一个圆按1:5缩小后,直径变成4cm,那么原来的直径,用“4×5”解答,再求出原来的圆的周长即可判断。
【解答】解:4×5=20(厘米)
3.14×20=62.8(厘米)
原来的圆的周长是62.8cm。说法正确。
故答案为:√。
【点评】求出原来的圆的直径是解答本题的关键。
四.计算题(共2小题)
16.(2023 邵阳县)把三角形A向右平移5格,得到三角形B,再将三角形B按3:1扩大,得到三角形C,请在下面方格纸中画出三角形B和三角形C。
【考点】图形的放大与缩小.
【专题】几何直观.
【答案】
【分析】根据平移的方法把三角形A的各个顶点向右平移5格,然后依次连接得到三角形B,再根据图形放大的方法,将三角形B的底和高分别扩大到原来的3倍,形状不变,即可画出按3:1扩大的三角形C。
【解答】解:如图:
【点评】本题考查了平移和图形的放大知识,结合题意分析解答即可。
17.将图1的三角形按比例缩小后得到图2的三角形,求未知数x.
【考点】图形的放大与缩小.
【专题】图形与变换;应用意识.
【答案】见试题解答内容
【分析】根据题意可知,缩小后的三角形与原三角形对应边成比例,所以设未知边为x,列比例为:1.6:x=3.2:4.8,利用比例的基本性质解比例即可.
【解答】解:设未知边为x,
1.6:x=3.2:4.8
3.2 x=1.6×4.8
x=2.4
答:未知数为2.4.
【点评】本题主要考查图形的放大与缩小,关键利用放大或缩小后的图形与原图形对应边成比例做题.
五.应用题(共3小题)
18.(2023春 揭东区期中)把一个长方形按1:3的比缩小,缩小后与缩小前的图形的面积相差64平方厘米。原来长方形的面积是多少平方厘米?
【考点】图形的放大与缩小.
【专题】应用意识.
【答案】72平方厘米。
【分析】一个图形按1:3缩小后,缩小后的图形的面积与缩小前图形的面积的比是(1×1):(3×3)=1:9;由此解答即可.
【解答】解:缩小后的图形的面积与缩小前图形的面积的比是(1×1):(3×3)=1:9
64÷(9﹣1)×9
=64÷8×9
=72(平方厘米)
答:原来长方形的面积是72平方厘米。
【点评】本题是考查图形的放大与缩小,一个图形放大或缩小n倍,它的面积将放大或缩小n2倍。
19.(2023 电白区模拟)把一张长7厘米、宽5厘米的长方形卡片按3:1的比例放大后,得到的卡片的面积是多少平方厘米?
【考点】图形的放大与缩小.
【专题】比和比例.
【答案】见试题解答内容
【分析】一个长7厘米、宽5厘米的长方形按3:1放大,即将这个长方形的长和宽同时扩大3倍,根据长方形的面积公式可知得到的图形的面积是:(7×3)×(5×3)=315(平方厘米).
【解答】解:(7×3)×(5×3)
=21×15
=315(平方厘米)
答:得到的卡片的面积是315平方厘米.
【点评】本题主要考查图形的放大或缩小,关键根据长方形的面积公式完成本题.
20.(2021 钦北区)李明在电脑上把一张长6厘米,宽4厘米的照片按比例放大,放大后照片的长是13.5厘米,宽是多少厘米?
【考点】图形的放大与缩小.
【专题】图形与变换;空间观念.
【答案】9厘米。
【分析】由题意可知:放大前后的长及放大前后的宽的比是一定的,即放大前后的对应的边成正比例,由此列出比例解决问题。
【解答】解:设放大后照片的宽应是x厘米,
6:13.5=4:x
6x=54
x=9
答:宽是9厘米。
【点评】解答此题关键是明确按比例放大长与长的比等于宽与宽的比。
六.解答题(共2小题)
21.(2024 播州区模拟)画一画.
(1)将三角形A的各条边按4:1放大,得到三角形B.
(2)将三角形B的各条边按1:2缩小,得到三角形C.
【考点】图形的放大与缩小.
【专题】图形与变换.
【答案】见试题解答内容
【分析】三角形A的两条直角边是2格,放大后两条直角边8格.据此画出图形B.
将B按1:2缩小后直角边变为4格,据此画出图形C.
【解答】解:所画图形如下:
【点评】本题考查图形的放大与缩小.
22.(2024 北川县)如图方格纸中小正方形的边长是1cm,按要求完成下面各题。
(1)圆O的圆心O点所在的位置用数对表示是( 3 , 8 )。画出将圆O向右平移4格后的图形。
(2)画出三角形ABC按2:1放大后的图形。原来三角形ABC的面积是放大后图形面积的 25 %。
【考点】图形的放大与缩小;数对与位置.
【专题】空间观念;几何直观.
【答案】(1)3,8;(2)25。
【分析】(1)用数对表示位置时,先表示第几列,再表示第几行,可知圆O的圆心O点所在的位置用数对表示是(3,8)。然后根据平移的方法,画出将圆O向右平移4格后的图形即可。
(2)根据图形放大的方法,画出三角形ABC按2:1放大到原来2倍后的图形即可。然后根据三角形的面积=底×高÷2,分别求出原来三角形ABC的面积和放大后图形面积,结合百分数的意义解答即可。
【解答】解:(1)圆O的圆心O点所在的位置用数对表示是(3,8)。画出将圆O向右平移4格后的图形。如图:
(2)画出三角形ABC按2:1放大后的图形。如图:
(3×2÷2)÷(6×4÷2)
=3÷12
=25%
答:原来三角形ABC的面积是放大后图形面积的25%。
故答案为:3,8;25。
【点评】本题考查了图形的平移、图形的放大、数对表示位置以及百分数的意义,结合题意分析解答即可。
21世纪教育网(www.21cnjy.com)
