空间距离上课课件(2)
图片预览


文档简介
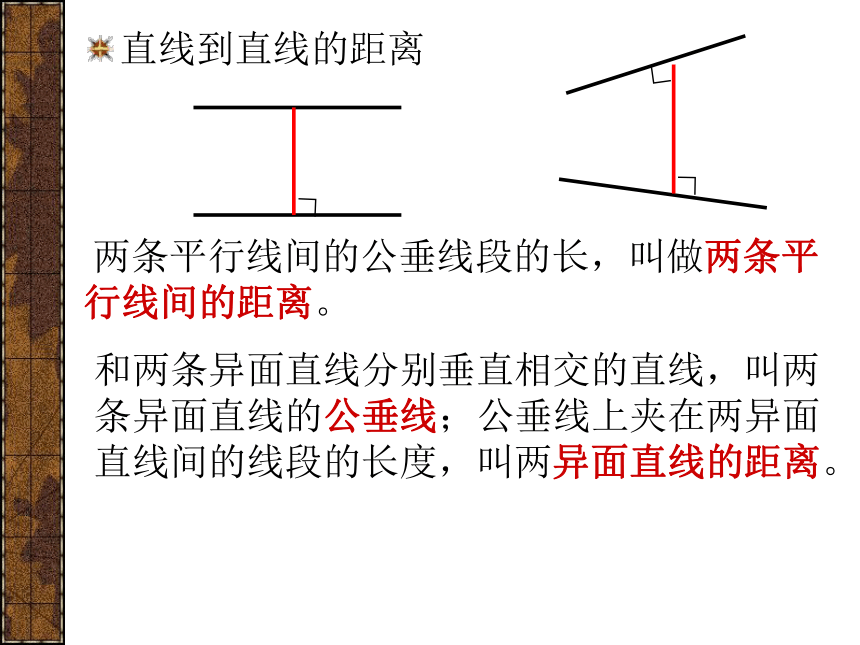
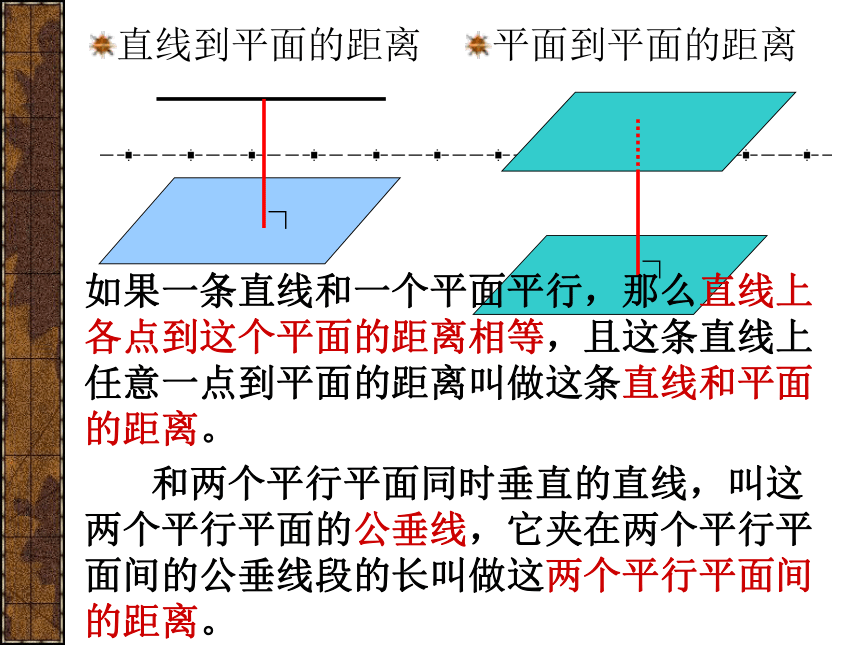
课件22张PPT。空间距离(二)直线到直线的距离 两条平行线间的公垂线段的长,叫做两条平行线间的距离。和两条异面直线分别垂直相交的直线,叫两条异面直线的公垂线;公垂线上夹在两异面直线间的线段的长度,叫两异面直线的距离。直线到平面的距离平面到平面的距离如果一条直线和一个平面平行,那么直线上各点到这个平面的距离相等,且这条直线上任意一点到平面的距离叫做这条直线和平面的距离。
和两个平行平面同时垂直的直线,叫这两个平行平面的公垂线,它夹在两个平行平面间的公垂线段的长叫做这两个平行平面间的距离。基本方法直接法
按定义直接作出垂线。
运用转化化归思想:面面距离→线面距离→点面距离→点点距离,即最终转化为两点间的距离来计算。通常将该线段置于一个直角三角形中求解。
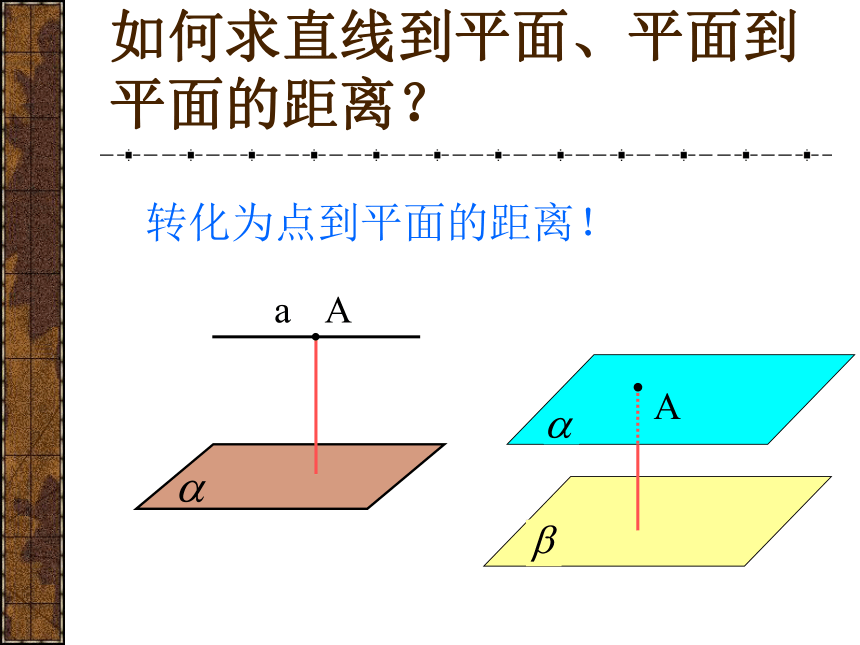
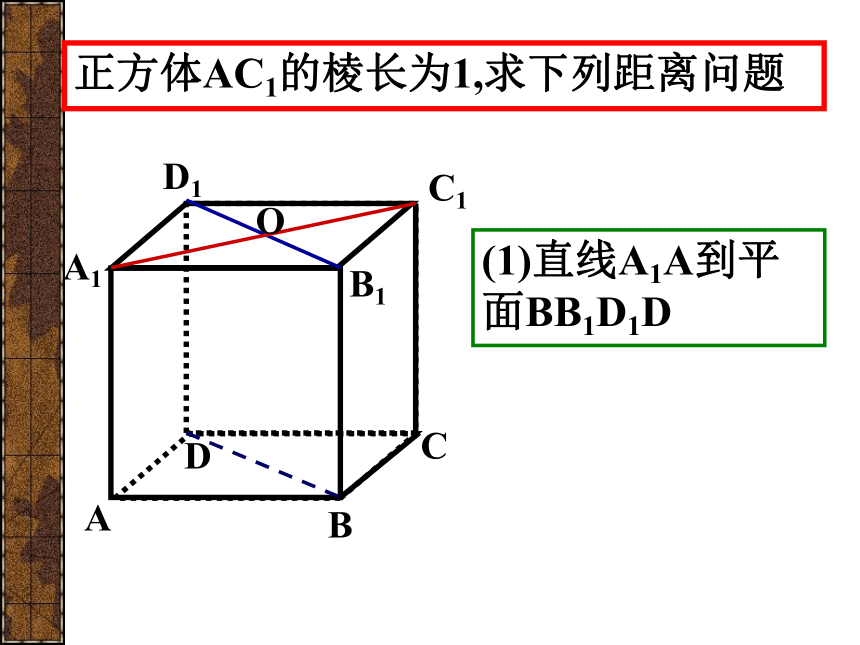
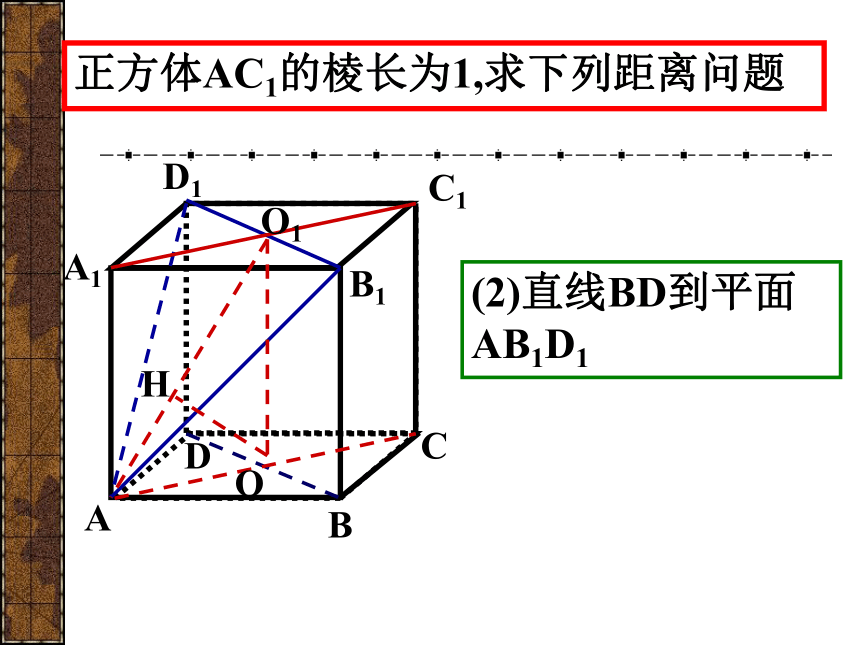
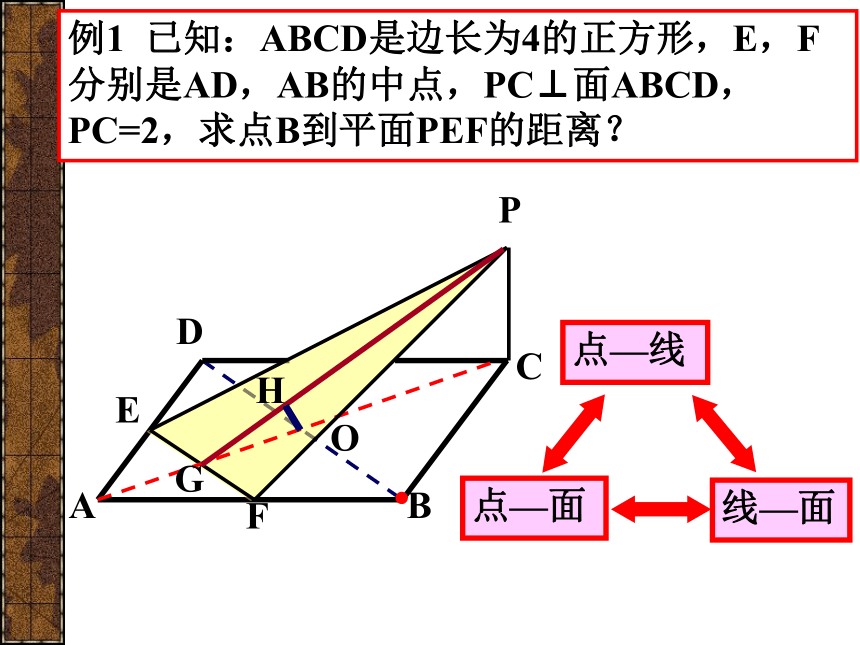
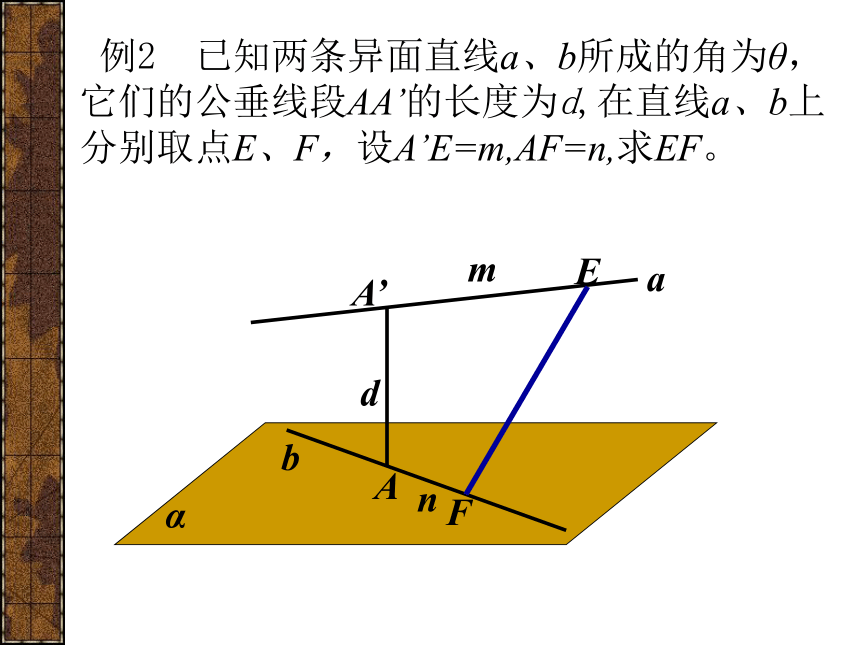
如何求直线到平面、平面到平面的距离?转化为点到平面的距离!AAABCA1B1D1C1正方体AC1的棱长为1,求下列距离问题D(1)直线A1A到平面BB1D1DOABCA1B1D1C1正方体AC1的棱长为1,求下列距离问题D(2)直线BD到平面AB1D1O1OH例1 已知:ABCD是边长为4的正方形,E,F分别是AD,AB的中点,PC⊥面ABCD,PC=2,求点B到平面PEF的距离?ABCDPFEGOH点—线点—面线—面 例2 已知两条异面直线a、b所成的角为θ,它们的公垂线段AA’的长度为d,在直线a、b上分别取点E、F,设A’E=m,AF=n,求EF。aA’AFmnEdαbabA’AFmnEαβθcd 例2 已知两条异面直线a、b所成的角为θ,它们的公垂线段AA’的长度为d,在直线a、b上分别取点E、F,设A’E=m,AF=n,求EF。abA’AFmnEαβθcGdFG = 例2 已知两条异面直线a、b所成的角为θ,它们的公垂线段AA’的长度为d,在直线a、b上分别取点E、F,设A’E=m,AF=n,求EF。abA’AFmnEαβθcGdFG = 例2 已知两条异面直线a、b所成的角为θ,它们的公垂线段AA’的长度为d,在直线a、b上分别取点E、F,设A’E=m,AF=n,求EF。abA’AFmnEαβθcGdEF = 例2 已知两条异面直线a、b所成的角为θ,它们的公垂线段AA’的长度为d,在直线a、b上分别取点E、F,设A’E=m,AF=n,求EF。abA’AFmnαdE 例2 已知两条异面直线a、b所成的角为θ,它们的公垂线段AA’的长度为d,在直线a、b上分别取点E、F,设A’E=m,AF=n,求EF。abA’AFmnαdEθGFG=?β 例2 已知两条异面直线a、b所成的角为θ,它们的公垂线段AA’的长度为d,在直线a、b上分别取点E、F,设A’E=m,AF=n,求EF。abA’AFmnαdEθGFG =β 例2 已知两条异面直线a、b所成的角为θ,它们的公垂线段AA’的长度为d,在直线a、b上分别取点E、F,设A’E=m,AF=n,求EF。abA’AFmnαdEθGEF=β 例2 已知两条异面直线a、b所成的角为θ,它们的公垂线段AA’的长度为d,在直线a、b上分别取点E、F,设A’E=m,AF=n,求EF。 例2 已知两条异面直线a、b所成的角为θ,它们的公垂线段AA’的长度为d,在直线a、b上分别取点E、F,设A’E=m,AF=n,求EF。aA’AFmnEdαb 例2 已知两条异面直线a、b所成的角为θ,在直线a、b上分别取点E、F,设A’E=m,AF=n, EF=l,求它们的公垂线段AA’的长度为d。aA’AFmnEdαblabA’AFmnαdE 例2 已知两条异面直线a、b所成的角为θ,在直线a、b上分别取点E、F,设A’E=m,AF=n, EF=l,求它们的公垂线段AA’的长度为d。OS练习:1.等边△ABC的边长为a,过△ABC的中心O作OP⊥平面ABC,且OP= ,则点P到△ABC的边的距离为
A.a B. C. D.2.设三棱锥S-ABC的底面为等腰直角三角形,斜边AC=10,侧棱SA=SB=SC=13,则顶点S到底面的距离为_________PONACBABCA练习:3正方形ABCD的边长是2,E、F分别是AB和CD的中点,将正方形沿EF折成直二面角(如图),M为矩形AEFD内的点,如果∠MBE=∠MBC,MB和平面BCF所成角的正切值为1/2,那么点M到直线EF的距离为______P
和两个平行平面同时垂直的直线,叫这两个平行平面的公垂线,它夹在两个平行平面间的公垂线段的长叫做这两个平行平面间的距离。基本方法直接法
按定义直接作出垂线。
运用转化化归思想:面面距离→线面距离→点面距离→点点距离,即最终转化为两点间的距离来计算。通常将该线段置于一个直角三角形中求解。
如何求直线到平面、平面到平面的距离?转化为点到平面的距离!AAABCA1B1D1C1正方体AC1的棱长为1,求下列距离问题D(1)直线A1A到平面BB1D1DOABCA1B1D1C1正方体AC1的棱长为1,求下列距离问题D(2)直线BD到平面AB1D1O1OH例1 已知:ABCD是边长为4的正方形,E,F分别是AD,AB的中点,PC⊥面ABCD,PC=2,求点B到平面PEF的距离?ABCDPFEGOH点—线点—面线—面 例2 已知两条异面直线a、b所成的角为θ,它们的公垂线段AA’的长度为d,在直线a、b上分别取点E、F,设A’E=m,AF=n,求EF。aA’AFmnEdαbabA’AFmnEαβθcd 例2 已知两条异面直线a、b所成的角为θ,它们的公垂线段AA’的长度为d,在直线a、b上分别取点E、F,设A’E=m,AF=n,求EF。abA’AFmnEαβθcGdFG = 例2 已知两条异面直线a、b所成的角为θ,它们的公垂线段AA’的长度为d,在直线a、b上分别取点E、F,设A’E=m,AF=n,求EF。abA’AFmnEαβθcGdFG = 例2 已知两条异面直线a、b所成的角为θ,它们的公垂线段AA’的长度为d,在直线a、b上分别取点E、F,设A’E=m,AF=n,求EF。abA’AFmnEαβθcGdEF = 例2 已知两条异面直线a、b所成的角为θ,它们的公垂线段AA’的长度为d,在直线a、b上分别取点E、F,设A’E=m,AF=n,求EF。abA’AFmnαdE 例2 已知两条异面直线a、b所成的角为θ,它们的公垂线段AA’的长度为d,在直线a、b上分别取点E、F,设A’E=m,AF=n,求EF。abA’AFmnαdEθGFG=?β 例2 已知两条异面直线a、b所成的角为θ,它们的公垂线段AA’的长度为d,在直线a、b上分别取点E、F,设A’E=m,AF=n,求EF。abA’AFmnαdEθGFG =β 例2 已知两条异面直线a、b所成的角为θ,它们的公垂线段AA’的长度为d,在直线a、b上分别取点E、F,设A’E=m,AF=n,求EF。abA’AFmnαdEθGEF=β 例2 已知两条异面直线a、b所成的角为θ,它们的公垂线段AA’的长度为d,在直线a、b上分别取点E、F,设A’E=m,AF=n,求EF。 例2 已知两条异面直线a、b所成的角为θ,它们的公垂线段AA’的长度为d,在直线a、b上分别取点E、F,设A’E=m,AF=n,求EF。aA’AFmnEdαb 例2 已知两条异面直线a、b所成的角为θ,在直线a、b上分别取点E、F,设A’E=m,AF=n, EF=l,求它们的公垂线段AA’的长度为d。aA’AFmnEdαblabA’AFmnαdE 例2 已知两条异面直线a、b所成的角为θ,在直线a、b上分别取点E、F,设A’E=m,AF=n, EF=l,求它们的公垂线段AA’的长度为d。OS练习:1.等边△ABC的边长为a,过△ABC的中心O作OP⊥平面ABC,且OP= ,则点P到△ABC的边的距离为
A.a B. C. D.2.设三棱锥S-ABC的底面为等腰直角三角形,斜边AC=10,侧棱SA=SB=SC=13,则顶点S到底面的距离为_________PONACBABCA练习:3正方形ABCD的边长是2,E、F分别是AB和CD的中点,将正方形沿EF折成直二面角(如图),M为矩形AEFD内的点,如果∠MBE=∠MBC,MB和平面BCF所成角的正切值为1/2,那么点M到直线EF的距离为______P
