2024-2025学年苏科版八年级数学下学期期中模拟试卷( 含解析)
文档属性
| 名称 | 2024-2025学年苏科版八年级数学下学期期中模拟试卷( 含解析) |  | |
| 格式 | docx | ||
| 文件大小 | 2.1MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-05-09 18:00:06 | ||
图片预览


文档简介
2024-2025学年八年级下学期期中模拟
数学试题
注意事项:
1.考试时间:100分钟,试卷满分:100分。本试卷分第Ⅰ卷(选择题)和第Ⅱ卷(非选择题)两部分。答卷前,考生务必将自己的姓名、准考证号填写在答题卡上。
2.回答第Ⅰ卷时,选出每小题答案后,用2B铅笔把答题卡上对应题目的答案标号涂黑。如需改动,用橡皮擦干净后,再选涂其他答案标号。写在本试卷上无效。
3.回答第Ⅱ卷时,将答案写在答题卡上。写在本试卷上无效。
4.测试范围:八年级数学下册第7章-第9章(苏科版2024新教材)。
第Ⅰ卷
一、选择题:本题共8小题,每小题2分,共16分。在每小题给出的四个选项中,只有一项是符合题目要求的。
1.在中国悠久的历史长河中,古窗作为建筑艺术的重要组成部分,展现了中华民族深邃的文化底蕴和审美情趣.下列窗户图案中,是中心对称图形的是( )
A.B.C.D.
2.某市某年约有51000名学生参加体育中考,为了解这51000名学生的体育成绩,从中抽取了2000名学生的体育成绩进行分析,以下说法正确的是( )
A.51000名学生是总体
B.每名学生是个体
C.抽取的2000名考生的体育成绩是总体的一个样本
D.样本容量是2000名
3.从一定高度落下的图钉,落地后针尖着地.这个事件是( )
A.必然事件 B.不可能事件 C.确定性事件 D.随机事件
4.如图,四边形的对角线相交于点,下列条件能判定四边形是平行四边形的是( )
A., B.,
C., D.,
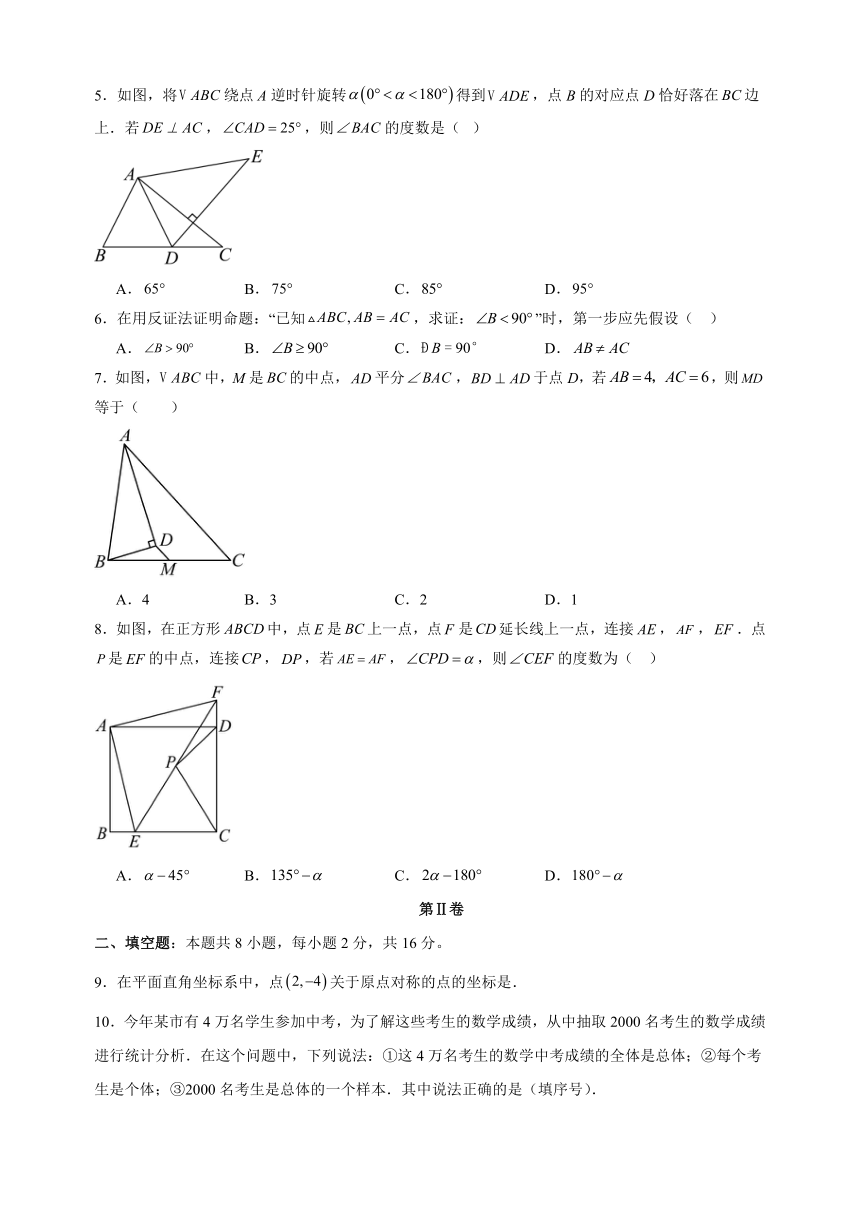
5.如图,将绕点A逆时针旋转得到,点B的对应点D恰好落在边上.若,,则的度数是( )
A. B. C. D.
6.在用反证法证明命题:“已知,求证:”时,第一步应先假设( )
A. B. C. D.
7.如图,中,M是的中点,平分,于点D,若,则等于( )
A.4 B.3 C.2 D.1
8.如图,在正方形中,点是上一点,点是延长线上一点,连接,,.点是的中点,连接,,若,,则的度数为( )
A. B. C. D.
第Ⅱ卷
二、填空题:本题共8小题,每小题2分,共16分。
9.在平面直角坐标系中,点关于原点对称的点的坐标是.
10.今年某市有4万名学生参加中考,为了解这些考生的数学成绩,从中抽取2000名考生的数学成绩进行统计分析.在这个问题中,下列说法:①这4万名考生的数学中考成绩的全体是总体;②每个考生是个体;③2000名考生是总体的一个样本.其中说法正确的是(填序号).
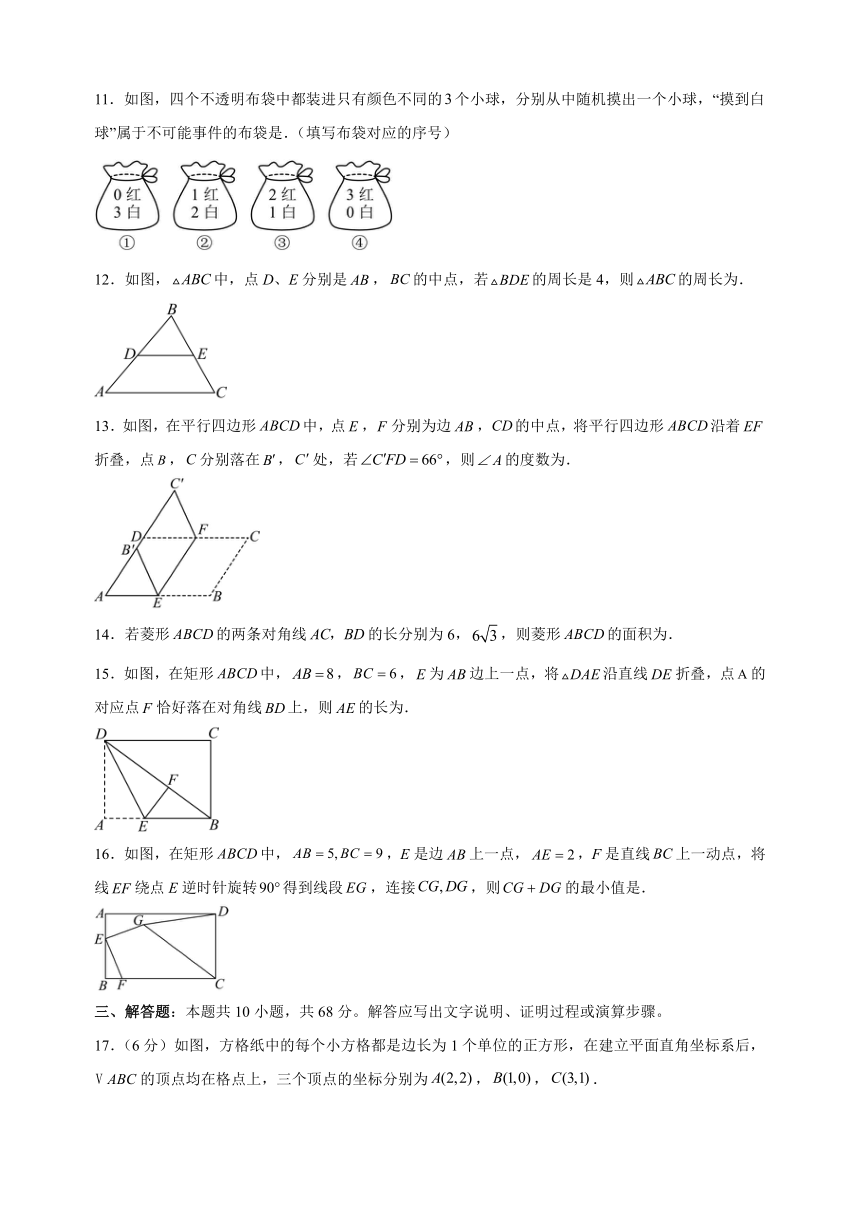
11.如图,四个不透明布袋中都装进只有颜色不同的个小球,分别从中随机摸出一个小球,“摸到白球”属于不可能事件的布袋是.(填写布袋对应的序号)
12.如图,中,点D、E分别是,的中点,若的周长是4,则的周长为.
13.如图,在平行四边形中,点,分别为边,的中点,将平行四边形沿着折叠,点,分别落在,处,若,则的度数为.
14.若菱形的两条对角线的长分别为6,,则菱形的面积为.
15.如图,在矩形中,,,为边上一点,将沿直线折叠,点的对应点恰好落在对角线上,则的长为.
16.如图,在矩形中,,E是边上一点,,F是直线上一动点,将线绕点E逆时针旋转得到线段,连接,则的最小值是.
三、解答题:本题共10小题,共68分。解答应写出文字说明、证明过程或演算步骤。
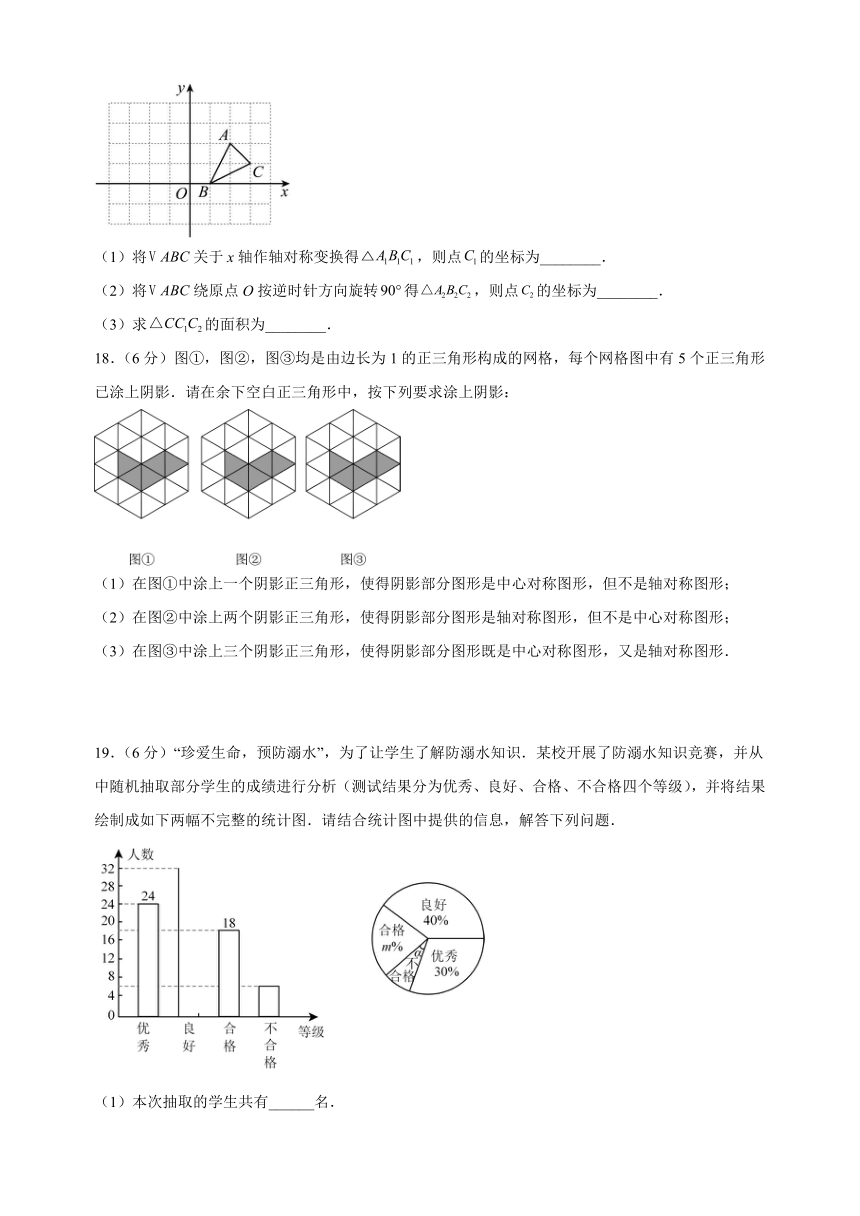
17.(6分)如图,方格纸中的每个小方格都是边长为1个单位的正方形,在建立平面直角坐标系后,的顶点均在格点上,三个顶点的坐标分别为,,.
(1)将关于x轴作轴对称变换得,则点的坐标为________.
(2)将绕原点O按逆时针方向旋转得,则点的坐标为________.
(3)求的面积为________.
18.(6分)图①,图②,图③均是由边长为1的正三角形构成的网格,每个网格图中有5个正三角形已涂上阴影.请在余下空白正三角形中,按下列要求涂上阴影:
(1)在图①中涂上一个阴影正三角形,使得阴影部分图形是中心对称图形,但不是轴对称图形;
(2)在图②中涂上两个阴影正三角形,使得阴影部分图形是轴对称图形,但不是中心对称图形;
(3)在图③中涂上三个阴影正三角形,使得阴影部分图形既是中心对称图形,又是轴对称图形.
19.(6分)“珍爱生命,预防溺水”,为了让学生了解防溺水知识.某校开展了防溺水知识竞赛,并从中随机抽取部分学生的成绩进行分析(测试结果分为优秀、良好、合格、不合格四个等级),并将结果绘制成如下两幅不完整的统计图.请结合统计图中提供的信息,解答下列问题.
(1)本次抽取的学生共有______名.
(2)请补全条形统计图.
(3)在扇形统计图中,“不合格”等级所对应的圆心角的度数是______,“合格”等级中的值为______.
20.(6分)在一个不透明的箱子里,装有若干个除了颜色外均相同的小球,某数学学习小组做摸球试验,将球搅匀后从中随机摸出一个球记下颜色,再把它放回箱子中,重复该操作.下表是活动进行中的一组统计数据:
摸球的次数
摸到白球的次数
摸到白球的频率
(1)上表中的_____,_____;
(2)“摸到白球”的概率的估计值是_____;(精确到)
(3)如果箱子中一共有个球,除了白球外,估计还有多少个其他颜色的球?
21.(6分)已知:互不重合的点、、、按图中顺序依次在同一条直线上,且,,,为锐角.
(1)求证:;
(2)连接、,若,求证:与互相平分
22.(4分)如图,是的中位线,的平分线交于点,连接并延长交于,若,,求的长.
23.(8分)中国古代数学家刘徽在《九章算术》中,给出了证明三角形面积公式的“出入相补法”,原理如下:
如图,在中,点D,E分别是的中点,连接,过点A作,垂足为F,延长至点G,使,连接,延长至点H,使,连接,则四边形的面积等于的面积.
(1)求证:四边形为矩形;
(2)若,利用上述结论求的面积.
24.(8分)如图,在矩形中,过对角线的中点O作的垂线,分别交、于E、F.
(1)求证:四边形是菱形;
(2)若,,求菱形的周长.
25.(8分)综合与实践
在综合与实践课上,赵老师让同学们以“正方形的折叠”为主题开展数学活动.
操作一:对折正方形纸片,使与重合,得到折痕,把纸片展平;
操作二:在上选一点P,沿折叠,使点A落在正方形内部点M处,把纸片展平.连接并延长交于点Q,连接.
(1)数学思考:
如图1,当点M在上时,与的数量关系是_______.
(2)拓展再探:
如图2,当改变点P在上的位置(点P不与点A,D重合),使点M不在上时,判断(1)中与的数量关系是否仍然成立?若成立,请证明;若不成立,请说明理由.
(3)迁移应用:
在(2)的探究中,连接,已知正方形纸片的边长为6,当的周长最小时,的长为多少?
26.(10分)对于点P,直线l和图形N,给出如下定义:若点P关于直线l的对称点在图形N的内部或边上,则称点P为图形N关于直线l的“镜像点”.
在平面直角坐标系中,已知的三个顶点的坐标分别为,,.设点,直线为过点且与y轴垂直的直线.
(1)若在点中,点________是关于直线的“镜像点”;
(2)当时,若x轴上存在关于直线的“镜像点”,则t的最小值为________;
(3)已知直线过点且与第一、三象限的角平分线平行.
①若直线上存在关于直线的“镜像点”,直接写出t的取值范围;
②已知边长为1的正方形的对角线的交点为,且正方形的边与坐标轴平行.若正方形边上的所有点都是关于直线的“镜像点”,直接写出t的取值范围.
参考答案
一、选择题:本题共8小题,每小题2分,共16分。在每小题给出的四个选项中,只有一项是符合题目要求的。
1.在中国悠久的历史长河中,古窗作为建筑艺术的重要组成部分,展现了中华民族深邃的文化底蕴和审美情趣.下列窗户图案中,是中心对称图形的是( )
A.B.C.D.
【答案】C
【详解】解:A、没有对称中心,不是中心对称图形,不符合题意;
B、没有对称中心,不是中心对称图形,不符合题意;
C、有对称中心,是中心对称图形,符合题意;
D、没有对称中心,不是中心对称图形,不符合题意;
故选:C .
2.某市某年约有51000名学生参加体育中考,为了解这51000名学生的体育成绩,从中抽取了2000名学生的体育成绩进行分析,以下说法正确的是( )
A.51000名学生是总体
B.每名学生是个体
C.抽取的2000名考生的体育成绩是总体的一个样本
D.样本容量是2000名
【答案】C
【详解】解:51000名学生的体育成绩是总体,每名学生的体育成绩是个体,抽取的2000名考生的体育成绩是总体的一个样本,样本容量是2000,因此选项A、B、D错误,选项C正确;
故选:C.
3.从一定高度落下的图钉,落地后针尖着地.这个事件是( )
A.必然事件 B.不可能事件 C.确定性事件 D.随机事件
【答案】D
【详解】解:从一定高度落下的图钉,落地后针尖着地.这个事件是随机事件.
故选D.
4.如图,四边形的对角线相交于点,下列条件能判定四边形是平行四边形的是( )
A., B.,
C., D.,
【答案】C
【详解】解:∵,
∴,
∵,
∴,
∴,
又∵,
∴四边形是平行四边形,故C符合题意,
但是A、B、D条件均不能证明,故不符合题意,
故选:C.
5.如图,将绕点A逆时针旋转得到,点B的对应点D恰好落在边上.若,,则的度数是( )
A. B. C. D.
【答案】B
【详解】解:根据题意,
∵,,
∴,
由旋转的性质可得,,
∴,
∴,
∴;
故选:B.
6.在用反证法证明命题:“已知,求证:”时,第一步应先假设( )
A. B. C. D.
【答案】B
【详解】解:“已知,求证:”时,结论为且反证法第一步应先假设结论不成立
第一步应先假设,
故选:B.
7.如图,中,M是的中点,平分,于点D,若,则等于( )
A.4 B.3 C.2 D.1
【答案】D
【详解】解:延长交于H,
,
,
,
是的中位线,
,
故选:D.
8.如图,在正方形中,点是上一点,点是延长线上一点,连接,,.点是的中点,连接,,若,,则的度数为( )
A. B. C. D.
【答案】A
【详解】解:如图,连接,
四边形为正方形,
,,,
在和中,
,
∴,
,
,
,
即,
为中点,
,
,为中点,
,
,
在和中,
,
,
,,
,
,
,
,,为中点,
,
,
,
,
,
故选:A.
第Ⅱ卷
二、填空题:本题共8小题,每小题2分,共16分。
9.在平面直角坐标系中,点关于原点对称的点的坐标是.
【答案】
【详解】解:点关于原点对称的点的坐标是,
故答案为:.
10.今年某市有4万名学生参加中考,为了解这些考生的数学成绩,从中抽取2000名考生的数学成绩进行统计分析.在这个问题中,下列说法:①这4万名考生的数学中考成绩的全体是总体;②每个考生是个体;③2000名考生是总体的一个样本.其中说法正确的是(填序号).
【答案】①
【详解】解:对于①,这4万名考生的数学中考成绩的全体是总体,故正确;
对于②,每个考生的数学中考成绩是个体,故错误;
对于③,2000名考生的中考数学成绩是总体的一个样本,故错误;
故①正确,
故答案为:①.
11.如图,四个不透明布袋中都装进只有颜色不同的个小球,分别从中随机摸出一个小球,“摸到白球”属于不可能事件的布袋是.(填写布袋对应的序号)
【答案】
【详解】解:①袋中有个白球,没有红球,摸到白球属于必然事件;
②袋中有个红球,个白球,摸到白球属于随机事件;
③袋中有个红球,个白球,摸到白球属于随机事件;
④袋中有个红球,没有白球,摸到白球属于不可能事件.
故答案为.
12.如图,中,点D、E分别是,的中点,若的周长是4,则的周长为.
【答案】8
【详解】解:∵点D、E分别是,的中点,
∴是的中位线,,
∴,
又∵的周长是4,
即,
∴的周长,
故答案为:8.
13.如图,在平行四边形中,点,分别为边,的中点,将平行四边形沿着折叠,点,分别落在,处,若,则的度数为.
【答案】
【详解】解:∵四边形是平行四边形,
∴,,
∴,
∵点,分别是,的中点,
∴,
由折叠可得:,
∴,
∴,
∵,
∴,
∴,
∴.
故答案为:.
14.若菱形的两条对角线的长分别为6,,则菱形的面积为.
【答案】
【详解】解:四边形是菱形,的长分别为6,,
菱形的面积.
故答案为:.
15.如图,在矩形中,,,为边上一点,将沿直线折叠,点的对应点恰好落在对角线上,则的长为.
【答案】3
【详解】解:∵四边形是矩形,
∴,,
∴,
∵将沿直线折叠,点的对应点恰好落在对角线上,
∴,,,
∴,
∵,
∴,
∴,
故答案为:3
16.如图,在矩形中,,E是边上一点,,F是直线上一动点,将线绕点E逆时针旋转得到线段,连接,则的最小值是.
【答案】13
【详解】解:将绕点逆时针旋转得到,延长交于点,延长至点,使,连接,
∵在矩形中,,,,
∴,,,
∴,,
∴,
∴四边形是矩形,
∴,,
∴,,
∴是的垂直平分线,
∴,
∵是直线上一动点,
∴,
∴当点,,三点共线时,取最小值,
在中,,,
,
∴的最小值是.
故答案为:.
三、解答题:本题共10小题,共68分。解答应写出文字说明、证明过程或演算步骤。
17.(6分)如图,方格纸中的每个小方格都是边长为1个单位的正方形,在建立平面直角坐标系后,的顶点均在格点上,三个顶点的坐标分别为,,.
(1)将关于x轴作轴对称变换得,则点的坐标为________.
(2)将绕原点O按逆时针方向旋转得,则点的坐标为________.
(3)求的面积为________.
【详解】(1)解:如图,即为所作
∴,
故答案为:;…………………………………2分
(2)解:即为所作,
∴,
故答案为:;…………………………………4分
(3)解:如图,的面积为
故答案为:4.…………………………………6分
18.(6分)图①,图②,图③均是由边长为1的正三角形构成的网格,每个网格图中有5个正三角形已涂上阴影.请在余下空白正三角形中,按下列要求涂上阴影:
(1)在图①中涂上一个阴影正三角形,使得阴影部分图形是中心对称图形,但不是轴对称图形;
(2)在图②中涂上两个阴影正三角形,使得阴影部分图形是轴对称图形,但不是中心对称图形;
(3)在图③中涂上三个阴影正三角形,使得阴影部分图形既是中心对称图形,又是轴对称图形.
【详解】(1)解:如下图为所作图形:
…………………………………2分
(2)解:如下图为所作图形:
…………………………………4分
(3)解:如下图为所作图形:
…………………………………6分
19.(6分)“珍爱生命,预防溺水”,为了让学生了解防溺水知识.某校开展了防溺水知识竞赛,并从中随机抽取部分学生的成绩进行分析(测试结果分为优秀、良好、合格、不合格四个等级),并将结果绘制成如下两幅不完整的统计图.请结合统计图中提供的信息,解答下列问题.
(1)本次抽取的学生共有______名.
(2)请补全条形统计图.
(3)在扇形统计图中,“不合格”等级所对应的圆心角的度数是______,“合格”等级中的值为______.
【详解】(1)解:(名),
答:本次抽取的学生共有名;…………………………………2分
(2)解:测试结果为良好的有:(名),
补全条形统计图如下:
;…………………………………4分
(3)解:“不合格”等级所对应的圆心角的度数是:,“合格”等级中的值为:,
故答案为:,.…………………………………6分
20.(6分)在一个不透明的箱子里,装有若干个除了颜色外均相同的小球,某数学学习小组做摸球试验,将球搅匀后从中随机摸出一个球记下颜色,再把它放回箱子中,重复该操作.下表是活动进行中的一组统计数据:
摸球的次数
摸到白球的次数
摸到白球的频率
(1)上表中的_____,_____;
(2)“摸到白球”的概率的估计值是_____;(精确到)
(3)如果箱子中一共有个球,除了白球外,估计还有多少个其他颜色的球?
【详解】(1)解:,
,
故答案为:;;…………………………………2分
(2)“摸到白球”的概率的估计值是,
故答案为:;…………………………………4分
(3)(个),
∴除白球外,还有大约个其它颜色的小球.…………………………………6分
21.(6分)已知:互不重合的点、、、按图中顺序依次在同一条直线上,且,,,为锐角.
(1)求证:;
(2)连接、,若,求证:与互相平分
【详解】(1)证明:,
,即,
,,
;…………………………………3分
(2)证明:如图,连接,,,
,
,
,,
,,
,
四边形是平行四边形,
与互相平分.
…………………………………6分
22.(4分)如图,是的中位线,的平分线交于点,连接并延长交于,若,,求的长.
【详解】解:∵是的中位线,
∴,,
∵是的平分线,
∴,
∵,
∴.
∴.
∴.
∴,
∴.…………………………………4分
23.(8分)中国古代数学家刘徽在《九章算术》中,给出了证明三角形面积公式的“出入相补法”,原理如下:
如图,在中,点D,E分别是的中点,连接,过点A作,垂足为F,延长至点G,使,连接,延长至点H,使,连接,则四边形的面积等于的面积.
(1)求证:四边形为矩形;
(2)若,利用上述结论求的面积.
【详解】(1)证明:点D,E分别是的中点,
.
,
,
.
同理可得:,,
,
∴四边形BCHG是平行四边形,
又∠H=90°(已证),
四边形为矩形.…………………………………4分
(2)解:点D,E分别是的中点,
是的中位线,
,
由(1)可知,,
,
.…………………………………8分
24.(8分)如图,在矩形中,过对角线的中点O作的垂线,分别交、于E、F.
(1)求证:四边形是菱形;
(2)若,,求菱形的周长.
【详解】(1)证明:∵四边形是矩形
∴
∴
∵点是的中点
∴
在和中
∴
∴
已知
∴四边形是平行四边形
∵
∴四边形是菱形;…………………………………4分
(2)解:∵四边形是矩形
∴
∵四边形是菱形
∴
设菱形的边长为,
则,
在中
即
解得
∴菱形的周长为20.…………………………………8分
25.(8分)综合与实践
在综合与实践课上,赵老师让同学们以“正方形的折叠”为主题开展数学活动.
操作一:对折正方形纸片,使与重合,得到折痕,把纸片展平;
操作二:在上选一点P,沿折叠,使点A落在正方形内部点M处,把纸片展平.连接并延长交于点Q,连接.
(1)数学思考:
如图1,当点M在上时,与的数量关系是_______.
(2)拓展再探:
如图2,当改变点P在上的位置(点P不与点A,D重合),使点M不在上时,判断(1)中与的数量关系是否仍然成立?若成立,请证明;若不成立,请说明理由.
(3)迁移应用:
在(2)的探究中,连接,已知正方形纸片的边长为6,当的周长最小时,的长为多少?
【详解】(1)证明:∵四边形是正方形,
∴,,
由折叠得,,,
∴,
在和中,
,
∴,
∴,
∵,,
∴,
∴;…………………………………2分
(2)解:成立,
∵四边形是正方形,
∴,,
由折叠得,,,
∴,
在和中,
,
∴,
∴,
∵,,
∴,
∴;…………………………………5分
(3)解:由折叠得,,
∴的周长为,
当取最小值时,的周长最小,
∵点的轨迹是以点为圆心,的长为半径的圆弧;
以点为圆心,的长为半径画圆,当点D,M,B共线时,最小,
设,则,
由折叠得,,,
∵,
∴,
在中,,
∴,
∴,
∴…………………………………8分
26.(10分)对于点P,直线l和图形N,给出如下定义:若点P关于直线l的对称点在图形N的内部或边上,则称点P为图形N关于直线l的“镜像点”.
在平面直角坐标系中,已知的三个顶点的坐标分别为,,.设点,直线为过点且与y轴垂直的直线.
(1)若在点中,点________是关于直线的“镜像点”;
(2)当时,若x轴上存在关于直线的“镜像点”,则t的最小值为________;
(3)已知直线过点且与第一、三象限的角平分线平行.
①若直线上存在关于直线的“镜像点”,直接写出t的取值范围;
②已知边长为1的正方形的对角线的交点为,且正方形的边与坐标轴平行.若正方形边上的所有点都是关于直线的“镜像点”,直接写出t的取值范围.
【详解】(1)解:将各个点标示在平面直角坐标系中,
∵关于直线的对称点为,,,
∴点和点是关于直线的“镜像点”.
故答案为:点和点;…………………………………3分
(2)解∶求t的最小值,这个最小值必然是负值,对称轴直线是平行x轴的,
所以观察竖直方向,上离x轴最远的点为C,
则x轴上的关于直线的“镜像点”在竖直方向的最远距离就是在点C.
此时,直线位于x轴和点C的正中间.
因此,t的最小值为,
故答案为:;…………………………………6分
(3)解∶①由题意可知直线的解析式为,
则直线上的点关于的对称点为,
那么,过点的直线为,
∴与直线有交点,且交点的临界值为和.
∴当过点A时,t的最大值为;当过点C时,t的最小值为,
故直线上存在关于直线的“镜像点”,t的取值范围为.
②正方形的对角线交点为,边长为1,则四个顶点坐标分别为,,,.
如果设正方形边上一点,过点P作交直线:于点B,则点,连接,结合直线和对称性即可知,
那么,点关于直线:的对称点.
∴正方形四个顶点及对角线交点关于直线:的对称点的坐标分别为,,,,,
∵正方形边上的所有点都是关于直线的“镜像点”,并且正方形位于直线的右下方,
∴对称正方形的左边顶点的横坐标不小于,对称正方形的上面顶点的纵些标不大于1,
即,解得,
同时,对称正方形的对角线交点纵坐标不能小于0(不能在x轴以下),即,解得,
综上,t的取值范围为.…………………………………10分
数学试题
注意事项:
1.考试时间:100分钟,试卷满分:100分。本试卷分第Ⅰ卷(选择题)和第Ⅱ卷(非选择题)两部分。答卷前,考生务必将自己的姓名、准考证号填写在答题卡上。
2.回答第Ⅰ卷时,选出每小题答案后,用2B铅笔把答题卡上对应题目的答案标号涂黑。如需改动,用橡皮擦干净后,再选涂其他答案标号。写在本试卷上无效。
3.回答第Ⅱ卷时,将答案写在答题卡上。写在本试卷上无效。
4.测试范围:八年级数学下册第7章-第9章(苏科版2024新教材)。
第Ⅰ卷
一、选择题:本题共8小题,每小题2分,共16分。在每小题给出的四个选项中,只有一项是符合题目要求的。
1.在中国悠久的历史长河中,古窗作为建筑艺术的重要组成部分,展现了中华民族深邃的文化底蕴和审美情趣.下列窗户图案中,是中心对称图形的是( )
A.B.C.D.
2.某市某年约有51000名学生参加体育中考,为了解这51000名学生的体育成绩,从中抽取了2000名学生的体育成绩进行分析,以下说法正确的是( )
A.51000名学生是总体
B.每名学生是个体
C.抽取的2000名考生的体育成绩是总体的一个样本
D.样本容量是2000名
3.从一定高度落下的图钉,落地后针尖着地.这个事件是( )
A.必然事件 B.不可能事件 C.确定性事件 D.随机事件
4.如图,四边形的对角线相交于点,下列条件能判定四边形是平行四边形的是( )
A., B.,
C., D.,
5.如图,将绕点A逆时针旋转得到,点B的对应点D恰好落在边上.若,,则的度数是( )
A. B. C. D.
6.在用反证法证明命题:“已知,求证:”时,第一步应先假设( )
A. B. C. D.
7.如图,中,M是的中点,平分,于点D,若,则等于( )
A.4 B.3 C.2 D.1
8.如图,在正方形中,点是上一点,点是延长线上一点,连接,,.点是的中点,连接,,若,,则的度数为( )
A. B. C. D.
第Ⅱ卷
二、填空题:本题共8小题,每小题2分,共16分。
9.在平面直角坐标系中,点关于原点对称的点的坐标是.
10.今年某市有4万名学生参加中考,为了解这些考生的数学成绩,从中抽取2000名考生的数学成绩进行统计分析.在这个问题中,下列说法:①这4万名考生的数学中考成绩的全体是总体;②每个考生是个体;③2000名考生是总体的一个样本.其中说法正确的是(填序号).
11.如图,四个不透明布袋中都装进只有颜色不同的个小球,分别从中随机摸出一个小球,“摸到白球”属于不可能事件的布袋是.(填写布袋对应的序号)
12.如图,中,点D、E分别是,的中点,若的周长是4,则的周长为.
13.如图,在平行四边形中,点,分别为边,的中点,将平行四边形沿着折叠,点,分别落在,处,若,则的度数为.
14.若菱形的两条对角线的长分别为6,,则菱形的面积为.
15.如图,在矩形中,,,为边上一点,将沿直线折叠,点的对应点恰好落在对角线上,则的长为.
16.如图,在矩形中,,E是边上一点,,F是直线上一动点,将线绕点E逆时针旋转得到线段,连接,则的最小值是.
三、解答题:本题共10小题,共68分。解答应写出文字说明、证明过程或演算步骤。
17.(6分)如图,方格纸中的每个小方格都是边长为1个单位的正方形,在建立平面直角坐标系后,的顶点均在格点上,三个顶点的坐标分别为,,.
(1)将关于x轴作轴对称变换得,则点的坐标为________.
(2)将绕原点O按逆时针方向旋转得,则点的坐标为________.
(3)求的面积为________.
18.(6分)图①,图②,图③均是由边长为1的正三角形构成的网格,每个网格图中有5个正三角形已涂上阴影.请在余下空白正三角形中,按下列要求涂上阴影:
(1)在图①中涂上一个阴影正三角形,使得阴影部分图形是中心对称图形,但不是轴对称图形;
(2)在图②中涂上两个阴影正三角形,使得阴影部分图形是轴对称图形,但不是中心对称图形;
(3)在图③中涂上三个阴影正三角形,使得阴影部分图形既是中心对称图形,又是轴对称图形.
19.(6分)“珍爱生命,预防溺水”,为了让学生了解防溺水知识.某校开展了防溺水知识竞赛,并从中随机抽取部分学生的成绩进行分析(测试结果分为优秀、良好、合格、不合格四个等级),并将结果绘制成如下两幅不完整的统计图.请结合统计图中提供的信息,解答下列问题.
(1)本次抽取的学生共有______名.
(2)请补全条形统计图.
(3)在扇形统计图中,“不合格”等级所对应的圆心角的度数是______,“合格”等级中的值为______.
20.(6分)在一个不透明的箱子里,装有若干个除了颜色外均相同的小球,某数学学习小组做摸球试验,将球搅匀后从中随机摸出一个球记下颜色,再把它放回箱子中,重复该操作.下表是活动进行中的一组统计数据:
摸球的次数
摸到白球的次数
摸到白球的频率
(1)上表中的_____,_____;
(2)“摸到白球”的概率的估计值是_____;(精确到)
(3)如果箱子中一共有个球,除了白球外,估计还有多少个其他颜色的球?
21.(6分)已知:互不重合的点、、、按图中顺序依次在同一条直线上,且,,,为锐角.
(1)求证:;
(2)连接、,若,求证:与互相平分
22.(4分)如图,是的中位线,的平分线交于点,连接并延长交于,若,,求的长.
23.(8分)中国古代数学家刘徽在《九章算术》中,给出了证明三角形面积公式的“出入相补法”,原理如下:
如图,在中,点D,E分别是的中点,连接,过点A作,垂足为F,延长至点G,使,连接,延长至点H,使,连接,则四边形的面积等于的面积.
(1)求证:四边形为矩形;
(2)若,利用上述结论求的面积.
24.(8分)如图,在矩形中,过对角线的中点O作的垂线,分别交、于E、F.
(1)求证:四边形是菱形;
(2)若,,求菱形的周长.
25.(8分)综合与实践
在综合与实践课上,赵老师让同学们以“正方形的折叠”为主题开展数学活动.
操作一:对折正方形纸片,使与重合,得到折痕,把纸片展平;
操作二:在上选一点P,沿折叠,使点A落在正方形内部点M处,把纸片展平.连接并延长交于点Q,连接.
(1)数学思考:
如图1,当点M在上时,与的数量关系是_______.
(2)拓展再探:
如图2,当改变点P在上的位置(点P不与点A,D重合),使点M不在上时,判断(1)中与的数量关系是否仍然成立?若成立,请证明;若不成立,请说明理由.
(3)迁移应用:
在(2)的探究中,连接,已知正方形纸片的边长为6,当的周长最小时,的长为多少?
26.(10分)对于点P,直线l和图形N,给出如下定义:若点P关于直线l的对称点在图形N的内部或边上,则称点P为图形N关于直线l的“镜像点”.
在平面直角坐标系中,已知的三个顶点的坐标分别为,,.设点,直线为过点且与y轴垂直的直线.
(1)若在点中,点________是关于直线的“镜像点”;
(2)当时,若x轴上存在关于直线的“镜像点”,则t的最小值为________;
(3)已知直线过点且与第一、三象限的角平分线平行.
①若直线上存在关于直线的“镜像点”,直接写出t的取值范围;
②已知边长为1的正方形的对角线的交点为,且正方形的边与坐标轴平行.若正方形边上的所有点都是关于直线的“镜像点”,直接写出t的取值范围.
参考答案
一、选择题:本题共8小题,每小题2分,共16分。在每小题给出的四个选项中,只有一项是符合题目要求的。
1.在中国悠久的历史长河中,古窗作为建筑艺术的重要组成部分,展现了中华民族深邃的文化底蕴和审美情趣.下列窗户图案中,是中心对称图形的是( )
A.B.C.D.
【答案】C
【详解】解:A、没有对称中心,不是中心对称图形,不符合题意;
B、没有对称中心,不是中心对称图形,不符合题意;
C、有对称中心,是中心对称图形,符合题意;
D、没有对称中心,不是中心对称图形,不符合题意;
故选:C .
2.某市某年约有51000名学生参加体育中考,为了解这51000名学生的体育成绩,从中抽取了2000名学生的体育成绩进行分析,以下说法正确的是( )
A.51000名学生是总体
B.每名学生是个体
C.抽取的2000名考生的体育成绩是总体的一个样本
D.样本容量是2000名
【答案】C
【详解】解:51000名学生的体育成绩是总体,每名学生的体育成绩是个体,抽取的2000名考生的体育成绩是总体的一个样本,样本容量是2000,因此选项A、B、D错误,选项C正确;
故选:C.
3.从一定高度落下的图钉,落地后针尖着地.这个事件是( )
A.必然事件 B.不可能事件 C.确定性事件 D.随机事件
【答案】D
【详解】解:从一定高度落下的图钉,落地后针尖着地.这个事件是随机事件.
故选D.
4.如图,四边形的对角线相交于点,下列条件能判定四边形是平行四边形的是( )
A., B.,
C., D.,
【答案】C
【详解】解:∵,
∴,
∵,
∴,
∴,
又∵,
∴四边形是平行四边形,故C符合题意,
但是A、B、D条件均不能证明,故不符合题意,
故选:C.
5.如图,将绕点A逆时针旋转得到,点B的对应点D恰好落在边上.若,,则的度数是( )
A. B. C. D.
【答案】B
【详解】解:根据题意,
∵,,
∴,
由旋转的性质可得,,
∴,
∴,
∴;
故选:B.
6.在用反证法证明命题:“已知,求证:”时,第一步应先假设( )
A. B. C. D.
【答案】B
【详解】解:“已知,求证:”时,结论为且反证法第一步应先假设结论不成立
第一步应先假设,
故选:B.
7.如图,中,M是的中点,平分,于点D,若,则等于( )
A.4 B.3 C.2 D.1
【答案】D
【详解】解:延长交于H,
,
,
,
是的中位线,
,
故选:D.
8.如图,在正方形中,点是上一点,点是延长线上一点,连接,,.点是的中点,连接,,若,,则的度数为( )
A. B. C. D.
【答案】A
【详解】解:如图,连接,
四边形为正方形,
,,,
在和中,
,
∴,
,
,
,
即,
为中点,
,
,为中点,
,
,
在和中,
,
,
,,
,
,
,
,,为中点,
,
,
,
,
,
故选:A.
第Ⅱ卷
二、填空题:本题共8小题,每小题2分,共16分。
9.在平面直角坐标系中,点关于原点对称的点的坐标是.
【答案】
【详解】解:点关于原点对称的点的坐标是,
故答案为:.
10.今年某市有4万名学生参加中考,为了解这些考生的数学成绩,从中抽取2000名考生的数学成绩进行统计分析.在这个问题中,下列说法:①这4万名考生的数学中考成绩的全体是总体;②每个考生是个体;③2000名考生是总体的一个样本.其中说法正确的是(填序号).
【答案】①
【详解】解:对于①,这4万名考生的数学中考成绩的全体是总体,故正确;
对于②,每个考生的数学中考成绩是个体,故错误;
对于③,2000名考生的中考数学成绩是总体的一个样本,故错误;
故①正确,
故答案为:①.
11.如图,四个不透明布袋中都装进只有颜色不同的个小球,分别从中随机摸出一个小球,“摸到白球”属于不可能事件的布袋是.(填写布袋对应的序号)
【答案】
【详解】解:①袋中有个白球,没有红球,摸到白球属于必然事件;
②袋中有个红球,个白球,摸到白球属于随机事件;
③袋中有个红球,个白球,摸到白球属于随机事件;
④袋中有个红球,没有白球,摸到白球属于不可能事件.
故答案为.
12.如图,中,点D、E分别是,的中点,若的周长是4,则的周长为.
【答案】8
【详解】解:∵点D、E分别是,的中点,
∴是的中位线,,
∴,
又∵的周长是4,
即,
∴的周长,
故答案为:8.
13.如图,在平行四边形中,点,分别为边,的中点,将平行四边形沿着折叠,点,分别落在,处,若,则的度数为.
【答案】
【详解】解:∵四边形是平行四边形,
∴,,
∴,
∵点,分别是,的中点,
∴,
由折叠可得:,
∴,
∴,
∵,
∴,
∴,
∴.
故答案为:.
14.若菱形的两条对角线的长分别为6,,则菱形的面积为.
【答案】
【详解】解:四边形是菱形,的长分别为6,,
菱形的面积.
故答案为:.
15.如图,在矩形中,,,为边上一点,将沿直线折叠,点的对应点恰好落在对角线上,则的长为.
【答案】3
【详解】解:∵四边形是矩形,
∴,,
∴,
∵将沿直线折叠,点的对应点恰好落在对角线上,
∴,,,
∴,
∵,
∴,
∴,
故答案为:3
16.如图,在矩形中,,E是边上一点,,F是直线上一动点,将线绕点E逆时针旋转得到线段,连接,则的最小值是.
【答案】13
【详解】解:将绕点逆时针旋转得到,延长交于点,延长至点,使,连接,
∵在矩形中,,,,
∴,,,
∴,,
∴,
∴四边形是矩形,
∴,,
∴,,
∴是的垂直平分线,
∴,
∵是直线上一动点,
∴,
∴当点,,三点共线时,取最小值,
在中,,,
,
∴的最小值是.
故答案为:.
三、解答题:本题共10小题,共68分。解答应写出文字说明、证明过程或演算步骤。
17.(6分)如图,方格纸中的每个小方格都是边长为1个单位的正方形,在建立平面直角坐标系后,的顶点均在格点上,三个顶点的坐标分别为,,.
(1)将关于x轴作轴对称变换得,则点的坐标为________.
(2)将绕原点O按逆时针方向旋转得,则点的坐标为________.
(3)求的面积为________.
【详解】(1)解:如图,即为所作
∴,
故答案为:;…………………………………2分
(2)解:即为所作,
∴,
故答案为:;…………………………………4分
(3)解:如图,的面积为
故答案为:4.…………………………………6分
18.(6分)图①,图②,图③均是由边长为1的正三角形构成的网格,每个网格图中有5个正三角形已涂上阴影.请在余下空白正三角形中,按下列要求涂上阴影:
(1)在图①中涂上一个阴影正三角形,使得阴影部分图形是中心对称图形,但不是轴对称图形;
(2)在图②中涂上两个阴影正三角形,使得阴影部分图形是轴对称图形,但不是中心对称图形;
(3)在图③中涂上三个阴影正三角形,使得阴影部分图形既是中心对称图形,又是轴对称图形.
【详解】(1)解:如下图为所作图形:
…………………………………2分
(2)解:如下图为所作图形:
…………………………………4分
(3)解:如下图为所作图形:
…………………………………6分
19.(6分)“珍爱生命,预防溺水”,为了让学生了解防溺水知识.某校开展了防溺水知识竞赛,并从中随机抽取部分学生的成绩进行分析(测试结果分为优秀、良好、合格、不合格四个等级),并将结果绘制成如下两幅不完整的统计图.请结合统计图中提供的信息,解答下列问题.
(1)本次抽取的学生共有______名.
(2)请补全条形统计图.
(3)在扇形统计图中,“不合格”等级所对应的圆心角的度数是______,“合格”等级中的值为______.
【详解】(1)解:(名),
答:本次抽取的学生共有名;…………………………………2分
(2)解:测试结果为良好的有:(名),
补全条形统计图如下:
;…………………………………4分
(3)解:“不合格”等级所对应的圆心角的度数是:,“合格”等级中的值为:,
故答案为:,.…………………………………6分
20.(6分)在一个不透明的箱子里,装有若干个除了颜色外均相同的小球,某数学学习小组做摸球试验,将球搅匀后从中随机摸出一个球记下颜色,再把它放回箱子中,重复该操作.下表是活动进行中的一组统计数据:
摸球的次数
摸到白球的次数
摸到白球的频率
(1)上表中的_____,_____;
(2)“摸到白球”的概率的估计值是_____;(精确到)
(3)如果箱子中一共有个球,除了白球外,估计还有多少个其他颜色的球?
【详解】(1)解:,
,
故答案为:;;…………………………………2分
(2)“摸到白球”的概率的估计值是,
故答案为:;…………………………………4分
(3)(个),
∴除白球外,还有大约个其它颜色的小球.…………………………………6分
21.(6分)已知:互不重合的点、、、按图中顺序依次在同一条直线上,且,,,为锐角.
(1)求证:;
(2)连接、,若,求证:与互相平分
【详解】(1)证明:,
,即,
,,
;…………………………………3分
(2)证明:如图,连接,,,
,
,
,,
,,
,
四边形是平行四边形,
与互相平分.
…………………………………6分
22.(4分)如图,是的中位线,的平分线交于点,连接并延长交于,若,,求的长.
【详解】解:∵是的中位线,
∴,,
∵是的平分线,
∴,
∵,
∴.
∴.
∴.
∴,
∴.…………………………………4分
23.(8分)中国古代数学家刘徽在《九章算术》中,给出了证明三角形面积公式的“出入相补法”,原理如下:
如图,在中,点D,E分别是的中点,连接,过点A作,垂足为F,延长至点G,使,连接,延长至点H,使,连接,则四边形的面积等于的面积.
(1)求证:四边形为矩形;
(2)若,利用上述结论求的面积.
【详解】(1)证明:点D,E分别是的中点,
.
,
,
.
同理可得:,,
,
∴四边形BCHG是平行四边形,
又∠H=90°(已证),
四边形为矩形.…………………………………4分
(2)解:点D,E分别是的中点,
是的中位线,
,
由(1)可知,,
,
.…………………………………8分
24.(8分)如图,在矩形中,过对角线的中点O作的垂线,分别交、于E、F.
(1)求证:四边形是菱形;
(2)若,,求菱形的周长.
【详解】(1)证明:∵四边形是矩形
∴
∴
∵点是的中点
∴
在和中
∴
∴
已知
∴四边形是平行四边形
∵
∴四边形是菱形;…………………………………4分
(2)解:∵四边形是矩形
∴
∵四边形是菱形
∴
设菱形的边长为,
则,
在中
即
解得
∴菱形的周长为20.…………………………………8分
25.(8分)综合与实践
在综合与实践课上,赵老师让同学们以“正方形的折叠”为主题开展数学活动.
操作一:对折正方形纸片,使与重合,得到折痕,把纸片展平;
操作二:在上选一点P,沿折叠,使点A落在正方形内部点M处,把纸片展平.连接并延长交于点Q,连接.
(1)数学思考:
如图1,当点M在上时,与的数量关系是_______.
(2)拓展再探:
如图2,当改变点P在上的位置(点P不与点A,D重合),使点M不在上时,判断(1)中与的数量关系是否仍然成立?若成立,请证明;若不成立,请说明理由.
(3)迁移应用:
在(2)的探究中,连接,已知正方形纸片的边长为6,当的周长最小时,的长为多少?
【详解】(1)证明:∵四边形是正方形,
∴,,
由折叠得,,,
∴,
在和中,
,
∴,
∴,
∵,,
∴,
∴;…………………………………2分
(2)解:成立,
∵四边形是正方形,
∴,,
由折叠得,,,
∴,
在和中,
,
∴,
∴,
∵,,
∴,
∴;…………………………………5分
(3)解:由折叠得,,
∴的周长为,
当取最小值时,的周长最小,
∵点的轨迹是以点为圆心,的长为半径的圆弧;
以点为圆心,的长为半径画圆,当点D,M,B共线时,最小,
设,则,
由折叠得,,,
∵,
∴,
在中,,
∴,
∴,
∴…………………………………8分
26.(10分)对于点P,直线l和图形N,给出如下定义:若点P关于直线l的对称点在图形N的内部或边上,则称点P为图形N关于直线l的“镜像点”.
在平面直角坐标系中,已知的三个顶点的坐标分别为,,.设点,直线为过点且与y轴垂直的直线.
(1)若在点中,点________是关于直线的“镜像点”;
(2)当时,若x轴上存在关于直线的“镜像点”,则t的最小值为________;
(3)已知直线过点且与第一、三象限的角平分线平行.
①若直线上存在关于直线的“镜像点”,直接写出t的取值范围;
②已知边长为1的正方形的对角线的交点为,且正方形的边与坐标轴平行.若正方形边上的所有点都是关于直线的“镜像点”,直接写出t的取值范围.
【详解】(1)解:将各个点标示在平面直角坐标系中,
∵关于直线的对称点为,,,
∴点和点是关于直线的“镜像点”.
故答案为:点和点;…………………………………3分
(2)解∶求t的最小值,这个最小值必然是负值,对称轴直线是平行x轴的,
所以观察竖直方向,上离x轴最远的点为C,
则x轴上的关于直线的“镜像点”在竖直方向的最远距离就是在点C.
此时,直线位于x轴和点C的正中间.
因此,t的最小值为,
故答案为:;…………………………………6分
(3)解∶①由题意可知直线的解析式为,
则直线上的点关于的对称点为,
那么,过点的直线为,
∴与直线有交点,且交点的临界值为和.
∴当过点A时,t的最大值为;当过点C时,t的最小值为,
故直线上存在关于直线的“镜像点”,t的取值范围为.
②正方形的对角线交点为,边长为1,则四个顶点坐标分别为,,,.
如果设正方形边上一点,过点P作交直线:于点B,则点,连接,结合直线和对称性即可知,
那么,点关于直线:的对称点.
∴正方形四个顶点及对角线交点关于直线:的对称点的坐标分别为,,,,,
∵正方形边上的所有点都是关于直线的“镜像点”,并且正方形位于直线的右下方,
∴对称正方形的左边顶点的横坐标不小于,对称正方形的上面顶点的纵些标不大于1,
即,解得,
同时,对称正方形的对角线交点纵坐标不能小于0(不能在x轴以下),即,解得,
综上,t的取值范围为.…………………………………10分
同课章节目录
